Dislocation reactions, grain boundaries, and irreversibility in two-dimensional lattices using topological tweezers

Significance

The properties of real-world materials are typically determined by small collections of defects within them. One common defect––a dislocation––results from removing half a row of atoms from a crystal, leaving behind the other half that now ends abruptly at a tip in the crystal. The termination point behaves like a point “particle” that carries a topological charge, obeys dynamical laws, and interacts with other such particles to create grain boundaries. We report a method to precisely manipulate dislocations by using specially designed light fields (“topological tweezers”) to massage an experimental model system consisting of microscopic colloids. We use this tool to study their interactions and complex collective dynamics that are not always as reversible as one might think.

Abstract

Dislocations, disclinations, and grain boundaries are topological excitations of crystals that play a key role in determining out-of-equilibrium material properties. In this article we study the kinetics, creation, and annihilation processes of these defects in a controllable way by applying “topological tweezers,” an array of weak optical tweezers which strain the lattice by weakly pulling on a collection of particles without grabbing them individually. We use topological tweezers to deterministically control individual dislocations and grain boundaries, and reversibly create and destroy dislocation pairs in a 2D crystal of charged colloids. Starting from a perfect lattice, we exert a torque on a finite region and follow the complete step-by-step creation of a disoriented grain, from the creation of dislocation pairs through their reactions to form a grain boundary and their reduction of elastic energy. However, when the grain is rotated back to its original orientation the dislocation reactions do not retrace. Rather, the process is irreversible; the grain boundary expands instead of collapsing.

Topological defects such as disclinations and dislocations play an essential role in determining the allowed phases and the elastic and rheological properties of materials (1–6). They are particularly important for understanding the nature of phase transitions in 2D systems and their thermodynamics have been studied extensively. However, the dynamics and reactions of such defects are less well known. Topological defects in a lattice are nonlocal imperfections which correspond to singularities in an order parameter characterizing a broken symmetry, e.g., disclinations (rotation) or dislocations (translation). These defects have quantized “charges” which interact with the stress field. As nonlocal objects they cannot be controlled simply by acting on particles near the singularity. As charges, however, they can be manipulated by controlling the surrounding fields. Here, we produce stress fields which create and manipulate dislocations. Further, we induce reactions corresponding to fission and fusion leading to the formation of more complex structures such as grain boundaries. Although all defect motion and reactions are dissipative, we find that simple two-defect reactions tend to be reversible whereas more complex reactions are irreversible.

Optical tweezers (7) have proven a flexible tool to control colloidal particles in a wide variety of condensed matter experiments (8). Typically used to grab individual particles in strong traps, they have been used in the study of lattices to grab a particle and remove it from a lattice to produce a vacancy (9, 10). A different mode explored here is the use of tailored patterns of traps (produced holographically, refs. 11–13) that weakly interact with many particles in a lattice to create stress fields designed to manipulate topological defects (where by weak we mean that each individual trap is capable of displacing an individual particle by of the distance to its nearest neighbor, at which point the interparticle potential results in the particle exiting the trap).

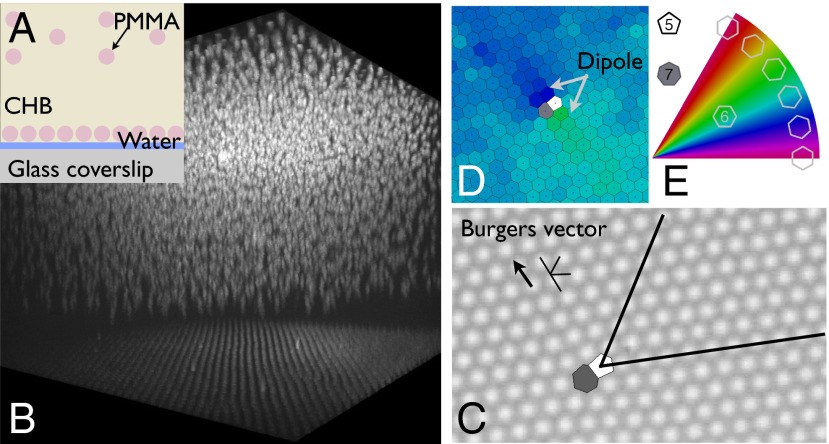
Colloidal crystals (14) offer a unique opportunity to study basic problems in condensed matter and in particular the physics of 2D statistical systems (3–5, 15–18). The colloidal crystals used here (Fig. 1) consist of a monolayer of charged micrometer-sized poly(methyl methacrylate) (PMMA) particles (19) bound to an oil (cyclohexyl bromide/dodecane)–water interface by electrostatic forces. Because the particles are superhydrophobic they sit entirely in the oil phase, minimizing wetting-induced interactions (20). Both the image-charge binding and the surface tension that resists deformation of the interface are very strong compared with any residual optical force perpendicular to the interface plane. We prepare a millimeter-scale, flat oil–water interface on a microscope coverslip (Materials and Methods); the particles bind to the interface and organize into a hexagonal lattice. A 3D confocal view of a sample cell, with the interfacial crystal at the bottom, is shown in Fig. 1B. Fig. 1 C and D shows a section of the lattice that has a single dislocation “frozen-in” by the fabrication process.

Fig. 1.

Lattice used in the experiments presented here. (A) Charged PMMA particles in CHB/dodecane are bound, by image charge attraction, to an oil–water interface formed on a glass coverslip. (B) Confocal image of a sample cell shows the lattice on the interface with a few dislocations frozen in by the fabrication process. Above (displaced by a vertically applied electric field to better view the 2D lattice) is a 3D Wigner lattice of the PMMA particles in CHB/dodecane. (C) Bright-field image of a section of the lattice showing a single dislocation. The extra half-rows that give rise to the dislocation (shown in black) meet at the core, which is also characterized by a pair of particles having five and seven nearest neighbors. A dislocation will be represented interchangeably by a bound (5–7) pair of Voronoi cells (overlaid), or by a line parallel to the Burgers vector and a V along the extra half-rows. The corresponding topological charge of the dislocation, its Burgers vector, is also shown. (D) Lattice can be represented through its Voronoi cells, colored by orientation. (E) In this picture the dipole in orientation which surrounds a dislocation is clearly visible. Only cells with six nearest neighbors are colored this way. Cells with five and seven neighbors are colored white and gray, respectively.

A dislocation in a hexagonal lattice consists of a pair of extra half-rows of particles that meet at the “core” (Fig. 1C). A dislocation disrupts crystalline translational order, and has as topological charge the Burgers vector (Fig. 1C), which has length a (the lattice constant) and can point in one of the six crystallographic directions. A single disclination results from an extra (missing) 60° wedge in the lattice and disrupts orientational order; its elementary topological charge is a multiple of 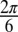. Disclinations are not usually seen in a flat 2D lattice owing to the large elastic energy cost of accommodating an extra wedge in the lattice. The disclinations proliferate on entering the isotropic liquid phase.

The core of a disclination can be found by Voronoi tessellation and corresponds to a single cell having five or seven nearest neighbors. The core of a dislocation corresponds instead to a neighboring pair of cells with five and seven nearest neighbors. This is because a dislocation can be seen as a dipole of disclinations, which is visible in the orientational order surrounding a dislocation shown in Fig. 1D. We represent dislocations interchangeably either as a line along the glide plane (parallel to the Burgers vector) with a “V” along the missing half-rows, or as the Voronoi cells of the 5–7 pair (Fig. 1C).

In a continuum model of a 2D lattice, the elastic energy is given by (21)

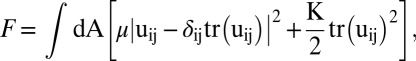where 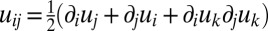is the strain tensor defined in terms of the particle displacement field u_i, μ is the shear modulus, and K is the bulk modulus. The particle displacements can be determined either from a single experimental image by comparing each Voronoi cell to an ideal one, by Fourier analysis (22), or from a sequence of images as the difference between instantaneous and mean position of each particle. From these measurements, fluctuations in area and orientation of a subset of the lattice can be obtained and used to determine the elastic moduli (23) μ and K. We find typical values of 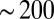and 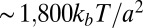for μ and K, respectively.

As a symmetric two-by-two matrix, the strain tensor can be expressed as the sum of two terms: an isotropic component (compression/dilation) proportional to the identity matrix, and a symmetric traceless (shear) part which can in turn be represented as a reflection matrix about an axis with orientation 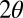multiplied by a magnitude γ:

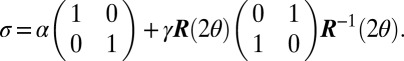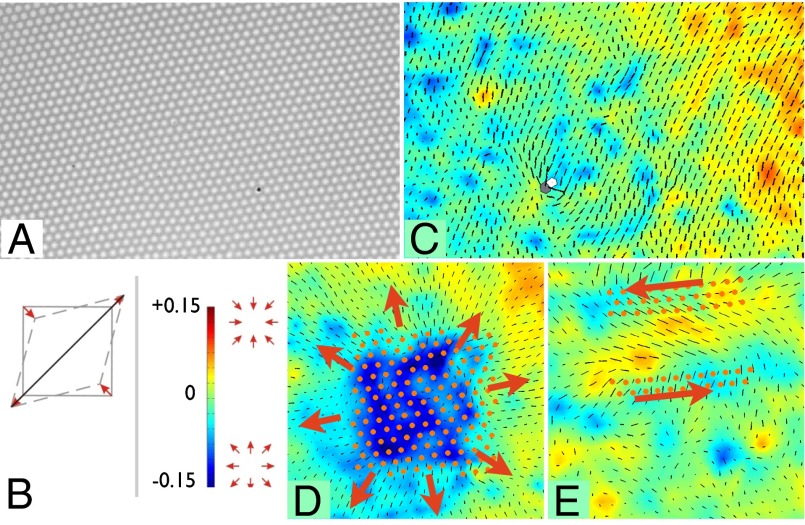
To visualize the strain tensor field in a single image, we developed the following scheme (Fig. 2): we represent the compressive part with color and the shear component by a rod along the direction of the shear elongation (which is aligned with the reflection axis) having length proportional to the magnitude of the shear strain (Fig. 2B). Fig. 2A shows an image of a 2D lattice and Fig. 2C shows the corresponding strain field. The visualization makes immediately apparent strains which are not evident to the eye. What appears is a combination of long-range strains created either by boundary conditions or by defects outside of the field of view, and shorter-range strains induced either by local defects or, as will be seen below, by the application of topological tweezers. The long- and short-range components can be separated by Fourier analysis. Fig. 2 D and E shows the filtered strain field induced by imposing shear with two domains of optical traps (Fig. 2E) and an incommensurate (dilating) potential on the lattice (Fig. 2D).

Fig. 2.

Representation of the strain field. Starting from an image of the lattice (A), the particle displacement field was determined by comparing each Voronoi cell to an ideal one. We represent the strain tensor, derived from the displacement field, as follows. (B) The isotropic (compression/dilation) part is represented with color and the shear component by a rod along the direction of the shear elongation having length proportional to the magnitude of the shear strain. (C) Visualization of the strain field of the lattice shown in A makes immediately apparent strains which are not evident from the bright-field image. The strain is a combination of long-range strains created either by boundary conditions or by defects outside the field of view and shorter-range strains induced either by local defects or the application of topological tweezers (D and E). (D) Application of an incommensurate dilated potential produces a patterned dilation (blue) strain. The patterns visible in the strain have a length scale corresponding to a beat frequency between the incommensurate potentials. (E) Application of shear stress produces a matching shear strain visible in the region in between the shearing traps.

Glide, dislocation motion along a Burger’s vector, involves a slight rearrangement of the particle positions. Climb, motion perpendicular to the Burgers vector, involves mass transport of the two additional half-rows out to the end of the crystal. Typically, only glide is observed in most crystal deformations. With our tweezers we can easily produce a simple shear strain around an isolated dislocation and induce glide. The glide is in the direction in which the shear rod and extra half rows are closest. (Fig. 3A and Movie S1). Using the tweezers to relax the strain field by bringing the lattice back to its original position, we find that the dislocation returns to its original position. Glide in our system is reversible, implying a very small periodic Peierls potential.

Fig. 3.

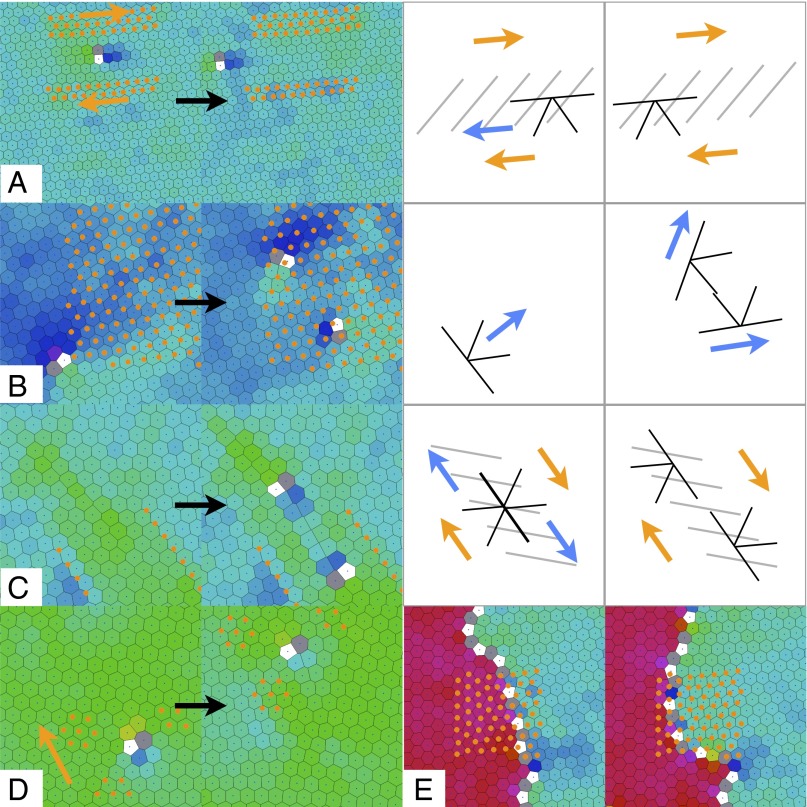
Control of dislocations with topological tweezers. (A) (See also Movie S1.) Glide can be induced by shearing the lattice on either side of a dislocation. This corresponds to a stress represented schematically on the right. (B) (See also Movies S3 and S4.) A climb force applied by dilating the lattice on one side of the dislocation results in the fissioning of the dislocation into a pair which by its joint gliding motion moves in the climb direction of the original dislocation. (C) (See also Movie S2.) Fissioning of a pair of dislocations by shearing a defect-free region of the lattice beyond the elastic regime. (D) (See also Movie S6.) Opposing shear stresses trap a dislocation which can then be moved along its glide plane. (E) (See also Movie S7.) Application of a commensurate potential, aligned with one side of a grain over a grain boundary, is capable of moving the grain boundary.

If a simple shear moves a dislocation to the right and the opposite shear displaces it to the left, then application of the first on the left and the second on the right makes a “dislocation tweezer” (Fig. 3D and Movie S6) capable of trapping the dislocation or moving it anywhere in its glide plane. Our dislocation tweezer grabs a nonlocal object by generating a stress pattern around its core and is an example of a topological tweezer.

We now focus on dislocation reactions. In all reactions the Burgers vector, like charge, is conserved. There are two reaction types: (i) creation (annihilation) of a dislocation pair with opposite Burgers vectors laying on the same glide line and (ii) fission of a single dislocation in a hexagonal lattice to form two dislocations with 60° between their Burgers vectors whose sum is equal to the original. Likewise, a noncollinear (60°) pair can undergo fusion. The pair creation can be demonstrated by applying shear to a dislocation-free region as in Fig. 2E. When the shear strain exceeds a certain threshold, pairs of dislocations unbind and glide in opposite directions to relieve the strain (Fig. 3C and Movie S2). When the applied shear strain is relieved by moving the tweezers and lattice back to their original positions, the dislocations glide toward each other and annihilate. So, simple creation and annihilation are reversible.

We have found two configurations that induce the fissioning of a dislocation. Dilating the lattice in the vicinity of the dislocation induces a Peach–Koehler force (24) 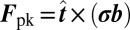in the climb direction in which the dislocation cannot move. Once this force reaches a certain threshold, the dislocation reacts by fissioning into two which can, by their combined glide motion, effectively “climb” by gliding (Fig. 3B and Movies S3 and S4). A different method is to impose a periodic potential on top of the dislocation that is commensurate with the defect-free lattice. This creates an anisotropic stress field which corresponds to the strain field of a dislocation with opposite Burgers vector. A pair of dislocations that would attract and react to form the original dislocation will be repelled by this inverted stress. The dislocation under this stress therefore fissions in either of the two possible configurations (Movie S5). Typically the fission products separate sufficiently fast and far enough that relaxing the stress does not reverse the process.

Beyond controlling individual defects, it is also possible to control groups of interacting defects aligned along a grain boundary. Fig. 3E and Movie S7 show how the application of a commensurate potential, aligned with one of the two sides of the grain boundary, moves the boundary. This can be used to “clean up” a lattice by selectively growing a particular grain and was used in the preparation of many of the experiments presented here.

The creation of a grain in a perfect lattice is a complex process involving formation of dislocation pairs, cooperative reactions, and dislocation organization into a grain boundary. We study this process in detail by using topological tweezers to rotate a region of the crystal clockwise by 60° and subsequently reversing the rotation returning the region to its original orientation, allowing us to probe how collective defect dynamics can achieve the formation of a grain and how irreversibility can arise from such coordinated dynamics (Movies S8–S11). Naively, one could expect the following sequence of events in a reciprocated rotation by 60° in a hexagonal lattice: (i) creation of dislocations in response to the applied shear (ii) correlation of the defects to form a grain boundary (iii) increase of dislocation density along the boundary to a maximum as the rotation approaches 30°, (iv) reversal of the dislocation orientation beyond 30° (v) decrease of the dislocation density as the rotation approaches 60°. (vi) Dislocations disappear as perfect registry is restored at 60°. (vii) A similar (reverse order) process on the way back.

We observe that steps i–iii proceed as expected, with the organization of unbound dislocations into a boundary revealed to proceed through a minimal set of reactions (Fig. 4B). The process is simple and elegant in our hexagonal lattice. A hexagonal region is trapped and rotated. A shear strain field with maxima along the edges surrounds the region and the elastic energy increases. Further rotation of the topological tweezer array to an angle that is offset by 12° from the far-field crystal orientation induces a lattice rotation of 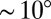within the tweezer array (corresponding to an angular strain between the crystal orientation inside the array and the far field of 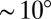), increases the energy, and after a short time there is dislocation pair creation along the edges. The strain field forces the pair to separate by gliding to opposite corners of the edge. At the corners, fusion of dislocations from adjoining edges produces dislocations oriented in the clockwise pattern of a grain boundary. The linear density of dislocations (Fig. 4C) dictates the orientational mismatch of the crystal on crossing the grain boundary. The creation and rearrangement of the dislocations lowers the elastic energy. With further rotation the density increases by reactions creating more dislocations.

Fig. 4.

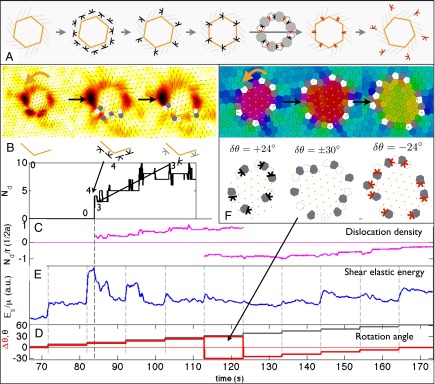
Topological defect dynamics in the formation and rotation of a grain. (See also Movies S8 and S9.) A commensurate set of traps was rotated counterclockwise from 0° to 60° in 6° steps (D, gray line), giving rise to a grain with boundary. A cartoon of the idealized process is shown in A. The initial response is an elastic pure-shear deformation (B) with a corresponding build-up in shear elastic energy 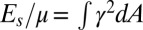(E). At a rotation angle of 12°, the shear stress makes defects unbind along the edges after a short delay (A and B), glide to relieve the stress (E, blue line), and react to form a grain boundary (A and B). Further unbindings, annihilations, and glide movements produce an oriented dislocation line density (C, purple line) along the grain boundary that mediates the difference in angle between the lattice and grain 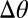(D, red line). As the rotation angle reaches 30° 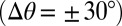, 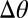reaches a maximum and becomes ambiguous in sign. The defect density reaches a corresponding maximum. Beyond 30°, 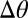becomes negative and the defect orientation must change from clockwise (black) to counterclockwise (red). If all defects along the boundary are in contact (the appropriate density to mediate a difference in orientation of 30°), simple disclination reassociation from clockwise to counterclockwise reverses the dislocations smoothly (A, step v). In the experiment we observe this mechanism along part of the boundary; however, in regions in which the defect density does not reach unity, the defects unbind into disclinations separated by a lattice constant (F) and these recombine with their counterparts from a neighboring dislocation. For further rotation, the dislocation line density is reduced as the defects are pushed outward.

The maximum density occurs when the grain is oriented at 30° from the surrounding lattice. Because of the sixfold symmetry of the hexagonal lattice, this orientation could likewise have been obtained by a rotation of 30° in the opposite sense, which would have produced a counterclockwise set of dislocations on the grain boundary. Further rotation should decrease the density of this counterclockwise boundary. If the dislocations formed a touching ring of fives and sevens, then the reversal just involves changing partners from right to left. However, the reversal in step iv (Fig. 4F) in our case is seen to occur partly by 5–7 reassociation and partly by an unusual “ionization” of dislocations into unbound disclinations as depicted in Fig. 4.

Importantly, the remaining steps v and vi are not simply the reverse of the initial rotation (from 0° to 30°); in particular, we do not observe the dislocations to fission and annihilate, but rather their number remains fixed and they are repelled by the grain. Note that the mismatch in orientation of the grain relative to the outside crystal is governed by the linear dislocation density in the grain boundary. The density can decrease either by keeping the boundary the same length and lowering the number of dislocations or by fixing the number of dislocations and increasing the circumference, hence radius, of the boundary. In our experiment we see that the dislocations remain and move away from the boundary.

We start with a perfect lattice, no local defects, rotate the grain by 60° so it again matches the lattice, but we end up with six dislocations within a distance of several grain sizes. To complete the picture we rotate the grain by 60° back to its original orientation. The local dislocations are pulled back to form a grain boundary, reverse direction at 30°, but rather than annihilate as we approach 0° they are again repelled from the grain. The cyclic rotation of the grain 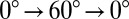is irreversible, leaving the originally perfect lattice littered with dislocations. The origin of the irreversibility appears to be associated with the interactions of many dislocations, because in our study each of the isolated reactions, creation, annihilation, fission, and fusion is reversible.

In conclusion, we have shown that whereas local individual dislocation reactions are reversible, complex reactions are not. (All dislocation motions are dissipative.) Simple reciprocating motion can lead to the proliferation of dislocations even in a 2D crystal. We have also presented topological tweezers acting on multiple particles simultaneously to generate stresses capable of completely controlling individual dislocations. Beyond applications in controlling and studying defects, the lattice stress tweezers can be used to apply a variety of potentials, including random, periodic, or aperiodic to study problems such as pinning and formation of Larkin domains (25, 26). Such sets of tweezers can also be used to study defect dynamics in curved spaces (27–29) and probe the local rheology of disordered systems (30, 31).

Materials and Methods

Lattice Preparation.

PMMA particles (diameter ∼2 μm) prepared using the methods of refs. 19, 32 were suspended in a mixture of cyclohexyl bromide (CHB) and dodecane (80/20 wt/wt). A glass coverslip was cleaned by sonication in acetone, followed by rinsing in isopropyl alcohol, followed by oxygen-plasma etching. The coverslip was then glued onto a channel (height ∼ 100 μm, width ∼2 mm, length ∼20 mm) formed by bonding two additional coverslips to the surface of a glass microscope slide. The channel was first filled with deionized water (Millipore 18.3 MΩ) and then cleared by wicking with a thin piece of absorbent paper inserted into one end. This procedure leaves a thin coating of water on the coverslip surface. The channel then is filled with the oil-phase colloidal dispersion, and the sample is allowed to equilibrate for 30 min. This procedure yields uniform regions of oil–water interface on the coverslip that extend for several millimeters on a side.

Tweezer Pattern Preparation.

To project tailored patterns of traps, we used a holographic optical tweezer setup (8). To calculate the trap positions appropriate for each operation, the following steps were taken. A bright-field image of the lattice, taken immediately (15 s) before the experiment, was used to determine the particle positions (33) from which the lattice spacing and the positions of defects could be determined by triangulation. A particular defect was then selected by user input. A fast Fourier transform of the lattice image was then used to determine the lattice vectors, in terms of which the absolute trap positions appropriate for a given configuration relative to the defect can be easily computed. The relevant hologram was then numerically computed (12) and projected on the Spatial Light Modulator.