Watching energy transfer in metalloporphyrin heterodimers using stimulated X-ray Raman spectroscopy

Significance

Energy transfer in multiporphyrin arrays is of fundamental interest and plays an important role in natural and artificial light harvesting. In this work, we show how ultrafast hard X-ray pulses may be used to create localized electronic wavepackets in a metalloporphyrin dimer. Energy migration between monomers is detected through a stimulated Raman process, resonant with the metal core. Combining the broad bandwidth of attosecond pulses with the localized nature of core orbitals results in a much higher degree of localization and temporal resolution than is possible with optical pulses.

Abstract

Understanding the excitation energy transfer mechanism in multiporphyrin arrays is key for designing artificial light-harvesting devices and other molecular electronics applications. Simulations of the stimulated X-ray Raman spectroscopy signals of a Zn/Ni porphyrin heterodimer induced by attosecond X-ray pulses show that these signals can directly reveal electron–hole pair motions. These dynamics are visualized by a natural orbital decomposition of the valence electron wavepackets.

Porphyrin rings are pyrole-based cyclic conjugated systems that serve as the main building blocks in many devices that depend on their high excitation energy transfer (EET) efficiency (1–4). Because of their stability and interesting structural, electronic, and optical properties, porphyrin compounds have a wide range of uses as chemical sensors (5), photosensitizers in photodynamic therapy for cancer (6), nonlinear optical materials (7–9), and molecular electronic (10–12) and spintronic devices (13, 14).

Porphyrin-based molecules hold a pivotal position in the chemistry of engineered photoactive organic compounds, and extensive electronic structure calculations of monomeric (15) and oligomeric (16, 17) porphyrin molecules, porphyrin structures in biomacromolecules (18, 19), and quasi-1D and -2D porphyrin systems with infinite sizes have been carried out (13, 14, 20–23). Most applications involve multiporphyrin arrays, either in linear or in cyclic shape, or dendrimers (24). Porphyrin dimers, which are still small enough to be treated with relatively high-level modern quantum chemistry methods, can offer basic clues to track down the more complicated EET dynamics in multiporphyrin arrays.

The kinetics of EET in multiporphyrin systems have long been studied by time-resolved fluorescence anisotropy decay (25) and pump–probe techniques, using visible light (26).

Here we present a simulation study that shows how recently developed attosecond sources of X-ray pulses may be used to probe the energy transfer dynamics in a porphyrin dimer. Intense attosecond X-ray pulses, recently made available by new X-ray free electron laser (XFEL) (27, 28) and higher harmonic generation (29, 30) sources, have bandwidths covering multiple electron volts and can prepare coherent superpositions of valence electronically excited states through an impulsive Raman process (31). The short durations of these pulses make them ideal for tracing valence electronic dynamics that evolve with extremely short periods. X-ray pulses can also exploit the spectrally isolated core-excitation frequencies to create valence excitations in the neighborhood of a selected atom, a type of localized excitation not generally accessible using visible or UV pulses. An experimental realization of a two-color pump–probe X-ray source from XFEL radiation was recently reported (32). These new sources have also been used in time-dependent X-ray diffraction studies (33), to monitor ultrafast changes in the conductivity of semiconductors (34) and measure metal-to-ligand charge transfer in inorganic complexes (35) and the ultrafast dissociation of molecules adsorbed on a metal surface (36). Many of these techniques use the X-ray light source only for the probing pulse (37, 38) or depend on a detection method relying on ion or electron capture after the molecule interacts with the X-rays (39). All-X-ray photon-in, photon-out measurements are experimentally very difficult, and X-ray pump–probe measurements with attosecond pulses have yet to be performed. A series of theoretical studies on the time-domain, impulsive X-ray Raman signals of small organic molecules at the K-edges of second- and third-row elements have explored some of the unique capabilities of this technique (31).

The porphyrin ring can chelate different metal atoms, changing the properties of the chromophore. This variability makes porphyrin systems ideal candidates for stimulated X-ray excitation; the spectrally isolated core transitions of the central metal atom allow them to act as X-ray dyes, creating local excitations through an X-ray Raman process.

In this paper we simulate the stimulated X-ray Raman spectroscopy (SXRS) signals of a Zn-Ni porphyrin dimer linked by an ethynyl group. A natural orbital analysis (40, 41) of the electronic wavepacket that evolves during the delay between pulses is used to characterize the electron and hole dynamics after excitation.

Stimulated X-Ray Raman Spectroscopy

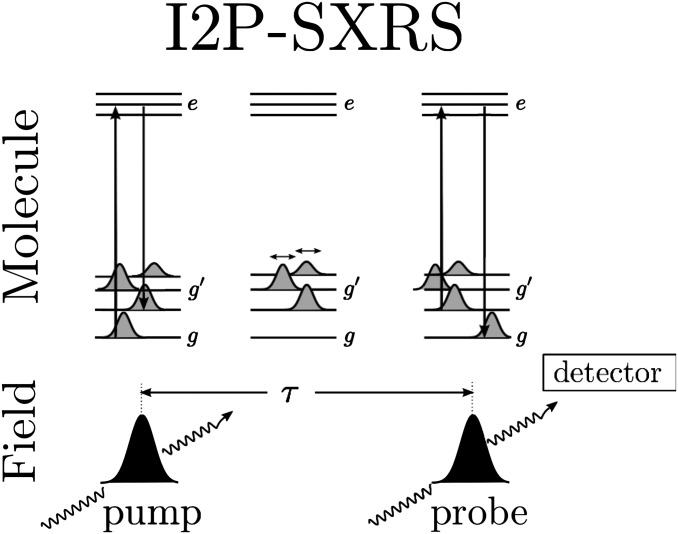
Stimulated X-ray Raman spectroscopy uses ultrashort X-ray pulses to probe valence excitations. In this technique, the system is excited by a pump pulse and the transmission of the probe pulse is recorded after a delay τ (31). Each pulse interacts with the system twice via a stimulated Raman process. A core electron is excited into an unoccupied orbital during each pulse; the excited system then evolves for a short period in the core-excited state before a second interaction with the same pulse stimulates a valence electron to destroy the core hole, emitting an X-ray photon in the process. The system is left in a coherent superposition of valence-excited states after interaction with the first X-ray pulse. The second pulse interacts with this wavepacket via a second Raman process, and the change in its transmitted intensity is detected. We focus on the integrated two-pulse (I2P) SXRS signal defined as the change in the transmission of the second pulse with or without the pump pulse, recorded as a function of the time delay between the two pulses (Fig. 1). Because the core to valence transition frequency is element specific, this technique can be spatially selective. The signal is averaged over the isotropic distribution of molecular orientations. The probe polarization is set at the magic angle 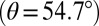with respect to the pump polarization, which allows the effective polarizability to be treated as a scalar rather than a tensor (31).

Fig. 1.

The sequence of events underlying the SXRS signal. The molecule is initially in the ground electronic state g. The pump pulse creates a valence excitation 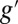through transient occupation of a core-excited state e. After a variable delay time τ, the probe pulse returns the system to the ground state via another core excitation. The signal is given by the change in the transmitted intensity of the probe due to the presence of the pump.

In addition to valence excitations, nuclear motions are also excited impulsively by the X-ray Raman process and should be taken into account for delays longer than the vibrational period 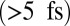. They are expected to add a vibronic fine structure to the valence electronic transitions that feature in the SXRS signals calculated here. Incorporating vibrational motions in superpositions of electronic states is an open computational challenge (42).

The I2P-SXRS signal is collected in the time domain, and a Fourier transform reveals the excitation frequencies of the valence-excited states that contribute. Expressions for the time- and frequency-domain I2P-SXRS signal are given in Eqs. S1 and S3 in SI Text, respectively. The signal is given by the imaginary part of the overlap 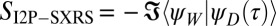between a time-dependent doorway state created by the first pulse and a window state created by the second pulse. When the pump pulse is tuned to the core edge of a selected atom, the valence wavepacket created by Raman interaction will initially be localized near that atom. In a porphyrin dimer two-color I2P-SXRS can directly monitor EET by tuning the pump and probe to be resonant with atoms located on different monomers. The signal vanishes for short delays and the time required to achieve the first maximum gives the EET coupling between monomers. The magnitude of the EET process is proportional to the spatial overlap between doorway and window states prepared on different monomers.

The feasibility of stimulated X-ray Raman in molecules using XFEL radiation has been examined by Patterson (43) and was demonstrated by recent pump–probe experiments in atoms (44, 45).

Results and Discussion

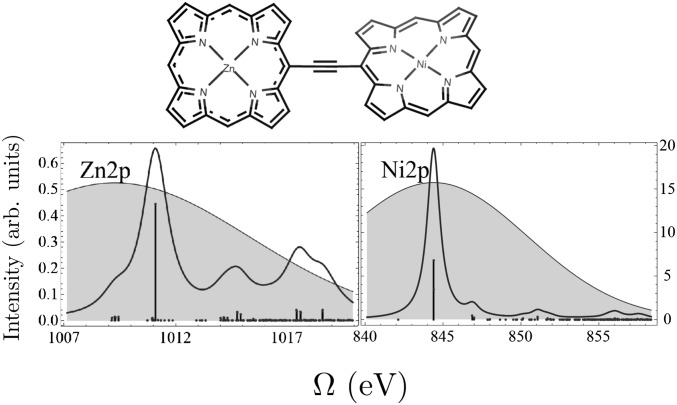
The chemical structure of the porphyrin dimer and the simulated X-ray absorption near-edge structure (XANES) for the nickel and the zinc 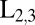-edge are shown in Fig. 2, together with the power spectra for the pulses used in our simulations. The zinc porphyrin ring is almost planar, whereas the nickel ring is distorted. In SI Text we show the calculated UV absorption spectrum and the XANES for the nickel and zinc K-edges in Figs. S1 and S2, respectively.

Fig. 2.

(Upper) Chemical structure of the porphyrin heterodimer. (Lower) Simulated XANES for zinc and nickel 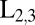-edge. All transitions have the same line width, 0.7 eV and 0.5 eV, respectively, taken from the ref. 46. Shaded areas show the power spectra of the transform-limited pulses used in our simulations with FWHM of 166 as (10.9 eV).

Note that the Raman process involves both photon absorption and emission. In a single-particle picture, a core electron is excited into a virtual orbital after which an electron from a valence orbital falls down and fills the core hole. The pulse bandwidth must encompass both the absorption and the emission frequencies. The XANES spectra in Fig. 2 reveal the pulse frequencies that contribute to the absorption, with the pulse center set to the core–edge transition. To see which frequencies contribute to the emission, it is necessary to collect the frequency-dispersed SXRS signal (47).

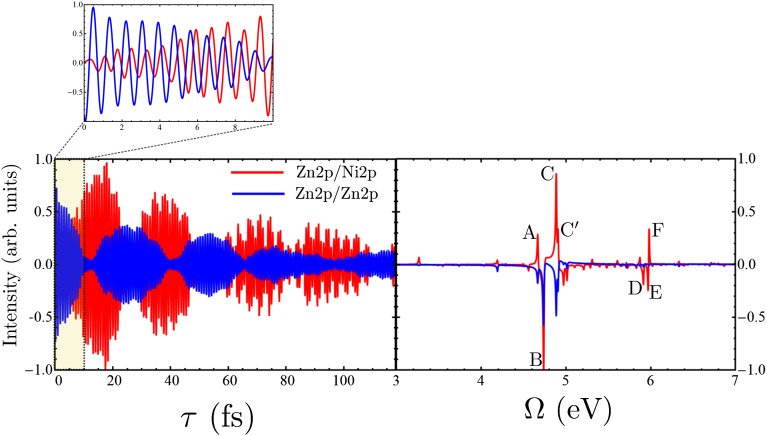
The I2P-SXRS signals in the time and frequency domain for the case where the pump is resonant with the zinc L-edge and the probe is resonant with either the zinc (Zn2p/Zn2p) or the nickel L-edge (Zn2p/Ni2p) are shown in Fig. 3. By tuning the pump and probe to either the K- or L- edge of nickel or zinc, there are sixteen different possible SXRS signals, which are depicted in Figs. S3–S5. Note from Fig. 2 that the amplitudes of the nickel 2p dipoles are larger than those for zinc, making the Zn2p/Zn2p signal weaker than the Zn2p/Ni2p signal. Peaks in the Fourier transform spectra correspond to electronic eigenstates of the dimer. In Fig. 3, Right, peaks labeled A, B, C, and contribute to both signals, whereas peaks D, E, and F are visible only in the two-color signal.

Fig. 3.

(Left) The time-resolved I2P-SXRS signals for the porphyrin dimer for 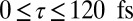(given by Eq. S1). Shown are single-color Zn2p/Zn2p signal (in blue) and two-color Zn2p/Ni2p signal, with a zinc pump and nickel probe (in red). Inset shows the first 10 fs of the signals (Left, shaded region) on an expanded scale. (Right) Fourier transform of the Left (given by Eq. S2).

The one-color Zn2p/Zn2p I2P-SXRS signal is maximal at 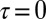, as the valence wavepacket is created and probed on the same atom. As τ grows, the excitation may spread throughout the molecule and onto the neighboring monomer, leading to a decrease in the signal amplitude. The signal shows strong beating, with a period of 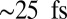that equals the inverse frequency difference between the two dominant peaks at in the frequency domain, located at 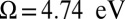(peak B in Fig. 3, Right) and 4.89 eV (peak C in Fig. 3, Right). Because these two peaks have the same sign in the frequency domain, this oscillation starts on a maximum rather than a minimum. [When two peaks in the frequency domain have the same (opposite) sign, the time-domain signal is proportional to the cosine (sine) of the frequency difference.] The signal is high initially, reaches a minimum near 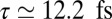, and peaks again at .

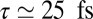The Zn2p/Ni2p signal starts at zero and grows to a maximum near 16 fs, a minimum at 28 fs, and another maximum near 38 fs. The maxima in the Zn2p/Ni2p signal roughly match with the minima in the Zn2p/Zn2p signal at the early time. However, there are many more spectral components and the time-domain signal is correspondingly richer at later times.

In SI Text, we also show the simulated frequency-dispersed two-pulse (D2P) SXRS signals in Figs. S6–S9. Experimentally, these are obtained by frequency resolving the probe pulse rather than recording its integrated intensity (47). These signals show the correlation between the valence-excited states that make up the I2P signal and the core-excited states off of which they scatter. The blue peaks in Fig. 3, Right are coupled to a Zn2p core-excited state with a frequency of 1,009.3 eV, which is not the dominant peak in the Zn2p XANES in Fig. 2. The red peaks are coupled to Ni2p core states with frequencies 844.4 eV and 846.9 eV, the latter of which is the dominant peak in the Ni2p XANES. In SI Text we show all of the 16 possible SXRS signals, where the pump and probe can be tuned to the K- or the L-edge of zinc or nickel, for reference.

Natural orbitals (NOs) (40) obtained through a singular-value decomposition of transition density matrices give a compact representation of single-particle valence excitations. When there is a single dominant NO transition (occupation number near 1), the excited state can be well described by an independent electron and hole. States with multiple NOs with nonnegligible occupation are inherently multiconfigurational in nature, and the electron and hole are entangled. A useful measure of this entanglement (41) is the participation ratio (PR) 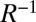, where R is the sum of the squared occupation numbers for all NO pairs (Eq. S22 in SI Text). The PR varies between 1 (no entanglement, uncorrelated electron and hole) and the number of possible excitations. The PRs for the peaks in Fig. 3 are given in Table 1. Fig. S10 shows the NOs for the valence-excited states corresponding to the peaks in Fig. 3. Only the valence state corresponding to peak E is well represented by a single NO electron-hole pair, with an occupation number of 0.85. As we see from the integrated densities in Table 1, peak E is also the only valence eigenstate which is largely localized to a single monomer.

Table 1.

Frequencies, participation ratios, and integrated electron and hole densities for the states corresponding to the major peaks in Fig. 3, Right

			Hole density		Electron density
Peak			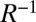Ni monomer	Zn monomer	Ni monomer	Zn monomer
A	4.67	1.57	0.41	0.59	0.38	0.62
B	4.74	2.45	0.37	0.63	0.29	0.71
C	4.89	4.48	0.34	0.66	0.40	0.60
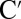	4.91	3.42	0.57	0.43	0.46	0.54
D	5.91	4.51	0.45	0.55	0.44	0.56
E	5.97	1.39	0.92	0.08	0.99	0.01
F	5.98	3.82	0.60	0.40	0.84	0.16

The natural orbital decomposition was used to visualize the superposition of the excited states created by the Raman excitation (see SI Text for detailed expressions). We show the dominant NO for the real-valued Ni2p window wavepacket in Fig. 4, Lower. Both electron and hole are entirely localized to the nickel monomer, with the hole more tightly focused near the nickel atom and with a participation ratio of 1.15, unentangled. The doorway state is time dependent and complex valued, but the signal is proportional to its imaginary part. In Fig. 4, Upper we plot NOs for the imaginary part of the Zn2p doorway for five time points, corresponding to peaks and troughs in the Zn2p/Zn2p signal. At all times, the doorway is multiconfigurational in nature, as can be seen in the time-dependent PR shown in Fig. 5; we show only the two with the highest occupation numbers. Initially, the doorway resides entirely on the zinc monomer. At times 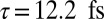and 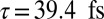, it has delocalized over the whole dimer. At times 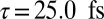and 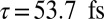, the doorway has relocalized on the zinc monomer.

Fig. 4.

(Upper) Dominant natural orbitals (NOs) for the Zn2p doorway wavepacket at different times. (Lower) NOs for the Ni2p window. Left, nickel monomer; Right, zinc monomer.

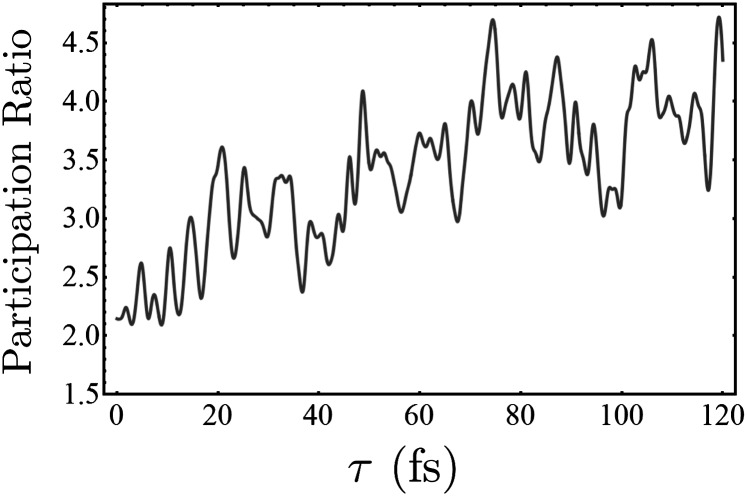
Fig. 5.

Participation ratio for the time-dependent Zn2p doorway wavepacket. A value of 1 indicates the electron and hole are uncorrelated, and a higher value indicates the greater degree of entanglement between different electron–hole pairs.

In Fig. S11, we give the time-dependent participation ratio for doorway wavepackets created at the K- and L-edges of zinc and nickel. The Zn2p wavepacket is unique in having a large PR, which starts at a value of 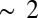and grows as high as 4.5 in the first 120 fs after excitation. The PR for Zn1s excitation stays below 2 for all times, and the Ni1s and Ni2p PRs stay below 1.5. Interestingly, it is only the Zn2p wavepacket that exhibits strong EET. This can be seen by comparing the Zn2p/Zn2p I2P-SXRS signal, which shows strong low-frequency oscillations, with the other three one-color signals that exhibit only exponential decay. These results suggest a correlation between a high PR and efficient EET. The theoretical basis for this observation is not obvious.

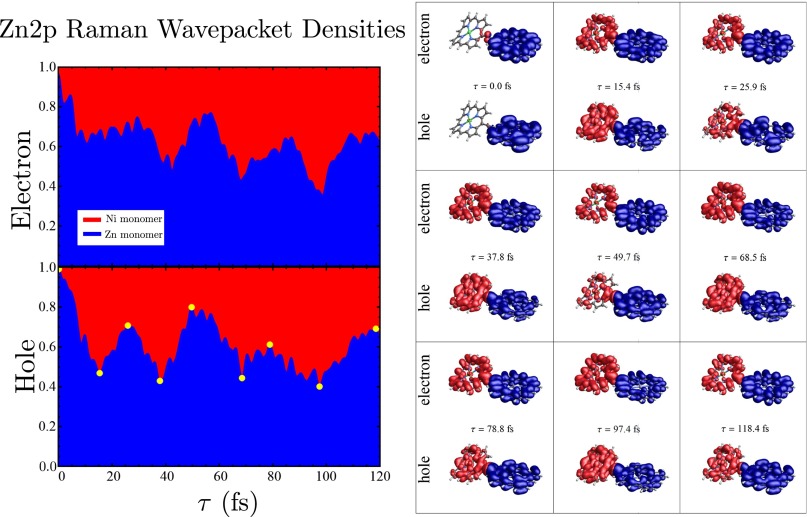
To further visualize the excited state dynamics, we examine the time-dependent electron and hole densities, integrated over spatial regions containing either the zinc or the nickel monomers, using the method described in SI Text. A perpendicular plane through the center of the carbon triple bond was used to separate the zinc and nickel monomer regions. In Fig. 6 we show the integrated densities for the zinc doorway, as well as the densities for various time points. Movie S1 shows the electron and hole densities for the first 120 fs following Zn2p excitation. We can see clearly from Fig. 6, Left and Right that the electron and hole densities change in the same phase. Each ring remains neutral; this is energy, not charge, transfer.

Fig. 6.

(Right) Electron and hole densities for the Zn2p valence superposition state prepared by SXRS for various times after excitation. The isosurfaces are colored according to which monomer they reside on, red for nickel and blue for zinc. (Left) Spatially integrated densities over each ring. (Lower Left) The yellow dots correspond to the time points for which snapshots are shown on the Right. Movie S1 shows the electron and hole motion.

Conclusions

The I2P-SXRS technique is ideally suited for creating localized excitations in molecules and monitoring the ensuing dynamics with attosecond time resolution, taking advantage of the current- and next-generation XFEL sources. Here we have shown that the time-dependent signal reveals the back-and-forth energy transfer in this model system. Compared to optical pulses, X-ray pulses create more localized excitations, so that they can trigger and measure excited state dynamics at specific positions in a molecular system. In addition, the X-ray Raman technique, thanks to the large bandwidth of attosecond pulses, can populate high-energy valence-excited states that may not be accessible from the ground state by visible pulses. Both of these features make stimulated X-ray Raman spectroscopy a powerful tool to observe EET in complex molecular systems.

Materials and Methods

Computational Details.

A restricted excitation window time-dependent density functional theory (REW-TDDFT) formalism was recently extended to treat X-ray core excitations, using a realistic treatment of valence electron correlation (48), which scales well to larger systems. The ground-state geometry of a Zn/Ni porphyrin heterodimer (Fig. 2) was optimized using Gaussian09 (49) at the B3LYP (50, 51)/6-31G* level of theory. Transition dipoles and core excitation frequencies were calculated using REW-TDDFT (48, 52–54). We adopt the computational protocol in ref. 55. All REW-TDDFT calculations were performed with a locally modified version of NWChem code (56) at the CAM-B3LYP (57)/6-311G** level of theory and within the Tamm–Dancoff approximation (58). We assume transform-limited Gaussian pulses in our simulations with FWHM of 166 as (10.9 eV). The pulse power spectra are shown as shaded areas along with the XANES in Fig. 2.