Nuclear quantum effects and hydrogen bond fluctuations in water

Significance

There is no doubt about the importance of liquid water for climate and life on Earth. Correctly modeling the properties of this substance is still a formidable challenge, however. Here, we show, using state-of-the-art techniques that allow for quantum mechanical effects in the motion of the electrons and nuclei, that room-temperature water is not simply a molecular liquid; its protons experience wild excursions along the hydrogen bond (HB) network driven by quantum fluctuations, which result in an unexpectedly large probability of transient autoionization events. Moreover, these events are strongly correlated across neighboring bonds so that perturbations disrupting the HB network (pressure, confinement, solvated ions, and interfaces) could enhance in a concerted way their impact on water’s behavior.

Abstract

The hydrogen bond (HB) is central to our understanding of the properties of water. However, despite intense theoretical and experimental study, it continues to hold some surprises. Here, we show from an analysis of ab initio simulations that take proper account of nuclear quantum effects that the hydrogen-bonded protons in liquid water experience significant excursions in the direction of the acceptor oxygen atoms. This generates a small but nonnegligible fraction of transient autoprotolysis events that are not seen in simulations with classical nuclei. These events are associated with major rearrangements of the electronic density, as revealed by an analysis of the computed Wannier centers and ¹H chemical shifts. We also show that the quantum fluctuations exhibit significant correlations across neighboring HBs, consistent with an ephemeral shuttling of protons along water wires. We end by suggesting possible implications for our understanding of how perturbations (solvated ions, interfaces, and confinement) might affect the HB network in water.

Despite its apparent simplicity, liquid water exhibits a number of anomalous properties, such as a decrease in density on freezing, an isobaric density maximum, and its unusually high dielectric constant and heat capacity (1). These, together with its unquestionable importance for climate and life on Earth, have made this substance a subject of intense research by both experiments and simulations.

The central concept that has been used to rationalize the peculiar behavior of water is that of the hydrogen bond (HB) (2). The nature of this bond in water has been studied in depth by atomistic computer simulations, which have investigated how it is affected by ionic and electronic polarizability (3, 4), pressure and temperature (5, 6), and nuclear quantum effects (NQEs) (7–9). Furthermore, ab initio molecular dynamics (MD) simulations have been used to shed light on autoionization (10, 11), a process with profound implications for the chemistry of aqueous solutions.

In this paper, we investigate the impact of NQEs on the HB in pure water, finding a qualitative increase in fluctuations that leads to a partial dissociation of the covalent O–H bond. The weakening of this covalent bond in the presence of hydrogen bonding is consistent with the red shift of the stretching mode of water upon condensation, as well as with recent experiments demonstrating that selectively exciting the O–H stretch in water leads to a pronounced delocalization of the proton toward the acceptor oxygen atom (12). However, the role of NQEs in governing the extent of this delocalization has not been investigated before now.

Our analysis is based on MD simulations of water at different thermodynamic state points, with an ab initio description of the interactions among the nuclei. We also account fully for the quantum nature of the nuclear motion, using a recently developed combination of imaginary time path integral and colored noise thermostating techniques (13–15). The efficiency of this combination allows us to investigate the statistics of the quantum HB fluctuations in ab initio water in far more detail than has been possible before. The use of an ab initio description of the chemical bonding also allows us to investigate the correlation between HB fluctuations and electronic rearrangements, as well as to comment on the implications of our findings for ¹H NMR spectroscopy.

Results

Structural Fluctuations of HBs in Water.

The analysis we perform requires the definition of one or more structural parameters that (i) clearly identify the protons involved in HBs and (ii) characterize HB fluctuations in such a way that makes proton delocalization apparent. The HB in water involves a hydrogen atom H, the oxygen O to which it is covalently bound, and a second acceptor oxygen atom O′. Different geometric definitions of the HB use various combinations of the distances between these three atoms. Any such combination contains a degree of arbitrariness, but the essential requirement is simply that the probability density of the chosen structural parameter(s) should be multimodal (16). It is this multimodality that makes it possible to associate HBs with a specific range of parameters in an unambiguous fashion.

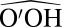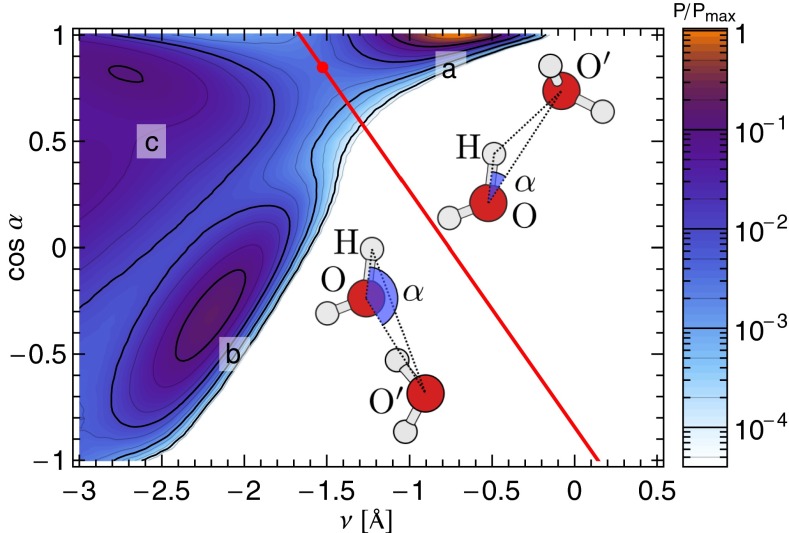
The angle α is often used as one of the parameters because it discriminates well among different O′ atoms within the first coordination shell of O. However, it is not very effective in describing fluctuations of the proton, so a second coordinate is needed. Rather than the O–O′ or H–O′ distance, we have chosen to use the proton-transfer coordinate 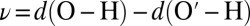, a choice that proves to be particularly convenient, as we shall see below. Fig. 1 shows that the joint probability density relative to ν and cos α displays a clear-cut clustering in which the hydrogen-bonding region can be defined unambiguously.

Fig. 1.

Joint probability density P(ν, cosα) of finding an O–H–O′ geometry with a given ν–α configuration in a classical simulation of ab initio water at 300 K and the experimental density, normalized over its maximum P_max. One can clearly identify a cluster of hydrogen-bonded configurations (a) and a cluster corresponding to the other first neighbors of the tagged molecule (b). Features at more negative values of ν are less clear-cut (c). They correspond to farther neighbors and are irrelevant to the present work. The red line marks the dividing surface one should ideally use to define the hydrogen-bonded region, which is obtained by moving away from the saddle point on the probability distribution in the direction of the negative eigenvector of the Hessian.

In the present study, we shall be more interested in investigating the fluctuations of the proton in well-formed HBs than in resolving borderline configurations. For this purpose, it is clear from Fig. 1 that the proton-transfer coordinate alone suffices to identify configurations in the region 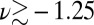Å as hydrogen-bonded and to characterize the extent of their fluctuations.

Having introduced this analysis framework, let us now use it to investigate the impact of NQEs on HB fluctuations. As detailed in Materials and Methods, the technique we have used to include NQEs combines path integral MD, which maps the partition function of a system of distinguishable quantum particles onto the partition function of a classical ring polymer consisting of several replicas of the system connected by harmonic springs (17, 18) with a generalized Langevin equation that reduces the number of replicas needed for convergence [PIGLET (15)].

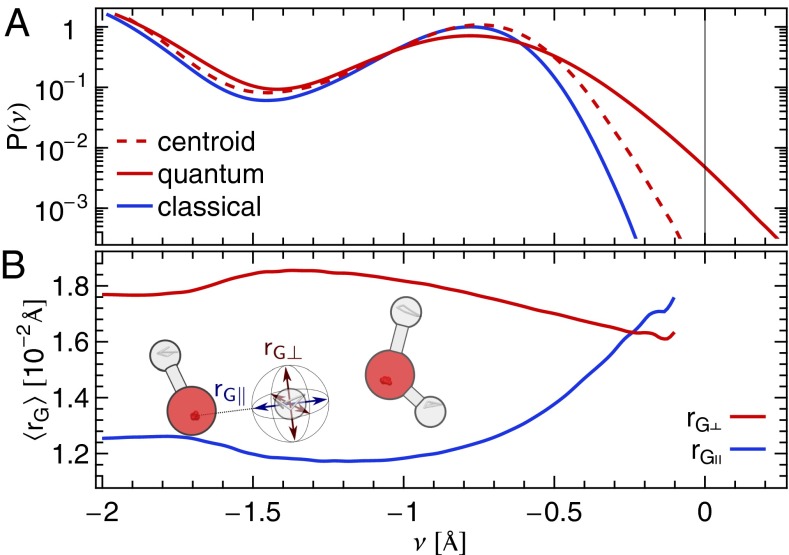
Fig. 2 shows that the impact of NQEs on the HB fluctuations in liquid water is actually quite dramatic, far more so than one would have anticipated on the basis of previous work (7–9). We find that quantum protons exhibit broad fluctuations that bring a small but significant fraction of HB configurations (about 1 in 1,000) into the 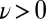region, the region that corresponds, at least from a geometric perspective, to autoprotolysis. This should be contrasted with our classical simulations in which we have only observed negative values of ν, and we estimate that the probability of reaching 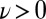is four orders of magnitude smaller (10⁻⁷; SI Appendix).

Fig. 2.

(A) Distribution of the proton-transfer coordinate in ab initio simulations of water at 300 K. The three curves correspond to a classical simulation, to the distribution of the ring polymer beads in a simulation that includes quantum effects, and to the distribution of the centroid of the ring polymer in the quantum simulation. (B) Conditional average of the gyration radius of the ring polymer in the directions parallel 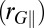and perpendicular 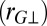to the O–H covalent bond for different values of ν for the centroid.

One might be tempted to attribute the extreme HB fluctuations seen in our quantum calculations to the excessive charge delocalization that is known to affect generalized gradient approximation density functionals (19–21). However, we have verified this is a qualitative effect that is only slightly altered by the use of a hybrid functional, which typically reduces charge delocalization (22), or by other changes to our computational details. As discussed in more detail in SI Appendix, the robustness of the effect can be attributed to the large amount of zero point energy in the covalent O–H stretch.

We should stress that the extreme autoprotolysis fluctuations are very short-lived and that they are a genuinely quantum mechanical effect. This becomes clear on examining the distribution of ν for the center of mass of the ring polymer, and its gyration radius in the directions parallel and perpendicular to the covalent O–H bond. The distribution of the centroid along the proton-transfer coordinate is only marginally broader than the classical distribution. The transient autoprotolysis events are due to the quantum mechanical fluctuations. Interestingly, the character of these fluctuations changes depending on the position of the centroid along the proton-transfer coordinate. For 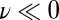, the ring polymer is considerably less spread out in the direction parallel to the stiff covalent bond than in the softer directions perpendicular to it. As the centroid approaches 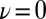, the ring polymer spreads out in the direction parallel to the O–H bond, effectively delocalizing onto the acceptor atom O′.

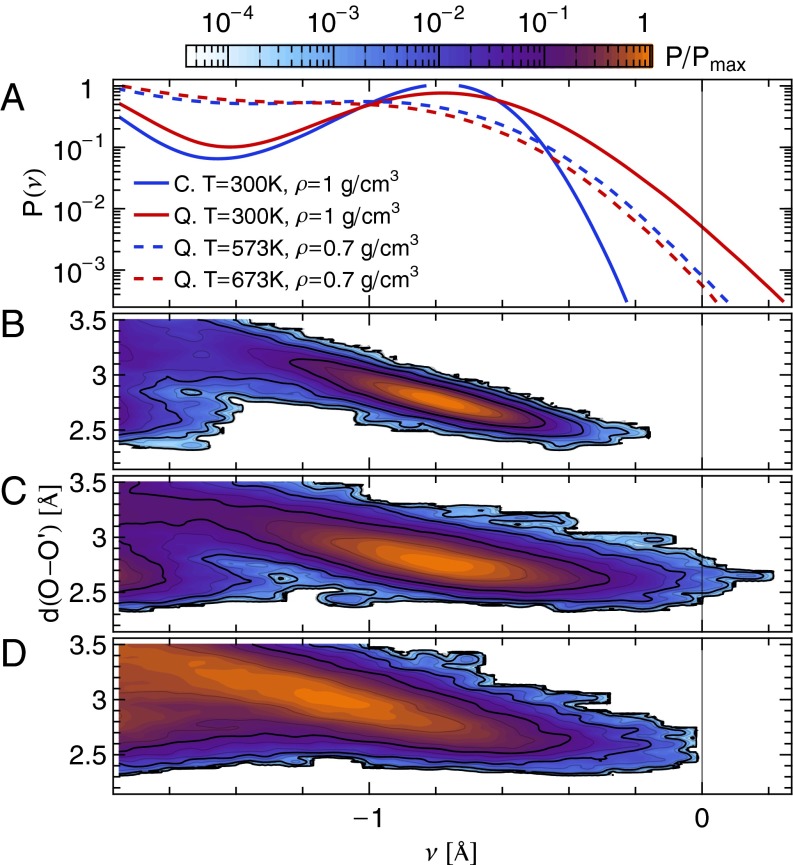
The quantum nature of the extreme HB fluctuations is confirmed by examining their temperature and density dependence. In Fig. 3A, we compare the distributions of ν at different thermodynamic state points. Temperature alone has little effect on the fluctuations toward 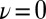: Raising the temperature from 573 K to 673 K actually results in a small reduction in the probability of autoprotolysis events, emphasizing once more that they cannot be traced to thermal fluctuations. A 30% decrease in the density leads to a more noticeable reduction in the probability of finding the proton at 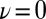. Even this change, however, is still negligible compared with the effect of neglecting NQEs.

Fig. 3.

(A) Distribution of the proton-transfer coordinate ν for water at different thermodynamic state points. (B–D) Joint probability distribution of the proton-transfer coordinate and the distance d(O–O′) between the covalently bound and acceptor oxygen atoms: (B) classical nuclei, , 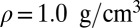; (C) quantum nuclei, 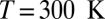, 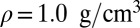; and (D) quantum nuclei, , .

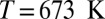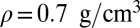Changes in density have the primary effect of modifying the average O–O′ distance. As in the case of solvated proton species (23, 24), one observes a strong correlation between the compression of the O–O′ distance and the excursions along the proton-transfer coordinate. A reduction in density leads, on average, to larger O–O′ distances and, consequently, to more negative values of ν. Quantum effects, on the other hand, do not change the average values of d(O–O′) and ν appreciably but increase significantly their fluctuations around the mean. In light of these observations, it would be interesting to revisit the problem of autoionization at high pressure (6), including the effects of quantum fluctuations.

Electronic Properties and Wannier Analysis.

We have found that the transient autoprotolysis events are dramatically less common in simulations based on an empirical force field, even when one uses a water model that includes anharmonic terms in the description of the covalent O–H bond (25) (SI Appendix). This suggests that the extreme fluctuations toward are not due simply to the anharmonicity of the O–H stretching coordinate but, rather, that they are stabilized by a rearrangement of the electron density.

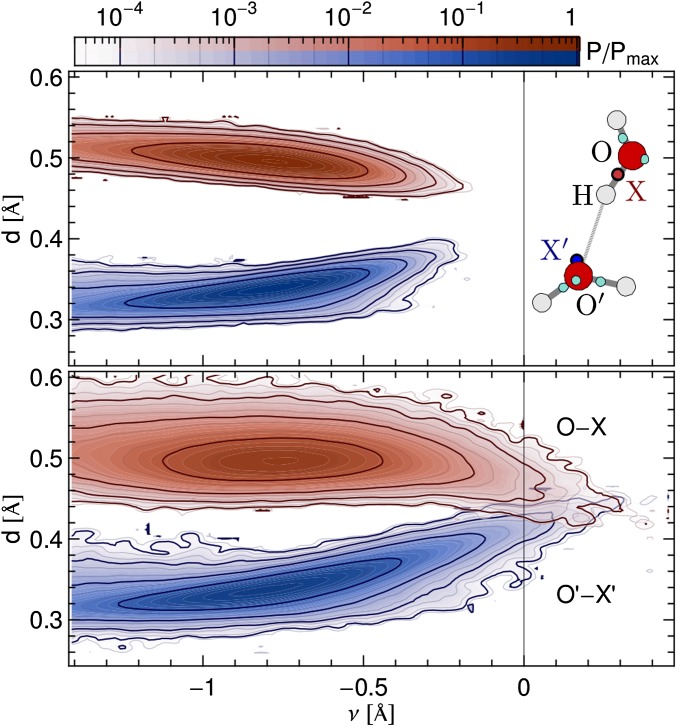
To verify this hypothesis, we have analyzed our trajectories in terms of their electronic structure. In several instances, maximally localized Wannier functions (26) have been proven to provide a powerful tool to rationalize the electronic structure of water (4–6, 8). The center of the charge density associated with a Wannier orbital can be thought of as representing an electron pair. Each oxygen atom is surrounded by four such centers. Two are at a distance of 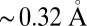from the atom and can be interpreted as the lone pairs, whereas the other two are at a distance of 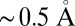from the oxygen, midway between the O and the covalently bound hydrogens, and can be interpreted as the bonding pairs of the water molecule.

An analysis of the positions of the Wannier centers as a function of ν demonstrates unambiguously that extreme fluctuations of the HB are associated with major rearrangements of the electron density (Fig. 4). As ν approaches zero for a tagged hydrogen, the electron pair X associated with the covalent bond moves closer to the oxygen atom, approaching the distance characteristic of a lone pair. At the same time, the distance between the lone pair X′ and the acceptor oxygen becomes larger and approaches the distance corresponding to a covalent O–H bond (Fig. 4). This charge transfer is already evident in the classical simulations, but it becomes more pronounced in the simulations with quantum nuclei: In the most extreme cases, one even sees an inversion, with .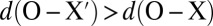

Fig. 4.

Given a tagged H atom, the oxygen atom O it is covalently bound to, and the acceptor atom O′, X and X′ are the Wannier centers of the two O atoms that are closest to H. The plots report the joint probability distribution of ν and of the distances of the Wannier centers to the corresponding O. A classical simulation of liquid water (Upper) and a simulation that includes NQEs (Lower) are shown.

¹H NMR Chemical Shifts.

The connection we have made between the structural parameter ν and the electronic structure of the HB can be used to assist the interpretation of experimental results, such as those of ¹H NMR spectroscopy. The ¹H NMR chemical shift of liquid water from room temperature to above the critical point has been measured using an isolated water molecule in a dilute gas at 473 K as an external reference (27, 28). The observed variations of the chemical shift were linked to variations in the hydrogen bonding as a function of the thermodynamic state point.

Pioneering density functional theory simulations (29, 30) have obtained qualitative agreement with these experiments. Unfortunately, however, the NMR chemical shift computed by density functional perturbation theory does not yet allow one to achieve the same exquisite level of accuracy that is characteristic of NMR experiments: Details of the calculation, such as the exchange-correlation functional, pseudopotential, and system size, can change the results by more than 1 ppm (31). On the other hand, simulations do offer useful insight when it comes to unraveling the connections between the chemical shielding of an atom and its environment, because the chemical shielding can be computed for individual atoms in a simulation, whereas only averages are available to experiments. Furthermore, the ¹H NMR chemical shift can be viewed as a concise indicator of the electronic structure in the neighborhood of a tagged atom, which complements the more complex information that can be extracted from an analysis of Wannier centers.

Early simulations of the isotropic chemical shift 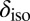in water and ice found that in the solid state, 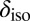correlates very well with the elongation of the O–H covalent bond (29). However, Fig. 5 shows that the correlation obtained with this structural parameter is highly sensitive to the thermodynamic state point, suggesting that it may not be the most transferable indicator of the connection between structural and electronic fluctuations in water. On the other hand, exactly the same dependence of 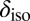on ν is observed at three radically different thermodynamic state points. This clearly indicates that the proton-transfer coordinate ν is a more natural structural parameter to use to characterize the electronic rearrangements associated with hydrogen bonding.

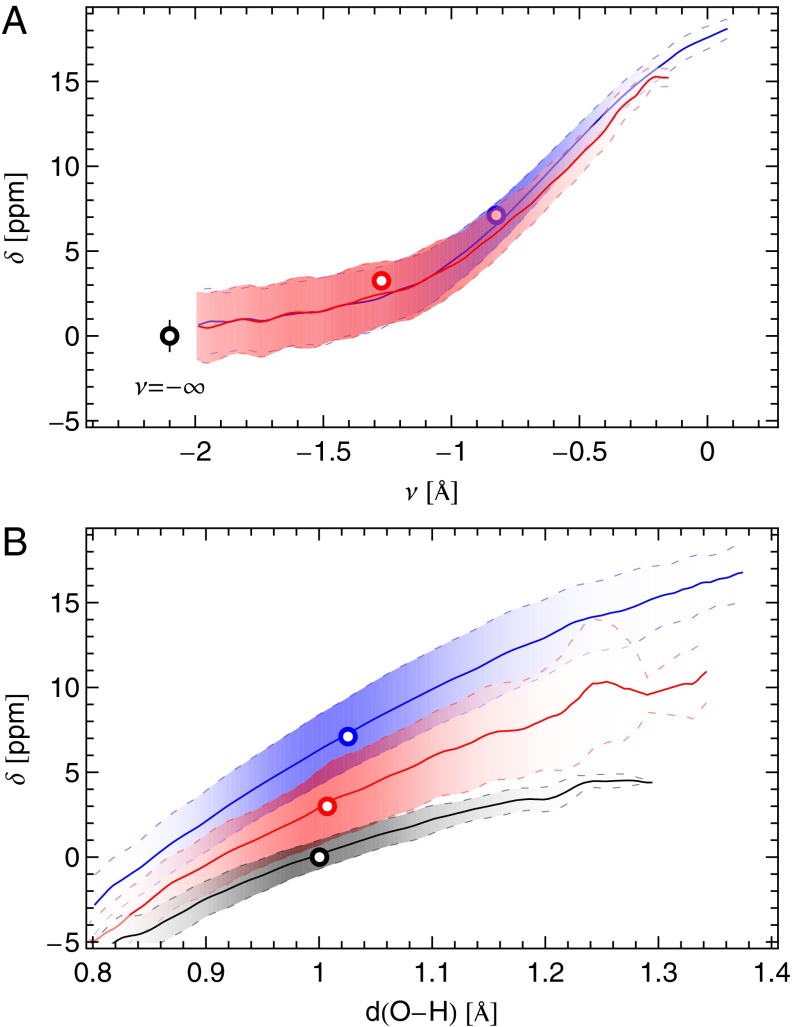
Fig. 5.

Compact illustration of the relation between the instantaneous chemical shift and the structural properties of the O–H bond at three different thermodynamic state points: the liquid at 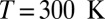and 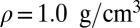(blue), supercritical water at 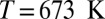and 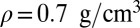(red), and an isolated gas-phase water molecule at 473 K (black). In all cases, NQEs were included using PIGLET. The continuous lines correspond to conditional averages of the chemical shift as a function of the structural parameter, the dashed lines delimit the area within 1 standard deviation from the mean, and the shading is proportional to the probability distribution of the structural parameter. The dots indicate the means of the structural parameter and the chemical shift. (A) Proton-transfer coordinate ν is used as the structural parameter, the gas-phase molecule corresponding to an asymptotic value of . (B) Covalent bond length 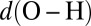is used.

This observation allows us to rationalize some of the qualitative experimental observations of Matubayasi et al. (27, 28). The ¹H chemical shift of the liquid was observed to decrease with increasing temperature, saturating to a near-constant value in the proximity of the critical temperature. This can be understood by noting that the mean value of the distribution of ν is shifted by density rather than by temperature. The chemical shift changes significantly only as long as there is liquid–gas coexistence in the (constant volume) sample holder; in this regime, an increase in temperature lowers the density of the liquid phase resulting in a decrease in the chemical shift.

Furthermore, our simulations provide a direct test of the impact of NQEs on the chemical shift. As discussed in a recent study of solid-state models of the solvated proton (24), the inclusion of NQEs will not change the experimentally observable (average) NMR chemical shift unless either the instantaneous chemical shift or its fluctuations have a strongly nonlinear character. The 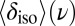curve in Fig. 5 is nearly linear from 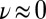to 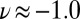, but it then saturates for 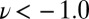to a value that corresponds to a broken HB, which is very close to the value for a gas-phase molecule. This kind of nonlinear behavior is precisely what is needed to have NQEs produce a net effect on the average chemical shift.

Our computed average ¹H chemical shift relative to a gas-phase molecule at temperature 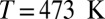amounts to 7.1 ppm for the room-temperature liquid (6.6 ppm for snapshots from a classical simulation, 4.27 ppm in experiments), 3.5 ppm for 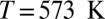at density 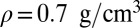(3.1 ppm for a classical simulation, 2.12 ppm in experiments), and 3.0 ppm for supercritical water at 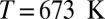and 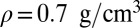(2.8 ppm for a classical simulation). Thus, NQEs change the computed 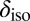by as much as 0.5 ppm, which is of the same order of magnitude as the errors arising from the use of an approximate description of the electronic structure. NQEs should therefore certainly be included in any future attempt to predict quantitatively the proton chemical shifts in aqueous systems.

Discussion

Provided that one singles out major qualitative effects, ab initio computer simulations can contribute a great deal to our understanding of the behavior of matter at the atomistic level. Here, we have shown that quantum mechanical effects in the nuclear motion have a qualitative impact on the HB fluctuations in water, and presumably also in other hydrogen-bonded systems.

Although the competition between intra- and intermolecular quantum effects that appears to be ubiquitous in water reduces the impact of neglecting NQEs on average properties (9, 25, 32, 33), the protons should always be treated as quantum particles in studies aimed at capturing rare events or, more generally, properties that depend on the tail of the equilibrium distribution. For instance, a recent study (34) suggests that conflicting interpretations of the X-ray absorption spectroscopy of water (35, 36) can be reconciled based on the presence of asymmetrical configurations of HBs in water. The enhancement of fluctuations due to the quantum nature of nuclei will inevitably generate a larger fraction of asymmetrical configurations (a detailed discussion is provided in SI Appendix), and may therefore be an important ingredient in the solution of this puzzle.

As we discuss in more detail in SI Appendix, the transient autoprotolysis events are strongly correlated across the HB network. In our quantum simulations, about 1 in 1,000 HBs has a value of 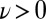, so one would expect a chance of 1 in 1 million of finding two HBs simultaneously involved in extreme excursions, were they uncorrelated. However, we observe significant deviations from this uncorrelated prediction when we consider pairs of HBs around a given water molecule. The probability of the two HBs donated by a water molecule experiencing autoprotolysis at the same time is reduced by a factor of 10, and the probability of a simultaneous fluctuation of one donated HB and one accepted HB involving the same molecule is increased by a factor of 5, relative to the uncorrelated prediction. This latter scenario corresponds to an ephemeral proton shuttling across a segment of a water wire, similar to what has been seen before in simulations of aqueous protons and hydroxide ions (37–39).

This, together with the finding that the electronic properties of the HB in neutral water correlate very naturally with the proton-transfer coordinate, suggests that one could imagine perturbations to the HB network (e.g., solvated ions, interfaces, confinement) as modulating the stability of the quantum fluctuations (40) that are already present in neat water rather than introducing completely new effects.

The recent methodological developments we have exploited in this paper (13–15) have greatly facilitated collecting the extensive dataset that underlies our statistical analysis. We anticipate that the routine inclusion of NQEs in ab initio simulations, which is made viable by these techniques, will contribute greatly to our future understanding of aqueous systems, including the solvation of the proton and its mobility in bulk water, in confinement (41, 42), and at interfaces.

Materials and Methods

MD Simulations.

Ab initio MD simulations were performed using Quickstep, one of the modules of the CP2K package (43). The electronic structure calculations were based on density functional theory, using the Becke–Lee–Yang–Parr (BLYP) exchange-correlation functional (44, 45) and Goedecker–Teter–Hutter (GTH) pseudopotentials (46). Wave functions were expanded in the Gaussian polarized double-zeta split-valence (DZVP) basis set, whereas the electronic density was represented using an auxiliary plane wave basis, with a kinetic energy cutoff of 300 Rydberg. We have verified that changing the details of the calculation and the choice of functional does not affect the qualitative conclusions of this work (SI Appendix). We have also performed calculations using q-TIP4P/F, an empirical potential specifically designed to be used in conjunction with path integral simulations (25).

Classical MD trajectories 100 ps in length were performed at a constant volume, using a time step of 1 fs, with a stochastic velocity rescaling thermostat (47), starting from a snapshot equilibrated with the empirical force field and discarding the first 6 ps for equilibration. We used the final configurations of these trajectories as the starting point for our simulations with quantum nuclei. These simulations used a path integral MD formalism, supplemented with a colored noise tailored to accelerate convergence (15), so that quantitative accuracy was reached with as few as six replicas. The parameters of the colored noise were downloaded from an online repository (48) and are provided in SI Appendix. Most of these PIGLET simulations used a time step of 0.5 fs and were 15 ps long, with the first 3 ps discarded for equilibration. The simulation at 300 K was run for a further 35 ps to allow for the slower relaxation time at this temperature than at higher temperatures.

Conditional Averages.

We have presented several conditional averages as a function of the value of the proton-transfer coordinate ν. These quantities correspond to the ensemble averages

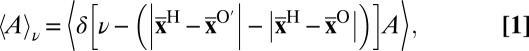where A is a placeholder for any estimator that one might want to average conditionally, 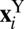indicates the position of the ith replica of the atom Y, 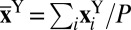indicates the position of the corresponding centroid, and P is the number of path integral beads. For instance, one can define the (directionally resolved) gyration radius of the ring polymer as

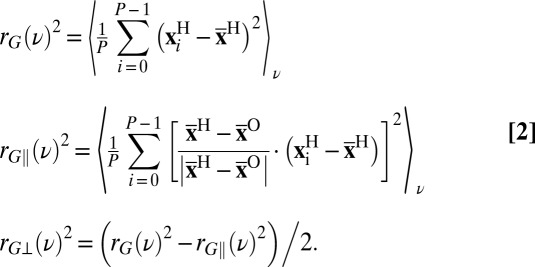Wannier Center Calculations.

All the Wannier centers (26) have been calculated using the algorithm implemented in the CPMD package, version 3.15.1 (49). The corresponding electronic structure was determined for each frame using fully nonlocal norm-conserving pseudopotentials as proposed by Troullier and Martins (50), in combination with a 80-Rydberg plane-wave energy cutoff and a Γ-point sampling of the first Brillouin zone. Our distributions encompass 2,000 frames for each trajectory.

Chemical Shift Calculations.

All the ¹H NMR isotropic chemical shieldings 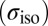have been calculated using the gauge-including projector-augmented-wave (51) method as implemented in the QUANTUM EXPRESSO package, v. 4.3.2 (52). For each MD simulation discussed in this paper, we calculated the ¹H 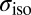of 400 frames (2,000 frames for the isolated water molecule) uniformly sampled along the trajectory. The electronic structure was calculated using fully nonlocal norm-conserving pseudopotentials (50), a plane wave basis with a 90-Rydberg energy cutoff, and a 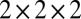Monkhorst–Pack k-point grid (53). These parameters yield fully converged ¹H 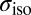values. The chemical shifts 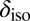were calculated using 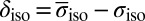, where 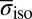is the average chemical shielding of an isolated quantum water molecule simulated at 473 K (30).