Decisions on the fly in cellular sensory systems

Significance

Cell-signaling pathways are often presumed to convert just the level of an external stimulus to response. However, in contexts such as the immune system or rapidly developing embryos, cells plausibly have to make rapid decisions based on limited information. Statistical theory defines absolute bounds on the minimum average observation time necessary for decisions subject to a defined error rate. We show that common genetic circuits have the potential to approach the theoretical optimal performance. They operate by accumulating a single chemical species and then applying a threshold. The circuit parameters required for optimal performance can be learned by a simple hill-climbing search. The complex but reversible protein modifications that accompany signaling thus have the potential to perform analog computations.

Abstract

Cells send and receive signals through pathways that have been defined in great detail biochemically, and it is often presumed that the signals convey only level information. Cell signaling in the presence of noise is extensively studied but only rarely is the speed required to make a decision considered. However, in the immune system, rapidly developing embryos, and cellular response to stress, fast and accurate actions are required. Statistical theory under the rubric of “exploit–explore” quantifies trade-offs between decision speed and accuracy and supplies rigorous performance bounds and algorithms that realize them. We show that common protein phosphorylation networks can implement optimal decision theory algorithms and speculate that the ubiquitous chemical modifications to receptors during signaling actually perform analog computations. We quantify performance trade-offs when the cellular system has incomplete knowledge of the data model. For the problem of sensing the time when the composition of a ligand mixture changes, we find a nonanalytic dependence on relative concentrations and specify the number of parameters needed for near-optimal performance and how to adjust them. The algorithms specify the minimal computation that has to take place on a single receptor before the information is pooled across the cell.

The exigencies of operations research during the second world war led to the following problem: Given a stream of data that is drawn from one of two prescribed models M1 or M2, what is the quickest way to decide between them subject to bounds on the errors? The solution found by Wald (1, 2) computes the ratio of two conditional probabilities using the data up to time t,

and calls M1 when 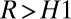and M2 when 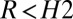and waits for more data otherwise. The thresholds H control the errors; e.g., larger 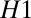decreases the odds of deciding M1 when the data come from M2. For the task of distinguishing two Gaussians with different means, the average decision time for Wald’s algorithm is a factor two times shorter than using a fixed averaging time for the same error rate. This is a simple example of a general class of problems termed “exploit–explore”; i.e., either decide or accumulate more data (3, 4). They are used in medical statistics to decide when a clinical trial has generated enough data for a conclusion.

For the problems that concern us, the next step in complexity was taken by Shiryaev (5–7), who considered the optimal detection of change points. A stream of data is presented and the model changes from M1 to M2 at an unknown time θ. The algorithm calls the change point at time t to minimize a linear combination of the false positive rate (e.g., 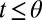) and the decision time mea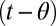n when 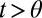. Again the algorithm “knows” the models M1, M2.

Another step in complexity, about which we have little to say, corresponds to situations where the statistics of the hypotheses to be discriminated are not available or too elaborate to be exploited. An example in case is when the statistics of the stream of data are actively modified by the actions of the receiver; i.e., the decision process feeds back onto the input statistics. Optimal strategies are then difficult to prove but the “infotaxis” heuristic may apply in very uncertain situations, e.g., for biological problems such as searching for a source of molecules dispersed in a turbulent environment (8).

Neurobiology presents many examples of optimal decision problems as suggested by the title of a recent review, “Seeing at a glance, smelling in a whiff: Rapid forms of perceptual decision making” (9). These problems are amenable to experiment, typically posed in the Wald limit, and there are quantitative bounds on performance that are independent of neural parameters (10). The appeal is similar to that of investigating the performance of the eye, subject to the physical constraints of optics. However, when moving from mathematics to neural systems even theoretically, additional questions arise, such as, How well can neural circuits compute the optimal algorithm? How much memory is required? And is there some neuron whose firing level encodes the likelihood ratio R (11)?

In contrast to the extensive neurobiology and psychology literature, optimal decision theory has largely been neglected at the level of cell signaling, with the exceptions of refs. 12 and 13, in contrast to information theory that readily passes between the two domains (14–16). Rapid and accurate decisions seem as much a part of the cellular world as of the neural one. T cells in the immune system have to sample many protein fragments for potential antigens (17). Greater speed at fixed accuracy allows more extensive sampling. Bacteria have to sense DNA damage and respond appropriately (18). Chemotaxis by bacteria or eukaryotic cells such as neutrophils clearly is facilitated by rapid detection of gradients (19, 20). There is a plausible fitness gain if embryonic development is accelerated in species such as insects and amphibians that develop outside of the mother.

However, the signaling context requires different models than in neural systems. A natural model for a receptor, the signal transduction layer in neural terms, assumes that only the ligand binding times are available for downstream decisions. We show how simple analog computation built from standard biochemical components can come close to the optimal performance. We consider both the fixed-time origin (Wald) and change-point problems. In each case we pose two computational tasks: sensing the absolute level of a single protein and detecting when the composition of a mixture changes at fixed total concentration. The uncorrelated nature of protein binding events implies that the accumulation of a single decision variable suffices for optimal performance, and no additional memory is needed. Parameter selection for the circuit doing the discrimination is clearly essential for optimal performance. Thus, we address the number of parameters needed for a good approximation and a plausible mechanism for their selection in vivo. In the embryo it may be reasonable to assume evolution has jointly optimized the signal and receiver to ensure rapid information transmission.

The statistical theory of Wald and his successors is predicated on the assumption that the data presented to the decision machinery are derived from one of the two models being compared. Mathematics furnishes no guidance as to how Eq. 1 performs otherwise. We show by example that counter to intuition, when the data are “easier”, i.e., present a greater contrast than the model assumes, the performance of Eq. 1 can actually degrade. This problem can be “cured” by suitably generalizing the states being compared. This complicates the calculations, but is required for biological realism.

Results

The typical vertebrate signaling pathway has over 10 genes that operate from the presentation of a signal to its realization through transcription (www.stanford.edu/group/nusselab/cgi-bin/wnt/; refs. 21, 22). This complexity seems in excess of what is needed to transmit merely level information and the component overload is attributed to the exigencies of biochemistry or evolutionary accident. We consider the alternative that natural signals are dynamic and the pathway uses that temporal history to make decisions. Because there are few single-cell experiments that present complex signals, we suggest some problems the cell may need to solve and compute the performance of simple biochemical systems.

We assume that the only information a single receptor has about the extracellular environment is whether it is bound by a ligand or not. Binding can of course elicit downstream changes in receptor conformation, binding to other receptors, and phosphorylation cascades, all of which we consider as possible analog “computations” performed on the time history of receptor occupancy. We consider two idealized tasks: (a) distinguishing two concentrations of the same ligand and (b) detecting a new component (or agonist in the immune context) added to a preexisting “pure” or “self” state. We keep total concentration fixed when the composition changes in b to distinguish the problem from a. The temporal context can be either (i) data from one of the possible states are presented at a defined time 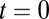or (ii) the data change from state i to state ii at an unknown time that is to be determined. For all combinations of tasks and contexts, the cell has to decide as rapidly as possible subject to an error bound. We first pose our two computational tasks (a, b) in the Wald limit with a defined initial time, i.e., a ratio test, Eq. 1, and then consider the more realistic (time) change-point problem.

Ratio Test for Concentrations.

Consider a single receptor that is empty/occupied for a series of times 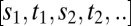; then the probability for observing the corresponding transitions is

where k is the on rate and ν is the off rate and the string of events is cut off by the current time t. Because we are interested in the long time limit, we do not consider the initial state and assume t falls just after one of the 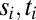. With only one species of ligand, the Wald sequential probability ratio test (SPRT) takes the ratio of Eq. 2, evaluated for the two concentrations under consideration. Then the factors 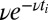cancel because the dissociation events do not distinguish between the hypotheses; the off rates are identical. Setting 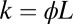for the two ligand concentrations 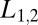, one finds

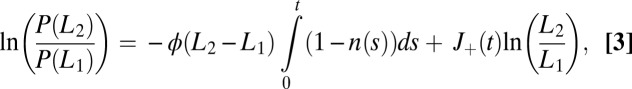where 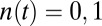is the receptor occupancy at time t and 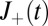is the number of 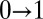transitions up to t.

For times much longer than the typical binding/unbinding times, we expect that the log-likelihood ratio is well approximated by Gaussian diffusion with drift. In SI Appendix, we detail the calculation of the receptor occupancy statistics that allows us to obtain the mean and the diffusivity for the log-likelihood. The expression for the drift reads

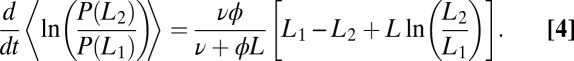The concentration L corresponds to the real process generating the data, which can possibly differ from the concentrations assumed in computing the probability ratio, Eq. 3. Note that the drift, Eq. 4, is defined as the rate of information production since the left-hand side (for data generated by one of the two models) is the rate of increase of the Kullback–Leibler relative entropy between the two distributions to be discriminated, which controls the error in hypotheses discrimination (Chernoff–Stein lemma; see, e.g., p. 383 in ref. 23).

It is important to consider the behavior of the average drift, Eq. 4, when the data presented to the ratio test, represented by L, do not correspond to either of the two ligand concentrations, 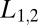assumed in constructing the ratio. For 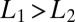the drift is a monotone decreasing function of L. Thus, if 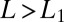or 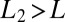, i.e., the data are easier to discriminate than the model assumes, the average drift will move the probability ratio more rapidly toward the decision thresholds. (The analogous remarks hold if 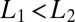.) More formally, if one desires to distinguish two states of concentration that can lie above or below a band around 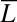, then the strategy that ensures that the most difficult case is done as well as possible (Maxi-Min strategy in game theory) would be to chose 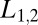in Eq. 4, as the concentrations defining the excluded band.

The diffusion approximation to the SPRT log-likelihood maps the decision process into the first passage time for two adsorbing boundaries and permits the analytic calculation of the decision time in terms of the imposed error rates (SI Appendix). The diffusion approximation works well provided the decision is based on several binding/unbinding events, as shown in Fig. 1. An important consequence of the analytical formula that we derive in SI Appendix is that the average decision time behaves as 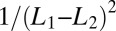for small differences between the two levels to be discriminated. It follows that the discrimination of a difference requires times of the order of 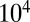(in units set by the timescale of the elementary events) (Fig. 1).

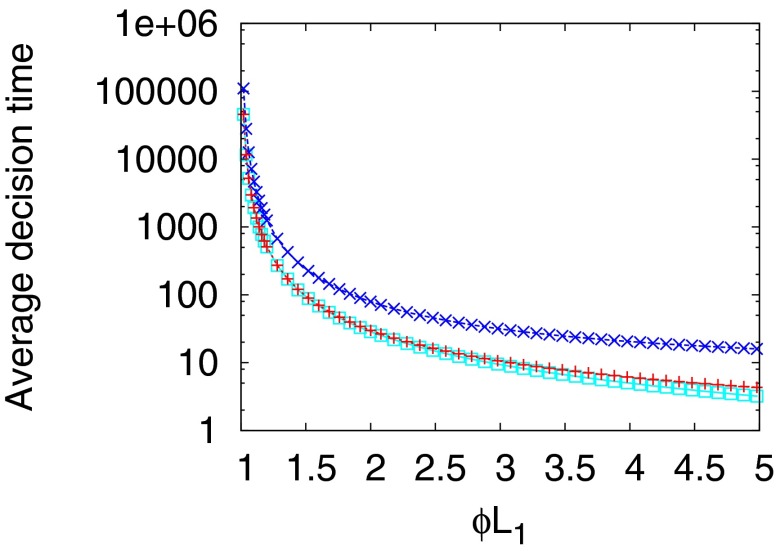
Fig. 1.

Average decision time for the Wald SPRT (red +) and its diffusion analytical approximation (aqua squares) derived in SI Appendix. The model parameters are 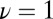, , 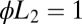with variable 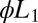on the abscissas. The data for discrimination are sampled with an on rate 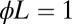. Precisions (false positive and false negative fractions) are 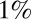. The blue Xs are the times that would be required by standard maximum-likelihood decisions, using a fixed sample size, the length of which is chosen to ensure the same 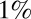precision (see SI Appendix for details). Note that Wald’s SPRT is more than twofold faster than standard maximum likelihood even in the asymptotic regime of small .

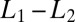The scaling of the inverse decision time with the square of the concentration difference is just a restatement of the law of large numbers and was first used in chemo-sensory context by Berg and Purcell (24) and refined as a maximum-likelihood calculation in ref. 25. The question being addressed in these papers is: How accurately can the concentration be measured from binding events occurring over a prescribed length of time? The SPRT asks a different question and although the scaling with concentration is the same, the average decision time must be faster and Fig. 1 shows a speedup by two to three times for the same error rate. Although the maximum-likelihood calculation is of course a valid bound, if one thinks mechanistically about a gene network, it is more likely that a “decision” is made when sufficient information accrues, rather than after a prescribed averaging time encoded in the genome. Note also that the distribution of completion times for a gene network, such as one would compute by Laplace transforming the master equation, is logically distinct from the SPRT that gives the optimal bound for the average decision time for any algorithm.

Ratio Test for Mixtures.

Consider a situation where a ligand with off rate 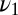is presented to the receptor alone or mixed with a second ligand with off rate 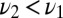. We assume the on rates per molecule are the same and the total concentration is invariant so now only the off rates survive when the ratio of Eq. 2 is formed. The analog to Eq. 3 is constructed by taking the ratio of the probability per time for a jump off the receptor under the mixture assumption, 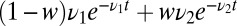, to the same quantity with 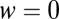, which is the probability density in the pure ensemble,

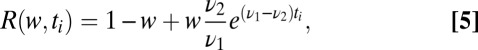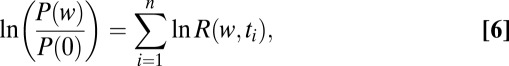where 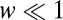is the fraction of the second ligand in the mixture, 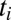are the binding times, and the sum on n is constrained by the total time t. If the ligand is bound at the current time t, the last term in the sum is slightly different as it does not contain the factor 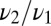; we neglect here this minor correction to simplify notation (see SI Appendix for more details). Note that the optimal function to discriminate between the two hypotheses, pure vs. mixture, contains three parameters characterizing the data: w, .

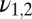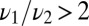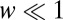The immune system presents a typical example of the type of discrimination task we are studying. Thus, one interesting limit is and ; there are a few agonists that bind to the T-cell receptors for more than twice as long as self. Then the leading terms in both the average and the variance of Eq. 5 (and thus the decision time) are nonanalytic in the admixture and scale as 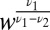. To be explicit, the sum over the independently sampled 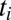in Eq. 6 converges to the integral of ln(R) in Eq. 5 over either the pure 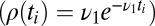or the mixture 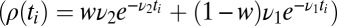distributions. The leading, and singular term for small w can be derived explicitly by changing variables in the integral average over the distributions and agrees with the exact hypergeometric function in SI Appendix, Eqs. 24 and 25,

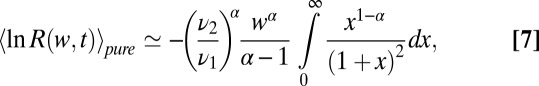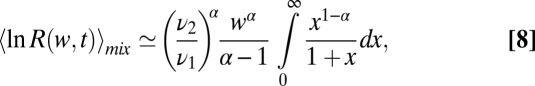where 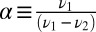and 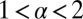. Numerically Eqs. 7 and 8 are 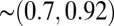times the exact values for 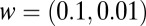, respectively, and corrections scale as 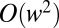. For 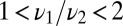all quantities scale as 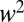and Eqs. 7 and 8 do not apply.

The average decision time is shown in SI Appendix to be 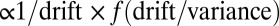, where f is a function computed explicitly and drift and variance refer to the log-likelihood of ln(R) in Eq. 5. The formula is derived using the diffusion approximation, which is justified as decision times are very long in the limit 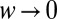. Because the average and the variance of ln(R) in Eq. 5 have the same scaling in the limit of small w, we conclude that the decision time behaves as 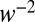or 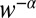, depending on the ratio .

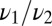The fractional power of w in the decision time for 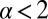can be derived in elementary terms by posing a suitable statistical test. Given a total of N samples, define a cutoff time T such that 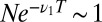; i.e., we expect to see only one event longer than T in the pure ensemble. Then the minority constituent of the mixture is visible in the tail of the distribution if the expected number of LONG events for the mixture, 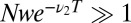. Eliminating T from the two equations gives 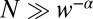, which agrees with the exact calculation. It is obviously easier to detect a minority constituent with a longer rather than shorter off time than that of the host.

When 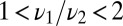, we can estimate how the decision time varies with w by comparing the difference in mean receptor occupancy times in the pure and mixed ensembles and comparing with the standard deviation (SD). That is, 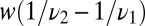exceeds the variance, 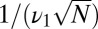, provided 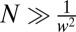. This agrees with the previous estimate when 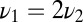and is less stringent, i.e., allows smaller N, when .

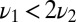Now in analogy with the discussion of Eq. 4 when the data L differ from the concentrations 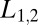assumed in the model, we inquire how the ratio test for mixtures performs when the off rate for the majority component of the data 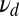is larger than the analogous parameter, 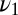, in Eq. 5. This should make it easier to detect when the minority species with a smaller off rate 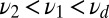is present. However, for large enough 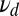the ratio test will classify the mixture data as pure (Fig. 2). The long binding events correctly favor the mixture, but the excess of short events contributes a negative drift to 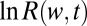that eventually overwhelms the positive drift from the long events (SI Appendix, Fig. S4). To fix this problem we need to include a realistic formulation of the pure system, namely of the fact that it might be composed of several types of ligands and that its exact composition is generally unknown.

Fig. 2.

The ratio test can fail when the data presented do not conform to the model. The average of the log-likelihood ratio as defined in Eqs. 5 and 6 is plotted vs. the off rate of the majority component in the data, 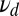. The model has 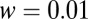, , 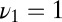and 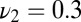. The upper curve (crosses) refers to mixture data with the same w and off rates 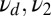whereas the lower one (squares) refers to data generated entirely with the off rate 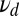. The upper curve is positive for 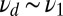, but ultimately becomes negative, implying a failure to detect the mixture.

Assume the pure system consists of a mixture of M species with off rates 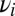and unknown weights 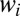that sum to one. Then the probability of observing a string of times 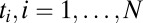is computed from the probability of the times conditioned on the weights followed by an integral over the 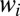with a prior we take as flat,

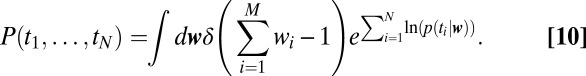For large N the integral over 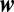can be evaluated by a saddle point. The sum over the 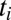in the saddle equation for the 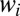should self-average and can be replaced by the time ensemble average. It is easy to check that the saddle equation for 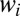is always solved by the 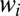used to generate the data if the 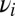of data and model are the same; otherwise the solution is nontrivial. The 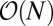term from the saddle has calculable 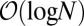corrections from fluctuations around the saddle (SI Appendix). The choice of prior, provided it is smooth and nonzero around the saddle, contributes only a constant. The same calculation can be done for the mixture data, with of course an independent integral over the relevant weights and a new saddle point (SI Appendix).

Thus, the optimal decision method to distinguish the admixture of a minority of long-lifetime species in a soup of shorter residence times implicitly determines the composition of the soup. This would seem to make an analog biochemical calculation insurmountable. However, the existence of a saddle point approximation does imply that the optimal algorithm can estimate the ratio by two terms of the form in Eq. 9 with distinct and unknown values of 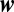. We develop below an approximation to Eq. 9 that can be easily optimized and biochemically implemented. Thus, optimizing the parameters in a biochemical model that locates the time change point will implicitly incorporate information about the saddle approximation, without requiring the intermediate solution of Eq. 10. The existence of a saddle approximation suggests that optimization of the complete problem could be simple, and indeed it is, as shown below.

Change Point for Mixtures.

We now shift from the problem of distinguishing two states presented at a defined time to finding the time when the state changes in a defined way. In the previous case where the statistics of the log probability ratio were Gaussian and easy to calculate with no further approximations, the change-point problem is more overtly dynamic.

Shiryaev (5, 6) considered the process 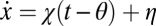, where χ is the Heaviside step function, 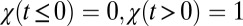, η is δ-correlated noise, and the change-point θ has a Poisson distribution defined by its rate. The task is to define an algorithm to determine θ from a stream of data 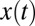that minimizes a linear combination of the false positive rate or precision and the decision time [average of 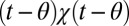]. We assume θ is Poisson distributed, so ultimately the change happens, but one can equally formulate a stationary problem with a limit on the false positive rate per time (7).

As before the optimal solution computes the probability ratio that the change at time θ happens before the current time, normalized by the probability it has not yet happened, with all probabilities conditioned on the history of 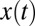; symbolically, 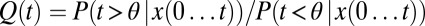. A decision is made when , where H is a numerical parameter related to the assumed error function. When x derives from white noise, Q can be computed incrementally in time with no auxiliary memory, and explicit expressions are given in SI Appendix for several cases.

We can again time slice the continuous-time recursion for Q after each off event n as was done in Eqs. 5 and 6. The discrete iteration reads in the simplest case of only two off rates (see SI Appendix for details),

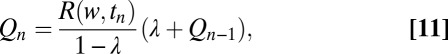where is the conditional probability ratio, just defined, after the series of the unbinding events, 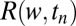is the probability ratio defined in Eq. 5, and λ is the probability per iteration for the change of statistics; i.e., 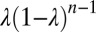is the probability that the change point will occur for the nth binding event. To bridge the reduction of Eq. 11 to an analog computation and deal with extensions, e.g., Eqs. 9 and 10, it is expedient to introduce the following iterative model for the mixture change-point problem that can be solved analytically and is derived by taking the log of Eq. 11:

Its relation to Eq. 11 is apparent if we set 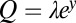, approximate 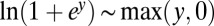and 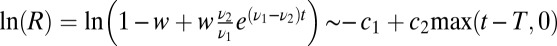, and finally rescale both 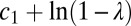and y to eliminate 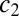. The true probability ratio directly translates to the error rate and the decision threshold, H, for 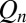in Eq. 11 is largely independent of the data. However, because of rescalings, the threshold for Eq. 12 is contingent on the data, as are 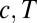. The entire parameter space of the model is thus 3D 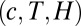. The piecewise linear approximation to Eq. 5 is accurate in mean square to 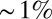for all .

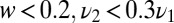Eq. 12 makes it intuitive that the optimal decision algorithm takes either a small downward step of 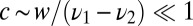with probability 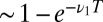or an occasional 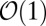step upward. The floor on y encodes the prior expectation of a fixed probability per time for a change in data to occur. Clearly an accurate decision based on the criterion 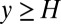requires a positive drift 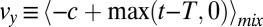in the mixture ensemble and a near zero or negative drift 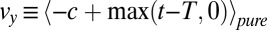in the pure ensemble to avoid reaching the threshold before the switch of the statistics, i.e., typically 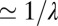iterations.

In the pure ensemble, y has a stationary distribution that can be calculated along with the rate per iteration, γ, that y hits H. The drift-diffusion approximation that we used for the probability ratio accumulated from a fixed time does not work for Eq. 12 but we can use the so-called Poisson clumping heuristics (26) to obtain the corresponding error rate (see SI Appendix for details). We work in the limit 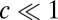and lump all instances of 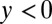into ,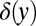

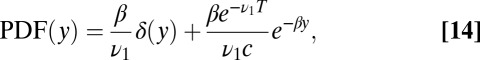The parameter γ is the intrinsic characterization of the false positive rate, i.e., per iteration of Eq. 12. The false positive rate per trial used for Eq. 11 is recovered by multiplying γ by the expected waiting time, i.e., the average of θ or 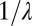. Using Eq. 15, the threshold H can be calculated from the false positive rate. To find the average decision time one can then initialize y by sampling from Eq. 14 to generate binding times from the mixture ensemble and iterate until hitting H.

We can now quantify the errors inherent in the Eq. 12 model by using the natural error metric of the average decision time at a fixed false positive rate. If we take data generated with the same parameters 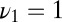and as in Fig. 2, 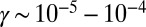, and , then Eqs. 11 and 12 give decision times within 10% (Fig. 3). In fact, simulating Eq. 12 over a grid of 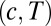parameters shows a limited band where the drift velocity, 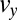, has the appropriate sign for both the pure and the mixed data. The shape of the decision-time landscape in Fig. 4 shows that the optimum is easy to reach by any gradient-descent evolution. This observation is relevant for the biochemical implementation of Eq. 12 that is described below.

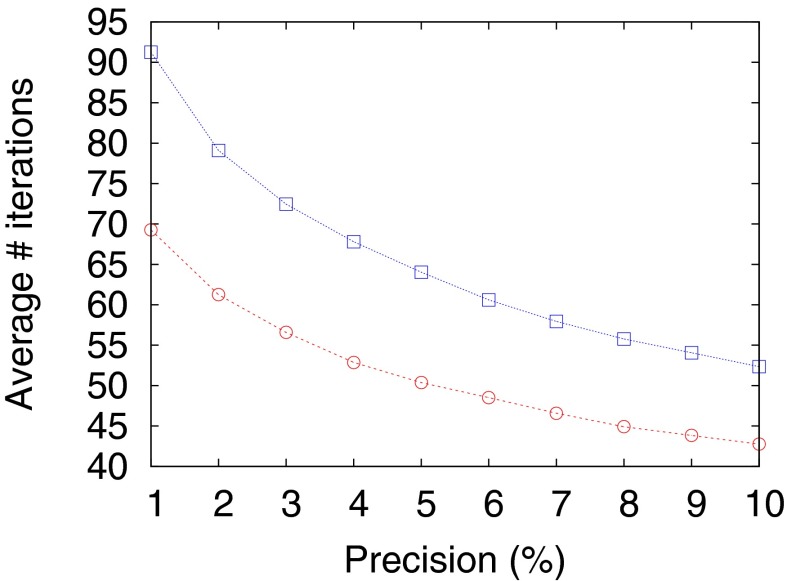
Fig. 3.

Decision time for the optimal strategy, Eq. 11 (circles), compared with the three-parameter model, Eq. 12 (squares), for a range of precisions. (In addition, Eq. 11 uses the actual composition of the data.) The mixture is generated with three frequencies 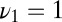, , 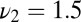and 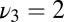and its composition is random. The agonist species with 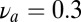, is added to the mixture at a Poisson-distributed time with mean 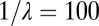in iteration units.

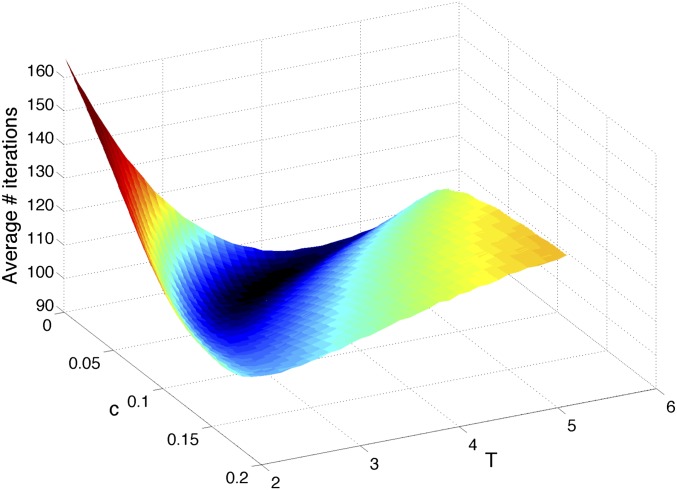
Fig. 4.

The landscape of the average number of iterations required for decision vs. 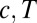for the Eq. 12 model. The precision of the decisions is 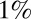and averages are obtained over 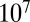realizations. The parabolic shape makes parameters easy to optimize by evolutionary gradient descent.

When multiple frequencies are included in the pure ensemble, the situation is as follows. If the weights of the various frequencies composing the data are known to the model, then Eq. 11 still applies with the probability ratio Eq. 5 replaced by

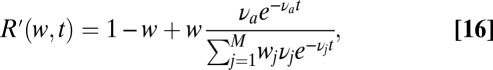where the denominator coincides with the likelihood previously defined in Eq. 9 and 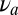is the frequency of the new molecular species (antigen) added into the mixture at a random time.

If the weights 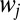in Eq. 16 are not a priori known, then Bayesian integrals as in Eq. 10 are required. When a new binding event 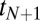is added to the sum in the exponential of the integrand in Eq. 10, the value of the resulting integral 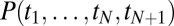is not obviously related to and 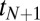(except in the limit of large N when a saddle approximation is justified) (SI Appendix). Determining the Bayesian optimal decision becomes then quite involved even from a purely computational perspective, let alone implementing it biochemically.

However, as shown in Fig. 3, the three-parameter Eq. 12 model cuts this Gordian knot, ensuring sensible speed and accuracy. Comparing its performance to that of Eq. 11 for a random ensemble of mixtures, we see indeed that speed is slower by 20–30% only, over a broad range of precisions. It is worth remarking that in Eq. 16 we are using the information on the weights in the mixture for each realization of the data. We have checked on a few realizations that discarding this information and calculating the optimal decision with Bayesian integrals as in Eq. 10 yields, as expected, a decision-time intermediate between Eq. 11 and Eq. 12.

The histogram of decision times for both the ratio test and the change-point problems is contained in SI Appendix, Fig. S2. Both distributions have an exponential tail that is 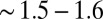times narrower than a Poisson distribution, when normalized by the mean time.

Biochemical Networks to Implement the Ratio Test for Concentrations.

We now show that the calculation of the log-likelihood ratio Eq. 3 can be realized with standard biochemical reactions. This is particularly simple because we just have to simulate by analog means an initial value problem: The ratio test presumes an origin of time, i.e., when the receptor is first exposed to ligands of either concentration.

A simple procedure that gives a good approximation is to have two chemical species 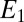and 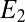. We assume 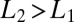(the opposite case is treated similarly). The first enzyme decays exponentially when the receptor is unbound as 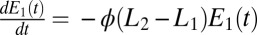whereas the second decays when the receptor is bound as 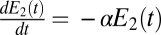, where α is a constant. The two species represent, respectively, the exponential of the first and the second term (with the sign inverted) in the expression Eq. 3. The 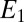equation is exact, whereas the one for 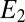is just an approximation because the decay in Eq. 3 is proportional to the binding time and not fixed.

As for the choice for the constant α, when many binding events accumulate, the average binding time will be 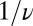. If we want to reproduce at least on average the correct result that upon binding there should be a factor 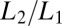in the likelihood ratio, then we should choose 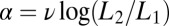. Validity of the choice is confirmed numerically in SI Appendix.

The next biochemical layer computes 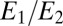, which approximates the likelihood ratio and switches when it reaches an appropriate threshold. A biochemical switch that produces such an output is the Goldbeter–Koshland module (27). The two species 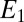and 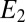act enzymatically in opposite directions on the conversion between two forms A and 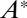. The detailed scheme is

The association/dissociation rates in the bidirectional reactions are denote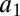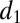d , and 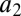, , 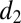respectively. The two subsequent dissociation reactions proceed at rates 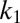and 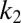. In the limit when the total amount of the two enzymes 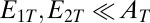, the steady-state normalized concentrations 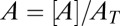and 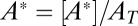depend on the ratio 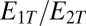only,

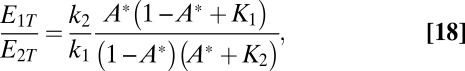where 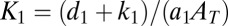and 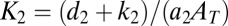. Inspection of [18] shows that for 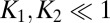, a sharp switch occurs around 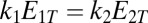and the output 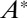features a jump from values very small to close to unity. This is the regime that is of interest to us. We can then use two Goldbeter–Koshland modules with rates 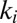adjusted so that they switch to signal a decision at the high or low threshold values of the probability (enzyme) ratio. The response time of the Goldbeter–Koshland (GK) system does slow down at the transition point, but this is not a serious issue for us, because either the forward or the backward rate is monotone increasing and thus moves through the transition region, and the decision becomes rapid. Our simulations of course include proper dynamics at the transition point in the GK system.

Results of numerical simulations for the previous model are shown in Fig. 5. The main source of error is due to the fact that 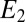decays at an average rate for the whole period of measurement rather than separately and discretely registering each binding as in Eq. 3. The quality of the approximation can therefore be improved by assuming adaptation mechanisms for the receptors. In refs. 12 and 13 it was for example assumed that receptor inactivation is the most rapid time. We have verified that fast adaptation permits the system to approach the optimal behavior when measuring on rates but obviously sacrifices all sensitivity for off rates and thus is not a strategy we could use to detect a small admixture of agonist. It is also not clear for all classes of receptors that the requisite speed is molecularly achievable. We thus present data without any receptor adaptation to show that results are still very good and deviate by a factor two times that of optimal over a broad range of precisions.

Fig. 5.

The behavior of the biochemical Goldbeter–Koshland (GK) module for concentration discrimination (with a constant decay rate for 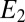) compared with the optimal solution. The two ensembles that are compared have vs. 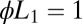(the unbinding rate 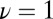). For the leftmost points in the graphs 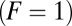, the ratio of the kinetic parameters 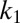and 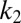appearing in Eq. 18 was fixed to have the critical values (where the GK module switches states and “decides”) 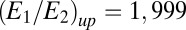and , which ensure 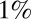false positive and false negative errors. For the other points in the graphs, the upper/lower critical value was divided/multiplied by the factor F shown on the x axis. (Left) The classification error for data with 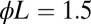(upper curve) and (lower curve) vs. F. (Right) The average decision times for the GK module (two upper curves) compared with the optimal solutions (two lower curves) vs. F. The thresholds for the Wald optimal solutions were adjusted to give the same error rate as the GK module with corresponding data. The slower/faster curves for each algorithm refer to data with 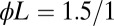, respectively; e.g., red squares show GK presented with .

An alternative to regulated decay that computes an exponential is autophosphorylation, analogous to simple noncooperative feedback of a transcriptional activator on itself. If receptors that dimerize and transactivate were able to rapidly exchange partners, then the number of activated receptors would grow exponentially. We are not aware whether this possibility has been considered experimentally.

Biochemical Networks to Detect a Mixture Change Point.

A true ratio test, in the sense of the previous section, would occur in a cell if there was an initial signal to start the process and a second system that did the comparison as an initial value problem. More likely is a single receptor that continuously monitors the environment and needs to detect when the composition changes, i.e., the Shiryaev problem.

The near optimal computation of a change point with the model of Eq. 12 simplifies its realization in biochemical terms. Consider a typical system with slow on, fast off dynamics; e.g., the ligand-bound receptor complex has a sequence of phosphorylation states, 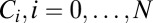. There is a forward rate ω for , a ligand unbinding rate ν, and a rapid reversion of any 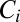to the unphosphorylated receptor when the ligand falls off. Only 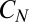can activate downstream events. If 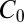is initialized at 1, then 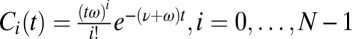and .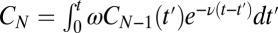

If instead we ask for the probability of 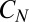conditioned on the receptor being continuously bound for a time span t, then we can remove the unbinding event ν from the rate equations and find

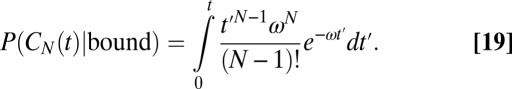For large t, Eq. 19 tends to 1 as it should, and it is 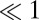for 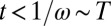. To reproduce 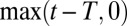in Eq. 12 it is then sufficient to let 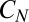act enzymatically on some substrate present in excess. The small constitutive negative drift in Eq. 12 could be replicated by an enzymatic degradation in a saturated regime (see ref. 28 for a biological instance of such a mechanism). In summary, the proposed chemical equivalent to Eq. 12 in differential form reads

The positivity of y in Eq. 12 is naturally encoded by a concentration, z. The decision is made when z hits some value H and any scale factor multiplying can be adsorbed into H. Provided 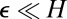, precisely how the degradation saturates does not matter, because it influences the distribution of z only when it is small. (In the derivation of Eqs. 14 and 15 we observed that a δ-function approximation for the weight around 0 was adequate in a continuum limit.) A more serious issue is molecular noise in the phosphorylation cascade leading to 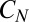. However, for N-Poisson events in series the SD in the sum scales as , so the time to activate 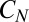becomes sharper with N. To simulate Eq. 20, one would sample the binding time 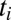to the receptor and then compare it with the (random) time for transitioning from state 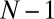to N, which is distributed according to the time derivative of Eq. 19. The end result for 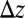is manifestly a smoothed version of .

Biochemical Networks to Detect a Concentration Change Point.

The optimal decision algorithm to detect a change in concentration, e.g., from 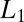to 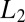, in a stream of data is governed by the same Eq. 11 derived previously but the probability ratio 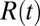in Eq. 5 is replaced by 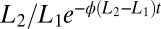. This form simplifies the equation corresponding to Eq. 12, which becomes

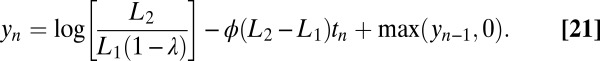Here, we have used again the approximation but the rest is now exact. Eq. 21 can be simulated biochemically by the same scheme as above, i.e., Eq. 20.

Pooling the Output of Many Receptors.

Having multiple receptors is clearly a bonus as it allows the cell to sample the ligand-binding statistics more rapidly and accelerates the decision process. Processing of information from receptor occupancy and calculating the optimal decision can be complicated, however, by coupling among receptors. This occurs when ligand sequestration effects are important, so that the likelihood of binding histories involves the configuration of the entire pool of receptors. Although these situations are possible, we show in Fig. 6 for the case of discriminating concentrations that a few-fold excess of ligands over the corresponding number of receptors is already sufficient to make an effective description with uncoupled receptors quite accurate.

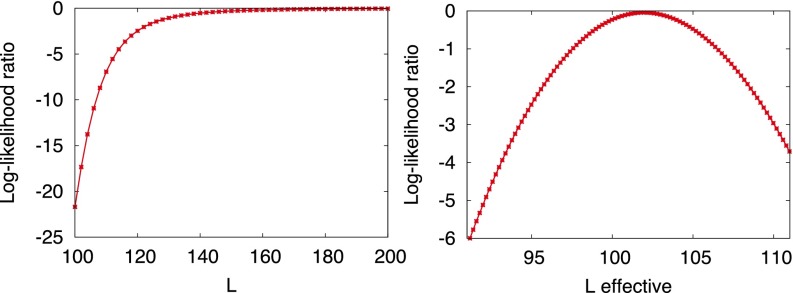
Fig. 6.

The comparison between the full dynamics with receptors coupled and the dynamics with decoupled receptors and a fixed effective number 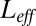of free ligands. For both panels the number of receptors is 100, 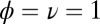. (Left) The log-likelihood ratio between the actual (coupled) model generating the data and the effective model vs. the total number of ligands L. ( 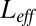is optimized separately for each L.) The ratio is computed in the asymptotic regime at time 10. (Right) The behavior of the log-likelihood ratio vs. the effective number of free ligands around its maximum. The total number L of ligands is 200.

Data are generated by Gillespie simulations of the binding/unbinding process for 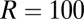receptors and a variable number of ligands L, Fig. 6. The number of nonoccupied receptors is denoted by . We compare the log-likelihood ratio between the actual model generating the data [that depends on the instantaneous value of free ligands 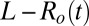] and an effective model where free ligands are fixed at 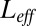. Note that receptors are uncoupled for the latter model. Proceeding as for Eq. 3, we obtain for the log-likelihood ratio of a trajectory extending up to time t,

where 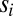are the times when binding events occur and their total number up to time t is 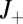. The graph of the log-likelihood ratio (for the best choice of 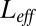at any given L) vs. the number of ligands L clearly shows that an effective description is accurate even for a twofold excess of ligands. Furthermore, the graph of the log-likelihoods vs. 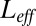shows simple concave curves, the maximum of which is easy to find. Note that the best 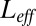corresponding to the maximum is, as expected, close to the average number of free ligands 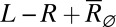, where 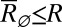is the solution to the quadratic stationary equation .

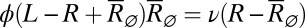The biochemical models that we have developed above for a single receptor immediately generalize to many receptors if we decouple the receptors by using a fixed . For the discrimination of concentrations, it is for example sufficient that unbound/bound receptors additively contribute to the instantaneous decay rate of the two enzymes 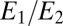. For the detection of a change in composition, the sequence of successive phosphorylations takes place on each individual receptor and then the end-point, 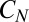, activities for all receptors are pooled to determine downstream events. Because receptors are independent for effective models, the rate of information acquisition is proportional to their number R and the average decision time will therefore reduce as .

Discussion

The wealth of genetic and biochemical information about signaling pathways contrasts with the paucity of data on pathway dynamics. At the population level most data are interpreted around the paradigm that a ligand elicits a proportional response. The widespread realization that the same pathway is used in many different contexts, such as NFκB in inflammation and TGFβ in development, cancer, and immunology, does raise the question of whether pathways are more than passive transmission lines and in fact “compute” or act as dynamically reprogrammable filters (29). Posttranscriptional modifications of proteins are a natural substrate in which to implement analog chemical computation, and Jacob’s old adage of bricolage suggests that signal transduction in cells might exploit this freedom to temporarily process signals. The canonical receptor systems as well as ion channels (30) possess a rich repertoire of interactions and modifications that could implement computation (31). One should note also a distinction between embryonic signaling where both the emitter and the receiver can be jointly tuned by evolution to process information and true environmental sensing where the signal has a more autonomous origin. Thus, in development, and even yeast mating, extracellular ligand processing may be as important as receptor interactions and posttranslational modifications in regulating pathway behavior (32, 33).

In the hope of stimulating experiments, and to explore the potential of analog biochemical computation in a concrete and nontrivial context, we have posed the problem of optimal decision theory for cells, in the context of detecting a change in concentration or composition. The problem is inherently dynamic, in that a stream of data is presented and a decision has to be made on the basis of the entire history. Thus, it is noteworthy, although simple to show, that optimal performance can be realized by accumulating a single variable in time. In a gene network context, it would seem that decisions on the fly are much more natural than the alternative of averaging for a predefined time and then deciding, which has become the calculational default.

We have reduced the biochemical complexity of real systems to a ligand-binding step governed by equilibrium thermodynamics followed by downstream enzymology. More complexity is unnecessary because we have shown that ubiquitous small enzymatic systems suffice for near optimal performance. For the Wald problem, the ratio of two quantities, probabilities in our case, is naturally computed by the push–pull mechanism of Goldbeter and Koshland (27). The probabilities themselves are the exponential of a function of the input signal. Exponentials can be simulated with regulated decay and more speculatively by catalytic amplification. The most common amplification cascade as exemplified by phototransduction does not compute an exponential. What we require is the positive feedback of a transcriptional activator on itself with signal-dependent modulation, so that the factor grows exponentially in time. Using receptors that dimerize to signal, the same function could be realized if the dimers exchanged partners so that the fraction of active receptors grows exponentially (34).

The computation of change points can naturally be implemented with any system that encodes a time lag, such as a phosphorylation cascade. The computation is easiest for the log probability ratio, because the decision is one sided: When the indicator is large, decide; otherwise, continue. Thus, we do not have to take the ratio of two quantities and threshold separately on very small or very large values. A phosphorylation cascade is indeed observed in early T-cell activation yet the kinetic proofreading scheme is supplemented by the negative feedback by the phosphatase SH2 domain-containing tyrosine phosphatase (SHP-1) (35, 36). The functional reasons for this feedback are interesting.

T cells have to discriminate agonists from a far larger concentration of self antigens on the basis of only a three- to fivefold difference in off rates and plausibly do so quickly. This is analogous to our formulation of the mixture discrimination problem. However, in the immune system the total number of ligands can fluctuate, whereas we kept it fixed. Comparing the two schemes, the role of the negative feedback by SHP-1 appears then to buffer variations in the total concentration of ligands (36). The T cell also has to respond when a few agonists bind, whereas we have posed the mixture change-point problem with concentrations, so many receptors can be bound by agonist and yet not contribute to the decision. The optimal discrimination time T in Eq. 12 may be large enough to exclude most agonist binding events (recall in this context the heuristic argument for the nonanalytic decision time 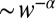after Eq. 8).

We have focused on the decision process for a single receptor and it may be objected that cells are never challenged by the bounds we have placed on the decision time because they can always use many receptors in parallel and decide after a few on/off times. Even in this limit performance is improved by setting the receptor kinetic parameters as we have derived. Furthermore, we noted throughout the paper that decision times can easily become very long, e.g., elementary events for a 1% discrimination in concentration. The cell may optimize subsets of receptors for various tasks by tuning cofactors or controlling access, and thus the number of receptors available in any one context may be less than the whole. Sheer increase of the number of receptors might therefore not be sufficient and evolving decision strategies as discussed here would be relevant to increase fitness.

How can one determine whether a cell is implementing a decision on the fly as opposed to computing for a fixed time? First, one would expect the decision time to scale with the strength of the signal. The high signal–short time limit would furnish a bound on the biochemical cascades induced by the receptor. Then for lower stimulation, does the decision time increase while the error rate remains fixed or does the opposite occur? Measuring a fractional power of w for the scaling of the decision time for the mixture change point when 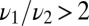would be a good indication of optimality. Comparing the actual decision time with theory would be difficult due to uncertainties surrounding cellular parameters and variation among cells. The histogram of decision times is not Poisson and if well fitted by the data would suggest an optimal decision. More loosely, if one measured the distribution of several parameters that plausibly impact the signaling cascade and found their distribution individually is much broader than the distribution of decision times, it would be circumstantial evidence that the decision time is acting as a constraint on cell parameters.

Another class of tests uses microfluidics to flip the environment between the two states being compared. It would be possible to find conditions where a probability ratio test yielded a decision only after an immense time. The ability to control the environment dynamics and predict the consequences would be a strong check on the theory, but the details are very dependent on the experimental setup.

These considerations all apply to independent cells. Its an interesting and related question as to how a collection of interacting cells subject to a common external signal makes a rapid decision to respond, but as a collective with 100% participation. It is not obvious that the most rapid individual response followed by signaling to neighbors outperforms a more deliberate response at the cellular level with lower variance. Cell sorting is another response to signals that can contribute to the optimization problem. Thus, bounds on dynamics through statistical optimization may be a richer field of study in the cellular context than the physical limits to performance.