Significance
Two models compete to explain the way proteins transit through the Golgi, a cellular organelle consisting of stacked membrane-bound compartments (cisternae) and responsible for protein maturation and sorting. The cisternal maturation model proposes that cisternae created de novo move through the stack, carrying their content with them. The vesicular transport model views cisternae as static structures between which proteins are exchanged by vesicular transport. We have developed a transport model that can quantify the importance of intercisternal exchange by analyzing the spatiotemporal evolution of a protein distribution within the Golgi. Intercisternal exchange is confirmed both for small membrane proteins and large protein complexes. This suggests the involvement of membrane carriers much larger than typical protein-coated vesicles.
Keywords: Golgi apparatus, secretory pathway, quantitative transport model, resident golgi enzymes, convection-diffusion
Abstract
The mechanisms controlling the transport of proteins through the Golgi stack of mammalian and plant cells is the subject of intense debate, with two models, cisternal progression and intercisternal exchange, emerging as major contenders. A variety of transport experiments have claimed support for each of these models. We reevaluate these experiments using a single quantitative coarse-grained framework of intra-Golgi transport that accounts for both transport models and their many variants. Our analysis makes a definitive case for the existence of intercisternal exchange both for small membrane proteins and large protein complexes––this implies that membrane structures larger than the typical protein-coated vesicles must be involved in transport. Notwithstanding, we find that current observations on protein transport cannot rule out cisternal progression as contributing significantly to the transport process. To discriminate between the different models of intra-Golgi transport, we suggest experiments and an analysis based on our extended theoretical framework that compare the dynamics of transiting and resident proteins.
The Golgi apparatus, a complex cellular organelle responsible for lipid and protein maturation and sorting, has attracted a great deal of attention, with many conflicting viewpoints regarding its mechanisms of transport. The Golgi of plant and animal cells consists of a stack of 5–20 cisternae (1), possibly interconnected by membrane tubules (2), which exchange material by vesicle budding and fusion (3, 4) (Fig. 1). Each cisterna has a distinct chemical identity, allowing progressive protein maturation from the cis to the trans face (5).
Fig. 1.
Sketch of the Golgi apparatus as a polarized stack of connected cisternae exchanging material. (A) Proteins synthesized in the ER go through the ER-Golgi intermediate compartment (ERGIC) before entering the Golgi through its cis face. After biochemical maturation and sorting, they exit the Golgi through the trans face to join the trans-Golgi network (TGN). (B) Relevant transport processes, including cisternal progression (translation), diffusion through connecting membrane tubules, vesicular transport, and exit. (C) Spatiotemporal evolution of an initially narrow protein distribution (as produced by a pulse of secretion from the ER); pure convection produces a uniform translation of the peak (dashed line), diffusion broadens the peak, and exit exponentially decreases the protein content.
There is a long-standing argument about the way proteins are transported through the Golgi, an issue intimately tied to the structure and dynamics of the organelle itself. The Golgi could be a rather static structure, in which cisternae keep constant positions and identities, and exchange proteins by vesicular transport. Alternatively, cisternae could progress from the cis end to the trans end without exchanging their cargo (6). Biochemical maturation of individual cisterna is known to occur in yeast (Saccharomyces cerevisiae) Golgi, which is not stacked but made of dispersed cisternae (7, 8). The cisternal progression model posits that this maturation translates into a physical progression of the cisternae (and their content) along the stack. It is supported by the observation that large molecules such as procollagen aggregates, presumably unable to enter conventional transport vesicles, nonetheless progress through the stack, suggesting that cisternae are created at the cis face and destroyed at the trans face (9). This picture was recently challenged (10) by the observation that proteins do not exit the Golgi linearly with time (as a model purely based on cisternal progression would predict) but exponentially, as can be explained by intercisternal exchange. These are however two extreme models, and cisternal progression and intercisternal exchange could act concomitantly. This is clear even in the cisternal progression model, which requires that resident Golgi enzymes (which are found in particular location in the Golgi stack) undergo specific retrograde (vesicular) transport.
Existing quantitative models are often tailored to support (11) or disprove (10) the cisternal progression model, and their comparison with quantitative data involves a large number of fitting parameters (10).
However, the relevance of each mode of transport can only be identified by an unbiased quantitative model based on the general formalism of transport phenomena (12). We report here that all available quantitative data on a variety of cargo, including large procollagen aggregates, can be reproduced by a combination of (i) global protein translation from the cis- to the trans-Golgi, (ii) diffusive-like protein exchange between cisternae, and (iii) protein exit throughout the stack. As shown below, the diffusive component implies that intercisternal exchange is not restricted to small protein-coated vesicles, and involves large transport carriers. We rigorously establish that transport data based on tagging a single molecular species can be argued to be consistent with many different models of transport and therefore cannot provide an unequivocal picture of intra-Golgi transport. To reach this goal, we propose experimental strategies based on dynamical correlations between transiting and resident Golgi proteins. A useful virtue of our formalism is that it can include the influence of the local biochemical and physical environment within the different cisternae as an energy landscape through which proteins diffuse, and thus permits a description of transiting proteins and resident Golgi enzymes within the same mathematical framework.
Model
Transport Equations for Intercisternal Exchange.
Treating the Golgi stack as composed of distinct cisternae, we analyze protein transport along its axis of polarity (the cis–trans axis), for which the cisterna number n, varying between 1 (the cis-most) and N (the trans-most) plays the role of a discrete spatial coordinate. The distribution of a chemical species A within the Golgi may be characterized by its concentration 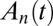 in cisterna n at time t. Intercisternal exchange is restricted to “jumps” between adjacent cisternae (with rates
in cisterna n at time t. Intercisternal exchange is restricted to “jumps” between adjacent cisternae (with rates 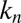 for
for 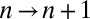 and
and 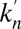 for
for 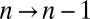 ; Fig. 1). We emphasize that the rates
; Fig. 1). We emphasize that the rates 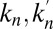 , and
, and  characterizing the coarse-grained dynamics may be used regardless of the microscopic details of the exchange process. For vesicular transport, they are the product of the rates of fission, translocation, and fusion of vesicles carrying A, and include the waiting time of A within a cisterna. They are not restricted to processes involving protein-coated vesicles, and may include transport through connecting membrane tubules and contributions from any fragment that detaches from one cisterna and fuses with a neighboring cisterna. These rates may depend on the local concentration
characterizing the coarse-grained dynamics may be used regardless of the microscopic details of the exchange process. For vesicular transport, they are the product of the rates of fission, translocation, and fusion of vesicles carrying A, and include the waiting time of A within a cisterna. They are not restricted to processes involving protein-coated vesicles, and may include transport through connecting membrane tubules and contributions from any fragment that detaches from one cisterna and fuses with a neighboring cisterna. These rates may depend on the local concentration 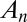 . A master equation (12) can be written for the concentration
. A master equation (12) can be written for the concentration 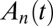 :
:
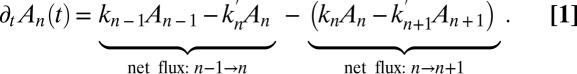 |
A straightforward generalization of the model could include transport between distant cisternae. This however does not bring new insight, nor does it improve the comparison with available experimental data on transiting proteins.
We will rewrite Eq. 1 in a continuous formalism, because this allows for a better description of cisternal progression. The coordinate n (the cisterna number) can be written as a continuous variable, and spatial variations are then written as a derivative:  , with distances normalized by the intercisternal distance (the connection between the discrete and continuous models is described in detail in SI Appendix). If the different exchange rates do not depend too drastically on position
, with distances normalized by the intercisternal distance (the connection between the discrete and continuous models is described in detail in SI Appendix). If the different exchange rates do not depend too drastically on position 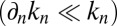 , Eq. 1 can be transformed into a Fokker-Planck equation (12). In this continuous description, intercisternal exchange amounts to an effective translation with velocity
, Eq. 1 can be transformed into a Fokker-Planck equation (12). In this continuous description, intercisternal exchange amounts to an effective translation with velocity 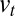 , combined with an effective diffusion with a diffusion constant
, combined with an effective diffusion with a diffusion constant 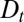 :
:
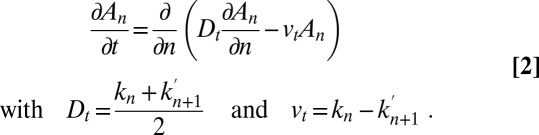 |
This illustrates that intercisternal exchange always yields an effective diffusion coefficient, even if all transport steps are anterograde  , as we discuss below.
, as we discuss below.
Including Cisternal Progression and External Fluxes.
Proteins may be transported toward the Golgi trans face by cisternal progression, defined as the process by which the entire content of a cisterna moves from position n to position  in the stack over a time
in the stack over a time 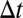 . The progression velocity is thus defined as
. The progression velocity is thus defined as 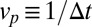 , and is the same for all cisternae. Furthermore, the species A may in principle be imported to or exported from any cisterna along the stack. These processes, which include direct recycling to the endoplasmic reticulum (ER), may be expressed as an external flux
, and is the same for all cisternae. Furthermore, the species A may in principle be imported to or exported from any cisterna along the stack. These processes, which include direct recycling to the endoplasmic reticulum (ER), may be expressed as an external flux 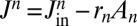 composed of an influx
composed of an influx 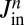 to cisterna n, that could come from outside the Golgi or from distant cisternae, and a rate of exit
to cisterna n, that could come from outside the Golgi or from distant cisternae, and a rate of exit 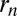 from cisterna n. Eq. 2 becomes
from cisterna n. Eq. 2 becomes
 |
The influx is not expected to contribute significantly to the dynamics of transiting proteins coming from the ER. It is ignored for now but is reintroduced in Results, where we derive the distribution of resident Golgi enzymes. Fluxes entering at the cis face and exiting from the trans face of the stack are included in the model as boundary fluxes (see below).
Eq. 3 illustrates three fundamental mechanisms governing the temporal evolution of a protein distribution within the Golgi: (i) protein exchange between neighboring cisternae introduces an effective diffusion of the concentration along the Golgi stack, characterized by a diffusion coefficient 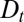 , (ii) directed protein transport from the cis- to the trans-Golgi leads to protein translation at a velocity
, (ii) directed protein transport from the cis- to the trans-Golgi leads to protein translation at a velocity 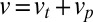 ; this accounts both for cisternal progression (at velocity
; this accounts both for cisternal progression (at velocity 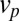 ) and for a bias for anterograde
) and for a bias for anterograde 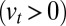 or retrograde
or retrograde 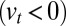 intercisternal exchange, and (iii) proteins may in principle exit from any Golgi cisterna to join other organelles (the ER or lysosomes) at a rate
intercisternal exchange, and (iii) proteins may in principle exit from any Golgi cisterna to join other organelles (the ER or lysosomes) at a rate  , which may be zero. Note that because the spatial coordinate is a dimensionless number, all three parameters have units of rates
, which may be zero. Note that because the spatial coordinate is a dimensionless number, all three parameters have units of rates 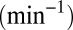 .
.
Because it does not depend on the microscopic processes responsible for transport, Eq. 3 constitutes the most rigorous quantification of an arbitrary transport process, and should be used as a first approach to characterize Golgi transport. The impact of the three main parameters on the distribution of proteins throughout the Golgi is best seen when analyzing the propagation of an initially localized protein distribution (pulsechase experiments, Fig. 1). The translation velocity displaces the concentration peak (linearly in time if v is constant), diffusion broadens the peak (its width increases as the square root of time if 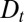 is constant), and protein exit decreases the total protein concentration (exponentially with time if r is constant). The various rates could vary for different proteins, possibly transported by different mechanisms, and should in particular be very different for transiting proteins and resident Golgi enzymes.
is constant), and protein exit decreases the total protein concentration (exponentially with time if r is constant). The various rates could vary for different proteins, possibly transported by different mechanisms, and should in particular be very different for transiting proteins and resident Golgi enzymes.
Cisternal progression only affects the translation velocity in Eq. 3, whereas anterograde intercisternal exchange affects both the velocity and the diffusion coefficient. Our formalism thus readily shows a fundamental qualitative difference between the two contending models. Within the cisternal progression model, the movement of transiting proteins may occur in the absence of intercisternal exchange, thus 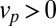 ,
, 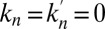 . This amounts to a perfect translation, without broadening, of a peak of concentration, i.e.,
. This amounts to a perfect translation, without broadening, of a peak of concentration, i.e., 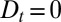 . Intercisternal exchange, on the other hand, necessarily involves some broadening, with an apparent diffusion coefficient directly related to the translation velocity (
. Intercisternal exchange, on the other hand, necessarily involves some broadening, with an apparent diffusion coefficient directly related to the translation velocity (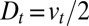 in the absence of retrograde transport, i.e., when
in the absence of retrograde transport, i.e., when 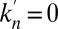 , and
, and 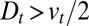 if
if  ). This immediately leads to a powerful conclusion: if the analysis of the pulse-chase data using Eq. 3 suggests that
). This immediately leads to a powerful conclusion: if the analysis of the pulse-chase data using Eq. 3 suggests that 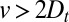 , then we can unambiguously conclude that the data are incompatible with a transport based purely on intercisternal exchange and must allow for some cisternal progression. This illustrates how a quantitative analysis based on generic transport equations may shed light on the nature of intra-Golgi transport, without requiring the knowledge of microscopic details of individual transport steps. We show in the next section that all available data for transiting proteins are well fitted by assuming constant exchange rates. Spatial variations of the transport rates are then introduced to study the dynamics of resident Golgi enzymes.
, then we can unambiguously conclude that the data are incompatible with a transport based purely on intercisternal exchange and must allow for some cisternal progression. This illustrates how a quantitative analysis based on generic transport equations may shed light on the nature of intra-Golgi transport, without requiring the knowledge of microscopic details of individual transport steps. We show in the next section that all available data for transiting proteins are well fitted by assuming constant exchange rates. Spatial variations of the transport rates are then introduced to study the dynamics of resident Golgi enzymes.
Boundary Fluxes.
Eq. 3 must be supplemented by boundary conditions at the cis
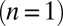 and trans
and trans
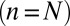 faces of the stack. At the cis face, the influx of material
faces of the stack. At the cis face, the influx of material 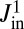 from the ER is taken as a parameter (possibly varying with time), imposed by the experimental procedure (e.g., in pulse-chase or incoming wave protocols, see below). The rate of protein exit at the cis face is taken as a fitting parameter
from the ER is taken as a parameter (possibly varying with time), imposed by the experimental procedure (e.g., in pulse-chase or incoming wave protocols, see below). The rate of protein exit at the cis face is taken as a fitting parameter 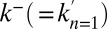 . The outflux of material at the trans face
. The outflux of material at the trans face  includes contributions both from vesicles secreted at the trans-Golgi and from the maturation of the trans cisterna:
includes contributions both from vesicles secreted at the trans-Golgi and from the maturation of the trans cisterna: 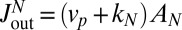 . As can be seen from Eq. 3, these two contributions may not be easily distinguished, as the net flux throughout the Golgi involves the net velocity
. As can be seen from Eq. 3, these two contributions may not be easily distinguished, as the net flux throughout the Golgi involves the net velocity 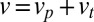 . We thus write the exit flux
. We thus write the exit flux 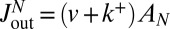 , where
, where 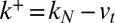 is the fitting parameter of trans-Golgi exit. In addition to the transport parameters (v and
is the fitting parameter of trans-Golgi exit. In addition to the transport parameters (v and 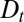 ) and the exit rate r, there are thus two additional boundary parameters
) and the exit rate r, there are thus two additional boundary parameters  and
and 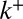 in the model. Boundary conditions do affect the spatiotemporal distribution of proteins inside the Golgi, but we show below that the (bulk) parameters
in the model. Boundary conditions do affect the spatiotemporal distribution of proteins inside the Golgi, but we show below that the (bulk) parameters 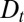 and v, which control the actual transport through the Golgi, can nevertheless be determined with reasonable accuracy.
and v, which control the actual transport through the Golgi, can nevertheless be determined with reasonable accuracy.
Results
Confrontation with Experimental Data on Transiting Proteins.
Our theoretical framework was used to analyze different experimental observations, collectively illustrated in Fig. 2. Fluorescence recovery after photobleaching experiments (FRAP) performed on the whole Golgi gives access to the total concentration of tagged proteins inside the Golgi. An exponential recovery dynamics is reported in ref. 10, both for small membrane proteins (glycoprotein of vesicular stomatitis virus, VSVG) and for large cytosolic protein complexes (procollagen). This was used as an argument against pure cisternal progression, for which a linear recovery dynamics is expected.
Fig. 2.
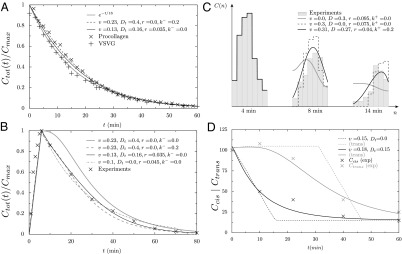
Quantitative analysis of data from different experimental protocols using a numerical solution of Eq. 3. (A and B) Optical microscopy assays. A whole Golgi FRAP experiment probing the exit of tagged proteins from the Golgi following (A) a steady influx, abruptly stopped at 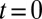 , of a small transmembrane protein (VSVG) and a large soluble protein aggregate (procollagen), and (B) a short influx, starting at
, of a small transmembrane protein (VSVG) and a large soluble protein aggregate (procollagen), and (B) a short influx, starting at 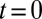 and stopping at
and stopping at 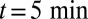 , of VSVG (10).
, of VSVG (10).  was set to zero in the fits because it does not influence the early relaxation. (C and D) EM assays. (C) Pulse-chase experiment for VSVG (13). Setting either convection (gray curve) or diffusion (dashed curve) to zero cannot reproduce the data. Fits are constrained so that the total protein concentration matches the data at
was set to zero in the fits because it does not influence the early relaxation. (C and D) EM assays. (C) Pulse-chase experiment for VSVG (13). Setting either convection (gray curve) or diffusion (dashed curve) to zero cannot reproduce the data. Fits are constrained so that the total protein concentration matches the data at 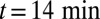 .
. 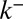 was set to zero because it has the same effect as r. (D) Evolution of the concentration of procollagen aggregates in the cis (black) and trans (gray) face of the Golgi upon sudden blockage of ER secretion (exiting wave experiment) (9). Data are in percentage of the concentration in normal conditions (steady ER secretion), and are not sensitive to exit rate. More information on the fitting procedure and experimental uncertainty is given in SI Appendix.
was set to zero because it has the same effect as r. (D) Evolution of the concentration of procollagen aggregates in the cis (black) and trans (gray) face of the Golgi upon sudden blockage of ER secretion (exiting wave experiment) (9). Data are in percentage of the concentration in normal conditions (steady ER secretion), and are not sensitive to exit rate. More information on the fitting procedure and experimental uncertainty is given in SI Appendix.
Our analysis shows (Fig. 2A) that the recovery profile is rather insensitive to the mode of intra-Golgi transport, and in particular to the effective diffusion coefficient  , the only parameter that solely depends on intercisternal exchange. We fit the data with a single exponential decay of characteristic time 16 min, which could be accounted for by any one of the following: protein exit throughout the Golgi (parameter r), early exit from the cis face (parameter
, the only parameter that solely depends on intercisternal exchange. We fit the data with a single exponential decay of characteristic time 16 min, which could be accounted for by any one of the following: protein exit throughout the Golgi (parameter r), early exit from the cis face (parameter 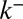 ), late exit via the trans face (parameter
), late exit via the trans face (parameter 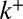 ), or any combination of the three. The dynamics of small inert soluble cargo molecule reported in ref. 10 follows a similar, although slightly faster, exponential recovery, with similar conclusions regarding its means of transport. When fluorescent VSVG proteins were only allowed to enter the Golgi for a short time, the exponential recovery started immediately after the cessation of the fluorescence influx (Fig. 2B). This shows that proteins do not need to reach the trans face to exit the Golgi, because recovery would otherwise show a delay (gray curve in Fig. 2B), and suggest that proteins can exit at the cis face (parameter
), or any combination of the three. The dynamics of small inert soluble cargo molecule reported in ref. 10 follows a similar, although slightly faster, exponential recovery, with similar conclusions regarding its means of transport. When fluorescent VSVG proteins were only allowed to enter the Golgi for a short time, the exponential recovery started immediately after the cessation of the fluorescence influx (Fig. 2B). This shows that proteins do not need to reach the trans face to exit the Golgi, because recovery would otherwise show a delay (gray curve in Fig. 2B), and suggest that proteins can exit at the cis face (parameter 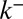 ) or throughout the stack (parameter r). Although these experiments give important information concerning the rate at which proteins are exported from the Golgi, such average measures of Golgi dynamics do not yield any clear-cut conclusion on the dominant means of transport across the Golgi stack. For instance, the exponential fluorescence decay of both FRAP experiments is consistent with a transport solely based on cisternal progression
) or throughout the stack (parameter r). Although these experiments give important information concerning the rate at which proteins are exported from the Golgi, such average measures of Golgi dynamics do not yield any clear-cut conclusion on the dominant means of transport across the Golgi stack. For instance, the exponential fluorescence decay of both FRAP experiments is consistent with a transport solely based on cisternal progression 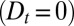 , provided proteins are allowed to exit throughout the Golgi at a sufficient rate
, provided proteins are allowed to exit throughout the Golgi at a sufficient rate 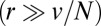 . A quantitative assessment of intra-Golgi transport, which is tantamount to obtaining numerical values for v and
. A quantitative assessment of intra-Golgi transport, which is tantamount to obtaining numerical values for v and 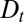 , requires the knowledge of the protein distribution inside the entire organelle.
, requires the knowledge of the protein distribution inside the entire organelle.
Following the transport of a pulse of protein (pulse-chase protocol, Fig. 1C), or the evolution of the protein distribution across the Golgi after ER secretion has been suddenly blocked (exiting wave protocol), could in principle yield independent measurements of the various parameters. Our analysis of pulse-chase data on small membrane proteins (VSVG, Fig. 2C) (13) clearly shows a combination of translation 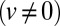 , broadening
, broadening 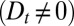 , and decay (at least one nonvanishing parameter among
, and decay (at least one nonvanishing parameter among 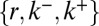 ) of the peaked concentration distribution. The best fit (black curve in Fig. 2C) suggests that all transport rates have similar values (
) of the peaked concentration distribution. The best fit (black curve in Fig. 2C) suggests that all transport rates have similar values ( ). The value of the velocity corresponds to a transit time across the Golgi of order
). The value of the velocity corresponds to a transit time across the Golgi of order 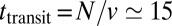 min (where
min (where 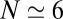 is the number of cisternae). More importantly, the high value of the diffusion coefficient indicates that VSVG is exchanged between cisternae during its transport through the Golgi.
is the number of cisternae). More importantly, the high value of the diffusion coefficient indicates that VSVG is exchanged between cisternae during its transport through the Golgi.
For large cytosolic procollagen aggregates, the exiting wave protocol reported in ref. 9 shows that concentration differences between the cis- and trans-Golgi relax rather smoothly after secretion is stopped, unlike what would be expected within a pure cisternal progression model (solid lines compared with dashed lines in Fig. 2D). Our analysis of the (rather scarce) data suggests that, just as VSVG, procollagen undergoes intercisternal exchange with a fairly large diffusion coefficient,  . This large value of
. This large value of 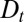 is rather surprising for such large protein complexes and of fundamental significance.
is rather surprising for such large protein complexes and of fundamental significance.
Experimental limitations, such as variability within and between cells or the finite amount of time needed to set up transport block, could be argued to smoothen concentration gradients in a way similar to intercisternal exchange. We show in SI Appendix that given the experimental error (below 10% for data of Fig. 2D, ref. 9), a finite diffusion coefficient must be invoked to explain the procollagen exiting wave data provided ER export ceases within 10 min of the initiation of the block. For a 5-min block, we find 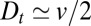 for procollagen (SI Appendix).
for procollagen (SI Appendix).
The analysis of Fig. 2 C and D provides compelling evidence that the two cargo molecules studied undergo retrograde transport during their journey through the Golgi apparatus. Indeed, our formalism enables us to determine the average number of intercisternal exchange steps experienced by a protein. In a stack with N cisternae, it is equal to  times the average time
times the average time 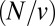 spent in the Golgi, or equivalently to
spent in the Golgi, or equivalently to 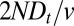 . We thus predict an average of
. We thus predict an average of 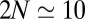 exchange steps for VSVG, and 5–10 steps for procollagen. Because
exchange steps for VSVG, and 5–10 steps for procollagen. Because 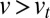 and using
and using 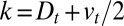 and
and 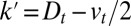 , we find that at least one-fourth of these transport steps is backward (toward the ER).
, we find that at least one-fourth of these transport steps is backward (toward the ER).
Protein Retention Inside the Golgi.
We now apply our formalism to resident Golgi proteins (e.g., glycosylation enzymes) that define the identity and function of specific cisternae and thus must remain in particular locations along the stack. Scenarios for protein retention in the Golgi usually involve either fast recycling of proteins by transport vesicles and/or localization by interaction with the surrounding membrane environment. A popular mechanism for the latter is the hydrophobic mismatch (14, 15), in which proteins are sorted by the span of their transmembrane domains compared with bilayer thickness.
In our framework (Eq. 3), localization by recycling corresponds to an influx of protein targeted to a particular cisterna  combined with protein exit at every cisterna (
combined with protein exit at every cisterna (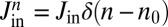 and
and 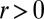 ). The stationary protein distribution along the stack is the stationary solution to Eq. 3. (see SI Appendix):
). The stationary protein distribution along the stack is the stationary solution to Eq. 3. (see SI Appendix):
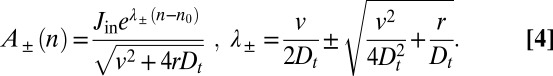 |
The protein distribution is peaked at 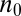 and is asymmetric,
and is asymmetric, 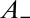 corresponding to
corresponding to 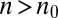 and
and 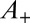 to
to 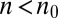 . It is spread over
. It is spread over 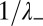 (respectively,
(respectively,  ) cisternae toward the trans (respectively, cis) Golgi face, and is broader toward the trans face due to protein convection. Accurate protein localization requires
) cisternae toward the trans (respectively, cis) Golgi face, and is broader toward the trans face due to protein convection. Accurate protein localization requires 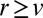 , as illustrated in Fig. 3A, a much faster rate than the one we measured for the transiting protein VSVG
, as illustrated in Fig. 3A, a much faster rate than the one we measured for the transiting protein VSVG 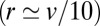 . The stationary distribution (Eq. 4 and Fig. 3A) requires that the influx is balanced by the outflux
. The stationary distribution (Eq. 4 and Fig. 3A) requires that the influx is balanced by the outflux 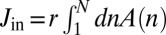 , but is not sensitive to details of the recycling pathway. Whether proteins leaving the Golgi are recycled to cisterna
, but is not sensitive to details of the recycling pathway. Whether proteins leaving the Golgi are recycled to cisterna  directly or via a more complex pathway (e.g., involving the ER or lysosomes) does not modify the steady-state profile.
directly or via a more complex pathway (e.g., involving the ER or lysosomes) does not modify the steady-state profile.
Fig. 3.
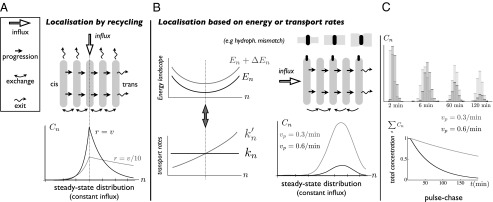
Localization of Golgi resident proteins. (A) Fast recycling of proteins imported at specific Golgi location leads to a peaked protein distribution around the import location. The steady-state distribution profile is shown for parameter values corresponding to VSVG (not a resident protein, 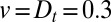 ,
, 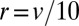 , gray curve) and for a recycling 10 times faster (black curve). (B) Local variation of the transport rates k and
, gray curve) and for a recycling 10 times faster (black curve). (B) Local variation of the transport rates k and 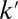 can be converted into energy landscapes
can be converted into energy landscapes 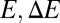 and related to physical mechanisms, such as hydrophobic mismatch. The example shows a quadratic landscape
and related to physical mechanisms, such as hydrophobic mismatch. The example shows a quadratic landscape 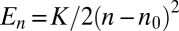 and the corresponding rates. The steady-state distribution shows a peak where the net velocity
and the corresponding rates. The steady-state distribution shows a peak where the net velocity 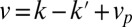 vanishes. (C) Pulse-chase experiment on resident proteins in a quadratic energy landscape, showing the evolution of a protein distribution initially localized at the cis face at
vanishes. (C) Pulse-chase experiment on resident proteins in a quadratic energy landscape, showing the evolution of a protein distribution initially localized at the cis face at 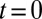 , and the variation of the total protein content with time. Variation of the progression velocity strongly influences the protein distribution and lifetime in the Golgi. Larger
, and the variation of the total protein content with time. Variation of the progression velocity strongly influences the protein distribution and lifetime in the Golgi. Larger 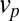 (black curve) displaces the peaks toward the trans face and promotes protein exit.
(black curve) displaces the peaks toward the trans face and promotes protein exit.
The effect of the biochemical environment on protein retention corresponds to a variation of the transport coefficients 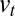 and
and 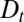 along the stack. Generically, protein movement in the Golgi can be written as a diffusion in an effective energy landscape
along the stack. Generically, protein movement in the Golgi can be written as a diffusion in an effective energy landscape 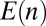 characterizing the protein’s energy in the different cisternae, supplemented by an activation energy
characterizing the protein’s energy in the different cisternae, supplemented by an activation energy 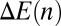 associated with transport intermediates. In SI Appendix, we show that
associated with transport intermediates. In SI Appendix, we show that
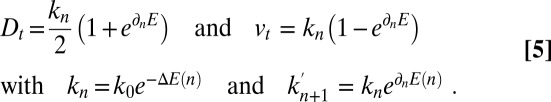 |
A landscape that promotes localization near a particular cisterna 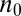 can locally be written as a quadratic potential:
can locally be written as a quadratic potential: 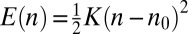 , where K is the coupling strength. About half the proteins moving through such a landscape would be localized at or near the minimum
, where K is the coupling strength. About half the proteins moving through such a landscape would be localized at or near the minimum 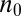 with a spread
with a spread 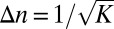 cisternae. A bulk flow (e.g., due to cisternal progression) with velocity
cisternae. A bulk flow (e.g., due to cisternal progression) with velocity  displaces the energy minimum by an amount
displaces the energy minimum by an amount 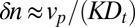 (Fig. 3B and SI Appendix). Thus, precise and robust localization require a large coupling strength
(Fig. 3B and SI Appendix). Thus, precise and robust localization require a large coupling strength  .
.
The landscape approach allows us to test the relevance of the hydrophobic mismatch mechanism, for which the energy 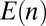 can be computed. The membrane thickness of organelles is known to continuously increase along the secretory pathway from about 3.7 nm in the ER to 4.2 nm at the plasma membrane (16), and proteins could be confined to membranes that best match the length of their hydrophobic domains. The energy of hydrophobic mismatch leads to a quadratic energy landscape with
can be computed. The membrane thickness of organelles is known to continuously increase along the secretory pathway from about 3.7 nm in the ER to 4.2 nm at the plasma membrane (16), and proteins could be confined to membranes that best match the length of their hydrophobic domains. The energy of hydrophobic mismatch leads to a quadratic energy landscape with 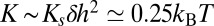 (17) (
(17) (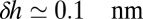 is the mismatch between adjacent cisternae and
is the mismatch between adjacent cisternae and 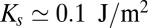 is the bilayer stretching modulus). Hydrophobic mismatch can thus in principle localize proteins against thermal fluctuations with an accuracy of about
is the bilayer stretching modulus). Hydrophobic mismatch can thus in principle localize proteins against thermal fluctuations with an accuracy of about  cisternae, and protein localization is indeed known to be affected by the length of its transmembrane domain (18, 19). It is however not robust against variation of the anterograde flux because
cisternae, and protein localization is indeed known to be affected by the length of its transmembrane domain (18, 19). It is however not robust against variation of the anterograde flux because 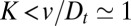 , consistent with the observation that the transmembrane domain length was not the sole factor affecting protein localization in the Golgi (18).
, consistent with the observation that the transmembrane domain length was not the sole factor affecting protein localization in the Golgi (18).
The two mechanisms above (localization by recycling and by an energy landscape) were used to analyze the distribution of the resident enzyme Man I in Arabidopsis thaliana Golgi stacks; SI Appendix, Fig. S2. This enzyme is localized to cisternae 3 and 4 of the stack with a 90% accuracy (20). Such strong confinement requires either fast recycling  or a deep energy well
or a deep energy well 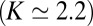 . Such large value of K is inconsistent with retention solely based on hydrophobic mismatch
. Such large value of K is inconsistent with retention solely based on hydrophobic mismatch  .
.
Discussion
Cisternal Progression or Vesicular Transport.
Our framework produces two strong predictions: (i) the level of intercisternal exchange (although not its directionality) can be directly quantified by measuring the coarse-grained diffusion coefficient 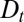 , and (ii) measuring a convection velocity
, and (ii) measuring a convection velocity 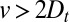 would necessarily imply some level of cisternal progression. We stress that cisternal progression cannot be disproved in case
would necessarily imply some level of cisternal progression. We stress that cisternal progression cannot be disproved in case 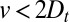 , because this could correspond to progression combined with retrograde vesicular transport. Our analysis of the data clearly shows the existence of some degree of diffusion, including significant backward transport steps, both for the small membrane protein VSVG and for the large protein complex procollagen (Fig. 2). Furthermore, we find that
, because this could correspond to progression combined with retrograde vesicular transport. Our analysis of the data clearly shows the existence of some degree of diffusion, including significant backward transport steps, both for the small membrane protein VSVG and for the large protein complex procollagen (Fig. 2). Furthermore, we find that 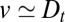 for both species. This implies that (i) intercisternal exchange is confirmed in both cases, and (ii) cisternal progression cannot be proved or disproved by the existing transport data. We emphasize that this follows from a strict application of general transport principles, and reflects the inadequacy of the existing experimental data to be more discriminating. Detailed microscopic models used to interpret coarse-grained experimental transport data (10) should be viewed with caution, confirming both the utility and necessity of our coarse-grained approach.
for both species. This implies that (i) intercisternal exchange is confirmed in both cases, and (ii) cisternal progression cannot be proved or disproved by the existing transport data. We emphasize that this follows from a strict application of general transport principles, and reflects the inadequacy of the existing experimental data to be more discriminating. Detailed microscopic models used to interpret coarse-grained experimental transport data (10) should be viewed with caution, confirming both the utility and necessity of our coarse-grained approach.
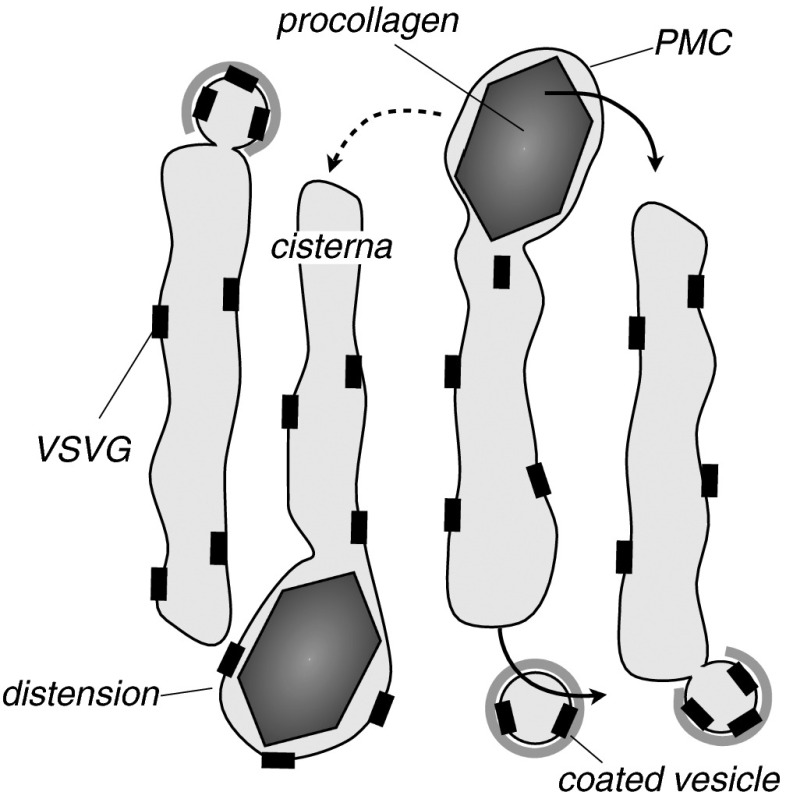
Our analysis shows that procollagen is exchanged between cisternae despite its size. This is at odds with packaging and transport in conventional small protein-coated transport vesicles, and implies that transport is at least partly mediated by large “pleiomorphic membrane carriers” (PMCs), as sketched in Fig. 4. PMCs containing procollagen aggregates could take the form of “megavesicles” such as those involved in the transport of large (engineered) protein complexes (21), or of large tubulo–vesicular connections such as those connecting the Golgi to surrounding organelles (22). Such large transport intermediates have not yet been seen, but recent experiments suggest indirectly that largo cargo can indeed be exchanged between cisternae (23). A mechanism based on lateral segregation in the cisternal membranes caused by a Rab cascade, the cisternal progenitor model (24), has recently linked the formation of large intra-Golgi transport carriers to the maturation of membrane components. The present work directly infers their involvement in intra-Golgi transport from quantitative transport data. Note that intercisternal exchange could be quite fast, so a given procollagen aggregate could only spend a very short fraction of its transit time outside cisternae. If an exchange step takes ∼1 s and there are 10 such steps for a transit time of ∼15 min, an aggregate spends about 99% of its time inside cisternae. This suggests that the formation of megavesicles could be a rare event.
Fig. 4.
Given the evidence for intercisternal exchange during the transit of large protein complexes through the mammalian Golgi apparatus (procollagen is exchanged on average 6 times during its journey according to our analysis), we propose that PMCs could be involved in intercisternal exchange, possibly triggered by distensions in procollagen-containing cisternae. The sketch presents a snapshot of a dynamic process, showing a PMC being exchanged between two cisternae: according to our analysis, a procollagen complex is exchanged an average of six times between cisternae during its journey through the Golgi (∼20 min). This may not lead to a net progression along the stack, and does not invalidate cisterna progression as the main cause for anterograde protein transport.
Finally, it is intriguing that diffusion and convection are found to occur at similar rates 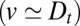 for both cargoes. This could indicate that these two processes share the same underlying mechanisms and/or that one process is coupled to the other, as suggested by the cisternal progenitor model (24). More insight could be gained by comparing values for v and
for both cargoes. This could indicate that these two processes share the same underlying mechanisms and/or that one process is coupled to the other, as suggested by the cisternal progenitor model (24). More insight could be gained by comparing values for v and  in different organisms. Scale-forming algae such as Scherffelia
dubia have a regularly stacked Golgi of 15–20 cisternae. Proteoglycan scales readily identifiable by EM and too large to fit in conventional transport vesicles transit through the stack without ever being seen outside cisternae (20). The absence of scale-containing megavesicles would imply that these scales undergo pure convection in the Golgi. A quantitative incoming wave experiment, yet unavailable to our knowledge, should produce data along the dashed lines of Fig. 2D, corresponding to the absence of diffusion.
in different organisms. Scale-forming algae such as Scherffelia
dubia have a regularly stacked Golgi of 15–20 cisternae. Proteoglycan scales readily identifiable by EM and too large to fit in conventional transport vesicles transit through the stack without ever being seen outside cisternae (20). The absence of scale-containing megavesicles would imply that these scales undergo pure convection in the Golgi. A quantitative incoming wave experiment, yet unavailable to our knowledge, should produce data along the dashed lines of Fig. 2D, corresponding to the absence of diffusion.
Experimental Proposal.
We have shown that all available data on the transport of two very different types of cargo through the Golgi (the small membrane protein VSVG and the large collagen complex procollagen) are reproduced by a model of intra-Golgi transport involving constant anterograde and retrograde transport rates, corresponding to a net constant velocity v and constant effective diffusion coefficient 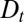 . Models involving more than these two or equivalent parameters for intra-Golgi transport are not falsifiable by current transport experiments and should be treated with caution.
. Models involving more than these two or equivalent parameters for intra-Golgi transport are not falsifiable by current transport experiments and should be treated with caution.
Our analysis shows that diffusion, a signature of intercisternal exchange, contributes to the transport of both types of cargo. This is rather surprising for the large protein complex procollagen and should therefore be confirmed by additional transport data with high statistical significance, and using a fast  transport block protocol. We advocate the use of high-resolution microscopy instead of low resolution optical assays (FRAP), because the latter are dominated by the boundary conditions (Fig. 2 A and B) and do not give sufficient insight into the intra-Golgi dynamics.
transport block protocol. We advocate the use of high-resolution microscopy instead of low resolution optical assays (FRAP), because the latter are dominated by the boundary conditions (Fig. 2 A and B) and do not give sufficient insight into the intra-Golgi dynamics.
Direct evidence for cisternal progression may be obtained only if 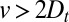 ; however, our analysis of the transport data showed
; however, our analysis of the transport data showed 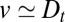 for both types of cargo. More information on the nature of protein transport could be gained by studying correlation in the transport dynamics of different protein species. A promising technique is the newly developed Retention Using Selective Hooks method (25), which allows one to precisely control the release of proteins from the ER into the Golgi, following which their progression and export can be monitored by optical or electron microscopy.
for both types of cargo. More information on the nature of protein transport could be gained by studying correlation in the transport dynamics of different protein species. A promising technique is the newly developed Retention Using Selective Hooks method (25), which allows one to precisely control the release of proteins from the ER into the Golgi, following which their progression and export can be monitored by optical or electron microscopy.
More insight on the interplay between progression and exchange could be gained by comparing the dynamics of transiting and resident Golgi proteins. Monitoring the distribution and dynamics of resident proteins under conditions that affect the transport of transiting proteins could be a promising strategy, as the localization of resident proteins is affected by cisternal progression. One first needs to identify the mechanism by which particular resident proteins are localized, fast recycling (Fig. 3A) and localized retrograde transport related to an energy landscape (Fig. 3B) being the two generic ones. The distribution of resident proteins within the stack should then be determined, by high-resolution microscopy, under conditions affecting the transit time of proteins putatively transported by cisternal progression, such as drugs targeting the cytoskeleton. According to our prediction, this distribution should correlate with the transport rate of transiting proteins in one of two ways if transit is due to cisternal progression. The distribution of proteins localized by fast recycling should broaden, whereas the distribution of proteins localized by retrograde transport should be displaced (and not broaden) toward the trans-Golgi face, under conditions that decrease the Golgi transit time (Fig. 3). Finding such correlations would bring support to the cisternal progression mechanism.
We close by recalling that transport solely based on cisternal progression cannot be reconciled with existing transport data (10). Exchange mediated by large membrane structures (the PMCs) seems the most reasonable compromise, and can be linked to biochemical maturation by the cisternal progenitor model (24). In fact, the distinction between cisternal progression and intercisternal exchange becomes less clear if transport involves large PMCs (Fig. 4) of size possibly close to the cisterna size, that undergo frequent scission and fusion. A more crucial question is rather whether there exists a bulk anterograde flow of material in the Golgi, or whether transport is mainly protein-specific. Dynamical correlation between different transiting proteins could inform us of the extent to which they use the same carrier. It would in particular be very interesting if the transport of VSVG, for instance, was increased by the presence of procollagen. That would suggest that procollagen can create its PMCs and that VSVG can be exchanged between cisternae by riding along these structures.
Supplementary Material
Acknowledgments
We acknowledge stimulating discussions with Bruno Goud, Vivek Malhotra, Satyajit Mayor, and Franck Perez. This work was supported by the foundation Pierre-Gilles de Gennes pour la Recherche.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1303358110/-/DCSupplemental.
References
- 1.Polishchuk RS, Mironov AA. Structural aspects of Golgi function. Cell Mol Life Sci. 2004;61(2):146–158. doi: 10.1007/s00018-003-3353-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Marsh BJ, Volkmann N, McIntosh JR, Howell KE. Direct continuities between cisternae at different levels of the Golgi complex in glucose-stimulated mouse islet beta cells. Proc Natl Acad Sci USA. 2004;101(15):5565–5570. doi: 10.1073/pnas.0401242101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Orci L, Malhotra V, Amherdt M, Serafini T, Rothman JE. Dissection of a single round of vesicular transport: Sequential intermediates for intercisternal movement in the Golgi stack. Cell. 1989;56(3):357–368. doi: 10.1016/0092-8674(89)90239-0. [DOI] [PubMed] [Google Scholar]
- 4.Malhotra V, Orci L, Glick BS, Block MR, Rothman JE. Role of an N-ethylmaleimide-sensitive transport component in promoting fusion of transport vesicles with cisternae of the Golgi stack. Cell. 1988;54(2):221–227. doi: 10.1016/0092-8674(88)90554-5. [DOI] [PubMed] [Google Scholar]
- 5.Wilson C, Ragnini-Wilson A. Conserved molecular mechanisms underlying homeostasis of the Golgi complex. Int J Cell Biol. 2010;2010:758230. doi: 10.1155/2010/758230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Marsh BJ, Howell KE. The mammalian Golgi—complex debates. Nat Rev Mol Cell Biol. 2002;3(10):789–795. doi: 10.1038/nrm933. [DOI] [PubMed] [Google Scholar]
- 7.Matsuura-Tokita K, Takeuchi M, Ichihara A, Mikuriya K, Nakano A. Live imaging of yeast Golgi cisternal maturation. Nature. 2006;441(7096):1007–1010. doi: 10.1038/nature04737. [DOI] [PubMed] [Google Scholar]
- 8.Losev E, et al. Golgi maturation visualized in living yeast. Nature. 2006;441(7096):1002–1006. doi: 10.1038/nature04717. [DOI] [PubMed] [Google Scholar]
- 9.Bonfanti L, et al. Procollagen traverses the Golgi stack without leaving the lumen of cisternae: Evidence for cisternal maturation. Cell. 1998;95(7):993–1003. doi: 10.1016/s0092-8674(00)81723-7. [DOI] [PubMed] [Google Scholar]
- 10.Patterson GH, et al. Transport through the Golgi apparatus by rapid partitioning within a two-phase membrane system. Cell. 2008;133(6):1055–1067. doi: 10.1016/j.cell.2008.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Glick BS, Elston T, Oster G. A cisternal maturation mechanism can explain the asymmetry of the Golgi stack. FEBS Lett. 1997;414(2):177–181. doi: 10.1016/s0014-5793(97)00984-8. [DOI] [PubMed] [Google Scholar]
- 12.Van Kampen N. Stochastic Processes in Physics and Chemistry. Amsterdam: Elsevier; 2007. [Google Scholar]
- 13.Trucco A, et al. Secretory traffic triggers the formation of tubular continuities across Golgi sub-compartments. Nat Cell Biol. 2004;6(11):1071–1081. doi: 10.1038/ncb1180. [DOI] [PubMed] [Google Scholar]
- 14.Webb RJ, East JM, Sharma RP, Lee AG. Hydrophobic mismatch and the incorporation of peptides into lipid bilayers: A possible mechanism for retention in the Golgi. Biochemistry. 1998;37(2):673–679. doi: 10.1021/bi972441+. [DOI] [PubMed] [Google Scholar]
- 15.Füllekrug J, Nilsson T. Protein sorting in the Golgi complex. Biochim Biophys Acta. 1998;1404(1-2):77–84. doi: 10.1016/S0167-4889(98)00048-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mitra K, Ubarretxena-Belandia I, Taguchi T, Warren G, Engelman DM. Modulation of the bilayer thickness of exocytic pathway membranes by membrane proteins rather than cholesterol. Proc Natl Acad Sci USA. 2004;101(12):4083–4088. doi: 10.1073/pnas.0307332101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Phillips R, Ursell T, Wiggins P, Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459(7245):379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Machamer CE. Targeting and retention of Golgi membrane proteins. Curr Opin Cell Biol. 1993;5(4):606–612. doi: 10.1016/0955-0674(93)90129-E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rayner JC, Pelham HRB. Transmembrane domain-dependent sorting of proteins to the ER and plasma membrane in yeast. EMBO J. 1997;16(8):1832–1841. doi: 10.1093/emboj/16.8.1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Donohoe BS, et al. Cis-Golgi cisternal assembly and biosynthetic activation occur sequentially in plants and algae. Traffic. 2013;14(5):551–567. doi: 10.1111/tra.12052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Volchuk A, et al. Megavesicles implicated in the rapid transport of intracisternal aggregates across the Golgi stack. Cell. 2000;102(3):335–348. doi: 10.1016/s0092-8674(00)00039-8. [DOI] [PubMed] [Google Scholar]
- 22.Luini A, Ragnini-Wilson A, Polishchuck RS, De Matteis MA. Large pleiomorphic traffic intermediates in the secretory pathway. Curr Opin Cell Biol. 2005;17(4):353–361. doi: 10.1016/j.ceb.2005.06.012. [DOI] [PubMed] [Google Scholar]
- 23. Lavieu G, Zheng H, Rothman JE (2013) Stapled Golgi cisternae remain in place as cargo passes through the stack. eLIFE, 2:e00558. [DOI] [PMC free article] [PubMed]
- 24.Pfeffer SR. How the Golgi works: A cisternal progenitor model. Proc Natl Acad Sci USA. 2010;107(46):19614–19618. doi: 10.1073/pnas.1011016107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Boncompain G, et al. Synchronization of secretory protein traffic in populations of cells. Nat Methods. 2012;9(5):493–498. doi: 10.1038/nmeth.1928. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.