Haplotype Block Structure and Its Applications to Association Studies: Power and Study Designs

Abstract

Recent studies have shown that the human genome has a haplotype block structure, such that it can be divided into discrete blocks of limited haplotype diversity. In each block, a small fraction of single-nucleotide polymorphisms (SNPs), referred to as “tag SNPs,” can be used to distinguish a large fraction of the haplotypes. These tag SNPs can potentially be extremely useful for association studies, in that it may not be necessary to genotype all SNPs; however, this depends on how much power is lost. Here we develop a simulation study to quantitatively assess the power loss for a variety of study designs, including case-control designs and case-parental control designs. First, a number of data sets containing case-parental or case-control samples are generated on the basis of a disease model. Second, a small fraction of case and control individuals in each data set are genotyped at all the loci, and a dynamic programming algorithm is used to determine the haplotype blocks and the tag SNPs based on the genotypes of the sampled individuals. Third, the statistical power of tests was evaluated on the basis of three kinds of data: (1) all of the SNPs and the corresponding haplotypes, (2) the tag SNPs and the corresponding haplotypes, and (3) the same number of randomly chosen SNPs as the number of tag SNPs and the corresponding haplotypes. We study the power of different association tests with a variety of disease models and block-partitioning criteria. Our study indicates that the genotyping efforts can be significantly reduced by the tag SNPs, without much loss of power. Depending on the specific haplotype block–partitioning algorithm and the disease model, when the identified tag SNPs are only 25% of all the SNPs, the power is reduced by only 4%, on average, compared with a power loss of ∼12% when the same number of randomly chosen SNPs is used in a two-locus haplotype analysis. When the identified tag SNPs are ∼14% of all the SNPs, the power is reduced by ∼9%, compared with a power loss of ∼21% when the same number of randomly chosen SNPs is used in a two-locus haplotype analysis. Our study also indicates that haplotype-based analysis can be much more powerful than marker-by-marker analysis.

Introduction

Genomewide association studies have recently received a great deal of attention as a tool for detecting the genetic variation responsible for human common diseases. Unlike traditional linkage studies, which can use recombination information only in pedigrees, association methods use recombination information at the population level. Thus, association methods have greater power to detect small and moderate genetic effects than does linkage analysis (Risch and Merikangas 1996). SNP markers are preferred over microsatellite markers for association studies, because of their high abundance along the human genome (SNPs with minor allele frequency >0.1 occur once every ∼600 kb) (Wang et al. 1998), their low mutation rate, and the accessibility of high-throughput genotyping. The power of association studies based on SNPs depends not only on the sample size and density of the marker map but also on many other factors, such as the age and frequency of the disease mutations and SNPs and the extent of linkage disequilibrium (LD) in the region.

The study of LD patterns in human and other organisms is a topic of great interest. In a simulation study, Kruglyak (1999) found that LD was unlikely to extend beyond an average of 3 kb in general populations and in most isolated populations, so that ⩾500,000 SNPs would be required for whole-genome association studies. On the other hand, Reich et al. (2001) showed that LD in a U.S. population of northern European descent could extend 60 kb for common alleles, so that only 50,000 SNPs would be needed in these populations. Several studies have observed substantial variation of LD patterns across the human genome in different populations (Dunning et al. 2000; Taillon-Miller et al. 2000; Eisenbarth et al. 2001; Reich et al. 2001). The regions of long-range LD over several hundred kilobases are usually interspersed with regions of short-range LD spanning only several kilobases along the chromosome.

Recent studies (Daly et al. 2001; Johnson et al. 2001; Patil et al. 2001; Dawson et al. 2002; Gabriel et al. 2002) have shown that the human genome can be partitioned into blocks with limited haplotype diversity, such that only a small fraction of SNPs captures most haplotypes. Patil et al. (2001) studied the global haplotype structure on chromosome 21 for 24,047 SNPs (⩾10% minor allele frequency). The 20 haplotypes identified by a rodent-human somatic cell hybrid technique were partitioned into 4,135 haplotype blocks, such that, in each block, repeated haplotypes accounted for ⩾80% of the observed haplotypes. A total of 4,563 SNPs (tag SNPs) were identified as distinguishing these repeated haplotypes (which they referred to as “common” haplotypes). For the same data, Zhang et al. (2002) reduced the number of blocks and tag SNPs to 2,575 and 3,582, respectively, through use of a dynamic programming algorithm. Thus, 15% (3,582) of all the SNPs (24,047) are sufficient to account for 80% of all the haplotypes in each block. Others have studied haplotype structure in smaller regions. Johnson et al. (2001) genotyped 122 SNPs in a 135-kb region for nine genes and found that 34 SNPs were sufficient to characterize the haplotypes in 384 European individuals. Daly et al. (2001) studied a 500-kb region, on human chromosome 5q31, that may contain a genetic variant responsible for Crohn disease, by genotyping 103 SNPs with minor allele frequency >5% for 129 triads. They found that the region could be divided into 11 blocks, in which only four common haplotypes accounted for nearly all (>90%) observed haplotypes. Although they did not determine the tag SNPs for each block, this step is straightforward once the blocks have been identified.

Haplotype blocks, together with the corresponding tag SNPs and common haplotypes determined by haplotype block–partitioning algorithms, can be used in genomewide association studies, as well as in the fine-scale mapping of complex disease genes. First, a small number of samples (e.g., 10 or 20 individuals) are chosen to be genotyped at a very dense SNP map in a region, and the haplotypes of these individuals are identified simultaneously. Second, an algorithm for haplotype block partitioning is employed, to identify haplotype block structure and a set of well-spaced tag SNPs. Third, a larger number of samples are genotyped only at these tag SNP marker loci. Fourth, association studies are conducted using all the genotyped samples, with knowledge of the haplotype block structure.

It is clear that the above approach can significantly reduce the genotyping cost (Johnson et al. 2001). What is not clear is how much power is lost. In the present study, we investigate how the power of association studies depends on the way in which the SNPs are chosen, using a variety of disease models and test statistics.

Methods

The Coalescent Process with Recombination

To perform our study, we first simulate a large number of haplotypes consisting of many consecutive SNPs across a genomic region, using the coalescent process with recombination (Hudson 1983; Kaplan and Hudson 1985; Griffiths and Marjoram 1997). In each simulation, the genealogies of 2,000 haplotypes are generated, with a population recombination rate (θ) over the region of interest chosen under the assumption that recombination occurs uniformly over the region. For simplicity of exposition, we denote the region of interest to be the interval [0,1]. Once the ancestral relationship between haplotypes has been generated, SNPs are added using an infinite-many-sites model with a population mutation rate μ. The infinite-many-sites model assumes that mutations occur uniformly in the interval [0,1] and that a new mutation creates a new SNP that does not already exist in the population; recurrent mutations are not allowed. In our simulations, we set both θ and μ equal to 200. These parameters correspond to ∼200 kb in humans (Nordborg and Tavaré 2002).

The following method is used to simulate a disease with a high-risk allele frequency of 0.10–0.15. Once the haplotypes have been generated, we choose a marker locus as the disease locus if it satisfies two conditions: (1) the frequency of the minor allele is 0.10–0.15, and (2) the position of the marker is between 0.45 and 0.55—that is, the location of the disease locus is approximately in the middle of the region. The first condition restricts the disease allele frequency, and the second condition constrains the disease locus to be approximately in the middle of the region of interest. If no such marker loci exist, this data set is discarded. If several marker loci satisfy these conditions in a data set, the marker locus closest to 0.50 is chosen as the disease locus. The marker loci are selected sequentially from left to right along the chromosome, according to the following conditions: (1) the frequency of the minor allele is ⩾10%, and (2) the distance between any two adjacent marker loci is >0.005. If the length of the simulated genetic region corresponds to ∼200 kb, then the distance between two adjacent markers is ⩾200×0.005=1 kb, resulting in ∼200 markers total. The haplotypes at these marker loci and the disease locus are retained for further analysis.

To generate the case-control and case-parent samples, we assume a multiplicative disease model—that is, the penetrances for genotypes dd, dD, and DD are c, cγ, and cγ², respectively, where c is the phenocopy rate and γ is the genotype relative risk. D and d are the high- and low-risk alleles, respectively, at the disease locus. For a given disease prevalence P, genotype relative risk γ, and disease allele frequency p, the phenocopy rate c can be calculated by the equation P=c[p²γ²+2p(1-p)γ+(1-p)²]. For example, if P=0.05 and p=0.125, the phenocopy rates corresponding to γ=2, 4, and 6 are 0.04, 0.026, and 0.019, respectively.

A Haplotype Block–Partitioning Algorithm

To make this article self-contained, we briefly describe the haplotype block definition that was proposed by Patil et al. (2001) and was later extended by Zhang et al. (2002), together with the dynamic programming algorithm used by the latter to find the block partition and tag SNPs. Suppose we have a number of haplotypes consisting of a set of consecutive SNPs. A segment of consecutive SNPs is a block if at least α percent of haplotypes are represented more than once (Patil et al. 2001; Zhang et al. 2002). The tag SNPs are selected on the basis of the measure of haplotype quality in each block. Different block quality measures can be used, depending on the purpose of a study. For example, when the criterion of Patil et al. (2001) is used, the tag SNPs are selected to minimize the number of SNPs that can distinguish at least α percent of the haplotypes. If we follow Johnson et al. (2001), the haplotype quality can be the haplotype diversity in a block, and the tag SNPs are selected to minimize the number of SNPs that can account for at least β percent of the haplotype diversity. Given α, β, and the criterion to identify the tag SNPs, Zhang et al. (2002) developed a dynamic programming algorithm, for haplotype block partitioning, that finds the partition with the minimum total number of tag SNPs. The algorithm can be briefly described as follows.

Let r₁,r₂,…,r_n be the SNPs. We define a Boolean function block(r_i,r_i+1,…,r_j)=1 if α percent of the haplotypes formed by the SNPs r_i,r_i+1,…,r_j are represented more than once, and block(r_i,r_i+1,…,r_j)=0 otherwise. Let f(·) be the number of tag SNPs in a block. Given a block partition—that is, B₁,B₂,…,B_I—the total number of tag SNPs for these blocks is f(B₁)+f(B₂)+…+f(B_I). The optimal block partition is defined to be the one that minimizes the total number of tag SNPs. Our goal is to find the optimal block partition for all the SNPs. Define S_j to be the number of tag SNPs for the optimal block partition of the first j SNPs, r₁,r₂,⋅⋅⋅,r_j, and set S₀=0. Then, applying dynamic programming theory,

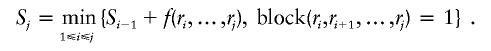Using this recursion, we can design a dynamic programming algorithm to compute the minimum number of tag SNPs for the optimal block partition of all the SNPs.

In practice, there may exist several block partitions that give the minimum number of tag SNPs. We want to find the partition with the minimum number of blocks. Let C_j be the minimum number of blocks of all the block partitions requiring S_j tag SNPs in the first SNPs and C₀=0. Then, applying dynamic programming theory again,

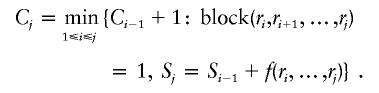By this recursion, the minimum number of blocks in the partition can be computed.

Test for Associations by LD

We consider two types of association studies: (1) case-control, in which both case and control individuals are unrelated individuals from a population; and (2) family-based, in which the control individuals are the parents of the affected individuals.

When the parents of case individuals are chosen as the control individuals, the transmission/disequilibrium test (TDT), introduced by Spielman et al. (1993), can be used to test for linkage in the presence of association. The TDT method has been extended to multiallelic markers (Sham and Curtis 1995; Spielman and Ewens 1996; Cleves et al. 1997), as well as to multiple markers (Clayton and Jones 1999; Dudbridge et al. 2000; McIntyre et al. 2000; Zhao et al. 2000). Here, we use an extended multiallelic TDT proposed by Spielman and Ewens (1996). Assuming we have the genotypes of n affected individuals with their parents at a marker with k alleles, A_1,A₂,⋅⋅⋅,A_k, we construct a k×k transmission/nontransmission table:

where t_ij represents the number of parents who have the genotype A_iA_j and transmit allele A_i to the offspring, and 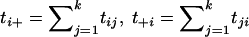, for i=1,2,…,k and j=1,2,…,k. A common test statistic for the marginal homogeneity is

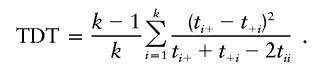This test statistic has an approximate χ² distribution with k-1 df when the sample size is large under the null hypothesis of no association.

For unrelated control individuals, a test for association is usually based on the differences in allele frequency between case individuals and control individuals (Olsen and Wijsman 1994). It should be noted that such tests are not robust to the effects of population stratification. Suppose that we have the genotype of n case individuals and n control individuals at a marker with k alleles A_1,A₂,⋅⋅⋅,A_k; we may construct a 2×k contingency table:

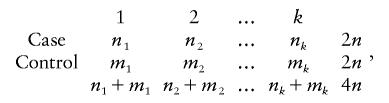where n_i and m_i are the number of alleles A_i in case and the control individuals, respectively. The test statistic is

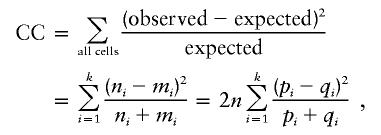where p_i and q_i are the frequency of allele A_i in case and control individuals, respectively. The above statistic has an approximate χ² distribution with k-1 df under the null hypothesis of no association.

When the haplotypes are known and treated as alleles at a single multiallelic marker locus, the above statistics can be directly applied to haplotype data. However, the number of different haplotypes increases rapidly with the number of marker loci, and the increase in the degrees of freedom in the χ² test will lower the power of these tests. An alternative is to apply the tests to a number of SNPs, but this runs into problems with multiple testing. Typically, a Bonferroni correction for the P value is employed to protect against inflated type I errors (here, “P value” refers to the probability of obtaining the observed data under the null hypothesis). However, the Bonferroni correction does not consider the dependence of tightly linked marker loci and may lead to a conservative test. Monte Carlo permutation methods have been developed to address this problem (e.g., see McIntyre et al. 2000). Usually, the maximum value of statistics, denoted as “TDT_max” or “CC_max,” over all the markers is taken as the statistic. TDT_max or CC_max are calculated on the basis of the original data and the permuted data. The overall P value is estimated by the proportion of permuted samples with a statistic bigger than that in the original data. In the present study, we assume that the haplotypes of samples are known, and we perform two-locus haplotype analysis for all the adjacent markers, using the TDT and CC statistics. The following Monte Carlo procedure is used to evaluate the overall P value:

• 1. Calculate the statistic TDT for case-parent data or CC for case-control data, at each marker locus. Then choose the maximum of each, TDT_max and CC_max, as the test statistics.
• 2. Randomly permute the data. For each trio, randomly permute the transmitted and nontransmitted haplotypes. For case-control data, randomly permute labels of the case individuals and the control individuals.
• 3. Calculate TDT_max and CC_max for the permuted data, as in step 1.
• 4. Repeat two to three times and estimate the overall P value by the proportion of these samples in which the value of TDT_max and CC_max for the permuted data is greater than the value of TDT_max and CC_max obtained from the original data.
• 5. Reject the null hypothesis if the overall P value is less than the given type I error rate.

Results

We used coalescent simulations to generate 10 populations of 2,000 haplotypes. The number of marker loci, the disease allele frequency, and the disease locus position vary in the 10 simulated populations. The number of markers varies from 120 to 134, with an average of 128. The disease allele frequency varies from 0.106 to 0.147, with an average of 0.123. The disease locus position varies from 0.479 to 0.501, with an average of 0.495, which is very close to the center of the marker map. The 10 populations are used as the pool to construct case-parent or case-control data. For each population, we generated 100 family data, consisting of 100 trios with an affected individual and their parents, as well as 100 case-control data, with 100 case individuals and 100 control individuals chosen on the basis of the specific penetrance. We used a rejection scheme to generate the trios for case-parent samples. Two haplotypes were randomly chosen from the haplotype pool and were then assigned to the parent, and one of them is randomly transmitted to the offspring. We retained only the trios that have an affected offspring. A total of 1,000 samples were generated. For each sample in the case-parent design, the haplotypes of a small fraction (λ, the percentage of tagged samples) of parents were randomly selected to obtain haplotype block partitions and the tag SNPs, by the dynamic programming program developed by Zhang et al. (2002). An equal number of case and control individuals were randomly selected in the case-control design.

The statistics TDT and CC were calculated on the basis of the SNPs or two-locus haplotypes, respectively. The P values over all the markers were obtained by either Bonferroni correction or the Monte Carlo procedure. Table 1 summarizes the methods compared in the present study. For each test, three different kinds of data were used to compare its power: (1) all of the SNPs and the haplotypes comprised by them; (2) the tag SNPs and the haplotypes comprised by them; and (3) the same number of randomly chosen SNPs and the haplotypes comprised by them.

Table 1.

Summary of Methods Compared in the Present Study

Test Method	Description
TDT-SNP-B	TDT using individual SNPs and Bonferroni correction for family data
TDT-SNP-M	TDT using individual SNPs and Monte Carlo procedure for family data
TDT-Hap-B	TDT using two-locus haplotypes and Bonferroni correction for family data
TDT-Hap-M	TDT using two-locus haplotypes and Monte Carlo procedure for family data
CC-SNP-B	χ2 using individual SNPs and Bonferroni correction for case-control data
CC-SNP-M	χ2 using individual SNPs and Monte Carlo procedure for case-control data
CC-Hap-B	χ2 using two-locus haplotypes and Bonferroni correction for case-control data
CC-Hap-M	χ2 using two-locus haplotypes and Monte Carlo procedure for case-control data

Type I Errors

We first verify that the proposed Monte Carlo methods have the correct nominal false-positive rates under different conditions. We randomly chose 200 individuals, 100 of whom were randomly assigned as control individuals and the other 100 of whom were treated as case individuals. This procedure was repeated 100 times for each of 10 populations, to obtain 1,000 samples. To obtain the haplotype block partitions and the tag SNPs, we set the percentage of common haplotypes, α, to either 0.80 or 0.70. The percentage of tagged samples, λ, was set to 0.05. The tag SNPs in the block were defined as the minimum number of SNPs that can distinguish at least α percent of haplotypes (Patil et al. 2001). The type I error rate was set to 5% and 1%. In table 2, we summarize the estimated type I error rates for all the statistical tests, for different α. For 1,000 replicated samples, the SE for the type I error rate estimate is 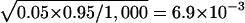when the true type I error rate is set to 5% and 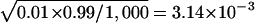when the true type I error rate is set to 1%. As shown in table 2, the estimated type I error rates when a Bonferroni correction is used tend to be conservative, and the type I error rates for the Monte Carlo methods tend to be larger than for the Bonferroni correction. However, none of these values are statistically significantly different from the nominal level.

Table 2.

The Type I Error (%) for the Proposed Methods, with α=.80 and λ=.05, for Different Type I Error Rates^[Note]

	Type I Error = 1%			Type I Error = 5%
Test Method	AllSNPs	TagSNPs	RandomSNPs	AllSNPs	TagSNPs	RandomSNPs
TDT-SNP-B	1.1	1.1	.8	2.8	3.3	3.8
TDT-SNP-M	1.4	1.4	.9	4.2	4.4	5.0
TDT-Hap-B	1.0	.8	1.1	3.8	4.6	5.1
TDT-Hap-M	1.1	1.0	.9	4.8	5.0	5.7
CC-SNP-B	.7	.9	.8	4.0	5.1	4.6
CC-SNP-M	.9	1.2	.9	5.4	5.6	5.3
CC-Hap-B	.3	.7	.3	2.6	3.9	2.9
CC-Hap-M	.8	1.5	.9	5.3	5.2	5.2

Note.— The tag SNPs are chosen as the minimum number of SNPs that can distinguish at least α percent of haplotypes. The results are based on 1,000 simulations.

Power Comparisons

Here we describe the results from our power study that used the above methods with various parameters and a type I error rate of 5%. We set the prevalence of the disease, P, to be 0.1, 0.05, and 0.01, corresponding to common, moderate, and rare diseases, respectively. We also varied the genotype relative risk, γ, between 2, 4, and 6. To investigate the effect of the coverage, we let α be either 0.70 or 0.80. Finally, the fraction of tagged samples used in the haplotype partitioning algorithm, λ, was either 0.05 or 0.10.

The power results for P=0.05 with various values of γ are given in table 3. α is set to 0.80 and λ is set to 0.05. The tag SNPs were chosen as the minimum number of SNPs that can distinguish at least α percent of the haplotypes. As expected, when the genotype relative risk γ=2, the power of all the methods is rather low, <0.2 in most cases. When γ=6, the power of all the approaches is very high, close to 1.0 in most cases. The most interesting case is when γ=4, in which case the power is 0.80–0.90 for most of the methods. It is also evident that the Monte Carlo methods are always more powerful than the Bonferroni correction. Qualitatively similar results were observed for P=0.1 and P=0.01 (data not shown). In the rest of this section, we use P=0.05 and γ=4 to compare the power of the different methods.

Table 3.

Power Results for Different Disease Models, with α=.80 and λ=.05^[Note]

	Power
	P=.05, γ=2			P=.05, γ=4			P=.05, γ=6
Test Method	AllSNPs	TagSNPs	RandomSNPs	AllSNPs	TagSNPs	RandomSNPs	AllSNPs	TagSNPs	RandomSNPs
TDT-SNP-B	.17	.16	.16	.91	.84	.77	1.00	.99	.96
TDT-SNP-M	.24	.20	.19	.94	.86	.80	1.00	.99	.97
TDT-Hap-B	.18	.19	.18	.93	.89	.83	1.00	1.00	.98
TDT-Hap-M	.23	.21	.21	.94	.91	.83	1.00	1.00	.98
CC-SNP-B	.19	.19	.17	.93	.87	.80	1.00	1.00	.97
CC-SNP-M	.24	.20	.19	.94	.88	.83	1.00	1.00	.97
CC-Hap-B	.15	.17	.15	.94	.91	.82	1.00	1.00	.97
CC-Hap-M	.23	.22	.19	.97	.93	.86	1.00	1.00	.99

Note.— The tag SNPs are chosen as the minimum number of SNPs that can distinguish at least α percent of haplotypes. The results are based on 1,000 simulations.

Haplotype Analysis versus Marker-by-Marker Analysis

One of the main points from table 3 is that the loss of power when tag SNPs are used is less than when the same number of randomly chosen SNPs are used, for both marker-by-marker and haplotype analysis. When only the tag SNPs are used, the average power of the marker-by-marker tests (TDT-SNP-B, TDT-SNP-M, CC-SNP-B, and CC-SNP-M) is reduced by ∼7%, 9%, 6%, and 7%, respectively, compared with the power when all SNPs are used. When the same number of randomly chosen SNPs is used, the corresponding numbers are 15%, 15%, 14%, and 13%, respectively. The power loss when randomly chosen SNPs are used is twice as large as when tag SNPs are used. For two-locus haplotype-based approaches (TDT-Hap-B, TDT-Hap-M, CC-Hap-B, and CC-Hap-M), the power when the tag SNPs are used is reduced by only ∼5%, 3%, 3%, and 4%, respectively, whereas the power of the tests when the same number of randomly chosen SNPs is used is reduced by ∼11%, 11%, 13%, and 11%, respectively. Thus, the power loss when tag SNPs are used for two-locus haplotype analysis is much less than that for marker-by-marker analysis. For haplotype approaches, the difference between using tag SNPs and using random SNPs is also larger than when using marker-by-marker approaches. It can also be seen that haplotype-based analysis is always more powerful than marker-by-marker analysis, in our simulations. Since the number of tag SNPs (31) is only ∼25% of the number of all the SNPs (128), the genotyping effort is substantially reduced without much loss of power.

The Effect of Coverage, Fraction of Tagged Samples, and Criterion for Defining Tag SNPs

To assess the influence that the haplotype block–partitioning algorithm has on the comparison, we also varied the coverage, α; the fraction of tagged samples, λ; and the criterion for defining the tag SNPs. The power results and the corresponding number of tag SNPs when P=0.05 and γ=4 are shown in tables 4 and 5, respectively. Several conclusions emerge. First, regardless of the values of α and λ, as well as the criterion for defining the tag SNPs, the differences between using all SNPs, the tag SNPs, and random SNPs are similar to what is described above. The power loss when tag SNPs are used is much less than when the same number of randomly chosen SNPs are used. Second, decreasing the coverage α in the block-partition algorithm decreases the number of tag SNPs and also reduces the power of the test statistics using the tag SNPs. For example, when λ=0.05 and Patil et al.'s (2001) criterion for defining the blocks is used, the average number of tag SNPs is reduced from 31 to 18, if we change α from 0.80 to 0.70. The corresponding power of the tests when the tag SNPs are used is also reduced. Third, on the basis of Patil et al.'s (2001) criterion for defining the haplotype blocks, the value of λ does not significantly change the number of tag SNPs required and the power of the tests using the tag SNPs, as expected. On the basis of the criterion of haplotype diversity (Johnson et al. 2001) for defining the haplotype blocks, both the number of tag SNPs and the power of the tests are significantly reduced when λ is changed from 0.05 to 0.10, which is not consistent with our intuition. This is probably caused by the definition of haplotype diversity. Fourth, when the third column and the seventh column in tables 4 and 5 are compared, the number of tag SNPs based on Patil et al.'s (2001) criterion is slightly higher than the number of tag SNPs based on the criterion of haplotype diversity (Johnson et al. 2001) (31 vs. 29). Similarly, the power of the tests when the tag SNPs are used is also similar for the two situations.

Table 4.

Power Results for Different α, λ, and Criteria for Defining Tag SNPs, with P=.05 and γ=4^[Note]

	Power
	Patil et al.'s (2001) Criteriona				Haplotype-Diversity Criterion(Johnson et al. 2001)b
	α=.70		α=.80		α=.70		α=.80
Test Method	λ=.05	λ=.10	λ=.05	λ=.10	λ=.05	λ=.10	λ=.05	λ=.10
TDT-SNP-B:
All SNPs	.88	.90	.91	.90	.90	.89	.89	.88
Tag SNPs	.75	.75	.84	.82	.79	.77	.80	.76
Random SNPs	.65	.68	.77	.77	.70	.66	.73	.70
TDT-SNP-M:
All SNPs	.92	.94	.94	.92	.93	.91	.91	.91
Tag SNPs	.76	.77	.86	.84	.80	.78	.83	.78
Random SNPs	.67	.71	.80	.79	.73	.69	.77	.72
TDT-Hap-B:
All SNPs	.90	.93	.93	.92	.93	.92	.93	.92
Tag SNPs	.82	.85	.89	.89	.87	.82	.88	.85
Random SNPs	.72	.76	.83	.84	.77	.74	.80	.77
TDT-Hap-M:
All SNPs	.92	.95	.94	.94	.94	.93	.95	.93
Tag SNPs	.84	.87	.91	.91	.88	.85	.90	.87
Random SNPs	.74	.77	.83	.85	.78	.75	.81	.79
CC-SNP-B:
All SNP	.94	.93	.93	.93	.94	.95	.94	.96
Tag SNPs	.80	.79	.87	.87	.82	.82	.87	.86
Random SNPs	.71	.73	.80	.81	.77	.74	.79	.77
CC-SNP-M:
All SNP	.95	.94	.94	.95	.95	.96	.95	.97
Tag SNPs	.81	.80	.88	.88	.83	.83	.87	.90
Random SNPs	.74	.75	.83	.82	.79	.76	.81	.78
CC-Hap-B:
All SNPs	.94	.95	.94	.94	.95	.95	.95	.95
Tag SNPs	.86	.87	.91	.91	.80	.83	.90	.90
Random SNPs	.73	.74	.82	.82	.78	.76	.81	.77
CC-Hap-M:
All SNPs	.96	.97	.97	.97	.97	.98	.97	.97
Tag SNPs	.89	.90	.93	.93	.91	.89	.93	.92
Random SNPs	.78	.78	.86	.86	.82	.79	.85	.80

Note.— The results are based on 1,000 simulations.

^aThe tag SNPs are chosen as the minimum number of SNPs that can distinguish at least α percent of haplotypes.

^bThe tag SNPs are chosen as the minimum number of SNPs that can explain at least β=.90 of overall haplotype diversity.

Table 5.

Number of Tag SNPs for Different α, λ, and Criteria for Defining Tag SNPs, with P=.05 and γ=4^[Note]

	No. of Tag SNPs
	Patil et al.'s (2001) Criteriona				Haplotype-Diversity Criterion(Johnson et al. 2001)b
	α=.70		α=.80		α=.70		α=.80
Sampling Scheme	λ=.05	λ=.10	λ=.05	λ=.10	λ=.05	λ=.10	λ=.05	λ=.10
Case-Parent Data	18	19	31	32	23	18	29	23
Case-Control Data	18	19	31	32	23	18	29	23

Note.— The results are based on 1,000 simulations.

^aThe tag SNPs are chosen as the minimum number of SNPs that can distinguish at least α percent of haplotypes.

^bThe tag SNPs are chosen as the minimum number of SNPs that can explain at least β=.90 of overall haplotype diversity.

Discussion

Genomewide association studies are likely to play a central role in the localization of genetic variants responsible for common human diseases. An understanding of haplotype block structure is essential for this effort. It is important to develop methods to identify block structure and the corresponding tag SNPs, as well as to understand the usefulness and limitations of tag SNPs for association studies. In the present study, we use Monte Carlo simulations to assess the power loss when tag SNPs instead of all SNPs are used in association studies. Using two-locus haplotype-based association tests, we find that, although the identified tag SNPs are only 25% of all the SNPs, the power is reduced by only 4%. When a comparable number of SNPs are chosen randomly, power loss is ∼12% when the same number of randomly chosen SNPs is used in a two-locus haplotype analysis. When the identified tag SNPs are ∼14% of all the SNPs, the power is reduced by ∼9%, compared with a power loss of ∼21% when the same number of randomly chosen SNPs is used in a two-locus haplotype analysis. It is generally believed that haplotype-based methods should outperform marker-by-marker–based methods, and this is confirmed in our study.

One of the critical assumptions in our study is that the population is homogeneous. Although the TDT method is valid even in structured populations, the simple case-control design can generate false-positive results due to population stratification. If the frequency of the SNPs and the haplotype distributions are different across populations, there will also be differences in haplotype block structure and tag SNPs. A possible way around this problem is to first use unrelated SNPs to divide a general population into several homogeneous populations (Pritchard and Rosenberg 1999) and then obtain the haplotype block partitions and the tag SNPs for each population.

Of course, population homogeneity is not the only important assumption that underlies our study. The coalescent simulations are based on several questionable assumptions, like a constant population size and uniformly distributed mutations and recombination break points. The approach we have taken is extremely flexible and could readily incorporate other assumptions. However, given the lack of reliable data to guide the modeling, we feel that the standard coalescent model is a reasonable first choice. The most important feature of population genetic data is the extremely complicated dependence structure, and this is efficiently captured by the standard coalescent.

In the present study, we keep only markers with a minor allele frequency of ⩾10% for further analysis. In further simulation experiments, we change this threshold to 5%, and the resulting haplotype block structure, tag SNPs, and qualitative results regarding the power of the different are very close to the results presented in the present article. In the present study, we assume that the haplotypes are completely known when we identify the haplotype blocks and the tag SNPs. In practice, the haplotype can be determined either experimentally, through methods such as allele-specific long-range PCR (Michlataos-Beloin et al. 1996) and diploid-to-haploid conversion (Douglas et al. 2001), or it can be extracted from genotype data through use of statistical methods (Clark 1990; Excoffier and Slatkin 1995; Hawley and Kidd 1995; Long et al. 1995; Stephens et al. 2001; Niu et al. 2002). Although current technologies are not suitable for the large-scale haplotyping, our study indicates that a small number of haplotypes suffice to determine the haplotype blocks. The power results when 5% of samples (20 haplotypes in our study) and 10% of samples (40 haplotypes in our study) are used to determine the haplotype blocks and the tag SNPs are essentially the same, on the basis of Patil et al.'s (2001) criterion for defining haplotype blocks. The experimental identification of such a small number of haplotypes can be achieved by the current technology. The effect that knowing genotypes instead of haplotypes has on haplotype block partition and tag SNP selection, as well as on the power of association studies, is a topic for future research.