Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2013 Nov 6;10(88):20130588. doi: 10.1098/rsif.2013.0588

Designing experiments to understand the variability in biochemical reaction networks

Jakob Ruess 1, Andreas Milias-Argeitis 1, John Lygeros 1,✉
PMCID: PMC3785824  PMID: 23985733

Abstract

Exploiting the information provided by the molecular noise of a biological process has proved to be valuable in extracting knowledge about the underlying kinetic parameters and sources of variability from single-cell measurements. However, quantifying this additional information a priori, to decide whether a single-cell experiment might be beneficial, is currently only possible in systems where either the chemical master equation is computationally tractable or a Gaussian approximation is appropriate. Here, we provide formulae for computing the information provided by measured means and variances from the first four moments and the parameter derivatives of the first two moments of the underlying process. For stochastic kinetic models for which these moments can be either computed exactly or approximated efficiently, the derived formulae can be used to approximate the information provided by single-cell distribution experiments. Based on this result, we propose an optimal experimental design framework which we employ to compare the utility of dual-reporter and perturbation experiments for quantifying the different noise sources in a simple model of gene expression. Subsequently, we compare the information content of a set of experiments which have been performed in an engineered light-switch gene expression system in yeast and show that well-chosen gene induction patterns may allow one to identify features of the system which remain hidden in unplanned experiments.

Keywords: continuous-time Markov chains, Fisher information, cell-to-cell variability, optimal experimental design, gene expression

1. Introduction

Quantitative studies of biological systems with mathematical models strongly depend on an appropriate characterization of the underlying system, that is on good knowledge about the underlying mechanisms and kinetic parameters. While extracting such knowledge from averaged cell population data is common practice, it has only recently been realized that also the molecular noise observed in single-cell measurements may be a rich source of information about the parameters of stochastic kinetic models [1–4]. Mathematically, one way to quantify the information provided by single-cell experiments is to determine the precision to which the model parameters can at best be estimated in a given experimental set-up, that is to determine the variances of the best possible unbiased estimators of the model parameters [5]. Thanks to the Cramér–Rao inequality these variances can be computed from the Fisher information matrix. To compute the Fisher information for stochastic kinetic models, one has to solve the chemical master equation (CME) [6] and take derivatives of its solution with respect to the model parameters. This is, however, only possible in the simplest cases and even approximation techniques either remain limited to very small systems [7] or are based on strong assumptions [8,9], which are not always fulfilled in real applications. Consequently, experiments are usually designed based on the intuition of the experimenter, rather than on information theoretic criteria.

A second difficulty in the analysis and design of single-cell experiments is that stochastic kinetic models are usually based on the assumption that the same process governs the evolution in all cells of the population. This, however, is generally not the case, because the process of interest often interacts with other unmodelled factors which are themselves subject to fluctuations and differ between the cells. For instance, differences in cell size, local growth conditions or expression capacity [10,11] may lead to additional variability in the cell population. In many instances, noise resulting from such extrinsic variability [12–14] has been reported to dominate the molecular noise of the process under study [15–17]. In such situations, methods which assume a homogeneous cell population and attribute all the observed variability to molecular noise of the modelled reactions may lead to biased results. Sometimes, it may be appropriate to assume that such unmodelled factors are static for the time scales of interest. For example, in the model of the stress response of budding yeast to osmotic pressure in Zechner et al. [3], the number of mitochondria affecting translation changes much more slowly than species in signalling and transcription cascades. In this case, the number of mitochondria can be taken as random but constant in time for the purposes of the model. In other cases, however, species which are not included in the model but affect reaction rates may evolve on time scales comparable to those of the reactions of interest [12,18,19], for instance global regulators affecting transcription. In theory, one should include such species in the model but this is often not practical because it would lead to models of intractable size. A convenient modelling abstraction may then be to include a stochastic process for some of the rates, to serve as a rudimentary abstraction of the complex mechanisms governing the fluctuations of the reaction rates [11].

In this paper, we propose a framework for optimally designing single-cell distribution experiments for identifying the parameters of stochastic kinetic models in which the reaction rates are possibly governed by stochastic differential equations. To this end, we first demonstrate on systems where one reaction rate is governed by a stochastic differential equation how equations describing the time evolution of the moments of the probability distribution can be derived. We then show how the Fisher information can be approximated from the first four moments and the parameter derivatives of the first two moments without the need of any assumption other than a sufficiently large measured cell population. Finally, we embed the approximated Fisher information into an optimization algorithm which returns the most informative experiment for a specified set of model parameters. This allows us to design optimal experiments for identifying specific features of the system. We demonstrate this by comparing dual-reporter and perturbation experiments in a simple model of gene expression, where the mRNA production rate is varying according to a stochastic differential equation. Finally, we study the variability in an engineered light-switch gene expression system in yeast. We use our methodology to evaluate the experiments that were performed in Milias-Argeitis et al. [20] and show that they strongly differ in the information provided about the unknown parameters. Furthermore, we show that an experiment found by using our optimal experimental design procedure would lead to far more information than any of the experiments reported in Milias-Argeitis et al. [20].

2. Material and methods

2.1. Moment equations for reaction systems with stochastically varying reaction rates

The time evolution of the probability distribution of stochastic kinetic models is governed by the CME. If variability in the reaction rates is present in a population, the distribution for each cell can be described by a CME, which is conditioned on the realizations of the reaction rates in the cell. In the study of Zechner et al. [3], it was shown how population moments can be computed from this conditional CME under the assumption that the reaction rates are constant in time. More generally, assume now that a reaction rate at is governed by a stochastic differential equation of the form

2.1. 2.1

where Wt is a standard Brownian motion. This process fluctuates around its mean μa, where the mean reversion speed r gives the autocorrelation time of the process, and thereby determines the time scale of the rate fluctuation. The noise coefficient s determines the size of the deviations from the mean, whereas the term 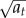Inline graphic prevents the process from taking negative values and is in accordance with the frequently used Langevin approximation for chemical reaction networks [9]. Note that this formulation includes constant reaction rates as for r = s = 0 the process at is constant and always distributed according to its initial distribution.

The system which jointly describes the time evolution of the species and the reaction rate is a stochastic hybrid system [21]. The time evolution of the moments can be computed as

2.1. 2.2

where x(t) = [x1(t) … xm(t)] is a vector containing the molecule counts of the m species and Inline graphic is chosen such that the left-hand side gives the derivative of the desired moment. L is the extended generator of the stochastic hybrid system, given by

2.1.

where f(a) = r(μa − a), νi are the stoichiometric transition vectors and wi(a, x) the propensities of the K reactions. Note that the resulting system of moment equations may be non-closed in the sense that the time evolution of the moments of any order depends on moments of higher order. In such cases, the moments cannot be computed exactly and approximation techniques have to be used [22–24].

2.2. Approximating the Fisher information

The amount of information about model structure or parameters, which can be gained from measurements, may be highly dependent on the experimental set-up that is chosen [25–29]. Carefully planning an experiment reduces experimental effort and resources and may even allow one to answer questions which cannot be answered from unplanned experiments.

One way to assess the information about a vector of unknown model parameters θ = [θ1 … θN]T that an experimental set-up can supply is through the computation of the Fisher information matrix I(θ) [5,30]. The diagonal elements of the inverse of I(θ) give lower bounds for the variances that any unbiased estimators of the model parameters can attain, and thus the Fisher information gives a measure of the accuracy to which the model parameters can be estimated in a given experimental setting (for a more detailed discussion, we refer the reader to [5]). The elements of the Fisher information matrix are given by

2.2.

where Y is the random variable which is experimentally measured and f(Y;θ) is its distribution. In stochastic kinetic models, the parameter vector θ typically contains reaction rates and possibly also parameters describing the variability in the reaction rates, for instance, moments of the parameter distributions [3] or the coefficients r, μa and s in equation (2.1). Because the values of the elements of the parameter vector often differ by orders of magnitude, it is sometimes more appropriate to compute the derivatives with respect to the logarithm of the parameters. It can be shown that these derivatives correspond to the sensitivity of the measured output with respect to the relative, instead of the absolute, changes in the parameters. The Fisher information matrix for a logarithmic parametrization can be readily obtained from the original Fisher information matrix (see electronic supplementary material, §S.1.5) and the parametrization is therefore not of importance for the formulae provided in this paper.

Population measurements, such as those provided by flow cytometry, can be viewed as a large number of independent samples Y1, … ,Yn, which are drawn from a marginal distribution f(Y;θ) of the underlying process. The computation of f(Y;θ) requires the solution of the CME, and therefore the computation of the Fisher information matrix which requires the parameter derivatives of the logarithm of f(Y;θ) is only possible in cases where the solution of the CME can be computed exactly or at least approximated accurately. An alternative approach for computing the Fisher information resorts to a Gaussian assumption on the underlying Markov process [5,31]. Under this assumption, the sample mean and variance of the measured population form a jointly sufficient statistic. Hence, computation of the Fisher information reduces to solving the differential equations that describe the dynamics of mean and variance of f(Y;θ) and computing their partial derivatives with respect to θ. There are, however, many systems where a Gaussian assumption is not appropriate [3,32]. In such cases, the method in [5] may lead to erroneous results for several reasons. First, the computed means and variances of f(Y;θ) may be inaccurate. Second, information that can be gained from higher order moments is neglected. And third, the Gaussian approximation implicitly assumes that sample mean and variance provide independent pieces of information, an assumption which is violated for all non-Gaussian distributions [33]. For instance, for a Poisson distribution the sample mean is already a sufficient statistic on its own and the variance adds no new information (see electronic supplementary material, §S.1.2).

In situations where a Gaussian assumption is not applicable, it may still be possible to approximate the information which is provided by sample mean and variance. If the sample size is sufficiently large, the central limit theorem implies that sample mean and variance are approximately jointly Gaussian. For simplicity, assume that there is only one unknown parameter θ and that only one species is measured (a more general case is treated in the electronic supplementary material, §S.1.3). The information given by the mean Im(θ) and the joint information given by mean and variance IJ(θ) can then be approximated using the special form of the Fisher information for multivariate Gaussian random variables (see electronic supplementary material, §S.1.1 and S.1.3), which results in

2.2. 2.3

and

2.2. 2.4

where n is the size of the sample, μ1 denotes the mean and μk the central moments of order k = 2, 3, 4.

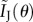These formulae are valid for any distribution which satisfies the requirements of the central limit theorem. Furthermore, it can be shown [34] that Inline graphic and Inline graphic provide lower bounds on the information of the whole sample. For a Gaussian distribution, as μ3 = 0 and Inline graphic, Inline graphic reduces to the correct expression for the complete information. For a Poisson distribution, as μ1 = μ2 = μ3, 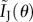Inline graphic reduces to 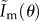Inline graphic, which again gives the correct expression for the complete information.

2.3. Designing optimal experiments

The goal of experimental design is to find the experiment which is optimal according to some criterion reflecting information about the unknown parameters. The most frequently used criteria are D-optimality, A-optimality and E-optimality which correspond to maximizing the determinant, minimizing the trace of the inverse and maximizing the minimal eigenvalue of the Fisher information matrix, respectively [27,35]. In biological applications, it is often desirable to design experiments which are targeted to specific parameters or to subsets of the parameter set. For instance, one might want to estimate the reaction rates of the model as well as possible, despite the presence of variability in some of the rates or parameters of a noise model which have no biological meaning. An optimality criterion targeted to such questions is Ds-optimality [36,37]. It is based on partitioning the parameter vector θ = [θ1 θ2]T in parameters of interest θ1 and nuisance parameters θ2. The experiment, which allows one to obtain the confidence region with minimum volume for θ1 can then be found by maximizing the determinant of

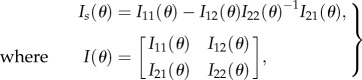2.3. 2.5

where I11(θ) and I22(θ) are the information matrices for θ1 and θ2, respectively, and I12(θ) and I21(θ) give the cross terms between θ1 and θ2.

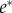The computation of I(θ) and Is(θ) requires knowledge of the true parameters θ, which are not available. This difficulty can be overcome by evaluating the information at some initial estimate Inline graphic [30]. If, however, this initial estimate differs significantly from the true parameter vector, the resulting experiment may be far from optimal. This is especially important for biological applications where initial estimates, if available at all, usually involve large uncertainties. Here, we chose an approach which includes the uncertainty of the initial estimate in the form of a prior distribution π(θ) and computes the expected information with respect to π(θ) [38,39] (for an overview of other methods, see electronic supplementary material, §S.4). The corresponding optimal experiment Inline graphic can then be obtained by solving the following optimization problem:

2.3. 2.6

where the expectation is taken over θ ∼ π(θ), Is(θ, e) is the information matrix for experiment e evaluated at θ and ℰ is the set of possible experiments. We can now state a procedure for designing optimal experiments for the estimation of parameters of stochastic kinetic models from single-cell measurements of a cell population.

Some comments on practical applicability of this procedure are given in the electronic supplementary material, §S.1.6.

This optimal experimental design procedure can be performed in iterations with experiments. Starting from some prior distribution π(θ), the computations lead to optimal experiments that yield data which can be used in a parameter inference scheme to compute posterior distributions. These can then in turn serve as new prior distributions for the computation of a new optimal experiment. This can be continued until the uncertainty about the parameters has been sufficiently reduced.

The optimal experimental design procedure

  • — Define a model, potentially including stochastic effects in reaction rates as in equation (2.1).

  • — Derive the differential equations for the required moments using equation (2.2). If the moment equations are non-closed and cannot be solved exactly then use an approximation method [22,23].

  • — Solve the differential equations to compute the moments and their partial derivatives with respect to the parameter vector as functions of θ and t.

  • — Choose a vector θ1 of parameters of interest and specify the distribution π(θ) according to prior uncertainty about θ.

  • — Solve the optimization problem in equation (2.6), where the total information Is(θ, e) is replaced by the approximated information of sample mean and variance according to equation (2.4).

3. Results

3.1. In silico study of a gene expression system

We demonstrate the proposed experimental design framework on a simple example of gene expression. The model we consider consists of the two species mRNA (M) and protein (P) and the four reactions

3.1.

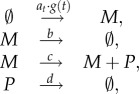where b = 0.03, c = 0.5, d = 0.04 and at is varying according to a stationary stochastic process of the form equation (2.1). The dynamics of the moments of order up to two of M and P are then completely determined by the mean reversion speed r and mean μa and variance Va of the stationary distribution of at (see electronic supplementary material, §S.2.1). Here, we assume that the values of these parameters are μa = 0.5, Va = 0.1 and r = 0.005. We further assume that the gene can be switched between an on state (where g(t) = 1) and an off state (where g(t) = 0) using some external input, for example, either by adding different nutrients in nutrient shift experiments [40], by adding salt to induce the osmotic stress response [41] or with light pulses [20]. Furthermore, throughout this section, we assume that it is known that no molecules are present at time t = 0 (loosely speaking, the gene has been off for some time at the start of the experiment) and that the degradation rates b and d are known, whereas μa, Va, r and c have to be determined from the measurements. Finally, for simplicity, all the computations of this section are performed locally at the ‘true’ parameter values and prior uncertainty about the parameters is not included.

We compare four experimental methods in terms of the information they can provide about the unknown parameters. For all methods, we assume that the experiments are limited to a time length of t = 300 time units and that at most 10 measurements of the protein distribution are taken during that time. The first two methods we consider are standard time course experiments, where the gene is switched on only at time zero and measurements are taken in regular time intervals (every 30 time units). In the first method (referred to as unplanned experiments), we assume that a single reporter protein is measured, whereas in the second method (unplanned dual-reporter experiments), an identical copy of the gene is added to the cells, such that a second reporter protein which is conditionally independent of P, given the history of at, can be measured [15,42,43]. These two methods are compared to more sophisticated experiments where informative gene-switching patterns and measurement times are identified using our experimental design framework.

For the optimally designed experiments, we again consider both single and dual-reporter experiments (referred to as optimal perturbation and optimal dual-reporter experiments, respectively). In both cases, the search for the most informative experiments proceeds in two steps. First, we fix equally spaced measurement times and use a Markov chain Monte Carlo-like algorithm to perform the optimization on the space of possible gene-switching pattern. Second, we fix the resulting gene-switching pattern and sequentially place the measurement times, where they yield maximal information. More details on this algorithm are given in the electronic supplementary material, §S.2.2. Figure 1 gives the resulting optimal perturbation experiments when either r or Va is taken as parameter of interest (θ1 in equation (2.5)) and the remaining parameters are taken as nuisance parameters (θ2 in equation (2.5)). Results for the remaining parameters and results for the optimal dual-reporter experiments are given in the electronic supplementary material, figures S2 and S3. It can be seen that different perturbations and measurement times are optimal for identifying different parameters.

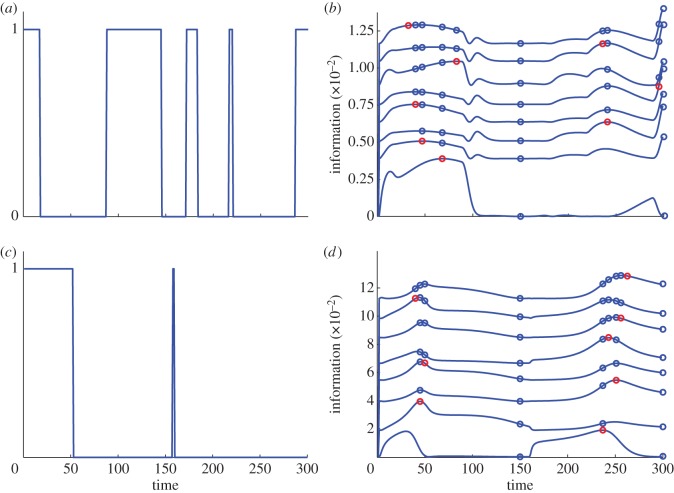
Figure 1.

Figure 1.

Open in a new tab

Optimal perturbation experiments for the parameters r (a,b) and Va (c,d). (a,c) Gene-switching patterns found by employing the experimental design procedure. A value of one corresponds to the gene being switched on, a value of zero to the gene being switched off. (b,d) Information (for a logarithmic parametrization) normalized by the sample size n for measurements at N + 1 time points, where the (N + 1)th time point is in addition to the N time points which were already placed. The different lines correspond to N = 2,3, … , 9. The blue circles correspond to the measurement time points which were already placed and the red circles correspond to the best choice for the (N + 1)th measurement time point.

The results of the comparison of the four methods are summarized in table 1. Note that the reported values correspond to a logarithmic parametrization to allow one to compare the information obtained for different parameters (rows). From the first column, we see that the information which can be gained from unplanned experiments is very small. This indicates that the parameters may be practically unidentifiable (see also the discussion in the electronic supplementary material, §S.2.3). Unplanned dual-reporter experiments, on the other hand, lead to much more information (second column in table 1) and appear to be suitable for identifying all the parameters of the system. Only r potentially remains difficult to identify. In general, r and Va are harder to identify than μa and c because the protein mean does not depend on r and Va, and hence they can only be identified from the protein variance. The information of the optimal perturbation experiments which were found by our experimental design procedure are given in the third column of table 1, where for all parameters the first value corresponds to the information which is obtained if the experiment is specifically targeted at the parameter (taking all other parameters as nuisance parameters) and the second value corresponds to the information which is obtained if the experiment is targeted at estimating all parameters. It can be seen that, compared to dual-reporter experiments, more information is obtained for the parameter r, whereas dual-reporter experiments lead to more information for μa, Va and c. Hence, depending on the objective of the study, different experimental strategies are preferable. The fourth experimental method, which combines optimal perturbations and dual reporters, naturally leads to the most information for all parameters (fourth column in table 1). Note, however, that the increase in information compared to unplanned dual-reporter experiments is very small if μa or c are the parameters of interest, which indicates that additionally perturbing the system may not be worth the effort. Furthermore, contrary to the optimal perturbation experiments, targeting the dual-reporter experiment at specific parameters (first value in the fourth column) yields only a minor increase in information compared with an experiment which is targeted at all parameters (second value in the fourth column). The experiment targeted at identifying r even leads to less information about r than the experiment targeted at all parameters which shows that the optimization algorithm used for finding informative experiments converged to a local minimum in the former case.

Table 1.

Comparison of different experimental approaches. Information normalized by the sample size n. Rows: information for different parameters of interest. Columns: information which can be gained by different experimental approaches. Computations corresponding to unplanned experiments were performed with the gene being switched on only once at time zero and equally spaced measurement times. Optimal experiments include optimal gene-switching patterns and sequentially placed measurement times (see electronic supplementary material, §S.2.2).

unplanned experiment unplanned dual reporter optimal perturbations targeted to particular parameter / all parameters optimal dual reporter targeted to particular parameter / all parameters
μa 0.0009 2.5776 1.1125 / 0.4063 2.7201 / 2.4877
Va 0.0002 0.1869 0.1286 / 0.0704 0.3690 / 0.3496
c 0.0009 2.8303 1.1817 / 0.4047 3.1083 / 2.7248
r 0.0012 0.0068 0.0129 / 0.0096 0.0244 / 0.0262
Open in a new tab

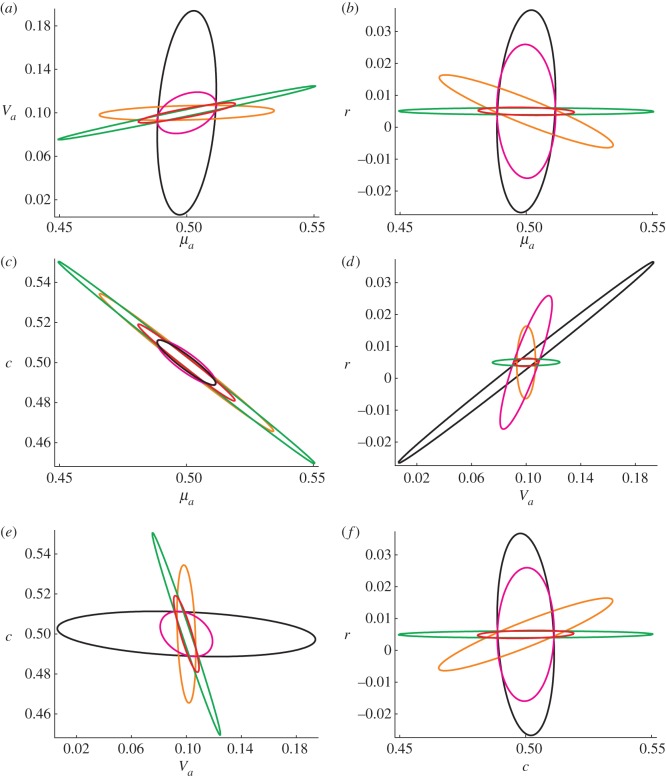
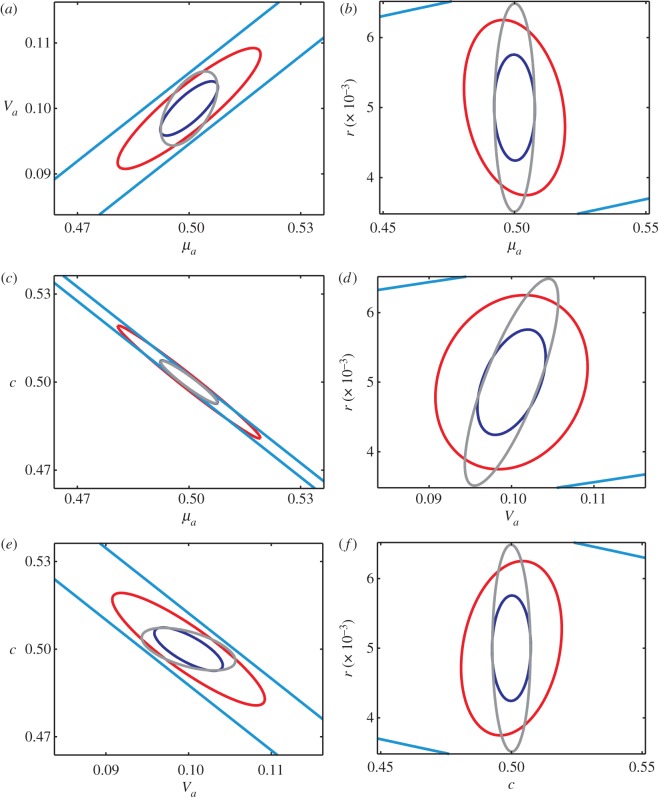
The maximum-likelihood estimator for the parameter vector is asymptotically normally distributed with covariance matrix equal to the inverse of the Fisher information matrix. We can therefore further visualize our results by computing confidence regions for the maximum-likelihood estimator in the different experiments. Figure 2 shows two-dimensional 95% confidence ellipses for all pairs of parameters for the optimal perturbation experiments targeted at each of the parameters where we assume that at each time point a cell population of size n = 10 000 is measured. The red ellipses correspond to the experiment which is targeted at all parameters and are therefore overall the smallest. However, the variance in the direction of each of the parameters can be reduced by specifically targeted experiments. The most significant difference can be seen in the experiments targeted either at μa or c (black and magenta) where the size of the ellipses is reduced in both the directions of μa and c at the cost of making r and Va much harder to identify. The parameter r is the hardest to identify and can only be reasonably constrained by experiments targeted either directly at r or at all parameters. Figure 3 shows two-dimensional 95% confidence ellipses for all pairs of parameters for the unplanned experiment, the unplanned dual-reporter experiment, the optimal perturbation experiment targeted at all parameters and the optimal dual-reporter experiment targeted at all parameters. Again, we assume that at each time point a cell population of size n = 10 000 is measured. As already indicated by the information values in table 1, the parameters are almost unidentifiable from unplanned experiments. All the other experiments, on the other hand, can constrain the parameters to relatively small regions.

Figure 2.

Figure 2.

Open in a new tab

Comparison of optimal perturbation experiments targeted at different parameters. Ninety-five per cent confidence ellipses for all pairs of parameters are shown in the different panels. Experiments are targeted at μa (black), Va (orange), c (magenta), r (green) and all parameters (red). Note that these ellipses correspond to confidence regions for the original parameters (not their logarithms).

Figure 3.

Figure 3.

Open in a new tab

Comparison of the different experimental approaches. Ninety-five per cent confidence ellipses for all pairs of parameters are shown in the different panels. Light blue, unplanned experiment; grey, unplanned dual-reporter experiment; red, optimal perturbation experiment targeted at all parameters; dark blue, optimal dual-reporter experiment targeted at all parameters. As in figure 2, the plots are in linear scale. Note that the red ellipses are the same as those shown in figure 2, with a different scaling of the axes.

Finally, we also computed the information under a Gaussian assumption. Our results (electronic supplementary material, table S1 and figure S4) show that for many objectives a Gaussian assumption leads to information estimates which are overly optimistic. This is most probably owing to the independence assumption of sample mean and variance which is implicitly imposed by a Gaussian approximation and is not valid for the system in question.

3.2. Characterizing variability in a light-induced gene expression system

Next, we study a light-switch gene expression system which has been engineered in yeast [20]. The authors used a light responsive module to initiate transcription by shining red light on the yeast culture and to terminate transcription by shining far-red light. They then proposed a control scheme to regulate the mean amount of protein in the population. The development of more sophisticated control schemes (for example, to allow one to also control the protein variance) requires a proper characterization of the sources of variability in the system. To this end, our framework can be used to compare the utility of different experiments, and ultimately to design the experiments which are optimal for the characterization of the different noise sources. We thus developed a stochastic version of the model [20] which includes a stochastic differential equation of the form equation (2.1) for the mRNA production rate. This introduced four additional parameters which were not identified in Milias-Argeitis et al. [20]. To characterize uncertainty about these parameters, we chose independent uniform prior distributions and computed the expectation of the information (for a logarithmic parametrization), which is provided by the experiments reported in fig. 1 of Milias-Argeitis et al. [20] about each of the additional parameters according to equations (2.5). Thereby, the remaining parameters which were already identified in Milias-Argeitis et al. [20] were fixed to their known values (see electronic supplementary material, §S.3.1 and §S.3.2). The results are shown in tables S2 and S3 in the electronic supplementary material. Which experiment is best again depends on the objective. For instance, the experiment where a red light pulse is applied at the beginning and a far-red light pulse after 30 min is best for identifying the protein production rate but worst for identifying the mean reversion rate r of the mRNA production rate. This is most probably owing to the fact that if the gene is switched off, the mRNA production rate is set to zero and the parameters describing this rate do not influence the dynamics anymore.

Furthermore, our results show that even though the experiments in fig. 1e of Milias-Argeitis et al. [20] were performed over a shorter time and contain fewer measurements than the experiments in fig. 1c of Milias-Argeitis et al. [20], they provide much more information about the parameter r. This suggests that experiments where the gene is expressed for short time intervals with silent periods in between could allow one to determine r, and thus to test whether the mRNA production rate can be assumed to be constant or whether a stochastic process description as used in this paper is required. Our results in the electronic supplementary material, §S.3.3 indicate that indeed, contrary to other experiments, the variance measured in the experiments in fig. 1e in Milias-Argeitis et al. [20] cannot be explained very well by a model with constant mRNA production.

Finally, we also employed our experimental design framework to search for experiments which carry high information about r. The light-pulse pattern and measurement times we determined with our method are shown in figure 4. They lead to an experiment which carries close to four times more information than any of the experiments in Milias-Argeitis et al. [20] suggesting that our experimental design framework can be a valuable tool for characterizing variability in this system.

Figure 4.

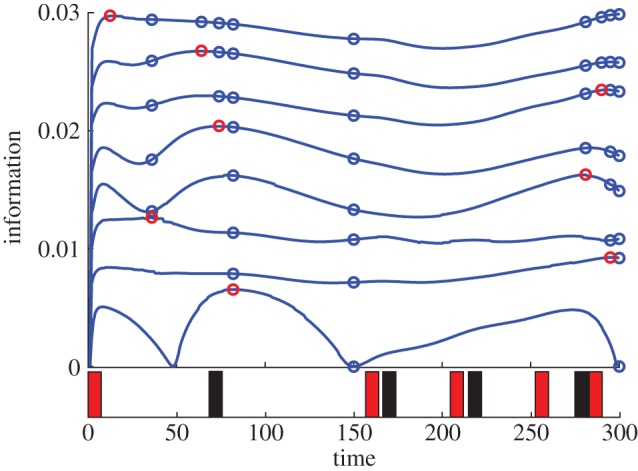
Figure 4.

Open in a new tab

Results of experimental design targeted at the parameter r for the light-switch gene expression system. The optimal light-pulse pattern is shown at the bottom of the figure. Red rectangles correspond to red light pulses and black rectangles correspond to far-red light pulses. The upper part of the figure shows the optimal measurement times, where the interpretation is the same as in figure 1.

4. Discussion

While knowledge about biological mechanisms is constantly growing, our understanding of the stochasticity of biological systems and its influence on system dynamics remains rather limited. Many different sources of variability may play a role and neglecting any one of them may lead to over- or underestimating the effect of others. In the gene expression model, for instance, one could use the methods of Friedman et al. [44] to estimate the protein burst size and frequency from measurements of the stationary protein distribution, under the assumption that the mRNA production is the same for all cells in the population. If, however, the data actually come from a population with variable mRNA production rate these estimates would be biased—potentially by more than an order of magnitude (see electronic supplementary material, §S.2.3). Allowing reaction rates to vary between individuals in a cell population offers a way to incorporate variability stemming from unknown factors and enables model-based studies of heterogeneous cell populations. We showed how the information about unknown parameters of such models which is provided by means and variances of measured populations can be approximated if the first four moments and the parameter derivatives of the first two moments of the underlying process can be computed. The derived formulae are applicable as long as the measured population is of sufficient size for the application of the central limit theorem. This opens up the possibility to pose many interesting questions: do the measurements contain enough information to separate different noise sources? How much information can be gained by measuring the variance in addition to the mean? And most importantly: what is the most informative experiment? By means of examples, we demonstrated that unplanned experiments may not contain enough information to identify the model parameters and that designing experiments based on intuition alone may not be sufficient. For instance, placing all the measurements either very early or very late in the experiment turns out to be better for identifying the mean reversion speed in our examples (figures 1 and 4) but appears very unintuitive at a first glance.

Our results (table 1 and figure 2; electronic supplementary material, figure S2) show that the optimal experiments are highly dependent on the chosen objective. In some cases, introducing a dual reporter yields high information, in other cases perturbing the system with input stimuli is preferable. A study of the system using the experimental design framework presented in this paper allows a comparison of the different experimental approaches and enables one to choose the approach which is most likely to be successful for the given objective. The resulting experiments can in turn be used to refine the model and to update the parameter estimates, giving rise to an iterative procedure of successive rounds of computations and experiments.

In the light-switch gene expression system, the computation of the information contents of the different experiments shows that perturbing the system with different light-pulse sequences can highlight different features of the system. This suggests that well-chosen gene induction patterns may allow one to uncover features of the system which remain hidden in unplanned experiments. For instance, the electronic supplementary material, figure S5 suggests that temporal fluctuations in the mRNA production rate may play a role for this system. Perturbing a system with light pulses to understand the variability may seem to be limited to this specifically engineered system. However, a similar strategy could also be employed by exploiting naturally occurring biological mechanisms. For example, in the study of Zechner et al. [3], the authors studied gene expression in yeast in response to osmotic pressure. Different salt concentrations led to different residence times of the signalling molecule Hog1 in the nucleus, and thereby created different input signals to the downstream gene expression system. In that system, multiple subsequent salt stresses, which can for instance be implemented using a microfluidic device as in Uhlendorf et al. [41], could serve as the equivalent of the multiple light pulses used in this paper and might give further insights into the specific nature of the system.

Acknowledgements

J.R. and J.L. designed research. J.R. developed the method and performed the computations. A.M. assisted with supplementary calculations. J.R. and J.L. wrote the paper.

Funding statement

The work was supported in part by the European Commission under the project MoVeS.

References

  • 1.Munsky B, Trinh B, Khammash M. 2009. Listening to the noise: random fluctuations reveal gene network parameters. Mol. Syst. Biol. 5, 318 ( 10.1038/msb.2009.75) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Neuert G, Munsky B, Tan RZ, Teytelman L, Khammash M, van Oudenaarden A. 2013. System identification of signal-activated stochastic gene regulation. Science 339, 584–587. ( 10.1126/science.1231456) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Zechner C, Ruess J, Krenn P, Pelet S, Peter M, Lygeros J, Koeppl H. 2012. Moment-based inference predicts bimodality in transient gene expression. Proc. Natl Acad. Sci. USA 109, 8340–8345. ( 10.1073/pnas.1200161109) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Singh A, Razooky B, Dar R, Weinberger L. 2012. Dynamics of protein noise can distinguish between alternate sources of gene-expression variability. Mol. Syst. Biol. 8, 607 ( 10.1038/msb.2012.38) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Komorowski M, Costa M, Rand D, Stumpf M. 2011. Sensitivity, robustness, and identifiability in stochastic chemical kinetics models. Proc. Natl Acad. Sci. USA 108, 8645–8650. ( 10.1073/pnas.1015814108) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Gillespie D. 1992. A rigorous derivation of the chemical master equation. Physica A 188, 404–425. ( 10.1016/0378-4371(92)90283-V) [DOI] [Google Scholar]
  • 7.Munsky B, Khammash M. 2006. The finite state projection algorithm for the solution of the chemical master equation. J. Chem. Phys. 124, 044104 ( 10.1063/1.2145882) [DOI] [PubMed] [Google Scholar]
  • 8.van Kampen N. 2006. Stochastic processes in physics and chemistry. Amsterdam, The Netherlands: Elsevier Science. [Google Scholar]
  • 9.Gillespie D. 2000. The chemical Langevin equation. J. Chem. Phys. 113, 297–306. ( 10.1063/1.481811) [DOI] [Google Scholar]
  • 10.Snijder B, Pelkmans L. 2011. Origins of regulated cell-to-cell variability. Nat. Rev. Mol. Cell Biol. 12, 119–125. ( 10.1038/nrm3044) [DOI] [PubMed] [Google Scholar]
  • 11.Shahrezaei V, Ollivier J, Swain P. 2008. Colored extrinsic fluctuations and stochastic gene expression. Mol. Syst. Biol. 4, 196 ( 10.1038/msb.2008.31) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Hilfinger A, Paulsson J. 2011. Separating intrinsic from extrinsic fluctuations in dynamic biological systems. Proc. Natl Acad. Sci. USA 108, 12 167–12 172. ( 10.1073/pnas.1018832108) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Koeppl H, Zechner C, Ganguly A, Pelet S, Peter M. 2011. Accounting for extrinsic variability in the estimation of stochastic rate constants. Int. J. Robust Nonlin. 22, 1103–1119. ( 10.1002/rnc.2804) [DOI] [Google Scholar]
  • 14.Hilfinger A, Chen M, Paulsson J. 2012. Using temporal correlations and full distributions to separate intrinsic and extrinsic fluctuations in biological systems. Phys. Rev. Lett. 109, 248104 ( 10.1103/PhysRevLett.109.248104) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Elowitz M, Levine A, Siggia E, Swain P. 2002. Stochastic gene expression in a single cell. Science 297, 1183–1186. ( 10.1126/science.1070919) [DOI] [PubMed] [Google Scholar]
  • 16.Colman-Lerner A, Gordon A, Serra E, Chin T, Resnekov O, Endy D, Pesce G, Brent R. 2005. Regulated cell-to-cell variation in a cell-fate decision system. Nature 437, 699–706. ( 10.1038/nature03998) [DOI] [PubMed] [Google Scholar]
  • 17.Volfson D, Marciniak J, Blake W, Ostroff N, Tsimring L, Hasty J. 2005. Origins of extrinsic variability in eukaryotic gene expression. Nature 439, 861–864. ( 10.1038/nature04281) [DOI] [PubMed] [Google Scholar]
  • 18.Chabot J, Pedraza J, Luitel P, Van Oudenaarden A. 2007. Stochastic gene expression out-of-steady-state in the cyanobacterial circadian clock. Nature 450, 1249–1252. ( 10.1038/nature06395) [DOI] [PubMed] [Google Scholar]
  • 19.Rosenfeld N, Young J, Alon U, Swain P, Elowitz M. 2005. Gene regulation at the single-cell level. Science 307, 1962–1965. ( 10.1126/science.1106914) [DOI] [PubMed] [Google Scholar]
  • 20.Milias-Argeitis A, Summers S, Stewart-Ornstein J, Zuleta I, Pincus D, El-Samad H, Khammash M, Lygeros J. 2011. In silico feedback for in vivo regulation of a gene expression circuit. Nat. Biotechnol. 29, 1114–1116. ( 10.1038/nbt.2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Hespanha J. 2006. Modeling and analysis of stochastic hybrid systems. IEE Proc. Control Theory Appl. 153, 520–535. ( 10.1049/ip-cta:20050088) [DOI] [Google Scholar]
  • 22.Ruess J, Milias-Argeitis A, Summers S, Lygeros J. 2011. Moment estimation for chemically reacting systems by extended Kalman filtering. J. Chem. Phys. 135, 165102 ( 10.1063/1.3654135) [DOI] [PubMed] [Google Scholar]
  • 23.Singh A, Hespanha J. 2011. Approximate moment dynamics for chemically reacting systems. IEEE Trans. Automat. Contr. 56, 414–418. ( 10.1109/TAC.2010.2088631) [DOI] [Google Scholar]
  • 24.Ale A, Kirk P, Stumpf M. 2013. A general moment expansion method for stochastic kinetic models. J. Chem. Phys. 138, 174101 ( 10.1063/1.4802475) [DOI] [PubMed] [Google Scholar]
  • 25.Bandara S, Schlöder J, Eils R, Bock H, Meyer T. 2009. Optimal experimental design for parameter estimation of a cell signaling model. PLoS Comput. Biol. 5, e1000558 ( 10.1371/journal.pcbi.1000558) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Busetto A, Ong C, Buhmann J. 2009. Optimized expected information gain for nonlinear dynamical systems. In Proc. 26th Annual Int. Conf. on Machine Learning, Montreal, Canada, 14–18 June, pp. 97–104. New York, NY: ACM. [Google Scholar]
  • 27.Franceschini G, Macchietto S. 2008. Model-based design of experiments for parameter precision: state of the art. Chem. Eng. Sci. 63, 4846–4872. ( 10.1016/j.ces.2007.11.034) [DOI] [Google Scholar]
  • 28.Liepe J, Filippi S, Komorowski M, Stumpf M. 2013. Maximizing the information content of experiments in systems biology. PLoS Comput. Biol. 9, e1002888 ( 10.1371/journal.pcbi.1002888) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Zechner C, Nandy P, Unger M, Koeppl H. 2012. Optimal variational perturbations for the inference of stochastic reaction dynamics. In IEEE 51st Annual Conf. on Decision and Control (CDC), Maui, Hawaii, 10–13 December, pp. 5336–5341. New York, NY: IEEE. [Google Scholar]
  • 30.Hagen D, White J, Tidor B. 2013. Convergence in parameters and predictions using computational experimental design. Interface Focus 3, 20130008 ( 10.1098/rsfs.2013.0008) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Wlodarczyk M, Lipniacki T, Komorowski M. 2013. Functional redundancy in the NF-κB signalling pathway. (http://arxiv.org/abs/1303.3109). [Google Scholar]
  • 32.Arkin A, Ross J, McAdams H. 1988. Stochastic kinetic analysis of developmental pathway bifurcation in phage lambda-infected Escherichia coli cells. Genetics 149, 1633–1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Lukacs E. 1942. A characterization of the normal distribution. Ann. Math. Stat. 13, 91–93. ( 10.1214/aoms/1177731647) [DOI] [Google Scholar]
  • 34.Jarret R. 1984. Bounds and expansions for Fisher information when the moments are known. Biometrika 71, 101–113. ( 10.1093/biomet/71.1.101) [DOI] [Google Scholar]
  • 35.Kreutz C, Timmer J. 2009. Systems biology: experimental design. FEBS J. 276, 923–942. ( 10.1111/j.1742-4658.2008.06843.x) [DOI] [PubMed] [Google Scholar]
  • 36.Hunter W, Hill W, Henson T. 1969. Designing experiments for precise estimation of all or some of the constants in a mechanistic model. Can. J. Chem. Eng. 47, 76–80. ( 10.1002/cjce.5450470114) [DOI] [Google Scholar]
  • 37.Walter E, Pronzato L. 1990. Qualitative and quantitative experiment design for phenomenological models—a survey. Automatica 26, 195–213. ( 10.1016/0005-1098(90)90116-Y) [DOI] [Google Scholar]
  • 38.Pronzato L, Walter E. 1985. Robust experimental design via stochastic approximation. Math. Biosci. 75, 103–120. ( 10.1016/0025-5564(85)90068-9) [DOI] [Google Scholar]
  • 39.Chaloner K, Larntz K. 1989. Optimal Bayesian design applied to logistic regression experiments. J. Stat. Plan Inference 21, 191–208. ( 10.1016/0378-3758(89)90004-9) [DOI] [Google Scholar]
  • 40.Menolascina F, di Bernardo M, di Bernardo D. 2011. Analysis, design and implementation of a novel scheme for in-vivo control of synthetic gene regulatory networks. Automatica 47, 1265–1270. ( 10.1016/j.automatica.2011.01.073) [DOI] [Google Scholar]
  • 41.Uhlendorf J, Miermont A, Delaveau T, Charvin G, Fages F, Bottani S, Batt G, Hersen P. 2012. Long-term model predictive control of gene expression at the population and single-cell levels. Proc. Natl Acad. Sci. USA 109, 14 271–14 276. ( 10.1073/pnas.1206810109) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Swain P, Elowitz M, Siggia E. 2002. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl Acad. Sci. USA 99, 12 795–12 800. ( 10.1073/pnas.162041399) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Bowsher C, Swain P. 2012. Identifying sources of variation and the flow of information in biochemical networks. Proc. Natl Acad. Sci. USA 109, E1320–E1328. ( 10.1073/pnas.1119407109) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Friedman N, Cai L, Xie S. 2006. Linking stochastic dynamics to population distribution: an analytical framework of gene expression. Phys. Rev. Lett. 97, 168302 ( 10.1103/PhysRevLett.97.168302) [DOI] [PubMed] [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES