An energetic model for macromolecules unfolding in stretching experiments

Abstract

We propose a simple approach, based on the minimization of the total (entropic plus unfolding) energy of a two-state system, to describe the unfolding of multi-domain macromolecules (proteins, silks, polysaccharides, nanopolymers). The model is fully analytical and enlightens the role of the different energetic components regulating the unfolding evolution. As an explicit example, we compare the analytical results with a titin atomic force microscopy stretch-induced unfolding experiment showing the ability of the model to quantitatively reproduce the experimental behaviour. In the thermodynamic limit, the sawtooth force–elongation unfolding curve degenerates to a constant force unfolding plateau.

1. Introduction

The past decade has shown a significant theoretical and experimental effort in the analysis of the thermomechanical behaviour of macromolecular materials such as muscle tissues [1], spider silks [2,3], polymers and biopolymers [4], polysoaps [5,6] and silks in general [7]. A common property of these materials [2,4,8–10] is that their macroscopic history-dependent, dissipative response is the result of complex evolutions of ‘semicrystalline’ microstructures. These are constituted by flexible (polymeric or protein) macromolecules reinforced by strong and stiff crystals (e.g. in the form of fillers or β-sheets [11,12]), undergoing typical hard–soft transitions owing to the unravelling of hard crystal domains into soft unfolded entropic domains. The deduction of predictive models describing the mechanical behaviour of macromolecular materials, connecting the macroscale response with the mesoscale behaviour, is crucial not only for the description of the fundamental polymeric and biopolymeric existing materials, but also in the perspective of the design of new bioinspired or reconstructed biological materials. As a consequence, an intense experimental, numerical and theoretical effort has been recently devoted in this field [11].

From an experimental point of view, a great impulse in the comprehension of the behaviour of these materials has been induced by new experimental techniques [13], such as atomic force microscopy (AFM) [14], laser optical tweezers [15], magnetic tweezers and single-molecule fluorescence techniques. The typical experiment is a mechanically induced unfolding of a macromolecule composed of n unravelling domains, such as a polymeric polypeptide, dextran [16], silks [7], proteins (see [14] for titin and [17] for fibrinogen), DNA/RNA strands [18].

From a theoretical point of view, the thermomechanical behaviour of multi-domain proteins has been investigated following different approaches: molecular dynamics (MD), off lattice models, all atom Monte Carlo approaches (see [19]), phenomenological approaches, statistical mechanics energy landscape analyses, with funnelling [20] and inherent structure models [21]. MD theories [19] have been restricted by the computational effort required to describe the unfolding of such large macromolecules at the AFM loading time scale. On the other hand, the statistical approaches for the discrete chain have been essentially based on numerical techniques, whereas analytical results have been obtained only in the thermodynamic limit hypothesis that hides the crucial role of finite size and discreteness of the unfolding phenomenon.

Schematically, we may describe a typical stretch-induced unfolding (figure 1) of a multi-domain macromolecule as follows [22]. At small elongations, the stiffness is principally regulated by the tertiary structure elasticity. Under increasing stretching, the force–elongation diagram shows periodic discontinuities resulting from (first-order) hard–soft transitions (owing to the secondary structure in the case of proteins where β-sheet unfolding is observed or to cross-link breakage in polymeric networks). These transitions have a main role in the energetics of the chain unfoldings owing to the two following effects: first, there is the enthalpic contribution of the transition itself (debonding energy), then there is an entropic contribution associated with the variation of the microstructure, leading to increased contour lengths of the chains. In the final stage, leading to the material failure, the behaviour is regulated by the entropic hardening of the fully unfolded macromolecules (primary structure).

Figure 1.

Scheme of the energetic decomposition of the external work into unfolding (dissipated) energy Q_i, i = 1,2,3,4 and elastic stored energy Φ_e (dashed region) for a typical unfolding force–elongation curve (continuous line) reproduced from [14]. Dashed lines represent approximating worm-like chain curves each characterized by a different contour length L_c(i), i = 1, … , 4; l_c represents the (fixed) contour length increase at each unfolding event.

To fix the ideas, in figure 1, we schematically show a typical AFM single-molecule stretching experiment reproduced from [14] on an engineering reconstructed macromolecule. The sawtooth force–length diagram can be described as a stick–slip dynamical evolution in a wiggly energy landscape, characterized by multiple energy wells, each corresponding to a given microstructure configuration. Thus, for growing assigned end-to-end length (see [23]), the chain alternates ‘slow’ (intrabasin) steps in energy wells at fixed folded/unfolded configuration, followed by ‘fast’ (interbasins) transitions corresponding to the unfolding of (typically single) crystals. These transitions are signalled by the periodic localized force drops induced by the entropy jumps owing to the creation of new free monomers. As a result, we observe hysteresis cycles (figure 1) with no permanent deformations resembling the pseudo-elastic hysteresis well known in metal alloys such as shape memory alloys (see [24]) or in rubber elasticity, owing to the polymeric network damage, known as the Mullins effect [25].

The MD approach in [23], based on the inherent structure formalism, clarifies that the observed unfolding is regulated by three main time scales: loading time τ_load, intrabasin relaxation time τ_intra and interbasin transition time τ_inter. Our theoretical model can be applied to the diffuse case when the following time-scale separation hypothesis can be assumed:

1.1

In this time-scale regime [23], unfolding results as an alternated sequence of purely elastic, intrabasin, stick evolutions and purely dissipative, interbasin, slip transitions, localized at fixed unfolding length thresholds.

In the case of AFM-induced unfolding, the non-dissipative hypothesis of the intrabasin evolution is supported by the observation [15,26] that during the (slip) evolution at fixed folded/unfolded configuration, the behaviour is fully reversible, thus indicating that the system relaxes to the local energy minimum. On the other hand, the fully dissipative hypothesis of the ‘fast’ (stick) interbasin transitions results from the observations (figure 1) that at the AFM loading time scale the β-sheet unfolding events are (mainly) localized at fixed macromolecule end-to-end lengths.

We remark that the time-scale separation (1.1) has been successfully adopted in other stick–slip evolutions associated with abrupt microstructure transitions in multi-valley energy landscapes at ‘low loading rates’ and ‘low temperature regimes’ such as depinning or nucleation of new defects, dislocations and Frank–Read sources in metal plasticity (see [24]), and Barkhausen jumps in ferromagnetism [27]. It is important to observe that under different time-scale regimes (see again [23]), e.g. 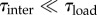, the system can show very different behaviours, with cooperative elastic transitions and no dissipation as observed in other protein unfolding experiments [28].

By energy conservation (Gibbs equation), under our hypothesis (1.1), the external work (see [24] for a theoretical discussion) can be decomposed as follows. By focusing again on the AFM experiment in figure 1, suppose that we begin stretching the macromolecule from its natural state. The macromolecule follows elastically the first equilibrium path (O–A in figure 1) with the external work W accumulated as elastic energy Φ_e (ΔW = ΔΦ_e). At the first β-sheet unfolding (path O–B)—here approximated as instantaneous with no external work W—there is an internal energy discontinuity [|Φ|]₁ (area O–A–B) that by energy conservation equals the unfolding energy Q₁ of the first hard domain. Similar considerations can be extended to the next elastic and dissipative steps, so that the total dissipation is Q = ∑Q_i = ∑[|Φ|]_i.

Based on previous considerations and inspired by the model in [2,29], where the authors describe the hysteresis of filled polymers and spider silks, here we propose an energetic approach and describe the unfolding macromolecule as a two-state material. Similarly, a two-state energetic approach was proposed in [30] to describe the helix → coil transition of polypeptide chains regulating the damage of multi-block copolymers. In this work, we obtained an analytic solution in the thermodynamic limit of a large number of breakable links. Recently [31] a statistical mechanics approach for a discrete two-well finite size chain has been proposed describing the force–extension diagrams of polymeric chains under assigned force (soft device) or end-to-end length (hard device). In particular, numerical results let us describe the sawtooth behaviour observed in a hard device.

In the field of protein mechanics, on the basis of the approach proposed in [30], an important step in the comprehension of the energy competition between the unfolding and entropic energy terms, has been delivered in [32]. In this paper, the author models the unfolding of a biomacromolecule as a chain composed of folded and unfolded domains, both elastic with Gaussian type response, combined with an Ising-type unfolding energy. The resulting MD simulation well describes the unfolding effect in a protein macromolecule, whereas analytical results are obtained only in the thermodynamic limit of many folded domains [32].

More recently, in [33], a statistical mechanics-based model for the stretching of titin proteins has been proposed, considering also the influence of the AFM loading device. A simple Ising model, neglecting the elasticity of both folded and unfolded domains in protein macromolecules, was instead proposed in [34] to describe the statistics of unfolding events. The described competition between the entropic energy of the unfolded fraction and the β-sheet unfolding energy has been analysed in [35,36] via Monte Carlo simulations combining a worm-like chain (WLC) with a two-state bell-type model for the unfolding. Finally, we recall the fully phenomenological continuum approaches recently proposed in [37,38] where the authors show the possibility of describing the protein unfolding as an energy minimization of a continuum system with a non-convex internal energy. In particular in [37], based on the general approach of [24,39] for the description of the mechanical behaviour of bistable discrete chains, the authors obtain an interesting characterization of an optimality condition of the number of β-sheet domains with respect to the toughness of the macromolecule.

The aim of this work is to obtain a fully analytical model, resulting from the energetic analysis and time-scale decomposition discussed previously, represented by a two-state lattice, describing the stretch-induced unfolding of macromolecules and the corresponding energy decomposition into stored and ‘dissipated’ energy. Interestingly, the analysis of this discrete bi-stable chain shows the existence of a fundamental, experimentally measurable, non-dimensional parameter ξ, defined in (3.8), representing the ratio of the elastic and unfolding energy of the single folded domains, that regulates the dissipation and the unfolding thresholds of each folded/unfolded phase configuration. The model is also extended to describe the possibility of the existence of a hierarchy of variable unfolding energies of the different folded domains. As we show, the effective distribution of unfolding energies can be deduced on the basis of the previously described energetic analysis, using the experimental force–elongation diagrams. Notably, after performing such an analysis for different macromolecule experimental curves, we obtain simple phenomenological linear dissipation energy distributions. The predictivity of the proposed model relies on the new theoretical (MD and all atom simulations) and experimental techniques permitting the independent evaluation of the main dimensional parameter ξ [40–42] and possibly its inhomogeneity and rate-dependent expression [36].

Aimed at the deduction of a three-dimensional continuum extension for biological tissues constituted by networks of modular macromolecules [43], we also deduce the thermodynamic limit of the proposed discrete model. The main advantage of our theoretical approach is that the behaviour of the single chain also in the continuum limit is regulated by the experimentally measurable parameter ξ that fully characterizes the unfolding behaviour of the macromolecule: unfolding force, initial unfolding stretch, stretch for unfolding saturation.

Finally, as an explicit example, we focus on the AFM experiments of titin unfolding. It is important to point out that such experiments often show rate-dependent effects, because at the AFM loading time scale the β-sheet unfolding transitions represent out of equilibrium events (e.g. the analysis performed by extending the Kramer reaction theory in [44,45] or the MD analysis in [23]). Here, aimed again to the deduction of a fully analytical approach, following [11,23,36,46], we take care of the described rate dependence by considering effective, rate-dependent unfolding energies.

2. Energetic assumptions

Because in macromolecules the hard crystal unfolding is typically an all-or-none transition, as confirmed also from the size of periodicity of the experimental unfolding lengths [14] in the case of titin, we model the molecule as a discrete lattice of n two-state (rigid-folded/entropic-unfolded) links (see the scheme in figure 1). The folded/unfolded state of the chain is assigned by a set of internal variables χ_i, i = 1, … , n, such that χ_i = 0 (χ_i = 1) denotes the folded (unfolded) state of the ith domain. Thus, in particular, 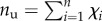is the number of unfolded elements and n_f = n − n_u is the number of folded elements.

As in the case of freely jointed chain or WLC models [47], we characterize the behaviour of each unfolded link through its contour length l_c and end-to-end length l, with a free energy density (energy per unit length) φ_e = φ_e(η), where η:= l/l^c represents a strain measure. We assume then the limit extensibility condition lim_{η → 1}φ_e(η) = ∞.

Consider first the entropic energy of the unfolded fraction. By neglecting non-local interactions (weak interaction hypothesis), it is possible to show that the total elastic energy 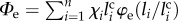can be simply expressed as

2.1

Here,

is the strain in the unfolded domain,

is (by neglecting the extension of the folded domains) the total end-to-end length, and

2.2

is the total contour length of the chain. In (2.2), L₀ denotes the ‘initial’ (virgin) contour length of the unfolded domain.

Indeed, at equilibrium, by neglecting the elastic energy of the (rigid) folded domains, the total elastic energy is given by 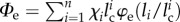, where 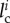and l_i are the (possibly variable) contour length and end-to-end length of the ith link in the unfolded state (χ_i = 1). Under an equilibrium hypothesis, we have a constant force F for all unfolded links, i.e. 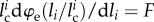. Thus, for a convex energy density (monotonic derivative 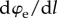), such as WLC or FLC, the strain is homogeneous in all unfolded elements, i.e. 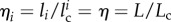, for all i = 1, … , n with χ_i = 1. Thus, we have .

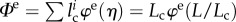Consider now the configurational energy associated with the different folded/unfolded states. Following [30,32], here we consider an Ising-type transition energy

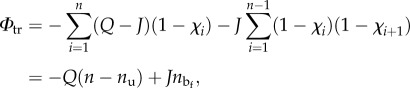depending on the internal variables χ_i and the number 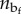of contiguous folded blocks in the folded/unfolded configuration. Here, Q is the unfolding energy for a single domain and J is a penalizing ‘interfacial’ energy term (measuring the loss of internal energy owing to the unbind terminal hydrogen bonds of each contiguous folded domain [30]).

To get the total energy 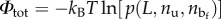(where T is the temperature and k_B is the Boltzmann constant), we have to know the probability 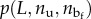of a given configuration of the chain with a microstructure corresponding to n_u and 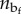and end-to-end length L. In particular, we have 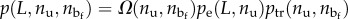, where 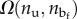represents the number of sequences with assigned n_u and 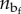, p_e(L,n_u) ∼ exp(−Φ_e(L,n_u)/k_BT) represents the probability of attaining a length L at given n_u and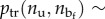 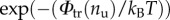is the probability of a state with assigned n_u. 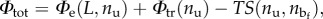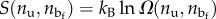So, we obtain where represents a mixing entropy component.

Observe that the coupling energy term J penalizes the multiplicity of folded blocks, whereas the mixing entropy term induces multi-domain configurations. In the following, we assume, as in [30], that the penalizing term J dominates this effect, so that we always consider single folded domain configurations (thus we assume 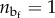: di-block approximation). This hypothesis is supported by the MD simulations [22] showing an unfolding strategy with always one single connected internal unfolded domain inside two boundary-folded domains.

Under these hypotheses, we obtain the simple expression of the total energy

2.3

We remark that to avoid the introduced di-block approximation, not always experimentally verified, one needs to evaluate the partition function [32,33] and only numerical results in the discrete model can be obtained. Moreover, stochastic processes considering fluctuations in both the unfolding forces [48] and the unfolding lengths are possible extensions of the proposed model. In addition, these extensions require the applications of numerical approaches.

3. Energy minimization

Consider the WLC force–length relation proposed in [49]

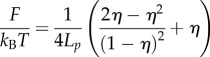3.1

corresponding to an energy density

3.2

Thus, using (2.1), the adimensionalized total entropic energy of the unfolded fraction can be written as

3.3

In order to obtain analytical solutions, we consider the following simplified expression of the WLC energy density:

3.4

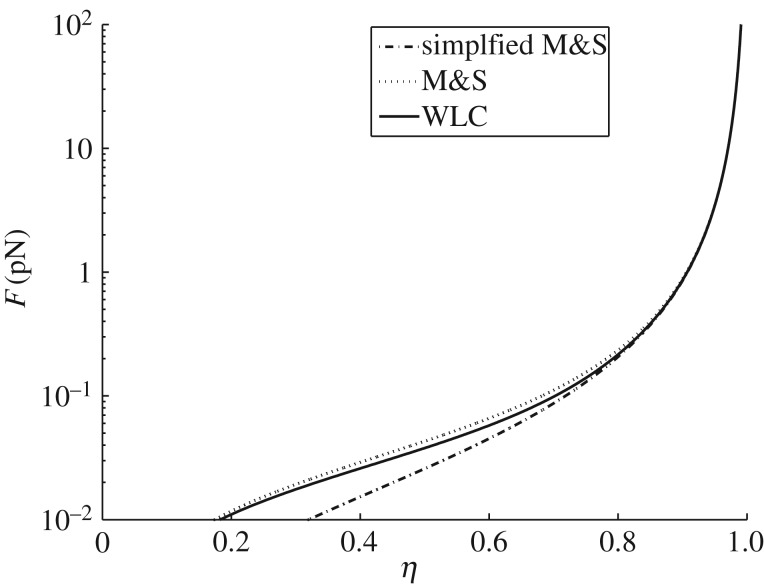
Observe that this approximation keeps the same asymptotic behaviour as l → l_c of the WLC model in (3.3). Figure 2 shows (in a log scale, stressing the differences at low values of the force) that, while for low forces (F < 10⁻¹ pN) the introduced approximation is significant (when compared with the approximation in [49]), for larger forces the approximation is of the same order (actually approximating better than [49] the WLC expression) as the one proposed by [49]. Because in the low force regime the elasticity is mainly regulated by the PEVK and tertiary structure elasticity (see [50,22] for details), this approximation appears inessential in both the qualitative and the quantitative analysis of the behaviour during the large-force unfolding regime of interest in this paper. Moreover, we remark that the approximation (3.1) has been shown to be inefficient in the low force regime in [51], where the authors introduce a Mooney–Rivlin-type correction to the WLC constitutive law.

Figure 2.

Force–strain curve (log-scale evidences the differences in the low force regime) for the WLC compared with the usual Marko & Siggia [49] approximation (M&S) and with the simplified model in (3.5) for l_p = 0.42 nm. Observe that the proposed approximation keeps the same asymptotic behaviour as l→l_c of (3.3) and that for F > 10⁻¹ pN the approximation is of the same order as that of [49].

Thus, using (2.1) and (2.2), the total elastic energy is

and, correspondingly, the total force–deformation relation is

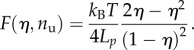3.5

Finally, according to (2.3), the total energy is

3.6

We follow a Griffith-like approach [52], minimizing the total unfolding (fracture) energy plus elastic (entropic) energy, and based on (1.1) we assume that the observed solutions are the global minima of Φ_tot in (3.6).

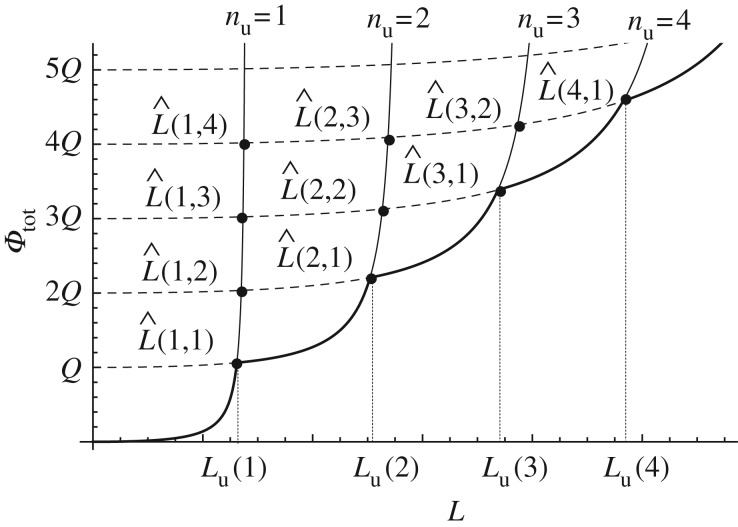
The first important step is to justify the experimental observation that the hard crystals unfold one at a time, resulting in a constant increase of the contour length (see [14]). To obtain this result, we begin by evaluating the solution of the equations Φ_tot(L, n_u + m) − Φ_tot(L, n_u) = 0 and get the intersection lengths (figure 3). The searched result follows by the observation that so that if 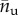is the branch corresponding to the global minimum at assigned end-to-end length L, by increasing L it loses its global stability at the intersection with the equilibrium branch 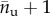(figure 3). Thus, the chain unfolds with a sequence of single hard domain transitions at the threshold assigned by :

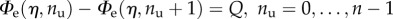3.7

(in this formula and in the following, we omit the n_u dependence of L_c).

Figure 3.

Scheme of the energy minimization: with bold line we represent stable (global energy minimum) solutions.

In (3.7), we introduced the main non-dimensional parameter of the model

3.8

representing a measure of the ratio between the elastic and fracture energy of the single β-sheet. Indeed, we observe that according to (3.2) we have that the term k_BTl_c/8L_p = φ_e(1/2)l_c, so that it measures the elastic energy of a single domain when the deformation is a half of the maximum elongation (contour length).

It is easy to verify that L_u∈(0, L_c) and that dL_u/dn_u > 0. As a result, the n_u branch corresponds to the global energy minimum for

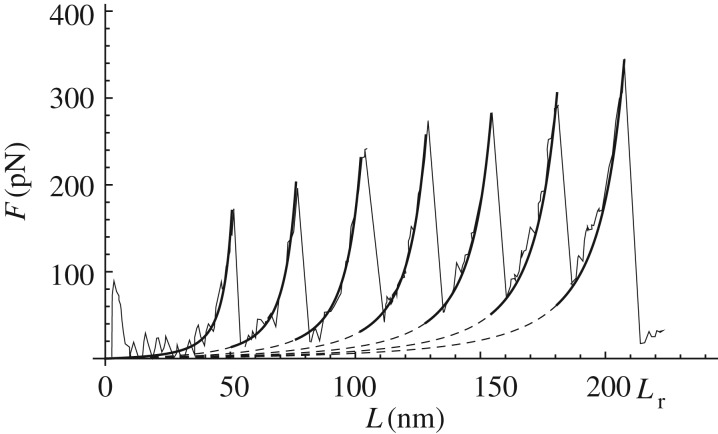
representing the existence domain of the n_u branch under our energy minimization hypothesis. In the special cases of the virgin curve, with n_u = 0, we have L∈(0, L_u(0)), whereas in the case of the fully unfolded chain, with n_u = n, we have L∈(L_u(n−1), L_r), where L_r is the fracture threshold of the fully unfolded chain (figure 6).

Figure 6.

Comparison between the AFM experiment for the titin protein reproduced from [14] (continuous curves) and the force versus elongation curves deduced by (3.5), (3.7), (4.3) and (4.2) (bold lines). Here, we considered the parameters: l_o = 58 nm, l_c = 28.43 nm, l_p = 0.36 nm, Q = 770k_BT, ΔQ = 420k_BT.

Using (3.5), we get the unfolding force F_u = F(L_u/L_c, n_u)

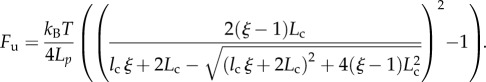3.9

Observe that using (3.7) and (3.9), it is also possible to obtain an explicit relation between the unfolding forces and the unfolding end-to-end lengths

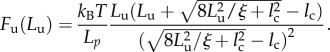3.10

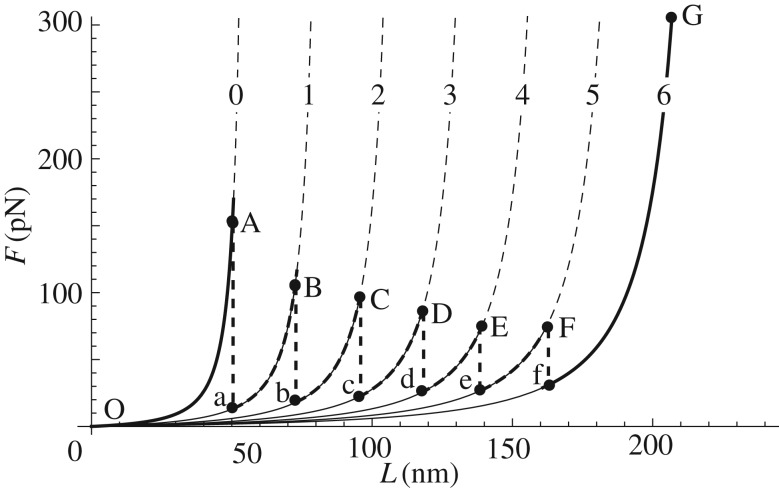
The stretch-induced unfolding of the system is shown with bold line in figure 4. The system reproduces the typical experimental behaviour of unravelling macromolecules with a regularly spaced sequence of unfolding events of the hard domains. Thus, if we start loading from the virgin configuration (n_u = 0, point O in figure 4), the system follows elastically the equilibrium curve n_u = 0 until the unfolding energy Q equals the jump of the entropic energy owing to the transition from the branch n_u = 0 to the branch n_u = 1 (path A–a in figure 4). By increasing further the assigned length, the system follows the new branch until another sudden transition to the branch n_u = 2 is observed when it becomes energetically favourable (path B–b). Similar transitions with single domain unfoldings are then observed, until all the crystals unfold and the system shows a hardening behaviour owing to the entropic elasticity of the fully unfolded chain (curve f–G in figure 4).

Figure 4.

Unfolding behaviour for a system of n = 6 initial folded domains. Here, we considered the parameters: l_o = 58 nm, l_c = 28.43 nm, l_p = 0.36 nm, Q = 770k_BT, ΔQ = 420k_BT. Each equilibrium path is labelled by the number n_u of unfolded domains.

Regarding the behaviour of the system under unloading, because typically at the AFM loading rate no refolding is observed [53], we assume irreversible (hard–soft) transitions. As a result if the system is unloaded at a given equilibrium branch 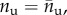the system follows this branch until both stretch and force go to zero. Under reloading the system instead changes again configuration with another hard–soft transition at the same value of primary loading 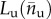. The memory of the system is then restricted to the only maximum value attained in the past by the end-to-end length L.

Finally, we observe that the theoretical model shows a softening behaviour during the unfolding regime, in the sense that the unfolding force decreases with the number n_u of unfolded domains. This can be analytically proved by observing that in view of (3.10) we have ∂F(L_u(n_u))/∂n_u < 0. Nevertheless, the experimental behaviour of stretch-induced unfolding of macromolecules shows a variable behaviour, with typically nearly constant unfolding forces [54], but with possibly increasing, decreasing or non-monotonic transition thresholds (see [14] for titin macromolecule and [55] for artificial elastomeric protein).

In the following section, we discuss this issue and propose an extension of our model able to reproduce the hardening effect observed, e.g. in titin macromolecule unfolding.

4. Unfolding energy hierarchy

The described variable observations on subsequent transition forces (force plateaux, hardening, softening) have been given different physical interpretations. A hierarchy of unfolding energies of the unfolding crystals may be simply due to inhomogeneity effects of the crystal domains [14,35,56], showing variable bond-breaking barriers [33] possibly owing to interfacial energy effects [57]. Another important effect is anisotropicity of the crystals with respect to the force direction—different paths in the wiggly energy landscape lead to different unfolding energy barriers [58]—so that different unfolding forces can be induced by variable crystal orientations in the macromolecule. Another known effect, that can induce hardening, is the so-called n-effect (see [58]) that, based on statistical considerations, leading to an unfolding force growth owing to a progressively reduced number of folded crystals available for unfolding in the macromolecule for growing elongations.

To check the possibility of variable unfolding energies, following the energetic decomposition schematized in figure 1, based on the experimental force–displacement unfolding diagrams we may estimate the fracture energy of each unfolding event using the relation

4.1

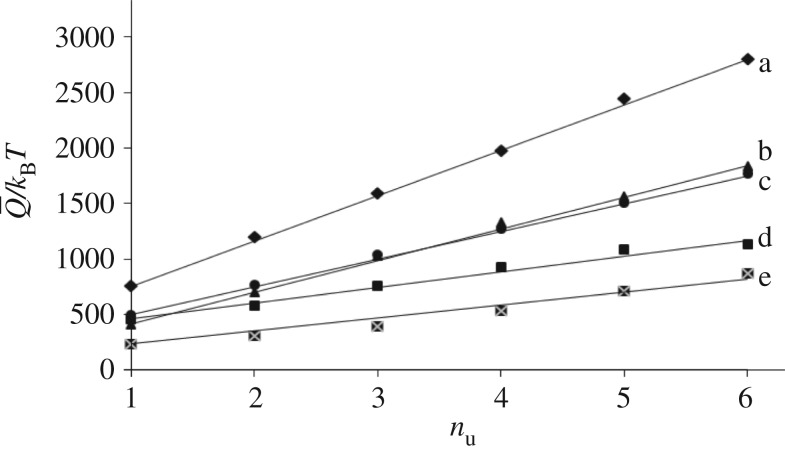
where 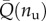represents the variable fracture energy of the n_u-th folded domain and η_u = L_u(n_u)/L_c(n_u) is the corresponding unfolding strain. Based on this relation, we analysed the experimental length–force diagrams for different unfolding macromolecules: titin in [14,48,59], TNfnAll protein from [60] and tenascin-C from [54]. The results are summarized in figure 5 and interestingly all show a linear phenomenological growing law for the dissipation energy of successive unfolding domains

4.2

where 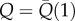represents the fracture energy of the weakest folded domain, which has the important role of regulating the stability of the initial unfolded configuration and the initial unfolding length L_u(1), whereas ΔQ is a fixed energy increment for successive unfolding events (figure 5).

Figure 5.

Unfolding energies as a function of n_u deduced from the following experiments: (a) AFM experiment on titin from [14]; (b) AFM experiment on TNfnAll protein from [60]; (c) AFM experiment on titin from [48]; (d) AFM experiment on tenascin-C from [54]; (e) AFM experiment on titin from [59].

It is important to remark that in the case of increasing unfolding energies, the di-block approximation can fail, with the order of unfolding that is regulated by the competition of mixing energy, interfacial energy effects and variability of the unfolding energy. This competition regulates in the quasi-static regime the order of transition and the hardening, softening or non-monotonic law of the successive unfolding force. Aimed again at a fully analytical result, we here suppose that both the mixing entropy contribution and the interfacial energy term are negligible when compared with the unfolding energy increment ΔQ so that the unfolding evolution strategy is regulated by the unfolding energy hierarchy and we may again describe the stretching behaviour of the macromolecule by minimizing an energy as in (3.6), but with variable unfolding energy increments. Indeed, (3.6) is obtained by simply considering ΔQ = Q in (4.2).

Under the considered assumption, we may first extend the considerations described in figure 3 to obtain that the domains unfold one at a time in the order of their unfolding energies. Then, we may again explicitly evaluate the unfolding lengths (3.7) and forces (3.9) by simply using (3.7) with a variable parameter

4.3

measuring the variable ratio of dissipated and elastic energy of the folded domains.

5. An explicit example: titin unfolding

To show the feasibility of the proposed model in quantitatively predicting the experimental behaviour of macromolecule unfolding, in this section, we analyse the diffusely studied AFM stretching experiments of titin, the protein responsible of the passive strength of muscles. These proteins are very long macromolecules with contour length larger than 1 μm [1], whose secondary structure is characterized by the presence of immunoglobulin (Ig) and fibronectin-type III (FNIII) domains, folded in forms of β-sheets, connected to the PEVK domain (rich in proline, glutamate, valine and lysine) [61]. At low forces, the elasticity is regulated by the tertiary structure and the (random coil) domain orientation, combined with the elasticity of PEVK domains [22,57,61]. At higher forces, the macromolecule response is dominated by an energetic competition of the entropic elasticity of the unfolded fraction of (Ig) and (FNIII) domains and by the enthalpic contribution of the folded → unfolded transition of the β-sheets.

One important effect in the case of titin is the rate-dependent behaviour of the unfolding events [14] whose detailed description has been addressed through MD approaches [23] and reaction theory approaches [44]. Here, as anticipated above, following [11,23,36,46], we take care of the observed rate dependence (i.e. rate-dependent unfolding energy barriers and dissipation) by considering effective rate-dependent dissipation energies Q_i.

In figure 6, we show the ability of the model in describing quantitatively the behaviour of titin unfolding experiments reported in [14] based on the obtained analytical relations (3.5), (3.7) and (4.3) with an energy hierarchy as in (4.2) deduced based on the experiments in [14] as reported in figure 5a.

6. Continuum limit

Here, aimed to a deduction of a continuum model for macromolecular materials [2], we analyse the continuum limit of the proposed model, obtained as a limit when n → ∞. To get this limit, we fix the total unfolded length that using (2.2) is given by

6.1

and consider the limit when both l_c → 0 and n → ∞. Introduce then the new continuum variable

representing the unfolded fraction. In the language of continuum mechanics ν_u represents a damage (internal) variable, with ν_u∈(0, 1) and ν_u = 0 in the virgin state and ν_u = 1 in the fully unfolded state [62,63]. The total contour length is then using (2.2) given by

6.2

Thus, the damage variable ν_u measures the change of contour length with in particular L_c = L₀ in the virgin configuration (ν_u = 0) and 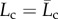, as in (6.1), in the damage saturation configuration of the fully unfolded state (ν_u = 1).

The total energy, using (3.6), can be rephrased as

6.3

where we introduced the rescaled unfolding energy

ensuring that decreases proportionally to the length l_c of the unfolded single elements. Here, in view of (6.2), the deformation variable depends on the continuum damage variable ν_u according to the following relation:

6.4

The obtained framework can be inscribed in the classical variational approach for damage known as pseudo-elasticity [64], requiring the minimization of the damage-dependent energy (6.3) under the constraint of irreversibility of unfolding. We refer the reader to [29] for the technical details of the variational approach, whereas we here resume the loading–unloading behaviour of the deduced continuum damage model. Based on our irreversibility assumption (no refolding), we may observe that also in the continuum damage model the memory of the loading history depends on the only value L_max of the maximum end-to-end length attained in the past that assigns ν_u. Indeed (see again [29] for technical details), during loading (L = L_max) to determine the global minimum of the energy (6.3), we minimize both with respect to L and ν_u. Minimization with respect to L (i.e. 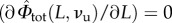) delivers the equilibrium force as in (3.5) with the deformation variable defined in (6.4). Minimization with respect to ν_u (i.e. 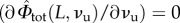) delivers the damage as a function of the assigned length

6.5

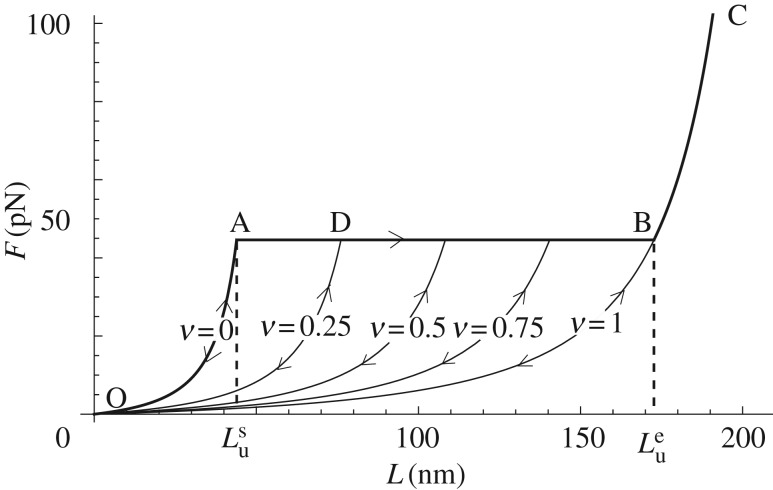
Interestingly, using (3.10), in this limit we obtain a constant unfolding force plateau

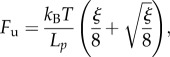that by (6.5) begins (ν_u = 0) at

and ends at

where the fully unfolded state (ν_u = 1) is attained. The obtained unfolding behaviour is shown in figure 7 (path OABC). During unloading (L < L_max), because we neglect refolding, the behaviour is again given by (3.5) with fixed damage that by (6.5) is given by 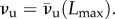Different unloading paths are shown in figure 7 (e.g. path DO is attained for an unloading at ν_u = 0.25).

Figure 7.

Unfolding behaviour of the lattice in the thermodynamic limit. Bold lines represent the loading path, whereas continuous lines the unloading paths at different values of the unfolded fraction ν_u and maximum end-to-end length. Here, we used the same parameters as figure 4.

7. Conclusion

In this paper, we propose, based on the time-scale separation (1.1), an energetic model for the description of the important phenomenon of stretch-induced unfolding of macromolecules. By considering a di-block approximation and by neglecting rate-dependent effects (possibly considering rate-dependent effective unfolding energies), we deduced a fully analytical model delivering the unfolding forces and lengths for the different equilibrium branches, all depending on a deduced main dimensional parameter ξ. Despite the important simplifications underlying the proposed model, the availability of a fully analytical model (available only in the thermodynamic limit for previously proposed models) let us clarify the main ingredients regulating the energetics underlying stretch-induced unfolding in multi-domain macromolecules. The analytical results for the (finite) discrete lattice have been also extended to the case of inhomogeneous unfolding energies based on the empirical law (4.2) that we deduced by analysing typical macromolecule unfolding experiments. The deduced analytical model shows a good qualitative (stick–slip unfolding evolution with regular spacing of the localized unfolding events) and quantitative agreement (figure 6) with the experimental behaviour and elucidates the experimentally determinable variables 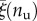in (4.3) regulating the mechanical behaviour of the chains. Finally, we deduced a continuum limit one-dimensional system available for three-dimensional extension to study the mechanical behaviour of biological and polymeric tissues and networks of modular macromolecules [43] that will be the subject of our future studies and that appears particularly valuable also in the perspective of analytical criteria in the new important technological field of the design of new bioinspired materials.

Funding statement

The work of D.D. and G.P. has been supported by Progetto di ricerca industriale-Regione Puglia, ‘Modelli innovativi per sistemi meccatronici’ and PRIN 2010–11: ‘Dinamica, stabilità e controllo di strutture flessibili’ (Dynamics, stability and control of slender structures).