Contractile Fibers and Catch-Bond Clusters: a Biological Force Sensor?

Abstract

Catch bonds are cellular receptor-ligand pairs whose lifetime, counterintuitively, increases with increasing load. Although their existence was initially pure theoretical speculation, recent years have seen several experimental demonstrations of catch-bond behavior in biologically relevant and functional protein-protein bonds. Particularly notable among these established catch-bond formers is the integrin α₅β₁, the primary receptor for fibronectin and, as such, a crucial determinant for the characteristics of the mechanical coupling between cell and matrix. In this work, we explore the implications of single catch-bond characteristics for the behavior of a load-sharing cluster of such bonds: These clusters are shown to possess a regime of strengthening with increasing applied force, similar to the manner in which focal adhesions become selectively reinforced. Our results may shed new light on the fundamental processes that allow cells to sense and respond to the mechanical properties of their environment and in particular show how single focal adhesions may act, autonomously, as local rigidity sensors.

Introduction

Most animal cells spend their days embedded in a supporting structure called the extracellular matrix (ECM). This complex medium is an interconnected, gel-like meshwork of glycosaminoglycans and fibrous proteins (collagen, fibronectin) that provides structural support and anchorage to the cells, as well as mechanical integrity and resilience to the tissue as a whole. More recently, its additional regulatory function has received considerable attention in the literature. More than passively anchored to it, cells actively sense (1,2) and alter (3) the mechanical properties of their surroundings which, in turn, may affect the fate of the cells embedded in it: the mechanical properties of the substrate have been implicated in the determination of the phenotype of otherwise indistinguishable stem cells (4,5). These findings have spawned considerable and renewed interest in the physical concepts and foundations underlying cell mechanosensing (6–8):

• How do cells couple to the environment?

• What information may they glean from it (mechanosensing), how can this information be internalized (mechanotransmission), and how is it processed (mechanotransduction)?

In this article, we consider the force-response of a cluster of catch bonds: integrin-ligand bonds, which display a regime of increasing bond lifetime with increasing loads (9). Although the molecular mechanisms responsible for this behavior remain debated (10), the behavior itself is by now firmly established and, in fact, has been demonstrated (11,12) in individual receptor-ligand pairs. We extract from these experiments operational parameters, and discuss collective behavior of a macroscopic assembly of catch bonds. Our results extend previous simulations in Sun et al. (13): We supply analytical results, consider the response to loading by molecular motors, and establish a direct link between external stiffness and bound integrin fraction.

Single Catch-Bond Characteristics

The equilibrium binding and unbinding kinetics of unforced noncovalent molecular bonds is generally summarized in binding and unbinding rates k_b⁰ and k_u⁰. The unbinding rate k_u⁰ determines the lifetime of the bond in the absence of bias. Consider a bond that is closed at time t = 0; the probability that it is still closed after a time t has passed is P_s(t) ∼ exp(−k_u⁰t), and the expectation value for its lifetime is 〈t〉 ≡ τ⁰ = 1/k_u⁰ (9). If an external force f is applied to the bond, unbinding is enhanced and Kramer’s rate theory (14) (alternatively known as Bell kinetics (15)) suggests the unbinding rate be modified as

$$k_u\left(f\right)=k_u^0\exp \left(\frac{+f\xi }{k_{\text{B}}T}\right),$$

with ξ a microscopic lengthscale characterizing the unbinding transition. Consequently, the bond lifetime is shortened exponentially as

$$\tau \left(f\right)={\tau }^0\exp \left(\frac{-f\xi }{k_{\text{B}}T}\right).$$

Bonds satisfying this relationship are called slip bonds. Catch bonds, however, behave in a markedly different manner when forced: Their bond lifetime initially increases when a force is applied. The single-bond lifetime of a catch bond is maximal at some finite force, after which it decays exponentially and recovers slip-type behavior. Although initially a purely theoretical speculation (16), catch bonds are by now a well-established phenomenon. Both the L- and P-selectins that feature prominently in neutrophil rolling have been shown to exhibit catch-bond behavior. The macroscopic phenomenon of a shear-threshold for the rolling adhesion of neutrophils is generally ascribed to a collective manifestation of individual catch-bond connections (17–19). Recent experiments have also demonstrated catch-bond behavior in single biological bonds (11,12)—in this work, we present results obtained by using numerical values for single bonds directly obtained from these experiments. Interestingly, among the receptor-ligand pairs for which this behavior was observed is the bond between the ECM component fibronectin FNIII_7–10 and the cellular integrin α₅β₁: the primary receptor for fibronectin (20). Fig. 1 plots the lifetime-force curve for this particular pair, clearly showing the initial rise in lifetime and the maximum lifetime at finite force. The solid curve is a fit to the data for the so-called two-pathway model (21), which considers unbinding of the receptor-ligand pair via two alternative routes—one catch path that is opposed by the applied force, and one slip path that is promoted by it. The values ξ_c and ξ_s are two distinct length scales for the two routes, and k_c and k_s the associated unforced unbinding rates. The two-pathway model predicts the lifetime of a catch bond to depend on the pulling as

$$\tau \left(f\right)={\left(k_s{e}^{\frac{f{\xi }_s}{k_{\text{B}}T}}+k_c{e}^{-\frac{f{\xi }_c}{k_{\text{B}}T}}\right)}^{-1}.$$ (1)

We are interested in the general behavior of coupled clusters of catch bonds, and choose to work with a simpler model that captures their essential behavior: We set the two unbinding lengths ξ_c and ξ_s equal, denoting the single length scale simply ξ. We use this length scale to set a force scale via k_BT ≡ f^∗ξ. All forces are nondimensionalized using this force scale: ϕ ≡ f/f^∗. Furthermore, Pereverzev et al. (21) argue that to get proper catch-bond behavior, one needs k_c ≫ k_s; we use this to rewrite k_c = k₀ exp(ϕ_c) and k_s = k₀ exp(−ϕ_s) with ϕ_s, ϕ_c > 0. Note that this is the regime in which a lifetime peak is encountered, but that positivity of ϕ_s and ϕ_c is not a hard constraint: In fact, the slip bond limit may be recovered by letting ϕ_c → −∞. We may set k₀ = 1 s⁻¹ without loss of generality. With these reductions and definitions, we shall write the dimensionless force-dependent unbinding rate

$$k_u^{\text{cb}}\left(\varphi \right)\equiv {\left(k_0\tau \left(\varphi \right)\right)}^{-1}$$

of the single catch bond as

$$k_u^{\text{cb}}\left(\varphi \right)=e^{-\left(\varphi -{\varphi }_c\right)}+e^{\left(\varphi -{\varphi }_s\right)}.$$ (2)

We have used this expression to fit the data from Kong et al. (12) for the FNIII_7–10-α₅β₁ bond; the results are plotted in Fig. 1. For future reference, we note that the maximal lifetime for the single bond is attained at

$${\varphi }_{\text{max}}=\frac{1}{2}\left({\varphi }_s+{\varphi }_c\right).$$

We now consider the consequences of this single-bond behavior for a cluster of catch bonds subjected to a fixed external force.

Figure 1.

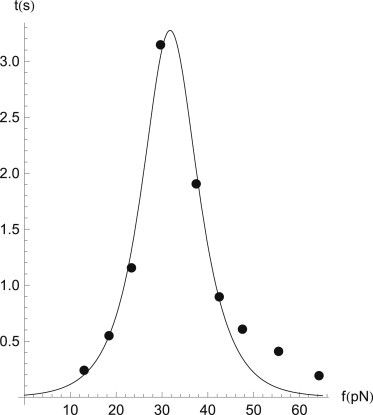
The catch bond between FNIII_7–10 and α₅β₁: (points) experimental results from Kong et al. (12); (solid line) fit to the two-pathway model from Pereverzev et al. (21), Eq. 2, with parameters ϕ_c = 4.02, ϕ_s = 7.78, and f^∗ = 5.38. In physical units, this corresponds to a slip-path unbinding rate of k_s = 4.2 × 10⁻⁴ s⁻¹, and a catch-path unbinding rate of k_c = 55 s⁻¹.

Catch-Bond Cluster: Fixed Force

Following the approach of Schwarz et al. (22) we consider a collection of N_t bonds, and let i denote the size of the cluster at time t, i.e., the instantaneous number of closed bonds. We may then summarize the evolution of p_i, the probability of having i closed bonds at a given time t, in a one-step master equation

$$\frac{\text{d}{p}_i}{\text{d}t}=r_{i+1}\left(F_{\text{t}}\right)p_{i+1}+g_{i-1}{p}_{i-1}-\left[r_i\left(F_{\text{t}}\right)+g_i\right]p_i,$$ (3)

where r_i(f) is the (force-dependent) rate at which one bond unbinds from a cluster of size i, and g_i is the rate at which an additional bond is formed when a cluster of size i is already present. The rate of rebinding may be assumed to be independent of the applied force, as the bond must be unstressed in its unbound state. We assume a simple relation of the form

$$g_i=k_0\gamma \left(N_{\text{t}}-i\right),$$

i.e., rebinding proportional to the number of available, unbound bonds with a uniform dimensionless rebinding rate γ. The unbinding rate is where the catch-bond nature of the individual bonds is injected into the model. We shall choose

$$r_i\left(F_{\text{t}}\right)=i{k}_0{k}_u^{\text{cb}}\left(\overline{f}\right),$$

which is proportional to the single-bond unbinding rate previously discussed, but evaluated at the force that single bonds actually experience in a cluster. The cluster is loaded collectively, and depending on the geometry of the cell, the alignment of the stress fiber attached to the focal adhesion, and the structure and shape of the substrate individual bonds in the cluster, may experience very different forces. In what follows, we will mostly consider only the simplest force distribution: a uniform distribution of the load across all closed bonds. The reasons for this choice is twofold:

• 1.Nonuniform loading requires additional assumptions on the distribution of forces that in general do not permit analytical treatment, and add further adjustable parameters to the system—we strive to keep the free parameters to a minimum.
• 2.More importantly, previous numerical work on nonuniform loading (13) has clearly delineated how different loading configurations quantitatively modify the binding, but mostly the unbinding, of integrin clusters.

We expect that our uniform loading configuration will be similarly modified in more complicated settings. In Cluster Lifetimes: Asymmetric Loading, we provide one explicit and analytical confirmation of this when we present lifetime results for a cluster that exhibits the typical asymmetric traction force distribution reported in Plotnikov et al. (23).

Assuming a uniformly distributed load, we shall choose $\overline{f}=F_{\text{t}}/i$. Under these assumptions, we may evaluate the temporal evolution of the cluster size N = 〈i〉:

$$\frac{\text{d}}{\text{d}t}N=\sum _{i=1}^{N_{\text{t}}}i\left(\frac{\text{d}{p}_i}{\text{d}t}\right)=-\langle r_i\rangle +\langle g_i\rangle .$$ (4)

We now pass to a mean-field picture and ignore fluctuation effects, writing the averages of the i-dependent functions r_i and g_i, respectively, as their values at the average of i:

$$\frac{\text{d}}{\text{d}t}N\approx -r_{\langle i\rangle }+g_{\langle i\rangle }=-N{k}_0{k}_u^{\text{cb}}\left(\frac{F_{\text{t}}}{N}\right)+k_0\gamma \left(N_{\text{t}}-N\right).$$ (5)

In the following, we shall take t to denote the dimensionless time k₀t. Defining the total scaled force Φ ≡ F_t/f^∗, we arrive at the full mean-field ordinary differential equation that governs the evolution of a catch-bond cluster sharing a force F_t:

$$\frac{\text{d}}{\text{d}t}N=-N\left(e^{-\left(\text{Φ}/N-{\varphi }_c\right)}+e^{\left(\text{Φ}/N-{\varphi }_s\right)}\right)+\gamma \left(N_{\text{t}}-N\right).$$ (6)

This equation is to be considered the catch-bond equivalent of the classical result derived for slip bonds by Bell (15). Its validity, of course, depends on the relative magnitude of the contribution of fluctuations. To establish this, we have checked the ratio between the variance

$${\sigma }^2=\langle {\left(i-\langle i\rangle \right)}^2\rangle$$

and the observed mean N = 〈i〉 itself. Interestingly, because we know the full stochastic structure underlying the mean-field system, we can also compute the variance from an ordinary differential equation similar to Eq. 6 (24,25). At very low forces, and therefore low N (roughly N below 10) the mean field approximation is seen to suffer from discreteness effects. Likewise, for very high forces, the fluctuations become larger and in particular lead to finite cluster lifetimes, as we shall detail in Cluster Lifetimes: Uniform Loading. In the slip-bond limit (ϕ_c → −∞), an analytical solution may be found for the saddle node bifurcation (15), which may be computed to occur at a critical force Φ_c = N_tplog(γ/e). In this case, the implicit equations determining this critical force

$$\left(\dot{N}=0,\frac{\text{d}}{\text{d}N}\dot{N}=0\right)$$

do not permit a closed-form solution. For some key quantities, however, we do present analytical results also for the catch-bond system. The equation is a mean-field approximation to the general, stochastic kinetics encoded by Eq. 3, and we will first explore the resulting behavior at this mean field level before presenting stochastic simulations of individual trajectories.

Equation 6 is appropriate for large systems, i.e., for adhesion clusters where many potential bonds are present. It allows us to determine the evolution of the number of closed bonds as a function of time, which of course asymptotes to the equilibrium number of bound bonds. This equilibrium cluster size is obtained numerically by solving dN/dt = 0, and the results are graphed in Fig. 2. This reveals the essential characteristics of the catch-bond cluster: As we increase the constant external force Φ, the number of closed bonds (normalized in the graph to the total number of bound bonds to yield the closed fraction) increases as well: The shared load makes for longer living single bonds. The rebinding rate remaining constant, the cluster is able to retain its closed bonds better at higher forces—as long as the average force per closed bond does not exceed ϕ_max. When it does exceed this maximal value, the equilibrium number of closed bonds drops rapidly as the cluster unbinds in avalanche-like fashion; each single bond unbinding resulting in a higher load per bond and hence (as the force per bond already exceeded ϕ_max), increased unbinding.

Figure 2.

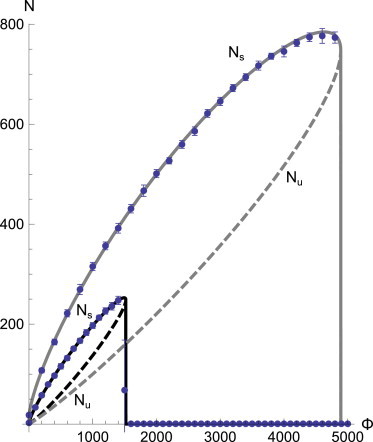
Equilibrium number of bound bonds in a catch-bond cluster as a function of the applied external force Φ. We graph the two solutions branches of d/dt N = 0, and label the stable (solid) and unstable (dashed) branches as N_s and N_u, respectively (see text). Different curves correspond to different values of rebinding rate: (solid curve) γ = 0.1; (shaded curve) γ = 1. Points and the error bars (RMSD for each single simulation trajectory) on these graphs correspond to the data obtained from the Gillespie simulations.

We may rewrite the right-hand side of Eq. 6 to yield

$$\frac{\text{d}}{\text{d}t}N=-2N\cosh \left(\frac{\text{Φ}}{N}-{\varphi }_{\text{max}}\right){\alpha }^{-1}+\gamma \left(N_{\text{t}}-N\right),$$ (7)

where

$$\alpha =\exp \left(\frac{1}{2}\left({\varphi }_s-{\varphi }_c\right)\right).$$

This produces the following analytical result for the curves in Fig. 2:

$$\text{Φ}\left(N\right)=N{\varphi }_{\text{max}}\pm N{\cosh }^{-1}\left(\frac{\alpha \gamma \left(N_{\text{t}}-N\right)}{2N}\right).$$ (8)

This equation describes both branches in Fig. 2 resulting from the saddle-node bifurcation. The upper branch, which we shall call N_s(Φ), is defined by the minus sign in Eq. 8 and is stable: small fluctuations in the number of bound bonds restore N to its equilibrium value N_s. The lower branch N_u(Φ), corresponding to the plus sign, is unstable: a slightly larger number of bound bonds causes N to shoot up to N_s, whereas a slightly lower value causes the cluster to unbind (N → 0). Eq. 8 also yields analytical expressions for the maximal cluster size N_max and the force at which it is attained, Φ_max:

$$\begin{array}{l}{N}_{\text{max}}=N_{\text{t}}\left(\frac{\alpha \gamma }{\alpha \gamma +2}\right);\\ {\text{Φ}}_{\text{max}}=N_{\text{t}}{\varphi }_{\text{max}}\left(\frac{\alpha \gamma }{\alpha \gamma +2}\right).\end{array}$$ (9)

Two points are worth noting here:

• 1.The force at which the maximal cluster size is attained is not simply the product of the total number of bonds N_t and the single-bond critical force ϕ_max; although this force is an upper limit, there is a prefactor that depends on the binding and rebinding rates, and varies continuously between 0 and 1. This factor is, in fact, the maximal probability that a single bond is bound.
• 2.While Φ_max is a lower bound on the force Φ_crit at which the cluster collectively unbinds, we have only found an implicit equation to define Φ_crit, given by

$${\frac{\text{d}}{\text{d}N}\text{Φ}|}_{{\text{Φ}}_{\text{crit}}}=0.$$

Solving this equation shows that, depending on the value of γ, Φ_max is either a good or a poor estimate for Φ_crit—in the regime 0 < γ < 2 the error is no larger than 9%. We do note, however, that Φ_crit is a biologically significant quantity. For instance, in rolling neutrophils, the catch bonds forged by l-, and to a lesser extent, P-selectins, collectively unbind at a critical shear stress (17–19) closely related to the critical cluster unbinding force. A final point of potential biological significance concerns the extent of the cluster reinforcement. By setting Φ(N) = 0, we can determine N₀, the equilibrium cluster size at zero force. Simple substitution yields

$$N_0=\left(\alpha \gamma N_{\text{t}}\right){\left(\alpha \gamma +2\text{cosh}{\varphi }_{\text{max}}\right)}^{-1}.$$

With this unforced occupation, we compute the ratio between the zero-force and the maximum cluster size:

$$\frac{N_{\text{max}}}{N_0}=\frac{\alpha \gamma +2\text{cosh}{\varphi }_{\text{max}}}{\alpha \gamma +2}=\frac{1+\gamma e^{\frac{1}{2}\left({\varphi }_s-{\varphi }_c\right)}+e^{{\varphi }_c+{\varphi }_s}}{\gamma e^{{\varphi }_s}+2e^{\frac{1}{2}\left({\varphi }_c+{\varphi }_s\right)}}.$$ (10)

This ratio is independent of the number of available bonds. Its behavior as a function of ϕ_c and ϕ_c is telling: while it plateaus for increasing ϕ_s, it may become arbitrarily big as ϕ_c is increased. Recalling the definition of ϕ_c, we see that biophysically, this limit corresponds to a high value for k_c and in particular, to the limit k_c ≫ k_s: an optimal regime for catch-bond functionality. Note, too, that we have not assumed in our catch-bond model that k_c ≫ k_s; we simply observe that, only in this regime, the single-bond lifetime curve displays a maximum at finite force. This analysis demonstrates that to ensure optimal collective functioning, individual bonds should show this behavior. And indeed, values reported for k_c obtained from fits of Pereverzev et al. (21) to single molecule experiments show that they are consistently higher than k_s, with the ratio k_c/k_s ranging from 5 to 480. Interestingly, our fit of the two-state model to the observed lifetime of the FNIII₇₋₁₀-α₅β₁ bond produces an even higher k_c/k_s ratio of 1.3 × 10⁵ (see Fig. 1). We interpret this as evidence that biophysical catch-bond links are designed such that when operating in concert, they provide maximal collective reinforcement.

So far, we have considered the mean-field, equilibrium properties of a cluster of catch bonds. We have shown that the equilibrium number of closed bonds rises with rising force, up to a point, and that aspects of this process may be understood analytically. In what follows, we analyze dynamical aspects of such clusters and will, in particular, address the lifetime: through a combination of factors, catch-bond clusters may become extremely long-lived.

Stochastic Simulations

We now turn to simulations of the time-dependent behavior of a cluster of catch bonds under a constant load. We start our runs with a cluster with some initial number of closed bonds N_i, apply a constant total force to this cluster, and observe how the fraction of closed bonds evolves in time. The one-step master equation lends itself well to simulations using the Gillespie algorithm (26), which simulates events in stochastically distributed time intervals.

The initial value N_i is significant for the typical evolution of the simulation. Consider Fig. 2, which shows the stable and unstable branches of the cluster size. For a fixed force Φ, there are two equilibrium cluster sizes; the unstable branch N_u and the stable branch N_s above it. For N_i, there are consequently three distinct possibilities:

• 1.N_i > N_s. Simulations starting here are expected to display a decrease in N up until the point where N attains its stable equilibrium value N_s.
• 2.N_u < N_i < N_s. Simulations starting in this regime will tend to show an increase in N until the stable value of N_s is attained.
• 3.N_i > N_u. Because the flow is away from the unstable branch, simulations starting in this regime will show complete detachment of the cluster until N = 0.

The first and second cases are indeed apparent—typical trajectories in this regime are plotted in Fig. 3, where we start simulations from above and below N_s. Fig. 3 also shows two typical unbinding events: when the fluctuating number of bound bonds stochastically drops below N_u, the entire cluster unbinds in cascade-like fashion. Note that even in the unbound state there is a finite number of bound bonds due to the random rebinding modeled by γ. Stochastic simulations, in principle, also offer direct access to the growth kinetics of a catch-bond cluster. This is a topic of great relevance, but to meaningfully address it, it must be considered jointly with the buildup of the traction force over time and, by extension, the evolution of the associated stress fiber. We choose here to consider the fixed force equilibria and lifetimes, and will not address the complex issue of cluster growth and maturation.

Figure 3.

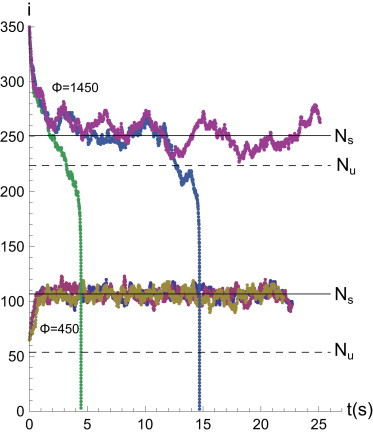
Stochastic trajectories for N_t = 1024, γ = 0.1 and two different values of the applied force Φ = 450 and Φ = 1450 (very close to Φ_crit), with N_i = 60 and 350, respectively. (Solid lines) The number of closed bonds either increases or decreases to reach its stable equilibrium value. (Dashed lines) Unstable solutions of Eq. 6. Two out of the three trajectories for the larger value of Φ correspond to cascade unbinding of a cluster. By compiling statistics on these unbinding events, we obtain the cluster lifetime from these simulations.

Cluster Lifetimes: Uniform Loading

How long will a cluster stay bound? We have been calling it stable, but at best it is metastable, because sooner or later, a fluctuation will come along that is sufficiently large to drive N below N_u and cause the entire cluster to unbind. There are several ways to compute or determine the lifetime τ. It is, however, difficult to obtain directly from simulations: As we will show, the lifetime becomes prohibitively large for realistic parameters and in simulational practice, the cluster never unbinds. One instructive way to view the lifetime is to construct the effective potential barrier that the cluster must cross to reach the unstable branch, starting from the stable region. To this end, we interpret the mean field evolution equation (Eq. 6) as a gradient flow of the form

$$\frac{\text{d}N}{\text{d}t}=-\frac{\text{d}U\left(N\right)}{\text{d}N},$$

which defines the effective potential U(N). Fig. 4 graphs the shape of this potential for various forces, and provides an intuitive interpretation for the unbinding transition: from the local minimum U_min = U(N_s) the cluster passes to the left over a barrier whose height we shall indicate with U(N_u) = U_min + ΔU. Fig. 4 b graphs this potential barrier as a function of the applied force, demonstrating a generic maximum at finite force.

Figure 4.

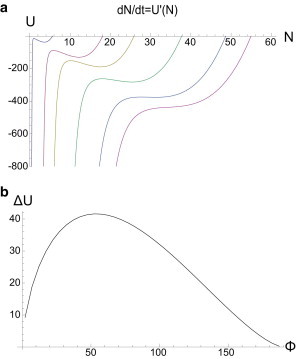
(a) The effective potential U(N) for Φ = 10, 50, 80, 130, 180, 210, and γ = 0.1. (b) The barrier height ΔU for γ = 0.1.

The height of the barrier will determine the lifetime of the cluster according to an Arrhenius law (24),

$$\tau ={\tau }_0{e}^{\text{Δ}U/U^{\text{⋆}}},$$ (11)

with τ₀ a reverse of the attempt frequency and U^∗ some reference effective potential (note that U is dimensionless—the time derivative in the gradient flow equation is taken with respect to a nondimensionalized time). We may estimate U^∗ as the effective potential lost per unbinding bond at zero force, i.e.,

$$U^{\text{⋆}}=\frac{\text{Δ}U\left(\text{Φ}=0\right)}{N_0=\frac{1}{2}\gamma N_{\text{t}}}.$$

The value τ₀ is a timescale on the order of the single-bond lifetime, i.e., seconds. Combined, this yields enormous lifetimes, and unbinding of the cluster is generally not expected to occur unless forces very close to Φ_crit are applied (see also Fig. 3).

A more direct, but perhaps less intuitive way to obtain the cluster lifetime is by explicitly constructing the lifetime by summing over all possible dissociation paths, weighed with their collective rates (27):

$$\tau =\sum _{i=1}^{N_s}\left[\frac{1}{r\left(i\right)}+\sum _{j=i+1}^{N_t}\frac{1}{r\left(j\right)}\prod _{k=i}^{j-1}\frac{g\left(k\right)}{r\left(k\right)}\right].$$ (12)

Fig. 5 compares directly the results from a small stochastic simulation to both the explicit summation method, and a best fit to the potential method, demonstrating that either works well. As expected, this small cluster displays a maximum in its lifetime at a finite force. What these considerations demonstrate is that not only do catch-bond clusters grow with increasing force, they also become longer-lived at higher forces. This enhancement of the lifetime is very pronounced: increasing the number of available receptors to 1024 (a number we have been using throughout this article in simulations) shows why we never see clusters unbind in previous simulations—the average lifetime at parameter values form single-bond experiments may become as long as 10²⁰ s (see also Fig. 6).

Figure 5.

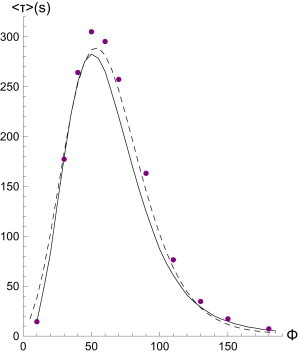
Lifetime of a catch-bond cluster with N_t = 128, γ = 0.1 (dashed line: Arrhenius law; solid line: pathway model; points: Gillespie simulations) as a function of force. Parameters in Arrhenius law were τ₀ = 3.2 and U^∗ = 9.2.

Figure 6.

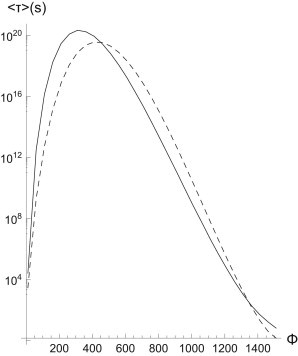
Lifetime of a catch-bond cluster with N_t = 1024, γ = 0.1 (dashed line: Arrhenius law; solid line: pathway model) as a function of force. Parameters in Arrhenius law were τ₀ = 1.4 and U^∗ = 59.4.

Slip-bond clusters, likewise, may be extremely long-lived (13,22,28). The principal cause for this is that, provided sufficiently many bonds are in principle available, the rupture of a single closed bond in the slip-bond cluster raises the force per bond on the remaining closed bonds, and therefore makes them more likely to unbind. However, this effect is offset almost completely for large clusters by the increased rebinding when more unbound bonds are available to do so. The catch-bond cluster, however, is even longer-lived because, in the stable regime, unbinding of a single bond also causes a higher force per remaining bond; but for catch bonds this may actually render them even longer-lived.

Cluster Lifetimes: Asymmetric Loading

In this section we consider one specific case of nonuniform loading, corresponding to the concentration of forces along the edges of a focal adhesion (FA) as reported in Plotnikov et al. (23). We divide the FA into distinct zones, and distribute the total force linearly across them. Unpeeling of the FA is implemented by fully detaching a zone once, for this zone, the average lifetime is exceeded. The detached zone is then prohibited from rebinding, which accounts for the spatial separation in the unpeeling region that renders rebinding highly unlikely. Once a zone is detached, the force that it was supporting is assigned, again in graded fashion, to the remaining bound zones. As in Sun et al. (13), these zones are now more likely to also unbind, causing a complete unpeeling of the structure. The total lifetime of the edge-loaded cluster is now equal to the lifetime of the rearmost zone. We collect our results in Fig. 7. The most striking finding is that for the same value of N_t, the cluster is much shorter-lived in edge-loading than in uniform loading. This is due to our choice of excluding unpeeled bonds from rebinding, and as we have seen in the preceding section, this rebinding is a strongly stabilizing process in the uniformly loaded cluster. We speculate that cells may actually use this force-distribution dependence to ensure that (for instance) filopodia-like processes provide quick and tentative probes of the external elasticity, but do not remain bound excessively long. The results we present in Fig. 7 are obtained by direct computation of lifetimes according to Eq. 12. For more elaborate or dynamic loading conditions one must turn to numerical simulation. Because our findings for nonuniform loading agree with those reported in Sun et al. (13), we expect qualitatively similar modifications of the adherent behavior under the additional loading protocols reported there.

Figure 7.

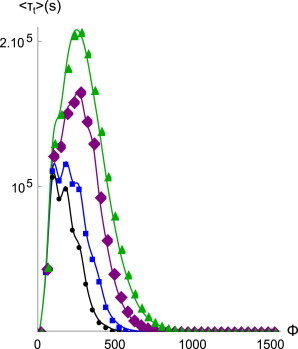
Lifetime of a catch-bond cluster with N_t = 1024, γ = 0.1 with total force distributed nonuniformly across four zones (line with points, 0.05Φ, 0.18Φ, 0.31Φ, and 0.45Φ; line with squares, 0.12Φ, 0.21Φ, 0.29Φ, and 0.38Φ; line with diamonds, 0.20Φ, 0.23Φ, 0.27Φ, and 0.30Φ; line with triangles, 0.25Φ per zone) as a function of force. Cluster lifetime shortens considerably with increasing asymmetry, and the unpeeling force diminishes.

Loading by Motors Pulling on Actin Stress Fibers

In this final section, we consider what happens to a catch-bond cluster when the force is not applied externally, but provided by motors actively pulling from the inside. Although motors are not the only source of force in cellular adhesions—polymerization forces, for instance, may contribute too—we choose to consider only active, motor-generated forces. For the catch bonds we consider here, Schiller et al. (29) report a strict dependence of FA formation and stability on myosin II-mediated forces for several catch bonds including α₅β₁. Thus, we consider focal adhesions connecting the passive ECM to actively contractile actin stress fibers inside the cell. Inspired by Schwarz et al. (22) and Erdmann and Schwarz (28), we represent the elastic media inside and outside the cell as elements connected in series (Fig. 8). In this simplified system, the mechanosensory question we address is the following: how can the number of closed bonds in the adhesion cluster—an internal measure—report on the extracellular stiffness, an external property. The effective spring constant of the outside-inside system is given by 1/K_eff = 1/K_ECM + 1/K_CSK, and we consider the force of the myosin motors pulling on the adhesion as given by a simple force-velocity relation that reflects the basic tendency to slow down upon increased counterloading. Letting X(t) represent the strain as a function of time—which equals the displacement against a fixed reference point of the contractile stress fiber—we express the evolution of the strain with time as

$$\frac{\text{d}X\left(t\right)}{\text{d}t}=v_0\left(1-\frac{F\left(t\right)}{F_s}\right),$$ (13)

where v₀ is the bare, unloaded velocity of the contractile fiber and F_s is its stall force: The force at which the fiber can no longer move. The choice for a linear force-velocity relation (identical to the one in Schwarz et al. (22)) deserves some motivation: Although it is well established that collective force-velocity relations may display complicated, concentration-dependent and nonlinear characteristics, we feel that, for our purposes and for the sake of transparency, our simplified approach is justified. For instance, in Erdmann and Schwarz (30) it is shown that small ensembles of myosin II motors display collective force-velocity relations that start at a finite unloaded velocity and monotonously (though not exactly linearly) decrease until a collective stall force is reached. In replacing this with a linearly decreasing force-velocity relation, we have sought to strike a balance between retaining the essential characteristics of collective behavior, while introducing a minimum of additional parameters.

Figure 8.

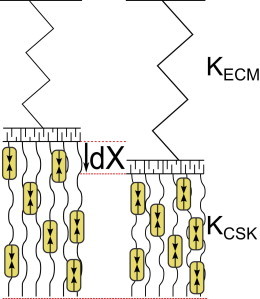
The spring-fiber system where the passive ECM with a spring constant of K_ECM is connected by a force bearing FA to the active contractile fiber with a spring constant K_CSK. Rather than have an external force effect a displacement on one of the springs, this displacement dX is now due to an active contraction of the stress fiber. We model the evolution of this displacement with the force-velocity relation Eq. 13.

In the two-spring system, the force F(t) itself is a simple function of X(t) through the elastic relation

$$F\left(t\right)=K_{\text{eff}}X\left(t\right)={\left(K_{\text{ECM}}^{-1}+K_{\text{CSK}}^{-1}\right)}^{-1}X\left(t\right).$$ (14)

Substituting Eq. 14 into Eq. 13, we solve for the evolution of the motor-supplied force with time, which expressed in the same dimensionless units as before yields a simple exponential approach to a plateau force,

$$\text{Φ}\left(t\right)={\text{Φ}}_s\left(1-e^{-t/{\tau }_K}\right),$$ (15)

where τ_K = F_s/v₀K is the relaxation time. Note that the stiffnesses K_ECM and K_CSK we define here have units of spring constants—force per length—rather than the force per area (Pascals) appropriate for 3D moduli. To translate our results to experimental stiffnesses, we must factor in the basic lengthscale over which these forces are applied. Although there is significant variation in the size and areas of FAs, most studies report typical dimensions of μm (see, e.g., Han et al. (31)). We therefore choose to convert our spring constants to effective moduli with this typical length, which is how the stiffness axis of Fig. 9 was obtained. To mark the distinction, we label this axis E_ECM to indicate moduli. This timescale is slow compared to the rapid exchange timescales of the catch-bond cluster, and we consider the situation where N(t), the instantaneous number of closed catch bonds, follows Φ(t) adiabatically. At present, regardless of the elasticity of ECM or CSK, Φ(t) will approach the stall force for long times. As such, this force evolution cannot help discern the extracellular stiffness. The cell as a whole, however, will invest a certain amount of energy into the contractile fibers. We hypothesize that this is equally distributed across each of its stress fibers (each receiving the average), in which case the system is operating under one further constraint: a set total energy expenditure. Similarly motivated hypotheses of constant work were put forward in Schwarz et al. (22) and Bischofs and Schwarz (8). The assumption of a fixed contractile energy investment is further supported by recent experimental determination of precisely this quantity: Schiller et al. (29) measure it to be ∼400 fJ for an entire cell which, assuming between 50 and 100 FAs per cell, comes to a few to tens of fJ per focal adhesion. We express the elastic work invested in a single focal adhesion, after a time t, as

$$W\left(t\right)=\underset{\text{path}}{\int }F\left(t\right)\text{d}X\left(t\right)=\frac{1}{2}\frac{F_s^2}{K_{\text{eff}}}{\left(1-e^{-t/{\tau }_K}\right)}^2.$$ (16)

Setting a limit on W(t) = W_max thus effectively terminates this process at a stop time t^⋆, defined implicitly by W(t^⋆) = W_max. The force at this time, Φ(t^⋆), may be computed to be

$$\text{Φ}\left(t^{\text{⋆}}\right)=\sqrt{2W_{\text{max}}{K}_{\text{eff}}}.$$ (17)

To complete the force sensor, we note that this force, which depends on the effective and therefore the external stiffness K_ECM, in turn defines a fraction of closed bonds N(Φ(K_ECM)): The asymptotic fraction of bound bonds—which is an internally observable quantity—directly reports on the external stiffness. Such mechanosensory relevance of catch bonds, and specifically α₅β₁, has been suggested before in Friedland et al. (10), but our direct correlation between an intracellular observable and the extracellular stiffness represents a very specific proposal for how this mechanosensory pathway is organized at the molecular level. As such, the catch-bond cluster provides the functionality of a mechanosensor. Our findings support the conclusions of Plotnikov et al. (23), the authors of which argue that each focal adhesion, individually and autonomously, acts as a local rigidity sensor and that the presence of forces is essential for focal adhesion formation and stabilization—as it is in our clusters. These findings are summarized in Fig. 9, which computes numerically the N(E_ECM) characteristics for realistic biophysical parameters, and different values of the work W_max. Note that for realistic energies per FA, the rigidity sensor itself functions (i.e., does not unbind) within a stiffness range of roughly 1–50 kPa. Most physiological environments for which this type of rigidity sensing could be relevant are well within this regime.

Figure 9.

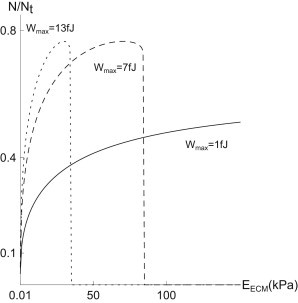
The fraction of closed bonds as a function of the ECM stiffness E_ECM. We consider here 120 parallel filaments, each of which is tensed by 4 × 10⁵ motors. Each of these motors possesses an effective stall force of 10 pN (34). The constant work W_max varies between the curves (dotted line depicts W_max = 13 fJ; dashed line, 7 fJ; solid line, 1 fJ), corresponding to between 0.6 and 8 k_BT per motor. If the external rigidity is too high, a catch-bond cluster is unable to hold on and detaches.

Recent experiments have also suggested an important role for fluctuating (23) or cyclically applied (32) forces in dynamical processes such as persistent motility, durotaxis, and cytoskeletal remodeling. We do not consider varying forces in the simulations presented here, but note that the relaxational timescales in our model (visible, for instance, in Fig. 3 as the cluster approaches equilibrium from N_i) do allow our results to be applied to relatively slowly varying load scenarios, where the cluster composition may adiabatically follow the load.

Our model predicts a very specific force-dependence of the diffusion of catch-bond integrins in focal adhesions. Bound bonds, anchored to the ECM, will exhibit lower diffusivity at larger applied forces, i.e., for higher external matrix stiffnesses, and more of them will be bound. This will result in a lower mobility, both collective and individual, as the force is raised—until the critical force at which very abruptly the catch bonds collectively detach and become mobile again. These effects should be measurable either by fluorescence recovery after photobleaching, but better still in experiments based on single molecule tracking or superresolution imaging such as those reported in Rossier et al. (33). Precise comparison between such experiments in systems such as Truong and Danen (20) requires further modeling of the spatial distribution of catch bonds, particularly in combination with pure slip bonds. As of this writing, we are in the process of simulating the mixed/diffusive system numerically, to determine the correlation between integrin mobility and FA traction force.

Conclusions

The fraction of bound integrin catch bonds, connecting a focal adhesion site to the ECM, shows a regime of increase with increasing force. As such, these clusters provide a stronger adhesive connection to the environment when the focal adhesion is under tension. In addition to becoming more tightly connected, the catch-bond cluster is also considerably longer-lived at higher forces—absent other cues to cause unbinding it may become, effectively, indefinitely adherent. In situations where the stress is actively generated by molecular motors pulling on an actin stress fiber, the fraction of bound bonds is a one-to-one reporter for the external ECM stiffness. This bound fraction, if properly coupled to further downstream intracellular sensory processes, may serve as a primary sensory link in a mechanosensing pathway.