Measuring the Lamellarity of Giant Lipid Vesicles with Differential Interference Contrast Microscopy

Abstract

Giant unilamellar vesicles are a widely utilized model membrane system, providing free-standing bilayers unaffected by support-induced artifacts. To measure the lamellarity of such vesicles, fluorescence microscopy is one commonly utilized technique, but it has the inherent disadvantages of requiring lipid staining, thereby affecting the intrinsic physical and chemical properties of the vesicles, and it requires a calibration by statistical analysis of a vesicle ensemble. Herein we present what we believe to be a novel label-free optical method to determine the lamellarity of giant vesicles based on quantitative differential interference contrast (qDIC) microscopy. The method is validated by comparison with fluorescence microscopy on a statistically significant number of vesicles, showing correlated quantization of the lamellarity. Importantly, qDIC requires neither sample-dependent calibration nor sample staining, and thus can measure the lamellarity of any giant vesicle without additional preparation or interference with subsequent investigations. Furthermore, qDIC requires only a microscope equipped with differential interference contrast and a digital camera.

Introduction

To dissect the complexity of cell membranes and to isolate the behavior of lipid bilayers in simple systems under controlled conditions, giant unilamellar vesicles (GUVs) are widely utilized model systems (1). Compared to supported planar lipid bilayers, GUVs have the advantage of being free-standing, hence free from support-induced artifacts, yet with sufficiently low curvature to well mimic cellular membranes. GUVs have been instrumental in studying fundamental questions in lipid biology, such as the existence of glycosphingolipid- and cholesterol-enriched domains (rafts) in natural membranes and their formation by lipid-lipid interactions (2).

In many studies, where a liposome serves as model system (3) it is preferable that the giant vesicle (GV) should consist of a single lipid bilayer, i.e., be unilamellar, such as an actual cellular membrane. However, formation techniques produce vesicles with a variety of sizes and lamellarities (4). Moreover, vesicles often display inclusions of smaller vesicles, lipid tethers, and membrane fragments, and/or droplets of bulk lipids. It is therefore necessary to be able to measure the membrane thickness of a GV over its entire surface, to identify uniform GUVs.

Optical imaging techniques appear ideally suited to nondestructively assess the shape, size, and uniformity of GVs. Because the thickness of a membrane bilayer (∼4 nm) is well below the spatial resolution of optical microscopy (≥200 nm), fluorescence intensity measurements have been used (5) to quantify the membrane thickness. However, fluorescence lipid staining can alter the intrinsic physical and chemical properties of the lipid bilayer and is prone to photobleaching (6). It is also limited to measuring the relative lamellarity within an ensemble of GVs under the same staining, excitation, and detection conditions, because the absolute intensity depends on the fluorophore concentration, which is difficult to accurately reproduce between different sample preparations. Furthermore, the assumption that the fluorescence intensity is proportional to the lamellarity requires a homogeneous distribution of the fluorophores in the membranes. In more complex GVs involving lipid mixtures with phase coexistence (2,7), changes in fluorophore concentration between the different phases thus severely complicate lamellarity assessments.

To overcome these limitations, we have developed a believed-novel method for quantitative determination of GV lamellarity based on label-free differential interference contrast (DIC) microscopy. DIC microscopy (8) is a wide-spread tool for observing transparent objects such as living cells and tissues. It measures the difference of the optical phase between two points in the sample plane, spatially separated by an amount typically comparable with the optical resolution. These changes in the optical phase are associated to changes in sample thickness and refractive index. Based on this principle, we have developed a quantitative DIC (qDIC) image acquisition and analysis procedure that enables the measurement of GV lamellarity in a rapid, noninvasive and reproducible way.

A population of GVs was produced using the electroformation method. Their lamellarity was quantified with qDIC on a statistically significant number of GVs (n = 77) and exhibited thickness quantization. For direct validation, the lamellarity on the same GVs was measured with fluorescence microscopy and agreement of the quantized lamellarity between the two methods on every investigated GV was found.

Materials and Methods

Commercial reagents

DOPC (1,2, dioleoyl-3-sn-glycero phosphatidylcholine) was purchased from Sigma-Aldrich (Dorset, UK) and used without further purification. A headgroup-modified, fluorescent lipid analog of DOPE (1,2, dioleoyl-3-sn-glycero phosphatidyl-ethanolamine) with the fluorophore ATTO-488 was purchased from ATTO TEC (Siegen, Germany). All other chemicals used were from Sigma-Aldrich and were of HPLC grade. Degassed Milli-Q grade water (18.5 MOhm, S. A. S., Molsheim, France) was utilized throughout.

Electroformation of GUVs

Giant thin-walled vesicles were created using an electroformation protocol based on the initial articles (9,10), which has been modified to increase the GUV yield (see Section S1 in the Supporting Material). A solution of DOPC containing 0.15 mol % ATTO-488 DOPE was applied onto the surface of two tantalum electrodes and dried. The electrodes were then suspended in water and an AC field sequence was applied, leading to formation of GUVs. For the optical microscopy, a 10× dilution of the resultant vesicle suspension in Milli-Q grade water (Millipore) was used.

DIC and fluorescence microscopy

Optical microscopy was performed using an Eclipse Ti-U microscope (Nikon UK Ltd, Kingston upon Thames, UK) and an objective (CFI plan Apochromat λ-series 20×, NA 0.75; Nikon). The 1.5× magnification multiplier of the Ti-U stand was used. For DIC, illumination was provided by a halogen tungsten lamp (V2-A LL 100 W; Nikon), followed by a blue-green filter (BG40; Galvoptics Ltd, Basildon, UK) to block near-infrared light for which the DIC polarizers do not have sufficient extinction, and a green filter (GIF, transmission band 550 ± 20 nm; Nikon) defining the wavelength range for the qDIC analysis and avoiding fluorophore excitation. A de-Sénarmont compensator was used for offset phase adjustment (a rotatable linear polarizer followed by a fixed λ/4 wave-plate, T-P2 DIC Polarizer HT; Nikon), followed by a Wollaston prism (T-C DIC Module High NA N2 Dry; Nikon) in the condenser unit, a Nomarski prism after the objective (D-C DIC Slider 20×; Nikon), and a linear polarizer (Ti-A-E DIC Analyzer Block; Nikon) in the filter turret. Epi-fluorescence microscopy was performed using a metal-halide lamp (Lumen L200/D; Prior Scientific, Rockland, MA) and an exciter/emitter/dichroic filter cube (GFP-A-Basic; Semrock, Rochester, NY) suitable for the ATTO-488 dye.

The vesicle suspension was pipetted into imaging chambers of 500-μm height and 20-mm diameter, formed by a microscope slide, an imaging gasket (Grace Bio-Labs, Bend, OR), and a No. 1 24 × 24-mm square coverslip. After mounting onto the microscope, the sample was equilibrated for a minimum of 30 min to reduce convection.

DIC and fluorescence images were acquired using a charge-coupled device camera (Orca 285; Hamamatsu, Hamamatsu City, Japan) with 1344 × 1024 pixels of 6.45-μm size. Considering 30× magnification, the pixel size corresponds to 0.215 μm at the sample plane, which was confirmed by a calibration sample within 0.5% accuracy. The camera has a 12-bit A/D converter, and the images were converted to 16-bit grayscale tiff files. An exposure time of 0.1 s was used for each frame in DIC images, limited by the readout speed, and the illumination intensity was adjusted to provide an average of ∼75% of digitizer range, corresponding to ∼3.8 × 10⁴ photoelectrons per pixel (at the lowest gain setting of the camera), and a relative shot noise of 0.5%. Whereas the camera has a specified full-well capacity of 18 ke, we found a linear response in the whole range of the camera up to ∼50 ke. Fluorescence images were acquired with an exposure time of 2.5 s, resulting in a maximum of ∼10⁴ photons/pixel for GUVs, leaving dynamic range for higher lamellarities. For each GV, 128 DIC images were acquired for opposite offset phases to analyze noise and movement. qDIC and fluorescence images were focused at the equatorial plane of the GVs. A typical single fluorescence image is shown in Fig. 1 a, and a single DIC image is shown in Fig. 1 c. Importantly, by performing DIC at 550 ± 20-nm wavelength where the absorption of the ATTO-488 fluorophore label is insignificant (see Section S2 in the Supporting Material), DIC and epi-fluorescence could be applied on exactly the same vesicle without mutual influence.

Figure 1.

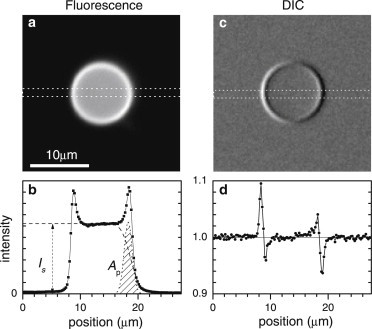
Images of a typical GUV made of DOPC labeled with 0.15 mol % DOPE-Atto488: (a) Fluorescence intensity image on a linear grayscale from zero (solid). (b) Fluorescence intensity along the cross-section indicated by the dotted rectangle in panel a. The intensity step I_s and the edge area A_p are indicated. (c) DIC image on a linear gray scale from 0.90I₀ (solid) to 1.16I₀ (open), where I₀ is the average intensity outside the GV. (d) DIC profile I/I₀ along the cross-section indicated by the dotted rectangle in panel c.

In general, qDIC requires equipment that is commercially available, affordable, and wide-spread. The essential parts are an optical microscope with DIC, a digital camera with a signal/noise > 100, and a computer to perform the image processing.

Fluorescence image processing

To quantify the vesicle lamellarity from fluorescence images, we calculated the average intensity in an annulus covering the edge of the vesicle with inner (outer) radius R₀ – ρ/2 (R₀ + ρ/2), where R₀ is the vesicle radius and ρ = 0.67 μm is given by the optical spatial resolution. We also calculate the average intensity within an inner circle of radius R₀ – 4ρ and the average intensity outside the vesicle (the background). In this way, we could quantify the average intensity at the edge of the vesicle and the average intensity of the step inside the GV, as shown in Fig. 1 b. When fluorescence images contained inclusions and/or stained lipid fragments that were out of focus but were still contributing to the measured signal, we used user-assigned regions to exclude those areas in the image analysis. The averaging procedure and all the following calculations were implemented in MATLAB ver. 2012a (The MathWorks, Natick, MA).

DIC Contrast Image Formation

We start by introducing the DIC contrast and the notations used in the image analysis. The sample is considered as a nonabsorbing object with phase retardation at each point in plane r = (x,y) given by the function φ(r). We use DIC with a de-Sénarmont compensator consisting of a polarizer and a quarter-wave plate in the illumination beam path. The angle θ of the polarizer with respect to the fast axis of the λ/4 plate is adjustable, resulting in elliptically polarized light after the λ/4 plate described as a field vector

$${\mathbf{E}}_{\text{in}}=E_0\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ e^{i\psi }\end{array}\right)$$ (1)

with a phase ψ = 2θ in the range from −π to π. The Wollaston prism in the back-focal plane of the condenser lens splits the two polarization components in direction, resulting in a shift of the illumination in the sample plane, such that one component passes through the point r + s/2, and the other through the point r − s/2, where s is the shear vector and r is the DIC image coordinate. We call the phases accumulated by the two beams in the sample φ₊(r) = φ (r + s/2) and φ₋(r) = φ (r − s/2). After propagation through the objective lens, the two beams are recombined by a Nomarski prism on the DIC slider, and pass through an analyzer oriented at −π/4 so that the final electric field is given by the Jones matrix expression

$${\mathbf{E}}_{\text{out}}=\frac{E_0}{2\sqrt{2}}\left(\begin{array}{cc}1& -1\\ -1& 1\end{array}\right)\left(\begin{array}{cc}{e}^{i{\phi }_{+}}& 0\\ 0& e^{i{\phi }_{-}}\end{array}\right)\left(\begin{array}{c}1\\ e^{i\psi }\end{array}\right).$$ (2)

The output intensity is thus given by

$$I_{\text{out}}\left(\mathbf{r},\psi \right)=\frac{I_{\text{ex}}}{2}\left[1-\text{cos}\left(\psi -\delta \left(\mathbf{r}\right)\right)\right],$$ (3)

with the phase difference δ = φ₊ − φ₋ and the excitation intensity I_ex ∝ E₀². To reduce the influence of a possible spatial dependence of I_ex(r), we acquire two images at opposite angles of the polarizer ±θ resulting in the output intensities I_± = I_out(r,±2θ). The contrast image is then defined as I_c = (I₊ − I₋)/(I₊ + I₋). If the phase retardation by the sample δ is small, as it is the case for GUVs, Eq. 3 can be linearized in δ, and for δ ≪ ψ < π the contrast image can be approximated as

$$I_{\text{c}}\left(\mathbf{r}\right)=\frac{\text{sin}\left(\psi \right)}{1-\text{cos}\left(\psi \right)}\delta \left(\mathbf{r}\right)\equiv K\left(\psi \right)\delta \left(\mathbf{r}\right),$$ (4)

with the transduction factor K. We note that K(π/2) = 1 such that for ψ = π/2 the contrast is equal to the phase difference. Decreasing ψ leads to an increase in K, thus enhancing the measured contrast at the expense of a smaller linear range in δ. Choosing ψ such that I_out = ηI_e, i.e., reduced to a fraction η compared to the maximum I_e reached for ψ = π, we find $K=\sqrt{1/\eta -1}$. In the data shown here, we used η = 0.05, which corresponds to K = 4.36 and a polarizer rotation angle of θ = 12.9°, requiring δ < 0.45 for the validity of Eq. 4, which is fulfilled for the measured GUVs having δ < 0.02 as visible in Fig. 1 d.

DIC Image Analysis

The image processing was divided into two major parts. In the first part, GVs were identified, centered, and the images were cropped to produce smaller images each containing only one GV (see Section S3 in the Supporting Material). Rigid GV movements during the acquisition of 128 images for each orientation of the polarizer were corrected by image registration. Averaging over 128 images was performed for noise reduction (see comparison between single acquisition in Fig. 2 a and averaging in Fig. 2 b) and the contrast image calculated according to Eq. 4. An analysis of the noise showed that a single DIC image with an acquisition time of 100 ms is sufficient to determine the quantized GV lamellarity. In the subsequent image processing, the contrast images were fitted to quantify vesicle lamellarity as detailed in the following subsections.

Figure 2.

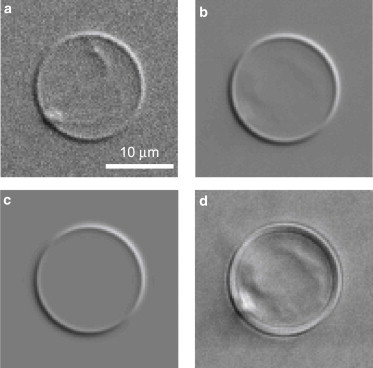
(a) Measured DIC of a GUV with a single acquisition. Displayed is the background subtracted and normalized image I₊/I₀ −1. (b) Measured DIC contrast image I_c averaged over 128 acquisitions for each polarizer angle. (c) Simulated DIC image I_p computed with the best fit parameters. (d) Difference between the measured contrast image b and the simulated image c. Linear grayscale, solid to open, from −0.1 to 0.1 (a–c), and from −0.02 to 0.02 (d).

DIC model images of giant vesicles

To extract a quantitative measure of the GV lamellarity, we used the simple and rather well-defined geometry of the GVs, being thin, nearly spherical shells. We created a model of the DIC images of GVs and optimized the model parameters to minimize the residuals of the fit. To inform this model, we use the measured epi-fluorescence intensity, which is averaged for each image point over the same light cone as DIC with matched objective and condenser NA, and therefore should be proportional to the phase shift assuming a homogeneously distributed fluorophore in the GV. We have thus modeled the optical phase retardation induced by a GV as

$$\phi \left(\mathbf{r}\right)=\frac{A_{\text{p}}}{w_{\text{p}}\sqrt{\pi }}\text{exp}\left[-{\left(\frac{\left|\mathbf{r}-{\mathbf{R}}_{\text{c}}\right|-R_0}{w_{\text{p}}}\right)}^2\right]+\frac{I_{\text{s}}}{2}\left[\text{erf}\left(\frac{\left|\mathbf{r}-{\mathbf{R}}_{\text{c}}\right|-R_0}{w_{\text{s}}}\right)+1\right],$$ (5)

resembling the fluorescence image in Fig. 1 b, with an area A_p under the peak at the vesicle rim and a step height I_s from the outside to the inside of the GV. R_c is the center of the GV, R₀ is its radius, and w_p and w_s are the widths of the rim and the step, respectively.

The choice of A_p, the area of the phase peak at the rim of the vesicle, is aimed at minimizing the effect of distortions of GVs. The translational motion of the vesicles as a whole is compensated by the registration procedure (see Section S3.2 in the Supporting Material). A temporally modulated distortion of the membrane shape by a distance less than the optical resolution will, in first-order, lead to an averaging of the phase over the motion, which retains the peak area. GVs showing larger motion are not reproduced by the fit and are discarded by the fit quality cutoff, as discussed in Section S3.2 in the Supporting Material. The step amplitude I_s is chosen as a fit parameter because it is not affected by small shape fluctuations of the GV. To account for distortions of the vesicles, we introduced an ellipticity in the model using |U(r – R_c)| in Eq. 5 instead of |r – R_c|, with a matrix U given by the ellipticity and its semimajor axis orientation. We found, however, that introducing the ellipticity was not improving the fit, such that we disregarded it in the following.

To model a DIC contrast image, Eq. 5 was used to calculate δ. We performed this operation in Fourier domain using the translation property of the Fourier transform $\mathcal{F}$,

$$\mathcal{F}\left[\delta \right]=2i\text{sin}\left(\frac{\mathbf{s}\cdot \mathbf{k}}{2}\right)\mathcal{F}\left[\phi \right].$$ (6)

We used the fast Fourier transform algorithm to reduce the computation time. An example of the resulting model contrast image is shown in Fig. 2 c. Adding an elliptical shape of the GV in the model function was evaluated, but did not lead to a better description of the measurements. The model contrast therefore uses a parameter vector p with 12 dimensions: the center R_c, the mean radius R₀, the ellipse orientation and eccentricity, the width w_p and area A_p of the rim, the width w_s and height I_s of the step, the shear vector s, and additionally a uniform offset.

Nonlinear least-squares fitting

For each parameter set p, the model contrast image I_p = Kδ was calculated and the norm of the difference $\text{Δ}=\left|\left|I_{\text{c}}-I_{\text{p}}\right|\right|$ to the measured image I_c was determined. The norm was defined as the sum of the squares of the elements in the two-dimensional image matrix divided by the total number of elements, i.e., the average of the squared elements. The value Δ was then minimized over p using a downhill simplex method, available as fminsearch in MATLAB. This locates a local minimum of an unconstrained multivariable function in a derivative-free algorithm (11). As discussed later, only a subset of parameters was free to vary. A typical residual image I_c − I_p is shown in Fig. 2 d on a scale stretched by a factor of 5 compared to Fig. 2, a–c, showing that the residual is small compared to I_c.

This procedure was applied automatically to measured images of a set of 145 different GVs. Some images were not fitted well due to the presence of defects such as inclusions or tethers. The fit was considered successful if $\left|\left|I_{\text{c}}-I_{\text{p}}\right|\right|/\left|\left|I_{\text{c}}\right|\right|<q$. The fit quality cutoff was chosen to be q = 0.5, resulting in ∼50% successful fits.

Results and Discussion

Lamellarity determined by fluorescence

Fluorescence images were acquired for every GV before DIC as described in Fluorescence Image Processing. The average fluorescence intensity at the vesicle ring, in the inner part (step), and the background outside the GV, are shown in Fig. 3 a. The background is virtually constant for all the images, and both the intensity at the ring and in the inner part show clear quantization. The azimuthal intensity at the GV perimeter, within equatorial sections, shows a monotonic increase with vesicle radius consistent with Akashi et al. (5), whereas the intensity in the center relating to the out-of focus polar regions is independent of the radius. This can be attributed to the geometry of the GV and the three-dimensional point-spread function (PSF) of the wide-field fluorescence microscope. When focusing in the sphere center, the area of GV surface within the lateral extension of the PSF grows quadratically with the GV radius. Simultaneously the PSF decays quadratically with the distance from the focus, providing an intensity independent of the GV radius. This is related to the missing sectioning capability of wide-field fluorescence. At the rim instead, the curvature of the GV determines how much GV surface lies within the PSF. We find that the data are consistent with a $\sqrt{R_0}$ radius dependence, as shown by the dotted lines in Fig. 3 a.

Figure 3.

Fluorescence of ATTO-488 labeled GVs. (a) Intensities of the background, the center, and the peak at the rim of the GV, as labeled; error bars are standard deviations of intensity within the appropriate areas. (b) Histogram of the center intensity with Gaussian fits.

The histogram of the fluorescence intensity at the GV center shown in Fig. 3 b reveals a 2:1 ratio of the two observed peaks, indicating the presence of double and single bilayers. The standard error of mean for the single bilayer distribution is ∼1% of the mean value, and its standard deviation is 17%. Using a bilayer thickness of 4 nm, this corresponds to a thickness fluctuation of 0.7 nm. The distinct quantization shown by this fluorescence analysis demonstrates that the electroformation method used allowed us to produce predominantly GUVs and serves as reference to validate our qDIC method.

Lamellarity quantification using qDIC

To determine the lamellarity from qDIC contrast images I_c, the fit procedure described in Section S3.2 in the Supporting Material was applied. To achieve convergence, the parameters were initialized, and then sequentially added to the fitted parameters using the following procedure: The GV center R_c and radius R₀ were initialized using moments of I_c as described in Section S3.1 in the Supporting Material. The initial amplitudes A_p and I_s were taken to be A_p = I_c,pp ⋅ 0.215 μm and I_s = 0.3I_c,pp using the peak-to-peak variation I_c,pp of I_c over the image. The values w_s and w_p were set to the image resolution w_s = λ/(2NA) ≈ 350 nm and w_p = λ/(NA) ≈ 700 nm.

The shear vector magnitude was set to |s| = 0.24 μm, which was independently determined as described in Section S3.7 in the Supporting Material. The shear vector direction was initially set to 135°, according to the microscope specification. Then, all other model parameters including the shear vector direction were set free, and the fitting was performed for the whole ensemble of the GUVs. The average shear vector direction of 135.7 ± 1.1° was determined. Fits, the shear vector direction was fixed at 135.7°.

The resulting distribution of A_p and I_s showed two branches versus R₀ similar to Fig. 3 a, with the radial dependencies of $A_{\text{p}}\propto \sqrt{R_0}$ and I_s being constant. Considering the lower branch as corresponding to unilamellar vesicles, consistent with the fluorescence results, we fitted the lower branch data using I_s = I_su and $A_{\text{p}}=A_{\text{pu}}\sqrt{R_0}$, yielding I_su = 0.058 and $A_{\text{pu}}=0.55/\sqrt{\text{nm}}$ (see Section S3.4 in the Supporting Material). The value of I_su = 0.058 corresponds to a phase shift of φ_u = I_su/K = 0.013. The phase shift created by a DOPC bilayer is given by φ_bl = 2πd(n_bl − n_w)/λ ≈ 0.0064, using the thickness (12) d = 4 nm and the refractive indices of a DOPC bilayer for in-plane polarization (12) n_bl = 1.47, and of water n_w = 1.333 at λ = 550 nm. We would expect φ_u = 2φ_bl = 0.0128 because the illumination passes through both surfaces of the GUV, which is in agreement with the measured value. We introduce the lamellarity parameter L giving the number of bilayers as

$$I_{\text{s}}=L{I}_{\text{su}}\text{and}{A}_{\text{p}}=L{A}_{\text{pu}}\sqrt{R_0},$$ (7)

because A_p and I_s are expected to scale proportional to L. We then refit the data having now only R_c, R₀, w_p, w_s, and L as free parameters. The result of this fit is given in Fig. 4 and shows quantization of the lamellarity L. The fit values of w_s and w_p were found to be uncorrelated to the other parameters, which we attribute to them being dominated by motion artifacts (blurring) due to dynamical GV distortion by thermal excitation. We note that the above procedure only needs to be done once to determine the instrument parameters s, I_su, and A_pu for a given DIC module, condenser, and objective NA. Once determined, we can measure the lamellarity of any GV repeating only the last fitting step.

Figure 4.

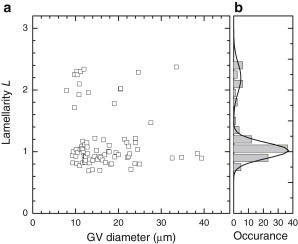
Vesicle lamellarity measured by qDIC. (a) Lamellarity as a function of GV diameter. (b) Histogram of the lamellarity; (solid lines) Gaussian fits.

The variation of the lamellarity within the two separate groups of points, corresponding to single and double bilayers, was estimated using a Gaussian fit to the histogram shown in Fig. 4 b. The standard deviation of 0.28 ± 0.02 in the subset of unilamellar vesicles corresponds to ∼1.1 nm, well below the thickness of a lipid bilayer, showing that qDIC is able to identify GUVs. Furthermore, we note that this variation is much larger than the measurement error of <0.01. It is thus dominated either by systematic errors such as the influence of out-of focus perturbations, or a noninteger lamellarity of the GVs, i.e., a measured membrane density not consistent with an integer multiple of lipid bilayers. This might arise from membranes incorporating additional lipid or other hydrophobic molecules, or having different order, being stretched, or having subresolution-sized domains of different lamellarities.

The lamellarity obtained by qDIC is correlated in Fig. 5 with the lamellarity obtained using fluorescence given by the fluorescence step intensity normalized to the mean value of the unilamellar distribution (see Fig. 3 b). We find a complete correlation between the lamellarities measured by the two techniques, verifying the validity and accuracy of the qDIC method.

Figure 5.

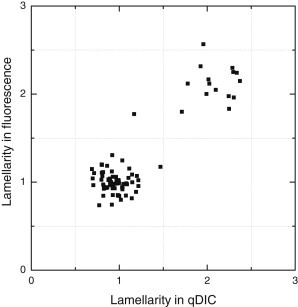
GV lamellarity measured by qDIC versus lamellarity measured by fluorescence.

The noise analysis (see Section S3.6 in the Supporting Material) shows that a single DIC image and a shorter exposure down to 1 ms is sufficient to determine the lamellarity, once the microscope has been calibrated. This reduces the sensitivity to drift and allows the measurement of the dynamics of objects, such as motion, vibrations, etc., from which important physical parameters such as membrane stiffness can be retrieved. The fitting model, Eq. 5, presently suited for spherical and elliptical geometries, can be adapted to other geometries. We are currently working on including phase-segregated domains in the membrane into the fit, motivated by the observation of such domains in measured data on GUVs of ternary lipid mixtures (DOPC/Porcine Sphingomyelin/cholesterol with 2:1:1 molar ratio) which showed domains with a 20% higher φ_u of the ordered domains. Even without a specific fitting model, the quantitative analysis can be done using the integration based on Wiener deconvolution (see Section S3.5 in the Supporting Material). This can be relevant for complex geometries like living cells.

GV systems are often not embedded in pure water, but in aqueous solutions of other substances such as buffers and sugars. The DIC contrast is determined by the refractive index difference between the bilayer and the inside and outside liquid. For equal refractive indices inside and outside, we discuss as example the specific case of a sucrose solution, which has a refractive index of n = n_w + kc, with the refractive index coefficient k = 0.049/M and the molarity c. Using a 100-mM solution instead of water results in a relative refractive index contrast change of −kc/(n_bl – n_w) = −4%. Accordingly, the qDIC parameters I_su and A_pu have to be reduced by 4%. We have measured GVs in 100-mM sucrose solution, and the qDIC analysis using the adjusted parameters results in a lamellarity quantization similar to the results in pure water, with GUVs having a lamellarity of L = 1.01 ± 0.15. This verifies that qDIC is able to determine the lamellarity of GVs also in homogeneous solutions.

In case inside and outside liquids have different refractive indices, an additional phase contrast component is created which is not considered in our fitting model, Eq. 5. The model can be modified to take such a difference into account, which would allow us to measure both the lamellarity and the refractive index difference. We note that a refractive index difference created by a molarity difference leads also to an osmotic pressure difference. The typical tensile strength of lipid bilayers of τ_lys ∼ 2 mN/m (13) allows for a maximum pressure p = 2τ_lys/R₀ ∼ 400 Pa (for R₀ = 10 μm) before rupture. Although generally osmolarity and molarity are different, we assume in the following discussion that they are equal. This is a good approximation for glucose and sucrose at low concentration, because they do not dissociate in aqueous solution and have an osmotic coefficient equal to unity within a few percent. Using the Morse equation for the osmotic pressure, we find the corresponding excess molarity inside the vesicle as δ_M = 2τ_lys/(TR_AR₀) with the gas constant R_A, yielding, for room temperature T = 300 K and R₀ = 10 μm, the upper limit of δ_M ∼ 0.16 mM. The resulting additional phase shift across the GV is δ_φ = 4πR₀kδ_M/λ, which for sucrose yields δ_φ = 0.0018, much smaller than φ_u and thus negligible, i.e., tolerable osmotic pressure differences do not lead to significant phase shifts. Significant refractive index differences between inside and outside can, however, be created using different solutes with equal osmotic pressure. As example, we consider glucose and sucrose. Assuming equal molarity c as dictated by the osmotic pressure, the corresponding phase shift is δ_φ = 4πR₀δ_kc/λ with the refractive index coefficient difference δ_k = 0.024/M between sucrose and glucose. We reach δ_φ = φ_u for a molarity of c = φ_uλ/(4πR₀δ_k) = 2.4 mM. We can conclude that for this system we need to take into account δ_φ in the fit for c > 0.5 mM. We also expect that for δ_φ ≫ φ_u, i.e., c > 20 mM, the error in the lamellarity determination would be significantly increased, possibly hindering the identification of GUVs.

Conclusions

We have demonstrated what we believe to be a novel method (qDIC) to quantify the lamellarity of giant vesicles based on differential interference contrast. We presented an experimental procedure to form a DIC contrast image proportional to the spatial change of the phase retardation at the sample. Fitting a model to the DIC contrast image provides the vesicle lamellarity. The method was validated by comparison with epi-fluorescence microscopy on an ensemble of fluorescently labeled vesicles. Importantly, qDIC is intrinsically label-free, overcoming the inherent drawbacks of fluorescent labeling such as sample modification and photobleaching. Particularly in the context of novel microscopy techniques that have recently emerged to image lipids in a label-free manner, such as coherent anti-Stokes Raman scattering (14,15), the method offers a platform for characterization of vesicle lamellarity compatible with subsequent label-free studies of GUVs. The method is capable to determine the lamellarity from a single DIC image, avoiding motion artifacts and opening up the study of vesicle dynamics. The method is also capable of label-free studies of phase-segregated domains in GUVs of lipid mixtures.