Use of Individual-level Covariates to Improve Latent Class Analysis of Trypanosoma Cruzi Diagnostic Tests

Abstract

Statistical methods such as latent class analysis can estimate the sensitivity and specificity of diagnostic tests when no perfect reference test exists. Traditional latent class methods assume a constant disease prevalence in one or more tested populations. When the risk of disease varies in a known way, these models fail to take advantage of additional information that can be obtained by measuring risk factors at the level of the individual. We show that by incorporating complex field-based epidemiologic data, in which the disease prevalence varies as a continuous function of individual-level covariates, our model produces more accurate sensitivity and specificity estimates than previous methods. We apply this technique to a simulated population and to actual Chagas disease test data from a community near Arequipa, Peru. Results from our model estimate that the first-line enzyme-linked immunosorbent assay has a sensitivity of 78% (95% CI: 62–100%) and a specificity of 100% (95% CI: 99–100%). The confirmatory immunofluorescence assay is estimated to be 73% sensitive (95% CI: 65–81%) and 99% specific (95% CI: 96–100%).

1 Introduction

Chagas disease is a vector-borne infection caused by the protozoan parasite Trypanosoma cruzi. In the Americas, Chagas disease is responsible for more morbidity and mortality than any other parasitic illness (World Health Organization, 2004). Transmission of T. cruzi typically occurs when contaminated feces of an infected blood-feeding triatomine insect enter a human host through the insect bite site or mucous membranes (Kirchhoff et al., 2004). T. cruzi can also be transmitted through blood transfusions (Young et al., 2007), organ transplants (Kun et al., 2009), consumption of contaminated food (Nóbrega et al., 2009), and congenitally from mother to child (Bern et al., 2009).

Many people infected with T. cruzi are unaware of their infection (Tarleton et al., 2007). For this reason, various serologic tests are used to detect infected individuals and protect the blood supply in Latin America (de Andrade et al., 1996, Blejer et al., 2001, Langhi Jr et al., 2002, Pirard et al., 2005) and the United States (Centers for Disease Control and Prevention, 2007). Proper interpretation of the results of these diagnostic tests requires knowledge of the sensitivity and specificity of each assay. Unfortunately there is no “gold standard” reference test for identifying T. cruzi infection (Tarleton et al., 2007). Parasitologic testing, which provides a clear definition of infection and is virtually 100% specific, is insensitive (Pirard et al., 2005). Serologic assays are frequently employed, but these also lack sensitivity due to their preparation from inappropriate stages of the parasite life-cycle (Tarleton et al., 2007) or because there is a great and largely unknown variety among T. cruzi strains in different regions (Verani et al., 2009). Absent a perfect reference test, the performance of Chagas disease assays can only be estimated by statistical methods that compare results from two or more imperfect tests.

Latent class analysis (LCA) is a popular approach to estimating performance of diagnostic tests in the absence of a gold standard. In LCA, a probabilistic model is assumed for the relationship between the diagnostic test results and the unobserved, or latent, disease status (Hui and Walter, 1980, Qu et al., 1996, Goetghebeur et al., 2000). In this paper we focus on LCA estimates in the commonly encountered scenario in which only two conditionally independent diagnostic tests are used (Hui and Walter, 1980, Joseph et al., 1995, Staquet et al., 1981, Walter and Irwig, 1988, Basáñez et al., 2004). We also perform a sensitivity analysis to investigate the effect of conditional dependence on our parameter estimates. An unbiased estimate for the two-test case is desirable in the context of Chagas disease, where limited resources restrict the number of tests that can be performed.

If the two tests are applied to a single population, then the model has five unknown parameters (the disease prevalence, the two sensitivities, and the two specificities) but the data contain only three degrees of freedom. Because the number of parameters exceeds the number of degrees of freedom, the model is nonidentifiable and estimates can only be obtained by introducing constraints (Walter and Irwig, 1988). One constraint technique consists of a Bayesian approach in which informative prior distributions are placed on at least two parameters (Joseph et al., 1995, Basáñez et al., 2004). A problem with this approach is that in nonidentifiable problems the posterior parameter estimates continue to be affected by the priors even as the sample size goes to infinity (Dendukuri and Joseph, 2001).

Alternatively, the two tests can be applied to two distinct populations. The model is then identifiable (provided that the two populations have sufficiently different disease prevalences) and can be solved by a maximum likelihood procedure (Hui and Walter, 1980). This approach has been used in the case of two geographically distinct populations with different prevalences (Hui and Walter, 1980, Johnson et al., 2001).

In this paper we describe a method for modeling the risk of disease as a function of multiple continuous individual-level covariates. Extended latent class models with covariates have been described previously (Huang and Bandeen-Roche, 2004, Hadgu and Qu, 1998, Dendukuri et al., 2009). Temporal covariates have been used, for example, to model test results as a function of days post infection (Engel et al., 2009) or to allow infection probability to depend on a covariate such as age (Branscum et al., 2008). We extend these analyses to consider a specific example of a population in which the probability of Chagas disease depends on several measurable temporal covariates. Our technique produces more precise parameter estimates than models that collapse the risk profile into a single binary covariate.

2 Methods

2.1 Specification of Covariate-Augmented LCA Model

We first review the likelihood computation for a two-test latent class model in which a single binary covariate separates tested individuals into two groups with different prevalences. We then show how to generalize this model to the case where the risk of disease is a continuous function of multiple covariates. Assume that two binary tests y_i (i = 1,2) are applied to N individuals. Positive test results are represented by y_i = 1 and negative results by y_i = 0. Let S_i and C_i be the sensitivity and specificity, respectively, of test y_i. S_i and C_i are assumed constant across all individuals. A binary covariate is measured and used to divide the sample N into two subpopulations of size N_g (where g = 1,2 and N₁ +N₂ = N) with distinct prevalences σ_g.

The likelihood l of the model is

$$l=\prod _{g=1}^2{\{{\sigma }_g{S}_1{S}_2+(1-{\sigma }_g)(1-C_1)(1-C_2)\}}^{N_{g11}}\times {\{{\sigma }_g{S}_1(1-S_2)+(1-{\sigma }_g)(1-C_1)C_2\}}^{N_{g10}}\times {\{{\sigma }_g(1-S_1)S_2+(1-{\sigma }_g)C_1(1-C_2)\}}^{N_{g01}}\times {\{{\sigma }_g(1-S_1)(1-S_2)+(1-{\sigma }_g)C_1{C}_2\}}^{N_{g00}},$$ (1)

where N_gjk (j, k = 0,1) is the number of individuals in population g with observed test results y₁ = j and y₂ = k. This likelihood is (apart from a constant coefficient) a multinomial likelihood. The goal of traditional LCA is to find parameters σ_g, S_i, and C_i that maximize l.

We now relax the assumption of a single binary covariate. For individual n (n = 1,…, N) in the sample, let the probability of disease σ_n be a function of M measurable covariates:

$${\sigma }_n=\text{Pr}(\text{disease}|\text{covariates})=f({\psi }_1(n),{\psi }_2(n),\dots ,{\psi }_M(n))$$ (2)

where ψ_m(n) (m = 1,…,M) is the value of the mth covariate in this subject. The covariates ψ_m may be continuous (e.g., age) or discrete. Specification of σ_n also requires a set of U risk parameters β = (β₁,…, β_U) that capture the manner in which the covariates influence the risk of disease. The functional form of σ_n is assumed to be known a priori and the model estimates the values of the risk parameters β. The likelihood L of this variable-risk model is

$$L=\text{Pr}(\text{observed data}|S_i,C_i,\beta )=\prod _{n=1}^N{\{{\sigma }_n{S}_1{S}_2+(1-{\sigma }_n)(1-C_1)(1-C_2)\}}^{{\delta }_{n11}}\times {\{{\sigma }_n{S}_1(1-S_2)+(1-{\sigma }_n)(1-C_1)C_2\}}^{{\delta }_{n10}}\times {\{{\sigma }_n(1-S_1)S_2+(1-{\sigma }_n)C_1(1-C_2)\}}^{{\delta }_{n01}}\times {\{{\sigma }_n(1-S_1)(1-S_2)+(1-{\sigma }_n)C_1{C}_2\}}^{{\delta }_{n00}},$$ (3)

where δ_njk = 1 if individual n has test results y₁ = j and y₂ = k, and δ_njk = 0 otherwise. It can be shown that when σ_n is a binary function of a single covariate, equation (3) reduces to the two test/two population likelihood function. The advantage of allowing σ_n to vary across all individuals is that in some cases the disease process may best be described as a function of one or more possibly continuous variables.

2.2 Chagas Disease Data and Infection Risk from Arequipa, Peru

The development of our model was motivated by Trypanosoma cruzi diagnostic test data from La Joya (population 2252), a community in the Peruvian department of Arequipa. In 2008 a cross-sectional serologic and socio-demographic study was conducted in La Joya. A total of 1333 individuals participated in the survey. Fifteen subjects were excluded from the following analysis due to missing or indeterminate data, making N = 1318 in the final sample.

Each individual’s serum was screened for T. cruzi infection with a commercially available enzyme-linked immunosorbent assay (ELISA) (Chagatek, Laboratorio Lemos SRL, Buenos Aires). All ELISA-positive sera and a random sample of 20% of ELISA-negative sera were also tested with an immunofluorescence assay (IFA) used as a confirmatory test (Table 1). The study protocol was approved by the institutional review boards of the Johns Hopkins Bloomberg School of Public Health and Universidad Peruana Cayetano Heredia, and analysis of data was approved by the University of Pennsylvania and Vanderbilt University.

Table 1.

Frequency of observed Trypanosoma cruzi diagnostic test results in La Joya, Peru.

	IFA+	IFA−	IFA not performed	Total
ELISA+	101	39	0	140
ELISA−	8	226	944	1178
Total	109	265	944	1318

Analysis of confirmed positive (ELISA+/IFA+) individuals showed that the yearly risk of T. cruzi infection in La Joya was greater prior to an insecticide spray campaign that occurred in 1995. The yearly infection risk for time lived outside the study community was also different than the risk during time spent in La Joya. The total probability of infection was best fit by an expanded catalytic model (Muench, 1959) given by

$${\sigma }_n(T_{\mathit{\text{pre}}}(n),T_{\mathit{\text{post}}}(n),T_{\mathit{\text{out}}}(n))=1-\text{exp}(-{\beta }_{\mathit{\text{pre}}}{T}_{\mathit{\text{pre}}}(n)-{\beta }_{\mathit{\text{post}}}{T}_{\mathit{\text{post}}}(n)-{\beta }_{\mathit{\text{out}}}{T}_{\mathit{\text{out}}}(n)-K),$$ (4)

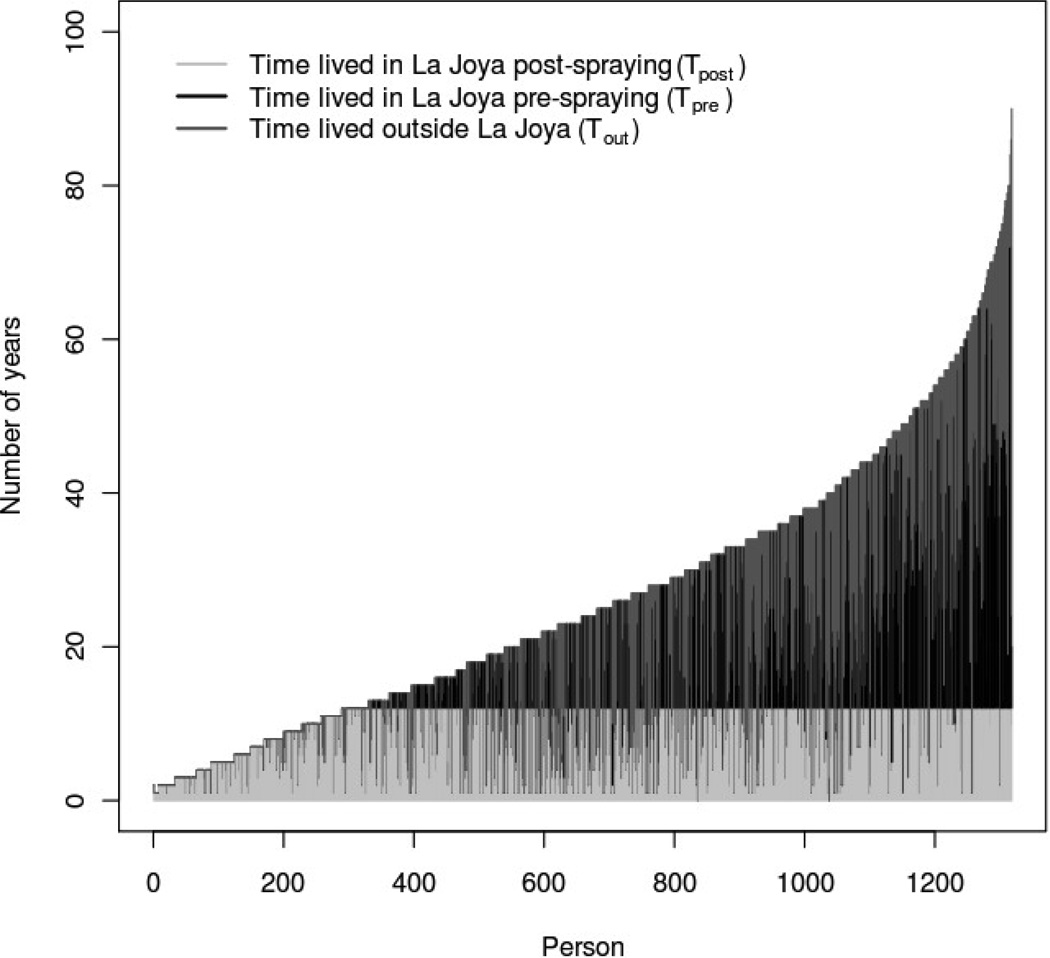
where the individual-level covariates are T_pre(n), T_post(n), and T_out(n) (Delgado et al., 2011). T_pre represents the number of years lived in the study community prior to 1996 (the first full calendar year in which vector-borne transmission was interrupted); T_post is the number of years lived in La Joya after transmission interruption; and T_out is number of years lived outside the study community. For each individual, T_pre(n) + T_post(n) + T_out(n) = age. Figure (1) shows the distribution of these temporal covariates in the sampled residents of La Joya. In the definition of σ_n, the coefficients β_pre, β_post, and β_out represent the differential risk factors for exposure to T. cruzi during each residence period. The final model parameter, K, is related to the probability of time-independent transmission of T. cruzi, including congenital transmission.

Figure 1.

Residence time history data for individuals tested for T. cruzi infection in La Joya, Arequipa, Peru. The 1318 subjects are ordered by increasing age on the x-axis. Transmission interruption due to insecticide spraying is presumed to have occurred twelve years prior to data collection, and thus T_post ≤ 12 for all subjects.

2.2.1 Verification Bias Correction

Only 20% of ELISA-negative individuals in La Joya underwent testing with IFA. This type of missing data, in which individuals with positive outcomes on a screening test are preferentially selected for subsequent confirmatory testing, is commonly referred to as verification bias (Greenes and Begg, 1985). Verification bias is problematic in our situation because the likelihood function derived in Section 2.1 includes contributions only from individuals tested with both assays. Thus useful covariate information from 80% of ELISA-negative individuals will be discarded. Furthermore, an attempt to apply equation (3) to the subset of individuals who underwent both diagnostic tests would result in inaccurate estimates of disease prevalence and ELISA sensitivity and specificity, due to the falsely low number of ELISA-negative individuals in the sample.

Fortunately equation (3) can be modified in a straightforward manner to allow all individuals, including those who underwent only one diagnostic test, to contribute to the likelihood function. Let α represent the fraction of individuals with y₁ = 0 who were tested with the confirmatory test (e.g., α = 0.2 in La Joya). There are five possible combinations of diagnostic test results whose probabilities are given by

$$P_{11}(n)=\text{Pr}(y_1=1,y_2=1)={\sigma }_n{S}_1{S}_2+(1-{\sigma }_n)(1-C_1)(1-C_2)P_{10}(n)=\text{Pr}(y_1=1,y_2=0)={\sigma }_n{S}_1(1-S_2)+(1-{\sigma }_n)(1-C_1)C_2{P}_{01}(n)=\text{Pr}(y_1=1,y_2=1)=\alpha [{\sigma }_n(1-S_1)S_2+(1-{\sigma }_n)C_1(1-C_2)]P_{00}(n)=\text{Pr}(y_1=1,y_2=0)=\alpha [{\sigma }_n(1-S_1)(1-S_2)+(1-{\sigma }_n)C_1{C}_2]P_{0X}(n)=\text{Pr}(y_1=1,y_2\text{not performed})=(1-\alpha )[{\sigma }_n(1-S_1)+(1-{\sigma }_n)C_1].$$ (5)

The proper covariate-augmented likelihood function, in the setting of verification bias, includes contributions from all five probabilities:

$$L=\text{Pr}(\text{observed data}|S_i,C_i\beta ,\alpha )=\prod _{n=1}^N{P}_{11}{(n)}^{{\delta }_{n11}}{P}_{10}{(n)}^{{\delta }_{n10}}{P}_{01}{(n)}^{{\delta }_{n01}}{P}_{00}{(n)}^{{\delta }_{n00}}(P_{0X}{(n)}^{{\delta }_{n0X}},$$ (6)

where δ_n0X = 1 if individual n has y₁ = 0 and is not tested with assay y₂, and δ_n0X = 0 otherwise.

2.3 Simulation Methods

To evaluate the accuracy and robustness of our proposed method, we performed four sets of simulations (hereafter referred to as Simulations A through D). The first three simulations were based on populations with epidemiologic characteristics similar to those found in our La Joya Chagas disease survey. In each case we created a set of N = 1318 individuals with values of T_pre(n), T_post(n), and T_out(n) identical to those in our La Joya sample (Figure 1). We then used equation (4) to assign a unique probability of infection, σ_n, to each individual. We fixed the population’s risk parameters at β_pre = 0.01, β_post= 0.001, β_out= 0.0015, and K = 0.005. For biological plausibility, these values were chosen to be similar to risk parameters estimated previously in La Joya by Delgado et al. (2011). Our choice of risk factors, combined with the measured temporal covariates, produced an overall disease prevalence of 8.5% in the simulated populations.

We next assigned a sensitivity and specificity to each diagnostic test. To measure the performance of our model over a range of diagnostic test parameters, we chose nine different combinations of S_i and C_i. Diagnostic test results for each individual were then assigned probabilistically using a random number generator. Given S_i, C_i, and an individual’s unique value of σ_n, the probabilities of being assigned each of the five possible combinations of test results were as given in equation (5). In the simulations with no verification bias, there were only four possible combinations of test results. We repeated this procedure to generate a total of 1000 simulated data sets per sensitivity/specificity combination.

The purpose of the Simulation A was to compare our method to the two test/two population LCA model described in Hui and Walter (1980). The simulated diagnostic test results were created with no verification bias (α = 1). To form two populations we divided the sample into “young” and “old” groups based on whether the individual was born before or after the 1996 transmission interruption. The two-population model assumed that the prevalences were distinct in the two groups, and equation (1) was used to define the model likelihood. We minimized – ln(l) using the nlminb function in R 2.8.1 (R Foundation for Statistical Computing, www.r-project.org). We also fit each data set with our variable-risk model described in Section 2.1. This model assumed that the functional form of σ_n was as given in equation (4). Equation (3) was used to define the model likelihood, and we used the R nlminb function to minimize – ln(L). Total computation time for all 9000 replicates of Simulation A was seven hours on a Linux-based machine with a single 2.0GHz Intel processor.

We performed a second set of simulations (Simulation B) to determine the effects of verification bias on our results. For this test we set α = 0.2 when creating the simulated diagnostic test data. Thus 80% of individuals with y₁ = 0 were not assigned a result on test y₂. Equation (6) was used to determine the likelihood of our proposed model, and we again used the R nlminb function to minimize – ln(L).

Two additional simulations were designed to evaluate our model’s robustness with respect to misspecification of the functional form of σ_n. In our third simulation (Simulation C) we generated diagnostic test results as above using the complex functional form of σ_n given in equation (4). We then conducted our latent class analysis under the erroneous assumption of the following simpler prevalence function in which the probability of infection depends only on age: σ_n(A_n) = 1– exp(–β_age A_n), where A_n is the age of the nth individual and β_age is a constant age-based risk parameter.

In our final simulation (Simulation D) we created a population of 1000 individuals with a flat age distribution uniform(0, 80 years). The disease prevalence as a function of age was quadratic: ${\sigma }_n(A_n)=0.00003\times A_n^2$ The value of the age coefficient was chosen such that σ_n = 0 in newborns and rises to σ_n = 19.2% in individuals with the maximum age of 80 years. Once again we chose nine different combinations of S_i and C_i and stochastically assigned diagnostic test results to each individual. We performed our parameter estimation using a misspecified LCA model that assumed a disease prevalence σ_n = β_ageA_n that varied linearly, rather than quadratically, with age.

2.4 Analysis of Peruvian T. cruzi Test Data

We analyzed the actual La Joya residence time data and Trypanosoma cruzi test results (Figure 1 and Table 1) with our variable-risk LCA technique. Equation (4) was used to specify the functional form of σ_n. Given this expression for σ_n, we constructed the model likelihood via equation (6). The nlminb function in R 2.8.1 was used to minimize –ln(L). In addition to computing the maximum-likelihood parameters, we employed a percentile bootstrap (1000 iterations) to compute 95% prediction intervals for each parameter (Efron and Tibshirani, 1993).

2.4.1 Relaxation of Conditional Independence Assumption

We extended our model to explore the possibility of covariance between the ELISA and IFA test results in La Joya. We specified the conditional dependence between the tests given a subject’s true infection status via two extra parameters, covs₁₂ and covc₁₂, that represent the covariance between the tests in infected and uninfected individuals, respectively (Dendukuri and Joseph, 2001). The effect of the covariance parameters is to increase the probability of identical test results (i.e., y₁ = y₂) by an amount covs₁₂ (in infected subjects) or covc₁₂ (in uninfected subjects) compared with the conditionally independent case. We restricted our analysis to the scenario in which the two diagnostic tests are positively correlated.

We modified equation (6), using the methods of Dendukuri and Joseph (2001), to compute the model likelihood in the conditionally dependent case. It has been shown that two-test latent class models that allow for unknown conditional dependence are nonidentifiable even when the two diagnostic tests are applied to a large number of distinct populations (Johnson and Hanson, 2005). Because the full model is nonidentifiable, we did not attempt to maximize the likelihood function to solve for all parameters simultaneously. Instead, we performed a sensitivity analysis to determine the effect of different covariance parameters on our La Joya parameter estimates.

For any given S_i and C_i, the covariance parameters must satisfy the relations covs₁₂ ≤ min(S₁,S₂) – S₁S₂ and covc₁₂ ≤ min(C₁,C₂) –C₁C₂ (Dendukuri and Joseph, 2001). If we assume the Chagas disease diagnostic tests used in La Joya have greater than 50% sensitivity and specificity, then covs₁₂ < 0.25 and covc₁₂ < 0.25. Thus for our sensitivity analysis we chose eleven different fixed combinations of covs₁₂ and covc₁₂ between 0 and 0.2. For each case we obtained maximum-likelihood estimates of diagnostic test sensitivity and specificity. We also computed 95% prediction intervals for each parameter using a percentile bootstrap with 1000 iterations.

3 Results

3.1 Simulation Results

Results of Simulation A are shown in Table 2. Our model produces more accurate sensitivity and specificity estimates than the two test/two population model, with a bigger gain in accuracy for sensitivity. For all settings considered and for both sensitivity and specificity, the mean square error (bias² + variance) of our model’s estimator is at least as small as that of the two test/two population model. Our model’s sensitivity estimate is considerably less biased than that of the two test/two population model when the true sensitivity is 95%. For other settings, both models estimate sensitivity with low bias. The standard deviation of our model’s estimate of sensitivity is more than 25% smaller than that of the two test/two population model in 8 of 9 settings for both S₁ and S₂. With respect to specificity, the bias of our model’s estimates and those of the two test/two population model are similar and small in all settings. The standard deviation of our model’s specificity estimate is always smaller than that of the two test/two population model.

Table 2.

Results of Simulation A. True values of each diagnostic test parameter are compared to estimates from a covariate-augmented LCA model with a variable risk function (“Modell”) and a model that used an age cutoff to divide the population into two groups with different prevalences (“Model2”). Each parameter estimate is presented as mean ± standard deviation (95% CI) of 1000 simulations. All values are reported as percents.

Modell
True	Estimated	True	Estimated	True	Estimated	True	Estimated
S1	S1	C1	C1	S2	S2	C2	C2
70	69 ± 17.4 (40,100)	70	71 ± 2.6 (67,77)	70	69 ± 17.2 (42,100)	70	71 ± 2.5 (67,77)
70	69 ± 7.2 (56,84)	70	70 ± 1.7 (67,74)	95	88 ± 13.6 (57,100)	95	95 ± 1.6 (93,99)
70	71 ± 9.7 (53,92)	95	95 ± 1 (93,97)	70	71 ± 9.8 (53,93)	95	95 ± 1 (93,97)
85	85 ± 10.5 (65,100)	85	85 ± 1.5 (82,88)	85	84 ±10.3 (64,100)	85	85 ± 1.5 (83,88)
85	85 ± 7.1 (71,100)	85	85 ± 1.2 (83,88)	95	93 ± 8.2 (74,100)	95	95 ± 1 (93,97)
85	85 ± 7.5 (71,100)	95	95 ± 0.9 (93,97)	85	85 ± 7.8 (70,100)	95	95 ± 0.9 (93,97)
95	92 ± 8.8 (71,100)	70	71 ± 2 (67,75)	95	91 ± 9.4 (69,100)	70	71 ± 1.9(67,75)
95	93 ± 7.3 (76,100)	85	85 ± 1.4 (83,88)	95	93 ± 7.5 (76,100)	85	85 ± 1.3 (83,88)
95	94 ± 5.3 (82,100)	95	95 ± 0.8 (94,97)	95	94 ± 5.4 (82,100)	95	95 ± 0.8 (94,97)
Model2
70	69 ± 22.3 (37,100)	70	73 ± 7.2 (66,100)	70	68 ± 22.4 (37,100)	70	72 ± 6 (66,95)
70	70 ± 10.1 (53,94)	70	71 ± 2.3 (67,76)	95	82 ± 20 (42,100)	95	95 ± 2.1 (92,100)
70	72 ± 14.6 (48,100)	95	95 ± 1.4 (93,98)	70	72 ± 14.6 (48,100)	95	95 ± 1.4 (93,98)
85	82 ± 15.1 (54,100)	85	86 ± 2.2 (82,91)	85	83 ± 15.1 (53,100)	85	86 ± 2.2 (82,91)
85	84 ± 10.3 (66,100)	85	86 ± 1.7 (83,90)	95	89 ± 12.8 (61,100)	95	95 ± 1.4 (93,98)
85	85 ± 11.2 (64,100)	95	95 ± 1.3 (93,98)	85	85 ± 11.5 (63,100)	95	95 ± 1.2 (93,98)
95	86 ± 14.5 (57,100)	70	72 ± 3.6 (67,80)	95	86 ± 14.9 (56,100)	70	72 ± 3.5 (67,81)
95	89 ± 11.9 (63,100)	85	86 ± 2 (83,90)	95	89 ± 11.5 (65,100)	85	86 ± 2 (83,91)
95	92 ± 8.1 (74,100)	95	95 ± 1.1 (94,98)	95	92 ± 8.1 (75,100)	95	95 ± 1.1 (93,98)

Table 3 shows results from Simulation B. Compared to “Model1” from Simulation A (Table 2), in which there is no verification bias, the sensitivity estimates from Simulation B have similar bias when the true sensitivity is 70%. Sensitivity estimates from Simulation B are slightly more biased when the true sensitivity is at least 85%. Standard deviations of the sensitivity estimates from Simulation B are 28–83% higher than those of Simulation B. The biases and standard deviations of the specificity estimates from Simulation B are similar to those of Simulation A across all values of true specificity.

Table 3.

Results of Simulation B: LCA in a La Joya-like population with verification bias (α = 0.2). True values of each diagnostic test parameter are compared to estimates from a covariate-augmented LCA model with a variable risk function. Each parameter estimate is presented as mean ± standard deviation (95% CI) of 1000 simulations. All values are reported as percents.

True	Estimated	True	Estimated	True	Estimated	True	Estimated
S1	S1	C1	C1	S2	S2	C2	C2
70	70 ± 22.2 (38,100)	70	72 ± 2.8 (67,79)	70	68 ± 18.1 (40,100)	70	73 ± 4.5 (65,83)
70	69 ± 13.2 (48,100)	70	71 ± 1.6(67,74)	95	87 ± 14.9 (55,100)	95	96 ± 2.6 (91,100)
70	70 ± 17.5 (41,100)	95	95 ± 1 (93,97)	70	70 ± 10.3 (52,94)	95	96 ± 2.1 (91,100)
85	82 ± 16.3 (51,100)	85	85 ± 1.6 (82,89)	85	83 ± 10.8 (63,100)	85	86 ± 3 (81,92)
85	84 ± 12.1 (62,100)	85	85 ± 1.3 (83,88)	95	93 ± 8.2 (74,100)	95	95 ± 1.9 (92,100)
85	84 ± 13.3 (58,100)	95	95 ± 0.9 (93,97)	85	85 ± 7.9 (69,100)	95	95 ± 1.9 (92,99)
95	85 ± 14.2 (57,100)	70	71 ± 2.1 (67,76)	95	89 ± 10.5 (66,100)	70	72 ± 4.2 (65,82)
95	89 ± 12.3 (63,100)	85	85 ± 1.4(83,88)	95	92 ± 7.8 (75,100)	85	86 ± 2.8 (81,92)
95	92 ± 9.5 (70,100)	95	95 ± 0.8 (94,97)	95	94 ± 5.5 (82,100)	95	96 ± 1.7 (92,99)

Results of Simulations C and D (Tables 4 and 5) demonstrate that when the LCA model’s assumed prevalence function differs from truth, the bias and the variance of the estimated diagnostic test parameters increase. However, the true values of S_i and C_i are still contained within the model’s 95% confidence intervals for all combinations of sensitivity and specificity considered. Furthermore, in these populations with low disease prevalence, even the misspecified models estimate C_i with small bias. In Table 5 we also present the mean value of – ln(L) for each simulation. In 8 of 9 simulations the properly specified quadratic model has a larger likelihood.

Table 4.

Results of Simulation C: LCA model with misspecified prevalence function that depends on age only. True values of each diagnostic test parameter are compared to estimates from a misspecified covariate-augmented LCA model. There was no verification bias (α = 1). Each parameter estimate is presented as mean ± standard deviation (95% CI) of 1000 simulations. All values are reported as percents.

True	Estimated	True	Estimated	True	Estimated	True	Estimated
S1	S1	C1	C1	S2	S2	C2	C2
70	69 ± 19.1 (39,100)	70	71 ± 2.6 (67,76)	70	69 ± 18.9 (39,100)	70	71 ±2.4 (67,76)
70	67 ± 6.9 (55,82)	70	71 ± 1.7 (68,75)	95	88 ± 16.3 (51,100)	95	96 ± 1.3 (94,99)
70	67 ± 12.3 (48,99)	95	95 ± 1.2 (93,98)	70	67 ± 11.8 (47,97)	95	96 ± 1.2 (93,98)
85	80 ± 13.1 (58,100)	85	86 ± 1.8 (83,90)	85	81 ± 13 (58,100)	85	86 ± 1.8 (83,90)
85	81 ± 8.5 (67,100)	85	86 ± 1.5 (83,89)	95	91 ± 10.6 (67,100)	95	96 ± 1.2 (93,98)
85	82 ± 9.9 (64,100)	95	95 ± 1.1 (93,98)	85	83 ± 10 (65,100)	95	95 ± 1.1 (93,98)
95	88 ± 11.5 (64,100)	70	71 ± 2.1 (68,76)	95	88 ± 11.1 (66,100)	70	71 ± 2.1 (68,76)
95	90 ± 9.8 (70,100)	85	86 ± 1.6 (83,89)	95	90 ± 9.6 (70,100)	85	86 ± 1.6 (83,89)
95	92 ± 7.4 (76,100)	95	95 ± 1 (94,97)	95	93 ± 7.3 (77,100)	95	95 ± 1 (94,97)

Table 5.

Results of Simulation D. The true prevalence function in the simulated populations was quadratic with age. Covariate-augmented LCA models that assumed both linear and quadratic prevalence functions were then fitted to the diagnostic test data. There was no verification bias (α = 1). Each parameter estimate is presented as mean ± standard deviation (95% CI) of 1000 simulations. All values are reported as percents. The negative of the natural logarithm of the model likelihood is also reported as mean ± standard deviation.

	Linear model
True	Estimated	True	Estimated	True	Estimated	True	Estimated
S1	S1	C1	C1	S2	S2	C2	C2	–ln(L)
70	66 ± 22.2 (36,100)	70	71 ± 2.6 (66,77)	70	67 ± 22.6 (35,100)	70	71 ± 2.7 (67,77)	1255 ± 16
70	63 ± 8.6 (49,82)	70	71 ± 2.2 (67,76)	95	79 ± 22.9 (36,100)	95	97 ± 1.3 (94,99)	946 ± 23
70	64 ± 15.8 (41,100)	95	96 ± 1.3 (93,98)	70	64 ± 15.5 (40,100)	95	96 ± 1.3 (93,98)	568 ± 29
85	76 ± 16.1 (49,100)	85	86 ± 1.9(83,91)	85	76 ± 16.5 (48,100)	85	86 ± 2 (83,90)	956 ± 27
85	78 ± 11.5 (59,100)	85	86 ± 1.8 (83,90)	95	85 ± 15.5 (54,100)	95	96 ± 1.3 (94,99)	777 ± 30
85	80 ± 13.9 (55,100)	95	96 ± 1.2 (93,98)	85	79 ± 13.2 (57,100)	95	96 ± 1.3 (93,98)	578 ± 30
95	84 ± 14.7 (56,100)	70	72 ± 2.4 (68,77)	95	83 ± 14.9 (55,100)	70	72 ± 2.4 (68,77)	1268 ± 16
95	85 ± 13.7 (59,100)	85	86 ± 1.9 (83,90)	95	84 ± 14.2 (57,100)	85	86 ± 1.9 (83,90)	963 ± 27
95	89 ± 10.9 (66,100)	95	96 ± 1.2 (94,98)	95	89 ± 10.3 (67,100)	95	96 ± 1.1 (94,98)	578 ± 32
	Quadratic model
70	72 ± 21.7 (37,100)	70	70 ± 2 (66,74)	70	72 ± 21.9 (37,100)	70	70 ± 2 (66,75)	1255 ± 16
70	70 ± 9.3 (54,90)	70	71 ± 1.8 (67,75)	95	85 ± 18.8 (44,100)	95	95 ± 1.1 (93,97)	944 ± 23
70	72 ± 14.1(49,100)	95	95 ± 1 (93,97)	70	71 ± 13.8 (49,100)	95	95 ± 1.1 (93,97)	566 ± 29
85	84 ± 13.3 (57,100)	85	85 ± 1.5 (83,88)	85	84 ± 13.6 (57,100)	85	85 ± 1.6 (82,88)	954 ± 27
85	85 ± 9.6 (68,100)	85	85 ± 1.4(83,88)	95	90 ± 11.6 (63,100)	95	95 ± 1.1 (93,97)	774 ± 30
85	85 ± 11.1 (64,100)	95	95 ± 1 (93,97)	85	85 ± 10.6 (65,100)	95	95 ± 1 (93,97)	575 ± 31
95	90 ±12.2 (62,100)	70	70 ± 1.9 (67,74)	95	89 ±12.5 (61,100)	70	70 ± 1.9 (67,74)	1267 ± 16
95	91 ± 10.1 (68,100)	85	85 ± 1.5 (83,88)	95	91 ± 10.4 (68,100)	85	85 ± 1.4 (83,88)	961 ± 27
95	93 ± 8 (76,100)	95	95 ± 1 (93,97)	95	93 ± 7.7 (75,100)	95	95 ± 0.9 (94,97)	574 ± 32

3.2 Results of Analysis of La Joya T. cruzi Data

Parameter estimates from our covariate-augmented LCA model applied to actual Chagas disease diagnostic test data from La Joya, Peru, are shown in Table 6. All estimates were calculated using the likelihood function with verification bias correction described in Section 2.2.1. The estimated specificities of ELISA and IFA in La Joya are nearly 100%. In contrast, the point estimates of the sensitivities of both tests are less than 80%. In the case of ELISA, however, the uncertainty is large enough that a sensitivity as high as 100% cannot be ruled out.

Table 6.

Parameter estimates and bootstrap confidence intervals from our latent class model with continuous covariates, applied to T. cruzi test data from La Joya, Peru.

Parameter	Model estimate (95% CI)
ELISA sensitivity (S1)	78% (62–100%)
ELISA specificity (C1)	100% (99–100%)
IFA sensitivity (S2)	73% (65–81%)
IFA specificity (C2)	99% (96–100%)
Pre-spray risk parameter (βpre)	0.019 (0.013–0.026)
Post-spray risk parameter (βpost)	0 (0–0.0005)
Parameter for risk outside La Joya (βout)	0.0031 (0.0016–0.0050)
Congenital transmission parameter (K)	0.0047 (0–0.014)

The model’s estimates of the risk parameters β_pre, β_post, β_out, and K confirm that the yearly risk of T. cruzi infection prior to the insecticide spray campaign (β_pre) was much greater than the post-spray risk, which was indistinguishable from zero. The estimated infection prevalence in the population (found by averaging σ_n across all subjects) is 13.4%.

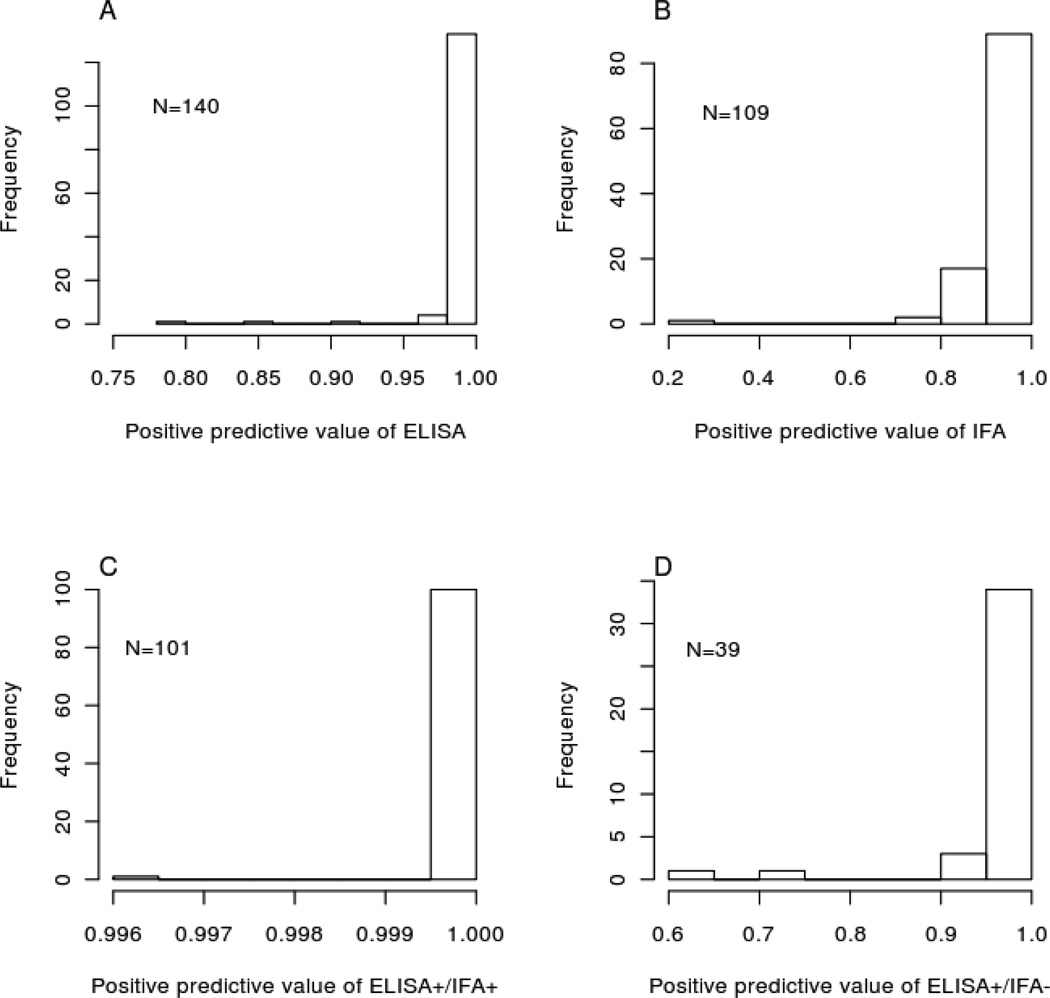
The estimated positive predictive values of ELISA and IFA in patients who tested positive on those assays are high (Figures 2A and 2B). Because of the tests’ high specificities in this population, most positive results represent true infections. Furthermore, using IFA to confirm positive ELISA results does not often significantly change the posterior probability of infection (Figures 2C and 2D).

Figure 2.

Covariate-augmented latent class estimates of positive predictive values of ELISA and IFA in La Joya, Arequipa, Peru. (A) and (B) Positive predictive value of each diagnostic test when used alone. (C) and (D) Positive predictive value of both possible outcomes when IFA was used as a confirmatory test in ELISA-positive individuals.

The estimated sensitivity and specificity of ELISA and IFA in La Joya are reduced when the diagnostic tests are assumed to be conditionally dependent (Table 7). The sensitivities of ELISA and IFA are as low as 67% and 58%, respectively, when covs₁₂ and covc₁₂ are at most 0.05. Larger covariances of up to 0.1 produce estimates of ELISA sensitivity as low as 47% and IFA sensitivity as low as 38%. With regards to specificity, the model predicts that ELISA and IFA are at least 88% specific even if the covariance between the tests is as high as 0.1. Covariances larger than 0.1 produce even smaller sensitivity and specificity estimates.

Table 7.

Analysis of the effect of conditional dependence on estimates of diagnostic test performance in La Joya. We maximized the likelihood of the model for nine different sets of covariances (column 1). Columns 2–5 give the maximum-likelihood estimates and bootstrap 95% confidence intervals of the diagnostic test sensitivities and specificities (expressed as percents) when these covariances are assumed.

	S1	C1	S2	C2
(covs12,covc12)	(95% CI)	(95% CI)	(95% CI)	(95% CI)
(0, 0)	78 (62,100)	100 (99,100)	73 (65,81)	99 (96,100)
(0, 0.05)	74 (56,100)	94 (94,95)	65 (55,81)	93 (91,95)
(0, 0.1)	55 (44,100)	89 (88,89)	54 (42,79)	89 (85,89)
(0.05, 0)	71 (55,93)	100 (99,100)	66 (58,75)	99 (96,100)
(0.05, 0.05)	67 (48,93)	94 (94,95)	58 (49,75)	93 (91,95)
(0.05, 0.1)	49 (36,91)	88 (88,89)	46 (35,76)	88 (85,89)
(0.1, 0)	63 (46,86)	100 (99,100)	57 (48,71)	99 (95,100)
(0.1, 0.05)	60 (43,84)	94 (94,95)	50 (41,70)	93 (90,95)
(0.1, 0.1)	47 (36,83)	88 (87,89)	38 (29,68)	88 (85,89)
(0.15, 0.15)	79 (33,80)	79 (78,82)	72 (29,79)	79 (78,82)
(0.2, 0.2)	31 (30,32)	54 (51,72)	29 (28,30)	44 (42,72)

4 Discussion

When estimating the sensitivity and specificity of diagnostic tests, the analyzed test results are often stripped of epidemiologic context. By treating all identical patterns of results as equivalent, algorithms such as latent class analysis may ignore vital information about differences between tested individuals. Many previous attempts to incorporate epidemiologic information into LCA have utilized two-tiered risk stratifications based on geographic location (Branscum et al., 2005, Hui and Walter, 1980, Johnson et al., 2001). If the probability of disease varies in a more complex manner, we show that careful measurement of individual-level risk allows LCA to estimate diagnostic test parameters more accurately.

With respect to Chagas disease in La Joya, Arequipa, Peru, our model estimates the specificity of the commercial Chagatek ELISA to be 100% (95% CI: 99–100%). Published Chagatek specificities from other sources range from 87.31– 100% (Blejer et al., 2001, Caballero et al., 2007). Our estimate is at the high end of this range. We estimate the specificity of IFA to be 99% (95% CI: 96–100%). The specificity of T. cruzi serum tests can be lowered by cross-reactivity with Leishmania spp. or Trypanosoma rangeli (Caballero et al., 2007, Malchiodi et al., 1994). Thus the near-perfect specificity that we observe in La Joya may reflect the fact that neither T. rangeli nor Leishmania spp. is endemic to the area (Levy et al., 2009, Lucas et al., 1998).

Our estimate of ELISA sensitivity is 78% (95% CI: 62–100%), much lower than other published estimates which range from 99.67–100% (Blejer et al., 2001, Caballero et al., 2007), although the upper end of our confidence interval includes these values. We also find a low sensitivity of 73% (95% CI: 65–81%) in the confirmatory IFA test. Our low sensitivity estimates corroborate a recent report that recombinant antigen-based rapid tests for Chagas disease exhibit much lower sensitivity in Arequipa than in Bolivia (Verani et al., 2009). The decreased sensitivities observed in Arequipa may be due to parasite heterogeneity, as the species T. cruzi is known to include various strains whose different antigenic properties may cause geographic variations in the performance of antigen-based diagnostic tests (Verani et al., 2009, Campbell et al., 2004).

Our simulations, as well as our analysis of actual Chagas disease test results, produce sensitivity estimates whose confidence intervals are much wider than those of the specificity estimates. Although verification bias has been shown to increase the variability of parameter estimates, our Simulation A (Table 2), in which all individuals underwent both diagnostic tests, demonstrates that the uncertainty in our sensitivity estimates is not entirely due to verification bias. Rather, our sensitivity estimates are uncertain because of the low disease prevalence in our samples. When prevalence is low, there are few subjects with positive test results, and thus it is difficult to estimate the rate of true positives (i.e., sensitivity) (Joseph et al., 1995).

Use of our technique requires a mathematical description of risk variability. In our study population, we chose a biologically plausible risk model that fits the observed test results better than several other candidate functions (Delgado et al., 2011). However, the true risk function is always unknowable, and even the best-fit model may not perfectly represent reality. Thus when applying our method to other disease states, care should be taken to verify the suitability of the proposed risk model. One way to do so is to create various risk functions and choose the one that maximizes a model selection criterion such as the Akaike Information Criterion (Akaike, 1974). Our simulations of misspecified models (Tables 4 and 5) show that in cases where the true risk function is unknown, a selection criterion based on the LCA likelihood could be used to choose between candidate prevalence functions.

Our primary results assume conditional independence between ELISA and IFA, but we have also explored the sensitivity of our estimates to this assumption. Addition of conditional dependence to the model reduces the estimated diagnostic test sensitivity and specificity. The sensitivity estimates are affected more than the specificity estimates. Although we cannot rule out the possibility of conditional dependence between ELISA and IFA, there is reason to believe that any covariance is likely to be small. A previous latent class analysis of Chagas disease diagnostic tests (including ELISA and IFA) found that a conditional independence model fit best (Pirard et al., 2005). And the choice of a conditional independence model is further justified by the observation, mentioned above, that Arequipa lacks cross-reacting organisms that could cause correlated false-positive results on multiple assays.

Similarly, throughout this paper we have assumed that diagnostic test sensitivity and specificity are constant across all subpopulations. Although beyond the scope of our current analysis, this assumption could in principle be relaxed. The model presented here could easily be expanded to include covariate effects on sensitivity and specificity, in addition to disease prevalence.

The observed lack of sensitivity of T. cruzi diagnostic tests in Arequipa is clinically problematic. Current protocols, which require two consecutive positive test results on different assays before treatment is initiated, exclude many infected individuals from consideration for pharmacological therapy. The magnitude of the undercount can be estimated by noting that our model predicts a T. cruzi infection prevalence of 13.4% in La Joya. In contrast, a much lower prevalence estimate of 101/1318 = 7.7% is produced when only ELISA+/IFA+ individuals are considered to be infected. This latter case definition was used in a previous analysis of T. cruzi transmission in La Joya, which explains why the predominant risk parameters measured in that study were roughly half as large as our estimates (Delgado et al., 2011).

Because the specificity of ELISA is very high in Arequipa, using IFA (or another test) to confirm positive ELISA results does little more than increase the rate of false negative. ELISA-positive individuals almost certainly represent true cases (Figure 2). The probability of infection remains high even if the subsequent IFA is negative. These findings are consistent with a recent report that ELISA+/IFA- individuals in Arequipa are geographically clustered around confirmed (ELISA+/IFA+) cases, making it likely that individuals with discordant results are in fact infected with T. cruzi (Levy et al., 2009). We suggest that clinical resources could be saved by reconsidering the need for confirmatory tests in ELISA-positive patients in settings with a reasonably high probability of infection. By analyzing diagnostic tests in context it may be possible to reduce expenses, which is particularly important when diagnosing neglected tropical diseases.