A Rapid Association Test Procedure Robust under Different Genetic Models Accounting for Population Stratification

Abstract

Objective

For genome-wide association studies (GWAS) in case-control data with stratification, a commonly used association test is the generalized Armitage (GA) trend test implemented in the software EIGENSTRAT. The GA trend test uses principal component analysis to correct for population stratification. It usually assumes an additive disease model and can have high power when the underlying disease model is additive or multiplicative, but may have relatively low power when the underlying disease model is recessive or dominant. The purpose of this paper is to provide a test procedure for GWAS with increased power over the GA trend test under the recessive and dominant models while maintaining the power of the GA trend test under the additive and multiplicative models.

Methods

We extend a Hardy-Weinberg disequilibrium (HWD) trend test for a homogeneous population to account for population stratification, and then propose a robust association test procedure for GWAS that incorporates information from the extended HWD trend test into the GA trend test.

Results and Conclusions

Our simulation studies and application of our method to a GWAS data set indicate that our proposed method can achieve the purpose described above.

1. Introduction

In genome-wide association studies with case-control designs, population stratification can happen when the participants are sampled from different subpopulations with significant allele frequency differences [1]. Population stratification can be a confounding factor in the association test and may produce spurious associations if not properly corrected [2, 3, 4]. Many methods have been developed to correct for stratification in association studies [3, 5, 6]. One of the most widely used methods is a generalized Armitage (GA) trend test implemented in the software EIGENSTRAT that uses principal component analysis (PCA) to correct for population stratification [3]. The GA trend test usually assumes that the underlying disease model is additive [3]. In this paper, we use “GA trend test” to denote the GA trend test assuming the additive model. One of the advantages of the GA trend test is that when the underlying disease model is additive or multiplicative, it can have high power in detecting causal variants. However, when the underlying disease model is dominant or recessive, it can have low power.

Some association tests that are robust to different genetic models have been developed for homogenous populations [7, 8, 9, 10]. For example, the MAX3 test statistic [7, 8] uses the maximum of the three Armitage trend test statistics [11] that assume the additive, dominant and recessive model, respectively. MAX3 has been extended to use top principal components (PCs) of genome-wide genotypes as covariates to correct for stratification [12]. This extended MAX3 method is referred to as MAX3-PC in this paper. However, MAX3-PC has two limitations: 1) compared to the GA trend test, when the underlying disease model is additive or multiplicative, MAX3-PC can have relatively lower power; 2) it can be computationally intensive for GWAS, especially for data with more than one million SNPs. Since the additive/multiplicative genetic model is often assumed and fits well for most identified genetic variants [13], in this article, we intend to propose a computationally efficient method for GWAS that can maintain the power of the GA trend test (EIGENSTRAT) under the additive and multiplicative models while it has improved power over the GA trend test under the recessive and dominant models.

To achieve this goal, first, we extend the Hardy-Weinberg disequilibrium (HWD) trend test of Song & Elston [14] for homogenous populations to account for population stratification. The extended HWD trend test can provide useful information under the dominant or recessive models which is different from that provided by the GA trend test. Second, for GWAS we apply the generalized sequential Bonferroni (GSB) procedure to incorporate information from the extended HWD trend test into the GA trend test. Simulation studies indicate that the proposed GSB procedure for GWAS can control the familywise error rate when stratification exists; it has comparable power to that of the GA trend test, when the underlying model is additive or multiplicative, and has higher power than the GA trend test when the underlying model is dominant or recessive. Simulation studies also indicate that MAX3-PC of So and Sham (2011) has relatively lower power than the GA trend test and the proposed GSB procedure under the additive and multiplicative models. Finally we applied our proposed method to four datasets provided by the Wellcome Trust Case-Control Consortium (WTCCC) [13].

2. Methods

In this section, we first extend the HWD trend test of Song & Elston [14] to account for population stratification, and then propose a GSB procedure for GWAS that incorporates information from the extended HWD trend test into the GA trend test. In this study, we assume independence among markers and ignore the LD among markers in the GWAS data.

2.1 Extended HWD trend test

By assuming that cases and controls are sampled from the same general homogenous population, Song & Elston [14] proposed a HWD trend test by comparing the HWD coefficient in cases D_case with the HWD coefficient in controls D_control. For a SNP with allele A and B, denote the genotype frequencies of AA, AB, BB in cases by p_AA, p_AB, p_BB and in controls by q_AA, q_AB, q_BB. Then we have D_case = p_BB − {p_AB/2 + p_BB}² and D_control = q_BB − {q_AB/2 + q_BB}². Let Δ = D_case − D_control. The null hypothesis is H₀: Δ = 0, which corresponds to testing whether the HWD coefficient for the test marker in the controls is equivalent to that in cases; if not, the test marker may be associated with the disease. The HWD trend test statistic is given by: $T_{HWDTT}=\widehat{\mathrm{\Delta }}/\sqrt{Va{\stackrel{⌢}{r}}_{H_0}({\widehat{\mathrm{\Delta }}}_i)}$ where Δ̂ = D̂_case − D̂_control , and D̂_case and D̂_control are the maximum likelihood estimates of D_case and D_control respectively. $Va{\stackrel{⌢}{r}}_{H_0}({\widehat{\mathrm{\Delta }}}_i)$ is the estimate of the variance of Δ̂ under H₀ [for details, see 14]. T_HWDTT asymptotically follows a standard normal distribution and the square of the test follows the chi-square distribution with 1 degree of freedom.

The HWD trend test statistic T_HWDTT can be used to test association between a marker and a disease under the assumption that Hardy-Weinberg equilibrium holds in the general population from which the cases and controls are sampled. Song & Elston [14] stated that the HWD trend test can automatically control for the genotyping errors, if the cases and controls are genotyped by the same methods at the same time, with the cases and controls randomized. However, a weakness of the HWD trend test is that it can have an inflated type I error rate when population stratification exists (see our simulation results below). Below we extend the HWD trend test to account for population stratification.

First, we assign cases and controls in the data into K groups (or clusters) that correspond to K putative subpopulations. Specifically, we calculate the top principal components (PCs), e.g., the top 10 PCs, of genome-wide genotypes and then apply a clustering algorithm, e.g., the k-means clustering algorithm [15], to the top PCs to partition the individuals into K groups.

In order to determine the number of subpopulations (K), we use the fpc package (http://cran.r-project.org/web/packages/fpc/index.html) that implements the k-means algorithm with options to determine the optimal number (K) of clusters [16]. More specifically, the fpc package uses the Duda-Hart test [17] to test if all individuals in the data are from one cluster. If they are not from one cluster, then the k-means cluster algorithm is executed with the cluster numbers k = 2, 3, …, K_max (we set K_max = 4 in our data analysis). The Calinski-Harabasz criterion is used to determine the optimal number of clusters from 2 to K_max [18]. The Calinski-Harabasz criterion can be calculated as $CH(k)=\frac{SSB/(k-1)}{SSB/(N-k)}$, where SSW is the sum of variances within the clusters, SSB is the sum of variances among the clusters, and N is the number of individuals in the case-control data. The number of subpopulations is selected as $K=\underset{k}{\text{arg max}}CH(k)$.

For the cases and controls assigned to the i-th group where i = 1, 2, …, K, we define an effect size to be the difference (Δ_i) of HWD coefficients between cases and controls, ${\mathrm{\Delta }}_i=D_{\mathit{\text{case}}}^i-D_{\mathit{\text{control}}}^i$ and denote its maximum likelihood estimation by β_i = Δ̂_i. Under the null hypothesis H₀: Hardy-Weinberg equilibrium holds in the i-th subpopulation (corresponding to the i-th group) and the test marker is not associated with the disease, the variance of the estimated effect Var_H0 (Δ̂_i) can be estimated (see Song and Elston [14]). If any assigned group only contains cases, then we set the HWD coefficient for the controls to $D_{\mathit{\text{control}}}^i=0$ and use the variance ${\mathit{\text{Var}}}_{H_0}({\widehat{D}}_{\mathit{\text{case}}}^i)$, as given in Song and Elston [14]. If any assigned groups only contain controls, this group is removed from the analysis because subpopulations consisting of controls only do not provide information for the association study.

Following the method in meta-analysis using a fixed effect model [19], the combined effect over the K groups (or subpopulations) is given by

$$E=\frac{\sum _{i=1}^K{\beta }_i{w}_i}{\sum _{i=1}^K{w}_i},$$

where $w_i={[Va{\stackrel{⌢}{r}}_{H_0}({\widehat{\mathrm{\Delta }}}_i)]}^{-1}$ is the inverse of the estimated variance of the estimated effect for the i-th subpopulation. The variance of the combined effect is given by $V={[\sum _{i=1}^K{w}_i]}^{-1}$. Under the null hypothesis that Hardy-Weinberg equilibrium holds in each of the subpopulation and the test marker is not associated with a disease, the extended HWD trend test statistic is then defined as E²/V, which has an approximate chi-square distribution with one degree of freedom.

2.2 Generalized Armitage (GA) trend test in EIGENSTRAT

To effectively control false positive rates caused by population stratification, Price et al. [3] proposed the GA trend test, which is implemented in the software EIGENSTRAT. The GA trend test calculates the top principal components (PCs) from genome-wide genotype values for each individual. To test the association between a marker and the disease status, the GA trend test adjusts the individual’s genotype value (assuming an additive model) at the marker by regressing out the top L PCs (e.g., L = 10) in a linear model (see Price et al. 2006) and then adjusts the phenotypic value (0 for a control and 1 for a case) by the same L PCs in the similar way. The GA trend test statistic is defined as (N-L-1)R², where R² is the correlation between the ancestry-adjusted genotype and ancestry-adjusted phenotype, and N is the number of individuals in the case-control study. Under the null hypothesis that the test marker is not associated with the disease, the GA trend test statistic asymptotically follows the chi-square distribution with 1 degree of freedom.

2.3 Generalized sequential Bonferroni procedure for multiple testing

For testing multiple hypotheses H₁, H₂, …, H_m, Holm [20] proposed a generalized sequential Bonferroni (GSB) procedure by assigning different weights to hypotheses of different importance. Let α denote the nominal familywise error rate (FWER), which is defined as the probability of rejecting at least one true null hypothesis. We describe the GSB procedure below.

Let p₁, p₂, ⋯, p_m denote the p-values from m tests corresponding to hypotheses H₁, H₂, …, H_m. Given weights w₁, w₂, …, w_m for these tests, define B-values as B_i = p_i / w_i. First we order B-values as B₍₁₎ ≤ B₍₂₎ ≤… ≤ B_(m), so that w₍₁₎, w₍₂₎, …, w_(m) and H₍₁₎, H₍₂₎, …, H_(m) are the corresponding weights and hypotheses of the ordered B-values. Starting from i = 1, given H₍₁₎, H₍₂₎, …, H_(i−1) have been tested and rejected, if $B_{(i)}\le \alpha /\sum _{k=i}^m{w}_{(k)}$, reject H_(i); otherwise, accept H_(i), H_(i+1), …, H_(m), and stop the GSB procedure. Holm [20] proved that the GSB procedure controls the FWER at the nominal significance level of α if the condition that the weights are independent of the m tests is satisfied. From the proof of Holm, we can see that the GSB is relatively conservative and that the condition that the weights are independent of the m tests is a sufficient condition but not a necessary condition. We will show by simulation studies (see Appendix) that under some situations, even though the weights are weakly correlated with the m tests, the GSB procedure can still control FWER well. In addition, from the rejection criteria above, in order to reject the hypothesis H_(i), the corresponding p-value p_(i) must be less than or equal to α, otherwise the GSB procedure will not reject the hypothesis H_(i).

We note that when the GSB procedure of Holm is applied to testing association at genome-wide markers, it cannot provide a p-value for each marker, which may be needed when comparing the GSB procedure with other methods in real data analysis. Therefore, we define the adjusted p-value for each test in the GSB procedure following the idea of Westfall and Young [21, p64]: Let p̃_(i) be the adjusted p-value corresponding to B_(i) and H_(i), i = 1, 2, …, m. Then we define ${\tilde{p}}_{(1)}=(\sum _{i=1}^m{w}_{(i)})B_{(1)},{\tilde{p}}_{(2)}=\text{max}((\sum _{i=2}^m{w}_{(i)})B_{(2)},{\tilde{p}}_{(1)}),\dots ,{\tilde{p}}_{(j)}=\text{max}((\sum _{i=j}^m{w}_{(i)})B_{(j)},{\tilde{p}}_{(j-1)}),\dots ,{\tilde{p}}_{(m)}=\text{max}(w_{(m)}{B}_{(m)},{\tilde{p}}_{(m-1)})$. Any adjusted p-value greater than 1.0 should be set to 1.0. The adjusted p-values should be compared to the nominal level α for the entire test procedure: if an adjusted p-value is less than or equal to α, then reject the corresponding hypothesis.

2.4 GSB procedure for GWAS in case-control data with population stratification

Here we describe how to apply the GSB procedure for multiple testing to GWAS data with population stratification. In the original GSB procedure, Holm [20] did not describe how to estimate the weights, although the GSB procedure has the potential to improve the power of multiple hypotheses testing when prior information is available to estimate the weights. Since the extended HWD trend test may provide different information from that provided by the GA trend test, we propose to use the extended HWD trend test to calculate a weight for each marker, and use the GA trend test to calculate a p-value for the marker. Then we use the weight to adjust the GA trend test p-value in the GSB procedure. Specifically, let q_i denote the p-value for the i-th marker calculated by the extended HWD trend test. We let the weight w_i for the i-th marker be the inverse of the extended HWD trend test p-value q_i, i.e., w_i = 1 / q_i. We then apply the GSB procedure to incorporate the weight into the corresponding GA trend test in GWAS.

As described in the previous section, to reject the null hypothesis that a marker is not associated with the disease, the p-value from the GA trend test at that marker must be less than or equal to the nominal FWER α. This property can prevent that a null marker, which usually has a p-value from the GA trend test greater than α (such as 0.05), to be called significant because of the extremely high weight that is calculated from the extended HWD trend test due to genotyping errors.

The extended HWD trend test can have high power under both the recessive and dominant models, but it has no (or almost no) power under the multiplicative (or additive) model. Therefore the weights calculated from the extended HWD trend test only generate noise when the underlying disease model is multiplicative or additive. This results in that under these two models, the GSB procedure (using p-values from the GA trend test) has relatively lower power than the GA trend test (with Bonferroni correction) in GWAS. On the other hand, when the underlying disease models are recessive or dominant, weights calculated from the extended HWD trend test can provide useful information, and the GSB procedure can have much higher power than the GA trend test (see our simulation results below).

Since the additive model is often assumed in association studies in the literature when the true underlying genetic models are unknown, we hope to modify the GSB procedure for GWAS so that it can maintain the power of the GA trend test under the additive and multiplicative models, but still have increased power under the dominant and recessive models. To achieve this goal, we employ a smoothing method of Roeder [22] to calculate smoothed weights. Suppose w_i is the original weight for the i-th marker, w̄ is the average value of the weights for all markers. We calculate a smoothed weight for the i-th marker as $w_i^{\prime }=(1-\lambda )w_i+\lambda \overline{w}$, where λ is a parameter and 0 ≤ λ ≤ 1. We call the GSB procedure using the smoothed weights smooth-GSB procedure. When λ is close to 1, then the smoothed weight is close to the constant w̄, and the GSB procedure has similar results as the GA trend test. On the other hand, when λ is close to 0, the smoothed weight is close to the original weight w_i, and the smooth-GSB procedure has similar results as the GSB procedure using the original weight w_i. Since we hope that the smooth-GSB procedure has power close to that of the GA trend test in GWAS under the additive and multiplicative models, the value of λ should be close to 1. On the other hand, if λ is very close to 1, only a little information from the original weight (i.e. from the extended HWD trend test) can be used, this will result in that the smooth-GSB procedure does not have much increased power compared to the GA trend test under the recessive and dominant models. As a tradeoff, we would suggest the value of λ should be greater than 0.5 but less than 0.9.

In the GSB procedure for GWAS, if the weight calculated from the extended HWD trend test is (asymptotically) independent of the GA trend test at each marker, then the GSB procedure for GWAS can control FWER. Joo et al. [23] proved that the HWD trend test statistic and the Cochran Armitage trend test statistic assuming the additive model are asymptotically independent in homogeneous populations. We expect that, as the extension of these two test statistics to correct for stratification, the extended HWD trend test statistic and the GA trend test statistic are approximately independent or at most are very weakly correlated. However, it is difficult to prove the independence theoretically. Below we will show by simulation studies that at a marker, the correlation between the extended HWD trend test statistic and the GA trend test statistic is negligible. We also show that in simulated case-control GWAS data, the GSB and smooth-GSB procedures can control FWER.

3. Simulation studies

3.1 Simulating case-control data with stratification

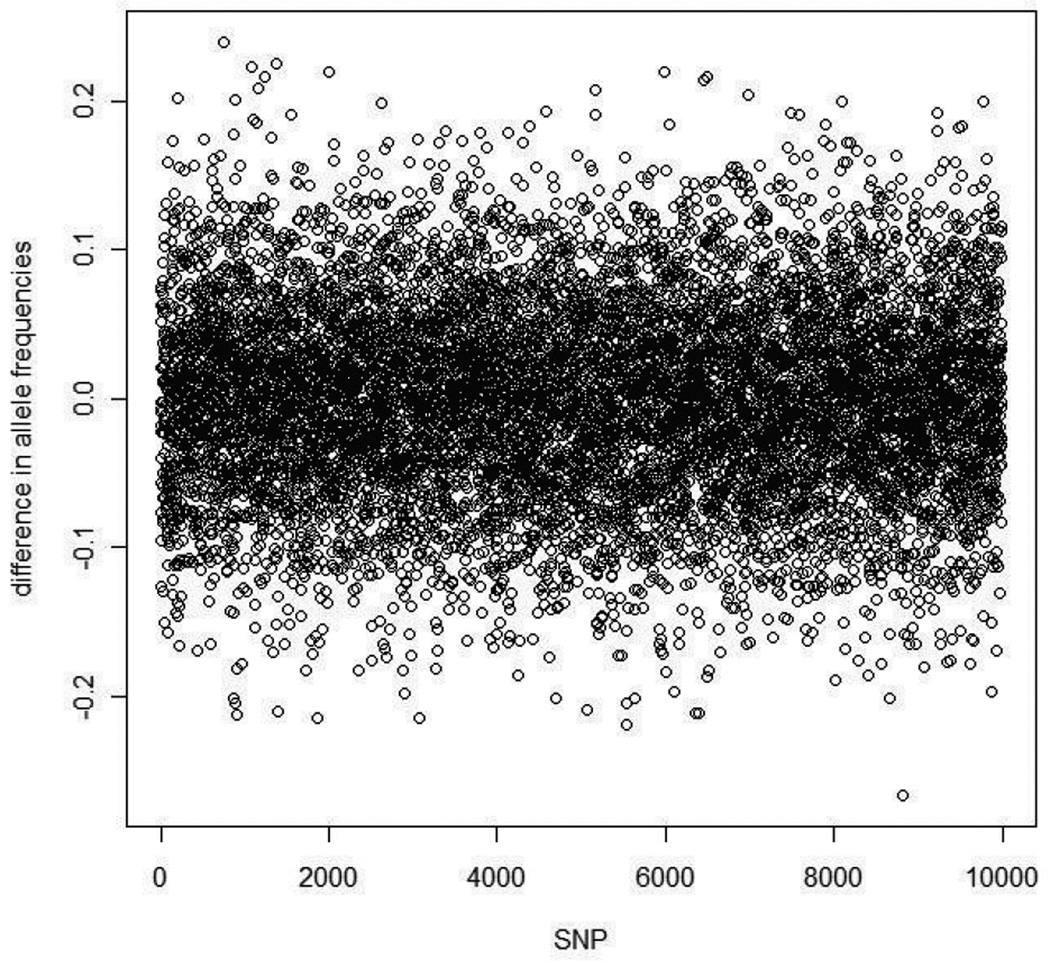
To evaluate the false positive rates and power of the extended HWD trend test and the proposed smooth-GSB procedure in case-control data with population stratification, we simulated data sets in a similar way to that in [3]. Each data set was simulated to include 2000 cases and 2000 controls with 10,000 random single nucleotide polymorphisms (SNPs). To simulate stratification, each individual was sampled from one of two populations. In cases, 40% were sampled from population 1 and 60% were sampled from population 2. In controls, 20% were sampled from population 1 and 80% were sampled from population 2. Allele frequencies for population 1 and population 2 at each of the 10,000 random SNPs were generated using the Balding-Nichols model with F_ST = 0.01. Specifically, at each random SNP, the allele frequencies for populations 1 and 2 were each drawn from a beta distribution with parameters p(1 − F_ST)/F_ST and (1 − p)(1 − F_ST)/F_ST, where the ancestral population allele frequency p was sampled from the uniform distribution in the interval [0.1, 0.9]. Usually the allele frequency differences between populations 1 and 2 are less than 0.1 [3]. In addition to the 10,000 random SNPs, we simulated 10 SNPs with differential frequencies in populations 1 and 2. For each of these 10 SNPs, the allele frequency difference between populations 1 and 2 was greater than 0.1, to approximate the effect of selection. In our simulation, we set the allele frequency to 0.2 in population 1 and 0.8 in population 2 as a demonstration of strong selection. As an example, Figure 1 shows the allele frequency differences at the 10,000 random SNPs between population 1 and population 2 in one replicate of our simulated data set. We can see that most of the allele frequency differences between the two populations are less than 0.1.

Figure 1.

The allele frequency differences between the two populations in one simulated data set.

3.2 Type I error evaluation of the original HWD trend test and the extended HWD trend test

To compare the type I errors of the original HWD trend test of song and Elston [14] and the extended HWD trend test, we chose a null SNP, i.e., non-disease-causing SNP, from the simulated 10,000+10 SNPs and evaluated the type I errors on this SNP. The null SNP was chosen in two ways: 1) from the 10,000 random SNPs and 2) from the 10 SNPs with differential frequencies, where we set the allele frequency as 0.2 in subpopulation 1 and 0.8 in subpopulation 2. We simulated 10,000 replicated data sets to estimate the type I error and the results are showed in Table I. We can see that with the random null SNP, both the original HWD trend test and the extended HWD trend test could control the type I error well. However, at the SNP with highly differentiated allele frequencies in the two subpopulations, the original HWD trend test had obviously inflated type I error and the extended HWD trend test could still control the type I error.

Table I.

Empirical type I error of the original HWD trend test (HWDTT) and the extended HWDTT (E-HWDTT) based on 10,000 replicates with significance level of 0.05.

Allele freqs	HWDTT	E-HWDTT
Randoma	0.0502	0.0459
0.2 – 0.8b	0.9809	0.0508

^aThe allele frequency differences of the candidate null SNP between the two populations were randomly simulated based on the F_st = 0.01

^bThe allele frequency differences of the candidate null SNP between the two populations were set to 0.2 and 0.8 respectively.

3.3 Evaluation of correlation between the GA trend test and the extended HWD trend test

We estimated the correlation coefficients between the GA trend test and the extended HWD trend test under the null hypothesis that no markers are associated with the disease and that Hardy-Weinberg equilibrium holds in each subpopulation. Under this null hypothesis we generated 10,000 replicates of the case-control data with 10,000+10 SNPs (see section 3.1). For each SNP, we calculated the GA trend test statistic and the extended HWD trend test statistic. The sample Spearman’s rank correlation coefficient between the GA trend test and the extended HWD trend test was calculated for each SNP based on the 10,000 replicates. The mean and variance of the absolute values of the Spearman’s rank correlation coefficients for the 10,000+10 markers were 0.00799 and 0.0060, respectively. These values indicate that the correlation between the two statistics is negligible.

3.4 FWER evaluation

To evaluate the FWERs of our proposed GSB procedures, we generated 100,000 replicates of the case-control data (with 10,000+10 SNPs) under the null hypothesis that no SNPs were associated with the disease (see the section on simulating case-control data above). The FWER was estimated as the proportion of replicates with at least one false discovery. We also estimated the FWERs of the extended HWD trend test and the GA trend test. For these individual SNP based tests, the significance level for individual SNPs was set using Bonferroni correction, i.e., the nominal FWER divided by the number of SNPs. For the smooth-GSB procedure, different values from 0.55 to 0.9 for λ were evaluated. The estimated FWERs were reported in Table II. We can see that all methods controlled the FWER well. We did not estimate the FWER of the MAX3-PC because of the high computational cost. The evaluation of the type I error of MAX3-PC can be found in So and Sham’s paper [12].

Table II.

Empirical FWER based on 100,000 replicates with nominal FWER = 0.01, 0.05 and 0.1^*.

FWER	E- HWDTTa	GA trendb	GSBc	S-GSBd
				λ=.55	λ=.6	λ=.65	λ=.7	λ=.75	λ=.8	λ=.85	λ=.9
.01	.0088	.0095	.0092	.0093	.0095	.0094	.0094	.0093	.0093	.0094	.0095
.05	.0417	.0478	.0487	.0478	.0477	.0476	.0475	.0473	.0473	.0473	.0475
.10	.0827	.0927	.0944	.0942	.0942	.0939	.0937	.0937	.0933	.0931	.0927

^*For the individual SNP based tests (E-HWDTT and the GA trend test), the significance level for individual SNPs was set using Bonferroni correction, i.e., the nominal FWER divided by the number of SNPs

^aE-HWDTT: the extended HWD trend test

^bGA trend = the GA trend test

^cGSB = generalized sequential Bonferroni procedure

^dS-GSB: the smooth-GSB procedure with different λ from 0.55 to 0.9.

3.5 Power evaluation

To evaluate the power of the proposed methods, we simulated a causal SNP besides the 10,000+10 non-causal SNPs as follows. At the causal SNP with allele A and B, let B denote the risk allele. We assume Hardy-Weinberg equilibrium in the subpopulations 1 and 2. Suppose p_k (k = 1, 2) is the frequency of allele B in population k. The genotype frequencies of (AA, AB, BB) for controls (population control) of population k are set to {(1 − p_k)², 2p_k(1−p_k), p_k²}. Let the genetic relative risks be R₁ = Pr (affected | AB) / Pr (affected | AA), R₂ = Pr (affected | BB) / Pr (affected | AA). When the genetic model is additive, multiplicative, dominant or recessive, we have R₂ = 2 R₁ − 1, R₂ = R₁², R₁ = R₂, or R₁ = 1, respectively. The genotype frequencies of (AA, AB, BB) in cases is set to {(1 − p_k)²/c, 2p_k(1−p_k)R₁/c, p_k²R₂/c }, where c = (1 − p_k)² + 2p_k(1−p_k)R₁ + p_k²R₂. With the specified genotype frequencies, cases and controls were sampled from the corresponding trinomial distribution with parameters {(1 − p_k)²/c, 2p_k(1−p_k)R₁/c, p_k²R₂/c } and {(1 − p_k)², 2p_k(1−p_k), p_k²}, respectively. We compared the power of five different methods: 1) the extended HWD trend test, 2) the GA trend test as implemented in EIGENSTRAT, 3) the GSB procedure, 4) the smooth-GSB procedure, and 5) MAX3-PC. The top 10 PCs of the genome-wide genotypes were used as covariates in the GA trend test and MAX3-PC. We simulated data under the four genetic disease models: the additive, multiplicative, dominant and recessive models, and considered different genotype relative risks. For each scenario, we simulated 10,000 replicates of the case-control data. The nominal FWER was set to be 0.05. For the individual SNP based tests (the extended HWD trend test, the GA trend test, and MAX3-PC), the corresponding significance level for each SNP was set to 0.05/m, where m is the number of SNPs. The power was estimated as the proportion of replicates with identified significant SNPs.

To test the influence of different values of λ on the smooth-GSB procedure, we estimated power of the smooth-GSB procedure with different λ values ranging from 0.55 to 0.90 based on 10,000 replicated data sets. Results were reported in Table III. We can see that the power of the smooth-GSB procedure is robust to different values of λ when 0.55 ≤ λ ≤0.9. When λ increased from 0.55 to 0.90, the power of the smooth-GSB procedure slightly increased under the additive and the multiplicative models and slightly decreased under the dominant and recessive models. More specifically as λ increased from 0.60 to 0.85, the power increase of the smooth-GSB procedure under the additive and multiplicative models was usually less than 0.02 and the power decrease under the dominant and recessive models was usually less than 0.03. Given this, we would further suggest setting the value of λ in the smooth-GSB procedure such that 0.60 ≤ λ ≤0.85. For example we can set λ = 0.7. Compared to the GA trend test, our smooth-GSB procedure has much higher power than the GA trend test under both the recessive and dominant models. On the other hand, the smooth-GSB procedure (when 0.60 ≤ λ ≤ 0.85) has power very close to the GA trend test (the difference is often less than 0.02) under both the additive and multiplicative models. For example, under the recessive model with genotypic relative risk R₂ = 1.5, the power of the smooth-GSB procedure with λ = 0.6 was 0.531, which was about 10% (in absolute terms) higher than the power 0.438 of the GA trend test. We can also see that the robust test MAX3-PC of So and Sham (2011) had relatively lower power than the GA trend test and our smooth-GSB procedure under the additive and multiplicative models while it had higher power than the other two methods under the dominant and recessive models. For example, under the additive model with genotype relative risk R₁ = 1.3, the power of the GA trend test, the smooth-GSB procedure (with λ = 0.6) and MAX-PC were 0.465, 0.448, and 0.420 respectively. The power of MAX3-PC was 4.5% (in absolute terms) lower than that of the GA trend test.

Table III.

Empirical power based on 10,000 replicates (the nominal FWER was 0.05).

Modela	R1	R2	E-HWDTTb	GA trendc	GSBd	S-GSBe								MAX3- PCf
						λ=.55	λ=.6	λ=.65	λ=.7	λ=.75	λ=.8	λ=.85	λ=.9
ADD	1.2	1.4	.000	.101	.065	.090	.091	.093	.094	.096	.098	.098	.099	.079
	1.3	1.6	.000	.465	.379	.445	.448	.451	.454	.456	.458	.460	.462	.420
	1.4	1.8	.000	.766	.705	.752	.755	.757	.758	.761	.762	.764	.764	.733
	1.5	2	.000	.888	.855	.882	.883	.883	.884	.885	.886	.887	.888	.873
DOM	1.3	1.3	.002	.069	.100	.095	.093	.092	.091	.089	.087	.085	.083	.103
	1.5	1.5	.030	.385	.499	.488	.485	.483	.480	.475	.470	.463	.455	.505
	1.7	1.7	.153	.556	.672	.657	.655	.652	.650	.647	.644	.638	.631	.687
	1.9	1.9	.352	.627	.743	.730	.728	.726	.723	.720	.717	.713	.705	.764
MUL	1.2	1.44	.000	.158	.104	.146	.148	.150	.151	.153	.154	.155	.156	.126
	1.3	1.69	.000	.640	.547	.621	.623	.626	.629	.631	.634	.636	.637	.597
	1.4	1.96	.000	.903	.861	.895	.897	.898	.898	.899	.900	.900	.902	.886
	1.5	2.25	.000	.971	.958	.967	.968	.968	.969	.969	.969	.970	.971	.966
REC	1	1.3	.002	.070	.093	.092	.091	.090	.089	.088	.087	.085	.083	.104
	1	1.5	.027	.438	.542	.534	.531	.528	.525	.520	.515	.512	.503	.555
	1	1.7	.121	.664	.775	.764	.762	.760	.758	.755	.752	.748	.742	.773
	1	1.9	.276	.750	.857	.847	.845	.843	.841	.838	.835	.831	.825	.853

^aADD: additive model; DOM: dominant model; MUL: multiplicative model; REC: recessive model

^bE-HWDTT = the extended HWD trend test

^cGA trend = the GA trend test

^dGSB = generalized sequential Bonferroni procedure

^eS-GSB = the smooth-GSB procedure with different λ from 0.55 to 0.9

^fMAX3-PC = the extended MAX3 with PCs as covariates.

Another advantage of the smooth-GSB procedure is that it is much faster than MAX3-PC. On a computer with CPU 3.47G Hz, with the principal components (PCs) already computed, to process 10,000+10 SNPs, our R implementation of the smooth-GSB procedure for GWAS took less than 15 seconds, while MAX3-PC implemented in the Robust SNP package (So and Sham 2011) took about 1,100 seconds if the absolute error of p-values was set to 10⁻⁶. It took about 2,500 seconds if the absolute error of p-values is set to 10⁻⁸. This means that for GWAS with about one million SNPs, the MAX3-PC will take about 70 hours with p-value accuracy level of 10⁻⁸, while the smooth-GSB procedure takes less than 25 minutes.

4. Application to WTCCC data

The WTCCC data contain seven different data sets of major diseases [13]. To evaluate the performance of the proposed method on real data, we chose four data sets on bipolar disorder (BD), coronary artery disease (CAD), Crohn’s disease (CD), and type 2 diabetes (T2D) from the WTCCC data. Each of the four data sets had the reported genomic control inflation factor > 1.06 [13], therefore there may be population stratification in each of these data sets. There were about 3,000 controls and about 2,000 cases in each data set.

We did the quality control according to the description in the WTCCC paper [13] to filter out some individuals and SNPs. The total number of SNPs after quality control was about 400,000. Following the suggestion of the WTCCC paper [13], we used only two top PCs as covariates to correct for population stratification in the GA trend test and MAX3-PC. These PCs were calculated based on about 190,000 SNPs which was obtained by pruning the whole genome SNPs using the software PLINK [24]. In each of the three single marker-based tests: the extended HWD trend test, the GA trend test and MAX3-PC, we can calculate a p-value at each of the about 400,000 SNPs. But in the smooth-GSB procedure, we can only calculate an adjusted p-value (see Section 2.3) for each SNP. In order to compare the adjusted p-value with the p-values from the three single marker-based tests, we define a p-value for each SNP in the smooth-GSB procedure as the adjusted p-value divided by the number of tests (m); however, if the adjusted p-value at a SNP is 1, then we will not define a p-value for that SNP because the null hypothesis will not be rejected at the SNP. When assuming the independence of markers, for the smooth-GSB procedure, comparing the adjusted p-value with the nominal FWER α is equivalent to comparing the new defined p-value with α/m.

Following the suggestion of the WTCCC paper [13], we used the threshold of 5×10⁻⁷ for individual SNPs. Table IV lists the significant SNPs identified by at least one of the three methods: the GA trend test, the smooth-GSB procedure, and MAX3-PC. For each significant region, only the SNP with the smallest p-value is listed. We can see that all the SNPs detected by the GA trend test, were also detected by the smooth-GSB procedure with different values of λ: 0.6, 0.7, and 0.8; the only exception is that SNP rs10761659 was not identified by the smooth-GSB procedure with λ = 0.6 (p-value=5.01×10⁻⁷,which is very close to the threshold 5×10⁻⁷). For the bipolar disorder, SNP rs420259 was detected by both the smooth-GSB procedure and MAX3-PC, but not by the GA trend test. This was reasonable because the best-fitting genetic model for SNP rs420259 was recessive [13]. As we described earlier, the GA trend test has low power under the recessive model. In addition, two SNPs, rs11747270 (for CD) and rs10806665 (for T2D), and their corresponding regions, were detected by both the GA trend test and the smooth-GSB procedure, but were not detected by MAX3-PC. The reason for this might be that the underlying disease models at these two SNPs are additive and MAX3-PC method has relatively lower power than the other two methods under the additive model. We note that the SNP rs10806665 (for T2D) was not identified significant by WTCCC [13]. We also note that for the coronary artery disease, two SNPs, rs4854090 and rs5007171, were detected by MAX3-PC but not by the GA trend test and smooth-GSB procedure. The underlying disease models at these two SNPs might be recessive or dominant, because under these two models, MAX3-PC has higher power than the other two methods. These two SNPs and their corresponding regions were not reported as significant by WTCCC [13].

Table IV.

P-values for the most significant SNPs in the regions identified by the GA trend test, the smooth-GSB procedure or MAX3-PC in four WTCCC data sets with population stratification.

Disease	Chr	SNP*	MAF	E-HWDTTa	GA trendb	S-GSBc			MAX3-PCd
						λ=0.6	λ=0.7	λ=0.8
BD	16	rs420259	.282	6.93×10−06	7.64×10−04	2.34×10−07	3.12×10−07	4.68×10−07	4.69×10−09
CAD	2	rs4854090	.251	4.31×10−06	6.97×10−02	NAe	NA	NA	3.26×10−08
	3	rs5007171	.210	5.15×10−07	1.21×10−01	NA	NA	NA	1.31×10−08
	7	rs17146094	.016	1.01×10−03	6.46×10−06	3.01×10−07	3.95×10−07	5.74×10−07	7.10×10−05
	9	rs1333049	.474	3.05×10−01	6.66×10−15	9.96×10−15	8.86×10−15	7.98×10−15	1.21×10−14
CD	1	rs11805303	.317	8.03×10−01	8.24×10−13	1.29×10−12	1.13×10−12	1.00×10−12	4.71×10−12
	2	rs10210302	.481	2.79×10−02	5.12×10−14	2.94×10−14	3.29×10−14	3.73×10−14	1.58×10−13
	5	rs17234657	.125	7.38×1001	2.19×10−14	3.40×10−14	2.99×10−14	2.66×10−14	5.17×10−13
	5	rs11747270	.068	7.13×10−01	2.57×10−07	3.99×10−07	3.51×10−07	3.13×10−07	1.51×10−06
	10	rs10761659	.461	8.95×10−01	3.18×10−07	5.01×10−07	4.38×10−07	3.89×10−07	6.14×10−07
	10	rs10883365	.477	2.74×10−01	3.39×10−08	4.73×10−08	4.30×10−08	3.95×10−08	7.82×10−08
	16	rs2076756	.242	4.36×10−01	3.77×10−15	2.83×10−15	3.02×10−15	3.24×10−15	5.73×10−14
	18	rs2542151	.163	3.54×10−01	1.09×10−08	1.59×10−08	1.43×10−08	1.29×10−08	6.75×10−08
T2D	6	rs10806665	.077	8.03×10−01	2.83×10−07	4.48×10−07	3.92×10−07	3.47×10−07	1.29×10−06
	10	rs4506565	.324	9.94×10−01	8.54×10−13	1.36×10−12	1.19×10−12	1.05×10−12	3.52×10−12
	16	rs7193144	.396	1.23×10−01	3.91×10−07	4.84×10−08	4.57×10−08	4.33×10−08	5.53×10−08

^*Only the SNP with the smallest p-value in each significant region is listed.

^aE-HWDTT: the extended HWD trend test

^bGA trend: the GA trend test

^cThe smooth-GSB procedure with different λ values; P-values for S-GSB was calculated as the adjusted p-values divided by the number of test

^dMAX3-PC: the extended MAX3 adjusting for top PCs.

^ethe adjusted p-value was equal to 1 and therefore the adjusted p-value for individual SNPs was not calculated. The p-values in bold mean they do not reach the genome-wide significant level 5×10⁻⁷. The SNP IDs with underscore and in italic style denote that the corresponding regions are not listed in Table 3 of the WTCCC paper, which lists the regions of the strongest association signals.

5. Discussion

In this study, we proposed a fast and robust association test procedure (the smooth-GSB procedure) which can be applied to GWAS data with case-control designs in the presence of subpopulations. As showed in the simulation studies, the smooth-GSB procedure can have significantly higher power than the GA trend test implemented in EIGENSTRAT when the underlying genetic model is dominant or recessive. It can also have power comparable to the GA trend test when the underlying genetic model is additive or multiplicative. Our simulation studies indicate that the existing robust test, MAX3-PC, can be computationally intensive for GWAS with a large number of SNPs and can have relatively lower power than the GA trend test when the underlying disease model is additive or multiplicative. Our proposed method can be viewed as an extension to account for population stratification of our previously proposed generalized sequential Bonferroni (GSB) procedure for GWAS in homogeneous populations [25].

The proposed smooth-GSB procedure is not appropriate for analysis of rare variants (for example with minor allele frequency (MAF) less than 0.05). When MAF < 0.05, the extended HWD trend test may not produce accurate p-values.

In our proposed smooth-GSB procedure, the parameter λ (0 ≤ λ ≤ 1) should be set empirically. If we choose λ = 1, then the smooth-GSB procedure becomes the Holm’s sequential rejective procedure [20] using the GA trend test and is approximately equivalent to the GA trend test with Bonferroni correction (if the number of markers is large enough such as in GWAS analysis). When λ = 1 the smooth-GSB procedure has the highest power if the underlying disease models are additive or multiplicative, but has relatively low power if the underlying disease models are recessive or dominant. On the other hand, in the smooth-GSB procedure, if we choose λ = 0, then it becomes the GSB procedure (see Section 2.4), which has the highest power when the disease models are recessive or dominant, but has lower power than the GA trend test if the underlying disease models are additive or multiplicative. In real data analysis, usually we don’t know the true disease models. Since most significant SNPs reported in the literature so far have demonstrated additive effects, based on our simulation studies, we would suggest choosing the value of λ such that 0.6 ≤ λ ≤ 0.85. For example, we can set λ = 0.7. As indicated by the results of our simulation studies, when the values of λ change from 0.6 to 0.85, the power of our smooth-GSB procedure is: a) very robust to different values of λ under different disease models, b) very close to that of the GA trend test if the underlying disease model is additive or multiplicative, and c) much higher than that of the GA trend test if the underlying disease model is recessive or dominant.

We note that in the extended HWD trend test, any proper clustering algorithm to partition the individuals into subpopulations can be applied, such as the more computationally intensive method proposed by Prichard et al. [26]. The k-means clustering method used in this paper has the advantage of low computation cost.

In the extended HWD trend test, we applied the k-means clustering algorithm to the top PCs of the genotype data to partition the individuals in the case-control data into several clusters corresponding to homogeneous subpopulations. This k-means clustering may not be appropriate for data from admixed populations, for which different partitioning methods may be needed. For example, we can partition individuals by the number of alleles at a marker inherited from an ancestral population. This partitioning method was used by Shriner et al. [27] in association studies in admixed populations.

In this article, we assume independence of markers in GWAS by ignoring the dependence among markers. The proposed methods under this assumption can be relatively conservative when applied to GWAS data analysis due to ignoring the LD among markers. Accounting for linkage disequilibrium among dense markers may increase power of association study methods in detecting causal variants. In our future study, we plan to incorporate SNP set (or gene)-based association tests, e.g., SKAT [28], which can account for dependence among markers, into our smooth-GSB procedure.

Appendix: Evaluation of FWER of the GSB procedures of Holm (1979) for multiple testing with weights weakly correlated with the tests

Here we show by simulation studies that under some situations, in the GSB procedure of Holm (1979) [20] for m independent hypotheses H₁, H₂, …, H_m, even though the weights are weakly correlated with the m tests, the GSB procedure can still control FWER well (see also section 2.3). Assuming all the null hypotheses H₁, H₂, …, H_m are true, the p-value p_j from the j-th test corresponding to hypothesis H_j follows the uniform distribution U[0,1] (j =1,…,m). Suppose we calculate a weight w_j for this p-value p_j by w_j=1/q_j, where q_j is a random variable whose marginal distribution is also the uniform distribution U[0,1], and q_j is weakly correlated with p_j, with q_j and p_j jointly following a bivariate uniform distribution. The correlation between the two variables q_j and p_j can be simulated by the bivariate copulas [29]. Suppose there were 1,000 tests (m=1,000). For the j-th test, we simulated a pair of q-value and p-value (q_j and p_j) from a bivariate uniform distribution with dependence between q_j and p_j by the Gaussian copula. We used Spearman’s rank correlation coefficient ρ_s to measure the dependency between the pair of q-value and p-value (q_j and p_j).

Once the pair of q-value and p-value was simulated for each test, we had 1,000 pairs of q-value and p-value corresponding to 1,000 tests. We calculated weights by using the q-values and then we applied the GSB procedure to the 1,000 tests. We replicated this simulation procedure 10⁷ times and therefore generated 10⁷ replicated “data sets”, each consisting of 1,000 pairs of q-value and p-values. We estimated the FWER of the GSB procedure over these 10⁷ replicated “data sets” with the nominal FWER as 0.01, 0.05 and 0.1. The FWER was estimated as the proportion of replicates with at least one false discovery. The results are showed in Table V. From the results we can see that the FWER of the GSB procedure was well controlled when the Spearman’s rank correlation coefficient ρ_s is equal to or less than 0.01 (i.e., q-value and p-value were weakly correlated).

Table V.

Empirical FWERs of the GSB procedures of Holm (1979) for 1,000 tests with weights weakly correlated with the tests^#.

	Nominal FWER (α)
ρs*	0.01	0.05	0.1
0.005	0.0103	0.0505	0.0987
0.01	0.0101	0.0495	0.0965

^#based on 10⁷ replicated datasets.

^*ρ_s is the Spearman’s rank correlation coefficient between the test statistics, respectively.

^#The nominal FWER used to reject null hypothesis.