Amputee locomotion: Spring-like leg behavior and stiffness regulation using running-specific prostheses

Abstract

Carbon fiber running-specific prostheses (RSPs) have allowed individuals with lower extremity amputation (ILEA) to participate in running. It has been established that as running speed increases, leg stiffness (K_leg) remains constant while vertical stiffness (K_vert) increases in able-bodied runners. The K_vert further depends on a combination of the torsional stiffnesses of the joints (joint stiffness; K_joint) and the touchdown joint angles. Thus, an increased understanding of spring-like leg function and stiffness regulation in ILEA runners using RSPs is expected to aid in prosthetic design and rehabilitation strategies. The aim of this study was to investigate stiffness regulation to various overground running speeds in ILEA wearing RSPs. Eight ILEA performed overground running at a range of running speeds. K_leg, K_vert and K_joint were calculated from kinetic and kinematic data in both intact and prosthetic limbs. K_leg and K_vert in both limbs remained constant when running speed increased, while intact limbs in ILEA running with RSPs have a higher K_leg and K_vert than residual limbs. There were no significant differences in K_ankle, K_knee and touchdown knee angle between the legs at all running speeds. Hip joints in both legs did not demonstrate spring-like function; however, distinct impact peaks were observed only in the intact leg hip extension moment at early stance phase, indicating that differences in K_vert between limbs in ILEA are due to attenuating shock with the hip joint. Therefore, these results suggest that ILEA using RSPs have a different stiffness regulation between the intact and prosthetic limbs during running.

Introduction

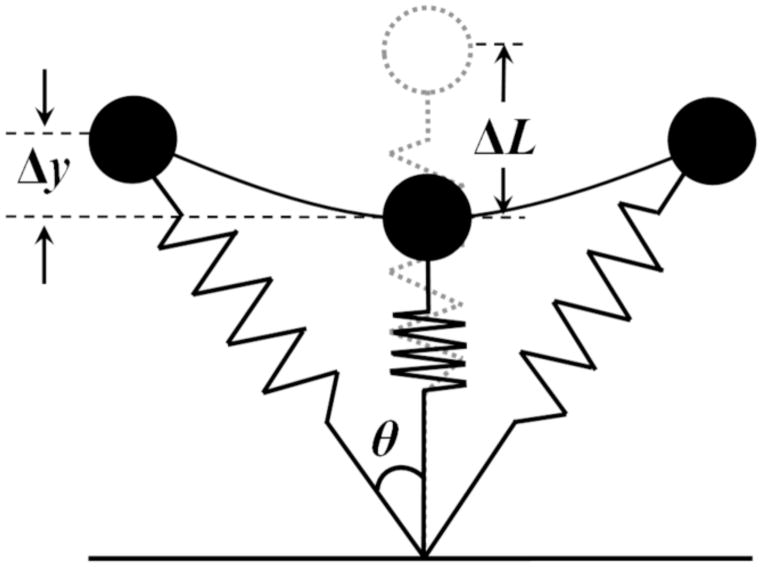
Recent carbon fiber running-specific prostheses (RSPs) have helped individuals with lower extremity amputation (ILEA) run by providing spring-like properties in their amputated leg. To describe the spring-like leg function during running, the whole body is often modeled with a “spring-mass model” which consists of a body mass supported by a spring (Figure 1; Blickhan, 1989; McMahon and Cheng, 1990). In this model, stiffness of the leg spring (leg stiffness; K_leg) is defined as the ratio of maximal vertical ground reaction force (F_peak) to maximum leg compression (ΔL) during the stance phase. Previous studies have demonstrated that able-bodied humans adjust the spring-like behavior for different running speeds by increasing the angle swept (θ) by the stance limb while keeping K_leg nearly constant (He et al., 1991; Farley et al., 1993; McMahon and Cheng, 1990; Morin et al., 2005, 2006), indicating that the constant-stiffness leg spring may be a basic and invariant characteristic of running. However, it is still unknown whether ILEA using RSPs show similar responses between the amputated limb and the intact limb. A better understanding of spring-like leg behavior and stiffness regulation using RSPs will lead to identifying potential risk factors of amputee running and optimizing prosthesis designs to mitigate these risk factors and improve prosthesis and individual performance through rehabilitation strategies.

Figure 1.

Spring-mass model for running. The leg spring is compressed during the first half of the stance phase and rebounds during the second half. Maximal vertical displacement of the center of mass and leg spring compression during ground contact is represented by Δy and ΔL, respectively. Half of the angle swept by the leg spring during the ground contact is denoted by θ.

It has also been shown that vertical stiffness (K_vert; ratio of F_peak to maximum vertical displacement of the center of mass at the middle of the stance phase) is a crucial parameter to determine the spring-like function in human running at a wide range of running speeds. Several studies have shown that vertical stiffness increases with an increase in running speed (Cavagna et al., 2005, 2012; He et al., 1991; Kuitunen et al., 2002; McGowan et al., 2012; Morin et al., 2005, 2006). In a multijointed system, K_vert further depends on a combination of the torsional stiffnesses of the joints (joint stiffness; K_joint, Kuitunen et al., 2002; Butler et al., 2003; Farley et al., 1998; Farley and Morgenroth, 1999; Hobara et al., 2010). Past findings demonstrated that the changes in K_vert during running primarily depend on K_knee (Kuitunen et al., 2002; Arampatzis et al., 1999; Günther and Blickhan, 2002; Stefanyshyn and Nigg, 1998). Furthermore, K_vert is also influenced by the changes in touchdown joint angle because this angle changes the distance of the moment arm of the ground reaction force (GRF) at each joint (Farley et al., 1998; Hobara et al., 2010; Moritz and Farley, 2004).

Despite several studies examining K_vert during ILEA running (McGowan et al., 2012; Wilson et al., 2009), little is known about stiffness regulation at joint levels. Understanding spring-like leg behavior and stiffness regulation in ILEA using RSPs is important for evaluating their running ability and developing RSP designs and effective rehabilitation strategies. The aim of this study was to investigate stiffness regulation to various overground running speeds in ILEA wearing RSPs.

According to previous studies, RSPs generated lower vertical GRFs than intact limbs (Brüggemann et al., 2009; Grabowski et al., 2010; Weyand et al., 2009). Hence, in the present study we hypothesized that (1) leg stiffness would remain constant with an increase in running speed, but the leg stiffness in the intact limb would be greater than the residual limb, (2) vertical and joint stiffness in both limbs would increase with an increase in running speed, (3) vertical stiffness in the intact limb would be greater than the residual limb and (4) the difference in vertical stiffness would be associated with differences in knee stiffness.

Methods

Participants

Eight male subjects with unilateral transtibial amputation volunteered to participate in the experiment (Table 1). Each ILEA used his own RSP. The study was approved by the local ethics committee of the University of Maryland, College Park Institutional Review Board and prior to testing, written informed consent was obtained.

Table 1.

Subject characteristics.

Subject	Age (years)	Height (m)	Total Mass (kg)	Running Experience (months)	RSP model	Amputated Limb	Cause of Amputation
1	48	1.75	73.4	46	Flex-Run	Right	Congenital
2	31	1.71	67.9	48	Flex-Run	Left	Trauma
3	34	1.72	110.2	60	Flex-Run	Left	Trauma
4	27	1.8	73.8	9	Cheetah	Left	Trauma
5	23	1.88	85.3	9	Cheetah	Right	Trauma
6	27	1.84	85.3	3	Flex-Run	Left	Trauma
7	46	1.81	84.3	256	Cheetah	Left	Trauma
8	20	1.89	78	12	Cheetah	Right	Trauma
Mean	32.0	1.80	82.3	55.4
SD	10.2	0.07	82.3	84.0

Task and procedure

Participants were instructed to run overground on a 100 m long track at 2.5, 3.0 and 3.5 m/s (Figure 2). Each subject continuously ran around the track and data were recorded whenever the subjects passed through the capture volume. Five successful trials for each leg at each of the three running speeds were taken and averaged for further analysis. A successful trial was defined as the subject running within ±0.2 m/s of the prescribed speed within the track section containing the force platforms and stepping within the boundaries of the force platforms during the trial. The order for prescribed running speeds was randomized. To facilitate control of the desired running speed, predetermined speeds were governed using concurrent biofeedback. Using four sets of laser sensors around the track, the average speed over the track section was instantaneously calculated when the subjects ran past the sensors, and verbal cues were provided if subjects were outside of the target speed range. Subjects rested for as long as needed between speed conditions to reduce the effects of fatigue.

Figure 2.

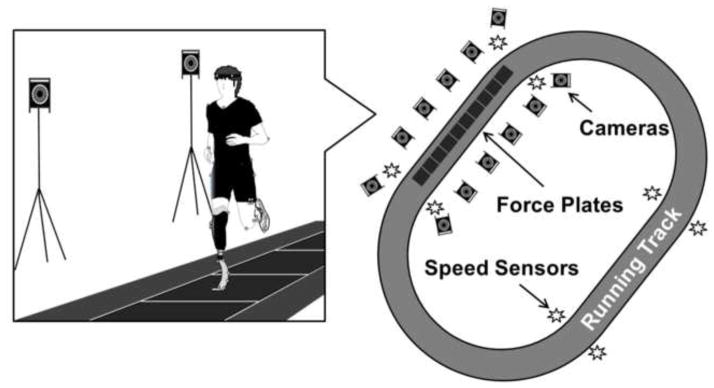
Schematic of experiment setup. Each subject ran around a 100m track containing 10 force plates that recorded ground reaction force data. Ten motion capture cameras collected 3D kinematic data and four sets of sensors around the track monitored running speed in real-time.

Data collection and analysis

Prior to beginning the experiment, retroreflective markers were placed bilaterally over the anterior and posterior iliac spines, heel, 3rd metatarsal head, 5th metatarsal head, and tip of the toe on the shoe. Marker clusters were placed bilaterally on the lateral thigh and shank segments. A static trial was collected prior to dynamic trials that included markers placed on the lateral and medial femoral condyles and the lateral and medial malleoli. On the amputated leg, the shank cluster was placed laterally on the socket and a marker was placed at the distal tip of the socket to define the long axis of the residual shank segment. According to a previous study (Buckley, 2000), the RSP “ankle” joint center was defined as the most acute point on the RSP curvature. Joint angular displacements were determined from the marker data using Visual3D (C-Motion, Germantown, MD) software.

Ten six-degree-of-freedom piezoelectric force platforms (60 cm × 50 cm each and the total measurement area of 600 cm × 50 cm; 9260AA6, Kistler, Amherst, NY) embedded in the track in series collected GRFs at 1000 Hz. The GRFs were filtered using a fourth order, zero lag low pass Butterworth filter with a cut-off frequency of 30 Hz. Further, we captured 3D positional data of the markers using a 10-camera motion capture system (Vicon, Centennial, CO) at 200 Hz. Raw marker data were filtered using a 4th order, zero lag low pass Butterworth filter with a cut-off frequency of 6 Hz.

From vertical GRF (vGRF) data, we determined step frequency (f), stance time (t_c) and maximal vGRF (F_peak) in both the intact and prosthetic limb (INT and PST, respectively). In the present study, we calculated K_leg utilizing the spring-mass model (Blickhan, 1989; Figure 1). During running, the peaks of vGRF and leg compression coincide in the middle of the ground contact phase. At this point, K_leg (N/m) can be calculated as the ratio of F_peak to peak leg compression in the spring (ΔL) when the leg spring is maximally compressed:

$$K_{\text{leg}}=F_{\text{peak}}/\mathrm{\Delta }L$$ (1)

ΔL was calculated from the maximum vertical displacement of the center of mass (COM; Δy), the initial length of the leg spring (L₀), and half of the angle swept by the leg spring while it was in contact with the ground (θ):

$$\mathrm{\Delta }L=\mathrm{\Delta }y+L_0(1-\text{cos}\theta )$$ (2)

with

$$\theta ={sin}^{-1}(u{t}_{\text{c}}/2L_0)$$ (3)

where u is the speed of the body (m/s) and t_c is the ground contact time at each step (He et al., 1991; Farley and Gonzalez, 1996; McMahon and Cheng, 1990). Based on the static standing trial, we calculated leg length in INT as the sum of lengths of the hip-knee-ankle joint centers to the ground. For the PST, we defined leg length as the sum of lengths of the hip-knee joint centers to the distal socket to the ground.

Following previous studies (Blickhan, 1989; Kuitunen et al., 2002; Morin et al., 2005; Farley and Gonzalez, 1996), K_vert was also calculated utilizing the spring-mass model. Assuming F_peak and Δy coincide in the middle of the ground contact phase, the K_vert (N/m) can be calculated as

$$K_{\text{vert}}=F_{\text{peak}}/\mathrm{\Delta }y$$ (4)

where Δy is the maximum vertical displacement of the COM during ground contact, which is obtained by integrating the vertical acceleration twice with respect to time (Cavagna, 1975). If F_peak and maximal COM displacement did not coincide in the middle of the ground contact phase, we calculated the K_vert as the ratio of F_peak and COM displacement between ground contact and the instant of F_peak (Hobara et al., 2008, 2009, 2010, 2012).

K_joint was calculated with the torsional spring model (Kuitunen et al., 2002; Farley et al., 1998; Farley and Morgenroth, 1999). The K_joint (Nm/deg) was calculated as a change in the joint moment (ΔM_joint) divided by the change in joint angular displacement (Δθ_joint) in the middle of the ground contact phase

$$K_{\text{joint}}=\mathrm{\Delta }{M}_{\text{joint}}/\mathrm{\Delta }{\theta }_{\text{joint}}.$$ (5)

In the present study, the joint moments were determined by utilizing rigid linked segment model, anthropomorphic data (Dempster, 1955), and inverse dynamics analysis (Winter, 1990). Since body mass influences the stiffness (Farley et al., 1993), K_leg, K_vert and K_joint were divided by the subject’s body weight (BW).

Statistical methods

A two-way repeated measures ANOVA with two factors, running speed (3 levels) and limbs (2 levels), was performed to compare INT and PST at three running speeds. Bonferroni post-hoc multiple comparison was performed if a significant main effect was observed. Statistical significance was set at p < 0.05. Statistical analysis was executed using SPSS (IBM SPSS Statistics Version 19, SPSS Inc., Chicago, IL).

Results

Leg and vertical stiffness

Figure 3 shows vGRF-COM displacement curves during the ground contact in running at 2.5, 3.0 and 3.5 m/s, respectively. Both INT and PST compressed after touchdown, and vGRF increased with decreased COM displacement. The vGRF peaked at the moment of maximum leg compression (middle of the stance phase), and subsequently, the vGRF decreased with leg extension until take-off.

Figure 3.

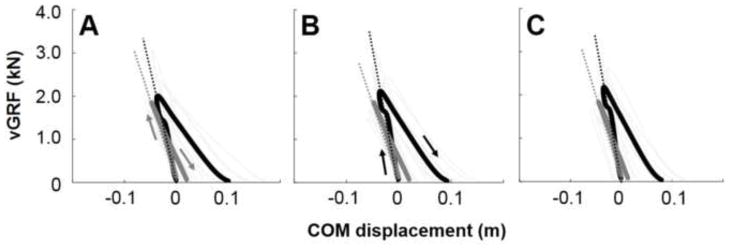
Time-normalized vGRF-COM displacement curves during the ground contact in running at 2.5 (A), 3.0 (B) and 3.5 m/s (C), respectively. Black thick (INT) and gray thick (PST) curves are means of 8 subjects. Gray thin curves represent mean curves for each individual in each leg. The slopes (dotted lines) of these curves represent vertical stiffness. K_vert is the slope of the vGRF-COM displacement curve in the leg compression phase

There was no significant main effect of running speed on K_leg, while there was a significant main effect of limbs (p < 0.05). K_leg was significantly greater in INT than PST at 2.5 and 3.5 m/s (Table 2; p < 0.05). No significant interaction existed between running speeds and limbs on K_leg. F_peak showed significant main effects of running speed (p < 0.05) and limbs (p < 0.05). F_peak was greater in INT compared to PST at each speed (Table 2). However, there was no significant speed by limb interaction effect on F_peak. Statistical analyses revealed main effects of speed on ΔL, θ, f and t_c (p < 0.01). However, there were no significant differences between limbs or interaction effects in these parameters (Table 2).

Table 2.

Comparison of kinetic and kinematic characteristics between the legs at all running speeds. Bold numbers and underlined bold numbers indicate significant differences between the limbs at p <0.05 and p <0.01, respectively.

	2.5 m/s		3.0 m/s		3.5 m/s
	INT	PST	INT	PST	INT	PST
Kleg, kN/BW/m	0.03 (0.02)	0.02 (0.01)	0.03 (0.01)	0.02 (0.01)	0.03 (0.03)	0.02 (0.01)
Kvert, kN/BW/m	0.07 (0.03)	0.05 (0.01)	0.09 (0.05)	0.05 (0.01)	0.09 (0.03)	0.05 (0.01)
Fpeak, N/BW	2.54 (0.31)	2.12 (0.22)	2.68 (0.25)†	2.29 (0.26) †*	2.76 (0.35) †	2.27 (0.22) **
ΔL, m	0.10 (0.02)	0.11 (0.02)	0.11 (0.02)	0.12 (0.02) *	0.12 (0.01) †#	0.12 (0.02) **
ΔCOM, m	0.04 (0.01)	0.05 (0.01)	0.04 (0.01)	0.05 (0.01)	0.03 (0.01)	0.04 (0.01)
tc, s	0.27 (0.02)	0.27 (0.03)	0.25 (0.01) ††	0.24 (0.02) **	0.23(0.02) ††##	0.22 (0.02) **$$
θ, deg.	20.24 (2.03)	20.52 (2.33)	21.57 (1.62) †	21.58 (2.02)	23.27 (1.64) ##	23.07 (2.23) **$$
f, Hz	2.73 (0.19)	2.73 (0.13)	2.76 (0.15)	2.79 (0.14) *	2.90 (0.15) ††##	2.94 (0.15) **$$
Kknee, Nm/BW/deg.	0.09 (0.04)	0.18 (0.19)	0.10 (0.04)	0.12 (0.06)	0.11 (0.05)	0.15 (0.12)
Kankle, Nm/BW/deg.	0.17 (0.08)	0.23 (0.04)	0.17 (0.08)	0.23 (0.04)	0.17 (0.07)	0.15 (0.12)
ΔMknee, Nm/BW	2.37 (0.64)	1.60 (0.59)	2.53 (0.77)	1.68 (0.65)	2.45 (0.76)	1.82 (0.64)
ΔMankle, Nm/BW	2.44 (0.39)	3.10 (0.69)	2.58 (0.38) †	3.33 (0.68)	2.73 (0.50) †	3.25 (0.67)
Δ θknee, deg.	27.28 (7.27)	15.53 (8.33)	26.62 (7.15)	16.85 (6.84)	23.97 (7.43) †#	16.27 (6.35)
Δ θankle, deg.	17.60 (8.31)	13.81 (3.04)	17.68 (8.03)	14.58 (3.03)	18.06 (7.89)	14.34 (3.14)
θhip, deg.	142.38 (6.65)	142.74 (6.89)	140.61 (6.45)	141.13 (6.12)	138.17 (6.48)	139.45 (5.29)
θknee, deg.	167.65 (7.18)	167.29 (7.91)	166.90 (6.68)	166.68 (7.69)	164.85 (6.42) #	165.32 (8.62) *
θankle, deg.	99.08 (10.35)	67.40 (10.99)	98.99 (9.68)	67.33 (10.83)	99.38 (9.49)	66.80 (10.90) *$
Peak Mhip	1.84 (0.31)	0.97 (0.23)	2.02 (0.28)	1.17 (0.26) *	2.36 (0.27) ††#	1.29 (0.31) *

^†significant differences from 2.5 m/s at p < 0.05 in INT.

^††significant differences from 2.5 m/s at p < 0.01 in INT.

^#significant differences between 3.0 m/s and 3.5 m/s at p < 0.05 in INT.

^##significant differences between 3.0 m/s and 3.5 m/s at p < 0.01 in INT

^*significant differences from 2.5 m/s at p < 0.05 in PST.

^**significant differences from 2.5 m/s at p < 0.01 in PST.

^$significant differences between 3.0 m/s and 3.5 m/s at p < 0.05 in PST.

^$$significant differences between 3.0 m/s and 3.5 m/s at p < 0.01 in PST

There was no significant main effect of running speed on K_vert while there was a significant main effect of limbs. K_vert was significantly greater in INT than PST at 3.5 m/s (Table 2; p < 0.05). There were no significant main effects of running speed and limb on ΔCOM, indicating that differences in stiffness were due to differences in F_peak rather than ΔCOM.

Joint stiffness

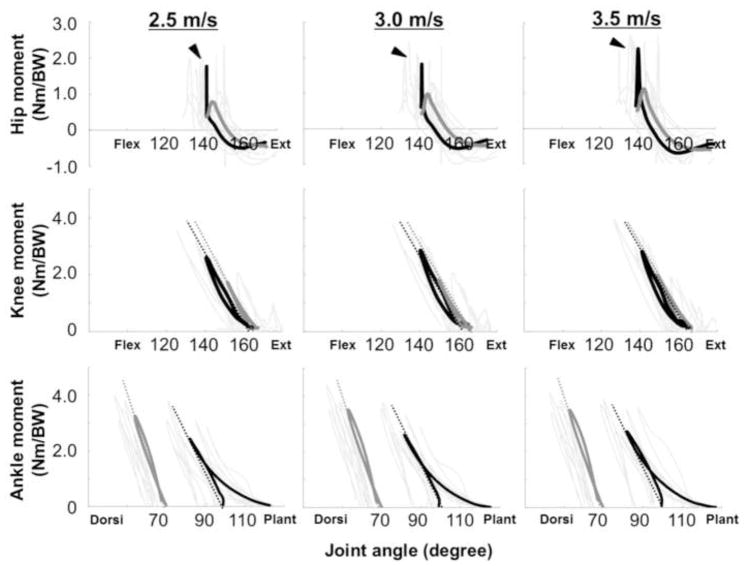
Figure 4 depicts moment-angle curves of the ankle, knee and hip joint during the ground contact in running at 2.5, 3.0 and 3.5 m/s, respectively. From the instant of touch down, the joints were flexed (dorsiflexed in ankle), and joint extension moments increased (plantarflexion moments in ankle). The joint moments of the knee and ankle peaked at maximum joint flexion (dorsiflexion), after which the joints began to extend (plantarflex) with decreases in joint moment until take-off. However, the hip joint in both legs did not show linear trends in the moment-angle relationships at any running speed; thus, we excluded the hip joint from joint stiffness calculations.

Figure 4.

Time-normalized moment-angle curves of the ankle, knee and hip joints during the ground contact in running at 2.5, 3.0 and 3.5 m/s, respectively. Arrows express the direction of the curve. In the figure, joint extension moments in each joint are represented as positive values. Black thick (INT) and gray thick (PST) curves are means of 8 subjects. Gray thin curves represent an individual value for each leg. The slopes (dotted lines) of these curves represent joint stiffnesses. Arrowheads indicate a peak hip extension moment at early stance phase in INT.

K_joint is the slope of the moment-angular displacement curve in the leg compression phase. Table 2 shows comparisons of K_knee and K_ankle between the legs across the three running speeds. Statistical analyses revealed that there were no significant main effects for running speeds or limb on K_knee and K_ankle.

Joint kinetics and kinematics

ΔM_knee was generally greater in INT than PST (p < 0.05), while there were no significant differences in ΔM_ankle between the legs. The ΔM_knee remained constant in both legs; however, ΔM_ankle in INT increased 10.9% when the speed increased (p < 0.05; Table 2). Further, Δθ_knee was generally greater in INT than PST (2.5 m/s: p < 0.01, 3.0 m/s: p < 0.01, and 3.5 m/s: p < 0.05), while there were no significant differences in Δθ_ankle between the limbs. Although Δθ_knee in INT decreased 13.8% when the speed increased (p < 0.05; Table 2), Δθ_ankle remained constant in both limbs.

As shown in Table 2, ankle angle at touchdown (θ_ankle) in PST was significantly extended compared to INT in all speeds (p < 0.01; Table 2). On the other hand, there was no significant bilateral difference in knee (θ_knee) and hip (θ_hip) angle at touchdown between the limbs.

Table 2 also shows a comparison of peak hip moments in early stance phase across three running speeds. The peak hip moment in early stance phase increased with increasing running speeds. Furthermore, the peak hip moment in early stance phase was generally greater in INT than PST at all running speeds (p < 0.01 at all speeds).

Discussion

The aim of this study was to investigate stiffness regulation to different overground running speeds in ILEA wearing RSPs. We found that K_leg remained constant in both legs for three speeds, but the K_leg in the intact limb was greater than the residual limb (Table 2). Current results support our first hypothesis, and agree with previous studies which stated that able-bodied runners keep K_leg constant for a range of running speeds (He et al., 1991; Farley et al., 1993; McMahon and Cheng, 1990; Morin et al., 2005, 2006). This suggests that a constant K_leg is a basic principle of running not only in able-bodied runners, but also in ILEA using RSPs. Maintaining a constant stiffness can be beneficial for the motor control of running when the running speed changes because other necessary kinematics and kinetics can be modulated with running speed without changing the stiffness.

Although changes in K_leg during running are associated with f and t_c (Farley and Gonzalez, 1996; Morin et al., 2007), there were no significant differences in f and t_c between the legs in any speed conditions in our study, indicating that differences in K_leg between limbs are not related to both f and t_c. As reviewed by previous studies (Brughelli and Cronin, 2008a, b), the results would indicate that as speed increases, the angle swept by the leg increases, which increases the change in ΔL. Thus, as the F_peak increases, the change in ΔL also increases, and therefore K_leg would not be altered significantly. Although our results contrast with a previous study (McGowan et al., 2012) which stated that there were no distinct differences in K_leg between the legs in ILEA running on a treadmill, the discrepancy between this study and our study may be explained by methodological differences. Further, current participants used their own RSP (2 in Cheetah, 4 in Flex-Run, 2 in Catapult), which is different from the previous study (4 in Cheetah, 1 in Sprinter and 1 in C-Sprint).

Our data showed that there was no significant main effect of running speed on K_vert (Table 2). Similarly, there was no significant main effect of running speed on K_knee and K_ankle in both limbs (Table 2). These results contrast with our second hypotheses which stated that vertical and joint stiffness in both limbs would increase with an increase in running speed. The lack of main effect of running speed on K_vert, K_knee and K_ankle might be due to the lower running speeds and smaller range of speeds in the present study compared with previous studies (Cavagna et al., 2005, 2012; He et al., 1991; Kuitunen et al., 2002; McGowan et al., 2012; Morin et al., 2005, 2006). Otherwise, small sample size might lead the invariant lower extremity stiffness according to the running speeds in the present study.

K_vert in INT was significantly greater than PST at 3.5 m/s (Table 2). However, the K_vert was not significantly greater at 2.5 and 3.0 m/s between the limbs. These results partly support our third hypothesis which stated that vertical stiffness in INT would be greater than PST. In other words, our third hypothesis was not fully supported at all speeds. A small sample size might have led to the non-significant differences in K_vert between the limbs.

Several studies demonstrated that changes in K_vert during running primarily depend on K_knee and not K_ankle (Kuitunen et al., 2002; Arampatzis et al., 1999; Günther and Blickhan, 2002; Stefanyshyn and Nigg, 1998). However, as shown in Table 2, we observed no significant differences in K_joint between the limbs at all running speeds. These results disagree with our final hypothesis, suggesting that differences in K_vert between the limbs probably depend upon something other than K_joint in ILEA runners. Although K_vert is also influenced by the changes in touchdown joint angle (Farley et al., 1998; Hobara et al., 2010; McMahon et al., 1987; Moritz and Farley, 2004), the subjects in the present study were not likely to control K_vert by altering touchdown joint angles. In fact, there were no significant differences in θ_knee between the legs (Table 2). θ_ankle in INT landed with more plantarflexed posture than PST; however, this comparison is dependent on how the prosthesis ankle joint and adjacent segments are defined. Moreover, the presence of a prosthetic limb may disrupt the normal joint/vertical stiffness relationships in running. Since identifying the major determinant of K_vert would be helpful in the development of more effective training methods both for able-bodied subjects (Hobara et al., 2011) and amputee athletes (Hobara et al., 2012), future studies should focus on investigating how to improve running performance in ILEAs.

A possible explanation for greater K_vert in the intact leg may be compensatory strategies involving the hip joint. In the present study, hip stiffness was not included in the stiffness calculations due to the lack of linearity between the moment-angle relationship of the hip joint in both legs. However, it is worthwhile to note that peak hip extension moment in INT demonstrated an obvious impact spike in early stance phase (arrowheads in Figure 4), while PST did not show such a distinct impact peak. This indicates the impact peak was not purely due to data processing artifacts (e.g. Bisseling & Hof, 2006; Edwards et al., 2011), else we would expect a distinct and consistent impact peak in both hips. These results suggest that the hip joints in ILEA with RSPs have a shock-absorbing function rather than a spring-like function. In fact, some previous studies demonstrated this unique compensatory strategy involving the hip joint during walking in transtibial amputees (Grumillier et al., 2008; Ventura et al., 2011). Further, Galli et al. (2008) demonstrated that a similar distinct impact of hip extension moment at early stance phase during walking was observed in subjects with Down syndrome, but not in a control group. The authors concluded that the extension moment pattern in the hip joint related to postural stability during dynamic movements. Therefore, less shock-absorption in INT might explain the differences in K_vert between the legs in ILEA running with RSPs. Furthermore, these compensatory movements may induce greater inefficiency and a higher injury risk during running as long term consequences.

There are some limitations in this study. First, although we observed that K_leg, K_vert and K_joint remained constant in both legs of ILEA for all three speeds (2.5, 3.0 and 3.5 m/s), these results might be due to the fact that the range of speeds was very limited in the present study. Therefore, future studies should focus on investigating the effect of greater running speeds on spring-like leg behavior of ILEA running. Second, although we used the most acute curve point on the RSP (Buckley, 2000) to define the “ankle” joint center, other studies placed a marker as an “ankle” joint center on the prosthetic foot at the same height as the lateral malleolus of the intact limb during normal standing (Brüggemann et al., 2009; Buckley, 1999). Thus, caution needs to be taken regarding the interpretation and generalization of these findings. Finally, due to the limited number of transtibial amputees who can perform overground running at the prescribed speeds, only eight ILEAs with a great variation in the running experience of the participants (3–256 months) were available for the present study. Running with prostheses can take some time to adjust to, and this may affect the current results by introducing greater variability in the ILEA group regarding their running mechanics. To verify the compensatory strategies observed in this study and establish practical gait rehabilitation and optimization of prosthesis designs, there should be more subjects in future research.

In summary, the results of the present study suggest that K_leg, K_vert and K_joint in both limbs remain constant when running speed increases. Intact limbs in ILEA running with RSPs have a higher K_leg and K_vert than residual limbs. Differences in the K_vert during running in ILEA might be due to attenuating shock with the hip joint, and not to differences in joint stiffness or touchdown joint angles.