Comparing statistical methods for removing seasonal variation from vitamin D measurements in case-control studies

Abstract

Vitamin D deficiency has been shown to be associated with multiple clinical outcomes, including osteoporosis, multiple sclerosis and colorectal cancer. In studies of vitamin D effect on disease outcome, vitamin D status is usually measured by a serum biomarker, namely 25-hydroxy vitamin D [25(OH)D]. Since the circulating 25(OH)D concentration varies from season to season and not all blood samples are collected at the same time, the disease-vitamin D relationship can be obscured if the seasonal variation is not adjusted properly. In the literature, a two-step procedure is usually adopted, with the vitamin D level adjusted for the seasonal variation being obtained in the first step, and the effect of vitamin D being assessed based on the adjusted vitamin D level at the second step. This two-step method can generate misleading results as the estimation variance arising from the first step is not taken into account in the second step analysis. We consider three alternative procedures that unify the two steps into a single model. We conduct an extensive simulation study to evaluate the performance of these methods and demonstrate their applications in a study of 25(OH)D effect on prostate cancer risk.

1. Introduction

Low levels of vitamin D have been associated with multiple clinical outcomes, including osteoporosis, multiple sclerosis, and assorted malignancies, such as colorectal cancer [12]. Among various vitamin D metabolites, 25-hydroxy vitamin D (25(OH)D) [10] is a major circulating form and is commonly considered to be the best indicator of vitamin D status, reflecting vitamin D intake and sunlight exposure, two major sources of vitamin D. A major challenge in studying the relationship between 25(OH)D levels and disease is how to quantify vitamin D levels appropriately in the human body because the circulating 25(OH)D level varies over the year; it tends to be higher in summer than in winter, due to the difference in sun exposure and sun intensity. Because the vitamin D level for each subject is usually measured only at one specific time point, it is important to adjust for the seasonal fluctuation in the measurement of the vitamin D level; otherwise, it would be difficult to assess the impact of vitamin D status on the disease risk. In fact, we will show that the seasonal variation can diminish the power to detect a vitamin D effect if it is ignored, even when the cases and the controls are well matched in their blood collection time.

In practice, a two-step method is commonly adopted for the adjustment of seasonal variation in a case-control study of disease-vitamin D association. In the first step, the seasonal pattern (i.e., the expected vitamin D level for the study population at observed time points) is estimated based on control samples. Then the disease-vitamin D relationship is assessed based on the residual vitamin D level, which is the difference between the original measure and the expected one at the blood collection time. Because of the periodic nature of the seasonal variation pattern, the ordinary linear model that treats the time of blood collection as a linear predictor is not suitable for modeling it. Instead, locally weighted polynomial regression, a semiparametric regression, has been used in the first step for the estimation of a seasonal pattern [3]. However, the variance of the seasonal pattern estimated in the first stage is not taken into account in the second stage and could result in inflated type I error in detecting the disease-vitamin D association.

In this paper, we propose a one-stage approach to model the relationship between the disease and vitamin D level with seasonal pattern being taken into account. To model the seasonal pattern function, we consider a parametric method and two semi-parametric methods. After making an appropriate transformation of the time of blood collection, it is possible to use ordinary linear regression to model the seasonal pattern as a linear function of the transformed blood collection time. Motivated by this observation, we consider a sine curve method in the context of a linear regression model for the adjustment of the seasonal variation in the study of vitamin D effect. The sine curve method models the seasonal pattern as a sine function of the blood collection time with only three parameters: angular frequency, amplitude, and phase. As suggested by [11], the sine curve can fit the seasonal variation pattern in 25(OH)D quite well. We also consider two semiparametric methods to model the variation pattern, namely the locally weighted polynomial regression and the penalized regression splines. We evaluate the relative performance of these methods under various scenarios and provide some guidance for future applications.

2. Method

2.1 Notation

Consider a case-control study with n₁ case patients and n₀ control subjects; the total number of sampled individuals is n = n₁ + n₀. Without loss of generality, we assume individuals 1, …, n₁ are cases and individuals n₁ + 1, …, n are controls. Suppose the ith individual's blood is collected at time t_i, with the measured vitamin D level being $x_i^{\ast }$. Here $x_i^{\ast }$ can be thought as a surrogate measure for the underlying vitamin D exposure level x_i, which is season independent but not observable. We assume the following model

$$x_i^{\ast }=x_i+\tau (t_i)+\gamma \prime u_i+e_i,i=1,\dots ,n,$$ (1)

where τ(·) is the unknown seasonal pattern function, u_i is a covariate vector accounting for other factors influencing vitamin D level (race, geographic latitude, and so on) and γ is the corresponding regression coefficient vector, and e_i is a random error term. Throughout this paper, we assume that {x₁, …, x_n1} are independent and identically distributed (i.i.d.) with mean μ₁ and variance σ², that {x_n1 + 1, …, x_n} are i.i.d. with mean μ₀ and variance σ², that e₁, …, e_n are i.i.d. random variables with expectation 0 and finite variance, and that the vectors (x_i, t_i, u_i, e_i), i = 1, …, n, are independent. Notice that we neither assume the distributions of (t_i, u_i) are the same for cases and controls nor assume any parametric form of the distribution of (x_i, t_i, u_i, e_i), which makes the methods considered later (SINE, LOESS, and PRS) applicable to a broad range of situations in practice.

In this paper, we are interested in detecting the difference in underlying vitamin D levels μ = μ₁ − μ₀ between cases and controls; the corresponding null hypothesis is H₀ : μ = 0. In this section, we do not consider disease-related risk factors other than vitamin D. Notice that the disease-related risk factors could be different from vitamin D-related factors. Instead, we will consider a more complicated model involving other disease risk factors in the Discussion section.

2.2 Naïve method

A naïve method ignores the seasonal pattern. The mean difference is simply estimated by ${\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast }$, and the standard error of ${\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast }$ is estimated by $s_{10}\sqrt{1/n_1+1/n_0}$, where $s_{10}=\{(n_1-1)s_1^2+(n_0-1)s_0^2\}/(n_1+n_0-2)$ is the estimated common variance, ${\overline{\mathit{\text{x}}}}_1^{\ast }$ and ${\mathit{\text{s}}}_1^2$ are the sample mean and sample variance of x₁, …, x_n1, respectively, and ${\overline{\mathit{\text{x}}}}_0^{\ast }$ and ${\mathit{\text{s}}}_0^2$ are the sample mean and sample variance of x_n1+1, …, x_n, respectively. The two-sample t-test statistic for detecting the mean difference is $({\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast })/(s_{10}\sqrt{1/n_1+1/n_0})$. We refer to this method as NAÏVE hereafter. In the following we derive the bias of the estimator ${\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast }$ and the power function for NAÏVE.

First, we assume that (t_i, u_i, e_i), i = 1, …, n, are i.i.d., and that x₁, …, x_n1 are i.i.d., and x_n1+1, …, x_n are i.i.d. These assumptions together with model (1) imply that the expectation of ${\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast }$ is the same as that of x̄₁ − x̄₀, the sample mean difference of underlying vitamin D levels. That is, NAÏVE does not produce bias in this situation. Let ${\sigma }_e^2$ denote the variance of τ(t_i) + γ′u_i + e_i. With the assumption of independence between x_i and (t_i, u_i, e_i), the variance of ${\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast }$ is equal to $({\sigma }^2+{\sigma }_e^2)(1/n_1+1/n_0)$, which is larger than σ²(1/n₁ + 1/n₀), the variance of x̄₁ − x̄₀. Therefore, the onesided tests (for the alternative hypothesis H₁ : μ < 0) based on underlying and measured vitamin D levels have asymptotic power functions $\Phi \left(z_{\alpha }+\mu /\sqrt{{\sigma }^2\left(1/n_1+1/n_0\right)}\right)$ and $\Phi \left(z_{\alpha }+\mu /\sqrt{({\sigma }^2+{\sigma }_e^2)(1/n_1+1/n_0)}\right)$, respectively, where z_α is the upper α-quantile of the standard normal distribution, and the power reduction depends on ${\sigma }_e^2/{\sigma }^2$, α, μ/σ, n₁ and n₀. In particular, the power loss is increasing in ${\sigma }_e^2/{\sigma }^2$.

When (t_i, u_i, e_i), i = 1, …, n, are not i.i.d., the expectation of ${\overline{x}}_1^{\ast }-{\overline{x}}_0^{\ast }$ could be different from that of x̄₁ − x̄₀, and the corresponding test could result in substantially inflated type I error, as will be shown in our simulation study.

2.3 Proposed model

Under the assumptions given in Subsection 2.2, the random variables {ε₁ = x₁ − μ₁ + e₁, …, ε_n1 = x_n1 − μ₁ + e_n1, ε_n1+1 = x_n1+1 − μ₀ + e_n1+1, …, ε_n = x_n − μ₀ + e_n} are i.i.d. with expectation 0, we can rewrite $x_i^{\ast }$ in the following form:

$$x_i^{\ast }={\mu }_0+\mu d_i+\gamma \prime u_i+\tau (t_i)+{\varepsilon }_i,i=1,\dots ,n.$$ (2)

The right hand side of the above model includes three terms: linear term μ₀ + μd_i + γ′u_i, nonparametric term τ(t_i), and error term ε_i. In the subsequent two subsections, we consider three methods with various modeling of the seasonal pattern function τ(t_i).

2.4 Sine curve method

Let I denote the period of the vitamin D variation pattern, for example, I = 365 in days, 52 in weeks, and 12 in months, respectively. We assume a sine curve τ(t) = β sin(ρt + θ), where ρ = 2π/I, β, and θ are the angular frequency, amplitude, and phase of the sine curve. It is clear that τ(t) is linear in sin(ρt) and cos(ρt):

$$\tau (t)={\beta }_1\text{sin}(\rho t)+{\beta }_2\text{cos}(\rho t),$$ (3)

where β₁ = β cos(θ) and β₂ = β sin(θ). This model has been applied by [2] to determine the effects of the seasonal variation of 25(OH)D on a previously selected minimum concentration for vitamin D sufficiency (50 nmol/L) and to evaluate whether fat mass modifies these effects.

From (2) and (3), we have the following linear model:

$$x_i^{\ast }={\mu }_0+\mu d_i+\gamma \prime u_i+{\beta }_1\text{sin}(\rho t_i)+{\beta }_2\text{cos}(\rho t_i)+{\varepsilon }_i,i=1,\dots ,n.$$ (4)

We can estimate the unknown parameters (μ₀, μ, γ, β₁, β₂) using the ordinary least squares principle. The null hypothesis H₀ : μ = 0 can be tested using the conventional Wald test. Hereafter, we refer to this method as SINE.

2.5 Semiparametric methods

Instead of modeling the seasonal pattern function τ(·) in a parametric form, one can also fit τ(·) by more flexible methods such as the locally weighted polynomial regression (LOESS) and penalized regression splines (PRS). The generalized additive model [9] given in (2) can then be fit by the backfitting algorithm described in [4].

LOESS was originally proposed by Cleveland [5] and further developed by Cleveland and Devlin [6]. The basic idea of LOESS is to fit a low-degree polynomial at each point using a subset of the data, using a weighted least squares method. The biggest advantage of LOESS is that it does not require the specification of a functional form of the regression model. With PRS, the problem is turned into a penalized generalized linear model fitting problem. Instead of fitting a low-degree polynomial at each time point, as in LOESS, one constructs a penalized regression spline [14] between any two adjacent knots, with the knots being placed evenly throughout the covariate values. For details of application of these two semiparametric methods to fitting generalized additive model, refer to [7] and [8], respectively.

The function “gam” in the R package “gam” [13] implements both LOESS and PRS, and it can be used to obtain the unknown parameter estimates and their standard errors. Again, the null hypothesis can be tested using the Wald test. Because our interest is μ and the seasonal pattern function is nuisance, we expect that the estimation/test is robust to the choice of the parameter setting for LOESS and PRS. Actually, our preliminary simulation results show that the argument options for “gam” do not produce substantial differences in the estimation/test results for μ, so we will adopt default arguments when applying “gam”. The major default settings are: all tuning parameters including the degree of freedom of polynomial in LOESS are determined by generalized cross validation, and the base for PRS is cubic smooth spline.

3. Simulation Study

To compare the performance of the aforementioned estimation/test methods, we conducted a simulation study. In the simulations, the uderlying vitamin D level x was assumed to follow the standard normal in the general population, and the measured vitamin D level was assumed to be

$$x\ast =x+u+\tau (t)+e,$$ (5)

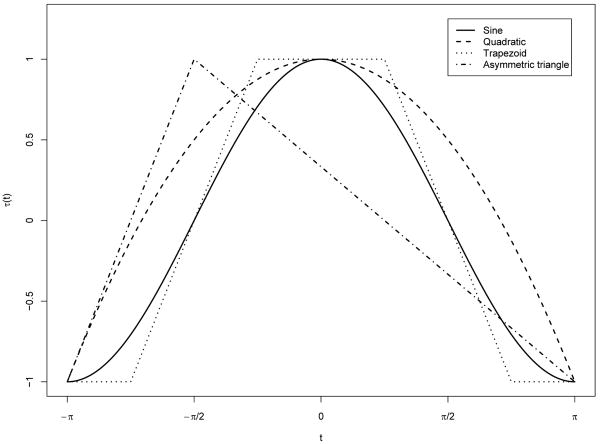
where u was a Bernoulli random variate with sucessful probability 0.5 and the random error e was standard normally distributed. For simplification of the notation, the blood collection times (radians) for both cases and controls were assumed to be distributed uniformaly in the time interval [−π, π), though the interval can be of any form, such as [0, 52) for weekly measurements. For the seasonal pattern function τ(·), we considered three symmetric functions as displayed in Figure 1. The first is a sine function, the second is a quadratic function, and the third is a trapezoid-shaped function. To relate the underlying vitamin D level with the disease status, we assumed a logistic regression model:

Figure 1. Seasonal pattern functions used in simulations.

$$\text{logit}\{P(d=1|x)\}=-4+\beta x,$$ (6)

where logit(t) = log{t/(1 − t)} and d is the disease status, taking a value of 1 if affected and 0 otherwise.

We considered the null hypothesis with β = 0 and alternative hypotheses under which the two-sample t-test based on the underlying vitamin D levels x has its powers around 0.8. For each combination of parameter β and seasonal pattern function τ(·), we generated a population of size 10 million, from which we independently drew 100,000 samples, with each sample consisting of n₁ cases and n₀ controls. We considered n₁ = n₀ = 50, 100, 200, or 500. To estimate/test μ in model (2), we applied NAÏVE, LOESS, PRS, and SINE to these 100,000 samples and calculated the bias of the resulting estimates (Bias), the standard error of the estimates (SE), the mean estimated standard errors (SEE), the 95% coverage probability (CP), and the type I error rate (Size) or power (Power) at a 0.05 nominal level. For comparison purposes, we also applied the conventional two-sample t-test and corresponding estimation method to the underlying vitamin D levels. We will refer to this method as TRUE hereafter, which has power close to 0.8 under the alternative hypothesis. The simulation results for sample sizes n₁ = n₀ = 50, 100, 200, and 500 are reported in Tables 1-4, respectively.

Table 1. Simulation results for sample size 50.

Seasonal pattern	Method	Null hypothesis					Alternative hypothesis
		Size1	Bias2	SE3	SEE4	CP5	Power6	Bias2	SE3	SEE4	CP5
Sine	TRUE	0.050	0.000	0.200	0.199	0.947	0.792	0.000	0.198	0.199	0.947
	NAÏVE	0.050	0.001	0.316	0.315	0.947	0.414	−0.001	0.313	0.315	0.948
	LOESS	0.053	0.000	0.289	0.285	0.944	0.490	0.001	0.286	0.284	0.945
	PRS	0.053	0.000	0.289	0.284	0.944	0.492	0.001	0.287	0.284	0.944
	SINE	0.050	0.000	0.287	0.286	0.947	0.486	0.001	0.284	0.286	0.949
Quadratic	TRUE	0.051	0.001	0.201	0.199	0.946	0.786	0.001	0.199	0.199	0.948
	NAÏVE	0.050	0.003	0.420	0.419	0.947	0.260	0.000	0.421	0.418	0.946
	LOESS	0.051	−0.001	0.288	0.284	0.946	0.492	0.000	0.29	0.283	0.942
	PRS	0.052	0.000	0.288	0.283	0.945	0.493	0.000	0.291	0.283	0.941
	SINE	0.050	0.002	0.347	0.347	0.948	0.354	0.002	0.351	0.346	0.945
Trapezoid	TRUE	0.050	−0.001	0.199	0.199	0.948	0.787	−0.002	0.199	0.198	0.946
	NAÏVE	0.048	−0.002	0.325	0.326	0.949	0.393	−0.001	0.324	0.325	0.949
	LOESS	0.053	0.000	0.290	0.286	0.944	0.486	−0.002	0.289	0.285	0.943
	PRS	0.054	0.000	0.290	0.285	0.943	0.488	−0.002	0.29	0.284	0.942
	SINE	0.050	0.000	0.288	0.287	0.947	0.483	−0.002	0.287	0.287	0.946

¹The type I error rate under the null hypothesis;

²The mean of the estimated difference minus the true difference;

³The standard deviation of the estimate;

⁴The mean estimated standard deviation of the estimate;

⁵The empirical coverage probability;

⁶The power under the alternative hypothesis.

Table 4. Simulation results for sample size 500.

Seasonal pattern	Method	Null hypothesis					Alternative hypothesis
		Size1	Bias2	SE3	SEE4	CP5	Power6	Bias2	SE3	SEE4	CP5
Sine	TRUE	0.049	−0.001	0.063	0.063	0.95	0.806	0.000	0.063	0.063	0.950
	NAÏVE	0.050	−0.001	0.100	0.100	0.950	0.436	−0.001	0.099	0.100	0.951
	LOESS	0.049	−0.001	0.089	0.090	0.951	0.514	−0.001	0.089	0.09	0.951
	PRS	0.049	−0.001	0.089	0.090	0.951	0.516	−0.001	0.089	0.09	0.951
	SINE	0.049	−0.001	0.089	0.090	0.951	0.516	−0.001	0.089	0.09	0.950
Quadratic	TRUE	0.049	0.000	0.063	0.063	0.951	0.808	0.000	0.063	0.063	0.952
	NAÏVE	0.050	0.000	0.133	0.133	0.950	0.270	0.000	0.133	0.133	0.952
	LOESS	0.051	0.000	0.090	0.089	0.949	0.516	0.000	0.089	0.089	0.952
	PRS	0.051	0.000	0.090	0.089	0.949	0.516	0.000	0.089	0.089	0.952
	SINE	0.051	0.000	0.109	0.108	0.949	0.377	0.000	0.108	0.108	0.951
Trapezoid	TRUE	0.049	−0.001	0.063	0.063	0.951	0.795	0.000	0.063	0.063	0.950
	NAÏVE	0.049	0.000	0.103	0.103	0.950	0.403	−0.001	0.103	0.103	0.950
	LOESS	0.050	−0.001	0.090	0.090	0.950	0.501	0.000	0.091	0.09	0.949
	PRS	0.050	−0.001	0.090	0.090	0.950	0.503	0.000	0.090	0.09	0.949
	SINE	0.050	0.000	0.090	0.090	0.950	0.505	0.000	0.090	0.09	0.949

¹The type I error rate under the null hypothesis;

²The mean of the estimated difference minus the true difference;

³The standard deviation of the estimate;

⁴The mean estimated standard deviation of the estimate;

⁵The empirical coverage probability;

⁶The power under the alternative hypothesis.

The third column of Tables 1-4 contains the results under the null hypothesis (H₀ : μ = 0). All the methods have very minor biases in the mean difference estimates, which vary from −0.003 to 0.002. Overall, SINE has virtually unbiased estimates of standard errors (SEE is very close to SE) and good control of coverage probabilities and type I error rates. When the sample size is small, LOESS and PRS have slightly conservative standard deviation estimates, and this results in slightly anti-conservative coverage probabilities and inflated type I error rates. For example, with sample sizes n₁ = n₀ = 50 and a trapezoidal seasonal pattern function, the type I error rate of LOESS and PRS are 0.053 and 0.054. As the sample size increases, the anti-conservativeness of LOESS and PRS become minor. For example, when the sample size is 500, the type I error rates of LOESS and PRS are controlled between 0.049 and 0.051.

The forth column of Tables 1-4 contains the results under the alternative hypothesis. Among all tests, NAÏVE is uniformly least powerful. When the seasonal pattern function is sine or trapezoid, LOESS, PRS, and SINE have comparable powers. When the seasonal pattern function is quadratic which is quite different from the sine function, SINE is less powerful than LOESS and PRS.

An important finding is that SINE is very robust to the misspecification of the seasonal pattern function. That is, when the underlying seasonal pattern function is quadratic or trapezoid but it is misspecified as sine, SINE maintains good control of coverage probabilities and type I error rates.

The above simulations assumed symmetric seasonal pattern functions. We also generated an asymmetric seasonal pattern function, which is a triangle function taking the minimal value −1 at −π and π and the maximal value 1 at −π/2. The function is displayed in Figure 1. The other settings are the same as those for Tables 1-4. The simulation results are reported in Table 5. Compared with LOESS and PRS, SINE has better control of type I error rates and coverage probabilities but is less powerful, when the sample size is small.

Table 5. Simulation results for the asymmetric triangle seasonal pattern.

Sample size	Method	Null hypothesis					Alternative hypothesis
		Size1	Bias2	SE3	SEE4	CP5	Power6	Bias2	SE3	SEE4	CP5
50	TRUE	0.050	0.001	0.200	0.200	0.947	0.792	−0.001	0.199	0.199	0.947
	NAÏVE	0.050	−0.001	0.306	0.305	0.947	0.430	0.001	0.304	0.304	0.945
	LOESS	0.052	0.000	0.289	0.285	0.945	0.482	0.002	0.289	0.285	0.943
	PRS	0.053	0.000	0.289	0.284	0.944	0.485	0.002	0.289	0.284	0.941
	SINE	0.050	−0.001	0.290	0.290	0.947	0.471	0.002	0.289	0.289	0.945
100	TRUE	0.051	−0.001	0.141	0.141	0.947	0.790	0.000	0.141	0.141	0.948
	NAÏVE	0.051	−0.002	0.217	0.216	0.948	0.438	0.000	0.218	0.216	0.945
	LOESS	0.054	−0.002	0.204	0.201	0.945	0.491	0.000	0.204	0.201	0.945
	PRS	0.054	−0.001	0.203	0.201	0.944	0.491	0.000	0.204	0.201	0.945
	SINE	0.052	−0.002	0.205	0.203	0.946	0.481	0.000	0.205	0.203	0.947
200	TRUE	0.049	0.000	0.100	0.100	0.950	0.806	0.000	0.100	0.100	0.949
	NAÏVE	0.050	0.001	0.153	0.153	0.949	0.458	−0.001	0.152	0.153	0.949
	LOESS	0.050	0.001	0.142	0.142	0.950	0.511	−0.001	0.142	0.142	0.95
	PRS	0.050	0.001	0.142	0.142	0.949	0.512	−0.001	0.142	0.142	0.949
	SINE	0.049	0.001	0.143	0.143	0.951	0.502	−0.001	0.143	0.143	0.949
500	TRUE	0.050	0.000	0.063	0.063	0.950	0.817	0.000	0.063	0.063	0.949
	NAÏVE	0.051	−0.001	0.097	0.097	0.948	0.461	0.001	0.096	0.097	0.950
	LOESS	0.052	0.000	0.090	0.090	0.948	0.518	0.001	0.089	0.090	0.951
	PRS	0.052	0.000	0.090	0.090	0.947	0.520	0.001	0.089	0.090	0.951
	SINE	0.051	0.000	0.091	0.090	0.949	0.512	0.001	0.090	0.090	0.951

¹The type I error rate under the null hypothesis;

²The mean of the estimated difference minus the true difference;

³The standard deviation of the estimate;

⁴The mean estimated standard deviation of the estimate;

⁵The empirical coverage probability;

⁶The power under the alternative hypothesis.

The blood collection times of cases and controls should be matched in a well designed case-control study of vitamin D-disease association. In practice, the matching might not be perfect. We conducted additional simulations to study the impact of unbalanced sampling. We generated the blood collection time of controls from the uniform distribution over the interval (−3π/4, 3π/4) and cases from the uniform distribution over the interval (−π, −3π/4) ∪ (−π/4, π). The seasonal pattern function is quadratic as displayed in Figure 1, and other settings are the same as those for Table 5. The simulation results are presented in Table 6. NAÏVE has very inflated type I error rates and non-ignorable biases in estimates, this is because the conditions for the validity of NAÏVE were not met. With unbalanced sampling, even when the sample size is large, LOESS and PRS can have minor inflated type I error rate and anticonservative coverage probabilities, while SINE has slightly deflated type I error rates and anticonservative coverage probabilities.

Table 6. Simulation results with mismatched blood collection time for cases and controls.

Sample size	Method	Null hypothesis					Alternative hypothesis
		Size1	Bias2	SE3	SEE4	CP5	Power6	Bias2	SE3	SEE4	CP5
50	TRUE	0.049	0.000	0.200	0.200	0.948	0.785	0.001	0.201	0.199	0.944
	NAÏVE	0.289	−0.555	0.393	0.391	0.701	0.802	−0.554	0.390	0.391	0.707
	LOESS	0.064	−0.020	0.305	0.288	0.932	0.507	−0.020	0.305	0.288	0.933
	PRS	0.069	−0.010	0.310	0.288	0.927	0.496	−0.010	0.310	0.287	0.928
	SINE	0.041	0.011	0.333	0.347	0.957	0.334	0.011	0.331	0.347	0.957
100	TRUE	0.049	−0.001	0.141	0.141	0.950	0.796	−0.001	0.141	0.141	0.948
	NAÏVE	0.506	−0.557	0.277	0.277	0.480	0.925	−0.557	0.276	0.277	0.477
	LOESS	0.062	−0.021	0.215	0.203	0.936	0.531	−0.022	0.213	0.203	0.935
	PRS	0.066	−0.011	0.219	0.203	0.932	0.512	−0.011	0.217	0.203	0.931
	SINE	0.041	0.009	0.233	0.244	0.958	0.340	0.009	0.232	0.244	0.960
200	TRUE	0.052	0.000	0.100	0.100	0.948	0.801	−0.001	0.100	0.100	0.951
	NAÏVE	0.804	−0.556	0.197	0.196	0.193	0.988	−0.553	0.197	0.196	0.197
	LOESS	0.066	−0.022	0.151	0.144	0.933	0.548	−0.020	0.152	0.144	0.933
	PRS	0.069	−0.011	0.154	0.143	0.930	0.521	−0.009	0.154	0.143	0.930
	SINE	0.042	0.010	0.165	0.172	0.957	0.338	0.012	0.165	0.172	0.960
500	TRUE	0.052	0.000	0.064	0.063	0.947	0.797	0.000	0.063	0.063	0.951
	NAÏVE	0.994	−0.556	0.124	0.124	0.006	1.000	−0.555	0.124	0.124	0.006
	LOESS	0.067	−0.020	0.095	0.091	0.933	0.583	−0.021	0.095	0.091	0.933
	PRS	0.067	−0.010	0.097	0.091	0.932	0.537	−0.011	0.096	0.091	0.932
	SINE	0.042	0.011	0.104	0.108	0.958	0.322	0.012	0.103	0.108	0.959

¹The type I error rate under the null hypothesis;

²The mean of the estimated difference minus the true difference;

³The standard deviation of the estimate;

⁴The mean estimated standard deviation of the estimate;

⁵The empirical coverage probability;

⁶The power under the alternative hypothesis.

4. Application to a Study of Prostate Cancer

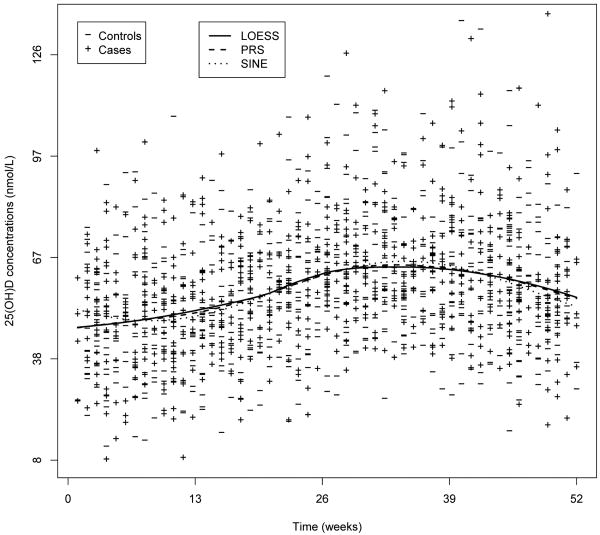
Ahn et al. [1] investigated the association between vitamin D status, as determined by 25(OH)D concentrations (nmol/L), and the risk of prostate cancer in a nested case-control study within the Prostate, Lung, Colorectal, and Ovarian Cancer Screening Trial (PLCO). This study included 749 case patients and 781 control subjects who were frequency-matchcd by cohort entry, time since initial screening, and calendar year of cohort entry. The scatter plot of the 25(OH)D concentrations is displayed in Figure 2. The mean vitamin D levels of cases and controls are 58.98 (SE: 19.12) and 57.68 (SE: 18.89), respectively. We applied NAÏVE, LOESS, PRS, and SINE to this data set, with further adjustment for study center. Presented in Table 7 are the resulting estimated vitamin D level differences (i.e., μ defined in (2)) between cases and controls and their estimated standard errors, and the p-values for one-sided tests. NAÏVE does not detect statistically significant difference between cases and controls at 0.05 level. The other three methods give similar significant results (p-values ranging from 0.041 to 0.043), indicating that the increased 25(OH)D concentration might be associated with reduced prostate cancer risk. The estimates of μ are also similar, with their absolute magnitudes (ranging from 1.58 to 1.60) being larger than that by NAÏVE (1.30). Figure 2 shows the predicted 25(OH)D concentrations for controls, from which we see that predicted seasonal patterns by three methods are very close to each other.

Figure 2. Scatter plot of 25(OH)D concentrations for cases and controls and predicted seasonal pattern functions for controls.

Table 7. Analysis results for an association study of 25(OH)D concentrations and prostate cancer.

Method	Est1	SE2	P-value3
NAÏVE	−1.30	0.972	0.091
LOESS	−1.58	0.920	0.043
PRS	−1.60	0.919	0.041
SINE	−1.60	0.921	0.041

¹The estimate of the mean difference of 25(OH)D concentrations (defined in (2)) between cases and controls;

²The estimated standard error of the vitamin D difference;

³The p-value of the one-sided test for the vitamin D difference.

This example illustrates the importance of the adjustment of seasonal variation. Without the proper account for the seasonal variation, the NAÏVE method fails to detect any difference in 25(OH)D level between cases and controls. Given the relatively large sample size, the well matched blood collection time, and the sine shaped seasonal variation pattern in 25(OH)D concentration, it is not surprising that the three considered tests with the adjustment of seasonal variation give similar results. This is consistent with what we have observed in the simulation study.

5. Discussion

The seasonal pattern for vitamin D has a substantial impact on power for testing its effect on the disease of interest. Using contaminated data without removing seasonal pattern can lead to substantial efficiency loss, and can result in serious false positive finding when the blood collection time for cases and controls are mismatched. We study three alternative approaches to model the vitamin D difference between cases and controls by taking into account the seasonal pattern. The seasonal pattern can be estimated using either a parametric sine form or a semiparametric form (LOESS and PRS). SINE has computational advantage over the semiparametric counterparts and it has better small sample behavior when the seasonal pattern resembles the sine curve. On the other hand, the semiparametric methods LOESS and PRS are comparable with SINE when the sample size is moderate or large even when seasonal pattern is sine, and they are more powerful when the seasonal patter departs from sine considerably. The matching of blood collection time for cases and controls are important. When the mismatching is serious, the parametric and semiparametric methods can be either anconservative or conservative. Based on the simulation results, we suggest SINE when the seasonal pattern function does not depart from a sine function too much; otherwise we recommend LOESS and PRS.

We model the vitamin D measure as the outcome and the disease status as a predictor in methods considered in this paper. Another commonly used two-step method is based on the following logistic regression model, in which the disease status is the response variable and the season adjusted vitamin D level x and some relevant covariate vector z are explanatory variables:

$$\{\begin{array}{l}\text{logit}\{P(d=1|x,z)\}=\alpha +H(x,z;\eta ),\hfill \\ x^{\ast }=\tau (t)+\gamma \prime u+x.\hfill \end{array}$$ (7)

Here α is an intercept and H is a function of x and z known up to a parameter vector η of finite dimension. For example, H(x, z; η) takes the form η₁x + η₂z + η₃xz with η = (η₁, η₂, η₃) when both main effects and interaction are considered. The first step is to remove the seasonal pattern using methods such as LOESS, PRS, or SINE and get an estimate of x, the season adjusted vitamin D level. The second step is to estimate/test η using the standard logistic regression model, with x being replaced by its estimate from the first step and treated as if it were observed. However, the variance estimated by this two-step method is not appropriate as it does not account for the uncertainty in the estimate of x. A bootstrap method can be used to estimate the variance appropriately, although it can be time-consuming. It would be of great interest to derive analytic asymptotic results for the inference of η under model (7).

Table 2. Simulation results for sample size 100.

Seasonal pattern	Method	Null hypothesis					Alternative hypothesis
		Size1	Bias2	SE3	SEE4	CP5	Power6	Bias2	SE3	SEE4	CP5
Sine	TRUE	0.050	0.000	0.142	0.141	0.949	0.796	−0.002	0.142	0.141	0.947
	NAÏVE	0.050	−0.001	0.224	0.223	0.949	0.423	−0.002	0.225	0.223	0.947
	LOESS	0.053	0.000	0.203	0.201	0.945	0.507	−0.002	0.203	0.201	0.947
	PRS	0.054	−0.001	0.203	0.201	0.945	0.510	−0.002	0.203	0.201	0.947
	SINE	0.051	−0.001	0.203	0.201	0.947	0.506	−0.002	0.202	0.201	0.948
Quadratic	TRUE	0.050	0.000	0.141	0.141	0.949	0.789	0.001	0.142	0.141	0.948
	NAÏVE	0.050	0.000	0.296	0.297	0.949	0.263	0.000	0.299	0.297	0.948
	LOESS	0.052	0.000	0.203	0.201	0.947	0.494	0.001	0.201	0.201	0.948
	PRS	0.052	0.000	0.203	0.200	0.946	0.494	0.001	0.201	0.200	0.948
	SINE	0.050	0.000	0.244	0.244	0.949	0.363	0.000	0.244	0.244	0.949
Trapezoid	TRUE	0.050	0.000	0.141	0.141	0.949	0.789	0.001	0.140	0.141	0.950
	NAÏVE	0.050	−0.002	0.231	0.231	0.948	0.394	0.000	0.229	0.230	0.950
	LOESS	0.051	−0.001	0.203	0.202	0.948	0.489	0.000	0.201	0.202	0.947
	PRS	0.051	−0.001	0.202	0.201	0.948	0.491	0.000	0.201	0.201	0.947
	SINE	0.049	−0.001	0.201	0.202	0.95	0.488	0.001	0.20	0.202	0.949

¹The type I error rate under the null hypothesis;

²The mean of the estimated difference minus the true difference;

³The standard deviation of the estimate;

⁴The mean estimated standard deviation of the estimate;

⁵The empirical coverage probability;

⁶The power under the alternative hypothesis.

Table 3. Simulation results for sample size 200.

Seasonal pattern	Method	Null hypothesis					Alternative hypothesis
		Size1	Bias2	SE3	SEE4	CP5	Power6	Bias2	SE3	SEE4	CP5
Sine	TRUE	0.049	0.000	0.100	0.100	0.950	0.799	0.000	0.100	0.100	0.950
	NAÏVE	0.050	0.000	0.158	0.158	0.950	0.424	−0.001	0.157	0.158	0.951
	LOESS	0.049	0.000	0.142	0.142	0.950	0.506	−0.001	0.142	0.142	0.947
	PRS	0.050	0.000	0.142	0.142	0.950	0.508	−0.001	0.142	0.142	0.947
	SINE	0.049	0.000	0.142	0.142	0.950	0.506	−0.001	0.142	0.142	0.949
Quadratic	TRUE	0.051	0.001	0.100	0.100	0.949	0.789	−0.001	0.100	0.100	0.950
	NAÏVE	0.050	0.002	0.210	0.21	0.949	0.26	0.000	0.212	0.21	0.946
	LOESS	0.049	0.002	0.142	0.142	0.950	0.495	0.000	0.141	0.141	0.948
	PRS	0.049	0.002	0.142	0.142	0.950	0.495	0.000	0.142	0.141	0.948
	SINE	0.049	0.002	0.171	0.172	0.950	0.358	−0.001	0.172	0.172	0.947
Trapezoid	TRUE	0.049	0.000	0.099	0.100	0.950	0.809	0.000	0.100	0.100	0.950
	NAÏVE	0.049	0.000	0.163	0.163	0.950	0.411	−0.001	0.163	0.163	0.950
	LOESS	0.050	0.000	0.142	0.143	0.949	0.511	0.000	0.142	0.143	0.949
	PRS	0.050	0.000	0.142	0.142	0.949	0.514	0.000	0.142	0.142	0.949
	SINE	0.049	0.000	0.142	0.142	0.950	0.514	0.000	0.142	0.142	0.950

¹The type I error rate under the null hypothesis;

²The mean of the estimated difference minus the true difference;

³The standard deviation of the estimate;

⁴The mean estimated standard deviation of the estimate;

⁵The empirical coverage probability;

⁶The power under the alternative hypothesis.