Abstract
In this paper, we analyze Markov Random Field (MRF) as a spatial regularizer in fMRI detection. The low signal-to-noise ratio (SNR) in fMRI images presents a serious challenge for detection algorithms, making regularization necessary to achieve good detection accuracy. Gaussian smoothing, traditionally employed to boost SNR, often produces over-smoothed activation maps. Recently, the use of MRF priors has been suggested as an alternative regularization approach. However, solving for an optimal configuration of the MRF is NP-hard in general. In this work, we investigate fast inference algorithms based on the Mean Field approximation in application to MRF priors for fMRI detection. Furthermore, we propose a novel way to incorporate anatomical information into the MRF-based detection framework and into the traditional smoothing methods. Intuitively speaking, the anatomical evidence increases the likelihood of activation in the gray matter and improves spatial coherency of the resulting activation maps within each tissue type. Validation using the receiver operating characteristic (ROC) analysis and the confusion matrix analysis on simulated data illustrates substantial improvement in detection accuracy using the anatomically guided MRF spatial regularizer. We further demonstrate the potential benefits of the proposed method in real fMRI signals of reduced length. The anatomically guided MRF regularizer enables significant reduction of the scan length while maintaining the quality of the resulting activation maps.
Keywords: fMRI Detection, Markov Random Field, Mean Field, Variational Approximation Method, Spatial Prior, Anatomical Information
1 Introduction
Functional magnetic resonance imaging (fMRI) provides a non-invasive dynamic method for studying brain activation by capturing changes in the blood oxygenation level. In this paper, we focus on intra-subject fMRI activation detection and aim to improve the accuracy of the activation localization in individual subjects. Most fMRI detection methods operate by comparing the time course of each voxel with the experimental protocol, labelling as “active” those voxels whose time courses correlate significantly with the protocol. The commonly used general linear model (GLM) [Friston et al., 1995, Worsley et al., 2002] further models the fMRI signal as an output of a linear system driven by the stimulus. Application of GLM to an fMRI time series results in the so-called statistical parametric map (SPM), which is often thresholded to produce a binary map of active areas or, more generally, areas that show different activation levels under different conditions during the experiment. However, because of low signal-to-noise ratio (SNR), the binary maps typically contain many small false positive islands.
One approach to reducing such false positives is to enforce spatial continuity of the data or the estimated activations as a pre-processing or post-processing step, respectively. Among the pre-processing approaches, smoothing with a Gaussian filter is the most popular method. It effectively increases the SNR of the signal. Unfortunately, Gaussian smoothing can produce overly smoothed SPMs, leading to a loss of details in the resulting binary activation maps. Alternatively, Descombes et al. [Descombes et al., 1998] employed the Markov Random Field (MRF) model to smooth the data, but their model required large amount of computation due to the application of MRF to the entire 4D fMRI volume. In contrast to smoothing in the spatial domain, Van De Ville et al. [Van De Ville et al., 2007] proposed a wavelet-based method to capture the underlying smooth activation pattern. As a post-processing step, Friston et al. [Friston et al., 1993] proposed an adaptive thresholding method that assesses the statistical significance of active regions according to their size based on the Gaussian Random Field theory.
An alternative is to integrate a model for spatial coherency of activation into estimation to avoid the above two-step procedure, in which the smoothing step in general may not adequately compensate for the estimation errors. MRFs and Laplacian models are widely used for encouraging spatial continuity. Penny et al. [Penny et al., 2005] employed a hierarchical model that imposed a Laplacian spatial prior on the regression coefficients of the GLM detector. Without the hyper prior, their approach effectively smooths the regression coefficients with a fixed spatial kernel that penalizes large magnitudes of the first order spatial derivatives of the regression coefficients. The hyper prior helps to obtain appropriate weights for the smoothing. Flandin and Penny [Flandin & Penny, 2007] extended this approach to the wavelets domain. Svensen et al. [Svensen et al., 2000] applied the MRF prior to the parameters of the hemodynamic response functions (HRF) in order to recover the missing activation regions in a fixed-HRF detector. Cosman et al. [Cosman et al., 2004], Rajapakse et al. [Rajapakse & Piyaratna, 2001], and Woolrich et al. [Woolrich et al., 2005] employed the MRF model to encourage adjacent locations to share similar activation states, for binary [Cosman et al., 2004, Rajapakse & Piyaratna, 2001] and trinary [Woolrich et al., 2005] activation models.
Motivated by the MRF model in [Cosman et al., 2004], we focus on MRFs for modeling spatial coherence of the activation maps and study their performance in conjunction with a refined version of the MRF model. Despite recent algorithmic development in capturing “continuous” activations, many fundamental neuroscience and surgical applications still employ binary activation maps to make inference about functional areas in the brain. In particular, neuroscientists and neurosurgeons are interested in identifying voxels that are consistently activated in a certain task [Amedi et al., 2001, Ashtari et al., 2005]. Since the fMRI voxels are relatively large, a one-to-two voxel shift often leads to activation localization in a different anatomical region. Therefore, there is still a real need to improve detector accuracy in delineating active/not active regions in an fMRI volume. Similar to previous work [Cosman et al., 2004, Rajapakse & Piyaratna, 2001, Woolrich et al., 2005], we assume that given the activation state of each voxel, the time courses of different voxels are conditionally independent. From the detection point of view, our model directly regularizes the detection results rather than a set of nonlinear HRF parameters implicitly connected to the activation maps of interest [Svensen et al., 2000]. More complex temporal models commonly used in fMRI detection, e.g., the autoregressive (AR) models [Burock & Dale, 1995], can be easily integrated into our framework by applying a pre-processing whitening step.
MRFs are known to be much more computationally intensive than linear filters, including the commonly used Gaussian filter. For an MRF with binary states, an exact solution can be obtained in polynomial time [Greig et al., 1989], but it is still too computationally demanding for fMRI detection applications due to a large number of voxels. An fMRI detection algorithm based on the GLM statistic and the binary activation states was demonstrated in [Cosman et al., 2004]. If one wants to go beyond binary states (e.g., treating positively and negatively activated voxels differently or including states corresponding to anatomical segmentation), estimation of the optimal activation configuration becomes intractable and approximation algorithms must be used. Prior work in solving the MRF model employed simulated annealing [Descombes et al., 1998, Rajapakse & Piyaratna, 2001], the iterated conditional mode algorithm [Besag, 1974, Salli et al., 2001], and the graph cuts algorithm [Boykov et al., 2001]. Recent work by Woolrich et al. [Woolrich et al., 2005] proposed to approximate the MRF using a mixture model. It effectively converts discrete inference into inference in Gaussian Random Fields in order to approximate the partition function. Although the method is computationally efficient, the results depend on the nonlinear logistic transform in the approximation, and the accuracy of the approximated partition function is not quantified. In this work, we adopt the Mean Field approach, developed in statistical physics [Parisi, 1998], and widely employed in MRF-based image processing applications [Kapur et al., 1998, Langan et al., 1992, Pohl et al., 2002]. We note that Svensen et al. [Svensen et al., 2000] also used Mean Field in application of MRFs to spatial regularization of the HRF shape.
We further refine the activation prior by incorporating anatomical information. Similar to the atlas-based segmentation that employs spatially varying priors on tissue types, the anatomy can provide prior information on the activation map. Intuitively speaking, we want the prior to reflect the fact that activation is more likely to occur in gray matter than in white matter, and is not at all likely in cerebrospinal fluid or bone. In addition, we expect the activation to be spatially coherent within each tissue type but not across tissue boundaries. We use a hidden state variable to encode both the tissue type and the activation state. Segmentation provides an additional, potentially noisy, observation at each node. We derive the detection algorithm for this model and evaluate it on simulated and real data, achieving high detection accuracy with significantly shorter time courses when compared to the standard GLM detector.
Anatomical scans have certainly been used in fMRI analysis and visualization before. Hartvig [Hartvig, 2002] used anatomical information in his marked point process spatial prior. Penny et al. [Penny et al., 2007] applied a tissue-type prior to explain the observed spatial variability in the temporal AR model. Mapping fMRI data to the cortical surface extracted from an anatomical scan, followed by activation detection on the surface, has been shown to achieve robust activation detection [Andrade et al., 2001, Kiebel et al., 2000]. Moreover, some systems, such as Brain Voyager and FSL, employ topologically correct representation of the neocortex for fMRI analysis and visualization [Dale et al., 1999, Goebel et al., 2006, Woolrich et al., 2001]. In contrast, our approach does not require a surface extraction algorithm but instead utilizes anatomical information to inject coherency bias into the detection algorithm while performing the computation directly on the volumetric data.
Similar to previous methods that rely on anatomical scans to provide guidance and visualization for fMRI detection, our technique depends on registration of fMRI data to the anatomical scan of the same subject. T2*-weighted echo-planar imaging (EPI) used in fMRI typically suffers from signal distortion or drop-out in certain areas due to magnetic field inhomogeneities. Recent work in parallel imaging acquisition promises to reduce such artifacts [Li et al., 2005]. Moreover, artifact correction and EPI unwarping based on field maps [Jezzard & Balaban, 1995] improve the quality of the fMRI alignment with anatomical MRI. In our real fMRI experiments, field map based unwarping was included.
Lack of ground truth activation in real fMRI data presents a serious challenge for validation of detection methods. Previously proposed methods for evaluating fMRI detectors [Genovese et al., 1997, Liou et al., 2006, Strother et al., 2002] focus on quantifying repeatability of the results on a large set of repeated trials. However, our model explicitly violates the voxel independence assumption required by these evaluation methods. Instead, we evaluate the detection results by comparing activation maps based on reduced-length time courses with pseudo ground truth activation maps created from full length time courses over multiple runs. This effectively evaluates how the reduction in observations degrades the ability of the method to detect activations.
This paper extends our preliminary results reported in [Ou & Golland, 2005]. Here we present an alternative formulation of the observation model in order to make the MRF model more transparent and refine the procedure for estimating the model parameters, leading to higher detection accuracy. In addition, we include an in-depth discussion on estimating the model parameters.
In the next section, we briefly review GLM, MRF, and the Mean Field algorithm. In Section 3, we demonstrate how to construct the likelihood term, closely related to the GLM framework, for the MRF model. Section 4 describes our MRF prior model for fMRI detection, and Section 5 extends the MRF model to include anatomical information. Section 6 reports experimental results on synthetic and real fMRI data sets, followed by conclusions and the discussion of future work in Section 7.
2 Background and Notation
In this section, we introduce notation and briefly review the necessary background on GLM detection, the MRF models, and the Mean Field approach to approximate inference on MRFs.
Throughout the paper, we use bold face to denote vectors in time, and “ → ” to denote vectors in space. We let random variable X⃗ = [X1, …, XN] represent an activation configuration of all N voxels in the volume, and let vector x⃗ = [x1, …, xN] be one possible configuration i.e., an activation map. In binary detection, the random variable Xi, which represents the activation state of voxel i, is also binary. We use random variable Yi to denote the time course of voxel i(i = 1, …, N). We let vector yi ∈ ℝT be the time course observed for voxel i in the fMRI scan, where T is the number of time samples in the scan. Given the fMRI scan y⃗ = [y1, …, yN], our goal is to produce an activation map x⃗* that represents the best estimate of the true activation map.
2.1 General Linear Model (GLM)
The GLM detector represents a time course as a linear combination of the protocol-dependent component B, and the protocol-independent component A, such as the cardiopulmonary contributions to the fMRI signal. For our purposes, it is convenient to represent activation detection as a binary hypothesis test for the presence of the protocol-dependent component B:
| (1) |
for i = 1, …, N, and . Appendix A shows that this formulation is equivalent to the more commonly used formulation of GLM that employs a contrast matrix to construct the test statistic. Matrix C = [A B] is referred to as the design matrix. The least squares estimates of the activation response βi and the protocol-independent factor αi
| (2) |
and the covariance of the estimates Σ̂βi are used to form the corresponding F-statistic for rejecting the null hypothesis, with (Nβ, T − rank(C)) degrees of freedom, where Nβ is the number of regression coefficients in βi. A detailed discussion on the GLM framework can be found in [Friston et al., 1995, Worsley et al., 2002].
Given an fMRI scan [y1, …, yN], the GLM detector produces an activation map x⃗* by thresholding the statistic value for each voxel at a user-specified level. Some variants of the GLM framework employ the Z-scores or the t-statistic instead. While the magnitude of the statistic could provide additional information about the nature of activation, the statistical framework above leads to a binary answer that is a map of all voxels whose activation scores passed the threshold for statistical significance. In this work, we adopt this commonly used convention of modeling activation maps as binary labels that contain voxels that are modulated significantly by the experimental protocol.
2.2 Markov Random Fields (MRFs)
MRFs are widely used in computer vision [Boykov et al., 2001, Freeman et al., 2000] as a prior for coherency of the underlying structure. For illustration purposes, we couple the review of MRFs with the concrete example of fMRI detection.
In this work, we impose the MRF prior on the hidden activation configuration X⃗:
| (3) |
where the singleton potential Φi(xi) provides bias over state values xi for voxel i, and the pairwise potential Ψij(xi, xj) models the compatibility of a pair of neighboring voxels. Z is the partition function. Here we consider two adjacent voxels as a clique of two, i.e., the first product in Eq. (3) is restricted to adjacent voxels 〈i, j〉. The Ising model is an MRF with binary state variables Xi's; the Potts model is an MRF with discrete state variables distributed over a finite set of values [Wu, 1982].
Given the time courses of all voxels y⃗ = [y1, …, yN], we seek the maximum a posteriori (MAP) estimate of the activation configuration:
| (4) |
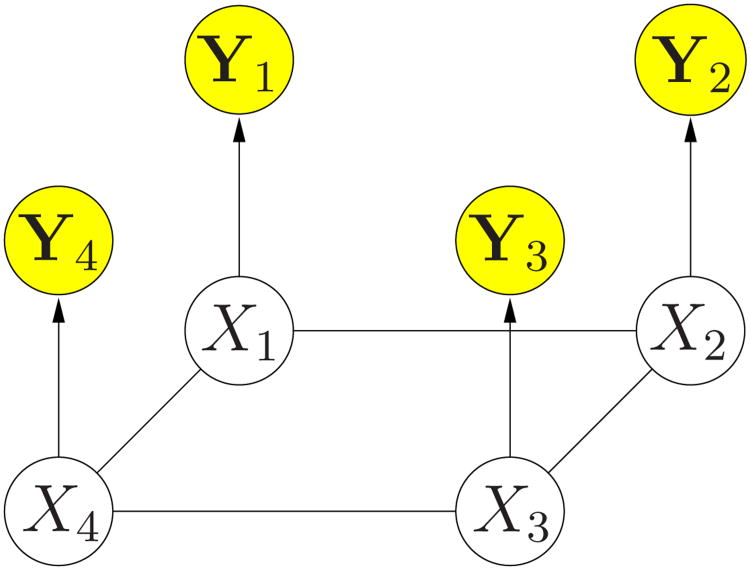
where PYi|Xi is the probability of the fMRI signal given the activation state of the voxel. The last equality is based on the assumption that the observations at different voxels are independent given the activation state of each voxel. Figure 1 shows the corresponding graphical model, using a 2-D grid for illustration purposes only. In all experiments reported in this paper, we perform the estimation fully in 3D, with six immediately adjacent voxels as neighbors. The observation model PYi|Xi and the potentials Φi and Ψij fully define the MRF model. The specifics of the model depend on the application of interest. This model explicitly introduces dependencies around the time courses of different voxels Yi's through the hidden activation state X⃗. We describe the details of MRF construction for fMRI detection in Section 3 and 4.
Fig. 1.
Graphical model for PX⃗,Y⃗. In fMRI detection, Xi is the hidden activation label, and Yi is the observed fMRI time course.
Direct search for the optimal activation configuration is intractable in general. A polynomial-time algorithm for exact MAP estimation exists for binary MRFs [Greig et al., 1989], based on a reduction to the Minimum-Cut-Maximum-Flow problem. We refer to this exact solver as Min-Max. Min-Max is still computationally intensive when applied to the volumetric data. Our experimental results in Section 6.2 show that the Mean Field solver provides a close approximation to the Min-Max solutions but requires much less computation.
2.3 The Mean Field Solver
The Mean Field algorithm can be derived in a number of ways. In Appendix B, we provide a detailed development based on the variational approach of approximating the posterior probability of configuration X⃗ given observation y⃗, PX⃗|Y⃗(x⃗|y⃗), by a product distribution through minimization of the KL-Divergence between the two distributions [Jaakkola, 2000]. The optimization leads to a fixed-point iterative update rule
| (5) |
where
 (i) is the set of voxel i's neighbors, and M is the number of possible values the state variables Xi can take. The normalization constant γ ensures the solution is a valid probability distribution (it sums to 1). At iteration t + 1, the voxel's belief is updated according to a linear combination of its neighbors' beliefs at iteration t. The probability model (i.e., PYi|Xi, Φi, and Ψij) determines the exact form of the update rule. We stop the iterations when the belief for each voxel changes less than a pre-selected threshold.
(i) is the set of voxel i's neighbors, and M is the number of possible values the state variables Xi can take. The normalization constant γ ensures the solution is a valid probability distribution (it sums to 1). At iteration t + 1, the voxel's belief is updated according to a linear combination of its neighbors' beliefs at iteration t. The probability model (i.e., PYi|Xi, Φi, and Ψij) determines the exact form of the update rule. We stop the iterations when the belief for each voxel changes less than a pre-selected threshold.
The resulting approximated posterior probability of activation has two interpretations. First, if we are interested in the MAP solution, we can assign each voxel the state value with the highest belief (for binary MRFs, voxel i is set active if bi(1) > bi(0)). Alternatively, we can use the belief bi as a detection statistic. We follow the latter strategy in the ROC analysis in Section 6.
3 Observation Model
In this section, we construct the observation model PYi|Xi that is consistent with the GLM framework for fMRI detection.
As demonstrated in [Cosman et al., 2004], the GLM detection can be equivalently formulated as a Generalized Likelihood Ratio (GLR) test:
| (6) |
It is easy to show that under the null hypothesis ℓ is a monotonic function of the F-statistic under the white noise assumption [Rencher, 2002]. If the noise has an unknown covariance, there is no longer an equivalence between the F-statistic and the GLR test. Moreover, neither the numerator nor the denominator in Equation (6) is a proper probability distribution function since they violate the normalization axiom. But since the maximum likelihood (ML) estimators asymptotically converge to the true values of the parameters under the correct hypothesis, and are asymptotically equivalent to the likelihood terms PYi|Xi (yi|xi = 1) and PYi|Xi (yi|xi = 0), respectively.
To augment the GLM detector with an MRF prior, we choose to approximate the observation model with the ML estimates of the corresponding parameters. We set
| (7) |
| (8) |
where α̂i, β̂i, and σ̂i are the ML estimates of the model parameters for voxel i. Since PYi|Xi (y|x = 1) is greater than PYi|Xi (y|x = 0) in the current likelihood setting, we design the prior on Xi to counter this bias as shown in the next section. In Appendix C, we also show an approach to constructing an MAP estimation procedure based on a voxel-independent prior, instead of the MRF prior, that yields activation maps identical to those obtained through the standard GLM detection.
4 Prior Model
We aim to set the prior model parameters to represent our knowledge about the statistical properties of the true activation maps. In this work, we employ a spatially stationary prior by using the same potential functions Φi and Ψij for all voxels in the volume. The observations (fMRI signals and anatomical information, if available) move the MAP estimate away from the configurations that are favored by the spatially stationary distribution. In this stationary model, the subscripts of the potential functions can be removed.
Setting the prior model parameters is a major challenge in MRF-based image analysis applications. Since no ground truth for fMRI detection is available, we choose to learn the model parameters from the data itself. While this approach represents an approximation for the optimal parameter setting, we found that it works reasonably well in practice. We use the results of the voxel-wise detector at a pre-specified threshold on activation values to estimate the expected number of active voxels in the volume. More specifically, we compute the GLR statistic in Equation (6) and threshold it to obtain an initial estimate of the activation map. We then use the appropriate voxel counts to estimate the model parameters for the MRF prior as described below.
We set the singleton potential Φ(a) to the expected percentage of voxels in state a. For example, in the binary activation scenario
| (9) |
where x̃j = 1 if the GLR statistic of Equation (6) at voxel j exceeds the detection threshold and x̃j = 0 otherwise. This effectively incorporates the detection threshold into the prior on the activation frequency in the volume.
The pairwise potential function Ψ(a, b) should encourage the neighboring voxels to share the activation state. Ideally, we should choose a value for the pairwise potential function in such a way that samples drawn from the resulting prior model agree with our notion of the spatial properties of true activation maps in fMRI experiments. However, the relationship between the potential functions and the statistical properties of samples drawn from the model is a complex one. In our earlier work [Ou & Golland, 2005], we used the frequency counts to set the pairwise potentials:
| (10) |
where an edge connects a pair of adjacent voxels in a 6-voxel neighborhood.
We observed in later experiments that it is easy to generate undesired configurations whose posterior probability, PX⃗|Y⃗ (x⃗|y⃗), is greater than that of a desired configuration under this model. A relatively large value of Ψ(a, b) indicates that co-occurrence of the corresponding states a and b is more likely than those with smaller values of the pairwise potential function. A typical Ψ estimated from our real fMRI data is around . However, the potential functions estimated from noisy frequency counts can over- or under-emphasize the relative likelihood of certain configurations. To enable training of the model, we add a modeling parameter λ that controls the overall “sharpness” of the joint component of the prior, replacing Ψ(a, b) with Ψ̃(a, b) = Ψλ(a, b). Varying this positive parameter λ controls the degree to which more favorable configurations are emphasized, but does not alter their ranking order. This parameter is important especially when working with noisy data because it can alleviate the effects of inaccurate estimation of Ψ.
In synthetic experiments, we estimate λ from half of the data by performing an exhaustive search with respect to the true positive rate while fixing the false positive rate at 10−3. Since ground truth activations are not available in real fMRI experiments, we cannot form a training set to estimate λ. In this work, we apply the estimated λ from the synthetic data to activation detection in real fMRI experiments. In order to obtain a sensible estimate of λ, we match the simulation parameters, such as the ratio of gray and white matter volumes and the proportion of active voxels, of the synthetic data with the real one.
The detection performance reported in this paper represents significant improvement over our earlier results [Ou & Golland, 2005], which did not include this modeling parameter λ (in other words, it used λ = 1). The improvement is particularly large for low SNR data. The augmented model also achieves a significant improvement in the detection accuracy for real fMRI data.
5 Anatomically Guided Detection
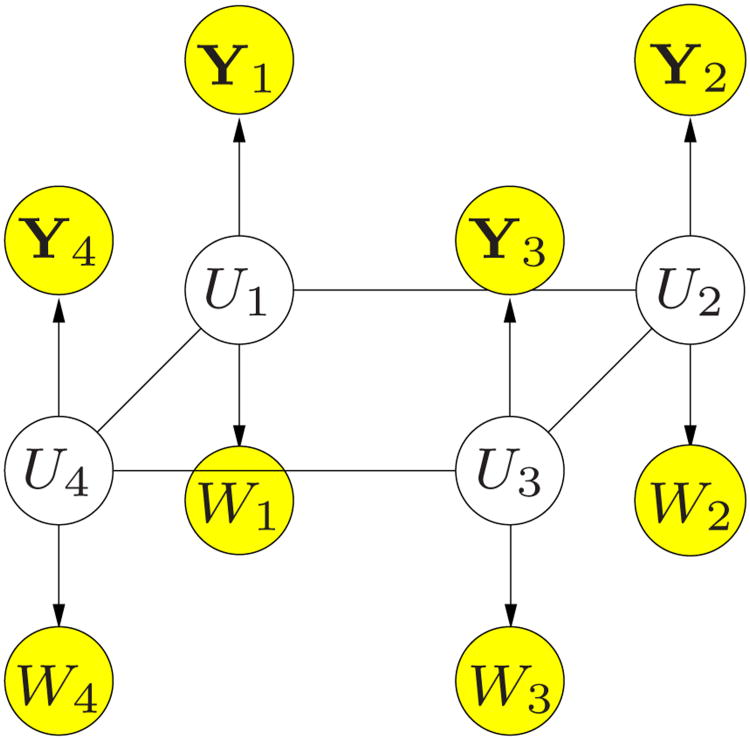
The general nature of the MRF framework enables a straightforward extension of the probabilistic model in the previous section to include a tissue type for each voxel. We define V⃗ = [V1, …, VN] to be the tissue types of all voxels, and W⃗ = [W1, …, WN] to be the tissue type observations, e.g., results of automatic segmentation of an MRI scan. Here we model both the hidden tissue type variables V⃗ and the observed anatomical labels W⃗ on the same grid of the fMRI scan.
Now each voxel has two hidden attributes: the activation state Xi and the tissue type Vi. We combine these attributes into a single hidden node Ui, as illustrated in Figure 2. For example, for binary activation states (active or not active) and three tissue types (gray matter, white matter, or other), Ui has six possible values. Since the segmentation labels W⃗ and the fMRI observation Y⃗ are obtained from two different images, it is reasonable to assume that they are conditionally independent given the hidden state.
Fig. 2.
Graphical model for PU⃗,Y⃗,W⃗.
We choose to treat the segmentation results as a noisy observation rather than the true tissue type. Imperfect registration between the fMRI images and the anatomical scan, partial volume effects, and the errors in the segmentation itself contribute to the “noise” in the anatomical information. Among these factors, partial volume has the strongest influence in our experiments because some brain structures have smaller dimensions than an fMRI voxel. For example, since the highly folded cortical sheet is approximately 3 mm thick, an fMRI voxel (2-4 mm) may correspond to multiple tissue types.
A straightforward extension of the model described in Section 2 leads to the MAP estimator for the new hidden variable
| (11) |
and the Mean Field update rule
| (12) |
This update rule is similar to Equation (5), with the exception of the extra likelihood term PWi|Ui(wi|ui) for the tissue type observation. The compatibility matrix Ψij is M × M, where M is the number of states in Ui.
Similar to the procedures for estimating the likelihood and prior model parameters in Section 3 and Section 4, we estimate the MRF model from thresholded GLR images. We estimate the likelihood term for the noisy segmentation W⃗ given the true hidden states from the corresponding counts of tissue labels in the high resolution segmentations, the coarse resolution subsampled images, and the initially thresholded GLM results. This accounts for the partial volume effects between the anatomical and the functional data. We also note that the inference framework can utilize probabilistic segmentations by incorporating them into the likelihood model.
Our procedure for the construction of the MRF prior is as follows:
Register the EPI images and the anatomical scan.
Downsample the anatomical images to fMRI resolution to establish correspondence.
Run standard GLM and obtain an SPM.
Construct the probabilistic model for noisy segmentation PWi|Ui(wi|ui) from the segmented anatomical scan and a thresholded SPM obtained in Step (3).
Estimate Φi(ui) and Ψij(ui, uj) from the segmented anatomical scan and the thresholded SPM.
6 Experiments
In this section, we first quantitatively evaluate the proposed spatial regularizers using synthetic data, followed by a comparison between the detection results computed using the Min-Max and the Mean Field solvers. We then present the experimental results using real fMRI data from the functional Biomedical Informatics Research Network (fBIRN) [Zou et al., 2005].
To compare the performance of the anatomically guided MRF detection with the traditional methods, we also implemented two types of anatomically driven extensions to the GLM detector and the Gaussian filter. In anatomically guided GLM detection, we suppress activations outside of the gray matter using the anatomical information as guidance. In this case, “soft” masking can also account for mis-registration and errors in segmentation. To incorporate anatomical information into the Gaussian filter, we adjust the weights of the filter based on the tissue types of the voxel's neighbors. When evaluating the filter at voxel i, we assign higher weights to the neighbors sharing the same segmentation results as voxel i. In this implementation, neighbors sharing the same segmentation results contribute twice as much as those sharing different segmentation results. In the later sections, we will refer to these two methods as GLM with anatomical information and anatomically guided Gaussian smoothing respectively.
We initialize the MRF by assigning equal beliefs to all states, i.e., bi(a) = 1/M for all activation states a. We stop the algorithm when the belief for each voxel changes by less than 0.01 between consecutive iterations. In all experiments reported in this paper, the Mean Field solver converged in 10 to 20 iterations.
6.1 Artificial Data
To quantitatively evaluate the performance of the method, we generated phantom data sets by applying the expectation-maximization (EM) segmentation algorithm [Pohl et al., 2004] to a 1 mm isotropic anatomical MRI scan and randomly placing activation areas of variable size (average diameter of 15 mm) in the gray matter. We then downsampled the scan to a typical fMRI resolution, 4 mm isotropic (64×64×64). In this synthetic data set, the gray matter voxels represent 10% of the total number of voxels in the volume, and the active voxels represent about 10% of the gray matter voxels. We then created simulated fMRI scans based on a fixed parametric hemodynamic response function (the two-gamma function) [Jezzard et al., 2002], using a block-design protocol. In this simplified model, we used the same noise level for all voxels in the volume to enable statistical comparison among different methods by averaging the detection rates over the volume.
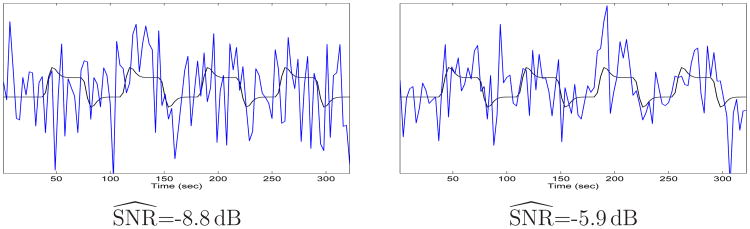
In our real fMRI studies, the estimated SNR, , varied from -4dB to -6.5 dB across sessions and across subjects. We used the estimated SNR to determine an observed level of the simulated noise as the true SNR is unavailable for real fMRI scans. To create realistic simulated signals, we used two levels of noise in these experiments. The resulting noisy signals have the estimated SNR of -5.9 dB and -8.8 dB that bracket the lowest SNR (-6.5 dB) in our real data. We chose such a conservative range of noise levels since the true SNR is typically lower than the estimated one in real fMRI data as part of the noise energy is assigned to the estimated signal during detection when the signal and the noise overlap in some frequency bands. Figure 3 shows example signals from our simulated data sets.
Fig. 3.
Example signals (blue) and their noise-free counterparts (black) at two different SNR levels.
To decouple testing from phantom generation, we used a GLM detector based on a 10-bin finite impulse response (FIR) hemodynamic response function in testing.
To compare the methods statistically, we generated 16 independent artificial data sets using the procedure mentioned above. We used eight data sets to learn the optimal model parameter λ for the MRF prior, as described in Section 4, and the remaining eight data sets for the evaluation of the methods. In the training phase, we explored the range of values for λ between 1 and 4. Most of our data sets show the best performance when λ is around 3. All 16 data sets were employed to evaluate the GLM detector with and without Gaussian smoothing, as well as their anatomically guided variants. Gaussian kernels of 7 mm full-width-half-maximum (FWHM) achieved the best performance in most simulated data sets when we varied the kernel width from 4 mm to 12 mm. We therefore report the results for the 7 mm FWHM Gaussian filter.
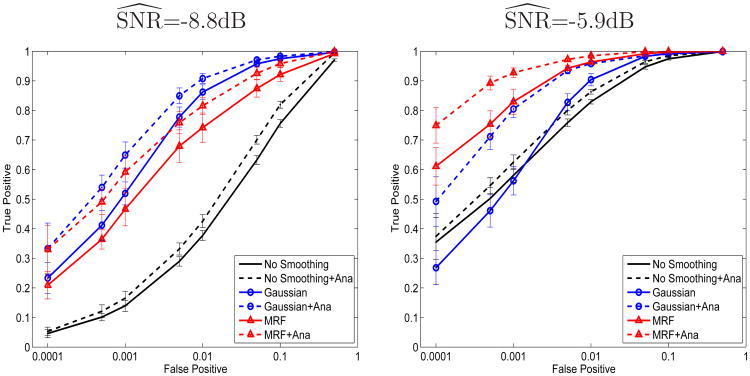
Figure 4 illustrates the ROC analysis for GLM, GLM with Gaussian smoothing, and GLM with MRF regularizer (solid curves) and their anatomically guided variants (dashed curves). The ROC curves were created by varying the threshold applied to the GLM statistic or the posterior probability. The error bars indicate the standard deviation of the true positive rate.
Fig. 4.
ROC curves for GLM, GLM with Gaussian smoothing, the MRF-based detector and their anatomically guided variants. False positive rate, shown on logarithmic scale, is computed using the brain voxels only.
Since we expect only a small fraction of voxels in the image volume to be active, a low false positive rate is necessary to prevent false detections from substantially outnumbering true detections (Figure 4). Here we focus on the false positive rates below 10−3, which correspond to about 10% of the total number of the active voxels, or approximately 250 voxels.
Let us first concentrate on the detection results without anatomical information (solid curves in Figure 4). As expected, the accuracy of all methods improves with increasing SNR. At high noise levels (low SNR), Gaussian smoothing outperforms MRFs. As the simplest smoothing technique, Gaussian smoothing is more robust to noise. As the SNR increases, the MRF provides better regularization of the activation state. For example, at SNR=-5.9 dB and at the false positive rate of 10−3, the MRF outperforms the Gaussian smoothing by about 30% in true detection accuracy; at 60% true detection, the MRF approximately achieves one tenth of the false detections compared to the Gaussian smoothing. We believe our current estimation procedure for the MRF potential functions Ψij and Φi partially degrades the MRF performance when SNR is relatively low. As mentioned earlier, these two parameters are estimated from the thresholded GLM activation map. Higher noise levels lead to increasingly inaccurate estimates for the model parameters and to sub-optimal detection results. However, with ongoing improvements of the imaging technology, we believe MRFs will become even more helpful in reducing spurious false detection islands.
Anatomical information significantly boosts the performance of all detectors at all noise levels (dashed curves). At high noise levels ( ) and false positive rates between 10−4 and 10−3 (26 and 262 false positive voxels respectively), both Gaussian smoothing and MRF gain at least 10% in true detection rate while using the anatomical information. At the lower noise level ( ), the basic GLM detector augmented with anatomical information exceeds the performance of the Gaussian smoothing. Since false detections occur relatively uniformly throughout the volume but activations are located in the gray matter, masking out irrelevant regions improves the performance substantially. At the 10−4 false positive rate, the anatomically guided MRF outperforms the anatomically guided Gaussian smoothing by about 20% in true detection rate, achieving over 90% detection accuracy.
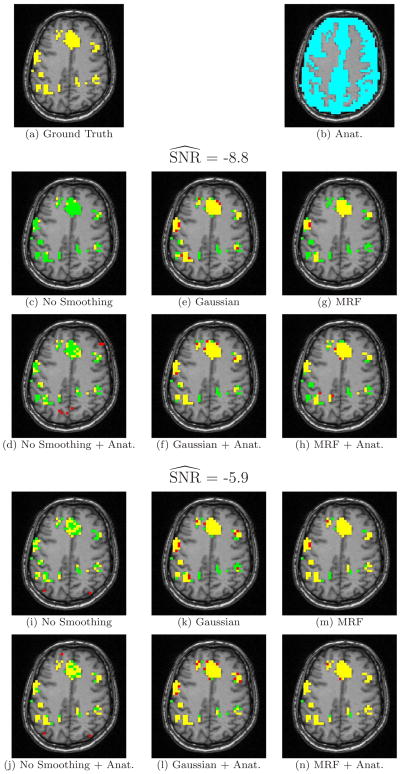
In addition to the quantitative ROC analysis, we find it useful to visually inspect the resulting activation maps. Figure 5 shows one axial slice of the activation phantom, the anatomical segmentation, and the detection results for the three methods and their anatomically guided versions at two different SNR levels. All the detections were performed at the false positive rate of 5 · 10−4. The basic GLM produces a fragmented activation map that shows very little of the original activation at low SNR (Figure 5c) and contains fragmented activation islands at high SNR (Figure 5i). Given either of these maps, users would have trouble inferring the true activation areas and disambiguating them from spurious false detections. Gaussian smoothing leads to a reasonable estimate of the ground truth; however, it tends to make the detections “spherical,” which may change the shape of the detected activation areas (Figure 5e,k). Consequently, many false positive voxels in the Gaussian smoothing occur at the boundaries of the activation regions. Anatomical information reduces this over-smoothing effect for some areas (Figure 5f,l). At low SNR (-8.8 dB), the MRF model fills in many of the active pixels that were missed by GLM (Figure 5g). At higher SNR (-5.9 dB), MRF produces relatively accurate results (Figure 5m). Not all of the scattered activation islands are removed through regularization, but the activation map looks more similar to the ground truth. The activation map is further improved when the anatomical information is integrated into the model (Figure 5h,n). Similar to our findings from the ROC analysis, at low SNR anatomically guided Gaussian smoothing achieves the best results, while at high SNR the anatomically guided MRF outperforms the rest of the detectors.
Fig. 5.
Axial slice of the ground truth, the segmentation and the estimated activation maps at the false positive rate of 5 · 10−4. True detections (yellow), false positive (red), and false negative (green) areas are shown.
6.2 Comparison to the Optimal Solution
In the binary case, we can evaluate the quality of the Mean Field solution by comparing it to the exact solution. The Min-Max solver mentioned in Section 2.2 runs in polynomial time and finds the activation map that achieves the global maximum of the posterior probability distribution for binary MRFs. We refer the readers to previously published work [Cosman et al., 2004] for implementation details on the Min-Max algorithm in application to MRF-based detection in fMRI.
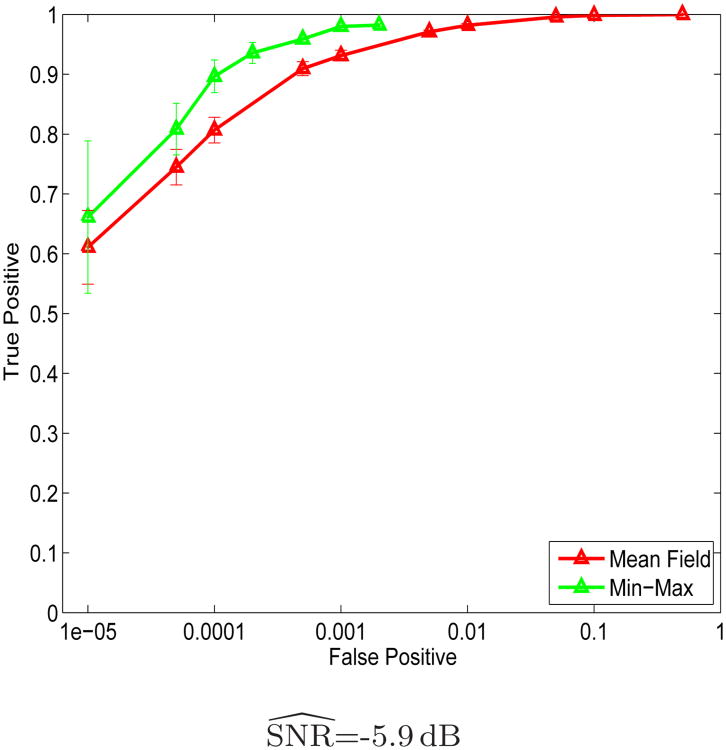
Figure 6 shows the ROC curves for the Mean Field and the Min-Max solvers applied to the binary activation data sets introduced in Section 6.1. The Mean Field ROC curve is identical to the corresponding one in Figure 4. The error bars for the Min-Max ROC curve were computed from the 16 artificial data sets. The Min-Max ROC curve is incomplete for large false positive rates, because extreme threshold values lead to demanding computation (more than ten hours for a single threshold value), and their corresponding false positive rate exceeds the acceptable region in practice. Because each run takes a long time, we did not optimize the shaping parameter λ for the Min-Max algorithm. Instead, we experimented with different values of λ, and displayed the best performance. As presented in Figure 6, Min-Max solution is roughly 5% more accurate than the Mean Field solution, suggesting that the Markov model captures the underlying activation pattern reasonably well. On the other hand, Min-Max's computational requirements are too demanding for the detection application. The Mean Field algorithm offers a good approximation to the globally optimal solution.
Fig. 6.
ROC curves for the MRF-based detection results using the Mean Field and the Min-Mix algorithms. False positive rate is shown on logarithmic scale.
The maximum flow in the Min-Max solver can be obtained via Edmonds-Karp algorithm [Cormen et al., 1997]. The run time complexity of the algorithm is O(N E2), where E is the number of edges in the graph. In our case, the number of edges per node in the graph is bounded by a constant, leading to O(N3) run time complexity. The run time complexity of the Mean Field update is O(N M), where M is the number of state values. In our experiments, the algorithm converged in 10 to 20 iterations. Our Mean Field with Matlab implementation usually converged in 5 to 10 minutes on a standard PC (2 GHz CPU and 2GB RAM), but it was slower than Gaussian smoothing which took less than a second. The Min-Max solver with Matlab implementation took 30 to 40 minutes for reasonable thresholds. The Mean Field algorithm requires O(N M) memory, which is comparable to the memory necessary to implement the Gaussian smoother and the standard GLM detector.
We note that the graph cuts algorithm [Boykov et al., 2001] is an extension of the Min-Max solver to multi-state MRF; it employs a series of binary Min-Max steps to achieve a good quality approximation. But since even a single run of a Min-Max solver on a 3-D fMRI volume is quite slow, we did not explore the graph cuts algorithms for approximate MRF inference any further.
6.3 Real fMRI Experiments
We demonstrate the method in application to a sensory-motor fMRI study. The study included five healthy right-handed subjects. Each subject performed four identical runs of a sensory-motor task. Each run consisted of nine rest epochs and eight task epochs (total 17 epochs), with each epoch lasting 15 seconds. A flashing checkerboard and a series of tones were presented at 3Hz during a task epoch, and the subject was asked to tap along in a regular 3 Hz rhythm. The original purpose of this fMRI study was to characterize cross-scanner variability [Magnotta et al., 2006, Zou et al., 2005], but we only use data from one scanner in the study. The fMRI images were acquired using a Siemens 3T machine (TR=3s, 64 × 64 × x35, 3.4 mm × 3.4 mm × 5 mm, dual echo EPI, echos at 20 and 50ms, EPI bandwidth of 2441 Hz, 90 degrees flip angle, single channel head coil). The estimated SNR in expert-selected ROIs relevant to the task varied between -4 dB and -6.5 dB. Each subject also underwent anatomical scanning (transverse three-dimensional magnetization prepared rapid acquisition gradient-echo protocol, 9.8/minimum, 15 degree flip angle, 22 × 16.5 cm field of view, 256 × 192 matrix, 124-128 sections, 1 mm × 1 mm × 1.2 mm, T1 =300 msec, bandwidth of 15,625 kHz, two signals acquired).
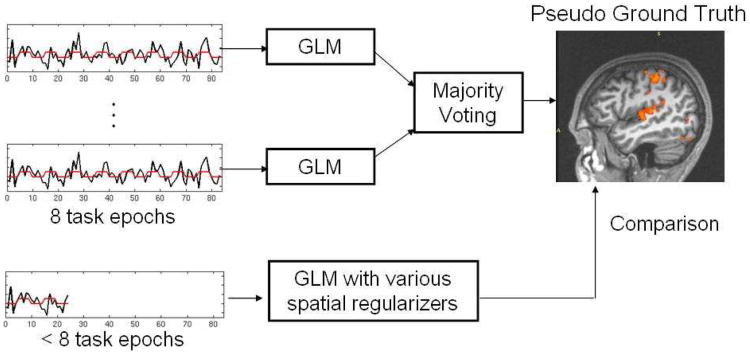
Since the ground truth activation is unknown in real fMRI experiments, we cannot construct ROC curves. In this work, we evaluated the proposed fMRI analysis methods with respect to their ability to detect activations from reduced-length time courses. Figure7 illustrates the flow chart of our evaluation process. We first applied the GLM detector, parameterized by the two-gamma function, without any smoothing to each of the four full-length runs for the same subject. We then employed majority voting among the resulting four activation maps to construct the pseudo ground truth activation map for the experiment. To evaluate the six methods we compared in Section 6.1, we first quantitatively compared each of their activation maps produced with varying length of time courses to the pseudo ground truth activation map (Figure 8). We then visually inspect the quality of the activation maps shown in Figures 9-11.
Fig. 7.
Our validation procedure for real fMRI data.
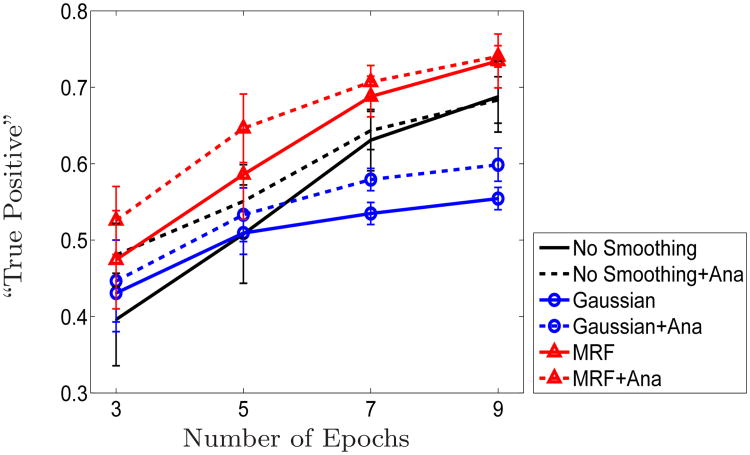
Fig. 8.
Detection sensitivity with respect to the length of time courses used in the detection. Results shown in Figures 9-11 correspond to detection using seven epochs. The map obtained through majority voting on four runs was used as “pseudo ground truth”.
Fig. 9.
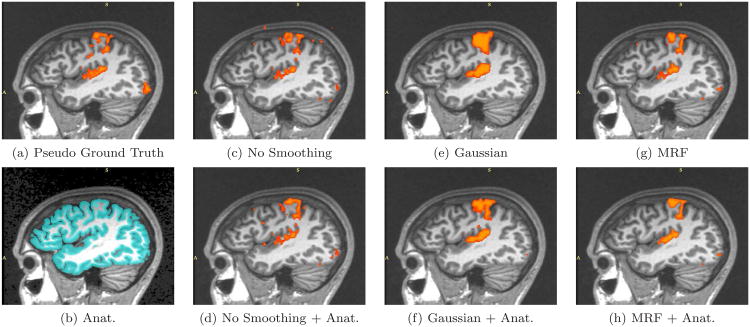
Real fMRI study. One sagittal slice in the estimated activation maps. (a) Pseudo ground truth created from four full-length sessions (17 epochs each). (b) High resolution segmentation result overlaid onto the corresponding MR image. (c)-(h) The activation maps obtained from the first seven epochs. (c) Plain GLM detection results. (d) A gray matter mask is employed to suppress GLM-detected activations which do not lie in the gray matter. (e) Isotropic Gaussian smoothing with 7mm FWHM is applied prior to the GLM detector. (f) A weighted Gaussian smoothing is applied prior to the GLM detector. (g) is generated by the GLM detector with MRF spatial prior. (h) further incorporates the anatomical information into the MRF prior.
Fig. 11.
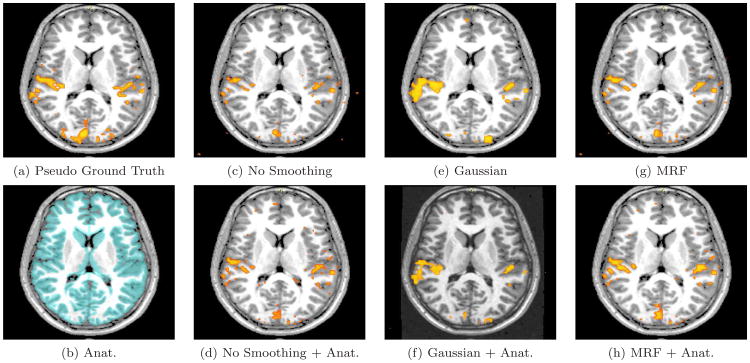
Real fMRI study. An axial slice in the estimated activation maps. The description of each subfigure follows the conventions of Figure 9.
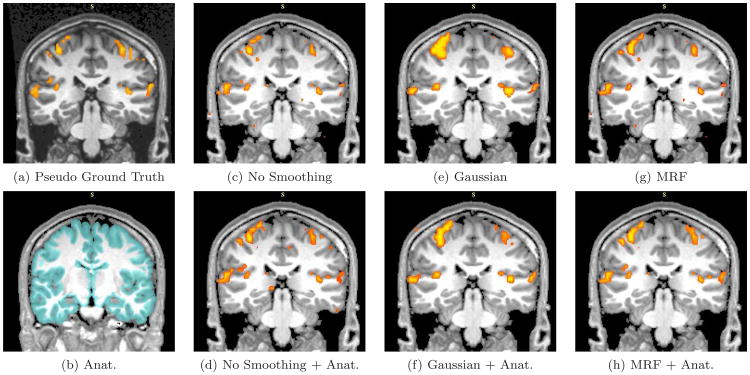
The pseudo ground truth activation map (Figures 9-11 (a)) exhibits a substantial amount of fragmentation. It often shows bias towards to the GLM detector, especially for the results obtained with relatively long time courses. At the same time, other detectors might produce perceptually more meaningful results. Hence, extra caution is needed while interpreting results based on this pseudo ground truth reference.
In contrast to our experiments with synthetic data, where the activation thresholds were chosen according to the required bound on the false positive rate, in real data we chose to select the top 1% of the voxels with the highest statistic or posterior probability when comparing the activation maps across detectors. Sophisticated threshold selection methods, such as controlling the false discovery rate [Benjamini & Hochberg, 1995] or controlling family-wise error rate, can be applied to statistics generated from the GLM detectors. When we introduce smoothing or spatial prior, the theory of statistical testing becomes substantially more complex. For the purpose of comparing different detectors, our threshold selection method effectively reveals the detected voxels and the spatial pattern when equal number of voxels pass the threshold.
Figure8 shows the fraction of detected activation matching with those in the pseudo ground truth versus the number of epochs included in the detection. We omit the corresponding figure for the false positive rate as the false positive rate can be straightforwardly derived from Figure 8 since we select the same number of voxels active in each experiment. We can see that spatial regularization, of either MRF or Gaussian smoothing, is crucial for detection with short time courses. Based on three epochs, GLM achieves 0.4 true positive rate, MRF and Gaussian achieve 0.48 and 0.44, respectively. The results of the MRF-based detectors show a much better agreement with the pseudo ground truth than the baseline methods. Furthermore, anatomical information significantly improves the performance of all detectors, boosting it by additional 5 to 8%.
We now inspect the activation maps from the six detectors with seven-epoch time courses (out of 17) in Figures 9-11(c)-(h). Subfigure (b) in all three figures displays the high resolution anatomical segmentation. Without spatial regularization, the GLM detector yields more fragmented activation map (c) due to loss in statistical power from reducing the length of the signal. Spatial masking removes some false detections outside of the gray matter in (d). Since we keep the number of active voxels constant, extra gray matter voxels are labelled as active in (d). The other four images illustrate the results of applying GLM with Gaussian smoothing and the MRF-based detector, as well as their anatomically guided versions. Although Gaussian smoothing (kernel width of 7 mm) removes most of the single-voxel activation islands, its activation map in (e) significantly over-smooths the activation areas when compared to (a). Anatomical weighting somewhat reduces the over-smoothing effect. MRF regularization ((g) and (h)) captures activations with elongated spatial structures. This highlights the potential benefit of using the Markov priors in fMRI detection. Furthermore, Figure 9(h) illustrates that a coherent activation pattern along the motor cortex is detected by the anatomically guided MRF detector. Similar to the Gaussian smoothing, the MRF model benefits from using anatomical information to remove spurious activations. Our experiments demonstrate that employing anatomically guided MRF spatial regularization leads to accurate detection from time courses of substantially reduced length.
7 Discussion and Conclusions
Our experiments confirm the importance of spatial regularization in reducing fragmentation of activation maps. We investigated two types of improvement in spatial modeling for fMRI detection: MRF priors and anatomical bias. The MRF provides a spatial prior that refines the structure of the resulting activation maps over Gaussian smoothing, as demonstrated by our experiments on phantom and real data. We explored the fast Mean Field approximate solver in application to MRF-based fMRI detection and showed that it provides good detection accuracy while taking substantially less time to evaluate than the exact solution. We note that since the Markov model itself is an approximation of the real geometry of the activation regions, we should not dwell on the small differences in the activation maps introduced by the approximate solvers but rather focus on their performance relative to the ground truth or the pseudo ground truth.
We also demonstrated that anatomical information provides helpful bias in fMRI detection. We derived an algorithm for anatomically guided MRF estimation and showed how Gaussian smoothing can be straightforwardly augmented with anatomical information by rescaling the coefficients of the smoothing kernel. Partial volume effects in reducing the anatomical segmentations to the fMRI resolution should be investigated further in the future. In this work, we downsample the anatomical scan to match the resolution of the functional scan. A better solution would be to use the high-resolution anatomical scans to resolve the activation in the functional voxels that are on the boundary of the gray matter, leading to a “super-resolution” detector.
In this paper, the detection method treats the anatomical segmentation as a noisy observation of the true tissue types. In addition, it utilizes anatomical information to estimate the pairwise and the singleton potential functions Ψij and Φi. If we treat the segmentation labels as the true tissue types for inference purposes, i.e., employ the graphical model from Figure 1 with spatially variant potential functions based on the segmentation label at each voxel, the method fails to produce accurate results. We believe that the mis-registration and subsampling noise in producing anatomical data on the same grid with fMRI measurements requires additional modelings and cannot be ignored in anatomically guided fMRI analysis. We can also use the anatomical information for inference only, but employ spatially stationary potential functions that are ignorant of anatomy. The structure of the corresponding graphical model is similar to that in Figure 2, except that each hidden node contains the activation state Xi only. In this model, the tissue type does not propagate between voxels. The resulting MRF prior does not encourage strong spatial coherency within tissue types and weak spatial coherency across tissue types. In our experiments, we found this method to produce similar results to those of the full model. To summarize, modeling the mismatch in alignment and resolution between the two modalities is crucial for accurate anatomically guided fMRI detection.
It has been suggested that anatomical information can be obtained from breath-hold fMRI experiments [Li et al., 1999], which would remove the effects of mis-registration and resolution mismatch between the functional data and the anatomical structure. The BOLD signal in the gray matter is highly correlated with the breath-hold experimental protocol, allowing gray matter segmentation with an appropriately selected threshold. In addition, a rough gray matter segmentation can be extracted from the AR(1) temporal model of noise [Worsley et al., 2002]. In our experiments, we found that the anatomical prior produced by these two approaches in general was of much lower quality than that obtained from anatomical segmentation followed by downsampling. We therefore focused on anatomical segmentation as a source of tissue type information.
We evaluated the methods by performing the ROC analysis on phantom data, and by studying their ability to recover activation from significantly shorter time courses on real data. In the high noise setting for the binary activation states, the Gaussian smoothing outperformed other methods, but the difference between Gaussian and MRF was marginal. As the SNR in the images increased, the Markov prior offered a substantial improvement in the detection accuracy.
Many fMRI studies aim to detect and characterize positive and negative activations separately [Allison et al., 2000, Aron et al., 2004, Seghier et al., 2004]. The negatively activated regions have also been shown to correlate with disease-induced neurodegeneration [Buckner et al., 2005, Greicius et al., 2004]. Most literature defines positive/negative activations as a comparison of responses to two different stimuli or as a comparison of responses to a stimuli versus baseline. Our model can capture both definitions by extending the activation state variables Xi to three states, i.e., {−1, 0, 1}. If more than one comparison of stimuli is of neuroscientific interest, our model can be adapted by handling each comparison independently. Recent work by Makni et al. [Makni et al., 2008] and Vincent et al. [Vincent et al., 2007] jointly estimate the positive/negative activations and the shape of HRF through a bilinear model. Their work requires an estimation on a set of pre-defined regions, such as the cortical parcellation from anatomical scans. We have completed preliminary evaluation of the six detectors discussed in Section 6.1 in the context of positive/negative activations [Ou, 2005]. The overall performance of these detectors is similar to the results for the binary activation cases, except that the MRF-based detectors show better performance in preserving the boundary between positively and negatively activated regions while Gaussian smoothing tends to average away positive and negative activation signals.
We used block design experiments to validate the method. We expect the MRF regularizer to perform somewhat worse in the event-related paradigms due to lower SNR. In our experiments, we observed that the proposed regularization methods improve detection accuracy at both SNR levels, but the effect is more substantial for higher SNR levels, suggesting that the utility of the method in analyzing real fMRI data will grow as the quality of the data improves.
We also note that localization response curve (LROC) analysis [Swensson, 1996] could explicitly incorporate location information into the ROC analysis for simulated data. In general, it is easy to detect some active voxels in or near the real activation region. However, correctly detecting the boundaries of the activation region is difficult, and it is not captured by the LROC. Our current approach to quantifying the detection performance by averaging the performance at each voxel using a standard ROC approach lacks the localization information, but it serves as a better evaluation tool as improving the boundary detection is one of the main goals of this work.
Evaluation is challenging in real fMRI data since no ground truth is available even for limited experiments. Alternative evaluation methods for fMRI detectors have been proposed, based on repeatability of activation results over multiple sessions [Genovese et al., 1997]. By modeling the distribution of detection results for a voxel over all sessions as a mixture of two binomial distributions, this method estimates the ROC curve. The underlying hidden activation state is estimated as part of the mixture model. Unfortunately, this model relies on a large number of independent sessions and on independence among voxels to provide reasonable estimates. Both assumptions may be too optimistic in fMRI experiments, and were certainly violated by our data and methods. Extensions of this procedure address multiple tasks [Liou et al., 2006] and non-parametric models [Strother et al., 2002] and allow characterization of prediction accuracy and the SNR associated with reproducible SPMs. However, the detectors in our comparison produce substantially different types of statistics (F-statistic for the GLM and posterior probability for the MRF-based detectors), presenting additional challenges for such methods. Here we chose to compare the method's ability to detect activations from reduced-length time courses as an evaluation criterion; further work in comparing activation detectors is needed. Maitra et al. extended work in [Genovese et al., 1997] to handle spatially-dependent fMRI detection [Maitra et al., 2002], and it is of our interest to compare their approach with ours in future work.
The anatomically guided Markov spatial prior enabled us to shorten the fMRI scan length from four runs of 17 epochs to nine-or-fewer epochs in one run while still retaining comparable detection power. We expect a similar effect to occur with respect to the spatial resolution when we extend the method to utilize the anatomical information at the original scan resolution. As the quality of the scanning equipment improves, the sophisticated spatial models, such as MRFs, will become even more important in recovering the details of the activation regions.
Fig. 10.
Real fMRI study. A coronal slice in the estimated activation maps. The description of each subfigure follows the conventions of Figure 9.
Acknowledgments
We thank Dr. Eric Cosman and Dr. Kilian Pohl for help on this article and Dr. Douglas Greve for pre-processing the fMRI data. This work was partially supported by the NIH National Center for Biomedical Computing Program, National Alliance for Medical Imaging Computing (NAMIC) Grant U54 EB005149, the NSF IIS 9610249 grant, the NIH NCRR mBIRN U24-RR021382 grant, the NIH NCRR NAC P41-RR13218 grant, the NIH NINDS R01-NS051826 grant and the NSF CAREER 0642971. fMRI acquisition was supported by the NCRR FIRST-BIRN (U24 RR021992) grant. Wanmei Ou is partially supported by the NSF graduate fellowship, and Dr. William M. Wells III is supported by the NCRR FIRST-BIRN grant and the Neuroimaging Analysis Center.
A Alternative GLM Formulation
Here we show that the formulation of Equation (1) is equivalent to the more typically employed application of a contrast matrix in conjunction with GLM. GLM models the BOLD response as a linear time-invariant system [Friston et al., 1995]:
| (A.1) |
where y is the voxel's fMRI time course and H is the design matrix, which may contain responses to different tasks or the same task but different types of stimulus. Since GLM models each voxel separately, we omit the voxel index i in the derivations here. Noise ∊ is assumed to be i.i.d. Gaussian noise. The vector of regression coefficients β includes both the coefficients in the signal space and the nuisance parameters. The contrast row vector c is defined to select the relevant components of the ML estimate of the regression vector β̂ for statistical testing. For example, we can construct the t-statistic as with T − rank(C) degrees of freedom, and Σ̂cβ is the estimated variance of cβ̂.
To show that Equation (1) is equivalent to this GLM formulation, we introduce transformation matrix TH. The first row of matrix TH is identical to the contrast row c; the remaining Nβ − 1 rows are constructed such that each row in TH is orthonormal to the remaining rows. We now consider β̃ = THβ. The first element of β̃ is the projection of the regression vector onto the signal space of interest, defined by c. The remaining elements of β̃ can be considered nuisance parameters. Therefore, we can rewrite Equation. (A.1) in the form of Equation (1) by setting :
| (A.2) |
The first term in the resulting sum corresponds to the signal space components. The second term in the sum represents contributions orthogonal to the signal space of interest.
B Mean Field Derivation
In this appendix, we demonstrate one possible derivation of the Mean Field iteration as a variational approximation of the original MAP problem, closely following the development in [Jaakkola, 2000]. The basic idea is to approximate the posterior probability PX⃗|Y⃗(x⃗|y⃗) by a simpler distribution through minimizing the KL-divergence between them and to use the mode of Q(·; b⃗) as an approximation for the mode of PX⃗|Y⃗(·|y⃗). b⃗ = [b1, b2, …, bN] is the vector of belief functions: bi(a) denotes the probability that voxel i is in state a. Clearly, , where M is the number of possible values that the state variable Xi can take. For example, M = 2 for binary MRFs. We note that the resulting distribution Q(·; b⃗) implicitly depends on the observations y⃗.
The KL-Divergence
| (B.1) |
serves as a distance between Q(·;b⃗) and PX⃗|Y⃗(·|y⃗); it is non-negative and is equal to zero only if Q = PX⃗|Y⃗. As an aside, the statistical inference theory implies that we should minimize the KL-divergence D(PX⃗|Y⃗║Q), which often leads to intractable problems. To overcome this difficulty, variational methods are usually formulated as a minimization of the KL-divergence D(Q║PX⃗|Y⃗).
It is easy to see that the minimum of D(Q(·; b⃗)║PX⃗|Y⃗) is achieved for the same belief vector b⃗* that minimizes the so called free energy,
| (B.2) |
since the last two terms are independent of b⃗. Substituting the definitions for Q(x⃗; b⃗) and for PX⃗|Y⃗(x⃗|y⃗), we obtain,
| (B.3) |
leading to the following constrained optimization problem:
| (B.4) |
Using Lagrange multipliers, we reduce the problem above to minimize
Differentiating with respect to bk(xk) yields
| (B.5) |
By setting the derivatives to zero and manipulating the expression above, we arrive at the fixed-point iteration for the belief functions
| (B.6) |
that immediately leads to the Mean Field update rule of Equation (5) if we set γ = e1 + ξk.
C Equivalence to the Joint MAP Solution
In this appendix, we present the connection between the MAP solution and the classical GLM inference in the binary activation scenario. In particular, we show that for a prior that models all voxels independently, there is a setting of the prior that forces the MAP solution to coincide with the classical solution. Furthermore, the two-step estimation procedure we outlined in Section 3, which first finds the ML estimates of the GLM parameters {α, β, σ2} and then uses them in the MAP estimation of the state variables X, is asymptotically equivalent to the optimal simultaneous MAP estimation of the activation state and the regression parameters in the case of the voxel-wise independent prior.
To simplify the derivations, we let be the parameters of the likelihood under H0 for voxel i, be the parameters of the likelihood under H1 for voxel i, and be the MAP (ML) estimates of Θ0i and Θ1i, respectively The activation state estimate obtained through the joint MAP estimation of the activation state and the GLM parameters
| (C.1) |
can also be expressed as
| (C.2) |
| (C.3) |
For a voxel-wise independent prior , the problem above can be solved for each voxel separately. In the remainder of this section, we omit the voxel index i.
| (C.4) |
| (C.5) |
| (C.6) |
| (C.7) |
| (C.8) |
We obtained Equation (C.6) by assuming a uniform prior distribution for Θx. Equation (C.8) is true asymptotically as the number of time points in a time course increases. Alternatively, we can express Equation (C.8) in terms of hypothesis testing:
| (C.9) |
As shown in [Rencher, 2002], the left-hand-size of Equation (C.9) is a monotonic function of the F statistic. Thus, we obtain the corresponding hypothesis testing threshold, η, according to the selected p value threshold in the classical GLM procedure:
| (C.10) |
This implies that selecting and causes the MAP with independent prior and the classical inferences to produce identical results.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Wanmei Ou, Email: wanmei@csail.mit.edu.
William M. Wells, III, Email: sw@bwh.harvard.edu.
Polina Golland, Email: polina@csail.mit.edu.
References
- Allison JD, Meador KJ, Loring DW, Figueroa RE, Wright JC. Functional MRI cerebral activation deactivation during finger movement. Neurology. 2000;54:135–142. doi: 10.1212/wnl.54.1.135. [DOI] [PubMed] [Google Scholar]
- Amedi A, Malach R, Hendler T, Peled S, Zohary E. Visuo-hapticobject-related activation in the ventral visual pathway. Nature Neuroscience. 2001;4:324–330. doi: 10.1038/85201. [DOI] [PubMed] [Google Scholar]
- Andrade A, Kherif F, Mangin JF, Worsley KJ, Paradis AL, Simon O, Dehaene S, Bihan DL, Poline JB. Detection of fMRI activation using cortical surface mapping. Human Brain Mapping. 2001;12:79–93. doi: 10.1002/1097-0193(200102)12:2<79::AID-HBM1005>3.0.CO;2-I. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aron AR, Shohamy D, Clark J, Myers C, Gluck MA, Poldrack RA. Human midbrain sensitivity to cognitive feedback and uncertainty during classification learning. Journal of Neurophysiology. 2004;92:1144–1152. doi: 10.1152/jn.01209.2003. [DOI] [PubMed] [Google Scholar]
- Ashtari M, Perrine K, Elbaz R, Syed U, Thaden E, McIlree C, Dolgoff-Kaspar R, Clarke T, Diamond A, Ettinger A. Mapping the functional anatomy of sentence comprehension application to presurgical evaluation of patients with brain tumor. American Journal of Neuroradiology. 2005;26:1461–1468. [PMC free article] [PubMed] [Google Scholar]
- Benjamini J, Hochberg Y. Controlling the false discovery rate: a practical powerful approach to multiple testing. Journal of the Royal Statistical Society Series B. 1995;57:289–300. [Google Scholar]
- Besag J. Spatial Interaction and the Statistical Analysis of Lattice Systems. Journal of the Royal Statistical Society Series B. 1974;36:192–236. [Google Scholar]
- Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001;23:1222–1239. [Google Scholar]
- Buckner RL, Snyder AZ, Shannon BJ, LaRossa G, Sachs R, Fotenos AF, Sheline YI, Klunk WE, Mathis CA, Morris JC, Mintun MA. Molecular, Structural, Functional Characterization of Alzheimer's Disease: Evidence for a Relationship between Default Activity, Amyloid, Memory. Journal of Neuroscience. 2005;25:7709–7717. doi: 10.1523/JNEUROSCI.2177-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burock MA, Dale AM. Estimation and detection of event-related fMRI signals with temporally correlated noise: A statistically efficient and unbiased approach. Human Brain Mapping. 2000;11:249–260. doi: 10.1002/1097-0193(200012)11:4<249::AID-HBM20>3.0.CO;2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cormen TH, Leiserson CE, Rivest RL. Introduction to algorithms. The MIT Press and McGraw-Hill; 1997. [Google Scholar]
- Cosman ER, Fisher JW, Wells WM. Exact MAP activity detection in fMRI using a GLM with an Ising spatial prior. In Proc Medical Image Computing and Computer-Assisted Intervention, LNCS. 2004;3217:703–710. [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis I: segmentation and surface reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Descombes X, Kruggel F, von Cramon DY. Spatio-temporal fMRI analysis using Markov random fields. IEEE Transactions on Medical Imaging. 1998;17:1028–1039. doi: 10.1109/42.746636. [DOI] [PubMed] [Google Scholar]
- Flandin G, Penny WD. Bayesian fMRI data analysis with sparse spatial basis function priors. Neurolmage. 2007;34:1108–25. doi: 10.1016/j.neuroimage.2006.10.005. [DOI] [PubMed] [Google Scholar]
- Freeman W, Pasztor EC, Carmichael OT. Learning low-level vision. International Journal of Computer Vision. 2000;40:25–47. [Google Scholar]
- Friston KJ, Worsley KJ, Frackowiak REJ, Massiotta JC, Evans AC. Assessing the significance of local activations using their spatial extent. Human Brain Mapping. 1993;1:210–220. doi: 10.1002/hbm.460010306. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Worsley KJ, Poline JB, Frith CD, Frackowiak RSJ. Statistical parametric maps in functional imaging: a general linear approach. Human Brain Mapping. 1995;2:189–210. [Google Scholar]
- Genovese CR, Noll DC, Eddy WF. Estimating test-retest reliability in functional MR imaging I: statistical methodology. Magnetic Resonance in Medicine. 1997;38:497–507. doi: 10.1002/mrm.1910380319. [DOI] [PubMed] [Google Scholar]
- Goebel R, Esposito F, Formisano E. Analysis of functional image analysis contest (FIAC) data with brainvoyager QX: From single-subject to cortically aligned group general linear model analysis and self-organizing group independent component analysis. Human Brain Mapping. 2006;27:392–401. doi: 10.1002/hbm.20249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V. Default-mode network activity distinguishes Alzheimer's disease from healthy aging: Evidence from functional MRI. National Academy of Sciences. 2004;101:4637–4642. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greig DM, Porteous BT, Gramon DY. Exact maximum a posteriori estimation for binary images. Journal of the Royal Statistical Society Series B. 1989;51:271–279. [Google Scholar]
- Hartvig NV. A stochastic geometry model for functional magnetic resonance images. Scandinavian Journal of Statistics. 2002;29:333–353. [Google Scholar]
- Jaakkola T. Advanced Mean Field Methods: Theory and Practice. MIT Press; 2000. Tutorial on variational approximation methods. [Google Scholar]
- Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magnetic Resonance in Medicine. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- Jezzard F, Matthews PM, Smith SM. Functional MIR – An Introduction to Methods. OXFORD: 2002. [Google Scholar]
- Kapur T, Grimson WEL, Wells WM, Kikinis R. Enhanced spatial priors for segmentation of magnetic resonance imagery. In Proc Medical Image Computing and Computer-Assisted Intervention, LNCS. 1998;1496:457–468. [Google Scholar]
- Kiebel SJ, Goebel R, Friston KJ. Anatomically informed basis functions. Neurolmage. 2000;11:656–667. doi: 10.1006/nimg.1999.0542. [DOI] [PubMed] [Google Scholar]
- Langan DA, Molnar KJ, Modestino JW, Zhang J. Use of the mean-field approximation in an EM-based approach to unsupervised stochastic model-based image segmentation. In Proc IEEE International Conference on Acoustics, Speech, and Signal Processing. 1992;3:57–60. [Google Scholar]
- Li TQ, Kastrup A, Takahashi AM, Moseley ME. Function MRI of human brain during breath holding by BOLD and FAIR techniques. NeuroImage. 1999;9:243–249. doi: 10.1006/nimg.1998.0399. [DOI] [PubMed] [Google Scholar]
- Lin FS, Huang TY, Chen NK, Wang FN, Stufflebeam SM, Belliveau JW, Wald LL, Kwong KK. Functional MRI using regularized parallel imaging acquisition. Magnetic Resonance in Medicine. 2005;54:343–353. doi: 10.1002/mrm.20555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liou M, Su HR, Lee JD, Aston JAD, Tsai AC, Cheng PE. A method for generating reproducible evidence in fMRI studies. NeuroImage. 2006;29:383–395. doi: 10.1016/j.neuroimage.2005.08.015. [DOI] [PubMed] [Google Scholar]
- Magnotta VA, Friedman L. FIRST BIRN Measurement of signal-to-noise and contrast-to-noise in the fBIRN multi-center imaging study. Journal of Digital Imaging. 2006;19:140–147. doi: 10.1007/s10278-006-0264-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maitra R, Roys S, Gullapalli R. Test-Retest Reliability Estimation of functional MRI Data. Magnetic Resonance in Medicine. 2002;48:62–70. doi: 10.1002/mrm.10191. [DOI] [PubMed] [Google Scholar]
- Makni S, Idier J, Vincent T, Thirion B, Dehaene-Lambertz G, Ciuciu P. A fully Bayesian approach to the parcel-based detection-estimation of brain activity in fMRI. NeuroImage. 2008;41:941–69. doi: 10.1016/j.neuroimage.2008.02.017. [DOI] [PubMed] [Google Scholar]
- Ou W, Golland P. From spatial regularization to anatomical priors in fMRI analysis. In Proc IPMI, LNCS. 2005;3565:88–100. doi: 10.1007/11505730_8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou W. MIT Master Thesis. 2005. fMRI detection with spatial regularization. [Google Scholar]
- Parisi G. Statistical Field Theory. Addison-Wesley; 1998. [Google Scholar]
- Penny WD, Trujillo-Barreto NJ, Friston KJ. Bayesian fMRI time series analysis with spatial priors. NeuroImage. 2005;24:350–362. doi: 10.1016/j.neuroimage.2004.08.034. [DOI] [PubMed] [Google Scholar]
- Penny WD, Flandin G, Trujillo-Barreto NJ. Bayesian comparison of spatially regularised general linear models. Human Brain Mapping. 2007;28:275–293. doi: 10.1002/hbm.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl KM, Wells WM, Guimond A, Kasai K, Shenton ME, Kikinis R, Grimson WEL, Warfield SK. Incorporating non-rigid registration into expectation maximization algorithm to segment MR images. In Proc Medical Image Computing and Computer-Assisted Intervention, LNCS. 2002;2488:564–571. doi: 10.1007/3-540-45786-0_70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl KM, Bouix S, Kikinis R, Grimson WEL. Anatomical guided segmentation with non-stationary tissue class distributions in an expectation-maximization framework. In Proc IEEE Symposium on Biomedical Imaging. 2004;1:81–84. doi: 10.1109/ISBI.2004.1398479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajapakse JC, Piyaratna J. Bayesian approach to segmentation of statistical parametric maps. IEEE Transactions on Biomedical Engineering. 2001;48:1186–1194. doi: 10.1109/10.951522. [DOI] [PubMed] [Google Scholar]
- Rencher AC. Methods of Multivariate Analysis. Wiley; 2002. [Google Scholar]
- Salli E, Aronen HJ, Savolainen S, Korvenoja A, Visa A. Contextual clustering for analysis of functional MRI data. IEEE Transactions on Medical Imaging. 2001;20:403–414. doi: 10.1109/42.925293. [DOI] [PubMed] [Google Scholar]
- Seghier ML, Lazeyras F, Zimine S, Maier SE, Hanquinet S, Delavelle J, Volpe JJ, Huppi PS. Combination of event-related fMRI and diffusion tensor imaging in an infant with perinatal stroke. NeuroImage. 2004;21:463–472. doi: 10.1016/j.neuroimage.2003.09.015. [DOI] [PubMed] [Google Scholar]
- Strother SC, Anderson J, Hansen LK, Kjems U, Kustra R, Sidtis J, Frutiger S, Muley S, LaConte S, Rottenberg D. The quantitative evaluation of functional neuroimaging experiments: the NPAIRS data analysis framework. NeuroImage. 2002;15:747–771. doi: 10.1006/nimg.2001.1034. [DOI] [PubMed] [Google Scholar]
- Svensen M, Kruggel F, von Cramon DY. Probabilistic modeling of single-trial fMRI data. IEEE Transactions on Medical Imaging. 2000;19:25–35. doi: 10.1109/42.832957. [DOI] [PubMed] [Google Scholar]
- Swensson RG. Unified measurement of observer performance in detecting and localizing target objects on images. Medical Physics. 1996;23:1709–1025. doi: 10.1118/1.597758. [DOI] [PubMed] [Google Scholar]
- Van De Ville D, Seghier ML, Lazeyras F, Blu T, Unser M. WSPM: wavelet-based statistical parametric mapping. NeuroImage. 2007;37:1205–1217. doi: 10.1016/j.neuroimage.2007.06.011. [DOI] [PubMed] [Google Scholar]
- Vincent T, Ciuciu P, Idier J. Spatial mixture modelling for the joint detection-estimation of brain activity in fMRI. Proc ICASSP. 2007;1:325–328. doi: 10.1109/IEMBS.2007.4353518. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Ripley BD, Brady M, Smith SM. Temporal autocorrelation in univariate linear modelling of fMRI data. NeuroImage. 2001;14:1370–1386. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Behrens TE, Beckmann CF, Smith SM. Mixture models with adaptive spatial regularization for segmentation with an application to fMRI data. IEEE Transactions on Medical Imaging. 2005;24:1–11. doi: 10.1109/tmi.2004.836545. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Liao CH, Aston J, Petre V, Duncan GH, Morales F, Evans AC. A general statistical analysis for fMRI data. NeuroImage. 2002;15:1–15. doi: 10.1006/nimg.2001.0933. [DOI] [PubMed] [Google Scholar]
- Wu F. The Potts model. Reviews of Modern Physics. 1982;54:235–268. [Google Scholar]
- Zou KH, Greve DN, Wang M, Pieper SD, Warfield SK, White NS, Manandhar S, Brown GG, Vangel MG, Kikinis R, Wells WM. Reproducibility of functional MR imaging: preliminary results of prospective multi-institutional study performed by biomedical informatics research network. Radiology. 2005;237:781–789. doi: 10.1148/radiol.2373041630. [DOI] [PMC free article] [PubMed] [Google Scholar]