Predicting efficacy of radiotherapy in individual glioblastoma patients in vivo: a mathematical modeling approach

Abstract

Glioblastoma multiforme (GBM) is the most malignant form of primary brain tumors known as gliomas. They proliferate and invade extensively and yield short life expectancies despite aggressive treatment. Response to treatment is usually measured in terms of survival of groups of patients treated similarly but this statistical approach misses the subgroups that may have responded to or may have been injured by treatment. Such statistics offer scant reassurance to individual patients who have suffered through these treatments. Furthermore, current imaging-based treatment response metrics in individual patients ignore patient-specific differences in tumor growth kinetics, which have been shown to vary widely across patients even within the same histological diagnosis and, unfortunately, these metrics have shown only minimal success in predicting patient outcome.

We consider nine newly diagnosed GBM patients receiving diagnostic biopsy followed by standard of care external beam radiation therapy (XRT). We present and apply a patient-specific, biologically-based mathematical model for glioma growth that quantifies response to XRT in individual patients in vivo. The mathematical model uses net rates of proliferation and migration of malignant tumor cells to characterize the tumor’s growth and invasion along with the linear-quadratic model for the response to radiation therapy. Using only routinely available pre-treatment MRIs to inform the patient-specific bio-mathematical model simulations, we find that radiation response in these patients, quantified by both clinical and model-generated measures, could have been predicted prior to treatment with high accuracy. Specifically, we find the net proliferation rate is correlated with the radiation response parameter (r = 0.89, p = 0.0007), resulting in a predictive relationship that is tested with a leave-one-out cross validation technique. This relationship predicts the tumor size post therapy to within inter-observer tumor volume uncertainty.

The results of this study suggest that a mathematical model can create a virtual in silico tumor with the same growth kinetics as a particular patient and can not only predict treatment response in individual patients in vivo but also provide a basis for evaluation of response in each patient to any given therapy.

Introduction

Glioblastomas are uniformly fatal primary brain tumors characterized by their extensive diffuse invasion of the normal brain parenchyma and associated with a median survival of 10–12 months (Alvord and Shaw, 1991). These characteristics lead to aggressive treatment strategies that most often include surgery, irradiation, and chemo-therapies. This somewhat algorithmic approach to treatment leads to prompt action once the tumor is diagnosed. Magnetic resonance imaging (MRI) is used to detect these tumors, and at the time of operation a second MRI image is often acquired for surgical guidance. It is from these two pre-treatment images that we are able to calculate kinetics of untreated tumor growth (Harpold et al., 2007; Swanson et al., 2002b; Wang et al., 2009), specifically estimating net rates of proliferation and invasion for the individual patient in vivo (Harpold et al., 2007). When combining these rates with our biologically-based mathematical model for glioma growth and invasion, the resultant in silico tumor accurately predicts subsequent untreated tumor growth in individual patients so well that it is a prognostic indicator of durations of survival before therapy even begins (Harpold et al., 2007; Wang et al., 2009). This study extends our prior successes with in silico prediction of tumor growth to incorporate the effects of external beam radiation therapy (XRT) in nine histologically diagnosed glioblastoma patients.

Background and Original PI Glioma Model

Our biologically-based modeling efforts are based on the hypothesis that, from a clinical standpoint, gliomas can be quantitatively characterized by two net rates: proliferation (ρ) and invasion (D) (PI model) – e.g., see Harpold et al (Harpold et al., 2007) for a recent review.

$$\stackrel{\begin{array}{c}\text{rate}\text{of}\text{change}\text{of}\\ \text{glioma}\text{cell}\text{concentration}\end{array}}{\overbrace{\frac{\partial c}{\partial t}}}=\stackrel{\begin{array}{c}\text{net}\text{dispersal}\\ \text{of}\text{glioma}\text{cells}\end{array}}{\overbrace{\nabla ·(D\nabla c)}}+\stackrel{\begin{array}{c}\text{net}\text{proliferation}\\ \text{of}\text{glioma}\text{cells}\end{array}}{\overbrace{\rho c\left(1-\frac{c}{k}\right)}}$$ Equation 1

Equation 1 is a reaction-diffusion partial differential equation that describes the density of glioma cancer cells (c) in terms of two net rates: proliferation (ρ) and invasion (D) (PI model). c = c(x,t) is the tumor cell density at time t and location x in units cells/mm³. D is the net invasion rate (mm²/year), ρ is the net proliferation rate (1/year), and k is the tumor cell carrying capacity of the tissue (10⁸ cells/mm³), supposing a 10-μm diameter tumor cell with logistic growth. We impose no-flux boundary conditions (n · ∇c = 0) to prevent tumor cells from leaving the brain domain B at its boundary ∂B. This model is not cell-based but describes the density of tumor cells and therefore reflects net measures of proliferation and motility for the entire population of tumor cells, down-stream from individual-cell behavior.

Major Assumptions of the PI Model

The PI model assumes glioma cell invasion throughout the brain is a diffusion process with diffusion coefficient D. The model also assumes logistic growth of the tumor cell population, so that the net proliferation rate (ρ) is lower in regions of high cell density (where c ≈ k) than in regions of low cell density (where c is much less than k). Our PI model for glioma growth uses a “tip of the iceberg” view of clinical imaging, where post-contrast T1-weighted (T1Gd) and T2-weighted MRI are associated with isosurfaces of constant density, and are used to infer a gradient of tumor cells (Harpold et al., 2007). The key consequences of this model (Equation 1) are 1) an approximately linear radial growth of the abnormality seen on imaging, which approaches a constant velocity of $2\sqrt{D\rho }$ defined by Fisher’s approximation (Fisher, 1937), and 2) a diffuse gradient of tumor cells peripheral to the imaging abnormality, characterized by an invisibility index, which is the ratio of the model parameters, D/ρ (Harpold et al., 2007; Swanson, 1999). A constant velocity of MR imageable growth has been demonstrated for 27 untreated low grade gliomas (Mandonnet et al., 2003) and for at least one untreated high grade glioma (Swanson and Alvord, 2002a; Harpold et al., 2007; Swanson and Alvord, 2002b) computed from serial MRI observations. Further, model-defined rates of biological aggressiveness (D and ρ) have been found to be predictive of survival, even when controlling for the standard clinico-pathologic prognostic parameters (Wang et al., 2009). The PI model has also been successfully applied to quantifying the effects of surgical resection in glioblastoma patients (Swanson et al., 2008b). Other modeling efforts have focused on non-clinical situations such as in vitro experiments or are not patient-specific due to the large number of parameters to be estimated (Ribba et al., 2006; Enderling et al., 2006; Stamatakos et al., 2006; Stamatakos et al., 2007).

Response to XRT is typically measured in terms of survival of groups of patients treated similarly. Additionally response to XRT can be quantified in individual patients in terms of changes in gross tumor volume (GTV) as observed on MRI and then classified according to the response criteria for solid tumors (RECIST) or MacDonald criteria, which classify response into one of four broad categories (Galanis et al., 2006; Padhani and Ollivier, 2001; Therasse et al., 2006), as illustrated in Figure 1. Not only is there an absence of a more quantitative measure of response, but currently there is no model for treatment delivery or response for individual patients, in vivo, that can extend beyond statistical measures of survival. We present and investigate an extension of a biologically-based mathematical model for glioma growth that quantifies the delivery of and response to XRT in individual patients, in vivo. Using the classic linear-quadratic model for radiation efficacy and following Swanson et al (Swanson et al., 2000), we model untreated glioma growth as well as XRT effects in individual glioma patients and consider patient-specific virtual controls to investigate model-predicted survival assuming a fatal tumor burden defined by both T1GD radius of 3.5 cm (Swanson et al., 2008a).

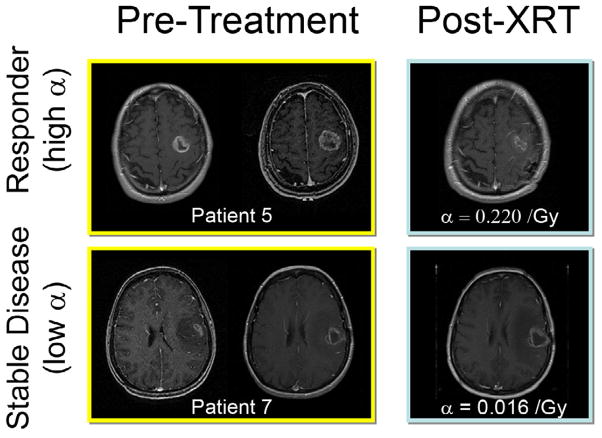
Figure 1.

Response to therapy is conventionally assessed by determining changes in gross tumor volume (GTV) on MRI prior to and after the administration of therapy. Post-contrast T1-weighted MRI images are shown for two glioblastoma patients that would typically be separated into generic groups: responder and stable disease. Radiation response parameter α gives an additional quantification of radiation response for each patient.

Materials and Methods

Radiation Therapy Model

We investigate an extension of the PI model (Equation 1) for untreated glioma growth to include the effects of XRT using the classic linear-quadratic model for radiation efficacy. Equation 2a is the well known linear-quadratic model for radiation efficacy (Hall, 1994) that relates the radiation Dose, defined in both space and time in units Gy (Gy = 1 J/kg), to a unitless effective dose E. The coefficients α (Gy⁻¹) and β (Gy⁻²) are the radiobiology parameters and determine the relative contribution of each term in the sum toward the total radiation effect and are sometimes interpreted biologically as repairable single and lethal double strand breaks to the cell’s DNA respectively (Hall, 1994). The linear-quadratic model is based on empirical dose-response data and is widely used in clinical applications. The ratio of the parameters α/β represents the tissue response: for early effects the ratio α/β is large and α dominates for small doses, for late effects, the ratio α/β is small and β dominates at small doses. In our model simulations the ratio α/β is held constant throughout the tumor, with α and the dose distribution determined by the individual patient data. Equation 2b is the probability of survival of glioma cells after the administration of radiation Dose such that the larger the dose, the smaller the probability of survival.

$$E=\alpha \mathit{Dose}+\beta {\mathit{Dose}}^2$$ Equation 2a

$$S=exp(-E)$$ Equation 2b

For each point in space and time, an effective dose and probability of cell survival can be calculated that corresponds uniquely to the individual patient’s treatment plan and radiobiology parameter (α). Increasing α decreases the probability of cells surviving, S, and therefore increases the probability of external beam radiation therapy (XRT) induced cell death.

$$\stackrel{\begin{array}{c}\text{rate}\text{of}\text{change}\text{of}\\ \text{glioma}\text{cell}\text{concentration}\end{array}}{\overbrace{\frac{\partial c}{\partial t}}}=\stackrel{\begin{array}{c}\text{net}\text{dispersal}\\ \text{of}\text{glioma}\text{cells}\end{array}}{\overbrace{\nabla ·(D\nabla c)}}+\stackrel{\begin{array}{c}\text{net}\text{proliferation}\\ \text{of}\text{glioma}\text{cells}\end{array}}{\overbrace{\rho c\left(1-\frac{c}{k}\right)}}-\stackrel{\begin{array}{c}\text{loss}\text{due}\text{to}\\ \text{radiation}\text{therapy}\end{array}}{\overbrace{R(\mathbf{x},t,\mathit{Dose})c\left(1-\frac{c}{k}\right)}}$$ Equation 3

where $R(\mathbf{x},t,\mathit{Dose}(\mathbf{x},t))\equiv \{\begin{array}{lll}0\hfill & \mathit{for}\hfill & t\notin \mathit{therapy}\hfill \\ \left(1-S(\alpha ,\beta ,\mathit{Dose}(\mathbf{x},t))\right)\hfill & \mathit{for}\hfill & t\in \mathit{therapy}\hfill \end{array}$

Equation 3 is a straight-forward extension of the PI model (Equation 1) to include the effects of XRT, represented by the coefficient R in the loss term. The effect of XRT is incorporated into model Equation 1 by considering the loss of cells due to XRT in terms of a death probability from Equation 2b. R represents the effect of XRT on the tumor cell population at a location x and time t where the effect is given by the probability of death (one minus the probability of survival) from the linear-quadratic model of radiation efficacy. Methodology and structure are detailed in Rockne et al (Rockne et al., 2009) and summarized in the supplementary material. The death probability is a function of the linear-quadratic model parameters α (Gy⁻¹) and β (Gy⁻²) and the radiation dose distribution (Dose(x, t) ) and is only applied during therapy. Similar to Equation 1, the model for radiation effect R is a net measure and considers the random damage, repair, and delivery of radiation to be upstream from the net deterministic measure of survival probability, although the linear-quadratic model can be derived from stochastic principles (Sachs et al., 2001).

Model assumptions

We assume XRT and its effect to be instantaneous, deterministic, and estimated by the linear-quadratic model and its corresponding probability of cellular survival/death. For low cell densities, the effect of XRT is manifest as a fraction of cells killed as a result of XRT. However, at large cell densities, it is assumed that the effect saturates in the same manner that the net proliferation saturates. Thus, the radiation effect R has the effect of mediating the net proliferation of the glioma cells to mimic a net slowing of proliferation in those regions occurring as a result of cell crowding and depletion of the microenvironment. This assumption is consistent with the classic radiobiological understanding that cells actively undergoing mitosis are more susceptible to DNA damage (Hall, 1994), which the linear-quadratic model for radiation efficacy assumes to be the mechanism for radiation-induced cell death (Sachs et al., 1997; Sachs et al., 2001; Cunningh and Niederer, 1972). For simplicity in our initial investigation, with the dose distribution and treatment schedule fixed, we regard α as our sole radiation efficacy parameter and leave α/β fixed at 10 Gy to approximate the radio-responsiveness of early responding tissue such as proliferating tumor cells (Hall, 1994; Sachs et al., 2001; Jones and Dale, 1995; Enderling et al., 2006; Jones and Dale, 1999; Lee et al., 1995; Garcia et al., 2006). An explicit model for the delivery of and response to chemotherapy is beyond the scope of this investigation, however, we assume that the effect of concurrent chemotherapy is included in the net response parameter α.

Patient Population

Three females and six males, with a mean and median age of 58 and 56 years, respectively, at the time of histologically diagnosed glioblastoma multiforme (WHO grade IV) (Kleihues et al., 2002) consented to this study approved by our local institutional review board. In addition to XRT details, recursive partitioning analysis (RPA) (Shaw et al., 2003) and extent of resection (EOR) were recorded for each patient (Table 1). All nine patients received XRT and had at least two pre-treatment and one post-XRT pair of T1Gd and T2 MRI observations.

Table 1.

Summary of model parameters and clinical information for all nine patients with glioblastoma multiforme included in the study. Survival is calculated in months, relative to the first MRI observation.

Patient	Age	EOR	T1Gd Velocity (mm/year)	T2 velocity (mm/year)	D (mm2/year)	ρ (/year)	α T1Gd (/Gy)	αT2 (/Gy)	Survival from 1st MRI observation (months)	Concurrent Chemo
1*	63	BX	50.9	32.1	18.43	35.13	0.244	0.162	88.0	TMZ
2*	43	BX	195.4	0.0	7.52	12.68	0.085	0.137	24.3	TMZ
3	53	BX	85.3	19.9	27.70	3.59	0.000	0.005	34.3	-
4	63	BX	83.8	21.9	7.88	15.24	0.004	0.000	13.2	TMZ
5	49	STR	42.3	66.9	8.90	50.29	0.222	0.265	18.8	BCNU + TMZ
6*	73	BX	24.3	−61.6	10.82	13.68	0.023	0.076	40.3	TMZ
7	56	BX	53.1	11.2	50.71	13.88	0.016	0.028	12.8	TMZ
8	63	BX	20.1	44.1	12.64	7.99	0.016	0.032	15.6	TMZ
9	45	STR	1.9	21.1	6.56	17.04	0.115	0.084	21.3	TMZ

^*indicates patient is still alive

MRI Segmentation

Gross tumor volumes (GTV) were calculated for each T1GD and T2 imaging pair through a semi-automated technique based on background subtraction, which allows a user to select only those voxels that contain tumor-related abnormal signal (Ridler and Calvard, 1978). Each segmented volume is translated to a mean radius by supposing the 4 3 geometry of a sphere with equivalent volume: $\mathit{GTV}=\frac{4}{3}\pi r^3$.

We averaged the GTV found by at least two independent observers for each image. Pre-treatment GTV measurements included regions of central necrosis (i.e. visible as hypo-intense on T1Gd). Post-operative scans also included regions of necrosis but excluded the resection bed from the GTV calculation, as the tumor cells are prevented from diffusing into that brain space, which hypothetically contains no tumor cells, dead or alive.

Velocity of Growth

Radial velocity of tumor growth was estimated using the slope of a line of best fit (linear regression) between the pre-treatment radii obtained from both T1Gd and T2 MRI GTVs. Mean and median T1Gd pre-treatment velocity for the population were 62 and 51 mm/year, respectively, with mean and median of 43 and 21 days between pretreatment scans. Mean and median velocity on T2 were 17 and 21 mm/year. We selected patients with a minimum of five days between pre-treatment images and/or at least a 1 mm increase in tumor radius on T1Gd in order to detect a significant non-zero velocity of growth. Fisher’s approximation for the velocity of radial growth provides a relationship between the model parameters (D, ρ) and the measured velocity, $v=2\sqrt{D\rho }$ (Fisher, 1937; Murray, 2003). Table 1 tabulates the patient characteristics.

Calculation of Patient-Specific Untreated PI Model Parameters

As established by us elsewhere (Harpold et al., 2007) the T1Gd MRI abnormality is associated with increased vascularity and “solid tumor,” while the T2 abnormality is associated with a low density of diffuse invasion (Harpold et al., 2007), from which a tumor cell gradient (D/ρ) is inferred. With the ratio D/ρ and velocity ( $v=2\sqrt{D\rho }$), both model parameters D and ρ can be calculated for each patient, uniquely characterizing that glioma’s untreated growth kinetics (Table 1).

Model Simulations

Three-dimensional simulations of untreated and XR-treated growth (Equation 3) supposing spherical symmetry were performed for each patient using the function pdepe in MATLAB (Skeel and Berzins, 1990). A small, Gaussian distribution of 2²⁰ cells, or almost 1 mm³ of initial tumor cells, is used to seed the tumor growth and is necessary to prevent gliomatosis cerebri, which is a diffuse saturation of malignant cells throughout the brain without the formation of a focal neoplasm (Rockne et al., 2009). With patient-specific PI model parameter values estimated (as above), a virtual tumor was created for each patient that matched the kinetics of that individual’s tumor. For each virtual patient, “clinical day zero” was defined to be the time point at which the simulated tumor volume matched the measured GTV from the first T1Gd observation. Resection to whatever extent applicable was then modeled by truncating the computational domain such that the simulated T1Gd radius matched that measured on the post-operative MRI observation, with boundary conditions adjusted accordingly to prevent tumor cells from migrating into the virtual resection cavity, following Woodward et al (1996) (Woodward et al., 1996) and Swanson et al (2003) (Swanson et al., 2003). Because of the assumption of spherical symmetry, only glioma patients receiving a biopsy or less than 25% resection of their pre-operative GTV were selected. For those patients with sub-total resections (STR), the spatial effect of surgical resection was minimal and assumed to take place at the center of the spherically symmetric tumor by matching the corresponding decrease in the measureable GTV. Patients receiving biopsy only were not considered to have had a significant surgical intervention and therefore no surgery was modeled.

Radiation Therapy Plan Details and Dose Distribution

XRT protocols and prescriptions were available for each patient. Six of the patients in the study received XRT at the University of Washington Medical Center (UWMC). The remaining three patients were treated at the University of California in Los Angeles. In accordance with the current standard of care at the UWMC, patients received 50.4 Gy to the T2-defined abnormality with a 2.5-cm margin, in equal doses of 1.8 Gy/day for six weeks for a dose of 54 Gy, followed by a boost defined by the T1Gd abnormality plus a 2-cm margin to a total of 59.4–61.2 Gy, in equal doses of 1.8 Gy/day for one week, with treatment administered on weekdays only. Spherically symmetric dose distributions were defined spatially by the UWMC protocol unless otherwise specified by prescription (see Supplemental Material, Rockne et al (Rockne et al., 2009) for methodology). Each simulated tumor received exactly the radiation dose and plan clinically prescribed, in both space and time.

Calculation of Patient-Specific Radiation Response Parameter

After the establishment of clinical day zero within the simulation, surgery to whatever extent was modeled, then XRT was simulated to precisely follow the patient’s individual treatment plan and time course relative to clinical day zero. Additionally, the day of the week on which treatment began was recorded in order to simulate therapy taking place only on weekdays. In order to estimate the value of radiation model parameter α (Gy⁻¹) (equation 2a) for each patient, a range of values for α are chosen and XRT is simulated for each, with the difference between the simulated T1Gd and T2 radii and the observed recorded for each patient (Figure 2). The first post-XRT MRI is considered the “XRT target date,” with its associated “target radius.” Increasing α decreases the probability of glioma cells surviving, S (equation 2b), and therefore increases the probability of XRT-induced glioma cell death. Therefore, for fixed growth kinetics D and ρ, simulations using a large α correspond to a large “effect,” or deviation from model-predicted untreated growth, while values of α near zero correspond to minimal to no deviation from the model-predicted untreated pattern of growth. We therefore consider α as a quantification of the degree of response to XRT. Since the relationship between D, ρ, and α is non-linear and spatially variable according to the patient-specific dose distribution and schedule, XRT was simulated several times, with a wide range of α values, yielding a relationship between α and the simulated imageable XRT response unique to the patient. Regression was then performed to yield a value of α that minimized the difference between the simulated and actual target radius, the accuracy of which is limited only by the resolution of the in silico computational grid, which is 0.12 mm—far beyond the most highly resolved MRIs considered in this study. To determine if there was any bias in choosing either of the MRI-defined abnormalities as the target, optimal values for α were found using both T1Gd and T2 post-XRT target radii and are denoted αT1Gd and αT2, respectively.

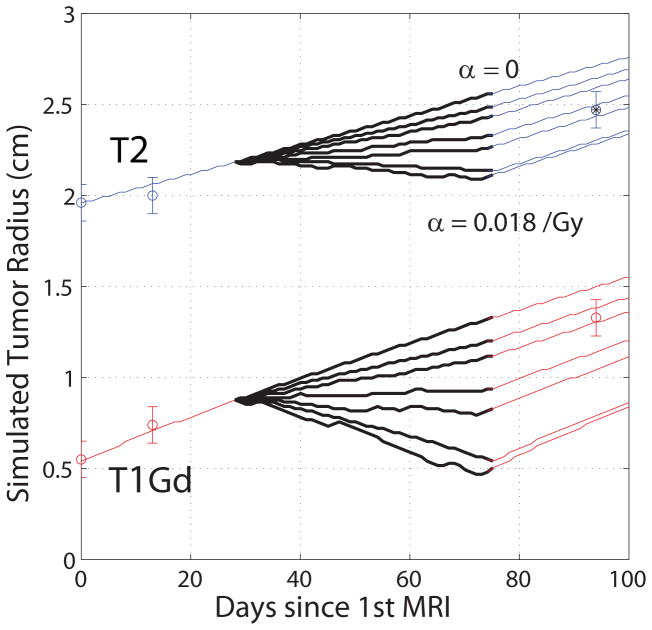
Figure 2.

Spherically symmetric, radial tumor growth and XRT for patient #7 for six values of α ranging from zero (no effect) to 0.018/Gy (high effect) in 0.003/Gy increments, with XRT interval denoted by thick black lines (~day 30 – day 75). We see the optimal value of α on T2 lies between the fourth and fifth curves from the top. Two pre-XRT and one post-XRT observations are shown. The asterisk indicates data point used to calculate an optimal value for α using a regression with α and the error between simulated and actual target radius.

Patients that were unable to meet the T1Gd or T2 post-XRT target radius for any nonnegative value of α were tabulated as having an α value of zero (see Table 1 and Supplemental Material). These patients had a velocity of growth during treatment greater than that measured prior to treatment. These patients were unable to meet the post-therapy target radius without an accelerating effect of XRT on the tumor growth, (α < 0), which we assumed not to exist.

Error and Uncertainty Analysis

Latin hypercube sampling (Helton and Davis, 2002) was used to test the sensitivity of model outcomes to perturbations in the original PI model parameters. A leave-one-out cross-validation (LOOCV) (Shao, 1993) was performed on the relationship between model parameters ρ and α to validate and assess the accuracy of our patient-specific XRT model outcome predictions. Each patient was systematically removed from the population and a new regression was established between α and ρ. Based on the new line of regression, a value for α was computed for the patient removed and XRT simulated. The difference between the simulated post XRT tumor size and the data was defined to be the error in the prediction. The median radial error for T1Gd and T2 post XRT tumor sizes were 2.4 mm and 4.5 mm respectively. By iterating through all nine patients in the population, error bars were determined for each patient by taking the maximum and minimum values of the range of the nine values of α determined by the leave-one-out process.

Metrics of Response

Glioma response to therapy is multivariate, with the additive, compounding effects of surgical resection and concurrent chemo-therapy influencing T1Gd and T2 abnormalities and GTVs, respectively. We considered several metrics for quantifying response to XRT in order to investigate their relationship to the radiation model parameter α.

• Last observation effect (LOE) is similar to that used for the response evaluation criteria in solid tumors (RECIST) (Galanis et al., 2006; Padhani and Ollivier, 2001; Therasse et al., 2006): the percent change in radius from the last pre-XRT observation to the first post-XRT observation.

• Cell kill (CK) is defined as the model-predicted ratio of the total number of simulated cells at the start to that at the end of therapy.

Patient-Specific Virtual Controls

Following our previous work modeling XRT in individual gliomas patients (Swanson et al., 2008a), we considered a fatal tumor burden (FTB) defined in terms of radius and compared actual survival relative to the first MRI observation to that predicted by the attainment of a FTB if left untreated using the patient’s specific model parameters and data.

Results and Discussion

Simulations of XRT on nine patients with histologically diagnosed glioblastoma multiforme (WHO grade IV) suggest that response to therapy, measured by changes in gross tumor volume observed on T1Gd and T2-weighted MRI, can be predicted and quantified based on relationships between model parameters and various measures of XRT response and effect.

To our knowledge, this is the first model for estimating radiobiologic parameters for individual patients, in humans, in vivo. Other models presented by Stamatakos, Enderling, Ribba and others (Enderling et al., 2007; Enderling et al., 2006; Ribba et al., 2006; Stamatakos et al., 2006; Stamatakos et al., 2007; Bauman et al., 1999b; Bauman et al., 1999a) either deal with tumor spheroids in vitro, or have yet to be applied to a patient population, and often rely on several parameters that cannot be tailored to the individual or calculated in vivo.

Patient-Specific Net Rate of Proliferation (ρ) and Radiobiologic Response Parameter (α) are Correlated

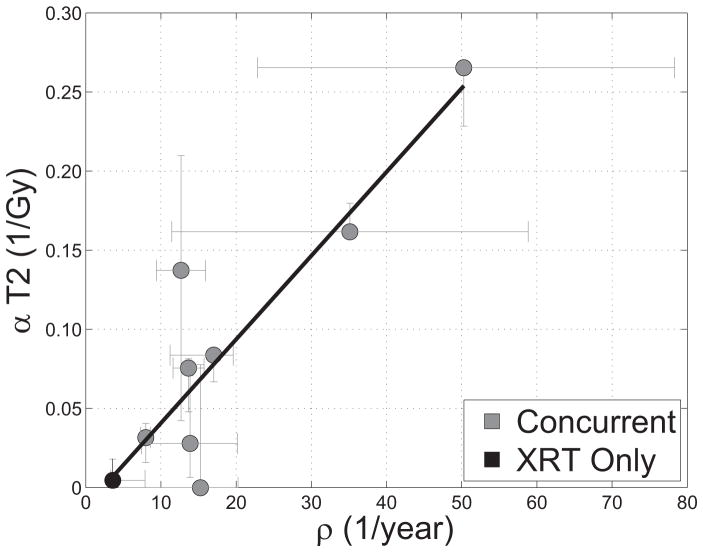
Each patient’s radiation response parameter α is strongly correlated to the pre-treatment net proliferation rate ρ (Figure 3, r = 0.89, p = 0.0007), suggesting that α can be predicted from ρ for any individual patient pre-treatment (Figure 3). From a mathematical perspective, this correlation is not surprising, since the model extension effectively varies only the proliferation rate through the probability of cell death (1 – S) as determined via the linear-quadratic model for radiation efficacy. However, the combination of spatial and temporal heterogeneity of the administered dose adds formal complexity to what might otherwise be considered a straight-forward relationship between the two parameters. Moreover, the relationship between α and ρ is an observed outcome from the data, which could easily have yielded a non-linear relationship between the model parameters. From a radiation oncology perspective, the relationship between proliferation rate and XRT response makes sense: actively proliferating cells are more susceptible and have greater response to XRT (Wilson et al., 2006). Moreover, our computed values for α lie within published ranges (Garcia et al., 2006; Qi et al., 2006; Yang et al., 1990) that use a variety of estimation methods, none of which are based upon clinical imaging. This suggests not only that this model provides a novel technique for assessing the untreated rate of invasion and proliferation of gliomas, but also that the classically defined XRT response parameter α can be estimated from clinical imaging and can potentially be predicted in vivo, prior to treatment.

Figure 3.

Relationship between radiation response and tumor proliferation rate parameters α (Gy⁻¹) and ρ (1/year), respectively, with α calculated relative to changes in T2 GTV post therapy r = 0.89, p = 0.0007 N = 9. Error bars on ρ are calculated by propagation of error in pre-treatment GTV as assessed by inter-observer variability of ± 1 mm in equivalent spherical radius. Error bars in α are computed by taking the maximum and minimum values of α in a leave-one-out cross-validation (LOOCV) technique.

Treatment Response can be Predicted in Individual Patients from Pre-Treatment Imaging

Our ability to predict α from ρ prior to treatment was confirmed with a leave-one-out cross-validation technique (LOOCV) (Shao, 1993; Martens and Dardenne, 1998) that, when translated to the difference in radius between the simulation and actual imaging data, gives a median error for T1Gd and T2 post XRT tumor sizes were 2.4 mm and 4.5 mm, respectively. We have estimated our inter-observer error tumor radius computed from the measurement of GTV to be ± 1 mm. This suggests that the predictive relationship between α and ρ is at least greater than the error expected in our data collection methodology and at the same time precise, given the limited number of patients in the study. The LOOCV technique also demonstrates the robustness of the prediction accuracy to outlying data points, such as patient #5. Although it is not surprising that a LOOCV technique is able to re-capitulate results of a fitted parameter, what is significant is that the model parameter ρ can be assessed prior to treatment. We can use pre-treatment kinetics to stratify, in a quantitative manner, patients into those more or less likely to respond to therapy prior to treatment.

Surprisingly, the radiation parameter α is not correlated to the rate of invasion D (r = −0.35), suggesting that tumor response may be independent of the degree of invasiveness, although the contribution of cells that lie below the threshold of detection cannot be underestimated.

Standard Treatment Response Metrics Do Not Correlate with Model Measures of Radiosensitivity

In order to compare our simulations to classical metrics of treatment response such as the RECIST (Padhani and Ollivier, 2001) or MacDonald (MacDonald et al., 1990) criteria, which rely on changes in GTV prior to and immediately following therapy, we considered alternative novel metrics of response. A less tangible, model-defined metric of cell kill provides a model-specific perspective on radiation efficacy and is correlated to α, which follows the interpretation of the linear-quadratic model as it relates to log cell kill. Table 2 summarizes the correlations between radiobiological model parameter α and response metrics.

Table 2.

Pearson correlation coefficient squared (r²) and p value for relationships between model radiation parameter α and measures of effect. Significant correlations are in bold.

Variable 1	Variable 2	r^2	P value
α (/Gy)	D (mm^2/year)	0.08	0.468
α (/Gy)	Last Observation Effect	0.25	0.166
α (/Gy)	Total Cells Effect	0.71	0.002

These novel and patient-specific metrics of response stand in stark contrast to the current schemes provided by the RECIST (Padhani and Ollivier, 2001) and MacDonald (MacDonald et al., 1990) criteria, which group patients into broad categories from stable disease to complete response with very little grey area between them. In light of the generally poor response seen in this patient population across all response metrics, combined with the overall poor response of high grade gliomas to any treatment whatever, a more highly resolved response scale is not only appropriate but could prove necessary in the future of glioma treatment. Our model of glioma growth and response to XRT provides an opportunity to develop response metrics that take into account invasive glioma cells that lie beneath the threshold of detection for standard clinical imaging techniques such as T1Gd and T2 MRI and to provide a more complete picture of disease response than those provided by the RECIST or MacDonald criteria, which are based solely on MRI abnormality defined volumes. Moreover, the last observation effect is not correlated with either ρ or α, suggesting that our definition and quantification of treatment response is not essentially equivalent to already established response metrics.

Metrics of Glioma Growth and Treatment Response are Robust to Uncertainty in GTV

We performed Latin hypercube sampling (LHS) uncertainty analysis on all model parameters: D, ρ, and α. Specifically, we performed LHS on the parameter ranges resulting from a ± 1 mm deviation in radius to our model parameter estimation. Unlike standard sensitivity analysis for which only one parameter is typically varied, in LHS all parameters (D, ρ, α) are allowed to vary at the same time. We applied LHS specifically to patient 6, with a sample size of 100, in which each simulation is a manifestation of randomly sampling parameter values from each respective parameter’s associated confidence interval. We assumed the parameter values to be normally distributed. The resulting collection of virtual tumors showed an amplifying uncertainty in our result as the virtual tumor progressed through simulated XRT. However, the magnitude of even the largest variation from either the mean or median of the simulation remained within our LOOCV envelope of 1.8 mm, suggesting that our model is robust to variations in both the untreated (D, ρ) model parameters as well as our radio-biological response parameter (α).

Effects of concurrent chemo-therapy and other medicines, including steroids prior to and during treatment were considered to be incorporated into the radiation parameter α, and therefore the value of α may be overestimated relative to XRT administered without chemo-therapy. We acknowledge the role chemo-therapy can and surely does play in tumor response to therapy, but at this time we do not explicitly incorporate its effects into the model. Swanson et al have previously investigated the role of steroids on the estimation of the ratio of PI model D/ρ and showed no statistical difference between two populations of patients, one receiving steroids and the other not (Swanson et al., 2002a).

XRT Response Metric is Robust to Choice of MRI Modality

Because T1Gd MRI is thought to represent the location of the bulk tumor mass as characterized by the leaky vasculature, it can be considered an indicator of tumor growth. It may not, however, be adequate at representing response to therapy, particularly XRT, as the XRT damage may not cause rapid shrinkage of the T1Gd abnormality. It is nevertheless used as a clinical indicator (MacDonald et al., 1990; Padhani and Ollivier, 2001) with some debate as to its true relationship to response (de Wit et al., 2004; Tsien et al., 2007). Similarly, increased signal from radiation-induced inflammation on T2-weighted MRI may be mistaken for actual disease-related edema. Interestingly, our values for radiation parameter α computed using T1Gd and T2 target radii were highly correlated, somewhat mitigating concern over which modality to select as a target. Regardless of the interpretation of T1Gd and T2 as indicators of response, this modeling approach connects the cell gradient (represented by the ratio of untreated model parameters ρ/D) to T1Gd and T2 MR imaging modalities. Therefore any change in GTV pre- to post-therapy is related to a corresponding change in the local cell density. Response rates as measured with T1Gd radius as target versus using T2 are highly correlated with r = 0.89, p = 0.0006. The T1Gd response parameter was also highly correlated with the net proliferation rate, r = 0.89, p = 0.0007.

Treatment Response and Pseudo Progression

In order to address concerns regarding robustness of our results to “pseudo-progression” (de Wit et al., 2004; Taal et al., 2008) of disease induced by therapy, we performed our analysis using the second post-XRT MRI observation (instead of the first) as our target for calculating α. The second MRI observation post XRT generally occurred 50–60 days after the end of therapy. This simply resulted in a translation of the range of α values, leaving all results intact (data not shown). This suggests that the value of α depends on the target observation time relative to the end of therapy and calls for a more detailed modeling approach that incorporates delayed radiation effects. Nevertheless, the robustness of the results relative to the time of the target observation suggests that the model remains useful as a predictor of response, as long as the limitations of the model prediction beyond the target date are kept in mind.

Efficacy of Radiotherapy is Predictable in Individual Glioblastoma Patients in vivo

This pilot study establishes a methodology that can be readily translated into a full three-dimensional, anatomically accurate, patient-specific simulation of virtual tumor growth and response to XRT. Further model development will include focal XRT resistance in the form of an oxygen enhancement ratio (OER) addition to the linear-quadratic model based on regions of hypoxia as defined by the ¹⁸F-Flouromisonidazole (FMISO) radiotracer used in PET imaging (Spence et al., 2008). Additionally, model extensions to incorporate normal tissue toxicity and delayed treatment effects will be investigated with the use of three-dimensional XRT dose plans and patient-specific tissue segmentation and anatomy. Optimization of treatment through altered fractionation and/or treatment field design can be investigated and compared to virtual controls, either untreated or with the conventional therapy course.

General Summary.

Glioblastoma multiforme (GBM) is the most malignant form of primary brain tumors known as gliomas. They proliferate and invade extensively and yield short life expectancies despite aggressive treatment. Response to treatment is usually measured in terms of survival of groups of patients treated similarly. Furthermore, current imaging-based treatment response metrics in individual patients ignore patient-specific differences in tumor growth kinetics, which have been shown to vary widely across patients even within the same histological diagnosis and, unfortunately, these metrics have shown only minimal success in predicting patient outcome.

We present a patient-specific, biologically-based mathematical model for glioma growth that quantifies response to external beam radiation therapy in individual patients in vivo. Using only routinely available pre-treatment MRIs to inform the patient-specific bio-mathematical model simulations, we find that radiation response in these patients, quantified by both clinical and model-generated measures, could have been predicted prior to treatment with high accuracy.