Physiologically Based Pharmacokinetic Modelling of Drug Penetration Across the Blood–Brain Barrier—Towards a Mechanistic IVIVE-Based Approach

Abstract

Predicting the penetration of drugs across the human blood–brain barrier (BBB) is a significant challenge during their development. A variety of in vitro systems representing the BBB have been described, but the optimal use of these data in terms of extrapolation to human unbound brain concentration profiles remains to be fully exploited. Physiologically based pharmacokinetic (PBPK) modelling of drug disposition in the central nervous system (CNS) currently consists of fitting preclinical in vivo data to compartmental models in order to estimate the permeability and efflux of drugs across the BBB. The increasingly popular approach of using in vitro–in vivo extrapolation (IVIVE) to generate PBPK model input parameters could provide a more mechanistic basis for the interspecies translation of preclinical models of the CNS. However, a major hurdle exists in verifying these predictions with observed data, since human brain concentrations can’t be directly measured. Therefore a combination of IVIVE-based and empirical modelling approaches based on preclinical data are currently required. In this review, we summarise the existing PBPK models of the CNS in the literature, and we evaluate the current opportunities and limitations of potential IVIVE strategies for PBPK modelling of BBB penetration.

INTRODUCTION

It has long been acknowledged that the early and accurate prediction of drug penetration across the blood–brain barrier (BBB) is vital during their development, given the high failure rate of drugs developed for central nervous system (CNS) indications (1). It is equally important to predict the brain penetration of non-CNS drugs in order to avoid complications in the later phases of drug development due to unforeseen neurotoxicity. The traditional modelling approaches used to predict the brain penetration of CNS drugs consisted of correlating the extent of their steady-state brain distribution in preclinical species, defined as the ratio of total drug concentrations in brain versus in blood or plasma (referred to as either K_p,brain or logBB), with their molecular properties (2–4). However, the use of such correlations to predict human brain/blood ratios have several limitations—They are based on total rather than unbound concentrations, they are single-point measures rather than pharmacokinetic profiles, and they represent the net effect of several different kinetic processes, which may differ between species (5). Low in vivo efficacy may arise for CNS drugs, which are developed based solely on optimising their K_p,brain values, since drugs with high K_p,brain values are generally lipophilic compounds, which rapidly cross the BBB, but which then exhibit a high degree of nonspecific binding within the brain. This trend has been demonstrated by a negative correlation obtained between K_p and the unbound fraction in brain (f_u,brain) for a dataset of 72 marketed drugs (6). Consequently, drugs under development for CNS indications should be selected based on optimising their unbound brain/blood ratios (K_p,uu,brain) since unbound brain concentrations are the driving force for receptor binding and membrane permeability, according to the free drug hypothesis (7,8). An improvement on the logBB approach therefore is the development of structure–brain exposure relationships based on K_p,uu,brain (9). Alternatively, correlations can be based on BBB permeability measured by in situ brain perfusion, which separates the notion of rate of brain penetration from distributional effects (10). However, significant limitations remain in the approach of using single parameters to reflect the net effect of the various kinetic processes defining the brain and blood pharmacokinetics of a drug.

Modelling and simulation is routinely carried out during drug development to estimate pharmacokinetic parameters from blood or plasma concentration–time profiles and to subsequently use these parameters to predict drug concentrations in various different scenarios. More recently, physiologically based pharmacokinetic (PBPK) modelling has gained popularity due to its ability to simulate drug concentrations in individual tissues and organs and to translate these predictions across different species and populations (11). These models account for the various kinetic processes affecting the absorption, distribution, metabolism and excretion of a drug, which can be predicted a priori based on mechanistic scaling of in vitro experimental data. Until recently, there have been relatively few published examples of PBPK models which use in vitro data to predict BBB permeability. This is largely due to the various limitations in the currently used experimental systems used to represent the complex and transporter-rich structure of the in vivo BBB and to the difficulty in obtaining the appropriate in vitro–in vivo scaling factors (12). Most of the PBPK models of the CNS published in the literature to date have concentrated on fitting model parameters to preclinical in vivo data in order to determine the extent of a drug’s brain distribution or to characterise its efflux at the BBB. However, the focus is increasingly on applying translational modelling approaches to enable predictions of the brain penetration of drugs in human (13,14).

This review is divided into three parts. First, a comprehensive summary of the PBPK models of the CNS published in the literature to date, with emphasis on their structural differences and their methods for the estimation or prediction of model parameters relating to blood–brain permeability. Second, in vitro–in vivo correlations and mechanistic approaches to predict BBB and blood–cerebrospinal fluid barrier (BCSFB) permeability measured in various in vitro models are discussed, with a view to their incorporation into PBPK modelling strategies. Finally, several translational approaches are considered for the transposition of preclinical or in vitro model parameters into human PBPK models of the CNS, along with a brief overview of the current in vivo methods, which could be used to evaluate the success of PBPK model predictions of the BBB transport of drugs in human.

PART ONE: CURRENT PBPK MODELS OF THE CNS

The representation of the CNS in a PBPK model requires careful consideration of its physiological structure (Fig. 1a). The major components of the CNS include the various cell types composing the brain tissue, the surrounding extracellular fluid (ECF) and the cerebrospinal fluid (CSF), as well as the barriers separating these structures from the systemic circulation, the BBB and BCSFB (Fig. 1b). However, it can be misleading to consider brain tissue or CSF as single entities, since they are heterogeneous structures subject to regional differences in cell type and receptor localisation, fluid flow rates and expression of transporter proteins along their various barriers. PBPK models often vary in the degree to which they represent the true anatomy and physiology of the organism, depending both on the goals of the model and the observation data available. Determination of model structure is often guided by the principle of parsimony—the selection of the simplest model that is suitable for the intended purpose—to avoid unnecessary complexity, which renders parameterisation of the model difficult (15). Therefore, these regional differences may not necessarily be taken into account in the model, and tissues can be grouped together as lumped compartments where appropriate.

Fig. 1.

Schematic representation of the macro- and micro-structures of the CNS, showing a brain tissue perfused by microvessels, the location of the choroid plexus and CSF, b the exchanges possible between brain compartments and barriers and c the cellular environments of the BBB and BCSFB

A tissue in which a drug is considered to obtain a rapid equilibrium with its vasculature is represented as a perfusion-limited compartment in a PBPK model. The rate of drug entry into the tissue is determined by the organ’s blood flow rate, and the extent of distribution is defined by a static tissue-to-blood partition coefficient, K_p. This assumption is generally appropriate for tissues with high blood flow rates and whose membranes are highly permeable to drugs via passive diffusion, with no significant transporter contributions. Clearly, this is not the case at the BBB and BCSFB, whose tight junctions and transporter-rich nature provide a barrier, which limits the rate of drug exchange between blood and tissue or CSF (Fig. 1c). The brain and CSF should therefore be considered as membrane permeability-limited compartments in a PBPK model, with one or more inter-compartmental rate constants representing the membrane permeability and/or transporter kinetic parameters.

Aside from structural differences, PBPK models may also vary in the way in which their model parameters are derived—either a priori from in silico predictions and in vitro–in vivo extrapolations (IVIVE), or they may be estimated by fitting the model to in vivo data. Whether in vivo data are used to provide estimates for model parameters, or whether it is used to evaluate the model predictions based on IVIVE approaches, the success of the modelling exercise is limited by the quantity and the quality of the observed data available (summarized in Table I). Ideally, if an organ or tissue is to be represented as an individual compartment, observed concentration data measured in this tissue should be obtained. However, this is not always feasible during drug development (16), and consequently, concentrations in a compartment lacking in vivo data may be replaced by surrogate data, or by applying suitable modelling approaches. Before the application of intra-cerebral microdialysis to measure the interstitial fluid (ISF) concentrations of drugs, CSF sampling was widely considered to provide an approximation of ISF concentrations for CNS drugs transported passively across the BBB and BCSFB (17–22). However, mixed results have been reported for drugs, which are substrates of active or carrier-mediated transporters, due to differences in transporter abundance and functionality across the respective barriers (23,24). Care must then be taken when compartments lacking observation data are included in a PBPK model. Figure 2 provides an example of two different model structures, which could be appropriate at different phases of drug development.

Table I.

Summary of PBPK Models for the CNS in the Literature

Compartmental PK
Drug(s)	Species	Experimental data	Model compartments	Reference
Sucrose, glycerol, mannitol, inulin	Rat	Plasma, brain total (homogenate)	Plasma, whole brain	Ohno et al. (28)
Antipyrine, caffeine, acetamide, propylene glycol, ethylene glycol, glycerol, thiourea, curare, formamide, urea, N-methylnicotinamide, methotrexate, mannitol, arabinose, erythritol, sucrose, TEA	Rat	Plasma, brain total (homogenate)	Plasma, whole brain	Rapoport et al. (29)
Gabapentin	Rat	Plasma, unbound ECF (microdialysis), brain total (homogenate)	Plasma, peripheral tissues, brain ECF, brain ICF	Wang and Welty (33)
Zidovudine	Rabbit	Plasma, unbound ECF (microdialysis), CSF	Plasma, peripheral tissues, whole brain, CSF	Wang et al. (34) Wang et al. (35)
Mannitol, Cefodizime	Rat	Blood, brain total (homogenate), CSF	Plasma, peripheral tissues, brain ECF, CSF	Suzuki et al. (36)
Morphine, Morpine-3-glucuronide, Morphine-6-glucuronide, oxycodone	Rat	Blood, unbound ECF (microdialysis)	Arterial blood, peripheral tissues, brain ECF 1, brain ECF 2	Bouw et al. (39)
				Xie et al. (40)
				Bouw et al. (41)
				Bostrom et al. (43)
Clozapine, N-desmethylclozapine, escitalopram, risperidone	Rat	Plasma, unbound ECF (microdialysis)	Plasma, peripheral tissues, brain ECF	Cremers et al. (44)
Fluvoxamine	Rat	Plasma, unbound ECF (microdialysis), brain total (homogenate)	Plasma, peripheral tissues, shallow perfusion-limited brain, deep brain	Geldof et al. (46)
Quinidine	Rat	Plasma, unbound ECF (microdialysis), brain total (homogenate)	Plasma, peripheral tissues, brain ECF, whole brain	Syvänen et al. (47)
Empirical PBPK
Norfloxacin, olfloxacin, fleroxacin, pefloxacin, Sparfloxacin, AM-1155	Rat	Blood, brain total (homogenate), CSF, V u,brain (microdialysis)	Plasma, peripheral tissues, brain ECF, whole brain	Ooie et al. (48)
Zidovudine, 2′,3′-dideoxyinosine (DDI)	Rat	Blood, brain total (homogenate), CSF, V u,brain (brain slice)	Plasma, peripheral tissues, brain ECF, whole brain	Takasawa et al. (49)
Caffeine, mannitol, tryptophan, compound A, compound B, compound C, compound D	Rat	Plasma, unbound ECF (microdialysis)	Plasma, peripheral tissues, brain ECF, brain ICF	Hansen et al. (50)
S18986, morphine, M6G	Rat	Plasma, unbound ECF (microdialysis), brain total (homogenate), CSF	Plasma, brain ECF, brain ICF, CSF	Bourasset et al. (51)
				Bourasset et al. (52)
Caffeine, CP-141938, fluoxetine, NFPS, propranolol, Theobromine, theophylline	Rat	Plasma, brain total (homogenate), f u,brain (equilibrium dialysis)	Plasma, peripheral tissues, brain vasculature, whole brain	Liu et al. (57)
Atomoxetine, duloxetine	Rat	Plasma, unbound ECF (microdialysis), brain total (homogenate), CSF	Plasma, brain ECF, brain ICF, CSF	Kielbasa et al. (58)
	Human
Acetaminophen	Rat	Plasma, unbound ECF (microdialysis), lateral ventricle CSF, cisterna magna CSF	Plasma, peripheral tissues, brain ECF, brain ICF, lateral ventricle CSF, third/fourth ventricle CSF, cisterna magna CSF, subarachnoid CSF	Westerhout et al. (60)
	Human
IVIVE PBPK
Paclitaxel, digoxin, saquinavir, topotecan, verapamil, talinolol, rifampicin, UK-224,671, domperidone	Mouse	Blood, brain total (homogenate), Caco-2 permeability, BMEC kinetics	Arterial blood, venous blood, adipose, bone, gut, heart, kidney, liver, lung, muscle, skin, spleen, brain vasculature, whole brain	Fenneteau et al. (61)
Morphine, oxycodone	Rat	Blood, brain total (homogenate), unbound ECF (microdialysis), f u,brain (equilibrium dialysis), V u,brain (microdialysis), Caco-2 permeability, BMEC kinetics	Arterial blood, venous blood, adipose, bone, gut, heart, kidney, liver, lung, muscle, skin, brain vasculature, whole brain	Ball et al. (66)
	Human

Fig. 2.

PBPK model structure is determined by the in vivo data available. a Simple model based on data available in plasma and brain tissue only. b Complex model based on data available in plasma, brain tissue, brain ECF and CSF

A review of the literature regarding PBPK models of the CNS models is now presented, with a discussion of the differences in model structure and parameterisation in relation to the observed data available (summarised in Table I). We have classified these models into three main groups: compartmental PK, empirical PBPK or IVIVE-based PBPK models (Fig. 3). While compartmental PK models include a separate compartment for the organ(s) of interest, such as the brain or CSF, they do not use fixed physiological values for anatomical model parameters including tissue volumes and fluid flow rates. These parameters are instead estimated by fitting the model to in vivo data obtained for a specific drug, in the tissue(s) of interest. Parameter estimates can then be compared to their corresponding physiological values, but much like classical compartmental pharmacokinetic models, they have limited predictive ability for interspecies translational approaches, with model parameters being specific to both the drug and the species they are estimated in. Empirical PBPK models provide a better basis for extrapolations between different species because most or all of the anatomical model parameters are fixed to their physiological values. An up-to-date listing of CNS physiological parameters for human, rat, mouse, monkey and dog has been recently reported in the literature (13). Drug-specific model parameters such as binding to brain tissue and permeability across the BBB and BCSFB are estimated from in vivo data, and as such represent an empirical ‘top–down’ approach. Caution must then be taken when extrapolating their values to other species, especially when these model parameters represent the net effect of several different kinetic processes such as transporter uptake or efflux, which may differ between species. IVIVE-based PBPK models are similar in structure to empirical PBPK models, but drug-specific parameters are predicted a priori using a mechanistic ‘bottom–up’ approach by extrapolating values measured in in vitro systems to their in vivo equivalents using appropriate physiological scaling factors (25).

Fig. 3.

An example of PBPK models published in the literature. a Hybrid PBPK model to analyse brain microdialysis data (37). b Empirical PBPK model to analyse CSF and brain microdialysis data (60). c IVIVE-PBPK model to predict BBB permeability and estimate RAF from in vitro and in vivo data (66). Figures were reproduced with permission from the authors

Compartmental PK Models

The earliest PBPK models of the CNS were developed with the goal of using compartmental modelling of time-dependent brain concentration profiles of a drug, rather than initial rate uptake analysis, to estimate BBB permeability (26). Similarly, models were also developed using drug CSF concentration profiles after intra-ventricular administration, in order to determine their BCSFB efflux kinetics (27). One of the first published examples of compartmental modelling to determine BBB permeability after systemic administration of vascular marker molecules was published by Ohno et al. who modelled plasma and brain concentrations of the ¹⁴C-labelled tracers sucrose, glycerol, mannitol and inulin, in order to estimate permeability of the BBB in different cerebral regions in the rat (28). Rapoport et al. (29) carried out a similar approach for 17 radiotracers, including several CNS drugs, and they also determined a correlation between the model-estimated BBB permeability of the drugs in their dataset and their octanol–water partition coefficients, as well as carrying out a sensitivity analysis on their model parameters to graphically show the impact of varying BBB permeability on brain concentrations. These models consisted of separate plasma and brain or CSF compartments, with a single bidirectional rate constant representing the permeability of the biological membrane separating them. In 1983, Collins and Dedrick (30) extended this approach by formally proposing a model for the simultaneous PK analysis of blood, brain and CSF concentrations, which they termed the ‘distributed model’. Theirs was a theoretical approach, rather than being based on data for a specific drug, and the authors carried out a sensitivity analysis and exploratory simulations for hypothetical drugs with certain predefined molecular properties.

The rise in the use of in vivo brain microdialysis to measure unbound drug concentrations in the brain ECF allowed the expansion of the distributed model to differentiate intracellular and extracellular spaces within the brain into separate compartments in the distributed model. A significant advantage of the microdialysis technique is that the frequent collection of dialysate samples can result in rich pharmacokinetic profiles, since no fluid is actually removed from the ECF (31). However, since drug concentrations are indirectly measured via equilibration across the probe membrane between drug in the ECF and drug in the dialysate, accurate determination of probe recovery in vivo is required to correct dialysate concentrations of a drug to the respective concentrations in the ECF (32). Modelling of microdialysis data allows BBB influx and efflux parameters to be determined based on unbound plasma and ECF concentration profiles, for the entire duration of the dialysate collection period. Wang and Welty (33) applied a modified version of the Collins and Dedrick distributed model to pharmacokinetic data obtained for gabapentin in the rat, first using unbound drug concentrations measured in brain ECF by microdialysis, and then using total drug concentrations obtained in brain homogenate. Although these data were modelled separately, they noted that since gabapentin concentrations were much higher in brain homogenate than in ECF, the BBB efflux permeability was likely to be underestimated by the model when using homogenate concentrations compared to ECF concentrations. This implies that incorporation of model parameters accounting for intracellular brain accumulation and binding is necessary in order to model the homogenate data and ECF data simultaneously. Wang et al. (34) also used the distributed model to characterise active efflux from CSF to blood of the anti-HIV drug zidovudine in the rabbit after intravenous and intrathecal administration. Blood, CSF and ECF concentrations of zidovudine were modelled simultaneously in order to estimate influx and efflux clearances across both the BBB and the BCSFB. In a subsequent study, they extended their model to include the saturation of zidovudine efflux across the BCSFB, after three different intrathecal doses of zidovudine (35). Their model results implied that zidovudine transfer across the BCSFB consisted of two linear processes—which they attributed to CSF bulk flow and passive diffusion—and one saturable process that they attributed to active transporter-driven efflux. They were thus able to estimate V_max and K_m values of 13.1 ± 14.2 nmol min⁻¹ kg⁻¹ and 475 ± 528 μM, respectively, for this active efflux, although they noted that the high standard errors that they obtained for their model parameters was likely due to limited observed data. These early examples demonstrated a sequential improvement towards more physiologically realistic model structures, and by considering BBB and BCSFB permeabilities as non-symmetrical rate processes, as well as differentiating the passive components from the active, saturable components.

In their review on the role of efflux transport of xenobiotics across the BBB and BCSFB, Suzuki et al. (36) evaluated the physiological reality of the Collins and Dedrick distributed model using CSF concentration data for mannitol as a probe compound not undergoing active efflux, and fitting the model to this data to estimate the physiological parameters of CSF volume and flow rate, and the ependymal surface area between brain ECF and CSF. They compared the model-estimated values to their corresponding physiological values reported in the literature and found them to be similar. They then fixed these physiological parameters in the model and used it to estimate the influx and efflux permeability of cefodizime across the BBB and BCSFB, obtaining a 4-fold higher efflux clearance across the BBB, compared to influx clearance. This represented the first step towards applying fixed physiological values to anatomical parameters in models of the CNS.

As an extension to the use of compartmental modelling to determine influx and efflux parameters across the BBB and BCSFB purely in order to explain pharmacokinetic observations, the focus shifted onto linking PK models based on brain ECF concentrations to pharmacodynamic (PD) observation data (Fig. 3a) (37,38). Hammarlund-Udenaes and colleagues (39) have published several mechanism based PK/PD models based on microdialysis data and antinociceptive effects for opioids in the rat, most notably for morphine, morphine-3-glucuronide (40), morphine-6-glucuronide (M6G) (41) and oxycodone (42). One of the goals of this modelling approach was to quantitatively explain how a similar in vivo potency of morphine and oxycodone in the rat was obtained for approximately the same plasma concentrations of the two drugs, despite their significantly different in vitro affinities for the μ-opioid receptor. The 6-fold higher unbound brain ECF concentrations seen for oxycodone compared to morphine were proposed to explain this phenomenon, and modelling of these concentrations supported this theory, as demonstrated by a higher uptake clearance than efflux clearance across the BBB for oxycodone, while the reverse result was obtained for morphine (43). Another example of application-based modelling for CNS drugs was presented by Cremers et al. (44) for the anti-psychotic drug clozapine and its active human metabolite N-desmethylclozapine. The highly variable response to clozapine treatment in patients with schizophrenia is thought to be due to inter-patient variability in ECF concentrations, for the same plasma concentrations. This is likely to be due to variability in P-gp-mediated clozapine efflux across the BBB. The authors carried out brain microdialysis in the rat for clozapine and N-desmethylclozapine, as well for a reference compound for passive BBB transport (escitalopram) and for a known P-gp substrate (risperidone). After comparison of their clozapine model results with risperidone, they concluded that the similarity in model parameters between the two drugs indicated that active P-gp-mediated efflux of clozapine and its metabolite was indeed likely. They proposed that their model, when coupled to receptor PD data, could be used to predict the pharmacological effects of clozapine in the rat, and could then serve as a basis for a subsequent model to enable human simulations.

It is only relatively recently that emphasis has been placed on distinguishing BBB permeability from intracellular brain distribution and tissue binding, which can also act as a driving force for the brain penetration of a drug (45). Simultaneous modelling of unbound drug brain ECF concentrations measured by microdialysis, with total drug concentrations measured in brain homogenate gives rise to a two-compartment brain model for which observed data are available in both compartments. Geldof et al. modelled the nonlinear efflux of fluvoxamine across the BBB by simultaneously fitting plasma, unbound brain ECF and total brain homogenate concentrations after three different intravenous doses of fluvoxamine in the rat (46). The brain was represented as two separate compartments—a shallow perfusion-limited brain compartment, and a deep brain compartment, which represented the brain ECF. Drug exchange between these two brain compartments was described by a passive diffusion term and a saturable active efflux term, while drug was assumed to equilibrate rapidly between the plasma and the shallow perfusion-limited brain compartment. Similarly, Syvänen et al. (47) also simultaneously modelled plasma, unbound brain ECF and total brain homogenate concentrations for the P-gp substrate quinidine. They investigated the efflux of quinidine at the BBB by co-administration with the P-gp inhibitor tariquidar, and using kainate-treated rats, which have been associated with an increase in P-gp expression. Their model also represented the brain as two separate compartments, but unlike Geldof et al., they considered that the rate-limiting barrier was situated between the plasma and the ECF compartment, and the secondary brain compartment was an intracellular compartment, responsible for intra-brain drug distribution. Rate constants for drug transfer between ECF and the intracellular compartment were estimated based on the total brain homogenate concentrations, and BBB efflux parameters were estimated between the plasma and ECF compartments. Although these two models differ slightly in their compartmental arrangements, they both reflect a more mechanistic approach by taking into account separately the rate processes relating to BBB permeability and intracellular brain distribution.

Empirical PBPK Models

The empirical PBPK models described in this section are similar in structure to the aforementioned compartmental PK models, with the exception that they use fixed physiological values obtained from the literature for some or all of the anatomical model parameters. The benefit of this approach is that the same model structure can be conserved to enable the rapid analysis of datasets containing many different classes of drugs, and it also allows a more precise estimation of drug-specific parameters such as BBB and BCSFB permeability, since there are fewer parameters to be estimated by the model. Ooie et al. (48) characterised the active efflux across the BBB of six quinolones in the rat, by fitting a version of the distributed model containing fixed physiological parameters, to total serum, brain and CSF concentrations of the quinolones, and correcting total brain concentrations to unbound ECF concentrations using the previously reported brain unbound volume of distribution, V_u,brain. V_u,brain was calculated by measuring both the unbound drug concentrations in the brain ECF by microdialysis, and the total concentrations in brain homogenate at steady state, and correcting for the amount of drug in brain capillaries. Similarly, Takasawa et al. (49) used this model for zidovudine and 2′,3′-dideoxyinosine (DDI) in the rat, with the exception that the unbound ECF concentrations were obtained by correcting total brain homogenate concentrations with V_u,brain measured in in vitro rat brain slices. In this method, the uptake of drug into the brain slice is measured over time, and at equilibrium with the buffer, V_u,brain is calculated from the total amount in the slice divided by the concentration, with correction for the adherent water volume around the slice. Both Ooie et al. and Takasawa et al. were able to estimate parameters for BBB and BCSFB transfer simultaneously. This type of model has also been used for datasets of compounds chosen for their broad range of physicochemical characteristics and in vitro BBB permeabilities, rather than compounds belonging to the same drug class. Hansen et al. (50) fitted their model to microdialysis data obtained in the rat for caffeine, mannitol and tryptophan, as well as four proprietary compounds. Unlike in the previous examples, the model did not contain a CSF compartment since CSF concentrations were not measured, but in this case, the unbound brain ECF concentrations of the drugs were available, allowing both the direct estimation of BBB unbound permeability, and of brain intracellular uptake parameters based on the measured brain unbound volume of distribution, since a physiological value was used for the ECF compartment volume. Bourasset et al. combined data obtained in the rat after brain microdialysis, brain tissue and CSF sampling, and in situ brain perfusion in a model for S18986, an alpha-amino-3-hydroxy-5-methyl-4-isoxazole-propionic acid allosteric modulator under development by Servier (51). Interestingly, they performed both microdialysis and in situ brain perfusion experiments in two brain regions, the frontal cortex and hippocampus. This allowed their model to distinguish membrane permeability from intra-brain and CSF distribution and to conclude that, while BBB permeability in the two regions was similar, the intracellular binding and/or accumulation was significantly greater in the hippocampus than the frontal cortex. Bourasset and Scherrmann (52) developed a similar model for morphine and M6G, in order to determine the kinetic parameters of capacity-limited processes at the various blood, brain and CSF interfaces. They found that morphine accumulated in the intracellular compartment from the ECF via a probenecid-sensitive, capacity-limited system, whereas M6G remained primarily in the ECF. Both of these examples demonstrate the advantage of obtaining rich data in various CNS locations, enabling the model to distinguish regional accumulation from membrane permeability.

Due to the increasing influence of PBPK modelling approaches in the pharmaceutical industry and by the regulatory agencies (53–55), as well as the improvements in software able to solve the complex differential equations required to code full body PBPK models (56), publications originating from the pharmaceutical industry concerning CNS PBPK modelling have become more frequent. Liu et al. (57) demonstrated the use of PBPK modelling of the brain as a method of screening compounds under development based on their BBB permeability. Their PBPK model represented the brain as a permeability-limited tissue consisting of two sub-compartments representing the intravascular space and extravascular space respectively, with the rate-limiting transfer coefficient between the two compartments representing the BBB. Since their dataset was made up of compounds, which were considered to cross the BBB mainly by passive diffusion, they estimated a single bidirectional permeability-surface area product for each of the compounds based on blood and brain total concentrations measured in the rat, and determined f_u,brain by dividing f_u,plasma by the brain/plasma ratio predicted by the model at steady state. While this model did not include a CSF compartment or separate compartments for ECF and intracellular spaces, it instead provided a practical example of a model, which could be easily implemented using the minimal amounts of in vivo data available at early stages of drug development. In another publication originating from the pharmaceutical industry, Kielbasa et al. (58) demonstrated an additional application of PBPK modelling of the CNS during drug development, the interspecies translation of BBB penetration to provide prediction of unbound brain concentrations in human. Their model was structurally more complex than that of Liu et al., consisting of separate compartments for blood, brain ECF, brain intracellular space and CSF. They used this PBPK model firstly to estimate BBB and BCSFB permeability in the rat for the CNS drugs atomoxetine and duloxetine, based on the approach previously applied for atomoxetine (59). Since their dataset consisted of in vivo unbound concentration profiles in both blood and brain ECF measured by microdialysis, and single time-point samples for CSF and brain homogenate at steady-state, they were able to estimate their model parameters with a good degree of precision. They then scaled the drug-specific model parameters to their corresponding human values based on an allometric relationship, simulated the unbound brain concentration profiles of atomoxetine and duloxetine in human. Although the authors acknowledged that their approach was not suitable for high-throughput application in early drug development, it nevertheless provides a rational means to carry out human predictions for more promising CNS drug candidates before clinical data becomes available.

Westerhout et al. recently published one of the most structurally complex PBPK models of the CNS to date, with the goal of carrying out a model-based investigation into whether different CSF sampling sites gave comparable PK profiles in rat, and therefore whether CSF could be used as a surrogate for ECF in human. Their model includes separate compartments for blood, brain ECF, and four different CSF locations (Fig. 3b) (60). The four CSF compartments were organised in series using a transit compartment arrangement, with drug able to pass sequentially from brain ECF to CSF in the lateral ventricle, the combined third and fourth ventricle, the cisterna magna and the subarachnoid space. The goal was to evaluate the use of a translational mechanistic modelling approach to use CSF sampled from the subarachnoid space in human as a means of estimating unbound brain ECF drug concentrations. Model parameters for acetaminophen were estimated by fitting to in vivo data obtained after intravenous administration in the rat, including concentration profiles obtained from two different CSF sampling locations (lateral ventricle and cisterna magna) along with brain ECF concentrations measured by brain microdialysis, and arterial plasma concentrations. The authors translated the rat model parameters to human values by assuming that the fold-relationships between the inter-compartmental rate constants were the same in human as for the rat. They then carried out human simulations to estimate brain ECF concentrations, based on fitting in vivo human plasma and subarachnoid CSF concentrations to the model, along with the human parameters scaled from the rat model. This example provides support for the prediction of ECF concentrations using CSF measurements in human, after accounting for the time delay caused by distribution between the ECF and the sampling site of CSF used in patients. A model of this complexity will rarely be necessary for drugs under development but it remains an interesting example of a mechanistic modelling approach to answer a relevant question.

Overall, the empirical models described in this section provide a good basis for both high-throughput analysis of the BBB transport of multiple drugs undergoing development, as well as a rational, physiological approach for predictions of unbound ECF drug concentrations in human. However, the success of these translational approaches also relies on certain important assumptions, such as similar mechanisms of transport across the BBB and BCSFB between species. This was considered to be the case for acetaminophen, atomoxetine and duloxetine as passive diffusion is the main process governing their BBB permeability. However, this may not always be the case for drugs in which active transporter-driven or carrier-mediated processes are dominant, and additional efforts may be required in order to model these processes.

IVIVE-PBPK Models

The in vitro–in vivo extrapolation strategy sometimes used to estimate certain drug-specific PBPK model input parameters is often referred to as a ‘bottom–up’ approach since parameters are scaled in a mechanistic, step-wise manner from the in vitro to in vivo level, using scaling factors to take into account the physiological and activity differences between kinetic processes measured for a drug under in vitro experimental conditions, and those occurring in the in vivo environment of the body (25). The IVIVE scaling of drug transporter-driven rate processes is challenging due to the relative lack of data concerning absolute protein expression levels of transporters both at the in vivo BBB, and in in vitro systems. Even when relative transporter expression levels are known, it is difficult to predict whether this would result in a corresponding relationship between their in vitro and in vivo activity. When in vitro drug permeability is measured in in vitro systems containing several transporters, the overall apparent permeability may be the net effect of several different rate processes, including passive diffusion and active transporter-driven or carrier-mediated processes.

There are currently very few published examples in the literature for which in vitro permeability has been used for the a priori prediction of permeability across the BBB or BCSFB, and incorporated into a PBPK model to predict the in vivo brain penetration of a drug. Fenneteau et al. (61) used an IVIVE-based approach in their whole body mouse PBPK model in order to evaluate the difference in model predictions when considering the brain and the heart as permeability-limited rather than perfusion-limited organs. Their model consisted of 11 tissue compartments and separate compartments for arterial and venous blood. The brain compartment was divided into two sub-compartments, representing brain vasculature and brain tissue, respectively, with drug transfer between the two compartments divided into passive and active efflux. Since their dataset included known P-gp substrates, they extracted data from the literature for bidirectional permeability measured across Caco-2 monolayers in order to calculate the efflux permeability, and they obtained passive permeability from apparent permeability measurements in Caco-2 cells in the presence of a P-gp inhibitor (GF-120918). Firstly, they performed an IVIVE assessment between Caco-2 permeability and in vivo permeability reported for wild type and P-gp-knockout Mdr1a/1b(−/−) mice (62). Positive linear correlations were obtained for both passive and efflux permeability (R² = 0.89 and 0.92, respectively). Secondly, they carried out a mechanistic IVIVE scaling approach for the P-gp substrate domperidone using their PBPK model and compared their model predictions to in vivo brain tissue concentrations obtained in both wild-type and knockout Mdr1a/1b(−/−) mice. Their IVIVE scaling approach consisted of scaling in vitro passive and efflux permeabilities to in vivo intrinsic permeabilities using the relationships obtained during the correlation analysis, then by scaling these in vivo intrinsic permeabilities to whole organ permeabilities using a physiological value for the in vivo membrane surface area obtained from the literature (Fig. 4). For passive permeability at the BBB, they decided to use the apparent permeability measured in bovine brain capillary endothelial cells, multiplied by a scaling factor of 150 that the authors used based on correlation with in vivo data for a dataset of 13 passively permeable drugs (63). In order to extrapolate in vitro Caco-2 P-gp efflux permeability to efflux permeability at the in vivo mouse BBB, they corrected the in vitro intrinsic P-gp efflux permeability by the relative fraction of Mdr1a/1b messenger RNA expression measured in the brain compared to that in the intestine, assuming that this accounted for the difference in P-gp activity between the two systems. Importantly, when model input parameters are predicted using a bottom–up scaling approach from in vitro data, it is vital to understand in a quantitative manner the extent to which experimental uncertainty and variability may affect the overall model predictions, and the impact of correlation of model input parameters. In a subsequent study, Fenneteau et al. (64) carried out a global sensitivity analysis which involved performing Monte Carlo simulations based on the generation of pharmacokinetic profiles via random sampling of model parameter values based on a log-distribution, and a multivariate sensitivity analysis to identify the input parameters with the greatest influence on model predictions, and to calculate the partial rank correlation coefficients. They found that BBB permeability and surface area were influential model parameters, noting that by considering them as two separate model parameters, rather than as a single permeability-surface area product as has been reported previously (65), their individual sensitivities on model predictions could be distinguished.

Fig. 4.

In vitro–in vivo extrapolation strategy used by Fenneteau et al. (61) for permeability rate-limited tissues in their mouse whole-body PBPK model. Diagram reproduced with permission from the authors; numbered references can be found in the original publication

We recently published a whole body PBPK model for the rat (Fig. 3c), in which BBB permeability was estimated using in vitro–in vivo scaling strategies to predict unbound brain concentrations of both efflux and influx transporter substrates (66). The brain was considered as two compartments representing the intravascular and extravascular spaces, separated by a rate-limiting membrane representing the BBB. Our goal was to evaluate two different IVIVE strategies for the extrapolation of transporter-driven influx and efflux at the BBB, using data from the literature, which would be available at different phases of drug development. Morphine and oxycodone were chosen as substrates of active efflux and influx transporters, respectively (43). Consistent with the aforementioned goals, the data chosen for morphine were intended to be representative of data, which would typically be available at the early stages of drug development (in vitro Caco-2 permeability, in vivo total concentrations in brain homogenate), while the data chosen for oxycodone were intended to reflect more the complicated experimental techniques, which may be employed later in the development phase (in vitro uptake kinetics in rat brain microvessel endothelial cells, in vivo unbound ECF concentrations obtained by microdialysis). In vitro–in vivo differences in transporter activity were represented in the model equations by a relative activity factor (RAF), which was estimated by fitting the model to the rat observed concentrations. We then used the whole body PBPK model carry out human predictions, by replacing physiological model parameters for the rat with their equivalent human values, and using the surface area of the human in vivo BBB to scale Caco-2 permeability for morphine, and the amount of human microvessel protein per gram of brain to scale the kinetic uptake parameters obtained in the brain cell culture for oxycodone. The values used for RAF in the human model were the same as those estimated using the rat model, although we noted that this assumption implied that the expression levels and activity of the relevant transporters per unit surface area of membrane, or per amount of microvessel protein is the same between the rat and human, which is not necessarily the case. In order to quantitatively assess the impact of this assumption, a sensitivity analysis was carried out on the model parameter RAF, to observe its influence on the overall model predictions.

The models reported by us and by Fenneteau et al. provide two promising examples of the use of IVIVE-based prediction strategies for the estimation of BBB permeability in PBPK models. While certain important assumptions remain for the extrapolation of transporter-driven permeability, these approaches should pave the way for additional studies of this type.

PART TWO: IVIVE STRATEGY FOR PBPK MODELS

The importance of applying a mechanistic IVIVE-based approach to determine drug-specific input parameter values for PBPK models has been emphasised in a recent review (67). When in vitro data is used to estimate model input parameters, extrapolation of these values to their in vivo equivalents using physiological scaling factors must be applied. This is an approach already routinely applied in PBPK models for the prediction of hepatic and intestinal intrinsic clearance and for permeability and transporter-driven active uptake and efflux in the liver and the gut. Scaling procedures in PBPK models were originally based on in vitro–in vivo correlation analyses, such as the relationship between apparent permeability measured across Caco-2 monolayers and human in vivo jejunal permeability measured by intestinal perfusion (68). While large-scale correlations are advantageous due to their rich, structurally diverse datasets, they are also limited by inter-laboratory differences in experimental conditions, or by being based on data from in vitro systems derived from a different cell type or species compared to the in vivo data. Recent efforts have concentrated on overcoming these limitations by focussing on the characterisation of individual kinetic processes at the in vitro level, as demonstrated by mechanistic modelling approaches applied to data obtained in hepatocytes and Caco-2 cells (69,70).

The current shortage of IVIVE-based mechanistic PBPK models of the CNS published in the literature can be attributed to the lack of established correlations due to the difficulty in measuring in vivo human BBB permeability and also because of the experimental limitations in the in vitro systems chosen to represent the BBB (71). Nevertheless, in recent years, progress has been made both in the improvement of experimental techniques, and the increase in the number of publications reporting in vitro–in vivo correlations for BBB permeability based on preclinical species (72). In this section, we will briefly summarise the in vitro models currently used to measure BBB and BCSFB permeability, their correlations with in vivo data obtained in preclinical species, and mechanistic approaches, which can be applied to improve their IVIVE for use in PBPK models.

In Vitro Models of the BBB and BCSFB

In vitro models of the BBB consist of primary or immortalised brain microvessel endothelial cell (BMEC) monolayers obtained from various species (73–78). Co-culturing brain cells with astrocytes, glial cells and/or pericytes has been shown to improve the integrity of inter-cellular tight junctions, by increasing trans-epithelial resistance values and decreasing the permeability of paracellular marker molecules, thereby better representing the in vivo BBB (79). In vitro models of the BCSFB are also available, and have been reviewed recently (80). However, these systems are not routinely used in drug development, due to practical limitations (expensive, low-throughput, technically challenging) and the debate surrounding their in vivo predictability for transporter substrates. Consequently, high-throughput artificial in vitro systems have been developed to predict passive diffusion across the BBB and BCSFB, such as the modified parallel artificial membrane permeability assay (PAMPA), which consists of porcine brain lipids, rather than the lipids typically used for intestinal absorption prediction (81). Alternatively, monolayers derived from non-BBB cell lines such as Caco-2, MDCKII and LLC-PK1, either in their wild-type or transporter-transfected forms, have also been considered as surrogate systems in which to predict BBB permeability (82). The advantage of using non-BBB in vitro systems is that they are often already routinely employed during drug development for the estimation of intestinal absorption, so permeability data can be exploited for the dual purpose of predicting both intestinal and BBB permeability.

In Vitro–In Vivo Correlations of BBB Permeability

Ideally, correlation analyses intended for implementation in PBPK models should be carried out on large datasets of compounds with a wide variety of molecular properties. It is more feasible to carry out large-scale correlations for BBB permeability by using high-throughput in vitro methods, such as PAMPA-BBB. Di et al. (83) developed a quantitative permeability relationship based on in vitro permeability in PAMPA-BBB (P_e,PAMPA-BBB) and rat in situ brain perfusion (P_{brain perfusion}) for 37 structurally diverse compounds.

$$P_{\mathrm{brain}\mathrm{perfusion}}\left(\times {10}^{-3}\mathrm{cm}/\mathrm{s}\right)=0.97\times P_{\mathrm{e},\mathrm{PAMPA-BBB}}\left(\times {10}^{-6}\mathrm{cm}/\mathrm{s}\right)+2.54$$

This correlation had an R² value of 0.47, compared to a value of 0.0071 when they compared the same dataset with permeability measured in MDR1-MDCKII cells. Tsinman and Avdeef subsequently developed an improved PAMPA-BBB system, which was intended to be more representative of the in vivo BBB than that used by Di et al. (84), consisting of a 5-fold higher lipid concentration, thinner membranes and a more viscous alkane solvent than dodecane. They carried out an even larger correlation analysis (n = 197) between intrinsic permeability measured in their new PAMPA-BBB (P^PAMPA-BBB₀), and permeability obtained from literature data for in situ brain perfusion in rodents (P^in situ₀), obtaining a correlation with an R² value of 0.77.

$$log{P}_0^{\mathit{in}\mathit{situ}}=-0.25+0.87\times P_0^{\mathrm{PAMPA-BBB}}$$

Correlations based on permeability measured across artificial membranes such as PAMPA-BBB are relevant for compounds whose BBB permeabilities are governed mainly by passive diffusion, but since these in vitro systems lack the transporters and carrier proteins, which are naturally present at the in vivo BBB and BCSFB, predictions may not be appropriate for drugs undergoing significant active uptake or efflux. The increasing use of BMEC systems to measure the BBB permeability of drugs has been accompanied by the publication of correlations with in vivo BBB permeability data. The following examples that will be discussed are by no means a comprehensive list, but are intended to demonstrate the various different approaches to carrying out correlation analysis. One of the first successful correlations reported for passively transported drugs (R² = 0.72, n = 13) was between permeability measured in in vitro primary bovine brain microvessel endothelial cells (BBMEC) and permeability obtained from rat in situ brain perfusion, although the in vitro permeabilities were on average 150-fold higher than their in vivo equivalents (63). The value of 150 was used by Fenneteau et al. (61)for domperidone in their PBPK model, as discussed in Part One of this review. However, it has also been seen that when correlations are based on in vivo data obtained using total, rather than unbound drug concentrations, correlations may require the correction of in vivo total concentrations by the fractions unbound in blood and brain. Summerfield et al. (85) found no overall correlation between P_app measured in MDR1-MDCKII and permeability determined using total concentrations measured by rat in situ brain perfusion for a dataset of 50 compounds. Since their dataset spanned a wide range of lipophilicities, the authors suggested that the poor correlation may have been due to the differences in brain binding of the various compounds in their dataset which may have affected the concentration gradient during perfusion. Their theory was supported by the fact that a much improved correlation was observed by selecting only the most hydrophilic drugs in the dataset, i.e. f_u,brain > 0.1 (R² = 0.82, n = 16). An example of an in vitro–in vivo correlation, which was improved by correcting for binding prior to performing the correlation analysis, was reported by Hellinger et al. (82). They obtained good correlations using a dataset of 10 passive and P-gp substrates between mouse in vivo permeability corrected for f_u,brain/f_u,plasma ratio, and various in vitro BBB (rat primary brain capillary endothelial cells co-cultured with astrocytes and pericytes) and non-BBB (MDR1-MDCK, MDCK, Caco-2 and highly P-gp expressing vinblastine-treated VB-Caco-2) systems, with R² values of 0.80, 0.78, 0.68, 0.61 and 0.72, respectively. In order to assess the prediction of active efflux at the BBB for P-gp substrates using in vitro systems, correlation analysis is carried out between in vitro efflux ratios (defined by the ratio between the permeabilities measured in different directions across the monolayer) and AUC_brain to AUC_plasma ratios in P-gp knockout mice versus wild-type mice. Feng et al. concluded that for MDCK, human MDR1-MDCK and mouse Mdr1a-MDCK cell lines, the in vitro efflux ratio was effective in identifying P-gp from non-P-gp substrates (n = 32) as determined by AUC ratios in wild-type versus knockout mice (86). Summerfield et al. (87) also found a good in vitro–in vivo correlation for the in vitro efflux ratio across MDR1-MDCK cells for P-gp substrates (R² = 0.93, n = 12), but only after this efflux ratio was corrected by the f_u,brain/f_u,plasma ratio in a manner analogous to that described above for permeability. As an alternative to using wild-type and knockout mice as the in vivo references for correlation analyses with P-gp substrates, Lacombe et al. (88) investigated correlating rat in vivo BBB permeability based on total brain concentrations with in vitro permeability measured in both rat- and human-derived primary brain endothelial and glial cells, for a dataset of 20 efflux substrates. They obtained a good correlation between P_app,AB in rat- versus human-derived in vitro systems (R² = 0.61 or R² = 0.91 when two outliers were removed), and also a good in vitro–in vivo correlation (R² = 0.67) between the rat in vivo AUC_brain and the corrected in vitro P_app,AB :

$$P_{\mathrm{app},\mathrm{A}:\mathrm{B},\mathrm{corrected}}=\frac{P_{\mathrm{app},\mathrm{A}:\mathrm{B},\mathrm{rat}\mathrm{vitro}}}{\mathit{ER}}\times \frac{f_{\mathrm{u},\mathrm{plasma}}}{f_{\mathrm{u},\mathrm{brain}}}\times {\mathrm{AUC}}_{\mathrm{plasma}}$$

where ER is the in vitro efflux ratio, f_u,plasma and f_u,brain are the in vitro fractions unbound in plasma and brain, and AUC_plasma is the area under the plasma concentration–time profile in vivo.

Since accounting for binding has been shown to improve correlations, a better alternative may be to carry out correlations permeability measured based on unbound ECF concentrations obtained using microdialysis as the in vivo reference data. Garberg et al. (89) measured the in vitro bidirectional permeability of a set of compounds with different transport mechanisms and permeabilities, in BMEC from four different species—primary human (HBMEC) and bovine (BBMEC) brain endothelial cells, immortalised rat (SV-ARBEC) and mouse (MBEC4) brain endothelial cells, as well as several non-BBB in vitro systems including Caco-2, wild-type MDCK, and MDR1-MDCK. Although they were only able to compare these in vitro efflux ratios with in vivo microdialysis AUC_brain/AUC_blood ratio in rats for six of the compounds in their original dataset of 23, they found that in general the in vitro efflux ratios were successfully able to detect whether the drug was an efflux substrate in vivo. Hakkarainen et al. (90) carried out a correlation analysis with rat microdialysis for nine drugs in BBMEC, Caco-2 and MDR1-MDCK cell lines. They found a linear correlation between the in vivo microdialysis AUC_brain/AUC_blood ratio and logP_app, whether for BBMEC (R = 0.99), Caco-2 (R = 0.91) or MDR1-MDCK (R = 0.85). Importantly, for all three cell systems, the correlation was only statistically significant when two outliers were removed from the regression, which were both known efflux transporter substrates (ondansetron and tolcapone). These two compounds had much higher in vitro permeabilities compared to their in vivo values, and the authors justified their removal from the correlation analysis by suggesting that the mechanism responsible for their in vivo efflux may have been saturated at the concentrations used in vitro. This highlights the importance of choosing physiologically relevant concentrations in vitro for transporter substrates, in order be able to obtain meaningful correlations with in vivo data. Further investigation into the in vitro–in vivo efflux relationship can be carried out using P-gp probe-inhibitor pairs to determine whether inhibition parameters obtained in vitro and in vivo are similar. This approach was demonstrated in a recent in vitro–in vivo correlation study for quinidine using PSC-833 as a P-gp inhibitor, and comparing inhibition parameters measured in wild-type MDCK, MDR1-MDCK and rat BMEC cell monolayers with those obtained in vivo by microdialysis in the rat (91).

Overall, it is conceivable that correlations such those described in this section could be implemented into PBPK model equations in order to scale in vitro permeability to in vivo BBB permeability, in a manner analogous to that used for the prediction of intestinal permeability using Caco-2 cells (68). However, care must be taken to correct in vivo data obtained using total concentrations by binding data in both plasma and brain.

Mechanistic Approaches

Recent efforts to improve the prediction of drug transfer across biological membranes from in vitro data have focussed on the development of mechanistic models at the in vitro level, in order to determine kinetic parameters for the individual rate processes relevant for a given drug, before transposing these values into a PBPK model. This could be challenging given the respective uncertainties associated with the measurement of certain physiological parameters, such as membrane surface area and relative transporter abundances, which may be hard to distinguish from each other due to difficulties in measuring their values in vitro and in vivo. Nevertheless, progress in this area continues to be made both through the improvement of experimental techniques, and in the analysis and interpretation of data.

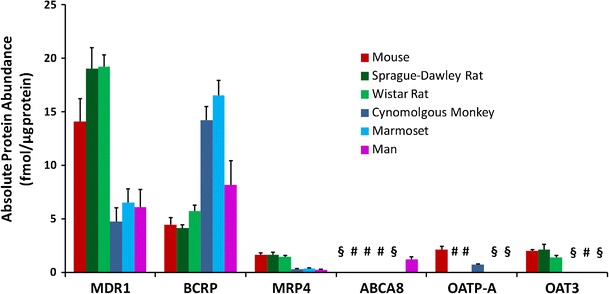
When sufficiently rich permeability data are available in in vitro monolayers, the passive and active components can be distinguishable from each other, as has been demonstrated in the Caco-2 system (92). Additional factors due to experimental conditions and inter-laboratory variability can also be quantified and removed from the measured apparent permeability, theoretically leading to a better correlation with the corresponding in vivo BBB permeability. This approach has recently been carried out by Avdeef through mechanistic modelling of permeability measured in in vitro brain microvessel endothelial cell cultures. Apparent permeability in BMEC systems originating from different species and different laboratories were used to evaluate a biophysical model proposed by the author to characterise the in vitro system in terms of parameters, which describe the nature of the paracellular pores and the aqueous boundary layer adjacent to the monolayer (93). This approach has also been used to successfully characterise other non-BBB in vitro systems such as Caco-2 (94,95) and PAMPA (96), and enables the extraction of intrinsic transcellular permeability from apparent permeability measurements. The benefit of this approach is that it can be used to overcome experimental limitations of in vitro BBB systems due to leaky inter-cellular junctions or low stirring speeds, to obtain a purely transcellular permeability, which is considered to be the appropriate parameter to relate to permeability from in situ brain perfusion, due to the tight inter-cellular junctions at the in vivo BBB and the well-mixed fluid dynamics in brain capillary microvessels. IVIVE scaling of transcellular, rather than apparent permeability, can then be envisaged as an input parameter for BBB permeability in a PBPK model, after scaling this value using the in vivo BBB surface area.

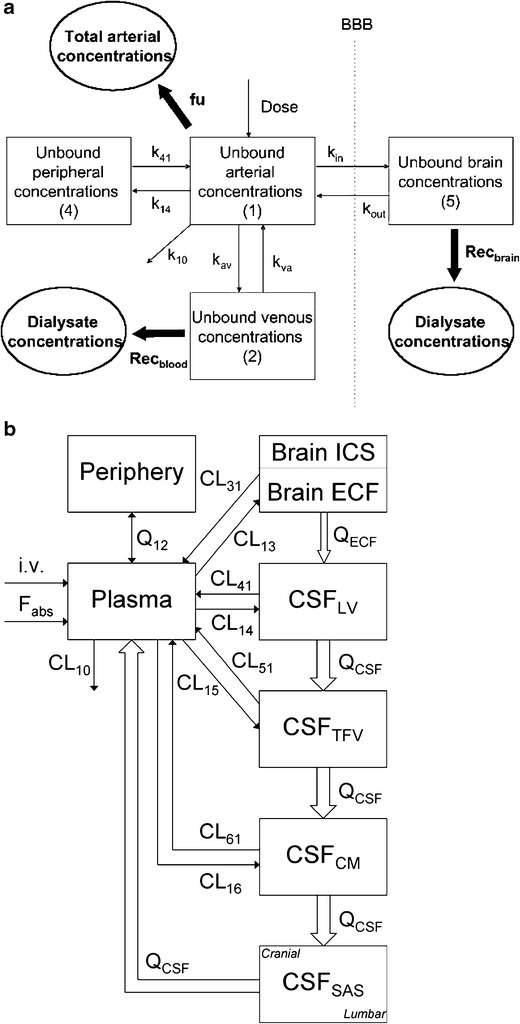
For substrates of drug transporters, relationships between transporter activity at the BBB and in in vitro models must be obtained. When the kinetic parameters for active transport of a drug are measured in representative BBB in vitro systems such as BMEC, they are often reported as normalised values to the quantity of protein in the incubation (97). These values can be scaled to whole-brain permeability by multiplying by the amount of microvessel membrane protein in the in vivo BBB (milligrams of protein per gram of brain), which has been measured using quantitative proteomic methods (98). Since this relies on transporter expression and activity levels being the same per unit mass of protein in both in vitro and in vivo, it may be more appropriate to scale based on the expression ratios of individual transporters. Since multiple efflux and influx transporters are known to be present at the BBB and BCSFB, recent focus has been on characterising their absolute protein abundances. It is only within the last few years that sufficiently sensitive techniques have been reported to successfully quantify transporter absolute abundances at the in vivo BBB (99). The quantitative proteomics approach developed by Terasaki and colleagues has enabled the comparison of BBB transporter absolute abundances between preclinical species and human, which may help to explain interspecies differences in the brain penetration of certain transporter substrates. BBB protein biomarkers including drug transporter abundances have been reported for the mouse (100), cynomolgous monkey (101), human (102), marmoset and rat (103). (Fig. 5.) A significant interspecies difference has been observed between the abundance of two major drug efflux transporters, P-gp and BCRP, between small and large species, with P-gp being the more abundant of the two transporters at the rat and mouse BBB, whereas BCRP was more abundant than P-gp at the monkey and human BBB. Therefore, the incorporation of transporter protein abundances into PBPK models will be essential for interspecies translational modelling of drugs which are substrates for these transporters.

Fig. 5.

Interspecies comparison of absolute protein abundances reported in the literature for selected drug transporters at the in vivo BBB, measured using the quantitative targeted proteomic technique (100–103). § denotes values below the limit of quantification, # denotes abundances were not determined

In order to use in vivo transporter abundance data in a PBPK model, the corresponding transporter protein abundances must also be measured in the relevant in vitro system used to determine BBB permeability. The ratio between in vivo and in vitro protein abundances is also known as a relative expression factor (REF) and can be used in place of the relative activity factor (RAF), which we estimated from in vivo data using our published PBPK model (66). Uchida et al. (104) used the quantitative proteomics technique to measure the P-gp abundance in P-gp-transfected LLC-PK1 cells (L-mdr1). They then aimed to ‘reconstruct’ the in vivo brain-to-blood concentration ratio (K_p,brain) for 11 P-gp substrates measured in wild-type and Mdr1a/1b(−/−) mice by combining measures of in vitro P-gp transport activity with the relative protein expression levels of P-gp in vivoversusin vitro. They found a good agreement (within 3-fold) for both K_p,brain and for K_p,uu,brain for 9 out of 11 compounds. The authors also noted that for similar in vitro–in vivo Mdr1a protein expression levels, P-gp activity is approximately the same by comparing literature values of in vivo permeability measured by in situ brain perfusion with their in vitro permeabilities. This ‘pharmacoproteomics (PPx)-based’ approach therefore represents a rational mechanistic approach for interspecies translation in PBPK modelling. Figure 6 summarises the IVIVE scaling strategies discussed in this section.

Fig. 6.

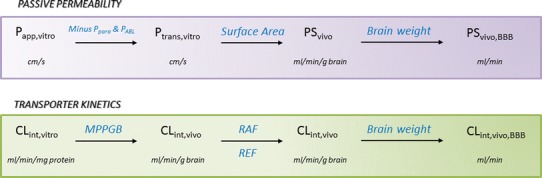
Our proposed mechanistic in vitro–in vivo extrapolation strategy for scaling in vitro-derived passive permeability and active transporter-driven kinetics to the in vivo BBB

However, complications may arise when predicting the BBB permeability of drugs, which are substrates of more than one drug transporter. Several tyrosine kinase inhibitors have been shown to be dual P-gp/BCRP substrates, and it has been demonstrated that these two transporters act synergistically both in vitro and in vivo to restrict the brain penetration of these drugs (105–111). By comparing brain/plasma ratios in single knock-out mice for either P-gp or BCRP, with the brain/plasma ratio in double knockout Mdr1a/1b(−/−) Bcrp1(−/−) mice, it has been shown that even for drugs known to be mainly substrates of either P-gp or BCRP, the brain/plasma ratios in the double knockout mice were much higher than those in either of the single knockout mice strains (112). This compensatory effect provides evidence for a synergy between different efflux transporters, which is likely to impact on predictions of drug–drug interactions (DDI) for non-CNS drugs, which are usually excluded from entering the brain by their strong active efflux. This suggests that in vitro systems, which express that all of the relevant transporters at the in vivo BBB may be more appropriate models with which to obtain DDI predictions for PBPK modelling, rather than cell models transfected with single transporters.

Intracellular Brain Distribution and Binding

Although the majority of the focus in this part of our review has been on the IVIVE of BBB permeability, the prediction of unbound ECF concentrations is also important in PBPK models during early drug development, where brain microdialysis is not routinely carried out. An estimate of unbound ECF concentrations can be obtained by multiplying total concentrations in brain homogenate by f_u,brain measured by equilibrium dialysis or in artificial systems such as TRANSIL®, which consists of porcine brain lipid membrane vesicles stabilised on silica beads (113). However since measurement of f_u,brain only takes into account nonspecific binding to brain tissue components, and not partitioning into brain cells, its validity in representing unbound ECF concentrations has been questioned (114,115). The in vitro brain slice method has been used for the measurement of the unbound volume of distribution, V_u,brain, of a drug in the ECF as it takes into account both nonspecific binding and intracellular partitioning, since cellular integrity is maintained (116,117). Friden et al. (114) reported that V_u,brain measured in brain slices was within 3-fold of the value obtained from in vivo microdialysis for 14 out of 15 of their test compounds, compared to 10 out of 15 when using f_u,brain measured by equilibrium dialysis of brain homogenate. While this remains a good agreement for the homogenate method, the authors noted that the failed predictions were for drugs residing predominantly in the interstitial space, or for those which tended to accumulate intracellularly. Since the brain slice method is a relatively low-throughput technique and is therefore not suitable for drugs in the early phase of development, the same group proposed a modelling approach to estimate V_u,brain from f_u,brain. The pH partition model published by Friden et al. (118) predicts the distribution of a drug from ECF into the more acidic intracellular and lysosomal compartments, based on its pK_a. This partitioning is assumed to be at instantaneous equilibrium, rather than a rate-limited process as it has been for some of the PBPK models mentioned in Part One of this review. The equations used for this pH partition model could then be implemented into PBPK models to predict V_u,brain from f_u,brain. It can be shown that for neutral molecules, V_u,brain equates to 1/f_u,brain, which implies that tissue binding is considered to be the only distribution mechanism. When active processes are thought to be responsible for intracellular uptake further mechanistic approaches may need to be applied, although little is currently known about the absolute transporter abundances in brain cell membranes.

PART 3: TRANSLATIONAL APPROACHES FOR HUMAN PREDICTIONS

The ultimate goal of PBPK modelling is the prediction of concentration profiles and drug–drug interactions in man, as early as possible in the development of a drug. The physiological structure of a PBPK model allows the physiological parameter values for the preclinical species to be replaced with their corresponding human values, for which data is widely available in the literature. In theory, drug-specific parameters should also be determined in in vitro systems of human origin. However, this may not always be feasible, due to the difficulty in obtaining human brain homogenate or in extracting primary brain endothelial cells from isolated microvessels. Consequently, alternative approaches include the direct use of the preclinical values in the human PBPK model, or translational scaling of in vivo-estimated or in vitro model parameters.

Good interspecies correlations have been reported for f_u,brain between rat and mouse (R² = 0.989, n = 25) (119), and rat, pig and human (R² > 0.9, n = 21) (120). Di et al. (121) also obtained high degrees of correlation for f_u,brain of 47 drugs in six different species (using orthogonal rather than linear regression) and in two different strains of rat. They concluded that interspecies similarities in f_u,brain are likely to be due to the primarily non-specific nature of drug binding to brain lipids, since the brain-lipid content is higher than that in plasma, and since protein binding within brain tissue is thought to be insignificant (122). This evidence supports the practice of using rat or mouse values of f_u,brain in human PBPK models, since brain homogenate is more easily obtained from rodents. For drugs whose brain distribution is influenced primarily by intracellular accumulation, rather than by nonspecific binding, the pH partition model described in Part Two of this review may also be applied, since it includes physiological parameters for brain compartment volumes and pHs, which can be replaced with the equivalent human values.

As previously mentioned, in vivo brain permeability of transporter substrates is likely to differ between species due to differences in transporter protein abundances at the BBB. Nevertheless, several interspecies translational approaches for BBB permeability have been published in the last 2 or 3 years. Doran et al. (123) evaluated an interspecies extrapolation approach using microdialysis data from the rat for two highly permeable non-P-gp substrates and for the P-gp substrate risperidone. They used unbound concentration ratio between brain and plasma in rat, multiplied by the unbound plasma concentrations in large species to obtain predicted unbound brain concentrations, and carried this out to obtain unbound brain pharmacokinetic profiles for two large species (dog and monkey). They then compared their predictions to the measured in vivo brain concentrations for these two species. In all three species, they calculated unbound brain and plasma concentrations by multiplying the measured total concentrations by the fractions unbound in brain and plasma measured by equilibrium dialysis. This method resulted in good predictions for the two highly permeable compounds, but a poor prediction for the P-gp substrate, suggesting a limitation in the use of this approach in the prediction of human unbound brain concentration profiles for poorly permeable transporter substrates.

An alternative approach consists of allometric scaling of drug-specific PBPK model parameters estimated by fitting the rat PBPK model to in vivo microdialysis and CSF data. Kielbasa et al. used the following allometric relationship to scale rat model parameters to their human equivalents:

$$P_{\mathrm{h}}=P_{\mathrm{r}}\times {\left(\frac{{\mathrm{Wt}}_{\mathrm{h}}}{{\mathrm{Wt}}_{\mathrm{r}}}\right)}^{0.75}$$

where P_h is the scaled human parameter, P_r is the model-predicted parameter in rat, Wt_h is the average human brain weight and Wt_r is the average rat brain weight. Westerhout et al. used a different approach when extrapolating their rat PBPK model parameters to human values, which was discussed in Part One of this review. Since they had human observed data in plasma and spinal CSF for acetaminophen, they were able to estimate certain model parameters based on this data, while scaling others based on parameter relationships obtained in the rat model. Both of these approaches may be suitable for drugs, which are mainly passively transported across the BBB, but for transporter substrates mechanistic or IVIVE-based approaches should be used to estimate human PBPK model parameters.

It can be considered that passive diffusion across biological membranes is similar between species, when differences in their respective surface areas are taken into account. Therefore, permeability measured across in vitro monolayers for passively transported drugs, or in the presence in suitable inhibitors of active transport for transporter substrates, can be used in human PBPK models. However, in order to scale the transporter-driven uptake and efflux from preclinical species to human, relative expression or activity factors should be incorporated in the human PBPK model. Relative expression factors can be obtained for human in a manner similar to that reported by Uchida et al. (104) for the mouse. When it is not possible to measure transporter protein abundances, RAF or REF in the human PBPK model may be fixed to the values estimated using preclinical PBPK models, as was the case in our reported PBPK models for morphine and oxycodone (66).

A significant challenge is the evaluation of model predictions with the human PBPK model, since observed brain concentrations are rarely obtainable. There are few examples of brain microdialysis and CSF sampling to determine drug pharmacokinetics due to the invasive nature of these techniques, and as such, they are only carried out on patients in specific disease states such as brain tumours, or acute brain injury (124). The most common non-invasive technique to assess the brain distribution of drugs in human is by imaging of radio-labelled drug. The use of positron emission tomography (PET) to assess P-gp function in vivo, along with suitable radiotracers has recently been reviewed (125). Although this technique can quantitatively measure the ratio of brain to blood concentrations, the number of probes available is limited, and when total radioactivity is measured this also includes any potentially active metabolites. Traditionally the most commonly used drug as a probe for P-gp functionality in both animal and human PET studies is [¹¹C] verapamil. Hsiao et al. did not observe any significant species differences between the increase in brain uptake of [¹¹C] verapamil after co-administration with the P-gp inhibitor cyclosporine A (CsA) between human and rat, for approximately the same verapamil blood concentrations in both species (126). The same group compared the in vitro inhibition of verapamil by CsA in MDR1-LLC-PK1 cells with that obtained using PET for both rat and human (127). The unbound EC₅₀ of CsA on verapamil was consistent between in vitro (0.6 μM) and the in vivo rat BBB (0.5 μM), and although an in vivo EC₅₀ was not obtained for human since a sufficient range of concentrations were not tested, another PET study showed that for a steady-state unbound CsA concentration of 0.2 μM there was a 79% increase in verapamil brain distribution (128), which Hsiao et al. considered to be similar to their in vitro result of 129%. However, questions remain on whether verapamil is a suitable probe for P-gp since efflux may be saturated at high concentrations, and verapamil may also transported at the BBB by other mechanisms such as organic cation transporters (129). Other probes have been tested but also show certain limitations. Syvänen et al. (130) observed species differences in K_p,brain measured by PET for humans, monkeys, rats, guinea pigs and minipigs for 3 P-gp substrates: [¹¹C] verapamil, [¹¹C] GR205171 and [¹⁸F] altanserin, even after inhibition of P-gp with cyclosporine A. They concluded that differences in P-gp activity alone did not explain these observed species differences, and that these probes may be substrates of other transport mechanisms at the BBB. More recently, loperamide has been proposed as a better P-gp probe since it seems to be more specific than verapamil. However, a limitation is that the prominent metabolite of loperamide, N-desmethyl-loperamide, is also a P-gp substrate; therefore; measurement of radiolabel combines the two (131). Therefore, using [¹¹C] N-desmethyl-loperamide itself as a probe for P-gp at the human BBB appears to be a promising approach (132,133). However, it has recently been questioned whether significant DDI of clinically used P-gp inhibitors are actually likely to be observed at the in vivo human BBB, since the ratio between the clinically relevant unbound inhibitor concentrations and their inhibition constant, K_i, are generally lower than 1 (134,135). Finally, an alternative approach to evaluate human PBPK predictions, which has not yet been thoroughly tested, is to link to the PBPK models to biomarkers or pharmacological effects in a PBPK/PD model, and to test whether the observed in vivo pharmacological observations are coherent with the model predictions. This depends on the early selection of appropriate biomarkers and the establishment of a reliable PK/PD relationship with the relevant biophase concentrations in preclinical species, in order to preserve the same mechanistic structure for the human predictions. Although this approach may introduce additional uncertainty regarding the PK/PD relationship, it may still be valuable for drugs for which imaging techniques are not possible.

CONCLUSION

To our knowledge, this is the first review focussing on PBPK modelling of blood–brain barrier transport. The increasing number of publications concerning PBPK models of the CNS, and in particular the prediction of BBB and BCSFB permeability, reflects both the urgent need for earlier and better predictions of unbound drug concentrations in the brain ECF, and the improvements in experimental techniques available to obtain the relevant in vitro and in vivo data. The area of focus has shifted from the generation of QSAR correlations for the prediction of total brain-to-blood steady-state concentration ratios for passively transported drugs, to the mechanistic prediction of BBB kinetics of transporter substrates either by interspecies translational modelling approaches, or by in vitro–in vivo extrapolation of permeability by scaling with absolute transporter abundances. PBPK models provide the ideal framework to incorporate this data and to carry out human predictions of unbound brain ECF concentrations of drugs during their development. More examples are needed to fully explore and evaluate the success of this approach, but the potential applications, in particular for the pharmaceutical industry, make this a highly promising area of research currently and in the years to come.