Decoding Sound Source Location and Separation Using Neural Population Activity Patterns

Abstract

The strategies by which the central nervous system decodes the properties of sensory stimuli, such as sound source location, from the responses of a population of neurons are a matter of debate. We show, using the average firing rates of neurons in the inferior colliculus (IC) of awake rabbits, that prevailing decoding models of sound localization (summed population activity and the population vector) fail to localize sources accurately due to heterogeneity in azimuth tuning across the population. In contrast, a maximum-likelihood decoder operating on the pattern of activity across the population of neurons in one IC accurately localized sound sources in the contralateral hemifield, consistent with lesion studies, and did so with a precision consistent with rabbit psychophysical performance. The pattern decoder also predicts behavior in response to incongruent localization cues consistent with the long-standing “duplex” theory of sound localization. We further show that the pattern decoder accurately distinguishes two concurrent, spatially separated sources from a single source, consistent with human behavior. Decoder detection of small amounts of source separation directly in front is due to neural sensitivity to the interaural decorrelation of sound, at both low and high frequencies. The distinct patterns of IC activity between single and separated sound sources thereby provide a neural correlate for the ability to segregate and localize sources in everyday, multisource environments.

Introduction

There is a clear understanding of the basic mechanisms by which the firing rates of neurons in the auditory brainstem become sensitive to the cues for the horizontal direction of a sound source—interaural time difference (ITD) and interaural level difference (ILD) (Grothe et al., 2010). What remains unclear is how the central auditory system combines information across these neurons to arrive at an estimate of location—i.e., how source location is decoded.

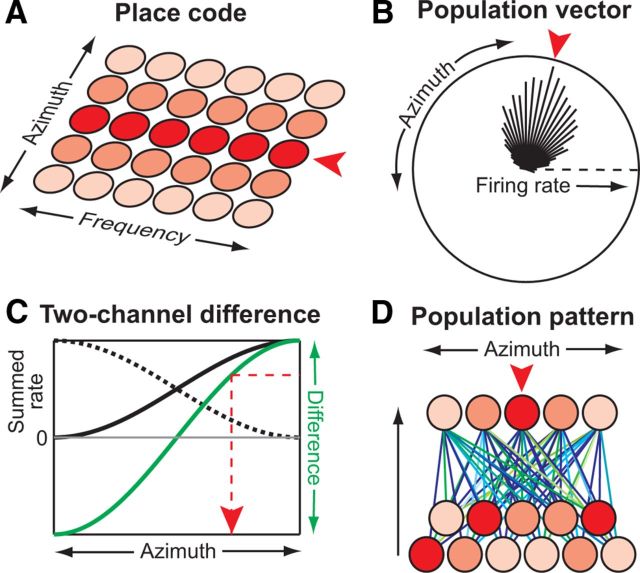
A place code of sound location was originally proposed by Jeffress (1948), who hypothesized that the central auditory system contains a topographic map of tuning to ITD (seeFig. 1A). Elaborations of this influential model (Colburn, 1977; Stern and Trahiotis, 1995) account for many psychophysical observations. However, after decades of neurophysiological research, no compelling evidence for a topographic map of ITD has been reported in mammals. On the other hand, a “population vector” decoder (Fig. 1B), which also characterizes tuning functions by their peaks but does not require systematic topography, predicts source azimuth consistent with behavioral measurements when tested on modeled neural activity in the optic tectum of barn owls (Fischer and Peña, 2011).

Figure 1.

Population decoding schemes. A, In a place code, azimuth (red arrow) is read out from the location of greatest activity along a topographic map of azimuth. B, For the population-vector decoder, the activity of each neuron is represented as a vector with magnitude equal to its firing rate and direction equal to its best azimuth (black lines). Azimuth is estimated as the direction of the vector sum. C, For the two-channel difference decoder, azimuth is estimated from the difference between the summed firing rates on the left and right sides. D, For the population-pattern decoder, each azimuth is estimated from the pattern of activity across the population. This can be visualized as a second layer of neurons associated with each azimuth that sum population activity weighted by different synaptic strengths. Azimuth is estimated as that associated with the neuron in the second layer with greatest activity.

The observation that the steepest slopes of tuning functions of inferior colliculus (IC) neurons tend to be near the midline motivated another population code for ITD in mammals (McAlpine et al., 2001). To take advantage of the large range of firing rates along tuning slopes, rates are summed separately in each IC and an estimate of ITD is then “read out” from the difference of summed rates (Fig. 1C). However, lesion and cortical cooling studies challenge this model by showing that localization only requires information from brain areas contralateral to the sound source (Jenkins and Masterton, 1982; Malhotra et al., 2004).

The above decoding models either reduce tuning functions to the locations of their peaks, or ignore the diversity in tuning functions by focusing on population-averaged activity. The present study tests a maximum-likelihood decoder operating on the pattern of activity across IC neurons (Fig. 1D), thereby using information in both the shapes of individual tuning functions and the distribution of peaks across the population. Pattern decoders have widely been used in visual cortex (Jazayeri and Movshon, 2006; Berens et al., 2012), but rarely in the auditory system. They have been applied to sound localization based on the responses of auditory cortical neurons in awake macaques (Miller and Recanzone, 2009) and on the responses of IC neurons in anesthetized gerbils to sources varying in ITD only (Lesica et al., 2010). Here, we demonstrate that a pattern decoder operating on the responses of IC neurons from one side in awake rabbits estimates source azimuth with a precision consistent with rabbit psychophysical measurements. We further show that, when tested with stimuli having incongruent ITD and ILD cues, the decoder behaves in a manner consistent with the long-standing “duplex theory” of sound localization (Strutt, 1907). Finally, we show that the decoder accurately predicts the ability to perceptually segregate two spatially separated sources (Best et al., 2004).

Materials and Methods

Experimental methods

Single unit activity was collected from the right IC of two female, Dutch-belted rabbits (Oryctolagus cuniculus). All procedures were approved by the Institutional Animal Care and Use Committees of Massachusetts Eye and Ear and the Massachusetts Institute of Technology. Data analyzed in the present study were described in a previous report (Day et al., 2012), which includes detailed experimental methods, including surgical and electrophysiological methods, and the generation and presentation of acoustic stimuli. Stimulus waveforms were given directional characteristics by filtering through rabbit directional transfer functions (DTFs), and acoustic stimuli were presented through ear inserts. DTFs were calculated from acoustic impulse responses measured in the ear canals of a cadaver rabbit. To remove detailed spectral features specific to an individualized DTF, simplified DTFs were constructed by extracting the first principal component of the log magnitude spectra of the measured DTFs (Kistler and Wightman, 1992). The resulting simplified DTFs capture the dependence of ITD and gross ILD on both frequency and azimuth (Day et al., 2012).

Single-unit recordings were collected from awake, head-restrained rabbits in daily sessions over a period of months, likely from the central nucleus of the IC (Day et al., 2012). Sound sources always consisted of the same token of 300 ms broadband noise (0.1–18 kHz; 4 ms on/off cos² ramp), presented every 500 ms. For the simultaneous presentation of two sound sources, an additional token of noise was used, incoherent with the first. In response to random tokens of noise, the variability of spike counts of IC neurons is dominated by intrinsic neural variability as opposed to variability due to different tokens (Shackleton and Palmer, 2006); therefore we do not expect our decoder results using frozen noise to be greatly different from those using random noise. For each neuron, single sources were presented at a sound level 23 dB above noise threshold, while two spatially separated sources were presented each at 20 dB above threshold, yielding equivalence in sound level when the two sources are colocated (two incoherent 20 dB noises at the same location are equivalent to a 23 dB noise).

Spike counts over the duration of the stimulus were measured for a single source presented at each of 13 azimuths in the frontal hemifield (±90° with 15° resolution, where 0° is straight ahead and positive indicates contralateral), using 3–10 repetitions (usually 8). This azimuth tuning function was also collected in the presence of an additional source fixed at 0°. Single-source and two-source azimuth tuning functions were also collected under two different manipulations of binaural cues. In the “ITD-only” condition, magnitude spectra of the DTFs were fixed to those at 0°, allowing only phase to vary naturally with azimuth. Conversely, in the “fixed-ITD” condition, phase spectra of the DTFs were fixed to those at 0°, allowing only magnitude to vary naturally with azimuth. Finally, new data were collected for the present study, from the same animals, where two sources were presented simultaneously in every location combination in the frontal hemifield, with a 30° resolution (7 single-source locations and 21 spatially separated location combinations).

Computational methods

Source azimuth was estimated from the spike counts of IC neurons using three different decoding models. Two main assumptions shared by all decoders are that spike counts in response to any sound stimulus have Poisson distributions, and that the spike counts of different neurons are statistically independent of each other for a given stimulus. Of the 1014 spike count distributions in our single-source dataset (78 neurons × 13 azimuths), 82% had a Fano factor within the 95% confidence intervals of that expected from a Poisson process (Eden and Kramer, 2010). Since we did not record simultaneously from multiple neurons, we could not directly assess the correlations in spike counts, and assumed statistical independence for simplicity. The limited available data from simultaneous recordings of neuron pairs in the IC of anesthetized gerbils to noise suggest that correlation coefficients between spike counts are small (Lesica et al., 2010, their supplemental Fig. 3; mean: 0.03, range: [−0.1, 0.225]).

Population-vector decoder.

For the “population-vector” decoder, we focused on the majority of neurons whose firing rates were sensitive to azimuth. Excluded were seven neurons with azimuth-insensitive firing rates (Day et al., 2012) and another neuron with very low firing rates in response to single sources. The best azimuth (BA) of each azimuth-sensitive neuron was defined as the azimuth with the highest firing rate, with a unit vector, θ_i, pointing in the direction of the BA. For any test azimuth, one spike count in response to that azimuth, n_i, was then selected randomly from each of N azimuth-sensitive neurons in the population. The estimated azimuth, θ̂, was computed as the angle of a weighted vector sum of BAs: $\widehat{\theta }=\angle {\displaystyle {\sum }_{i=1}^N{n}_i{\theta }_i}$. The estimated azimuth was then rounded to the nearest 15°. This procedure was iterated 500 times for each test azimuth to yield 500 estimates. In every iteration, the randomly selected test spike counts, n_i, were removed from the dataset before determining the BA of each neuron; therefore BAs were not influenced by the data used to test the decoder so as to avoid overfitting. We also alternatively normalized each n_i by the mean spike count at the BA of the corresponding neuron, but the performance of the decoder remained essentially the same.

To assess the influence of tuning function shape on the performance of the population-vector decoder, we compared decoder performance when tested on experimental data versus simulated data with homogeneous tuning shapes. Simulated azimuth tuning functions were Gaussian with means positioned at the same BAs as in the experimental data, and SD set to 31° to create an ipsilateral “slope” equal to that of the median slope across the experimental sample (52°; slope defined later in Results). Tuning functions had a maximum firing rate of 100 spikes/s. Spike counts were randomly drawn from a Poisson distribution.

Two- and single-channel decoders.

All neural data were obtained from the right IC. For the “two-channel difference” decoder, we simulated neural data for the left IC by assigning the response of each right-side neuron at a given azimuth to a “left-side” neuron's response at the same azimuth with the opposite sign (e.g., response of L neuron at +90° = response of R neuron at −90°). For each azimuth, θ, one spike count in response to that azimuth was selected randomly from each right and left neuron in the population. The difference, d_θ, was then taken between the sums of these spike counts on the left and right sides, l_θ and r_θ, respectively. This was repeated 50 times for different randomly selected spike counts to create 50 samples of d_θ. The probability distribution of d_θ was well approximated by a Gaussian function, with mean and variance, μ_θ and σ_θ², respectively, estimated from the 50 samples. To test the model, a difference of summed spike counts, d′, was computed for each azimuth from randomly selected spike counts in response to that azimuth. The estimated azimuth was then chosen to maximize the following likelihood:

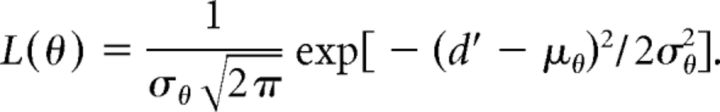This whole procedure was iterated 500 times for each test azimuth. As for the population vector, in every iteration spike counts used to compute d′ were removed from the dataset before μ_θ and σ_θ² were estimated; therefore the decoder was never tested on the data it was trained with to avoid overfitting. The “single-channel” decoder was implemented in the same way as the two-channel difference decoder, except d_θ and d′ were sums of spike counts on the right side only (r_θ and r′) instead of a difference of sums between sides.

The two-channel decoder was also used to distinguish between one and two spatially separated sources. In this case the two-source combination, θ, could be any spatially separated combination or colocated (single source) combination. Instead of operating on the difference of summed spike counts, d′, the decoder operated on both the left and right summed spike counts, l′ and r′. These summed spike counts were assumed to be statistically independent, therefore the likelihood was a product of Gaussians:

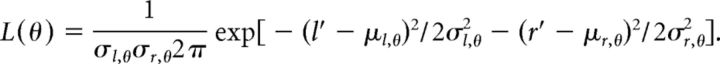The estimated two-source combination was chosen to maximize the likelihood. This estimate was then further categorized as “two sources” (any spatially separated combination) or “one source” (any colocated combination).

Population-pattern decoder.

For the “population-pattern” decoder, the tuning function of each neuron, f_i(θ), was defined as the mean spike count as a function of azimuth, θ. For each test azimuth, one spike count in response to that azimuth, n_i, was then selected randomly from each of N neurons in the population. As shown in Jazayeri and Movshon (2006), the logarithm of the likelihood given the assumption of independent, Poisson spike counts is as follows:

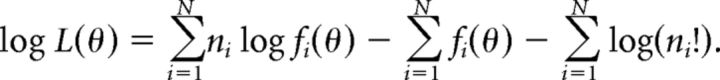The first term is a weighted sum of spike counts and the second term is independent of spike count, but dependent on θ. The third term may be ignored since it is independent of θ. The estimated azimuth was then chosen to maximize the log likelihood. To avoid taking the logarithm of zero whenever the mean spike count of neuron i at some azimuth, θ₀, was equal to zero, we set f_i(θ₀) to 1/(number of trials + 1). This effectively assumes that one spike would have occurred in response to an extra stimulus repetition. Similar to the other decoders, this procedure was iterated 500 times at each test azimuth, and in each iteration the test spike counts n_i were removed from the dataset before estimating f_i(θ) to avoid overfitting.

The population-pattern decoder was also used to distinguish between one and two separated sources. In this case, θ could be any two-source combination, and n_i represented the spike count of neuron i in response to some two-source combination. The same log likelihood as above was then used to determine the two-source combination most likely to give rise to the test spike counts. The estimated two-source combination was further categorized as one source or two sources.

Performance of the population-pattern decoder was also tested when the decoder was trained with “standard” data (normal binaural cues) and tested on altered-cue data (incongruent binaural cues). In this case tuning functions f_i(θ) were estimated from standard data and test spike counts n_i were selected from altered-cue data.

Performance of each decoder was summarized by the mean absolute error of localization over all source azimuths, ε. In some cases the mean absolute error was calculated over only contralateral or ipsilateral source azimuths (including 0°), ε_contra and ε_ipsi, respectively. Since decoder estimates were generated at each source azimuth over a finite number of iterations, there will be some variability in the calculation of ε. To estimate this variability, we calculated ε from the population-pattern decoder on 100 separate simulations; the SD of ε was only 0.06°.

Results

Poor source localization performance using previous decoders

We tested the performance of alternative neural population decoders in estimating the azimuth of single sources in the frontal hemifield. We used data from a previous study (Day et al., 2012) in which single units (N = 78) were recorded from the right IC of awake rabbits in response to broadband noise bursts presented in virtual acoustic space at horizontal locations between ±90°. The decoders operate on the spike counts of IC neurons, as opposed to the more general spike times. Spike counts have been shown to contain the majority of mutual information between the neural activity of IC neurons and ITD and ILD cues (Chase and Young, 2008). Best frequencies (BFs; the pure tone frequency yielding maximum firing rate) spanned 0.3–17 kHz across the neuron sample.

We first tested a “population vector” decoder (Georgopoulos et al., 1982; Fischer and Peña, 2011) of source azimuth. The response of each neuron to a given sound source was represented by a vector whose direction is the neuron's BA and whose magnitude is the neuron's firing rate in response to the source (Fig. 1B). The source azimuth is then estimated as the direction of the vector sum across the population.

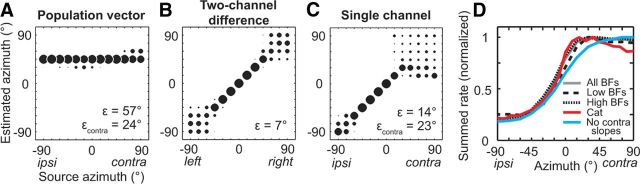
The population-vector decoder performed very poorly at localizing sources in the frontal hemifield, classifying every source to azimuths near 45° (Fig. 2A). This extreme contralateral bias occurred because 93% (65/70) of BAs were located on the contralateral side. A nonuniform distribution of tuning function peaks is known to bias estimates in a vector decoding scheme (Salinas and Abbott, 1994). However, the contralateral bias in the distribution of BAs does not entirely explain the poor localization of contralateral sources by the population vector; these estimation errors were also partly due to heterogeneity in the shapes of tuning functions across the sample (in particular, the marked asymmetry of tuning functions, which we describe below). To demonstrate this, we tested the population-vector decoder on a simulated dataset in which the distribution of BAs was identical to that measured in our sample but the tuning functions were all Gaussians with equal variance (SD = 31°). Using these simulated data, the decoder performed dramatically better at estimating the azimuth of contralateral sources (ε_contra = 9° vs ε_contra = 24° using the empirical data). The poor performance of the population-vector decoder was therefore due to both the bias in BAs and the heterogeneity in the shapes of azimuth tuning functions.

Figure 2.

Performance of previous decoders. A–C, Distribution of estimated azimuths at each source azimuth for the population-vector, two-channel difference, and single-channel decoders, respectively. Bubble diameter indicates fraction of estimates, where the sum in each column equals 1. ε and ε_contra, mean absolute error over all sources and only contralateral sources, respectively. For completely random estimates, ε_contra = 63°. D, Summed firing rate across either all neurons (N = 78), neurons with low BFs (<2 kHz; N = 21), neurons with high BFs (≥2 kHz; N = 57), or all neurons without a contralateral slope (N = 53). Summed rate for all BFs also plotted for azimuth tuning data from the IC of anesthetized cats (N = 105; Delgutte et al., 1999).

Next we tested the two-channel population decoder of McAlpine et al. (2001), modified to decode azimuth rather than ITD as in Stecker et al. (2005). Firing rates from neurons on the right and “left” sides (see Materials and Methods) were summed separately, and azimuth was estimated from the difference of the summed rates (Fig. 1C); we termed this the “two-channel difference” decoder. This decoder localized sources between ±30° nearly perfectly, but tended to blur source locations between 60 and 90° and between −60 and −90° (Fig. 2B). The mean absolute error of localization for this decoder was 7°.

Lesion-behavior studies strongly suggest that the neural information from the IC on one side is sufficient to localize sources on the opposite side (Jenkins and Masterton, 1982). Even stronger evidence for contralateral sufficiency is available for the auditory cortex using reversible cooling of specific fields while cats perform a localization task (Malhotra et al., 2004). Could a single-channel decoder (McAlpine et al., 2001) therefore localize contralateral sources? We tested this hypothesis by estimating azimuth from the summed rate on one side, instead of the difference of summed rates. The single-channel decoder largely failed to distinguish among source locations on the contralateral side (ε_contra = 23°), although ipsilateral sources were localized accurately (ε_ipsi = 3°; Fig. 2C). The reason for this poor performance is that the summed firing rate plateaus at contralateral azimuths (Fig. 2D), creating ambiguity between most contralateral locations. This ambiguity remained when we separately analyzed low-BF and high-BF neurons, using a 2 kHz BF cutoff to separate neurons whose azimuth sensitivity is determined by ITD in the temporal fine structure from neurons sensitive to ILD and/or envelope ITD (Devore and Delgutte, 2010; Day et al., 2012). We also performed the same analysis on azimuth tuning functions previously measured from IC neurons in anesthetized cats (Delgutte et al., 1999), using similar virtual acoustic space methods. The summed rate in cats reaches a maximum around 15° and decreases slightly at more lateral azimuths (Fig. 2D); therefore the ambiguity of the summed neural activity at contralateral locations is not unique to rabbits.

Why does the summed firing rate plateau at contralateral locations? Good decoder performance requires the summed rate to vary monotonically with azimuth, which would occur if the slopes of individual tuning functions were all oriented in the same direction and collectively spanned the entire range of contralateral azimuths. For each azimuth-sensitive neuron in our sample, we defined the “ipsilateral slope” of the azimuth tuning function as the range of azimuths ipsilateral to the BA where the firing rate grows from 10% of the maximum firing rate above the ipsilateral minimum to 90% of the maximum firing rate (Fig. 3A). The “contralateral slope” was defined in the same way, if existent, except it was referenced to the contralateral minimum. We further computed the ipsilateral and contralateral half-maximum azimuths—the azimuths at which the firing rate equaled 50% of the maximum rate, if existent. The distribution of ipsilateral slopes across the population of IC neurons nearly spanned the entire frontal hemifield (Fig. 3B). However, 37% of neurons, spread across the entire tonotopic axis, additionally had a contralateral slope, meaning the firing rate decreased contralateral to the BA by at least 20% of the maximum rate. Firing rate was not as strongly modulated contralateral to the BA; only 9% of neurons had contralateral slopes that decreased by at least 50% from the maximum rate. Nevertheless, the existence of a sizeable proportion of neurons with contralateral slopes causes the summed firing rate to plateau at contralateral locations: the summed rate excluding neurons with contralateral slopes was a monotonic function of azimuth (Fig. 2D). Performance of the single-channel decoder improved substantially when neurons with contralateral slopes were excluded from the sample (ε_contra = 9° vs ε_contra = 23° for all neurons).

Figure 3.

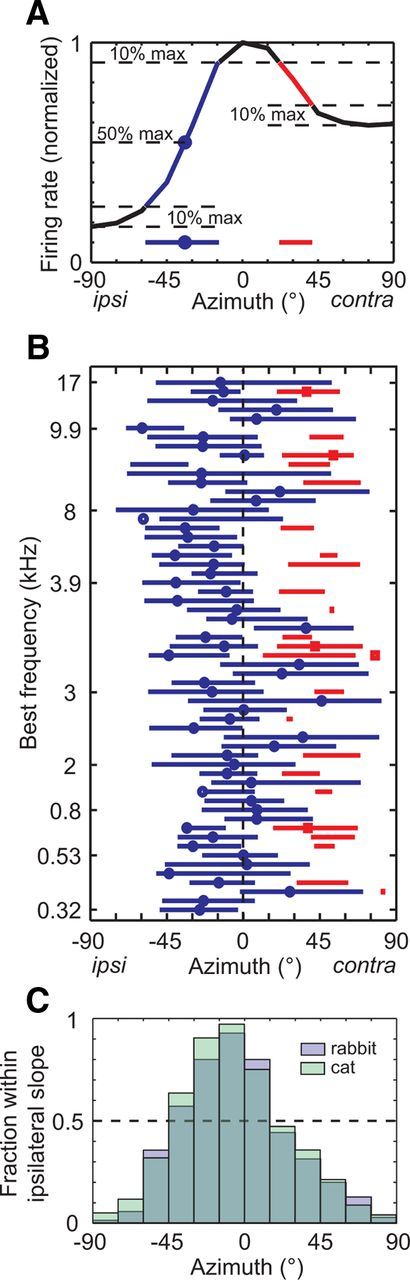
Heterogeneity of azimuth tuning functions. A, The tuning function of each azimuth-sensitive neuron was characterized by its ipsilateral slope (blue line), ipsilateral half-maximum azimuth (blue circle), contralateral slope (red line), and contralateral half-maximum azimuth (red square; none for this neuron). All features are projected onto the x-axis to show azimuth ranges. B, Features are displayed for all azimuth-sensitive neurons ordered by increasing BF (N = 59). Not shown are 11 neurons for which a BF was not measured. C, Bar graph shows the fraction of neurons that have an ipsilateral slope that overlaps with the azimuth on the x-axis (blue, N = 70). Data are also shown for IC neurons of anesthetized cats (green, N = 105; Delgutte et al., 1999). Dashed line indicates 50%.

Another trend apparent in Figure 3B is that ipsilateral slopes are biased toward ipsilateral locations. We collapsed ipsilateral slopes into the bar graph in Figure 3C, where each bar indicates the fraction of neurons that have an ipsilateral slope overlapping the corresponding azimuth bin. On the ipsilateral side, >50% of neurons encode azimuths between −45 and 0° in the firing rates of their ipsilateral slopes, while on the contralateral side this only holds between 0 and 15°. We performed the same analysis on azimuth tuning functions from IC neurons in anesthetized cats (Delgutte et al., 1999) and the results were much the same as for rabbits (Fig. 3C). The ipsilateral slopes of azimuth tuning functions of IC neurons are therefore biased to encode ipsilateral locations more than contralateral locations (Delgutte et al., 1999).

Accurate decoding of source location using the pattern of population activity

Although the diversity in the shapes of azimuth tuning functions across IC neurons causes poor performance of the population-vector and single-channel decoders, neural computations used further along the auditory pathway may make use of the information available in this tuning heterogeneity. For any source location, the pattern of activity across the population of IC neurons will be distinct from the patterns of activity evoked by sources at other locations due to heterogeneous tuning. For instance, Figure 4A shows the firing rates of neurons in our sample in response to a source at 30°, ordered from greatest to least. Maintaining the same order, the firing rates of the same neurons are also shown for a source at 45°. The shift in source location causes a slight change in the pattern of activity, which can be more clearly seen by calculating the difference in firing rates between the two locations (Fig. 4B). The patterns for 30 and 45° are clearly distinct, but we need to test whether the pattern for each source location is distinct from every other source location, and whether the differences are significant with respect to neural response variability. We therefore implemented a maximum-likelihood decoder operating on the pattern of spike counts (Jazayeri and Movshon, 2006) across every IC neuron in the sample. The pattern-matching computation can be interpreted as a summation of spike counts of IC neurons through a set of synaptic weights onto a second layer of neurons, where each second-layer neuron represents one possible response azimuth (Fig. 1D). Azimuth is then estimated as that of the second-layer neuron with the greatest activity.

Figure 4.

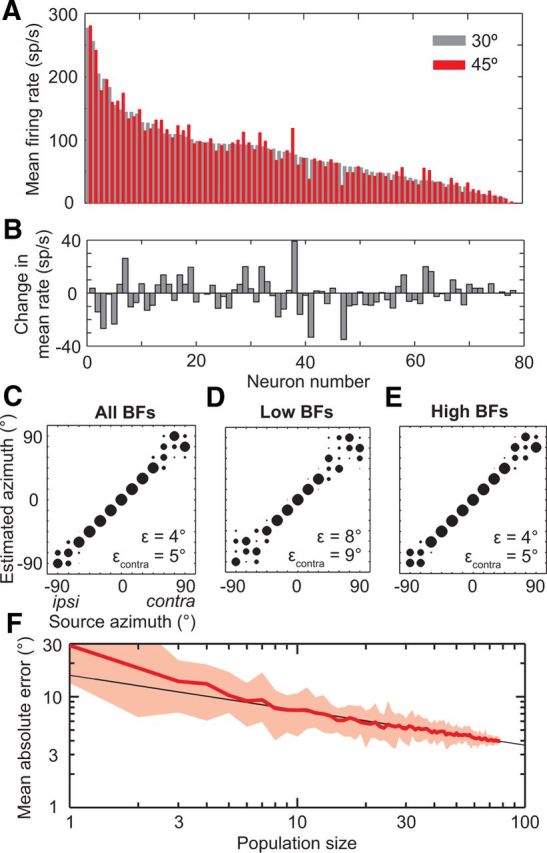
Pattern of activity across IC neurons can be used to decode source azimuth. A, Mean firing rates of all neurons to a source at 30°, ordered by decreasing rate (gray bars). Mean rates of the same neurons in the same order to a source at 45° (red bars). B, Change in mean firing rates across neurons from 30 to 45°, same order as in A. C–E, Localization performance of the population-pattern decoder using either all neurons (N = 78), neurons with low BFs (N = 21), or neurons with high BFs (N = 57), respectively. F, Mean absolute error of localization, ε, as a function of population size. Red line, mean ε over 25 randomly selected populations per size. Shaded area, range of ε. Black line, power law fit to the mean ε for sizes ≥5: y = 15.6x^–0.32.

The “population-pattern” decoder estimated azimuth nearly perfectly for sources located between ±45°, but tended to blur source locations between 60 and 90° and between −90 and −75° (Fig. 4C). The overall performance exceeded that of the two-channel difference decoder (ε = 4° and ε_contra = 5° vs ε = 7° for the two-channel difference decoder). Unlike the two-channel difference decoder, the performance of the population-pattern decoder depends only on responses from one IC, consistent with lesion studies (Jenkins and Masterton, 1982). We also trained and tested the population-pattern decoder separately on neurons with low BFs or with high BFs. Performance of the high-BF decoder was just as good as with all neurons (ε_contra = 5°; Fig. 4E), but the low-BF decoder tended to blur lateral locations slightly more (ε_contra = 9°; Fig. 4D). This may, in part, be due to the smaller number of low-BF neurons available in the dataset to train the decoder.

The all-BF pattern decoder also localized sources at ipsilateral locations well, and did so with even higher accuracy than at contralateral locations (ε_ipsi = 2° vs ε_contra = 5°). This is because the ipsilateral slopes of azimuth tuning functions provide a wide range of firing rates over which to encode azimuth, and ipsilateral slopes tend to over-represent ipsilateral azimuths (Fig. 3C). These results appear inconsistent with lesion studies in cats that show an inability to localize ipsilateral sources accurately with only a single intact IC (Jenkins and Masterton, 1982). Yet why would the azimuths of ipsilateral sources be accurately represented in the IC if this information were only to be “lost” at higher levels in the auditory system? It may be that neural information regarding only contralateral, but not ipsilateral, source locations remains reliable when stimulus parameters other than location are varied, such as sound level, spectrotemporal profile, or the presence of background noise or reverberation.

How many neurons does the population-pattern decoder need to accurately estimate the azimuth of a source? To answer this question, we examined how sensitive the performance of the decoder was to population size. We trained and tested a sequence of decoders of increasing population size with each population randomly selected from our sample without replacement, and repeated this selection 25 times for each size. Decoder performance improved with size approximately following a power law (Fig. 4F), with a decoder using 38 neurons performing on average with a mean absolute error < 5°.

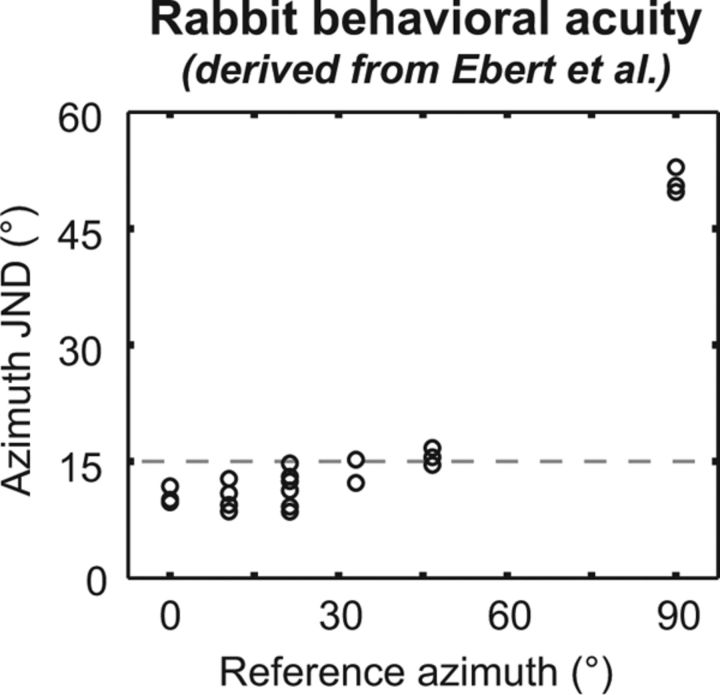
Although rabbit behavioral localization data are unavailable for comparison to decoder performance, our results can be indirectly related to rabbit behavioral ITD acuity. Ebert et al. (2008) measured just noticeable differences (JNDs) in ITD for low-frequency (0.5–1.5 kHz) noise presented to rabbits. Using a measured mapping between ITD and azimuth for rabbits (Day et al., 2012, their Fig. 2c), we converted these ITD JNDs into azimuth JNDs for each reference azimuth (Fig. 5). We assume that in a localization task, a rabbit would confuse the locations of two sources separated by less than one azimuth JND (Moore et al., 2008). Based on this assumption and the Ebert et al. (2008) data, we predict that (1) sources at 0 and 15° will not be mistaken for each other; (2) sources at 30 and 45° are on the threshold for being mistaken for each other; and (3) a source at 90° may be mistaken for one at 75°, 60°, or 45°. Since the behavioral measurements were conducted with low-pass noise, we compare these predictions to the performance of the population-pattern decoder trained only on low-BF neurons. Figure 4D shows that all three of the above predictions are met by the low-BF decoder using data from only 21 neurons; therefore performance of the population-pattern decoder is consistent with this limited behavioral dataset.

Figure 5.

Behavioral azimuth JND versus reference azimuth, for rabbits, derived from data in Ebert et al. (2008) (their Fig. 2c). Dashed line indicates a 15° JND. ITD JNDs from the Ebert et al. (2008) data were transformed into azimuth JNDs using the inverse of the equation, ITD = (275 μs) · sin(azimuth), taking reference location into account. JND data at the reference ITD of 300 μs were used to compute the azimuth JND at a reference of 90°.

ITD acuity in rabbits is much worse at a reference ITD pointing to 90° as compared with a reference ITD pointing to 0° (Fig. 5). This observation is correctly predicted by the low-BF pattern decoder (Fig. 4D). Some ambiguity at lateral azimuths remains even when the decoder is trained with neurons of all BFs (Fig. 4C). These estimation errors occur because the firing rates of most IC neurons tend to saturate at the most lateral azimuths, with very few neurons having ipsilateral or contralateral slopes that extend beyond 75° (Fig. 3). This saturation of rate is partly due to the compression of the dependence of ITD and ILD on azimuth at lateral positions (Day et al., 2012, their Fig. 2b,c). Rate ambiguity due to compression of binaural cues with azimuth could in theory be countered by placing sharper slopes in ITD and ILD tuning functions at ITDs or ILDs corresponding to lateral azimuths, but Figure 3 demonstrates that this rarely occurs among IC neurons.

Consistency of population-pattern decoder performance with the duplex theory

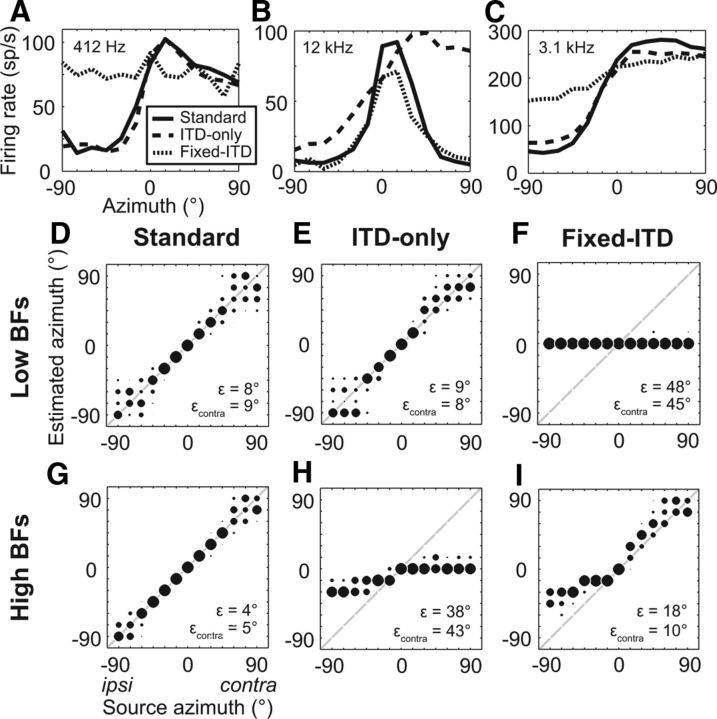
Early work by Lord Rayleigh (Strutt, 1907) determined that the primary cue used to lateralize a pure tone is ITD for low-frequency tones, and ILD for high-frequency tones. This “duplex” theory has been shown to largely hold for broadband noise when investigated using manipulations of binaural cues in virtual acoustic space (Wightman and Kistler, 1992; Macpherson and Middlebrooks, 2002). In previous work (Day et al., 2012), we investigated how IC neurons encode the azimuth of a noise source when sound to the two ears is presented in either of two conditions with incongruent binaural cues: (1) to allow the natural variation of ILD and spectral tilt with azimuth while ITD remains fixed to its value at 0° (“fixed-ITD”) or (2) to allow the natural variation of ITD with azimuth while ILD and spectral tilt remain fixed to their value at 0° (“ITD-only”). For low-BF neurons such as the example in Figure 6A, azimuth tuning functions measured in the ITD-only condition were nearly the same as those measured in the “standard” condition (where both ITD and ILD varied naturally), while tuning functions were usually flat in the fixed-ITD condition, showing that ITD cues were dominant. On the other hand, for a majority of high-BF neurons, fixed-ITD tuning functions tended to be similar to standard tuning functions, while ITD-only tuning functions were either flat or had shapes that did not match the standard tuning function (Fig. 6B). However, ITD-only tuning functions were similar to standard tuning functions in a minority of high-BF neurons (Fig. 6C). Most high-BF neurons in our sample were sensitive to the ITD in the fluctuating envelope induced by cochlear filtering of the broadband sound waveforms, as shown by the similarity of ITD tuning functions measured during the sustained portion of the response with either the same or opposite waveform polarities at the two ears (Joris, 2003; Devore and Delgutte, 2010; Day et al., 2012). While the examples in Figure 6, A–C, suggest a general consistency with duplex theory as far as the encoding of azimuth in the firing rates of IC neurons, it does not necessarily follow that the population decoding of azimuth would also be consistent with duplex theory, especially for high-BF neurons that are sensitive to multiple cues. We therefore examined the performance of the population-pattern decoder when tested on data from conditions with incongruent binaural cues.

Figure 6.

Population-pattern decoding is consistent with the “duplex theory” of sound localization. A–C, Azimuth tuning functions of 3 IC neurons under standard (solid line), ITD-only (dashed line), and fixed-ITD (dotted line) cue conditions. BF of each neuron indicated in upper left corner. D, G, Localization performance of the population-pattern decoder using low-BF (N = 11) or high-BF (N = 32) neurons, respectively. E, H, Performance of the decoder when trained on data in the standard condition and tested on data in the ITD-only condition, using the same neurons as in D and G, respectively. F, I, Same as in E and H except decoder is tested on data in the fixed-ITD condition. Unity lines shown in D–I (gray lines).

Using only neurons for which we had data from all three cue conditions, we first trained and tested the population-pattern decoder on data from the standard condition as a baseline of performance, separately for low-BF and high-BF neurons (Fig. 6D,G, respectively). We then tested the same decoders on data from either the ITD-only condition (Fig. 6E,H) or the fixed-ITD condition (Fig. 6F,I). This procedure is motivated by the idea that an animal is “trained” on sound sources with naturally covarying—as opposed to incongruent—binaural cues. Performance of the low-BF decoder was nearly the same when tested on data from the ITD-only condition (Fig. 6E) as when tested on data from the standard condition, but azimuth estimates when tested on data from the fixed-ITD condition (Fig. 6F) remained locked to the ITD cue (0°). Therefore decoder performance was completely determined by ITD for low-BF neurons, consistent with the duplex theory.

Performance of the high-BF decoder was more complex. Since lesion studies imply that localization depends only on neural information from the contralateral IC (Jenkins and Masterton, 1982), we focus on decoder performance for contralateral sources. Localization of contralateral sources was reasonably accurate in the fixed-ITD condition, although source laterality tended to be overestimated by the decoder (Fig. 6I). In contrast, azimuth estimates in the ITD-only condition (Fig. 6 H) remained locked to the ILD cue (0°). Therefore azimuth estimates for contralateral sources using the high-BF decoder were dominated by ILD, consistent with the duplex theory. On the other hand, the high-BF decoder severely undershot azimuth estimates of ipsilateral sources in the fixed-ITD condition (Fig. 6I), indicating a stronger influence of ITD than for contralateral sources.

The poor performance of the high-BF decoder tested on data from the ITD-only condition (Fig. 6H) may be simply due to a possible weak dependence of the firing rates of IC neurons on envelope ITD. To address this possibility, we both trained and tested the high-BF decoder on data from the ITD-only condition. In this condition, the performance of the high-BF decoder dramatically improved (ε = 9° vs ε = 38° when trained on the standard condition). Therefore, source azimuth is sufficiently encoded by the pattern of activity across high-BF neurons in response to stimuli varying only in ITD. The poor performance of the high-BF decoder in Figure 6H is due to differences between these ITD-only response patterns and the response patterns evoked by stimuli with both natural binaural cues.

Population-pattern decoder distinguishes single sources from two spatially separated sources

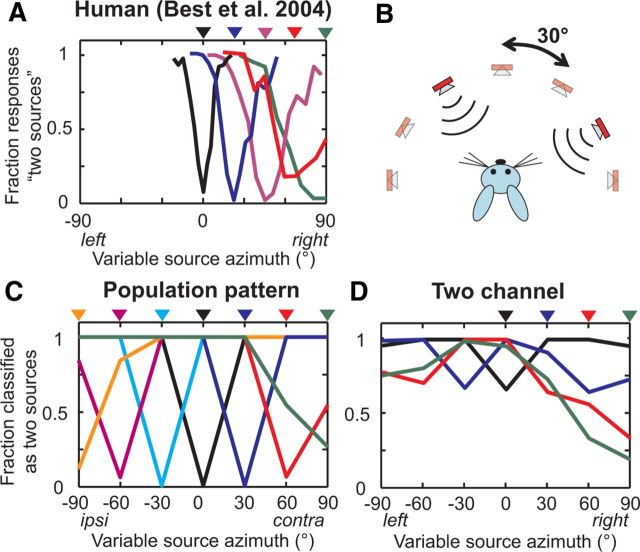
Best et al. (2004) measured the ability of human listeners to detect the spatial separation of two incoherent tokens of broadband noise presented concurrently in virtual acoustic space. When emitted from the same location, these stimuli are perceived as a single sound source. A percept of two sources was evoked by a separation of about 15° when one of the sources was fixed at 0°; a progressively larger separation was necessary for a two-source percept when one of the sources was fixed at more lateral azimuths (Fig. 7A).

Figure 7.

Patterns of activity across IC neurons are largely distinct between single sources and two concurrent, separated sources. A, Human perception of two sources as a function of separation between a fixed source and a variable source. Triangles indicate location of the fixed source, with color-matched response curves below. Data from Best et al., 2004. B, Experimental simulation for rabbits. Two sources are presented concurrently in virtual acoustic space in every possible two-source configuration in the frontal hemifield. C, Performance of the population-pattern decoder on distinguishing two concurrent, separated sources from single sources, using all neurons (N = 59). Triangles indicate location of the fixed source, same as in A. D, Performance of the two-channel decoder, same as in C.

The perceptual ability to distinguish the presence of two spatially separated sources from that of a single source suggests that the corresponding patterns of population activity in the IC must also be distinct. We tested this hypothesis using data from the rabbit IC. For each neuron, we recorded responses to two different tokens of broadband noise presented concurrently in every possible two-source combination in the frontal hemifield, in 30° steps (Fig. 7B). As before, we used a maximum-likelihood decoder operating on the pattern of spike counts from every neuron in the sample. This decoder classified each population response into one of 28 possible unique location combinations (7 single-source locations and 21 spatially separated combinations). Estimates were then further categorized into “one source” or “two sources.”

The population-pattern decoder performed very well (Fig. 7C), with 97% of population responses correctly distinguished between single sources and two spatially separated sources over all stimulus conditions. When one source was fixed at 0°, perfect distinction was obtained for a separation of 30°, while a 60° separation was necessary for perfect distinction when one source was fixed at either 90° or −90°. This trend approximates that of the human psychophysical data (Fig. 7A); however, the spatial resolution of our measurements was limited to 30° versus 3° in the human data. Spatial separation was successfully detected for two sources confined to the ipsilateral side as well as to the contralateral side. Further, the performance of the decoder when trained and tested on only low-BF neurons or only high-BF neurons was similar to that shown in Figure 7C using all neurons (91, 97, and 97% of responses were correctly distinguished for low-BF, high-BF, and all-BF decoders, respectively).

Could the two-channel difference decoder also distinguish between single sources and two spatially separated sources? This decoder classifies responses based on the difference of summed rates from each side. However, the difference operation is fundamentally incompatible with distinguishing between one and two sources because any two-source combination symmetric about 0° (e.g., 30 and −30°) would activate both sides equally, with a difference of zero. The same would be true for a single source at 0°. Therefore two sources symmetric about the midline will always be indistinguishable from a single source at 0° for this decoder. To address this problem, we modified the decoder to operate on both the left and right summed rates independently instead of their scalar difference (see Materials and Methods). This extended two-channel decoder was generally unable to distinguish between single sources and two spatially separated sources (Fig. 7D). In particular, single sources at 0°, 30°, or 60° were often misclassified as two separated sources. These errors occurred because the left and right summed rates in response to single sources were similar to those evoked by some spatially separated two-source combinations; for example, the left and right summed rates in response to a single source at 30° were nearly identical to those in response to two sources at 30 and 60°.

Neural sensitivity to interaural decorrelation underlies the accurate detection of separation in front of a listener

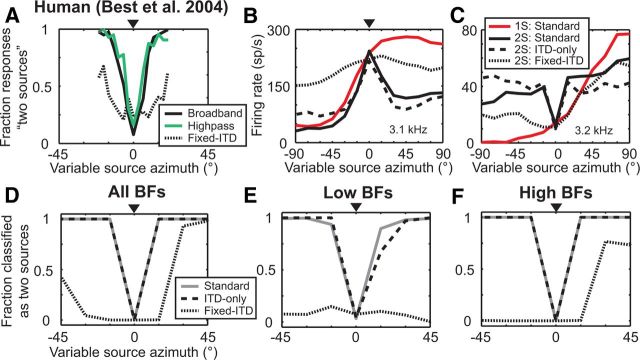
Best et al. (2004) performed additional psychophysical experiments to investigate the role of ITD in detecting the spatial separation from a fixed source directly in front of a listener (0°). Human listeners were able to detect the spatial separation of two high-pass noises with as little physical separation as when detecting the separation of two broadband noises (Fig. 8A). However, the separation of two broadband noises was more poorly detected in a fixed-ITD condition compared with the standard condition (Fig. 8A), despite the availability of high-frequency ILD cues in the fixed ITD condition. Together, these psychophysical results suggest that envelope ITD is an important cue for this task in the case of high-pass noise. However, Best et al. (2004) did not directly test the detection of separation of highpass noises in the fixed-ITD condition.

Figure 8.

Neural sensitivity to interaural decorrelation underlies the perception of source separation in front of a listener. A, Human perception of two sources as a function of separation between a fixed source (triangle) and a variable source for broadband noises (black solid line), high-pass noises (green line), and broadband noises in a fixed-ITD condition (dotted line). Data from Best et al., 2004. B, C, Azimuth tuning functions of two high-BF IC neurons to single sources (red line), and to a variable source in the presence of a concurrent fixed source (triangle) in the standard (black line), ITD-only (dashed line), and fixed-ITD (dotted line) conditions. BF of each neuron indicated in corner. D, Performance of the population-pattern decoder on distinguishing two concurrent, separated sources from single sources using all neurons (solid line; N = 43). Performance of the decoder using the same neurons when trained on data in the standard condition and tested on data either in the ITD-only (dashed line) or fixed-ITD (dotted line) conditions. E, F, Same as in D except the decoder used only neurons with low BFs (N = 11) or high BFs (N = 32), respectively.

In previous work (Day et al., 2012), we observed a characteristic firing rate suppression (Fig. 8B) or enhancement (Fig. 8C) occurring in most high-BF IC neurons when one broadband noise is separated from another broadband noise fixed at 0°. These dramatic rate changes were also observed under the ITD-only condition but not in the fixed-ITD condition, and we demonstrated that such changes are due to neural sensitivity to the interaural decorrelation of cochlea-induced envelopes that occurs when two sources are spatially separated. We proposed that the rate suppression or enhancement in high-BF neurons—evoked by interaural decorrelation—may underlie the detection of separation of high-frequency sources in front of a listener. To test this hypothesis, we investigated whether the performance of the population-pattern decoder tested on data from cue-manipulated conditions was consistent with the psychophysical results outlined above.

We tested the decoder using those neurons from Day et al. (2012) from which the following four sets of data were available (as represented by the different lines in Fig. 8B,C): (1) single-source azimuth tuning function measured in 15° steps; (2) azimuth tuning function measured in the presence of an additional source fixed at 0°; and the same two-source azimuth tuning function (3) in the ITD-only condition and (4) in the fixed-ITD condition. The population-pattern decoder was then trained on population responses to both single sources and two spatially separated sources in the standard condition and tested on responses in either the ITD-only or fixed-ITD conditions. For comparison we also tested the decoder on responses to two sources in the standard condition.

When the decoder was tested on responses in the ITD-only condition, perfect distinction between one and two sources was obtained with a separation of 15°, the same as when tested in the standard condition, while a 45° separation was necessary in the fixed-ITD condition to achieve perfect distinction (Fig. 8D). Therefore decoder performance was qualitatively consistent with human performance in the fixed-ITD condition (Fig. 8A).

We also tested the decoder on populations containing only neurons with either low BFs or high BFs. For the low-BF decoder (Fig. 8E) tested on the ITD-only condition, a majority of neural responses was classified as two sources when sources were separated by 15°. On the other hand, when tested on the fixed-ITD condition, no physical separation could cause a majority of responses to be classified as two sources. This result was expected given the dominance of ITD cues in the azimuth sensitivity of low-BF neurons.

For the high-BF decoder (Fig. 8F), performance was also good in the ITD-only condition, but poor in the fixed-ITD condition, very similar to the performance obtained with all neurons. This means that the patterns of activity across high-BF IC neurons used to distinguish one source from two separated sources are similar between conditions in which all natural binaural cues are available and conditions in which only ITD varies naturally, and are dissimilar when only ILD varies naturally. This result is interesting because decoder performance on single-source localization using these same high-BF neurons was largely dependent on neural sensitivity to ILD (Fig. 6 G–I). In summary, the detection of separation of two sources when one is fixed at 0° depends on strong neural sensitivity to interaural decorrelation, and this holds both at low and high frequencies.

Discussion

Our detailed analyses of single-unit data from the IC of awake rabbits show that decoders that reduce azimuth tuning functions to either their peaks (population vector) or to population-averaged activity on one side (single channel) fail to estimate accurately the azimuth of a broadband noise at locations contralateral to the IC. The poor performance of these decoders is due to heterogeneities in both the shapes of azimuth tuning functions and the locations of BAs across the population. In contrast, a decoder operating on the pattern of spike counts across IC neurons from a single side estimated sources at all locations with high accuracy (ε = 4°) and with precision comparable to rabbit behavioral data.

We further used the population-pattern decoder to link psychophysical observations to neural activity in the IC. Decoder performance was consistent with the duplex theory of sound localization when tested on sounds with incongruent binaural cues. Specifically, the ability of the low-BF decoder to localize sources required natural ITD cues, while the ability of the high-BF decoder to localize contralateral sources required natural ILD cues, despite sufficient information from envelope ITDs at high frequencies. Both of these findings parallel human performance in similar conditions (Macpherson and Middlebrooks, 2002). Moreover, the decoder could accurately distinguish between a single broadband noise and two concurrent noises spatially separated in the frontal hemifield, consistent with human performance (Best et al., 2004). Performance of the decoder when tested under incongruent cue conditions strongly suggests that the ability to detect small spatial separations directly in front of a listener is due to neural sensitivity to interaural decorrelation.

Pattern decoding could be implemented by simply integrating IC responses through synaptic weights onto a second layer of neurons (Fig. 1D). If this putative second layer were the anatomical target of IC projections in the thalamus, then we would expect thalamic neurons to have narrow azimuth tuning functions. However, azimuth tuning in medial geniculate neurons tends to be broad, similar to that of primary auditory cortex (Clarey et al., 1995). While it is unlikely that a pattern decoding computation is implemented in the tectothalamic circuit, our analyses generally suggest that a decoding circuit further along the auditory pathway should be able to accurately estimate source azimuth based on information contained in the spike counts of IC neurons if some of the location-specific information represented in the variation of tuning functions across neurons (both tuning peaks and shapes) is retained.

Comparison to previous sound localization decoding studies

Lesica et al. (2010) tested both the single-channel decoder and a variant of the population-pattern decoder on spike counts from low-BF IC neurons in anesthetized gerbils measured in response to broadband noise varying in ITD. Unlike the present results, they found that the single-channel decoder could estimate the stimulus ITD nearly as well as their population-pattern decoder. In particular, the dependence of summed firing rate on ITD within the range of ITDs used to localize sources was strictly monotonic for gerbils, unlike the plateau at contralateral azimuths observed in rabbits and cats (Fig. 2D). This discrepancy may be simply due to differences in the range of ITDs used to localize sound sources in each species. Best ITDs of IC neurons are generally distributed on the contralateral side between 0 and (2 · BF)⁻¹ ITD (the so-called “π-limit”; McAlpine et al., 2001; Hancock and Delgutte, 2004; Joris et al., 2006). The wider the ITD range used to localize sources, the more best ITDs will fall within this range, and therefore the more contralateral slopes of azimuth tuning functions will appear in the population (Fig. 3B), causing a plateau in the summed firing rate at contralateral azimuths. Since the ITD range of gerbils (Maki and Furukawa, 2005) is about one-half that of rabbits (Kim et al., 2010; Day et al., 2012) or cats (Tollin and Koka, 2009), and one-fifth that of humans, the success of the single-channel decoder in gerbils (at low frequencies) is therefore likely due to their small ITD range.

A previous study in anesthetized cat IC from our laboratory used a two-channel difference scheme to show parallel effects of reverberation on IC responses and on psychophysical lateralization judgments (Devore et al., 2009). While this study did not explicitly test the localization performance of the two-channel difference decoder, both the summed rate for cats shown in Figure 2D, and the difference of summed rates (Devore et al., 2009; their Fig. 6b) show that neither the single-channel nor two-channel difference decoders would match the behavioral acuity of cats at the most lateral azimuths (Heffner and Heffner, 1988). It remains to be seen whether the population-pattern decoder can account for localization performance in the presence of reverberation.

A recent azimuth decoding study in barn owls (Fischer and Peña, 2011) showed that the performance of the population-vector decoder operating on the firing rates of modeled optic tectum neurons was consistent with behavior. It is likely that the success of the population vector was due to the nearly symmetrical azimuth tuning of modeled neurons. Tuning functions were narrow and had BAs < 50°, thereby largely avoiding lateral azimuths where the compression of ITD with azimuth causes asymmetric tuning. In contrast, the azimuth tuning functions in rabbit are broad and have mostly asymmetrical shapes (Fig. 3), which leads to extremely poor performance of the population-vector decoder.

Neural pattern decoding of sound source location has also been studied in the auditory cortex. Using the same pattern decoder as in the present study, Miller and Recanzone (2009) found that the azimuth of sources far to the contralateral side, but not the ipsilateral side, could be estimated from firing rates of neurons in the auditory cortex (both core and belt areas) of awake macaques. However, estimation of frontal locations was substantially worse than with the present IC decoder, even with a cortical population size of 128 neurons. It may be that some of the location-specific information available in the temporal firing patterns of cortical neurons (Middlebrooks et al., 1994) is necessary to achieve the same level of performance as that based on IC spike counts. Nevertheless, a simple two-channel difference decoder operating on the summed rates of subpopulations of ipsilateral- and contralateral-tuned auditory cortical neurons from the same hemisphere in anesthetized cats could also localize sources with reasonable accuracy (Stecker et al., 2005); however, in this model, responses of neurons with BAs within ±30° were excluded from the computation. These excluded neurons would likely have tuning functions with contralateral slopes, which would cause the summed rate to plateau and degrade localization performance. It remains unclear how to reconcile the accurate performance of the suboptimal cortical two-channel difference decoder (Stecker et al., 2005) with the poor performance of the theoretically optimal cortical population-pattern decoder (Miller and Recanzone, 2009) on estimating frontal locations, unless the discrepancy is simply due to differences in species and anesthetic state.

Patterns of neural activity indicating “glimpses” of a source in isolation

A major unresolved question is how the auditory system localizes sound in realistic environments with multiple, concurrent sources and reverberation. The problem that confronts the auditory system is that spatially separated sources with overlapping spectral and temporal properties produce fluctuating binaural cues distorted from those that occur for each source independently (Day et al., 2012, their Fig. 1). Fortunately, most natural sounds are spectrotemporally sparse such that in the presence of multiple sources, the acoustic energy in certain frequency channels at certain moments in time will be dominated by a single source. One strategy to localize in a multisource environment is to accumulate evidence of spatial location during these glimpses of a source in isolation (Yost and Brown, 2013). However, some indicator would be required to identify which instants contain one source in isolation. Using a model of auditory signal processing, Faller and Merimaa (2004) showed that the correct ITD and ILD cues associated with each source in a multisource condition can be computed during those glimpses when the interaural coherence between left and right peripherally filtered signals is high.

Our decoder results show that the pattern of activity across IC neurons is highly dependent on interaural coherence in some conditions (Fig. 8), suggesting it may be a reliable indicator of the presence of single sources. Since the population-pattern decoder distinguishes between the presence of one and two sources, it may also be able to distinguish between the presence of one and many sources, or even between anechoic and reverberant conditions; both multisource and reverberant conditions cause interaural decorrelation and would therefore dramatically change the pattern of IC activity from that in response to a single, anechoic source. In this way, a decoder could accurately localize sources by only accumulating evidence during glimpses when the pattern of activity across IC (or perhaps a tonotopic subregion of IC) matches the known pattern for a single source in anechoic conditions. All other perceptual qualities of sound present in the neural representation during a glimpse might then be temporally bound to aid segregation of that source from others (Shamma et al., 2011).