Heterosynaptic Plasticity Prevents Runaway Synaptic Dynamics

Abstract

Spike timing-dependent plasticity (STDP) and other conventional Hebbian-type plasticity rules are prone to produce runaway dynamics of synaptic weights. Once potentiated, a synapse would have higher probability to lead to spikes and thus to be further potentiated, but once depressed, a synapse would tend to be further depressed. The runaway synaptic dynamics can be prevented by precisely balancing STDP rules for potentiation and depression; however, experimental evidence shows a great variety of potentiation and depression windows and magnitudes. Here we show that modifications of synapses to layer 2/3 pyramidal neurons from rat visual and auditory cortices in slices can be induced by intracellular tetanization: bursts of postsynaptic spikes without presynaptic stimulation. Induction of these heterosynaptic changes depended on the rise of intracellular calcium, and their direction and magnitude correlated with initial state of release mechanisms. We suggest that this type of plasticity serves as a mechanism that stabilizes the distribution of synaptic weights and prevents their runaway dynamics. To test this hypothesis, we develop a cortical neuron model implementing both homosynaptic (STDP) and heterosynaptic plasticity with properties matching the experimental data. We find that heterosynaptic plasticity effectively prevented runaway dynamics for the tested range of STDP and input parameters. Synaptic weights, although shifted from the original, remained normally distributed and nonsaturated. Our study presents a biophysically constrained model of how the interaction of different forms of plasticity—Hebbian and heterosynaptic—may prevent runaway synaptic dynamics and keep synaptic weights unsaturated and thus capable of further plastic changes and formation of new memories.

Introduction

Synaptic plasticity is considered a cellular mechanism of learning and memory (Bliss and Collingridge, 1993; Malenka and Bear, 2004). Spike timing-dependent plasticity (STDP) is experimentally well-characterized form of plasticity that modifies synaptic weights depending on the relative timing of presynaptic input and postsynaptic spikes. Inputs that were active before the postsynaptic spike and thus contributed to its generation are potentiated, while synapses that are active after the postsynaptic spike are depressed (Markram et al., 1997; Magee and Johnston, 1997; Abbott and Nelson, 2000; Caporale and Dan, 2008). These formal rules are broadly used in computational models of learning and developmental processes (Miller, 1996; Song et al., 2000; Kempter et al., 2001; Rubin et al., 2001; Song and Abbott, 2001; Clopath et al., 2010). However, STDP and other conventional Hebbian-type plasticity rules impose a positive feedback on synaptic changes, and are prone to produce runaway dynamics of synaptic weights. Potentiated synapses have higher probability to lead to spikes and be further potentiated; depressed synapses less probably lead to spikes and thus tend to be further depressed.

Potentiation or depression of synapses toward extreme weights may be useful for processes requiring strong synaptic competition including elimination of the “wrong” connections, such as segregation of inputs from two eyes during development of the visual cortex (Wiesel and Hubel, 1963; Thompson et al., 1983) or formation of other sensory representations (Aitkin et al., 1970; Merzenich et al., 1975; Feldman, 2009). However, learning of complex associations for both declarative and procedural memories would likely require a broad distribution of synaptic weights. To achieve this and to keep system susceptible for new learning, stabilization mechanisms are needed that prevent synapses from runaway potentiation or depression and associated overexcitability or complete silencing of neurons.

A number of stabilizing mechanisms have been suggested. In previous research, normalization was explicitly implemented in the equation for synaptic weight changes (von der Malsburg, 1973) or was achieved by introducing a dependence of the change on the actual weight, which provides an internal feedback control of synaptic modifications (Oja, 1982). Later studies expanded the use of normalization (Elliott and Shadbolt, 2002; Wu and Yamaguchi, 2006; Finelli et al., 2008) and elaborated tuning of the learning rules, e.g., by introducing weight-dependence of plastic changes and/or precise balancing of STDP rules for potentiation and depression (Bi and Poo, 1998; van Rossum et al., 2000; Abbott and Nelson, 2000; Kempter et al., 2001; Gütig et al., 2003; Hardingham et al., 2007; Delgado et al., 2010; Gilson and Fukai, 2011) and activity-dependent regulation of Ca²⁺ thresholds for potentiation and depression (Yeung et al., 2004). Total weight of synaptic inputs to a neuron could be also conserved by local balancing of potentiation and depression (Royer and Paré 2003). Some of these mechanisms were related to experimental results, while others did not have biological correlates.

In our previous work at neocortical synapses in vitro, we described a form of heterosynaptic plasticity that can be induced by intracellular tetanization—a purely postsynaptic protocol without presynaptic stimulation (Volgushev et al., 1994, 2000; Lee et al., 2012). We hypothesized that this form of heterosynaptic plasticity can serve as a normalizing mechanism and prevent runaway synaptic dynamics (Volgushev et al., 2000; Chistiakova and Volgushev, 2009). Here we test this hypothesis using a biophysically constrained neuron model. We show how interaction of different forms of plasticity—Hebbian and heterosynaptic—may produce unsaturated distribution of synaptic weights while still allow for synaptic changes required to form new memories.

Materials and Methods

In vitro experiments

Slice preparation.

All experimental procedures used in this study were in compliance with U.S. National Institutes of Health regulations and were approved by the Institutional Animal Care and Use Committee of the University of Connecticut. Details of slice preparation and recording were similar to those used in previous studies (Volgushev et al., 2000; Lee et al., 2012). Wistar rats (15–32 d old) of either sex were anesthetized with isoflurane and decapitated, and the brains were quickly removed and placed into an ice-cold oxygenated artificial CSF (ACSF) solution containing the following (in mm): 125 NaCl, 25 NaHCO₃, 25 glucose, 3 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, bubbled with 95% O₂/5% CO₂, pH 7.4. Coronal slices (350 μm thickness) containing visual or auditory cortex were prepared from the right hemisphere. Slices were allowed to recover for at least 1 h at room temperature. For recording, individual slices were transferred to a recording chamber mounted on Olympus microscope equipped with infrared differential interference contrast (DIC) optics. In the recording chamber, slices were submerged in oxygenated ACSF at 30–32°C.

Intracellular recording and synaptic stimulation.

Intracellular recordings in whole-cell configuration were made from layer 2/3 pyramidal cells from visual or auditory cortex using patch electrodes (4–7 MΩ) filled with a solution containing the following (in mm): 130 K-glutamate, 20 KCl, 10 HEPES, 10 Na-phosphocreatine, 4 Mg-ATP, 0.3 Na₂-GTP, pH 7.4 with KOH. Layer 2/3 pyramidal neurons were selected for recording using DIC microscopy. Our previous work with biocytin labeling and morphological reconstruction of recorded neurons demonstrated reliability of pyramidal cell identification using DIC microscopy (Volgushev et al., 2000).

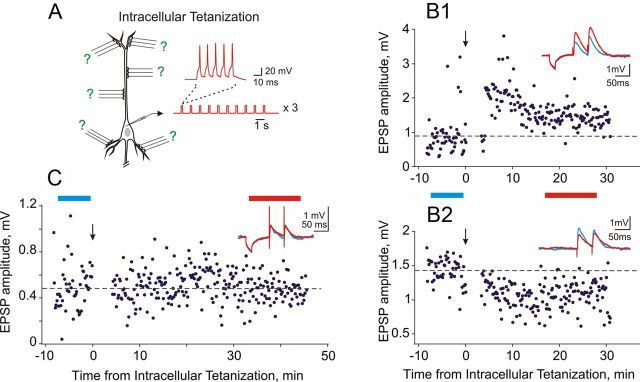
Two pairs of stimulating electrodes (S1 and S2) were placed in layer 4, below the layer 2/3 recording site. Stimulation current intensities were adjusted to evoke monosynaptic EPSPs in the layer 2/3 cell. We used paired-pulse stimulation protocol with a 50 ms interpulse interval. Paired stimuli were applied to S1 and S2 in alternating sequence once per 7.5 s, so that each input was stimulated with paired pulses each 15 s. Small-amplitude hyperpolarizing pulses were applied before S1 stimuli to access the input resistance. EPSPs in the layer 2/3 cell induced by layer 4 stimulation were recorded during a 10–12 min control period. Following the control period, synaptic stimulation was stopped, and intracellular tetanization was applied to the cell through the recording pipette. Intracellular tetanization consisted of three trains (one per minute) of 10 bursts (1 Hz) of five pulses (5 ms, 100 Hz, 0.4–1.1 nA; Fig. 1A). The current intensity was adjusted to evoke four to five spikes per burst. Following intracellular tetanization, synaptic stimulation was resumed, and EPSPs evoked by the test stimuli were recorded for another 30–50 min.

Figure 1.

Synaptic plasticity induced by intracellular tetanization. A, A scheme of intracellular tetanization experiment. Bursts of short depolarizing pulses (5 ms pulse duration, 5 pulses at 100 Hz; top) were applied through the recording electrode without presynaptic stimulation. The bursts were applied in trains of 10 (1 burst per second; bottom). Intracellular tetanization consisted of three such trains (1 train per minute). Synaptic responses to test stimuli were recorded before and after the intracellular tetanization. B1, B2, Long-term potentiation (B1) and depression (B2) induced by intracellular tetanization at two inputs to the same cell. Blue and red traces show averaged membrane potential responses to small steps of hyperpolarization current and to paired-pulse electric stimuli before (blue) and after (red) the intracellular tetanization. Respective time periods are labeled with blue and red bars between the panels. Time courses show the amplitudes of individual EPSPs evoked by first the first pulse in the paired-pulse stimulation paradigm. Vertical arrows indicate timing of intracellular tetanization. C, Responses to hyperpolarizing current steps and paired synaptic stimulation and time course of EPSP amplitude changes in another input that did not change after intracellular tetanization.

Database and data analysis.

Electrophysiological results presented here (Figs. 1, 2) include a total of N = 179 inputs to 117 neurons. Among these, N = 60 inputs to 41 neurons are new data. For the scatter plot in Figure 2, we also used data from previous publications [N = 43 inputs to 26 neurons (Volgushev et al., 2000; Chistiakova and Volgushev, 2009); N = 76 inputs to 50 neurons (Lee et al., 2012)]. All inputs included in the analysis fulfilled the criteria of (1) stability of EPSP amplitudes during the control period, (2) stability of the membrane potential throughout the recording, and (3) stability of the onset latency and kinetics of the rising slope of the EPSP. EPSP amplitudes were measured as the difference between the mean membrane potential during two time windows. The first time window was placed before the EPSP onset, and the second time window was placed just before the peak of the rising slope of the EPSP. Amplitude of the second EPSP in paired-pulse stimulation paradigm was measured using windows of the same duration, but shifted by the length of interpulse interval (50 ms). Paired-pulse ratio (PPR) was calculated as the ratio of averaged amplitude of the EPSP evoked by the second pulse over the averaged amplitude of the EPSP evoked by the first pulse.

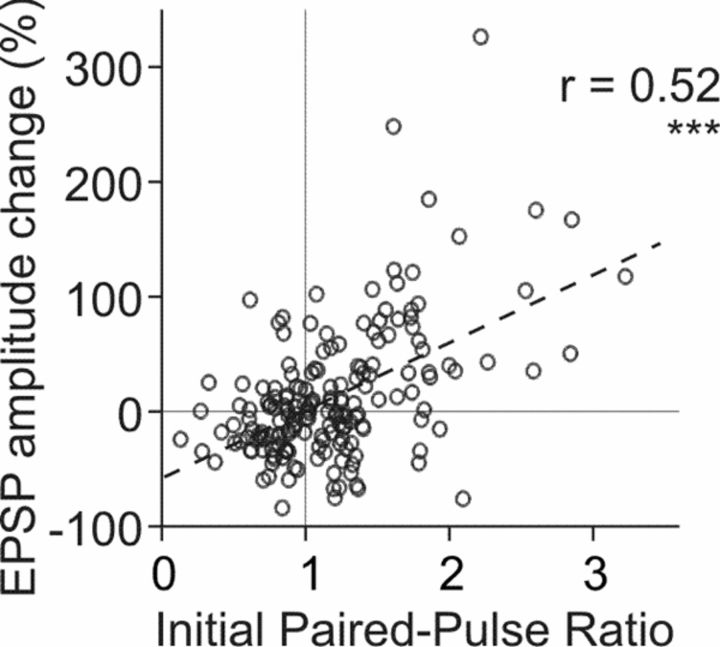
Figure 2.

Correlation between EPSP amplitude changes induced by intracellular tetanization and initial paired-pulse ratio in neocortical neurons. Data for N = 179 inputs. The sample includes new data (N = 60 inputs) as well as data used in our previous publications [N = 43 inputs (Volgushev et al., 2000); N = 76 inputs (Lee et al., 2012)].

For assessing changes of synaptic transmission, amplitude of EPSPs evoked by the first stimulus in a pair was used. The magnitude of plastic changes was calculated as the ratio of average EPSP amplitude after the tetanization over the average EPSP amplitude during the control period. The criterion for plasticity was a significant (p < 0.05, Student's t test) change in mean EPSP amplitude between the control and posttetanic time periods.

Computational model

Model of pyramidal neuron.

For all simulations we used an established reduced model of a cortical pyramidal cell (Mainen and Sejnowski, 1996; Timofeev et al., 2000; Bazhenov et al., 2002; Chen et al., 2012). This model was first proposed as a reduction of a multicompartmental pyramidal cell model (Mainen and Sejnowski, 1996) and consists of two electrically coupled compartments, dendritic and axosomatic. The current balance equations for the two compartments of the model are as follows:

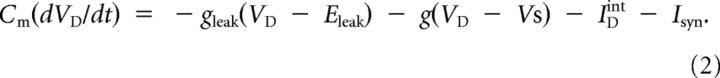where C_m is the membrane capacitance, V_S and V_D are the membrane potentials in the axosomatic and dendritic compartments, g is conductance coupling between the compartments, I_S^int and I_D^int are the sums of all active currents in the axosomatic and dendritic compartments, respectively, and I_syn is the sum of synaptic currents. Because Na⁺ and K⁺ conductances in the axosomatic compartment were much stronger than in the dendrite (Mainen and Sejnowski, 1996), Equation 1 can be rewritten in a form εdVs/dt = F(V_S), where ε is a small parameter, and F(V_S) represents normalized axosomatic currents that match the magnitude of the dendritic currents. Using singular perturbations analysis (Kuznetsov, 1995), it can be shown that the state variable V_S quickly reaches the manifold of slow motion defined by equation F(V_S) = 0 and, therefore, is always at equilibrium state. Thus, Equation 1 can be substituted by the following:

Furthermore, through bifurcation analysis, it was shown that the dynamics of the reduced model described by Equations 2 and 3 was equivalent to the full model (Eqs. 1, 2; for a similar analysis, see Fröhlich and Bazhenov, 2006, their Fig. 3). Thus, this reduced model can be used without losing the accuracy of simulation. Importantly, the reduced model allows simulations with time steps that are a few orders of magnitude larger than that required for a full model. This reduced model can closely match spiking patterns of different classes of cells and has been successfully used in many cortical network simulations (Timofeev et al., 2000; Bazhenov et al., 2002; Fröhlich at al., 2008, 2010; Chen et al., 2012).

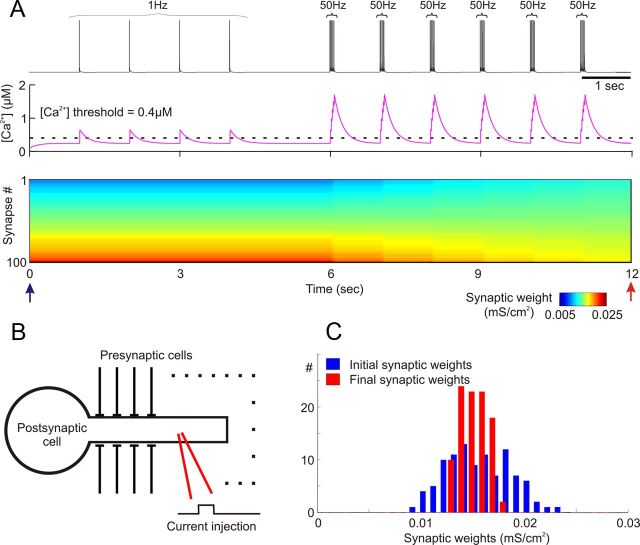
Figure 3.

Simulation of heterosynaptic plasticity in a model neuron. A, Membrane potential trace (top), changes of intracellular calcium concentration in the dendritic compartment (middle), and changes of synaptic weights (bottom) induced by intracellular depolarizing pulses. Current pulses were injected into the dendritic compartment of the postsynaptic neuron to evoke action potentials. Current pulses were applied to evoke single spikes at 1 Hz and then bursts of 5 spikes, with the frequency of spikes within the burst 50 Hz. Bursts of 50 Hz pulses were repeated six times. The dashed line in the middle panel shows the calcium threshold for heterosynaptic plasticity (0.4 μm). In the bottom panel, synaptic weights are color coded. Synapses were sorted by their weights at the beginning of the simulation experiment. Heterosynaptic plasticity led to changes of synaptic weights after bursts of spikes, but not after single spikes. B, A scheme of a model neuron receiving 100 synaptic inputs to the dendrite. Current pulses to evoke spikes were injected in the dendrite. C, Distribution of synaptic weights at the beginning (blue) and at the end of experiments (red) shown in A. Arrows in A indicate time moments when distributions were taken.

In the axosomatic compartment (S_soma = 1.0 × 10⁻⁶ cm²), the model contained a fast Na⁺ current, I_Na (g_Na = 3000 mS/cm²), a persistent sodium current, I_Na(p) (g_Na(p) = 0.07 mS/cm²; Alzheimer et al., 1993; Kay et al., 1998; Astman et al., 2006), and a fast delayed rectifier potassium K⁺ current, I_K (g_K = 200 mS/cm²). In the dendritic compartment (S_dendr = rS_soma), the model contained a fast Na⁺ current, I_Na (g_Na = 1.5 mS/cm²); a persistent sodium current, I_Na(p) (g_Na(p) = 0.07 mS/cm²); a slow voltage-dependent, noninactivating K⁺ current, I_Km (g_Km = 0.01 mS/cm²); a slow Ca²⁺-dependent K⁺ current, I_KCa (g_KCa = 0.3 mS/cm²); a high-threshold Ca²⁺ current, I_HVA (g_HVA = 0.01 mS/cm²); and a potassium leak current, I_KL = g_KL(V − E_KL) (g_KL = 0.0025 mS/cm²). The membrane capacitance was C_m = 0.75 μF/cm², and the leak conductance was g_L = 0.033 mS/cm². Equilibrium potentials were E_Na = 50 mV, E_K = −95 mV, E_leak= −68 mV, and E_Ca = 140 mV. The firing properties of the model depend on the ratio of dendritic area to axosomatic area, r (Mainen and Sejnowski, 1996). We used a model of a regular-spiking neuron, with r = 165. For all currents, the expressions of the voltage- and Ca²⁺-dependent transition rates are given by Timofeev et al. (2000) and Chen et al. (2012).

Synaptic currents.

One hundred synapses with AMPA-type channels were located at the dendritic compartment. The synaptic current at each synapse was simulated by the first-order activation kinetics (Destexhe et al., 1994):

where W_syn is the strength (weight) of a synapse, [O] is the fraction of open channels, E^syn is the reversal potential (E^syn = 0 mV for excitatory synapses), H(x) is the Heaviside (step) function, t₀ is the time instant of receptor activation, A = 0.5, and t_max = 0.3 ms. The rate constants, α and β, were α = 1.1 ms⁻¹ and β = 0.19 ms⁻¹. The synaptic weight was defined in the range between 0 mS/cm² and maximum of 0.03 mS/cm². The initial weights were randomly assigned to the 100 synapses from a Gaussian distribution with the mean 0.015 mS/cm² and SD 0.003 mS/cm². Short-term dynamics of synaptic transmission at each synapse were simulated using a simple phenomenological model (Abbott et al., 1997; Tsodyks and Markram, 1997; Galarreta and Hestrin, 1998; Timofeev et al., 2000). According to this model, postsynaptic current is a product of a maximal synaptic conductance W_syn and the depression variable D, which describes the amount of synaptic resources that remain available; D = 1 − [1 − D_i (1 − U)]exp[−(t − t_i)/τ], where U = 0.07 is the fraction of resources used per action potential, τ = 700 ms is the time constant of recovery of the synaptic resources, D_i is the value of D immediately before the ith event, and (t − t_i) is the time after the ith event.

Spike timing-dependent plasticity.

STDP was implemented as in previous modeling studies (Song et al., 2000; Kempter et al., 2001; Song and Abbott, 2001). The occurrence, direction and magnitude of synaptic modifications were determined by the time difference between presynaptic and postsynaptic spikes. If the presynaptic spike occurred before the postsynaptic spike within the time window for potentiation, the weight of that synapse increased. If the presynaptic spike followed the postsynaptic spike within the time window for depression, the weight of the synapse decreased. STDP was described by the following equations:

In Equations 7 and 8, dW_syn is the change of synaptic strength, a⁺ and a⁻ are the maximal amplitude of potentiation and depression that could be induced by a single postsynaptic spike, t^post and t^pre are the timing of postsynaptic and presynaptic spikes, and τ⁺ and τ⁻ are the time constants of potentiation and depression windows. As a standard setting, we used STDP with symmetrical potentiation and depression windows: a⁺ = a⁻ = 10⁻³ mS/cm² and τ⁺ = τ⁻ = 20 ms. To explore synaptic dynamics produced by potentiation-dominated or depression-dominated STDP, we kept parameters of the depression window constant (a⁻ = 10⁻³ mS/cm², τ⁻ = 20 ms), but varied parameters of potentiation window (maximal magnitude, a⁺ = 0.2 × 10⁻³ mS/cm² to 2.5 × 10⁻³ mS/cm²; time constant, τ⁺ = 5, 10, 20, 30, or 40 ms).

Heterosynaptic plasticity.

Heterosynaptic plasticity was implemented according to the rules derived from our in vitro experiments (Volgushev et al., 2000; Chistiakova and Volgushev, 2009; Lee et al., 2012). In slice experiments, induction of heterosynaptic plasticity required a rise of intracellular [Ca²⁺] in the postsynaptic neuron (Lee et al., 2012). This was implemented in the model by setting a calcium threshold at 0.4 μm in the standard model (tested range between 0.2 and 0.8 μm). Our experimental results also showed that the effect of heterosynaptic plasticity depended on the initial state of the synapse: synapses with initially low release probability have a tendency to be potentiated, while synapses with initially high release probability tended to be depressed or did not change after intracellular tetanization (Volgushev et al., 2000; Chistiakova and Volgushev, 2009; Lee et al., 2012). Furthermore, the probability of change was higher for the strong or weak synapses but lower for synapses of intermediate strength (Volgushev et al., 2000; Chistiakova and Volgushev, 2009; Lee et al., 2012; see Results). To implement these dependences, we used the following equations (Eqs. 9, 10) to calculate the probability of the synaptic change resulted from heterosynaptic plasticity and the magnitude of synaptic weight change:

where W_syn is the current synaptic strength, and W_max = 0.03 mS/cm² is the maximal synaptic strength. According to Equation 9, P = 0.1 for synapses with intermediate strength, and P = ∼0.775 for synapses with maximal/minimal strength.

The change of synaptic weight dW_syn was calculated according to following equation:

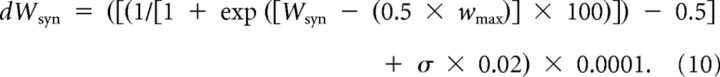In this equation, dW_syn indicates the change of synaptic strength, and σ is a random variable drawn from Gaussian distribution with mean equaling to zero and SD equal to 3.

To summarize, plastic changes could take place only when postsynaptic action potentials were generated. When a spike occurred, the algorithm checked whether postsynaptic [Ca²⁺] exceeded the threshold for heterosynaptic plasticity, and, if yes, it calculated for each synapse the synaptic weight change dW_syn (Eq. 10) and the probability of change P (Eq. 9). The probability of change P was compared to a random number X generated from a uniform distribution from 0 to 1. For P > X, the synaptic weight changed by dW_syn (Eq. 10).

Mechanisms of induction and expression of plasticity in the model.

We implemented STDP and heterosynaptic plasticity as phenomenological models, but did not model explicitly intracellular cascades that were activated during the induction of plasticity, nor intracellular mechanisms involved in the maintenance of plastic changes. We opted for phenomenological plasticity models for two main reasons. First, to explore the range of STDP parameters for which heterosynaptic plasticity could prevent runaway dynamics of synaptic weights, we needed to change the magnitude and time constant of STDP windows for potentiation and depression. Second, modeling of biochemical cascades that mediate the induction and maintenance of synaptic plasticity is a rapidly developing field, focused at a single-synapse level (Graupner and Brunel, 2010). Implementing these models in a neuron with numerous synapses would make the model too complicated and intractable, and thus preclude clear-cut interpretation of results. Furthermore, despite large number of existing models (over 100; Manninen et al., 2010), there is no consensus on specific details necessary for quantitative simulations at layer 2/3 pyramidal neuron synapses.

Induction of heterosynaptic plasticity in our model depended on the rise of intracellular [Ca²⁺] in accordance with experimental data (Lee et al., 2012). However, available experimental data do not provide an estimate of the threshold of calcium rise. The threshold value used here (0.4 μm in the standard model; tested range between 0.2 and 0.8 μm) corresponded to calcium rise produced in the model by a burst of several spikes, such as used in intracellular tetanization experiments (Volgushev et al., 2000; Lee et al., 2012; for comparison of intracellular tetanization to other plasticity induction protocols and to in vivo activity, see Chistiakova and Volgushev 2009). So, effectively, calcium rise above the threshold in our phenomenological model can be considered an indicator of strong postsynaptic activity.

Changes of synaptic weights (both STDP and heterosynaptic plasticity induced) were implemented in the model as changes of synaptic efficacy, and thus were purely postsynaptic. Experimental data indicate that expression of some forms of plasticity may involve both presynaptic and postsynaptic mechanisms (Malenka and Bear 2004; Hardingham et al., 2007; Sjöström et al., 2007), with preferential presynaptic versus postsynaptic contribution depending on initial state of synapses and specifics of the induction protocol (Larkman et al., 1992; Birtoli and Ulrich 2004; Seol et al., 2007), and that presynaptic and postsynaptic changes have differential effects on postsynaptic membrane potential fluctuations evoked by irregular presynaptic firing (Markram and Tsodyks, 1996; Tsodyks and Markram, 1997). However, the relative contribution of the presynaptic versus postsynaptic mechanisms has not been defined quantitatively. Introducing this additional undefined parameter would have complicated interpretation of the results (e.g., runaway dynamics of synaptic efficacy vs. runaway dynamics of the release probability). Indeed, modeling synaptic plasticity as purely postsynaptic changes of efficacy is commonly used in computational models (Song et al., 2000; Destexhe and Marder, 2004; Bazhenov et al., 2005).

Considering all of these factors, as well as the fact that heterosynaptic plasticity does induce postsynaptic changes, we opted modeling synaptic changes as changes of efficacy.

Input spike trains.

The model neuron received 100 synaptic inputs from 100 presynaptic neurons. Each synapse was driven by individual spike train with Poisson distributed interspike intervals. To test the impact of the structured input patterns on dynamics of synaptic weights, we varied degree of correlation between input spike trains using the following procedure (Destexhe and Paré, 1999). First, several (from 2 to 100) spike train templates with Poisson distributed interspike intervals were generated. Next, the spike train for each presynaptic neuron was created by randomly selecting spikes from one of the templates. The degree of correlation among input spike trains was controlled by the number of templates used. When the number of templates was increased, the correlation among input spike trains was reduced. In the current study, we used two templates to produce highly correlated input spike trains (averaged cross-correlation between spike trains, 0.605 ± 0.046), 10 templates to produce mildly correlated inputs (averaged cross-correlation, 0.348 ± 0.05), and 20 templates to produce the weakly correlated input spike trains (averaged cross-correlation, 0.336 ± 0.02).

Normality test of synaptic weight distribution.

Distributions of synaptic weights were tested for normality using the D'Agostino–Pearson K² test (D'Agostino et al., 1990) in Matlab. This test first quantifies the skewness and kurtosis of a sample distribution and then calculates how far these values deviate from the values expected with a normal distribution. For each distribution, the test returns a K² value (approximation to χ² distribution). If a sample distribution is close to a normal distribution, the K² value is low; high values of K² indicate significant deviation from normality. Distributions with probability associated to the χ² statistic higher than 0.05 were identified as normally distributed (Trujillo-Ortiz and Hernandez-Walls, 2003). This approach provides a goodness-of-fit measure of deviation of the distribution from a normal distribution due to either its skewness or kurtosis.

Results

We studied the effect of intracellular tetanization on synaptic transmission to layer 2/3 pyramidal neurons in slices of visual and auditory cortex of rats. Intracellular tetanization consisted of three trains (one per minute) of 10 bursts (1 Hz), each burst containing five pulses (duration, 5 ms; frequency, 100 Hz; amplitude, 0.4–1.1 nA; Fig. 1A). Tetanization was applied to the cell through the intracellular recording electrode without presynaptic stimulation. Thus, plastic changes induced by intracellular tetanization can be considered analogous to heterosynaptic changes (Fig. 1A, green question marks), i.e., changes at synapses that were not activated during a conventional pairing or afferent tetanization protocol. Figure 1 shows examples of EPSP amplitude changes induced by intracellular tetanization. Response amplitudes were stable during control period before the tetanization (Fig. 1B1,B2,C, periods marked with blue bars, blue averaged response traces). After the intracellular tetanization (Fig. 1B1,B2,C, the periods marked with red bars and red response traces), EPSP amplitude could increase (Fig. 1B1), decrease (B2), or not change (C). Changes of the EPSP amplitude were not accompanied by changes of the input resistance, as indicated by stable responses to hyperpolarizing pulses applied before test synaptic stimuli (Fig. 1B1,C). Notably, potentiation and depression could co-occur at two distinct synapses in one cell after the same intracellular tetanization (Fig. 1B1,B2). According to our previous study (Lee et al., 2012), induction of synaptic plasticity by intracellular tetanization required the rise of intracellular calcium concentration in the postsynaptic neuron.

Potentiation was observed in 65 of 179 inputs (36.3%); responses in these inputs increased to 170.1 ± 56.3% (average + SD) of the control. Depression was observed in 64 of 179 cases (35.8%); responses were decreased to 63.3 ± 17.1% of the control. Remaining inputs (50 of 179, 27.9%) did not change after intracellular tetanization (99.9 ± 8.0% of the control). Our previous work demonstrated that the direction and the magnitude of EPSP amplitude changes induced by intracellular tetanization were correlated with initial properties of synapses: synapses with initially high PPR, indicative of low release probability, had a tendency to be potentiated, while synapses with initially low PPR, indicative of high release probability, tended to be depressed or did not change. Figure 2 further illustrates this dependence for 179 inputs to 117 pyramidal neurons in layer 2/3 from the visual and auditory cortex (r = 0.52, p < 0.01).

Thus, our present and previous results reveal the following properties of synaptic plasticity induced by postsynaptic intracellular tetanization: (1) Its induction requires a substantial rise of intracellular calcium concentration. (2) It can lead to heterosynaptic changes at synapses that were not active during the induction. (3) The direction and magnitude of synaptic changes depended on initial properties of synapses: synapses with low release probability (“weak” synapses) had tendency to be potentiated, while synapses with high release probability (“strong” synapses) had tendency to be depressed or unchanged. (4) The likelihood of synaptic changes was low for synapses of intermediate-strength and high for strong or weak synapses. Specifically, we found that the occurrence of plastic changes was higher for the inputs with a PPR below 25% percentile or above 75% percentile (94 and 77%, respectively) than for inputs with a PPR in the second or third quartile (72 and 39%). We have hypothesized that a plastic process with such properties may serve as a mechanism of stabilization of synaptic weights and may prevent runaway dynamics of synaptic weights. In the following sections, we test this hypothesis using an established conductance-based model of a cortical pyramidal neuron receiving input from 100 synapses (Fig. 3B). Rules of STDP and heterosynaptic plasticity were implemented in the model. We then studied the dynamics of synaptic weights when these plasticity rules were applied separately or combined.

Heterosynaptic plasticity induced by intracellular tetanization in a model neuron

We first tested the induction of heterosynaptic plasticity in the model where action potentials were evoked in the postsynaptic neuron by depolarizing current pulses. The amplitude of depolarizing pulses injected into the dendrite of the postsynaptic neuron (Fig. 3B) was adjusted so that each pulse evoked a spike (Fig. 3A, top), and thus the number and frequency of postsynaptic spikes could be controlled precisely. Postsynaptic action potentials evoked at 1 Hz led to a transient, nonaccumulating rise of intracellular calcium (Fig. 3A, middle), and did not induce changes of synaptic weights (bottom). Increasing the frequency of depolarizing pulses and thus evoked spikes to 50 Hz (as used in intracellular tetanization experiments in slices) led to accumulation of intracellular calcium. By the time of arrival of the second spike in the 50 Hz burst, intracellular [Ca²⁺] was above the threshold required to induce plasticity (0.4 μm; Fig. 3A, middle, dashed horizontal line). This triggered heterosynaptic plasticity and led to a change of synaptic weights. The change of synaptic weights is evident as a disturbance in the color-coded plot of synaptic weights against time (Fig. 3A, bottom, around 6 s). Note that heterosynaptic plasticity in this model is triggered only if a postsynaptic spike is generated and [Ca²⁺]_i is above the threshold. The threshold was only exceeded after a burst of spikes, but an isolated spike was not sufficient to induce a required [Ca²⁺]_i rise. This assures that heterosynaptic plasticity is triggered only by strong postsynaptic activations in accordance with experimental results. Since there is no available estimate of the absolute level of calcium rise necessary to induce heterosynaptic plasticity, the rise above the threshold implemented in the model (0.4 μm in the standard model; range between 0.2 and 0.8 μm was tested) can be considered as an indicator of strong postsynaptic activity.

Figure 3 demonstrates that the following properties of heterosynaptic plasticity observed in slice experiments were reproduced in the model. First, changes of synaptic weights occurred in the absence of presynaptic activity, so activation of a synapse was not required to trigger changes of its weight. Second, the direction of plastic changes depended on the initial synaptic weight. In the color-coded plot of synaptic weight changes (Fig. 3A), synapses were sorted by their weight at the beginning of the simulation. During the simulation, heterosynaptic plasticity led to a substitution of colors representing strongest (dark red) and weakest (dark blue) synapses by colors representing intermediate synaptic weights. This effect is clearly evident by comparing the distributions of synaptic weights at the beginning and at the end of simulation (Fig. 3C). At the end of the simulation, synaptic weights shifted toward the values in the middle of the range, which resulted in a narrower final distribution (mean of final weights, 0.0152 ± 0.0013 mS/cm² versus initial weights, 0.0153 ± 0.0031 mS/cm²). This indicates that strong synapses were depressed and weak synapses were potentiated by the heterosynaptic plasticity.

Heterosynaptic plasticity prevents saturation of synaptic weights produced by STDP

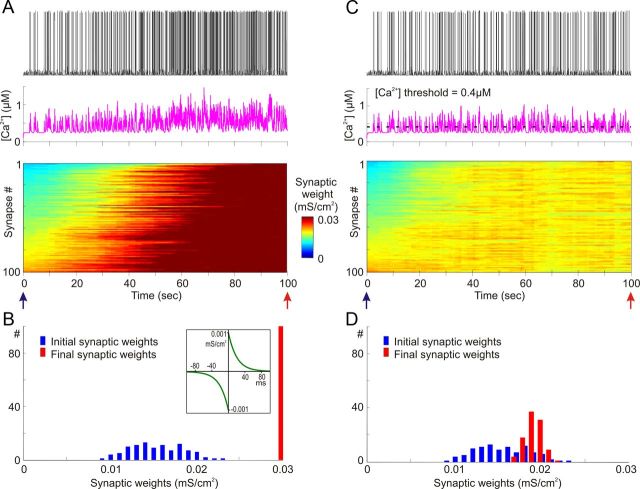
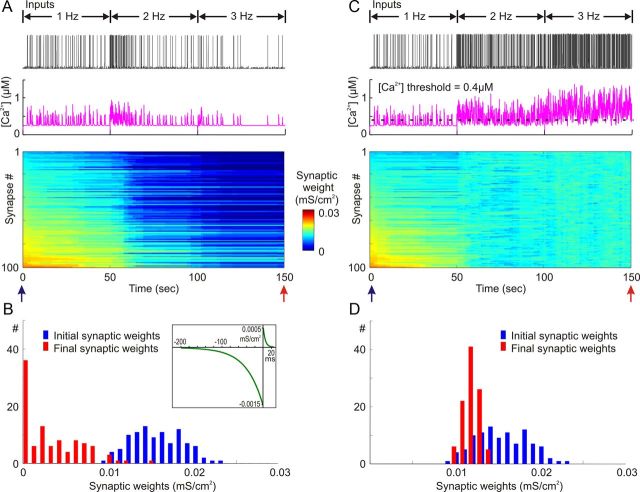
In agreement with previous results, STDP with symmetrical potentiation and depression windows led to runaway potentiation of synapses in the model with weakly correlated presynaptic activity. In the simulation illustrated in Figure 4, A and B, potentiation and depression windows were symmetrical, with time constants τ⁺ = τ⁻ = 20 ms and maximal magnitude a⁺ = a⁻ = 10⁻³ mS/cm² (Fig. 4B, inset). The averaged firing rate of each presynaptic neuron was 1 Hz, and averaged correlation between presynaptic spike trains was 0.348 ± 0.05. Synaptic weights showed clear runaway dynamics in this simulation, gradually increasing to saturation at the maximal value. This dynamic was due to an intrinsic positive feedback in Hebbian-type learning rules: an increase of the weight of a synapse increased the probability that activation of this synapse will lead to spike and thus increased the probability that this synapse will be be further potentiated. In Figure 4A, after ∼80 s of simulation, all synaptic weights were saturated at the maximum. Runaway increase of synaptic weights was accompanied by an increase of the postsynaptic firing rate and intracellular calcium concentration (Fig. 4A). The postsynaptic firing rate increased from 1.8 ± 2.1 Hz during the first 10 s of simulation to 6.3 ± 3.1 Hz during the last 10 s. Intracellular [Ca²⁺] increased from an average of 0.32 ± 0.13 μm during the first 10 s to 0.56 ± 0.22 μm during the last 10 s.

Figure 4.

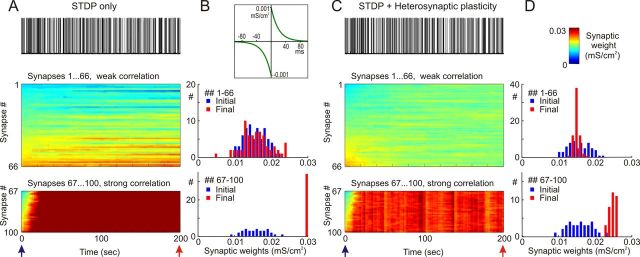
Heterosynaptic plasticity prevents saturation of synaptic weights produced by positively biased STDP. A, B, Synaptic activity produced by weakly correlated inputs leads to runaway dynamics of synaptic weights in a model with symmetrical STDP mechanism. Presynaptic spike trains (N = 100) had an average rate of 1 Hz; cross-correlation of spike trains was 0.348 ± 0.05. STDP rule with symmetrical potentiation and depression windows (τ⁺ = τ⁻ = 20 ms, a⁺ = a⁻ = 10⁻³ mS/cm²; B, inset) was implemented at each synapse. A, Membrane potential trace (top), changes of intracellular [Ca²⁺] (middle), and changes of synaptic weights, color coded, with synapses sorted by their synaptic weights at the beginning of the experiment (bottom). B, Distributions of synaptic weights at the beginning (blue; at 20 ms) and at the end (red; at 100 s) of simulation experiment shown in A. Note runaway dynamics of synaptic weights leading to their saturation at extreme value (0.03 mS/cm²) and associated increase of the firing rate of the postsynaptic neuron. C, D, Heterosynaptic plasticity prevents runaway dynamics of synaptic weights and associated increase of the firing rate. The same model as in A and B is shown, but with the mechanism for heterosynaptic plasticity as described in Figure 3, with the [Ca²⁺] threshold 0.4 μm (dashed line) added to each synapse. All conventions are same as in A and B. Note that synaptic weights are not saturated, but remain normally distributed within the operation rage. Also note that in contrast to the STDP-only model, postsynaptic firing rate does not express a dramatic increase.

Figure 4, C and D, shows results of simulation in the model in which a mechanism of heterosynaptic plasticity illustrated in Figure 3 was added. All other parameters—initial distribution of synaptic weights, presynaptic firing, and STDP rules—were the same as in the model shown in Figure 4, A and B. In the model equipped with both STDP and heterosynaptic plasticity, synaptic weights slightly increased, and their distribution became narrower after 100 s of simulation (0.015 ± 0.0031 at the beginning versus 0.019 ± 0.001 at the end of simulation; Fig. 4D). However, none of the synapses expressed runaway dynamics, and none was saturated. Distribution of synaptic weights remained normal within the operation range. An increase of the averaged synaptic weight led to a moderate increase of the firing rate of the postsynaptic neuron from 1.8 ± 2.1 Hz during the first 10 s of simulation to 2.6 ± 2.3 Hz during the last 10 s, and an increase of averaged [Ca²⁺]_i in the postsynaptic neuron from of 0.32 ± 0.13 μm during the first 10 s to 0.37 ± 0.14 μm during the last 10 s. Thus, heterosynaptic plasticity effectively counteracted the runaway potentiation and prevented saturation of synaptic weights.

In the previous simulation experiment described in Figure 4, STDP with symmetrical windows for potentiation and depression (a⁺ = a⁻ = 1 × 10⁻³ mS/cm², τ⁺ = τ⁻ = 20 ms) was tested. Next, we asked whether heterosynaptic plasticity can also prevent runaway depression of synaptic weights. To achieve runaway decrease of synaptic weights, we used a model with a strong bias of STDP windows toward depression (Fig. 5A,B). The time constant for the depression window was increased to τ⁻ = 40 ms, and the maximal depression magnitude was increased to a⁻ = 1.5 × 10⁻³ mS/cm². At the same time, the window for potentiation was narrowed (τ⁺ = 5 ms), and the maximum magnitude of potentiation was decreased to a⁻ = 0.5 × 10⁻³ mS/cm² (Fig. 5B, inset). Synaptic weights progressively decreased in the model with these settings. However, after ∼50 s of simulation, decreased synaptic weights could not induce postsynaptic activity sufficient to produce any further synaptic changes (Fig. 5A). To compensate for this effect of decreased synaptic weights and to restore the firing of the postsynaptic neuron, average input firing rates were increased to 2 Hz. After another 50 s of simulation, presynaptic activity in individual synapses was further increased to 3 Hz (Fig. 5A). The distribution of synaptic weights at the end of this simulation expresses clear signs of runaway depression. About 35% of synapses had zero weight, and the whole distribution was asymmetrical shifted toward zero (Fig. 5B). As a result of dramatically decreased synaptic weights, activity of the postsynaptic neuron was essentially abolished. During the last 10 s of simulation, the firing rate was 0.3 ± 0.48 Hz (versus 1.3 ± 1.5 Hz at the beginning), and averaged postsynaptic calcium concentration was 0.25 ± 0.043 μm (versus 0.296 ± 0.1 μm at the beginning), despite a threefold increase of presynaptic firing rate.

Figure 5.

Heterosynaptic plasticity prevents runaway dynamics of synaptic weights produced by STDP with a negative bias. A, B, STDP with a negative bias leads to runaway dynamics of synaptic weights toward zero during background activity produced by weakly correlated inputs. Presynaptic spike trains (N = 100) at an average rate of 1 Hz during first 50 s of simulation, 2 Hz during 50–100 s, and 3 Hz during 100–150 s are shown. Cross-correlation of spike trains throughout the simulation was 0.348 ± 0.05. STDP rule with negative bias (τ⁺ = 5 ms, a⁺ = 0.5 × 10⁻³ mS/cm², τ⁻ = 40 ms, a⁻ = 1.5 × 10⁻³ mS/cm²; B, inset) was implemented at each synapse. A, Membrane potential trace (top), changes of intracellular [Ca²⁺] (middle), and changes of synaptic weights, color coded, with synapses sorted by their synaptic weights at the beginning of the experiment (bottom). B, Distributions of synaptic weights at the beginning (blue; at 20 ms) and at the end (red; at 150 s) of the simulation experiment shown in A. Note runaway dynamics of synaptic weights leading to saturation at zero of about 40% of synapses, and associated dramatic decrease of postsynaptic firing rate despite an increase of presynaptic firing. C, D, Heterosynaptic plasticity prevents runaway synaptic dynamics toward zero weights and the associated decrease of postsynaptic firing. The same model as in A and B is shown, but with the mechanism for heterosynaptic plasticity as described in Figure 3, with the [Ca²⁺] threshold 0.4 μm (dashed line) added to each synapse. All conventions are same as in A and B. Note that synaptic weights are not saturated, but remain normally distributed within the operation range. Also note that in contrast to STDP-only model, postsynaptic firing rate does not express a dramatic decrease, but increases in parallel with increased presynaptic firing.

When heterosynaptic plasticity was added to this model, dynamics of synaptic weights and postsynaptic activity became completely different from those of the STDP-only model. Synaptic weights did not show runaway dynamics. Rather, after a slight initial decrease from 0.015 ± 0.0031 mS/cm² at the beginning to 0.0125 ± 0.0022 mS/cm² after 50 s of simulation with 1 Hz inputs, they were stabilized at a new balance and changed little during further simulation (Fig. 5C). Activity of the postsynaptic neuron changed in parallel to the change of frequency of its inputs. The firing rate of the postsynaptic neuron was 0.9 ± 0.88 Hz during the last 10 s of simulation with presynaptic firing at 1 Hz, 4.4 ± 1.6 Hz during the last 10 s with presynaptic firing at 2 Hz, and 9.2 ± 2.86 Hz during the last 10 s with presynaptic firing at 3 Hz. Averaged intracellular calcium concentrations in the postsynaptic neuron were 0.28 ± 0.081 μm, 0.45 ± 0.17 μm, and 0.69 ± 0.23 μm during these periods, respectively. Thus, heterosynaptic plasticity prevented both runaway potentiation and runaway depression of synaptic weights. It exerted a stabilizing effect on synaptic weights, keeping them within the operation range, away from extreme values, and normally distributed.

Note that the shape of the final steady-state distribution of synaptic weights in the models that implement both STDP and heterosynaptic plasticity depended on the details of plasticity rules and the initial distribution of synaptic weights. With initial weights normally distributed around the middle value, and the rules for heterosynaptic plasticity centered in the range of synaptic weights, final distributions were close to normal. However, skewed final distributions could be also obtained, including shapes close to Poisson or log-normal distributions, as reported experimentally (Song et al., 2005) when uniform distribution of initial weights and heterosynaptic plasticity rules shifted away from the midpoint weight were used (data not shown). One further reason for the highly asymmetrical distribution of experimentally measured synaptic weights, with a large number of zero weights, could be the presence of silent synapses, at which only NMDA, but no AMPA, receptors are present (for review, see Lüscher et al., 2000; Malinow et al., 2000). Pairing presynaptic activation with strong depolarization may lead to insertion of AMPA receptors in these synapses, thus “unsilencing” them. It remains, however, unclear whether postsynaptic firing alone is sufficient to influence insertion of AMPA receptors in previously silent synapses, and thus if heterosynaptic plasticity can influence these synapses.

Stabilizing effect of heterosynaptic plasticity on synaptic weights is long lasting and robust to changes of input activity patterns

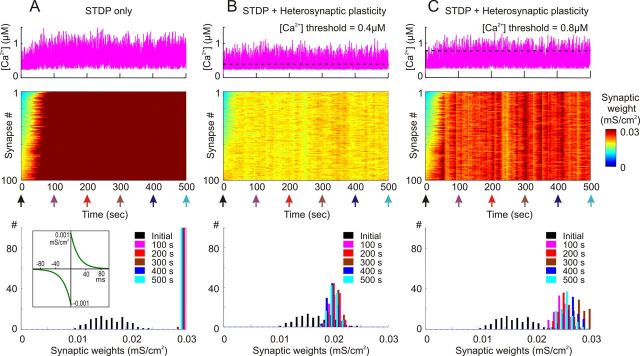
To test stability of the distribution of synaptic weights resulting from a combined action of STDP and heterosynaptic plasticity mechanisms, we performed simulations over longer periods. In the STDP-only model (Fig. 4A,B), synaptic weights, once they reached maximum after ∼70–80 s, remained saturated for the period of simulation (Fig. 6A). In the model equipped with both STDP and heterosynaptic plasticity, synaptic weights reached a new equilibrium state after ∼40–50 s of simulation (Fig. 6B). After that, synaptic weights exhibited some fluctuations, but remained normally distributed around the new equilibrium, with little changes of the mean and SD (0.0191 ± 0.001 mS/cm², 0.0192 ± 0.0008 mS/cm², 0.0195 ± 0.0009 mS/cm², 0.0189 ± 0.0008 mS/cm², and 0.0193 ± 0.0008 mS/cm² at 100, 200, 300, 400, and 500 s after simulation began, respectively; Fig. 6B, bottom). In simulations with the [Ca²⁺]_i threshold for heterosynaptic plasticity increased from the standard setting of 0.4 μm to 0.8 μm, runaway dynamics of synaptic weights were still prevented (Fig. 6C). Synaptic weights remained within the operation range, away from extreme values. Their distribution remained normal, although with higher values of the mean and SD (0.0243 ± 0.0012 mS/cm², 0.0252 ± 0.0012 mS/cm², 0.0281 ± 0.0014 mS/cm², 0.0266 ± 0.0015 mS/cm², and 0.0257 ± 0.0014 mS/cm² at 100, 200, 300, 400, and 500 s after simulation began, respectively; Fig. 6C). Furthermore, with a higher threshold of heterosynaptic plasticity, synaptic weights expressed larger fluctuation around the new equilibrium. Indeed, the distributions of synaptic weights in Figure 6, B and C, at time moments 100, 200, 300, 400, and 500 s after the beginning of simulation were significantly different (two-sample t test, p < 0.05).

Figure 6.

Normalizing effect of heterosynaptic plasticity on synaptic weights is long lasting and operates over a range of calcium thresholds. A, Weakly correlated inputs express runaway dynamics and lasting saturation of synaptic weights in a model with symmetrical STDP. Simulation had the same parameters as in Figure 4A (100 presynaptic spike trains at average rate of 1 Hz; cross-correlation was 0.348 ± 0.05; symmetrical STDP rule τ⁺ = τ⁻ = 20 ms; a⁺ = a⁻ = 10⁻³ mS/cm²; bottom, inset), but was run over 500 s. Changes of intracellular [Ca²⁺] (top), changes of synaptic weights, color coded, with synapses sorted by their synaptic weights at the beginning of experiment (middle) and distributions of synaptic weights at the beginning of the experiment (black; 20 ms) and after 100, 200, 300, 400, and 500 s of simulation, as indicated (bottom). Note that STDP produced runaway dynamics of synaptic weights leading to their saturation. Once saturated after about 80 s, synaptic weights remained at the extreme (0.03 mS/cm²). B, C, Heterosynaptic plasticity prevents runaway dynamics of synaptic weights and leads to a lasting stabilization of synaptic weight distribution within an operation range. The same model as in A is used, but with the mechanism for heterosynaptic plasticity (as described in Fig. 3) with [Ca²⁺] threshold 0.4 μm (B) or 0.8 μm (C) added to each synapse. Calcium thresholds are shown as dashed lines over the plots of [Ca²⁺] change. Other conventions are as in A. Note that synaptic weights are not saturated, but remain normally distributed within the operation rage. Also note that the final distribution of synaptic weights depends on calcium threshold of heterosynaptic plasticity.

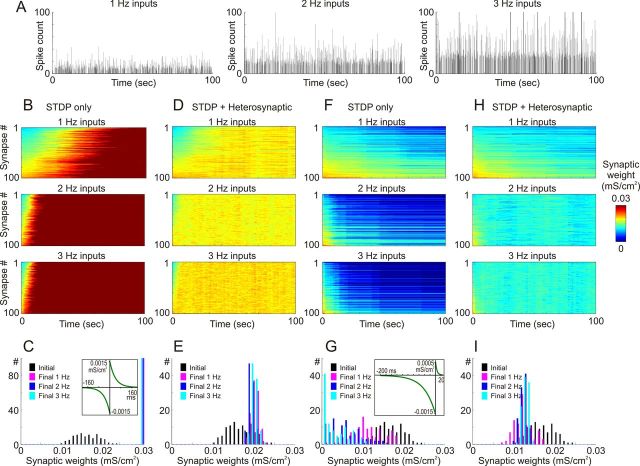
Next, we studied effects of STDP alone or in combination with heterosynaptic plasticity on dynamics of synaptic weights under conditions of different levels of presynaptic activity. Figure 7A shows time histograms of the total number of spikes in all presynaptic neurons firing at average rates of 1, 2, and 3 Hz. At all three levels of presynaptic activity, STDP with symmetrical windows (τ⁺ = τ⁻ = 20 ms, a⁺ = a⁻ = 1 × 10⁻³ mS/cm²; Fig. 7C, inset) produced runaway potentiation of synaptic weights (Fig. 7B,C). Saturation of all synaptic weights at the maximum value occurred after ∼70–80 s of simulation with 1 Hz of presynaptic activity, but much faster, after ∼15–20 s, at higher levels of presynaptic activity (Fig. 7B). When heterosynaptic plasticity was added to this model, runaway dynamics of synaptic weights were prevented at all three levels of presynaptic activity (Fig. 7F,G). The frequency of presynaptic firing affected the time required to reach the new equilibrium of synaptic weights, but in neither of conditions were synaptic weights saturated. In all three cases, synaptic weights remained normally distributed within the operation range (Fig. 7G).

Figure 7.

Normalizing effect of heterosynaptic plasticity on synaptic weights operates over a range of presynaptic activity rates. A, Cumulative histograms of presynaptic spike trains (N = 100) at average rates of 1 Hz (left), 2 Hz (middle), and 3 Hz (right) during a 100 simulation period. Bin size, 50 ms. In all three cases, cross-correlation of presynaptic spike trains was 0.348 ± 0.05. B, Changes of synaptic weights in a model with a symmetrical STDP rule (τ⁺ = τ⁻ = 40 ms, a⁺ = a⁻ = 1.5 × 10⁻³ mS/cm²; C, inset) subject to synaptic bombardment produced by spike trains at 1 Hz (top), 2 Hz (middle), and 3 Hz (bottom). Synaptic weights are color coded, and synapses were sorted by their initial weights at the beginning of a simulation. C, Distributions of synaptic weights at the beginning (black bars) and at the end (100 s, color coded) of simulations from B. Note runaway dynamics of synaptic weights and their saturation at the highest value (0.03 mS/cm²). D, E, Dynamics of synaptic weights in a model with a symmetric STDP rule as in B and C, but with added heterosynaptic plasticity as described in Figure 3, with [Ca²⁺] threshold 0.4 μm. Note that synaptic weights remain normally distributed and unsaturated (E). Conventions are as in B and C. F, G, Changes of synaptic weights (F) and their distributions at the beginning and at the end of simulations with negatively biased STDP (τ⁺ = 5 ms, a⁺ = 0.5 × 10⁻³ mS/cm², τ⁻ = 40 ms, a⁻ = 1.5 × 10⁻³ mS/cm²; G, inset). Conventions are as in B and C. H, I, Dynamics of synaptic weights in a model with negatively biased STDP rule as in F and G, but with added heterosynaptic plasticity as described in Figure 3, with [Ca²⁺] threshold 0.4 μm. Note that synaptic weights remain normally distributed and unsaturated (I). Conventions are as in B and C.

STDP with a strong negative bias (τ⁺ = 5 ms, a⁺ = 0.5 × 10⁻³ mS/cm², τ⁻ = 40 ms, a⁻ = 1.5 × 10⁻³ mS/cm²; Fig. 7G, inset) produced runaway depression and saturation of a portion of synaptic weights at zero when the neuron received intermediate (2 Hz) and high (3 Hz) levels of input activity (Fig. 7D,E). With a low rate of presynaptic firing, synaptic weights were only shifted to the left, but remained unsaturated. This effect was due to a dramatic decrease of postsynaptic activity (see Fig. 5 and related text): synapses did not change when weakened inputs were not able to evoke spikes. These abnormal kinds of dynamics of synaptic weights leading either to a ceased postsynaptic activity or to runaway depression were prevented when heterosynaptic plasticity was added to the model (Fig. 7H). With all three levels of presynaptic firing, synaptic weights remained unsaturated and normally distributed (Fig. 7I). With higher rates of presynaptic inputs (2 or 3 Hz), the new equilibrium was reached faster, and the resulting distributions of synaptic weights were narrower (0.0111 ± 0.0022 mS/cm² at 1 Hz of inputs, 0.0114 ± 0.0009 mS/cm² at 2 Hz of inputs, 0.0122 ± 0.00078 mS/cm² at 3 Hz of inputs) and significantly different (two sample t test, p < 0.05).

Results presented in Figures 6 and 7 show that the stabilizing effect of heterosynaptic plasticity on synaptic weights is long lasting and robust with respect to changes of the calcium threshold for heterosynaptic plasticity and the level of presynaptic activity.

Heterosynaptic plasticity can prevent runaway dynamics of synaptic weights for a broad range of STDP parameters

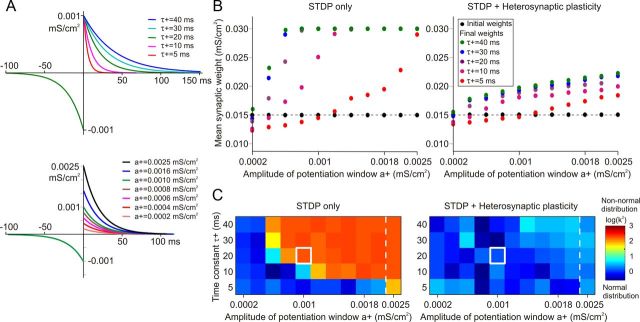
How effective is heterosynaptic plasticity in preventing runaway synaptic dynamics caused by different STDP rules? To address this question, we kept the LTD component of STDP unchanged (τ⁻ = 20 ms, a⁻ = 1 × 10⁻³ mS/cm²) and systematically varied the time constant of STDP potentiation window from τ⁺ = 5 ms to τ⁺ = 40 ms (5, 10, 20, 30, 40 ms) and its maximal magnitude from a⁺ = 2 × 10⁻⁴ mS/cm² to a⁺ = 2.5 × 10⁻³ mS/cm². The tested sets of STDP parameters (55 combinations in total) thus included symmetrical rules where windows for potentiation and depression were the same, rules that were biased toward potentiation with larger magnitude and/or duration of the window for potentiation than for depression, as well as rules that were biased toward depression with smaller magnitude and/or duration of the potentiation window than of the depression window. Figure 8A shows examples of STDP rules for different time constants and different maximal magnitudes of the potentiation window.

Figure 8.

Heterosynaptic plasticity prevents runaway dynamics of synaptic weights over a broad range of STDP parameters. A, Examples of potentiation windows in STDP rules, illustrating the range of tested parameters. Top, STDP potentiation windows with the same maximal magnitude of potentiation a⁺ = 10⁻³ mS/cm², but different time constants, τ⁺ = 5, 10, 20, 30, 40 ms. Bottom, STDP potentiation windows with the same time constant, τ⁺ = 20 ms, but different maximal magnitudes, a⁺ = 0.2 × 10⁻³ to a⁺ = 2.5 × 10⁻³ mS/cm², as indicated. In this series of simulations, the depression window of STDP was kept constant (a⁻ = 10⁻³ mS/cm²; τ⁻ = 20 ms), so the range of tested parameters of potentiation window a⁺, τ⁺ covered positively biased, negatively biased, and symmetrical STDP rules. B, Each data point shows the mean synaptic weight of 100 synapses after 100 s of simulation, for different values of a⁺ (x-axes) and τ⁺ (color coded, as indicated). Black circle symbols connected by a dashed line show the mean of the initial distribution of synaptic weights that was identical in all simulations. In all simulations, presynaptic spike trains had mean rate of 1 Hz, with 0.348 ± 0.05 correlation. Left, Results after 100 s simulations with STDP only. Right, Results after 100 s simulations with heterosynaptic plasticity (as described in Fig. 3) in addition to STDP. Note that in simulations with the STDP-only model, synaptic weights were most often saturated at maximal value (0.03 mS/cm²). In contrast, in simulations with STDP and heterosynaptic plasticity, synaptic weights were not saturated. C, Each box in the grids shows the D'Agostino–Pearson K² test for normality of synaptic weight distribution after 100 s of simulations with different STDP potentiation windows, with a⁺ and τ⁺ as indicated on the x- and y-axes. The same data as in B were used for this plot. Left, Results after 100 s simulations with STDP only. Right, Results after 100 s simulations with heterosynaptic plasticity (as described in Fig. 3) in addition to STDP. Note that in STDP-only models, distribution of synaptic weights after 100 s of simulation deviates from normal (K² values above 50) for a broad range of a⁺ and τ⁺. In contrast, in the models with STDP and heterosynaptic plasticity, distribution of synaptic weights remained normal over the whole range of tested a⁺ and τ⁺ values.

In the models without heterosynaptic plasticity, STDP with most of these parameter settings produced runaway dynamics of synaptic weights. For 45 of 55 parameter combinations, a significant net increase of the mean synaptic weight after 100 s of simulation was observed. In 33 of these 45 cases, synaptic weights were saturated at the maximum, so that their mean was at or close to the upper extreme (Fig. 8B, left, points at or close to 0.03 mS/cm²). In the remaining 12 cases in which the net potentiation was observed, but synaptic weights were not saturated after 100 s of simulations, longer simulation periods (or higher frequency of presynaptic inputs) were required for synaptic weights to become saturated at the maximum (data not shown). To further document the anomalous distributions of synaptic weights produced by runaway dynamics, we tested final distributions for their deviation from a normal distribution due to their skewness or kurtosis using the D'Agostino–Pearson K² test (see Materials and Methods). Figure 8C (left) shows that the final distributions of synaptic weights exhibit significant deviation from normality after 100 s of simulations with a⁺ > 0.6 × 10⁻³ mS/cm² and/or τ⁺ > 10 ms.

Addition of heterosynaptic plasticity to the models effectively prevented runaway dynamics of synaptic weights for the tested range of STDP parameters. When a model neuron was equipped with STDP and heterosynaptic plasticity, synaptic weights reached a new balance after 20–50 s of simulation, and remained normally distributed around these new equilibriums. The mean of the final distributions was shifted from the original value, but never reached the extremes (Fig. 8B, right). Final synaptic weights remained normally distributed in these simulations, as indicated by low K² values (Fig. 8C, right). This condition was maintained in longer simulations (Fig. 6B,C).

Results presented in Figure 8 show that heterosynaptic plasticity can counteract runaway trends caused by STDP plasticity rules and stabilize the operation of neurons over a broad range of STDP parameters.

Synaptic competition in the model with heterosynaptic plasticity

Results of the modeling experiments described above show that heterosynaptic plasticity can effectively prevent runaway dynamics of synaptic weights. Next, we asked whether this stabilizing effect of heterosynaptic plasticity still leaves room for synaptic competition. We segregated synaptic inputs to a model neuron into two groups. The first group (two-thirds of all synapses) consisted of 66 synapses that received weakly correlated input spike trains (average cross-correlation between spike trains, 0.336 ± 0.02). The second, smaller, group (one-third of all synapses) consisted of 34 synapses from neurons with highly correlated spike trains, with average cross-correlation between spike trains 0.605 ± 0.046 throughout the simulation period. In both groups, presynaptic neurons fired at an average frequency of 1 Hz, and synaptic weights had the same initial distribution. In the STDP-only model, synapses receiving highly correlated inputs were rapidly potentiated, and their weights saturated at the maximal value (Fig. 9A,B). Synapses receiving weakly correlated inputs expressed little plasticity, and their distribution essentially did not change after 200 s of simulation (Fig. 9A,B). In the model with both STDP and heterosynaptic plasticity, final synaptic weights of synapses from the two groups formed two compact and clearly separated distributions (Fig. 9C,D). Segregation of synaptic weights of two groups of synapses was a robust phenomenon, observed for different sizes of the groups (e.g., 30, 50, and 70 synapses out of 100 expressing high correlation), different values of input correlations in the “high” correlation group (averaged correlation between spike trains, 0.61 or 0.99), and zero or different levels of correlation in the “low” correlation group, and also in simulations where two groups of inputs had same averaged correlation but differed by their frequency, e.g., 1 versus 3 or 5 Hz (data not shown). In contrast to the STDP-only model, in none of these simulations did the synapses express runaway dynamics, but all synaptic weights remained within the operation range (Fig. 9C,D). Because the inputs were not saturated, they have preserved the ability for further learning. Switching to the input with the same (high) level of correlation for all synapses led to slow decay of the weight differences between the groups. Changing the pattern of input to the model with heterosynaptic plasticity (e.g., high correlation of a different, “new” group of synapses) led to redistribution of synaptic weights. The new group of highly correlated inputs acquired higher weights, whereas the weights of inputs with lower correlation decreased (data not shown).

Figure 9.

Segregation of synaptic weights of strongly versus weakly correlated inputs. A model neuron received input from N = 100 presynaptic neurons firing at average frequency of 1 Hz. Spike trains of 66 presynaptic neurons (inputs 1 to 66) were weakly correlated (cross-correlation, 0.336 ± 0.02); spike trains of 34 presynaptic neurons (inputs 67 to 100) were strongly correlated (cross-correlation, 0.605 ± 0.046). A, C, Membrane potential of a model neuron (top) and dynamics of synaptic weights of N = 66 weakly correlated inputs (synapses 1–66) and N = 34 strongly correlated inputs (synapses 67–100) in the model with STDP only (A) and the model with STDP and heterosynaptic plasticity (C). B, STDP rule used in the simulations (top): τ⁺ = τ⁻ = 20 ms; a⁺ = a⁻ = 10⁻³ mS/cm². Distributions of synaptic weights (bottom) at the beginning (blue bars) and at the end (red) of simulations from A, for the groups of weakly correlated inputs (1–66) and strongly correlated inputs (67–100). Note runaway dynamics of synaptic weights and their saturation at the highest value (0.03 mS/cm²) for the group of strongly correlated inputs. D, Distributions of synaptic weights (color bar) at the beginning (blue) and at the end (red) of simulation in C, with STDP and heterosynaptic plasticity for the groups of strongly and weakly correlated inputs.

Thus, although heterosynaptic plasticity effectively counteracts runaway dynamics of synaptic weights, it does not preclude activity-dependent plasticity: Synapses from presynaptic neurons that fire together (high-correlated inputs) acquire higher weights than synapses from presynaptic neurons that exhibit low-correlated firing.

Discussion

In this study, we present experimental data on heterosynaptic plasticity in two cortical areas, visual and auditory, and we develop a realistic model of a cortical cell driven by synaptic inputs to explore interaction between heterosynaptic plasticity and STDP. We show that direction and magnitude of heterosynaptic plastic changes in vitro depend on initial properties of synapses. Using a conductance-based model, we show that STDP operating alone on the input synapses to the cell driven by correlated spike trains often leads to unstable synaptic weight dynamics: a slight bias of STDP rules toward LTP or LTD triggers runaway dynamics with synaptic weights evolving toward the maximum or toward zero. When parameters tuned by experimental data were implemented in the model, heterosynaptic plasticity prevented the runaway dynamics and created a stable, unimodal and balanced distribution of synaptic weights for a broad range of STDP parameters.

Plasticity at nonstimulated synapses: heterosynaptic plasticity

Conventional forms of LTP and LTD can be induced by afferent tetanization (Bliss and Lomo, 1973) or pairing synaptic stimulation with postsynaptic spikes. The associative, Hebbian-type synaptic plasticity is triggered by the rise of intracellular [Ca²⁺] (Malenka et al., 1988; Bliss and Collingridge, 1993), whereby fast, large-amplitude [Ca²⁺]_i increases induce potentiation, but slower and low-amplitude Ca²⁺ rises induce depression (Bienenstock et al., 1982; Lisman, 1989; Hansel et al., 1997; Ismailov et al., 2004). This plasticity is homosynaptic: it occurs at the synapses that were active during the induction protocol. However, [Ca²⁺]_i rises are not restricted to the activated synapses, but take place also at synapses, which were not active during the plasticity induction, e.g., due to bursts of backpropagating action potentials (Yuste and Denk, 1995; Schiller et al., 1998). This [Ca²⁺]_i increase can lead to plasticity at nonactive synapses—heterosynaptic plasticity, often also referred to as nonassociative plasticity.

Heterosynaptic LTD was found to accompany homosynaptic LTP (Lynch et al., 1977). At short distances, the input specificity of LTP breaks down, and a pairing protocol leads to LTP in a local population of synapses, including those not activated during the induction (Bonhoeffer et al., 1989; Kossel et al., 1990; Engert and Bonhoeffer, 1997), and even synapses at neighboring neurons (Schuman and Madison, 1994). Heterosynaptic LTP at short distances and LTD at longer distances result in a Mexican hat-like profile of plastic changes around the activated synapses (White et al., 1990; Royer and Paré, 2003), resembling kind of lateral inhibition in synaptic plasticity space.

LTP or LTD can be induced even without synaptic activation, by photolytic release of caged Ca²⁺ in neurons (Neveu and Zucker, 1996; Yang et al., 1999), or intracellular tetanization—bursts of postsynaptic action potentials without presynaptic stimulation (Kuhnt et al., 1994; Volgushev et al., 1994, 1997, 1999, 2000; Chistiakova and Volgushev, 2009; Lee et al., 2012). Since neither protocol involves synaptic stimulation during the induction, plasticity at any cell's synapse can be considered heterosynaptic. These forms of heterosynaptic plasticity share some common properties with homosynaptic plasticity. They operate on the same time scale, are rapidly induced (within seconds or minutes), and are long lasting. Induction of both homosynaptic and heterosynaptic plasticity requires [Ca²⁺]_i rise, and thus strong postsynaptic activity. This may activate retrograde signaling via NO-dependent pathways (Volgushev et al., 2000; Lee et al., 2012), leading to both presynaptic and postsynaptic changes. Involvement of common biochemical pathways is further supported by the partial occlusion of the induction of homosynaptic and heterosynaptic plasticity (Kuhnt et al., 1994; Neveu and Zucker, 1996; Volgushev et al., 1999; Yang et al., 1999). An important feature that distinguishes heterosynaptic plasticity is that its induction does not require activation of that particular synapse, but can be triggered by Ca²⁺ rise produced by activation of other synapses. It remains to be elucidated how the rise of [Ca²⁺]_i may trigger both input-specific homosynaptic changes as well as cell-wide heterosynaptic changes. One possibility is that multiple sources of intracellular calcium create differential spatial distribution of intracellular calcium (Yasuda et al., 2003; Bloodgood and Sabatini, 2007), leading to preferential activation of location-specific calcium sensors. Another possibility is that homosynaptic and heterosynaptic plasticity are triggered by different [Ca²⁺]_i levels. In addition, synapses may have differential predispositions to undergo potentiation or depression or do not change (Abraham and Bear, 1996; Volgushev et al., 1997), whereby strong calcium increase may preferentially trigger respective processes. Weight dependence of heterosynaptic (Volgushev et al., 2000; Chistiakova and Volgushev 2009; Lee et al., 2012) and homosynaptic plasticity (Bi and Poo 1998; van Rossum et al., 2000; Hardingham et al., 2007) lends support for that latter possibility.

STDP and runaway synaptic dynamics

STDP is experimentally well-characterized form of plasticity that is broadly used in computational models of learning and developmental processes (Miller, 1996; Kempter et al., 1999, 2001; Song et al., 2000; van Rossum et al., 2000; Rubin et al., 2001; Song and Abbott 2001; Finelli et al., 2008). However, STDP and other conventional Hebbian-type plasticity rules are prone to produce runaway dynamics of synaptic weights and neuronal firing. Potentiated synapses have higher probability to lead to spikes and thus to be further potentiated, while depressed synapses less probably evoke spikes and thus tend to be further depressed. Mechanisms supporting runaway dynamics of synaptic weights combined with strong synaptic competition (Miller and MacKay 1993; Miller, 1996) are useful for formation of sensory representations (Wiesel and Hubel, 1963; Aitkin et al., 1970; Merzenich et al., 1975; Thompson et al., 1983; Feldman, 2009) and other “rewiring” processes. However, during learning processes that do not require elimination of synapses but are mediated by more subtle synaptic changes, stabilization mechanisms preventing runaway dynamics of plastic synapses toward extreme weights need to be in place.

Possible mechanisms preventing runaway synaptic dynamics

Local balancing of synaptic weights was suggested as one mechanism preventing runaway dynamics. In the hippocampus (White et al., 1990) and amygdala (Royer and Paré 2003), potentiation of the synapses activated during afferent tetanization was accompanied by the depression of neighboring synapses and vice versa. In the resulting Mexican hat-type profile of plastic changes, potentiation and depression can balance each other, so that net synaptic weight is preserved. Signal for this process is most probably local [Ca²⁺]_i rise and its gradient. Potentiation is induced at and around the stimulated synapses experiencing maximal [Ca²⁺]_i rise (Miyakawa et al., 1992; Magee and Johnston, 1997; Stuart and Häusser, 2001; Nevian and Sakmann, 2006), depression is induced at somewhat distant sites experiencing smaller [Ca²⁺]_i rises, and no changes occur yet more distantly, where [Ca²⁺]_i does not reach plasticity threshold (Bienenstock et al., 1982; Lisman, 1989; Yang et al., 1999).

Several mechanisms suggested to prevent the runaway synaptic dynamics are based on adjustment of learning rules per se. These include weight dependence, so that weaker synapses potentiate more while stronger synapses express less potentiation, and in the limit even depress (Bi and Poo, 1998; van Rossum et al., 2000; Hardingham et al., 2007), and/or precise balancing of STDP rules for potentiation and depression (Abbott and Nelson, 2000; van Rossum et al., 2000; Kempter et al., 2001; Gütig et al., 2003; Morrison et al., 2007; Babadi and Abbott, 2010; Delgado et al., 2010; Gilson and Fukai, 2011). It was rigorously shown that STDP can lead to stabilization of the mean firing rate of the postsynaptic neuron if the integral of the learning window is negative (Kempter et al., 2001). However, experimental evidence shows a great variety of the duration and magnitude of STDP windows for potentiation and depression (Nishiyama et al., 2000; Sjöström et al., 2001; Zhou et al., 2005; Haas et al., 2006; Feldman, 2009). Our simulation results show that STDP does not induce runaway synaptic dynamics only within a very narrow range of potentiation and depression windows. Because of these strict requirements, such a mechanism is unlikely to be a general tool for counteracting runaway dynamics, although it may work at some synapses.

Cell-wide mechanisms that can affect all, or most of, plastic synapses of a cell can counteract the runaway synaptic dynamics in a most robust way. Cell-wide synaptic weight normalization is commonly used in simulations of learning processes in neurons and neuronal networks (von der Malsburg, 1973; Elliott and Shadbolt, 2002; Wu and Yamaguchi, 2006; Finelli et al., 2008). A previously suggested mechanism involves regulation of the Ca²⁺ thresholds for potentiation or depression via a slow, activity-dependent homeostatic regulation of [Ca²⁺]_i levels (Yeung et al., 2004). Our results show that heterosynaptic plasticity, which operates as cell-wide mechanism due to its Ca²⁺ dependence, can rapidly and effectively prevent runaway dynamics of synaptic weights over a broad range of STDP parameters.

Our results show that runaway potentiation or depression in unbalanced STDP-only models disturbs input–output relations, leading to overreactivity or complete silencing of neurons. Heterosynaptic plasticity counteracts these effects by preventing the runaway dynamics of synaptic weights on a single-cell level. For a more robust control of neuronal activity, including conditions of lasting changes of the input level, mechanisms operating on the longer time scale at the network level would be required, such as homeostatic scaling of synaptic weights by overall level of postsynaptic activity (for review, see Turrigiano, 2008; Vitureira et al., 2012).

Outlook

Our results show that the net effect of correlated activity on synaptic weights depends on the relative strength of STDP and heterosynaptic plasticity. This suggests an interesting possibility that relative contribution of competition versus balancing mechanisms, and thus susceptibility of synapses to extreme potentiation or depression, can be fine-tuned by upregulation or downregulation of heterosynaptic plasticity. This kind of regulation may be one of the mechanisms involved in changing susceptibility of synapses for plasticity during wake–sleep cycles. Less heterosynaptic plasticity during waking may “allow” more room for STDP-related synaptic changes, including polarization of synaptic weights, while more heterosynaptic plasticity during sleep may lead to restoration of an overall balance of synaptic weights, though some of the changes may still be kept or strengthened due to repetition of specific activity patterns during slow-wave sleep, in a process of memory replay (Ji and Wilson, 2007; Peyrache et al., 2009). Indeed, our results show that despite the normalizing effect of heterosynaptic plasticity, synapses from neurons expressing higher level of correlation, such as neurons firing in synchrony, can still acquire and maintain higher weights.

To conclude, our study predicts that heterosynaptic plasticity can effectively counteract runaway dynamics of synaptic weights produced by STDP, and thus substantially broaden the range of possible STDP rules that are compatible with normal operation of neuronal networks.