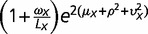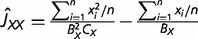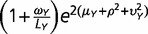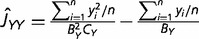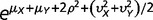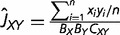Phylogenomic Distance Method for Analyzing Transcriptome Evolution Based on RNA-seq Data

Abstract

Thanks to the microarray technology, our understanding of transcriptome evolution at the genome level has been considerably advanced in the past decade. Yet, further investigation was challenged by several technical limitations of this technology. Recent innovation of next-generation sequencing, particularly the invention of RNA-seq technology, has shed insightful lights on resolving this problem. Though a number of statistical and computational methods have been developed to analyze RNA-seq data, the analytical framework specifically designed for evolutionary genomics remains an open question. In this article we develop a new method for estimating the genome expression distance from the RNA-seq data, which has explicit interpretations under the model of gene expression evolution. Moreover, this distance measure takes the data overdispersion, gene length variation, and sequencing depth variation into account so that it can be applied to multiple genomes from different species. Using mammalian RNA-seq data as example, we demonstrated that this expression distance is useful in phylogenomic analysis.

Introduction

Despite exciting achievements in transcriptome changes in genome evolution, mainly based on microarrays (Enard et al. 2002; Caceres et al. 2003; Gu and Gu 2003; Makova and Li 2003; Rifkin et al. 2003; Huminiecki and Wolfe 2004; Khaitovich et al. 2004; Gu et al. 2005; Gu and Su 2007), further investigation has been challenged by the availability of robust gene expression data across a broad range of species and tissues (Wang et al. 2009). Nevertheless, recent technological innovations called next-generation sequencing, particularly the development of RNA-seq technology, have shed some light to this problem, which can generate tens of millions of short sequence reads. These reads can be mapped to each gene through the reference genome or de novo assembling, enabling researchers to quantify the transcription level in ultra-high resolution (Cloonan et al. 2009; Morozova et al. 2009; Wang et al. 2009). Indeed, RNA-seq technology has already made unprecedented advances for revealing the complexity of transcriptional phenomena, ranging from the expression profiling, dissection of isoform, and allelic expression, to the extension of 3′-UTR regions, novel splice junctions, modes of antisense regulation, and intragenic expression (Carninci et al. 2005; Eveland et al. 2008; Mortazavi et al. 2008; Nagalakshmi et al. 2008; Sultan et al. 2008; Graveley et al. 2010; Trapnell et al. 2010).

The power of RNA-seq in the study of transcriptome evolution was well demonstrated by the recent work of Brawand et al. (2011). They reported a large-scale RNA-seq analysis of six mammalian tissues and showed the dynamics of transcriptome evolution that may underlie many phenotypic differences between species. However, despite many studies in RNA-seq data analysis (Lu et al. 2005; Robinson and Smyth 2007, 2008; Anders and Huber 2010; Di et al. 2011; Zhou et al. 2011; McCarthy et al. 2012), statistical methods designed specifically for evolutionary genomics have not been well developed. In this article we report a new method for estimating the genome expression distance based on RNA-seq data, which has explicit interpretations under the model of gene expression evolution. Using mammalian RNA-seq data as example, we show that this expression distance can be used in phylogenomic reconstruction and related phylogeny-based expression analysis.

Materials and Methods

New Methods

Statistical Framework of Transcriptome Evolution

Because RNA-seq technology provides readout counts, the sampling property is similar to some earlier data types such as SAGE (Velculescu et al. 1995) or EST (Audic and Claverie 1997; Ewing and Claverie 2000). A variety of statistical methods were proposed; see Zhou et al. (2011), McCarthy et al. (2012), and Di et al. (2011) for recent advances and references therein. Simply to say, these methods considered RNA-seq overdispersion as well as data normalization to remove nonbiological effects in the data processing, which will be also addressed in our method.

Though a simple Poisson distribution model p(x; λ), characterized by the variance equal to the mean (λ), can effectively handle substantial zero counts, many studies have shown that RNA-seq counts exhibit a greater variance across biological replicates than expected (Di et al. 2011; McCarthy et al. 2012). This phenomenon is called overdispersion in statistics. Among a number of statistical models proposed to remedy this problem (Lu et al. 2005; Robinson and Smyth 2007, 2008; Anders and Huber 2010; Di et al. 2011; Zhou et al. 2011; McCarthy et al. 2012), our study adopts the widely used negative binomial distribution (NBD). We choose a special form denoted by p(x; λ, ω), characterized by the mean parameter (λ) and the overdispersion parameter (ω) (see eq. 4 in Data Processing section). A large value of ω indicates a strong over-dispersion, and vice versa. When ω = 0, p(x; λ, ω) is reduced to the Poisson model.

Next we model the mean parameter λ as a random variable to describe the expression variability among genes. A typical RNA-seq sample may include many thousands of genes, showing a highly skewed distribution of read counts. For instance, in mammalian tissues (Brawand et al. 2011), the top 5% highly expressed genes received roughly 10²–10⁵ RNA-seq counts, whereas the bottom 40% lowly expressed genes received roughly 0–10 counts. We therefore implement a lognormal distribution, analogous to the log-transformation in the microarray data analysis (Kerr and Churchill 2001; Irizarry et al. 2003); the log of λ follows a normal distribution with the mean µ and variance η². Together, the RNA-seq counts in a sample follow a negative binomial-lognormal distribution denoted by f(x). Though the analytical form of f(x) is not available, the mean and variance of f(x) can be derived straightforwardly; see equation (5) in Data Processing section.

In the case of two RNA-seq samples of the same tissue from two species (genomes) X and Y, the mean parameter λ_X (or λ_Y) of genome X (or Y) follows a lognormal distribution accounting for the among-gene expression variability. Because λ_X and λ_Y are correlated by the evolutionary relatedness of genomes X and Y, without loss of generality the joint model of λ_X and λ_Y can be written as follows (Gu 2004):

(1)

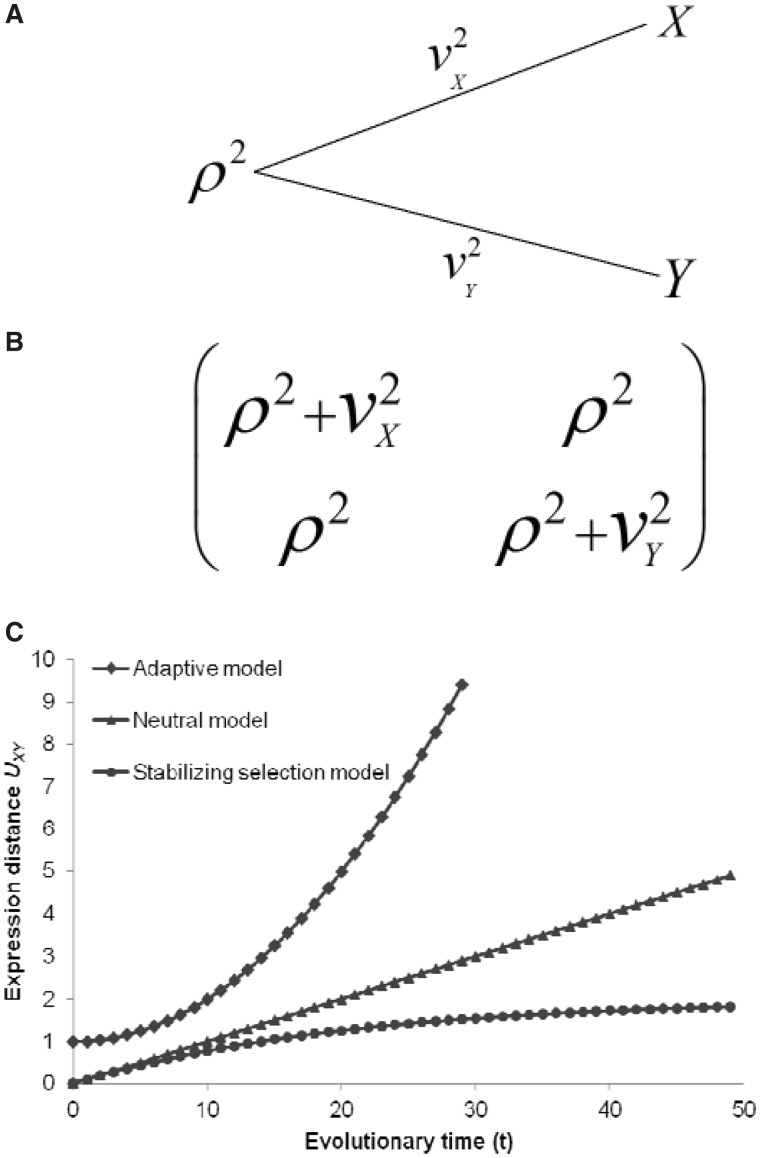
where α_XY is the ancestral genetic component shared by X and Y, β_X and β_Y are the independent genetic effects, and μ_X and μ_Y are the ground means. Together, α_XY, β_X, and β_Y describe the evolutionally correlated structure of the underlying regulatory machinery. To implement this model, we further assume that α_XY, β_X, and β_Y are mutually independent, each of which follows a normal distribution with the mean 0, and the variance ρ², v²_X, or v²_Y, respectively. As shown in figure 1, the variance component ρ² measures the expression variability at the common ancestor of species X and Y. Meanwhile, the variance component v²_X (or v²_Y) measures the expression variability generated during the evolution from the common ancestor to the current species X (or Y). For the current genome X, the marginal expression variability is given by γ_X = α_XY + β_X so that the variance of among-gene variability is given by η²_X = ρ² + v²_X. Similarly, for genome Y, we have γ_Y = α_XY + β_Y and η²_Y = ρ² + v²_Y.

Fig. 1.—

Model of transcriptome evolution between two species. (A) A schematic illustration for a rooted two-gene tree: ρ² refers to among-gene expression variability at the common ancestor of species X and Y; v²_X and v²_Y measure the among-gene expression variability in lineage X and Y since the split of common ancestor, respectively. (B) The variance–covariance matrix of genome expression between for current genomes X and Y. (C) The expression distance U_XY plotted against the evolutionary time t. Expression divergence is an accelerated process under the adaptive model, a constant-rate process under the neutral model, and a decelerated process under the stabilizing model. In particular, when W→0, we have U_XY →2σ2t, i.e., the stabilizing selection model is reduced to the neutral model; and when t→∞, U_XY →1/W, i.e., the expression divergence approaches a saturated level.

Definition of Expression Distance

For a given tissue, the expression distance should measure the expression divergence between two species that had diverged t time units ago, reflecting the underlying regulatory divergence. Because two variance components v²_X and v²_Y characterize the expression divergence along the lineages from the common ancestor to species X and Y, respectively, following our previous work (Gu 2004; Gu and Su 2007) we define the expression distance between species X and Y as

(2)

The biological interpretation of equation (2) can be briefly summarized as follows; also see figure 1C for numerical illustrations.

(i) Under the simple Brownian model that represents a selectively neutral expression evolution (Gu 2004), we have U_XY = 2σ²t, where σ² is the rate of mutational variance. Hence, under the neutral expression model, the expression distance U_XY increases proportionally with the evolutionary time t, and the rate (r) of expression divergence equals to the rate of mutational variance, i.e., r = σ².

(ii) Under the Ornstein-Uhlenback (OU) model (Gu and Su 2007), gene expression has been maintained around its optimum by the stabilizing selection and any deviation of expression profile may reduce the organismal fitness. It has been shown (Gu and Su 2007) that the expression distance is expected to be U_XY = (1 − e^−2βt)/W, where W describes the selection strength and the decay rate β = Wσ². Importantly, when t→∞, U_XY→1/W, which means that the expression distance approaches a saturated level determined by the strength of stabilizing selection. In a special case of W→0, i.e., very weak stabilizing selection, one can show U_XY→2σ²t, i.e., the neutral Brownian model. Intuitively, expression divergence under the stabilizing model evolves more slowly than the neutral expectation. Indeed, the rate of expression divergence (r) under the stabilizing model can be symbolically written by r = σ²f, where the expression constraint f < 1 measures the effect of purifying selection. In short, stabilizing selection model of expression divergence is consistent with the nearly neutral model.

(iii) Despite many forms of adaptive expression divergence, the general pattern is that the rate of expression divergence can be accelerated by the adaptive evolution, i.e., r > σ². For instance, gradual directive selection (Gu 2004) predicts that the expression distance is proportional to t².

Estimation of Expression Distance from RNA-seq Data

Suppose that we have RNA-seq data of a tissue from genomes X and Y, both of which contain n orthologous genes with RNA-seq counts denoted by x_1, … , x_n and y_1, … , y_n. When RNA-seq data contain multiple biological replicates, we use a simple mean. It is thus straightforward to obtain the estimates of first, second, and cross moments E[x], E[x²], E[y], E[y²], and E[xy], respectively; for instance, the estimate of E[xy] is given by Σ_i x_i y_i/n. On the other hand, the expectations of these moments under the NBD-lognormal model can be found in equations (5) and (6) in Data Processing section, allowing us to develop a simple method to estimate the expression distance U_XY = v²_X + v²_Y. To this end, we first define three basic quantities: J_XX = E[x²] − E[x], J_YY = E[y²] − E[y], and J_XY = E[xy]. The (mean-corrected) second moments J_XX and J_YY represent the expression variability in genomes X and Y, respectively, and the cross-product J_XY measures the co-expression pattern. Putting together with equation (2) and equations (5) and (6), one can derive the relationships of J_XX, J_YY, and J_XY with the underlying model parameters (presented in the second column of table 1). It follows that the expression distance defined by equation (2) can be rewritten as follows:

(3)

where Ω_X = ln(1 + ω_X /L_X) and Ω_Y = ln(1 + ω_Y /L_Y) are the effects of overdispersion; L_X and L_Y are the numbers of biological replicates of genomes X and Y, respectively.

Table 1.

Definitions, Theoretical Expectations, and Formulas of Statistical Estimation for Three Quantities J_XX, J_YY, and J_XY

Quantitya	Expectationb	Estimationc
JXX = E[x2] − E[x]
JYY = E[y2] − E[y]
JXY = E[xy]

^aE[.] is short form for expectation.

^bDerivation of each expectation can be found in Materials and Methods. See figure 1 and the text for the description of model parameters.

^cx_i. (or y_i.) is the mean RNA-seq count of gene i over its biological replicates in genome X (or Y); and n is the number of genes under study.

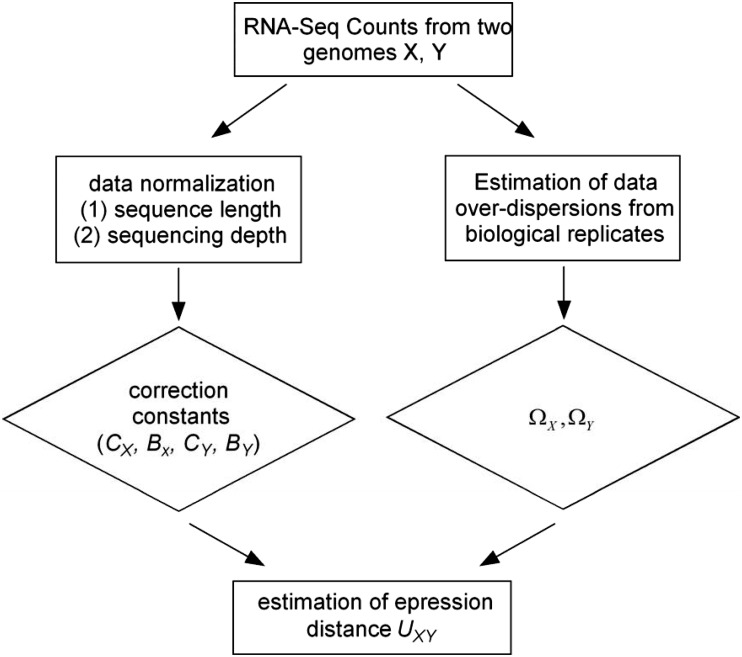
The flow chart in figure 2 shows the statistical procedure for the estimation of U_XY; see Data Processing section for technical details. In the first step of data normalization, we introduced two correction constants of each genome (X) to remove the overestimation of expression distance: constant C_X accounts for the effect caused by the sequence length variation among genes and B_X for the sequencing depth variation among genomes. After data normalization, one can compute J_XX, J_YY, and J_XY, respectively, by the formulas in the third column of table 1. When genes have the same sequence length and genomes have the same sequencing depth, we have C_X = 1 and B_X = 1; in this case, J_XX, J_YY, and J_XY are simply calculated by the method of moments. The next issue is to estimate overdispersion. We implemented a simple method to estimate Ω_X and Ω_Y even for only two biological replicates available. One may see Results and Discussion for a special treatment in the case of single biological replicate. Finally, the sampling variance of the estimated U_XY can be empirically determined by the bootstrapping approach or a simple approximate method.

Fig. 2.—

Flow chart for illustrating the statistical procedure of expression distance estimation.

Data Sets

We downloaded the mammalian RNA-seq data in five tissues (brain, cerebellum, liver, heart, and kidney) from Brawand et al. (2011). For simplicity, we used the total reads of all 5,636 1:1 orthologous genes, suggested by the original authors. Nevertheless, we obtain the RNA-seq counts independently from the raw reads and found virtually the same results.

Data Processing

Calculation of Moments

The specific form of NBD we used in our study is as follows:

(4)

where α = 1/ω. Let φ(λ) be a lognormal distribution φ(λ) such that the log of λ follows a normal distribution with the mean µ and variance η². Then, the negative binomial-lognormal distribution for RNA-seq counts (x) of genes is given by f (x) = ∫p(x; λ, ω) φ(λ) d λ. Next we derive first and second moments. From the conditional expectation E[x| λ] = λ according to equation (4), we have E[x] = E[E[x| λ]] = E[λ]. Similarly, we have E[x²] = E[E[x²| λ]] = E[λ + (ω + 1)λ²]. With respective the lognormal distribution φ(λ), we obtain

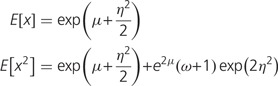(5)

In the case of two genomes X and Y, the first and second moments of x or y are given by equation (5). For the cross-moment of x and y, from equation (4) we have E[xy] = E[E[xy| λ_Xλ_Y]] = E[λ_Xλ_Y]. Together with the independent assumption of three components in equation (1) and the lognormal distribution φ(λ), we derive E[λ_Xλ_Y] = E[exp(μ_X + α_XY + β_X) exp(μ_Y + α_XY + β_Y)] = exp(μ_X + μ_Y) E[exp(2α_XY)] E[exp(β_X)] E[exp (β_Y)], resulting in

(6)

When the mean RNA-seq counts over L number of biological replicates is used to estimate the expression distance, the first, second, and cross-moments can be derived with a similar approach, except for the overdispersion parameters ω. = ω/L (omitting the subscripts X or Y).

RNA-seq Data Normalizations

Two main nonbiological effects inherited in the RNA-seq data processing need to be removed to avoid potential biases in the estimation of expression distance: sequence length variation and sequencing depth variation. To this end, we assume that the RNA-seq count of any gene (x_i) can be written as

(7)

where c_i and B_X are the normalization constants and variable z_i is the normalized count when all genes have the same length (equal to the genome mean) and the same sequencing depth (equal to the mean over the genomes under study). Similar to RPKM (reads per kilobase per million mapped reads), we set c_i = l_i/l, where l_i is the sequence length of gene i and l is the genome mean of sequence lengths. To correct sequencing depth variation, one has to consider the factor that the number (N) of genes may vary among genomes. Here we used a relative measure for any genome X by defining R_X = Total counts/N. That is, we actually normalize the data such that the mean count per gene is roughly the same among the genomes under study. Moreover, we choose B_X = R_X/R⁰, where R⁰ is the mean over all genomes under study.

Next we derive the formulas in the third column of table 1 to estimate the expression distance after the data normalization. From equation (7) we claim that the expectations E[x] is given by E[x] = B_X E[z] Σ_i c_i/n = B_XE[z] because Σ_i c_i/n = 1. Similarly, we have E[x²] = B_X²E[z²] Σ_i c_i²/n = B_X²C_XE[z²], where C_X = Σ_i c_i²/n. Therefore, after data normalization, we have J_XX = E[z²] − E[z] = E[x²]/(B_X² C_X) − E[x]/B_X. In the same manner, we have J_YY = E[y²]/(B_Y² C_Y) − E[y]/B_Y, and J_XY = E[xy]/(B_X B_Y C_XY), where C_XY = Σ_i c_i,X c_i,Y/n. After replacing these moments by their corresponding sampling moments, we obtain the results as shown in table 1.

Outlier Control

There are always a few outlier, i.e., extremely highly expressed genes. Their expression variations are very sensitive to the physiological or developmental condition when the sample was obtained. Because the distribution of RNA-seq is highly skewed, estimation of expression distance could be distorted by these outliers. As the first attempt, we implemented a simple cutoff to alleviate this problem: for the top 2.5% of highly expressed genes, we reset their RNA-seq counts to the value of the 97.5% quantile. Our preliminary analysis indicates that this approach is efficient and not sensitive to the selected cutoff (not shown).

Estimation of Overdispersion

If the number of biological replicates in RNA-seq data set is small, estimation of gene-specific overdispersion remains a difficult task. To deal with this problem, a number of statistical methods were proposed by sharing a certain amount of information between genes. For the practical reason, we implemented a fast but robust method to estimate the genome-wide overdispersion parameters ω (for ω_X or ω_Y) by maximizing the joint likelihood function of NBDs.

We use genome X for illustration. Suppose that x_ik is the RNA-seq count of the k-th biological replicate of gene i. The log-likelihood function of gene i, denoted by lik_i(λ_i, ω_X|x_ik), is formulated according to the NBD, whereas the mean (λ_i) is gene-specific and ω_X is the common parameter. Thus, the overall likelihood function Lik over all genes is the sum of all lik_i(λ_i, ω_X|x_ik). A standard numerical procedure can be applied to obtain the maximum likelihood estimate of ω_X, which is converged rapidly when the moment estimate is used as an initial value: Let x_i. and V_i,X be the sampling mean and variance of gene i. The initial estimate of ω_X can be calculated as Σ_i (V_i,X − x_i.)/Σ_i x_i.².

A Simple Method for Estimating Sampling Variance of U_XY

The sampling variance of the estimated expression distance can be numerically calculated by the bootstrapping method. Nevertheless, by computer simulations we found that the following simple formula is close to the bootstrapping result: Var(U_XY) = q/[(1 − q)n], where q = J²_XY/J_XX J_YY, and n is the number of genes.

Results and Discussion

Mammalian Tissue Expression Evolution

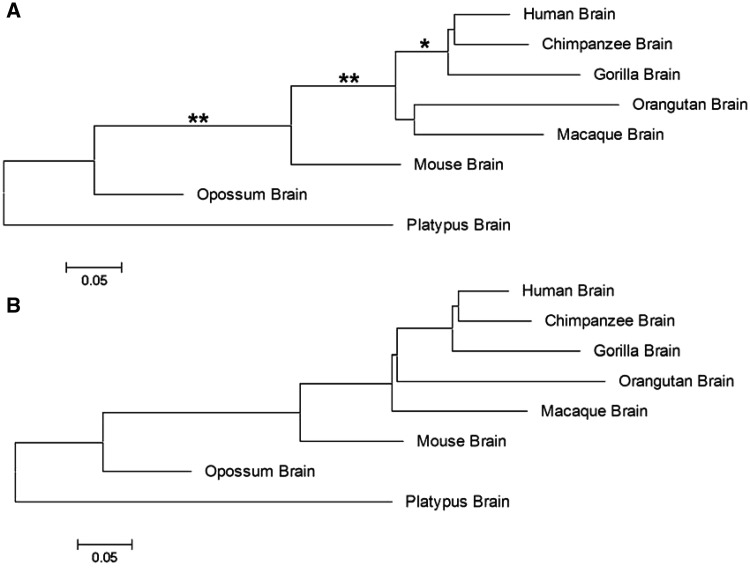
We used mammalian RNA-seq data (Brawand et al. 2011) in brain, cerebellum, kidney, heart, and lung to demonstrate the application of our newly developed method. For simplicity, we used the RNA-seq counts of 5,636 1:1 orthologous genes used by the original authors. We estimated C_X for the effect of sequence length variation in each genome. Since we observed that it has only a small-scale variation among genomes, we used the averaged correction constant C = 1.324 in the following analysis. By contrast, each tissue we have studied reveals a great deal of B_X variation, suggesting that the sequencing depth variation among genomes should be corrected appropriately (see table 2 for examples). After estimating the effects of overdispersion, we calculated the pairwise expression distances between mammalian genomes (the up diagonal in table 3 for brain and the down diagonal for cerebellum); the sampling variances of expression distance are presented in the form of standard error. Apparently, the expression distance is small between phylogenetically closely related genomes and large between distantly related genomes. Based on the expression distance matrices, we reconstructed the genome expression phylogeny by the neighbor-joining method. For illustration, figure 3A shows the expression phylogeny for the mammalian brain. With some minor exceptions, the inferred tree is consistent with the known mammalian phylogeny, which correctly resolved the lineage of placentals, or eutherians from marsupials and monotremes, and separated two major eutherian lineages (primates and rodents). On the other hand, we mapped the expression distances onto the known mammalian phylogeny, as shown in figure 3B. We have performed all analyses in the other four tissues. All inferred expression phylogenies are roughly consistent with the known mammalian phylogeny. Similar to Brawand et al. (2011), we found that different tissues and lineages may show different expression distances. For instance, the expression rate of testes is more rapid than the rest of tissues. Because of the space limit, we will show these results in detail elsewhere.

Table 2.

Summary for the Estimates of Deep-Sequencing Parameters and Overdispersed Parameters in Mammalian Brains and Cerebellums

	Bx		ΩX
	Brain	Cerebellum	Brain	Cerebellum
Human	0.619	1.183	0.165	0.034
Chimpanzee	0.660	0.831	0.102	0.049
Gorilla	1.215	1.063	0.051	0.034
Orangutan	1.462	0.970	0.039	0.033
Macaque	0.846	0.598	0.046	0.009
Mouse	1.439	0.876	0.162	0.054
Opossum	1.030	0.746	0.153	0.003
Platypus	1.093	0.999	0.034	0.013

Table 3.

Pairwise Tissue Expression Distance (U_XY) Matrix of Brain and Cerebellum in Mammals

	Human	Chimpanzee	Gorilla	Orangutan	Macaque	Mouse	Opossum	Platypus
Human	0	0.116 ± 0.038	0.174 ± 0.031	0.338 ± 0.021	0.247 ± 0.025	0.248 ± 0.025	0.473 ± 0.017	0.797 ± 0.012
Chimpanzee	0.304 ± 0.023	0	0.191 ± 0.029	0.300 ± 0.023	0.258 ± 0.025	0.333 ± 0.021	0.494 ± 0.017	0.799 ± 0.012
Gorilla	0.357 ± 0.021	0.329 ± 0.022	0	0.348 ± 0.021	0.299 ± 0.023	0.379 ± 0.020	0.512 ± 0.016	0.890 ± 0.011
Orangutan	0.523 ± 0.016	0.393 ± 0.019	0.511 ± 0.016	0	0.302 ± 0.023	0.426 ± 0.018	0.535 ± 0.016	0.912 ± 0.011
Macaque	0.468 ± 0.017	0.343 ± 0.021	0.456 ± 0.018	0.459 ± 0.018	0	0.306 ± 0.023	0.464 ± 0.018	0.852 ± 0.012
Mouse	0.493 ± 0.017	0.467 ± 0.017	0.549 ± 0.016	0.680 ± 0.014	0.518 ± 0.016	0	0.361 ± 0.020	0.704 ± 0.013
Opossum	0.810 ± 0.012	0.699 ± 0.013	0.785 ± 0.012	0.821 ± 0.012	0.672 ± 0.014	0.676 ± 0.014	0	0.512 ± 0.016
Platypus	1.010 ± 0.010	0.842 ± 0.012	0.976 ± 0.010	0.992 ± 0.010	0.823 ± 0.012	0.786 ± 0.012	0.777 ± 0.012	0

Note.—Up diagonal for brain and down diagonal for cerebellum; the sampling variances of expression distance are presented in the form of standard error.

Fig. 3.—

Mammalian brain expression phylogeny. (A) Expression phylogeny inferred by the neighbor-joining method based on expression distance matrix of brains. Nodes with * means bootstrapping values >0.95 and with ** values >0.99. (B) The result of mapping the expression distance to a given species tree, which is extracted from the tree of life (http://tolweb.org/, last accessed September 18, 2013).

Some Technical Comments

There are several ad hoc distance measures that have been used to analyze the divergence in expression. For instance, Brawand et al. (2011) used 1−R, where R is the Spearman’s correlation coefficient, and the Euclidean distance in their analyses. Although these measures are useful, our model-based expression distance has a unique strength for the study of transcriptome evolution because it provides a basis to generate testable hypotheses under the phylogenetic framework. In addition, our method has considered the effects of sampling and data processing so that the user can justify whether a conclusion is sensitive to the high throughput-dependent noise.

Our model implements a NBD to account for data over-dispersion. Though it is a common practice in statistics, some studies suggested that it may not be sufficient in RNA-seq analysis. Meanwhile, we use the lognormal-normal distribution to account for highly skewed RAN-seq variability. It remains our further work to evaluate whether the current model is the most appropriate for RNA-seq data, and how to improve the robustness of our method in the estimation of expression distance.

In real data analysis, application of new expression distance is difficult in the case of no biological replicate, because Ω_X and Ω_Y cannot be estimated. To resolve this problem, we suggest a modified expression distance by omitting the overdispersion effects, that is,

(8)

Though U*_XY tends to overestimate the expression distance, one can show that U*_XY satisfies the “four-point condition” (Gu and Li 1996). In other words, U*_XY is a paralinear distance to U_XY, which has the following properties: 1) Under the strict additivity, the phylogenetic topology inferred from U*_XY is the same as that from U_XY. 2) External branch lengths tend to be overestimated, whereas internal branch lengths are expected to be unbiased. Our software has the option of paralinear expression distance estimation.

Software Availability

We have developed a software system, called PhyExp, short for phylogenomic analysis of expression profiles, to help the evolutionary analysis of RNA-seq data. There are several commercially available platforms such as Illumina, SOLiD, or 454 Genome Sequencer, but the RNA-seq data processing and analysis is about the same. Two distribution R packages, compatible with Windows and Linux operating systems, respectively, are available at http://www.xungulab.com (last accessed September 23, 2013). The first version, PhyExp1.0, has implemented the following options: 1) After the input file (RNA-Seq counts of genes) has been loaded, the expression distance matrix, including the paralinear distances, as well as their sampling variances are calculated.2) Infer the expression phylogeny by the neighbor-joining method; the statistical reliability can be examined via the bootstrapping. 3) PhyExp1.0 has the option to input the amino acid sequence alignment, which allows the user to map the expression distances onto the inferred molecular phylogeny or to a user-provided phylogeny.

There are several directions in further improvements: 1) Implement a suite of phylogeny-based analysis tools, including testing asymmetry of expression divergence, ancestral expression inference, and phylogeny-dependent detection of differentially expressed genes (unpublished results). 2) Develop and implement advanced methods for dealing with data normalization and data overdispersion. And 3) for the practical purpose, implement the option of expression divergence analysis based on microarray data. Moreover, we are particularly interested how expression divergence is correlated with sequence divergence as well as related phenotypes along the phylogeny (Lartillot and Poujol 2011).