Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Oct 1.
Published in final edited form as: J Biomech. 2012 Jun 8;45(11):1934–1940. doi: 10.1016/j.jbiomech.2012.05.022

Initiation and progression of mechanical damage in the intervertebral disc under cyclic loading using continuum damage mechanics methodology: A finite element study

Muhammad Qasim a, Raghu N Natarajan a,b,*, Howard S An a, Gunnar BJ Andersson a
PMCID: PMC3787695  NIHMSID: NIHMS379913  PMID: 22682891

Abstract

It is difficult to study the breakdown of disc tissue over several years of exposure to bending and lifting by experimental methods. There is also no finite element model that elucidates the failure mechanism due to repetitive loading of the lumbar motion segment. The aim of this study was to refine an already validated poro-elastic finite element model of lumbar motion segment to investigate the initiation and progression of mechanical damage in the disc under simple and complex cyclic loading conditions. Continuum damage mechanics methodology was incorporated into the finite element model to track the damage accumulation in the annulus in response to the repetitive loading. The analyses showed that the damage initiated at the posterior inner annulus adjacent to the endplates and propagated outwards towards its periphery under all loading conditions simulated. The damage accumulated preferentially in the posterior region of the annulus. The analyses also showed that the disc failure is unlikely to happen with repetitive bending in the absence of compressive load. Compressive cyclic loading with low peak load magnitude also did not create the failure of the disc. The finite element model results were consistent with the experimental and clinical observations in terms of the region of failure, magnitude of applied loads and the number of load cycles survived.

Keywords: Lumbar spine, Disc degeneration, Fatigue failure, Finite element modeling, Continuum damage mechanics

1. Introduction

Low back pain is a major health condition affecting every population worldwide (Andersson, 1999). It can lead to decreased quality of life, diminished physical activity and psychological distress (Deyo and Tsui-Wu, 1987; Deyo et al., 2011). Intervertebral disc degeneration is associated with low back pain (Cheung et al., 2009; Luoma et al., 2000; Samartzis et al., 2011; Savage et al., 1997). Appearance of annular lesions has been suggested (Osti et al., 1992; Sharma et al., 2009a, 2009b; Vernon-Roberts et al., 2007a, b) as the first sign of the disc degeneration process. Epidemiological studies have identified frequent bending and lifting as a major risk for disc prolapse (Kelsey et al., 1984; KUMAR, 1990). Damage to disc structure has been reported in response to cyclic loading of the motion segment by a number of studies involving human cadavers and animal models (Adams and Hutton, 1983; Adams and Hutton, 1985; Adams et al., 2000; Goel et al., 1988a, b; Hansson et al., 1987; Liu et al., 1983; Liu et al., 1985; Yoganandan et al., 1994). Yu et al. (2003) reported presence of irregular fibres, buckling and bleeding in the porcine annulus in response to compressive cyclic loading. Gordon et al. (1991) reported disc herniation in 14 cadaveric lumbar motion segments, subjected to combination of flexion, axial rotation and compression for an average duration of 36,750 cycles. Liu et al. (1983) subjected cadaveric lumbar motion segments to cyclic axial loads ranging from 37%–80% of their failure load limit for up to 10,000 cycles. Disc injury was reported in 2 of 11 specimens while all the specimens experienced endplate or vertebral bone cracking. Parkinson and Callaghan (2009) conducted a series of in-vitro fatigue testing on porcine motion segments to understand the failure mechanism. They concluded that cyclic flexion/extension bending results in the failure of the disc while large cyclic compressive loading fractures the vertebral body. Average numbers of load cycles for disc injury were reported to be 9000 as compared to 930 for vertebral bone fracture. Marshall and McGill (2010) showed that cyclic flexion/extension bending of porcine motion segments caused nucleus tracking through the posterior annulus, while cyclic axial rotation resulted in the radial delamination of the annulus. In case of the human cadaver studies, it is difficult to obtain a large number of specimens without disc degeneration or pre-existing annular disruptions. With current imaging techniques it is not possible to identify the location and extent of damage during different stages of testing without interruptions. It is difficult if not impossible to apply complex loadings that are representative of daily life activities in the cadaver testing setup. These limitations make it hard to track the initiation and progression of structural damage in the intervertebral disc under complex loading conditions in the experimental setup.

Finite element (FE) modelling has been used extensively to explore the spine biomechanics. However most of the FE models of the spine are employed to elucidate the spine kinematics under single load cycle (Goel et al., 1995; Argoubi and Shirazi-Adl, 1996; Rohlmann et al., 2006; Little et al., 2007; Schmidt et al., 2007; Galbusera et al., 2011). Damage to disc structure had been studied using FE models but there is no FE study for lumbar spine that investigates the degradation of the disc due to cyclic loading to the best of the authors' knowledge (Shirazi-Adl, 1989; Natarajan et al., 1994; Schimdt et al., 2009). Initiation and progression of structural damage can be tracked in a motion segment by employing user written codes in conjunction with the FE model. The purpose of this study was to employ continuum damage mechanics methodology to predict damage initiation and progression in the disc under cyclic loading using a poro-elastic FE model of a lumbar motion segment. The current analysis was restricted to the damage analyses in the annulus only. The FE model considered annulus as a single continuum body reinforced by collagen fibres instead of multilayered structure. It was hypothesised that the (a) number of load cycles to disc failure will decrease as the motion segment is subjected to complex loading rather than uni-axial compressive loading and (b) damage will initiate and progress preferentially in the posterior region of the disc under all loading conditions.

2. Materials and method

2.1. 3D poro-elastic finite element model of L4/L5 lumbar motion segment

A previously validated (Natarajan et al., 2006; Natarajan et al., 2008; Williams et al., 2007; Tyrrell et al., 1985) three dimensional non-linear poro-elastic FE model of a healthy lumbar L4–L5 motion segment was modified for the current study. It included parameters such as porosity, osmotic pressure and the strain dependent permeability. Element and material model information for the FE model are listed in the Table 1 and detailed information is included in the appendix. FE analyses were carried out using a commercially available software package ADINA (ADINA R&D Inc., Watertown, Massachussetts).

Table 1.

Element and material model information for L4L5 finite element model. (Ebara et al., 1996; Elliott and Setton, 2001; Goel et al., 1988; Gu et al., 1999; Koeller et al., 1986; Panjabi et al., 1984; Sanjeevi et al., 1982; Sharma et al., 1995).

Structure Drained elastic modulus Poisson's ratio Type of element No. of elements Material model
Cortical bone 12 GPa 0.30 3-D Solid (8 node) 1759 Linear elastic
Cancellous bone 100 MPa 0.20 3-D Solid (8 node) 3112 Linear elastic
Posterior elements 3.5 GPa 0.25 3-D Solid (8 node) 2112 Linear elastic
Endplate 20 MPa 0.40 3-D Solid (8 node) 264 Linear elastic
Nucleus 1.0 MPa 0.40 3-D Solid (8 node) 720 Linear elastic
Annulus 4.2 MPa 0.10 3-D Solid (8 node) 1920 Linear elastic
Annular fibres – – Rebar Elements 1760 Non-linear elastic
Ligaments – – Truss 32 Non-linear elastic
Facet cartilage 11 MPa 0.4 3-D Solid (8 node) 192 Linear elastic
Facet contacts – – Contact 24 –
Open in a new tab

2.2. Continuum damage mechanics

Kachanov (1999) introduced a concept of damage being continuously distributed throughout the solid and proposed a damage variable as an internal state variable describing the state of degradation of the material. A computational methodology (Verdonschot and Huiskes, 1997) for the prediction of degradation of materials under cyclic loading based on Kachanov's concept was employed in the current study to investigate the failure progression in the annulus. Continuum damage mechanics formulation along with the FE modelling was employed to simulate the fatigue behaviour of the human cortical bone (Taylor et al., 1999a, b). Jeffers et al. (2007) and Lennon et al. (2007) also used it to investigate the cement mantle failure and loosening of femoral components in total hip arthroplasty respectively.

2.3. Application of continuum damage methodology to lumbar spine FE model

In the FE model, annulus was divided into 1920 elements. Element properties were calculated at eight integration points distributed within the element. At the beginning of the analysis each integration point in the elements representing annulus was assigned a value of zero for the damage variable d representing its healthy state (Fig. 1). The loading was applied to the FE model in incremental steps. At the maximum load step, principal tensile stress was calculated at each integration point in the annulus elements. The number of load cycles to failure (N) was calculated at each integration point in the annulus using a Stress–Failure (S–N) curve. The lowest number of cycles to failure (Nmin) corresponded to the integration point with the highest tensile stress value. Damage d at each integration point was incremented as

Fig. 1.

Fig. 1

Open in a new tab

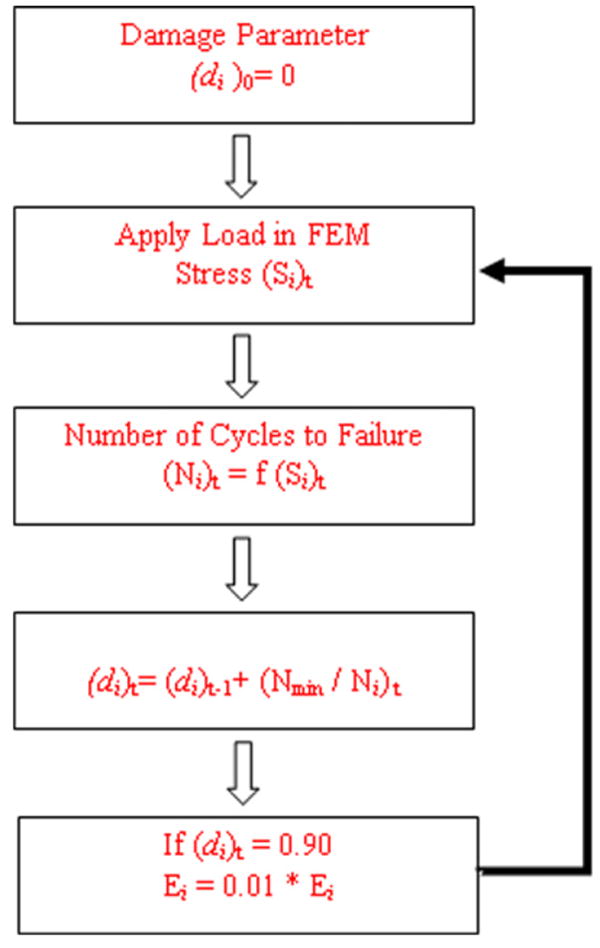
Numerical algorithm based on continuum damage mechanics methodology incorporated into finite element model to investigate the initiation and progression of structural damage in the annulus.

(di)t=(di)t−1+(Nmin/Ni)t

where i represents the integration point and t represent the iteration number.

When damage d for an integration point reached a predefined limit, the corresponding integration point in the element was assumed unable to share any load. The elastic modulus at the damaged integration points was reduced to a predetermined value thus introducing the degradation of the material at that location in the annulus. Even though the damage to the tissue occur only in the direction of tensile principal stress, the algorithm assumes damage equally occurs in all the three principal directions at each integrating point within an element. The number of load cycles required to cause the given damage in the annulus was equal to Nmin.. The stiffness matrix was then updated. The same loading was again applied to the motion segment and damage was incremented for each integration point following the above procedure. The damage initiation and progression was tracked by recording the damaged integration points. The procedure was implemented by introducing a FORTRAN code in the ADINA subroutine (“User Supplied Material”) that allowed changing elastic modulus at each integration point of the annulus.

2.4. Stress–failure (S–N) curve for annulus

The S–N curve for the annulus was developed by using the data from a cyclic cadaver study carried out by Green et al. (1993). They tested 22 annulus slices from the anterior and posterior regions of the lumbar discs (age range 19–71 years) under different magnitudes of tensile stress for up to 10,000 cycles. In situ tensile strength of the annulus was then estimated based on the size of the specimens. The numbers of cycles to failure at different magnitudes of stress for individual specimens were plotted. A curve fit based on the power–law represents the S–N curve for the annulus (Fig. 2). The logic behind using power–law model rather than a linear model as reported for other biological tissues (Schechtman and Bader, 1997; Wang et al., 1995) was to include the effect of endurance limit observed during cyclic testing of annulus fibrosus (Green et al., 1993).

Fig. 2.

Fig. 2

Open in a new tab

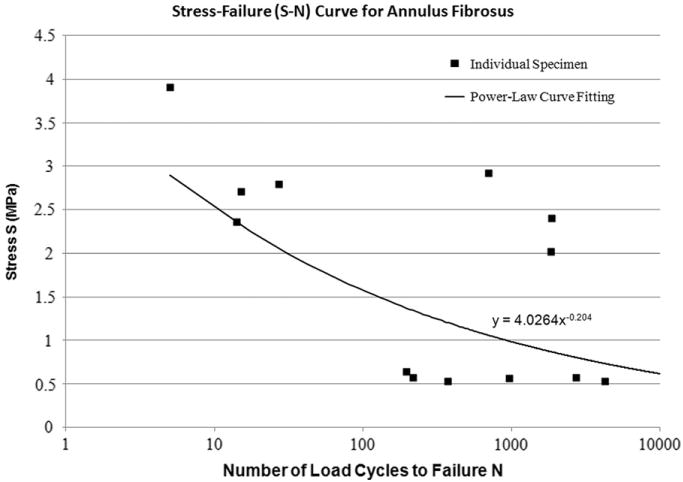
Stress–Failure (S–N) curve for annulus fibrosus. Annulus specimens from different discs were cyclically loaded in tension for up to 10,000 cycles by Green et al. (1993). Stress level and the numbers of load cycles to failure are plotted for each specimen. A trend line based on power function represents the fatigue behaviour of the annulus ground material.

2.5. Effect of magnitudes of elastic modulus and damage parameter at damaged integrating points on the damage progression

Analyses were carried out to investigate the effect of elastic modulus and damage parameter value at the damaged integration points on the damage accumulation in the annulus. For this the motion segment was subjected to a compressive cyclic loading with a peak load of 800 N. Analyses were conducted by reducing the elastic modulus at the damaged integration points to one tenth, one hundredth and one thousandth of its original value at three different values of damage parameter (0.99, 0.90, and 0.80). In total nine simulations were performed; three different values of damage parameter paired with three different values of elastic modulus at damaged integration points.

A much faster failure progression was observed when the elastic modulus was reduced to one hundredth than if it was reduced to one tenth of its original value (Fig. 3). However damage progression rate did not change appreciably when elastic modulus was reduced to one thousandth rather than one hundredth of its original value (Fig. 3). Thus the magnitude of the elastic modulus at the damaged integration point had a considerable effect on the rate of damage accumulation.

Fig. 3.

Fig. 3

Open in a new tab

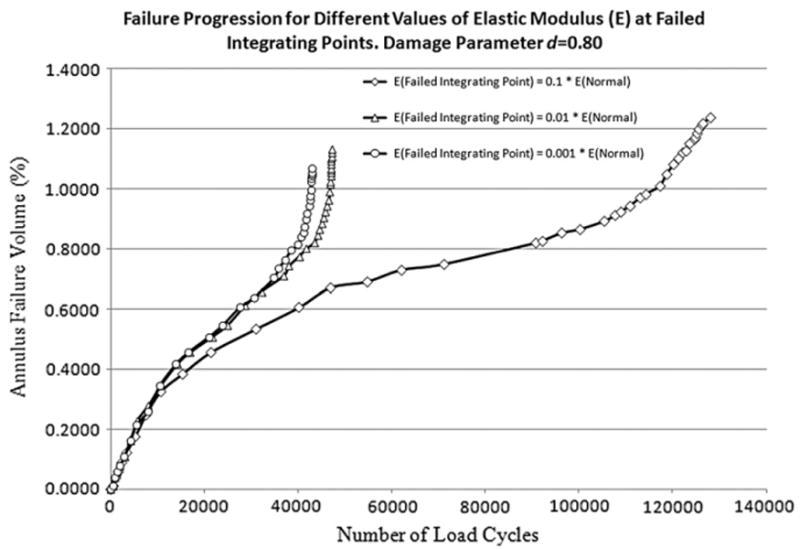
Failure progression for different values of elastic modulus for failed integrating point. Elastic modulus of failed integrating points was reduced by one tenth, one hundredth and one thousandth of its normal value.

The damage accumulation was faster with a decreasing value of d and became slower with an increasing value of d (Fig. 4). However, the difference between the three cases was not appreciable. Thus the damage parameter value at which the integration point was considered degraded did not have a considerable effect on the damage progression rate.

Fig. 4.

Fig. 4

Open in a new tab

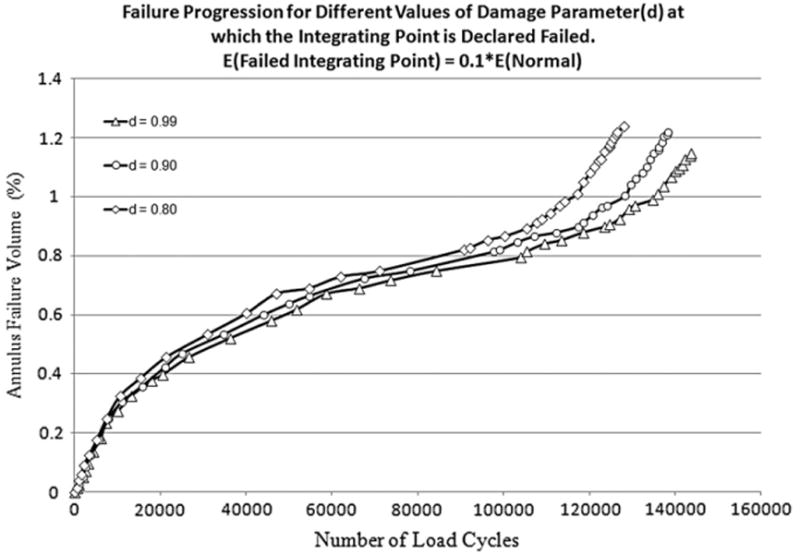
Failure progression for different values of damage parameter d at which integrating point is declared failed. A value of zero for d represents the normal state of the annulus with no damage. Analyses was carried out for three values of d i.e. 0.80, 0.90, 0.99.

Same conclusions were reached from all the nine combinations. Based on the above findings it was decided to reduce the elastic modulus of the integration point to one hundredth of its original value, if its damage parameter reached a value of 0.90 for subsequent analyses.

2.6. Validation of the FE model incorporated with damage accumulation formulation

The FE model incorporated with the continuum damage mechanics methodology was validated by comparing the results with the human cadaver study carried out by Gordon et al. (1991). They studied the disc rupture mechanism using 14 human lumbar motion segments (age range 18–65 years) under complex cyclic loading. 12 motion segments were from L1L2, L3L4 and L4L5 levels with four specimens at each level and two specimens were from L2L3 level. Testing was carried out under displacement control. Motion segments were subjected to 7° flexion, 0.93±0.56 mm compression and 1.9±0.6° axial rotation simultaneously. The testing was stopped when a sharp decrease in the forces was observed and the motion segment was considered failed at that load cycle. They reported mean failure cycles of 36,750 with a standard deviation of 12,612. Ten discs showed annular protrusion and four showed nuclear extrusion in the posterior region. Annular tears were found in all specimens in the posterolateral region. The current FE model was subjected to 7.16° flexion accompanied by 1.09 mm axial compression and 1.67° axial rotation simultaneously in order to compare the results with the in vitro study.

2.7. Loading conditions

In order to investigate the effect of different modes of loading on damage accumulation in a lumbar disc, simple and complex loadings were applied to the motion segment. Simple loading conditions involve the application of either the axial compressive load or the bending moments in one of the three principal directions (Table 2, Load cases 1–5). Complex loading scenarios were simulated by the application of the bending moments in single or multiple directions along with the compressive load (Load cases 6–10). Compressive load was simulated by applying a uniform pressure on the top of the superior endplate. Bending moments were simulated by applying equal and opposite forces at appropriate points on the top surface of L4 vertebra.

Table 2.

Failure initiation and progression was analysed under simple and complex loading modes. Loading conditions consisted of different combinations of bending moments and axial compressive load.

Load case Peak compressive load Peak bending moment (6 Nm)
400 N 800 N Flexion Torsion Lateral bending
1 x
2 x
3 x
4 x
5 x
6 x x
7 x x
8 x x
9 x x x
10 x x x x
Open in a new tab

3. Results

The FE model subjected to the loading conditions similar to the in vitro study predicted that the motion segment will require 31,855 cycles to fail for the given loading. The FE model identified damage initiation and progression in the posterior region of the annulus. The current FE study results thus matched well with the cadaver study observations in terms of number of load cycles to failure and location of damage accumulation (Gordon et al., 1991).

Damage accumulation in the annulus with increasing number of load cycles was plotted under different simple and complex loading conditions (Fig. 5). The damaged annulus volume increased almost linearly with increasing number of load cycles until the point of failure under all loading modes. At the failure point an exponential increase in the damaged annulus volume was observed against a very small increase in the number of load cycles. The number of load cycles to failure decreased as the motion segment was subjected to bending moments in addition to the compressive load. The failure load cycle was identified by sharp increase in failure volume against a very small increase in number of load cycles.

Fig. 5.

Fig. 5

Open in a new tab

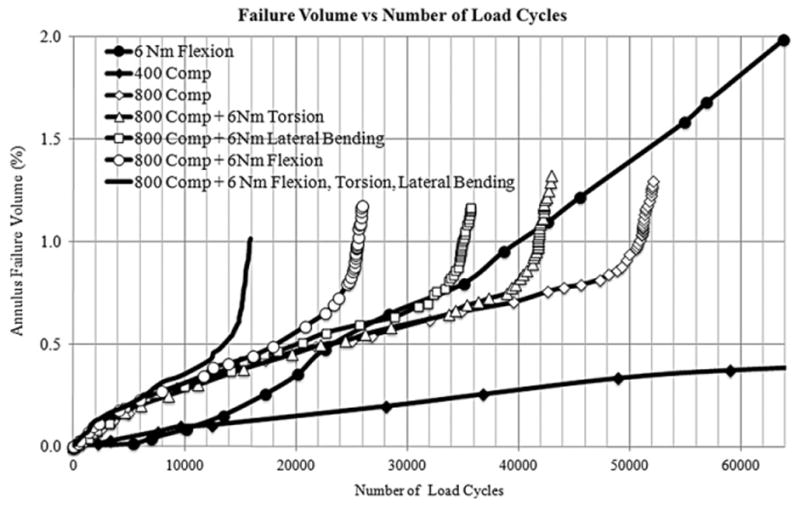
Damage accumulation in the annulus fibrosus under different loading conditions. Failure cycle is identified by sharp increase in the failure volume against a small increment in the number of load cycles.

Application of 6 Nm moments in the three principal directions without any compressive load (Load cases 3–5) did not create the failure of the disc, regardless of the number of applied load cycles. Similarly, cyclic compressive loading with a peak load of 400 N (Load case 1) did not fail the disc. The FE model predicted the failure of the disc in 50,798 load cycles under cyclic compressive loading with a peak load of 800 N (Load case 2). Introduction of 6 Nm moments in the three principal directions in concert with the cyclic compressive load (Load cases 6–8) decreased the number of load cycles to failure by 50%(flexion), 32%(lateral bending) and 18%(axial rotation) as compared to the uni-axial cyclic compressive loading (Load case 2). Application of 6 Nm moments in flexion, lateral bending and axial rotation simultaneously along with the compressive cyclic load (Load case 10), reduced the number of load cycles to failure by 71% as compared to the cyclic compressive loading (Load case 2).

FE model predicted the initiation of damage at the posterior region of the inner annulus next to the inferior endplate and progressed towards outer periphery under all loading conditions considered (Fig. 6). Damage was also identified at the mid disc height in the posterior annulus which did not propagate beyond few inner annulus layers. Introduction of bending moments caused the damage to progress preferentially in the posteriolateral region of the annulus.

Fig. 6.

Fig. 6

Open in a new tab

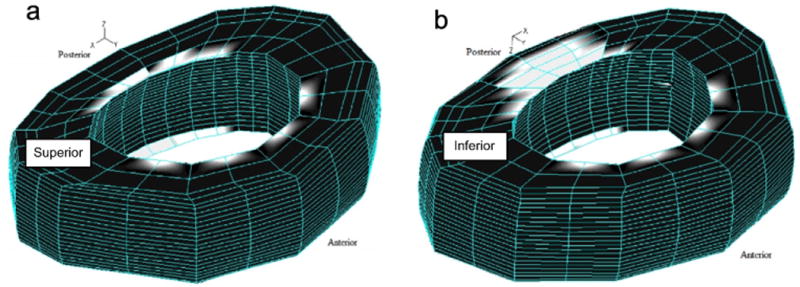
Damage accumulated in the annulus up to the failure cycle under cyclic compressive loading with a peak load of 800 N. White colour shows the volume of the annulus that has degraded while black colour represents the normal annulus.

Even though the failure of annular fibres based on maximum strain value (for assumed fibre failure strain of 15%) was also included in the analyses (Shirazi-Adl et al., 1986), no fibre damage was observed in any of the simulations.

4. Discussion

A poro-elastic FE model of L4/L5 lumbar motion segment incorporated with continuum damage mechanics methodology was presented that predicted structural damage in the disc under cyclic loading. Results of the validation study were consistent with the experimental observations in terms of the region of failure, magnitude of applied loads and the number of load cycles. In vitro and in vivo human studies have reported occurrence of radial fissures in the posterior annulus (Haefeli et al., 2006; Osti et al., 1992; Sharma et al., 2009a, 2009b; Vernon-Roberts et al., 2007a, b). Cyclic testing of porcine discs also reported failure in the posterior annulus (Marshall and McGill, 2010;Callaghan and McGill,2001). Thus damage accumulation in the posterior annulus as predicted by the current FE model matched well with clinical and experimental observations. The numbers of load cycles to failure predicted for complex loading modes were considerably smaller than those for uni-axial loading supporting the first hypothesis. Damage initiated and progressed preferentially in the posterior annulus under all loading conditions simulated in this study validating the other hypothesis.

Goel et al. (1988) subjected 11 cadaveric human lumbar spines T12-S1 to 3Nm flexion moment for up to 9600 cycles. They reported structural failure in none of the discs, which is consistent with the results from the current study. The FE model results showed that the repetitive bending without compressive load and cyclic compressive loading with low peak load magnitude did not create a failure in the disc irrespective of the number of load cycles. These findings compare well with the results presented by Callaghan and McGill (2001) who observed just an initiation of a fissure in the posterior region in only 1 out of 5 discs subjected to low compressive load. Marshall and McGill (2010) reported increased annulus damage in porcine discs subjected to combination of axial rotation and flexion/extension than those tested under flexion/extension alone. This result supports the less number of load cycles to failure predicted under complex loading modes than single axis bending in the current study.

One of the major limitations of the algorithm used here is that even though the damage to the tissue occurs only in the direction of tensile principal stress, the algorithm assumes damage equally occurs in all the three principal directions at each integrating point within an element. The current analyses also did not take into account the changes in the viscoelastic characteristics of the annulus due to the fluid flowing in an out of the disc with increasing number of load cycles which is another major limitation of the analyses. Instead, the damage accumulation methodology was employed as it enabled the simulation of large number of load cycles without having to run every load cycle, thus dramatically reducing the computational expense. Further, the change in permeability resulting from instantaneous disc volume change due to loading was approximated by the change in axial strain in the tissue rather than change in void ratio in the tissue. It should also be noted that the modulus values assumed for facet cartilage and AF matrix in the current analyses were based on tensile tests and much smaller values should be considered in compression.

Damage accumulation was designed as a linear process which is a fair assumption in absence of any experimentally derived data on damage propagation in the annulus. The analyses further assumed no rest periods between the loading cycles as well as the tissue healing process. Shearing between the annulus layers has been suggested to cause the delamination of the annulus layers (Iatridis and ap Gwynn, 2004; Marshall and McGill, 2010; Schmidt et al., 2009). However, lack of stress–failure curve based on shear stress made it impossible to include the damage mechanism due to shearing.

Supplementary Material

1

Acknowledgments

NIH AR48152-02.

Footnotes

Conflict of interest statement: None of the authors has any conflict of interest to report.

Appendix A. Supplementary material: Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jbiomech. 2012.05.022.

References

  1. Adams MA, Freeman BJ, Morrison HP, Nelson IW, Dolan P. Mechanical initiation of intervertebral disc degeneration. Spine. 2000;25:1625–1636. doi: 10.1097/00007632-200007010-00005. [DOI] [PubMed] [Google Scholar]
  2. Adams MA, Hutton WC. Gradual disc prolapse. Spine. 1985;10:524–531. doi: 10.1097/00007632-198507000-00006. [DOI] [PubMed] [Google Scholar]
  3. Adams MA, Hutton WC. The effect of fatigue on the lumbar intervertebral disc. The journal of bone and joint surgery. British Volume. 1983;65:199–203. doi: 10.1302/0301-620X.65B2.6826631. [DOI] [PubMed] [Google Scholar]
  4. ADINA Commercial Software. Version 8.4 Watertown, Massachussetts. ADINA R&D Inc.; Watertown, Massachussetts: [Google Scholar]
  5. Andersson GB. Epidemiological features of chronic low-back pain. Lancet. 1999;354:581–585. doi: 10.1016/S0140-6736(99)01312-4. [DOI] [PubMed] [Google Scholar]
  6. Argoubi M, Shirazi-Adl A. Poroelastic creep response analysis of a lumbar motion segment in compression. Journal of Biomechanics. 1996;29:1331–1339. doi: 10.1016/0021-9290(96)00035-8. [DOI] [PubMed] [Google Scholar]
  7. Callaghan JP, McGill SM. Intervertebral disc herniation: studies on a porcine model exposed to highly repetitive flexion/extension motion with compressive force. Clinical Biomechanics (Bristol, Avon) 2001;16:28–37. doi: 10.1016/s0268-0033(00)00063-2. [DOI] [PubMed] [Google Scholar]
  8. Cheung KM, Karppinen J, Chan D, Ho DW, Song YQ, Sham P, Cheah KS, Leong JC, Luk KD. Prevalence and pattern of lumbar magnetic resonance imaging changes in a population study of one thousand forty-three individuals. Spine. 2009;34:934–940. doi: 10.1097/BRS.0b013e3181a01b3f. [DOI] [PubMed] [Google Scholar]
  9. Deyo RA, Mirza SK, Martin BI. Error in trends, major medical complications, and charges associated with surgery for lumbar spinal stenosis in older adults. JAMA: The Journal of the American Medical Association. 2011;306:1088. doi: 10.1001/jama.2011.1300. [DOI] [PubMed] [Google Scholar]
  10. Deyo RA, Tsui-Wu YJ. Descriptive epidemiology of low-back pain and its related medical care in the United States. Spine. 1987;12:264–268. doi: 10.1097/00007632-198704000-00013. [DOI] [PubMed] [Google Scholar]
  11. Ebara S, Iatridis JC, Setton LA, Foster RJ, Mow VC, Weidenbaum M. Tensile properties of nondegenerate human lumbar anulus fibrosus. Spine. 1996;21:452–461. doi: 10.1097/00007632-199602150-00009. [DOI] [PubMed] [Google Scholar]
  12. Elliott DM, Setton LA. Anisotropic and inhomogeneous tensile behavior of the human anulus fibrosus: experimental measurement and material model predictions. Journal of Biomechanical Engineering. 2001;123:256–263. doi: 10.1115/1.1374202. [DOI] [PubMed] [Google Scholar]
  13. Galbusera F, Schmidt H, Neidlinger-Wilke C, Gottschalk A, Wilke HJ. The mechanical response of the lumbar spine to different combinations of disc degenerative changes investigated using randomized poroelastic finite element models. European Spine Journal: Official Publication of the European Spine Society, the European Spinal Deformity Society, and the European Section of the Cervical Spine Research Society. 2011;20:563–571. doi: 10.1007/s00586-010-1586-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Goel VK, Kim YE, Lim TH, Weinstein JN. An analytical investigation of the mechanics of spinal instrumentation. Spine. 1988a;13:1003–1011. doi: 10.1097/00007632-198809000-00007. [DOI] [PubMed] [Google Scholar]
  15. Goel VK, Voo LM, Weinstein JN, Liu YK, Okuma T, Njus GO. Response of the ligamentous lumbar spine to cyclic bending loads. Spine. 1988b;13:294–300. doi: 10.1097/00007632-198803000-00012. [DOI] [PubMed] [Google Scholar]
  16. Goel VK, Monroe BT, Gilbertson LG, Brinckmann P. Interlaminar shear stresses and laminae separation in a disc. Finite element analysis of the L3-L4 motion segment subjected to axial compressive loads. Spine. 1995;20:689–698. [PubMed] [Google Scholar]
  17. Gordon SJ, Yang KH, Mayer PJ, Mace AH, Jr, Kish VL, Radin EL. Mechanism of disc rupture. A preliminary report. Spine. 1991;16:450–456. doi: 10.1097/00007632-199104000-00011. [DOI] [PubMed] [Google Scholar]
  18. Green TP, Adams MA, Dolan P. Tensile properties of the annulus fibrosus II. Ultimate tensile strength and fatigue life. European Spine Journal: Official Publication of the European Spine Society, the European Spinal Deformity Society, and the European Section of the Cervical Spine Research Society. 1993;2:209–214. doi: 10.1007/BF00299448. [DOI] [PubMed] [Google Scholar]
  19. Gu WY, Mao XG, Foster RJ, Weidenbaum M, Mow VC, Rawlins BA. The anisotropic hydraulic permeability of human lumbar anulus fibrosus. Influence of age, degeneration, direction, and water content. Spine. 1999;24:2449–2455. doi: 10.1097/00007632-199912010-00005. [DOI] [PubMed] [Google Scholar]
  20. Haefeli M, Kalberer F, Saegesser D, Nerlich AG, Boos N, Paesold G. The course of macroscopic degeneration in the human lumbar intervertebral disc. Spine. 2006;31:1522–1531. doi: 10.1097/01.brs.0000222032.52336.8e. [DOI] [PubMed] [Google Scholar]
  21. Hansson TH, Keller TS, Spengler DM. Mechanical behavior of the human lumbar spine. II. Fatigue strength during dynamic compressive loading. Journal of Orthopaedic Research: Official Publication of the Orthopaedic Research Society. 1987;5:479–487. doi: 10.1002/jor.1100050403. [DOI] [PubMed] [Google Scholar]
  22. Iatridis JC, ap Gwynn I. Mechanisms for mechanical damage in the intervertebral disc annulus fibrosus. Journal of Biomechanics. 2004;37:1165–1175. doi: 10.1016/j.jbiomech.2003.12.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jeffers JR, Browne M, Lennon AB, Prendergast PJ, Taylor M. Cement mantle fatigue failure in total hip replacement: experimental and computational testing. Journal of Biomechanics. 2007;40:1525–1533. doi: 10.1016/j.jbiomech.2006.07.029. [DOI] [PubMed] [Google Scholar]
  24. Kachanov L. Rupture time under creep conditions. International Journal of Fracture. 1999;97:11–18. [Google Scholar]
  25. Kelsey JL, Githens PB, White AA, 3rd, Holford TR, Walter SD, O'Connor T, Ostfeld AM, Weil U, Southwick WO, Calogero JA. An epidemiologic study of lifting and twisting on the job and risk for acute prolapsed lumbar intervertebral disc. Journal of Orthopaedic Research: Official Publication of the Orthopaedic Research Society. 1984;2:61–66. doi: 10.1002/jor.1100020110. [DOI] [PubMed] [Google Scholar]
  26. Koeller W, Muehlhaus S, Meier W, Hartmann F. Biomechanical properties of human intervertebral discs subjected to axial dynamic compression—influence of age and degeneration. Journal of Biomechanics. 1986;19:807–816. doi: 10.1016/0021-9290(86)90131-4. [DOI] [PubMed] [Google Scholar]
  27. Kumar S. Cumulative load as a risk factor for back pain. Spine. 1990;15:1311. doi: 10.1097/00007632-199012000-00014. [DOI] [PubMed] [Google Scholar]
  28. Lennon AB, Britton JR, MacNiocaill RF, Byrne DP, Kenny PJ, Prendergast PJ. Predicting revision risk for aseptic loosening of femoral components in total hip arthroplasty in individual patients—a finite element study. Journal of Orthopaedic Research: Official Publication of the Orthopaedic Research Society. 2007;25:779–788. doi: 10.1002/jor.20346. [DOI] [PubMed] [Google Scholar]
  29. Little JP, Adam CJ, Evans JH, Pettet GJ, Pearcy MJ. Nonlinear finite element analysis of anular lesions in the L4/5 intervertebral disc. Journal of Biomechanics. 2007;40:2744–2751. doi: 10.1016/j.jbiomech.2007.01.007. [DOI] [PubMed] [Google Scholar]
  30. Liu YK, Goel VK, Dejong A, Njus G, Nishiyama K, Buckwalter J. Torsional fatigue of the lumbar intervertebral joints. Spine. 1985;10:894–900. doi: 10.1097/00007632-198512000-00006. [DOI] [PubMed] [Google Scholar]
  31. Liu YK, Njus G, Buckwalter J, Wakano K. Fatigue response of lumbar intervertebral joints under axial cyclic loading. Spine. 1983;8:857–865. doi: 10.1097/00007632-198311000-00008. [DOI] [PubMed] [Google Scholar]
  32. Luoma K, Riihimaki H, Luukkonen R, Raininko R, Viikari-Juntura E, Lamminen A. Low back pain in relation to lumbar disc degeneration. Spine. 2000;25:487–492. doi: 10.1097/00007632-200002150-00016. [DOI] [PubMed] [Google Scholar]
  33. Marshall LW, McGill SM. The role of axial torque in disc herniation. Clinical Biomechanics (Bristol, Avon) 2010;25:6–9. doi: 10.1016/j.clinbiomech.2009.09.003. [DOI] [PubMed] [Google Scholar]
  34. Natarajan RN, Ke JH, Andersson GB. A model to study the disc degeneration process. Spine. 1994;19:259–265. doi: 10.1097/00007632-199402000-00001. [DOI] [PubMed] [Google Scholar]
  35. Natarajan RN, Lavender SA, An HA, Andersson GB. Biomechanical response of a lumbar intervertebral disc to manual lifting activities: a poroelastic finite element model study. Spine. 2008;33:1958–1965. doi: 10.1097/BRS.0b013e3181822742. [DOI] [PubMed] [Google Scholar]
  36. Natarajan RN, Williams JR, Andersson GB. Modeling changes in intervertebral disc mechanics with degeneration. The Journal of Bone and Joint Surgery. American. 2006;88(2):36–40. doi: 10.2106/JBJS.F.00002. [DOI] [PubMed] [Google Scholar]
  37. Osti OL, Vernon-Roberts B, Moore R, Fraser RD. Annular tears and disc degeneration in the lumbar spine. A post-mortem study of 135 discs. The Journal of Bone and Joint Surgery. British. 1992;74:678–682. doi: 10.1302/0301-620X.74B5.1388173. [DOI] [PubMed] [Google Scholar]
  38. Panjabi MM, Krag MH, Chung TQ. Effects of disc injury on mechanical behavior of the human spine. Spine. 1984;9:707–713. doi: 10.1097/00007632-198410000-00010. [DOI] [PubMed] [Google Scholar]
  39. Parkinson RJ, Callaghan JP. The role of dynamic flexion in spine injury is altered by increasing dynamic load magnitude. Clinical Biomechanics (Bristol, Avon) 2009;24:148–154. doi: 10.1016/j.clinbiomech.2008.11.007. [DOI] [PubMed] [Google Scholar]
  40. Rohlmann A, Zander T, Schmidt H, Wilke HJ, Bergmann G. Analysis of the influence of disc degeneration on the mechanical behaviour of a lumbar motion segment using the finite element method. Journal of Biomechanics. 2006;39:2484–2490. doi: 10.1016/j.jbiomech.2005.07.026. [DOI] [PubMed] [Google Scholar]
  41. Samartzis D, Karppinen J, Mok F, Fong DY, Luk KD, Cheung KM. A population-based study of juvenile disc degeneration and its association with overweight and obesity, low back pain, and diminished functional status. The Journal of Bone and Joint Surgery American. 2011;93:662–670. doi: 10.2106/JBJS.I.01568. [DOI] [PubMed] [Google Scholar]
  42. Sanjeevi R, Somanathan N, Ramaswamy D. A viscoelastic model for collagen fibres. Journal of Biomechanics. 1982;15:181–183. doi: 10.1016/0021-9290(82)90250-0. [DOI] [PubMed] [Google Scholar]
  43. Savage RA, Whitehouse GH, Roberts N. The relationship between the magnetic resonance imaging appearance of the lumbar spine and low back pain, age and occupation in males. European Spine Journal: Official Publication of the European Spine Society, the European Spinal Deformity Society, and the European Section of the Cervical Spine Research Society. 1997;6:106–114. doi: 10.1007/BF01358742. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Schechtman H, Bader DL. In vitro fatigue of human tendons. Journal of Biomechanics. 1997;30:829–835. doi: 10.1016/s0021-9290(97)00033-x. [DOI] [PubMed] [Google Scholar]
  45. Schmidt H, Kettler A, Heuer F, Simon U, Claes L, Wilke HJ. Intradiscal pressure, shear strain, and fiber strain in the intervertebral disc under combined loading. Spine. 2007;32:748. doi: 10.1097/01.brs.0000259059.90430.c2. [DOI] [PubMed] [Google Scholar]
  46. Schmidt H, Heuer F, Wilke HJ. Dependency of disc degeneration on shear and tensile strains between annular fiber layers for complex loads. Medical Engineering and Physics. 2009;31:642–649. doi: 10.1016/j.medengphy.2008.12.004. [DOI] [PubMed] [Google Scholar]
  47. Sharma A, Parsons MS, Pilgram TK. Temporal association of annular tears and nuclear degeneration: lessons from the pediatric population. American Journal of Neuroradiology. 2009a;30:1541–1545. doi: 10.3174/ajnr.A1625. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Sharma A, Pilgram T, Wippold FJ., 2nd Association between annular tears and disk degeneration: a longitudinal study. American Journal of Neuroradiology. 2009b;30:500–506. doi: 10.3174/ajnr.A1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Sharma M, Langrana NA, Rodriguez J. Role of ligaments and facets in lumbar spinal stability. Spine. 1995;20:887–900. doi: 10.1097/00007632-199504150-00003. [DOI] [PubMed] [Google Scholar]
  50. Shirazi-Adl A. Strain in fibers of a lumbar disc. Analysis of the role of lifting in producing disc prolapse. Spine. 1989;14:96–103. doi: 10.1097/00007632-198901000-00019. [DOI] [PubMed] [Google Scholar]
  51. Shirazi-Adl A, Ahmed AM, Shrivastava SC. A finite element study of a lumbar motion segment subjected to pure sagittal plane moments. Journal of Biomechanics. 1986;19(4):331–350. doi: 10.1016/0021-9290(86)90009-6. [DOI] [PubMed] [Google Scholar]
  52. Taylor M, Verdonschot N, Huiskes R, Zioupos P. A combined finite element method and continuum damage mechanics approach to simulate the in vitro fatigue behavior of human cortical bone. Journal of Materials Science. Materials in Medicine. 1999a;10:841–846. doi: 10.1023/a:1008960630142. [DOI] [PubMed] [Google Scholar]
  53. Taylor M, Verdonschot N, Huiskes R, Zioupos P. A combined finite element method and continuum damage mechanics approach to simulate the in vitro fatigue behavior of human cortical bone. Journal of Materials Science. Materials in Medicine. 1999b;10:841–846. doi: 10.1023/a:1008960630142. [DOI] [PubMed] [Google Scholar]
  54. Tyrrell AR, Reilly T, Troup JD. Circadian variation in stature and the effects of spinal loading. Spine. 1985;10:161–164. doi: 10.1097/00007632-198503000-00011. [DOI] [PubMed] [Google Scholar]
  55. Verdonschot N, Huiskes R. The effects of cement-stem debonding in THA on the long-term failure probability of cement. Journal of Biomechanics. 1997;30:795–802. doi: 10.1016/s0021-9290(97)00038-9. [DOI] [PubMed] [Google Scholar]
  56. Vernon-Roberts B, Moore RJ, Fraser RD. The natural history of agerelated disc degeneration: the pathology and sequelae of tears. Spine. 2007a;32:2797–2804. doi: 10.1097/BRS.0b013e31815b64d2. [DOI] [PubMed] [Google Scholar]
  57. Vernon-Roberts B, Moore RJ, Fraser RD. The natural history of agerelated disc degeneration: the pathology and sequelae of tears. Spine. 2007b;32:2797–2804. doi: 10.1097/BRS.0b013e31815b64d2. [DOI] [PubMed] [Google Scholar]
  58. Wang XT, Ker RF, Alexander RM. Fatigue rupture of wallaby tail tendons. The Journal of Experimental Biology. 1995;198:847–852. doi: 10.1242/jeb.198.3.847. [DOI] [PubMed] [Google Scholar]
  59. Williams JR, Natarajan RN, Andersson GB. Inclusion of regional poroelastic material properties better predicts biomechanical behavior of lumbar discs subjected to dynamic loading. Journal of Biomechanics. 2007;40:1981–1987. doi: 10.1016/j.jbiomech.2006.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Yoganandan N, Cusick JF, Pintar FA, Droese K, Reinartz J. Cyclic compression-flexion loading of the human lumbar spine. Spine. 1994;19:784–90. doi: 10.1097/00007632-199404000-00010. discussion 791. [DOI] [PubMed] [Google Scholar]
  61. Yu CY, Tsai KH, Hu WP, Lin RM, Song HW, Chang GL. Geometric and morphological changes of the intervertebral disc under fatigue testing. Clinical Biomechanics (Bristol, Avon) 2003;18:S3–9. doi: 10.1016/s0268-0033(03)00078-0. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS379913-supplement-1.doc (27.5KB, doc)

RESOURCES