Dosimetric Effectiveness of Targeted Radionuclide Therapy Based on a Pharmacokinetic Landscape

Abstract

Assessment of targeted radionuclide therapy (TRT) agent effectiveness based on its pharmacokinetic (PK) properties could provide means to expedited agent development or its rejection. A broad PK model that predicts the relative effectiveness of TRT agents based on the relationship between their normal body (k₁₂, k₂₁) and tumor (k₃₄, k₄₃) PK parameters has been developed. A classic two-compartment open model decoupled from a tumor was used to represent the body. Analytically solved differential equations were used to develop a relationship that predicts TRT effectiveness. Various PK scenarios were created by pairing normal body PK parameters of 38 pharmaceuticals found in the literature with estimated tumor PK parameters. Each PK scenario resulted in a maximum permissible injected activity that limited the whole-body dose to 2 Gy and yielded a maximum delivered tumor dose. The model suggests that a k₃₄:k₄₃ ratio greater than 5 and a k₁₂:k₂₁ ratio less than 1 is effective at delivering doses that ensure sufficient solid tumor control. It was also shown that there is no direct relationship between tumor dose and acid dissociation constant (pK_a), lipophilicity (log P), and fraction unbound (fu), which are important physicochemical properties. This study suggests that although effective TRT may be difficult to achieve for solid tumors, good TRT agents must have extremely desirable normal body PKs in conjunction with very high tumor retention. The developed PK TRT model could serve as a tool to compare the relative dosimetric effectiveness of existing TRT agents and novel TRT agents early in the developmental phase to potentially reject those that possess unfavorable PKs.

Introduction

Targeted radionuclide therapy (TRT) aims to deliver therapeutic doses to a tumor while sparing normal tissues by selective retention of a radionuclide in a tumor.¹ Unlike external radiotherapy, the dosimetric effectiveness of TRT is dependent on a targeting moiety—the molecular constituent that either binds onto or is sequestered by tumor cells.^2–4 To be an effective targeting agent, the moiety must have a propensity for tumors over normal tissues, thus increasing its therapeutic efficacy. The radiochemistry of the moiety determines the therapeutic radionuclide that can be attached, whereas the pharmacokinetics (PKs) within the body influence the dose to critical organs.¹ The PKs of a targeting agent includes not only the biological path that the agent takes throughout the body but also the uptake and clearance characteristics within the tumor. Along with the physical characteristics of the chosen radionuclide, physical half-life, and dose deposition, the synergy between large body clearance and small tumor clearance can effectively deliver tumor radiation doses while preventing normal tissue complications.

TRT has been a mainstay in nuclear medicine departments since the 1950s, with the use of ¹³¹I for ablation after thyroid resection⁵ and treatment of differentiated thyroid cancer.^{6–10 131}I has proven to be efficacious because of the physiological propensity that the thyroid has for iodine. To target other malignancies, biochemical differences between normal tissues and tumors such as antigen expression have been exploited. Aiming to treat hematological malignancies, monoclonal antibodies (mAbs) have been radiolabeled. Two examples of radiolabeled anti-CD20 antibodies with FDA approval that have shown remarkable efficacy in the treatment of non-Hodgkin's lymphoma are ⁹⁰Y-ibritumomab tiuxetan (Zevalin) and ¹³¹I-tositumomab (Bexxar).^11–13 This particular tumor type is very radiosensitive, responding to a dose as low as 2 Gy.¹⁴ To target more radioresistant tumors, analogs of biological molecules that the tumor could not distinguish from biologically derived molecules have been radiolabeled. Uptake of meta-iodobenzylguanidine (mIBG), an arylalkylguanidine norepinephrine analog, has led to successful therapy of neuroectodermally derived tumors in adolescents with ¹³¹I-mIBG.¹⁵ Further, the overexpression of somatostatin receptors in neuroendocrine tumors affords the possibility of peptide receptor radionuclide therapy (PRRT).^{12 90}Y-DOTATOC and ⁹⁰Y-lanreotide are examples of somatostatin receptor analogs, which have shown success in PRRT.^12,16–18

The maximum radiation dose delivered to a tumor is contingent upon limits of normal tissue toxicity. The bone marrow is most often the dose-limiting organ for TRT and restricting its absorbed dose to less than 2 Gy is often the goal.⁷ However, the mode of excretion from the body is also important for some TRT agents whose dose-limiting organ is found within the excretion pathway. Normal tissue toxicity dictates the maximum permissible activity administered to a patient and is a motivation behind PK modeling. Most of the examples of PK models for TRT agents in the literature are for radiolabeled mAbs.^19–23 For example, Odom-Maryon et al. successfully used a three-compartment model to represent the concentration of radiolabeled chimeric anti-CEA antibody within the blood and urine¹⁹ in hopes of avoiding bladder and kidney radiation toxicity. Despite successfully predicting radiation dose to the kidneys and bladder, the model was unable to predict tumor radiation dose. A PK model that is able to relate tumor and normal body PKs to tumor radiation dose is warranted.

Assuming that all other parameters are equal, a simple PK model for TRT could serve as a tool to compare the relative dosimetric effectiveness of existing TRT agents. Such a model would also help to predict the relative effectiveness of potential TRT agents early in the developmental phase and provide a reason to reject potential TRT agents that possess unfavorable PKs. The aims of this study were to develop a PK model for TRT that could be used to predict relative effectiveness and to investigate or determine the most relevant physicochemical properties related to tumor dose.

Materials and Methods

A PK model for TRT

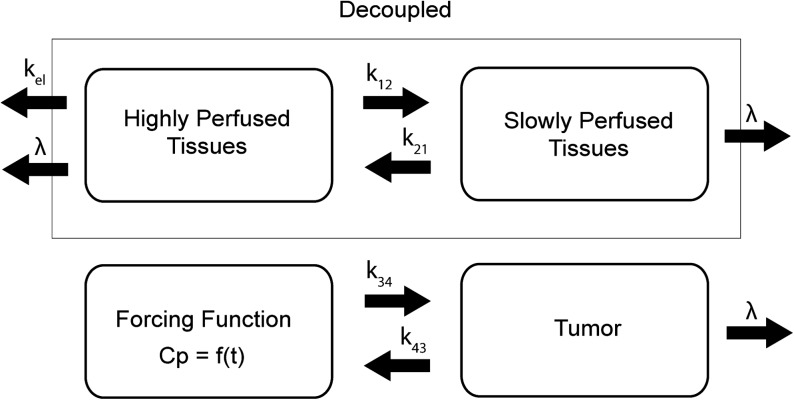
In this work, a classical two-compartment open model assuming bolus intravenous administration and central compartment elimination^24,25 was used, as shown in Figure 1. The tumor compartment within the linear system was assumed not to perturb the two-compartment open model of the body because of its negligible volume compared with the other two body compartments. Therefore, the tumor compartment was decoupled from the normal body compartments. The equations for the change in concentration of radioactivity for both normal body and tumor are given as follows:

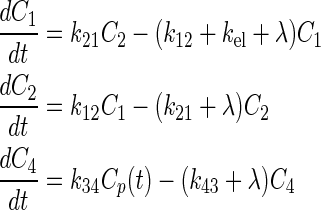(1)

FIG. 1.

A pharmacokinetic model representing the classical two-compartment model of the body, which is decoupled from the tumor compartment. The plasma concentration, Cp, becomes the forcing function for the tumor. The unit for the transfer constants is hour⁻¹. k, intercompartmental rate constant; λ, physical decay constant.

The unit of the intercompartmental rate constants, 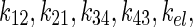and physical decay constant, λ, is hour⁻¹. The solution to each equation, solved via Laplace transforms, represents the time–concentration curve of each compartment that is used to determine radiation dosimetry. The analytical solutions of radioactivity–concentration, C(t), are converted to time–activity, A(t), by incorporating the volume of each compartment and A₀, the initial activity within compartment 1. An analytical PK model was derived for each compartment:

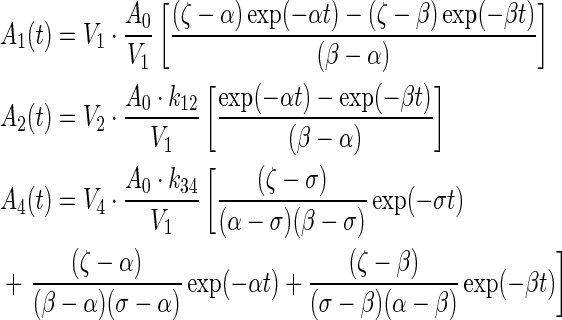(2)

where A₀ = injected activity, ζ = k₂₁ + λ, σ = k₄₃ + λ, γ =k₁₂ + k_el + λ.

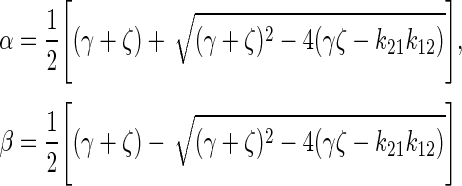(3)

The analytical PK model was adapted into a TRT model by relating whole-body dose threshold, D_thresh, to tumor dose, D_tumor, via specific PK parameters of each compartment. w₁ and w₂ are the proportion of the total body volume of each body compartment, respectively.

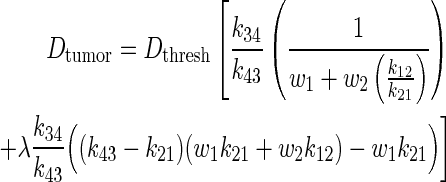(4)

The complete derivation of Eq. (4) is found in the Appendix. The present study model assumes bone marrow to be the dose-limiting organ. Because whole-body dose is a surrogate for bone marrow dose, the whole-body dose threshold, D_thresh, is set according to a bone marrow limit of 2 Gy.⁷ The present study model also assumes homogeneous uptake within each compartment, homogeneous dose deposition, and homogeneous tissue within each compartment. Lastly, each compartment only experiences self-dose, and neighboring dose deposition is neglected.

Relative effectiveness of TRT

Eq. (4) was used to derive a landscape of different PK scenarios that result in maximum doses delivered to a tumor. The ratio of k₃₄:k₄₃ was held constant while the ratio k₁₂:k₂₁ was varied. The maximum delivered tumor dose is dependent on both tumor and normal body PKs. The first two k₃₄:k₄₃ ratios that were investigated were 0.3 and 2.45, which are representative of two common chemotherapy agents, Topotecan and Carboplatin, respectively. Other hypothetical k₃₄:k₄₃ ratios were also investigated, which included 5, 10, 15, and 20. For each PK scenario, the targeting agent was assumed to be radiolabeled with a long-lived β-emitting radionuclide such as ¹³¹I (λ = 0.00361 hour⁻¹) or ⁹⁰Y (λ = 0.0108 hour⁻¹). This physical decay is reflected by λ in Eq. (1). Because the decay constant for most TRT radionuclides is very small, the second part of the Eq. (4) is negligible and the equation becomes

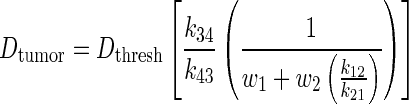(5)

w₁ and w₂ are the proportion of the normal body encompassed by each compartment, respectively. For the analysis, w₁ = 0.2 and w₂ = 0.8 were assigned, which are the assumed body fractions of highly and slowly perfused tissues, respectively. The organs comprising the first compartment—highly perfused tissues—were the heart, lung, hepatoportal system, and endocrine glands. The organs comprising the second compartment—slowly perfused tissues—were the skin, fat, muscle, bone, and bone marrow. The tumor is synonymous with Compartment 4.

PKs landscape of TRT

Data mining of the literature was performed to find human-derived intercompartmental microrate constants (k₁₂, k₂₁, k_elimination) of 38 pharmaceuticals that are commonly used for a wide variety of purposes. These pharmaceuticals are summarized in Table 1. Figure 2A and B demonstrates the magnitude of the k₁₂ and k₂₁ values used, as well as the ratio between the two variables, respectively. These intercompartmental microrate constants were used to construct a pharmaceutical landscape of possible PK parameters within the normal body for theoretical TRT agents. To assess the relative effectiveness of potential TRT agents, the microrate constants (k₃₄, k₄₃) of the tumor were parameterized with respect to each pharmaceutical's respective k₁₂ and k₂₁ values. For example, k₄₃ was varied over 1 order of magnitude, whereas k₃₄ was varied over 2 orders of magnitude.

Table 1.

Pharmacokinetic Parameters

Name	k12	k21	kel	Log P	pKa	fu	References
1. N-Acetylprocainamide	0.983	0.971	0.9	1.29	9.3	0.9	30,a–c
2. Ampicillin	0.4	0.73	1.71	0.4	2.6, 7.2	0.85	30,d–f
3. Benzylpenicillin	0.93	1.44	2.59	1.5	2.74	0.57	e,g,h
4. Carboplatin	0.011	0.018	0.015	−1.8	6.5	1	26, 30,i,j
5. Cefazolin	1.96	2.15	1.3	0.97	2.1	0.18	30,k–m
6. Cephalexin	1.27	2.68	1.62	0.6	4.5	0.85	30,e,k,n
7. Cephapirin	1.09	1.28	4.2	−0.61	2.15	0.55	30,d,e,o
8. Cephradine	2.39	1.73	2.12	−1.58	2.6, 7.4	0.95	30,k,l
9. Cyclophosamide	4.5	2.9	0.29	0.8	9.91	0.87	30,d,e,p
10. Cyclazocine	0.32	0.11	1.41	4.51	9.38	NF	q–s
11. Cytosine arabinoside	5.58	4.5	19.8	−2.46	4.2	0.87	d,r,t,u
12. Diazepam	2.29	0.85	0.225	2.9	3.4	0.023	30,d,e
13. Dicloxacillin	2	2	2.1	3.7	2.6	0.033	30,e,v,w
14. Digoxin	0.85	0.144	0.145	2.2	13.5	0.7	30,d,e,x
15. Doxorubicin	5.1	0.29	0.48	−0.5	8.3	0.28	30,d,e,y
16. Erythromycin	0.52	0.64	0.71	3.06	8.88	0.1	30,e,z
17. 5-Fluorouracil	12	12	10.8	−0.8	8.02	0.64	30,d,e
18. Hydrochlorothiazide	0.184	0.218	0.214	−0.5	7.9, 9.2	NF	e,t,aa
19. 6'-Hydroxycinchonine	8.04	2.22	7.98	2.73	NF	NF	bb,cc
20. Isosorbide dinitrate	4.2	7.2	3.6	0.87	NF	0.72	30,e,dd
21. Leuprolide	1.292	0.679	0.956	0.1	9.6	0.54	30,e,ee,ff
22. Lidocaine	2.46	1.74	1.32	2.1	8.01	0.33	30,e,gg
23. LSD	3.083	4.358	0.407	2.95	7.5	0.2	e,hh–jj
24. Methotrexate	0.0054	0.0448	0.33	−2.2	4.7	0.37	30,e,kk
25. Methyldopa	0.72	1.02	0.84	−1.7	2.2, 9.2, 10.6, 12	0.85	30,d,e,ll
26. Morphine	36	2.7	6	0.8	8.21	0.65	30,d,e
27. Naltrexone	0.0612	0.0996	0.6642	0.7	8.13	0.79	30,e,mm,nn
28. Oxacillin	2.22	3.6	3.42	2.4	2.72	0.07	30,d,e
29. Phosphonomycin	0.91	0.99	0.64	−1.6	8.3	1	30,e,oo,pp
30. Procainamide	3.252	1.398	0.972	1.3	9.32	0.84	30,e,qq
31. Propanolol	5.9	1.3	1.5	3	9	0.13	30,d,e,rr
32. Quinidine	13.56	1.14	12.42	2.6	8.56	0.26	30,e,bb
33. Sulfisoxazole	0.45	0.87	0.195	0.9	5	0.079	30,e,ss
34. Sulpiride	3.5	0.687	0.889	0.6	9.12	0.95	e,tt,uu
35. Theophylline	2.7	3.1	0.31	−0.8	8.81	0.61	30,d,e
36. Topotecan	0.01	0.025	0.022	0.8	7.2	0.65	26, 30,e,vv
37. Tubocurarine	2.34	2.76	1.02	3.12	8.1, 9.1	0.58	30,d,e,ww
38. Warfarin	1.61	1.52	0.033	3	5	0.015	30,d,e,xx

The intercompartmental microrate constants of various pharmaceuticals (unit: hour⁻¹). These are used to simulate a wide range of pharmacokinetic possibilities. The log P (lipophilicity), pK_a (acid dissociation constant), and fu (fraction unbound) are also reported.

NF, not found.

^aKamath BL, Lai CM, Gupta SD, et al. Pharmacokinetics of procainamide and N-acetylprocainamide in rats. J Pharm Sci 1981;70:299.

^beMolecules. N-Acetylprocainamide LogP. Online document at www.emolecules.com/cgi-bin/more?vid=488217 Accessed June 17, 2009.

^cMeyer W, Kaye CM, Turner P. A study of the influence of pH on the buccal absorption and renal excretion of procainamide. Eur J Clin Pharmacol 1974;7:287.

^dAbramson FP. Two-compartment pharmacokinetic models: Computer simulations of their characteristics and clinical consequences. J Pharm Sci 1981;70:141.

^eWishart DS, Knox C, Guo AC, et al. DrugBank: A knowledgebase for drugs, drug actions and drug targets. Nucleic Acids Res 2008;36(Database issue):D901.

^fSjovall J, Alvan G, Westerlund D. Oral cyclacillin interacts with the absorption of oral ampicillin, amoxycillin, and bacampicillin. Eur J Clin Pharmacol 1985;29:495.

^gJusko WJ, Gibaldi M. Effects of change in elimination on varous parameters of the two-compartment open model. J Pharm Sci 1972;61:1270.

^hVisser LG, Arnouts P, van Furth R, et al. Clinical pharmacokinetics of continuous intravenous administration of penicillins. Clin Infect Dis 1993;17:491.

ⁱTetko IV, Jaroszewicz I, Platts JA, et al. Calculation of lipophilicity for Pt(II) complexes: Experimental comparison of several methods. J Inorg Biochem 2008;102:1424.

^jReedijk J. New clues for platinum antitumor chemistry: Kinetically controlled metal binding to DNA. Proc Natl Acad Sci U S A 2003;100:3611.

^kGreene DS, Quintiliani R, Nightingale CH. Physiological perfusion model for cephalosporin antibiotics I: Model selection based on blood drug concentrations. J Pharm Sci 1978;67:191.

^lYang G, Cao W, Zhu T, et al. The QRAR model study of beta-lactam antibiotics by capillary coated with cell membrane. J Chromatogr B Anal Technol Biomed Life Sci 2008;873:1.

^mPharma Professional Services. Online document at www.druginfosys.com/ Accessed June 17, 2009.

ⁿSiarheyeva A, Lopez JJ, Glaubitz C. Localization of multidrug transporter substrates within model membranes. Biochemistry 2006;45:6203.

^oEMoT: Encyclopedia of Molecular Targets. Cambridge, MA: Massachusetts Institute of Technology. Online document at http://emot.mit.edu/ Accessed June 17, 2009.

^pChemical Book. Online document at www.chemicalbook.com/ProductIndex_EN.aspx Accessed June 17, 2009.

^qPeterson JE, Barnick CT, Benziger D, et al. Analysis of cyclazocine in plasma. J Pharm Sci 1979;68:1447.

^rNIAID—Division of AIDS HIV/OI/TB Therapeutics Database. Online document at http://chemdb2.niaid.nih.gov/struct_search/ Accessed June 17, 2009.

^sKaufman JJ, Semo NM, Koski WS. Microelectrometric titration measurement of the pKa's and partition and drug distribution coefficients of narcotics and narcotic antagonists and their pH and temperature dependence. J Med Chem 1975;18:647.

^tDrugs.com. Drug Information Online. Online document at www.drugs.com/ Accessed June 17, 2009.

^uSlevin ML, Johnston A, Woollard RC, et al. Relationship between protein binding and extravascular drug concentrations of a water-soluble drug, cytosine arabinoside. JR Soc Med 1983;76:365.

^vDoluisio JT, LaPiana JC, Dittert LW. Pharmacokinetics of ampicillin trihydrate, sodium ampicillin, and sodium dicloxacillin following intramuscular injection. J Pharm Sci 1971;60:715.

^wSrisom P, Liawruangrath B, Liawruangrath S. Micellar liquid chromatographic determination of penicillins in pharmaceuticals. Chromatographia 2007;65:687.

^xLam TN, Hunt CA. Discovering plausible mechanistic details of hepatic drug interactions. Drug Metab Dispos 2009;37:237.

^yAdams DJ. The impact of tumor physiology on camptothecin-based drug development. Curr Med Chem Anticancer Agents 2005;5:1.

^zWelling PG, Craig WA. Pharmacokinetics of intravenous erythromycin. J Pharm Sci 1978;67:1057.

^aaRedalieu E, Chan KK, Tipnis V, et al. Kinetics of hydrochlorothiazide absorption in humans. J Pharm Sci 1985;74:765.

^bbUeda CT, Nickols JG. Comparative pharmacokinetics of quinidine and its O-desmethyl metabolite in rabbits. J Pharm Sci 1980;69:1400.

^ccMackey ZB, Baca AM, Mallari JP, et al. Discovery of trypanocidal compounds by whole cell HTS of Trypanosoma brucei. Chem Biol Drug Des 2006;67:355.

^ddDoyle E, Chasseaud LF. Pharmacokinetics of isosorbide dinitrate in rhesus monkey, cynomolgus monkey, and baboon. J Pharm Sci 1981;70:1270.

^eeSennello LT, Finley RA, Chu SY, et al. Single-dose pharmacokinetics of leuprolide in humans following intravenous and subcutaneous administration. J Pharm Sci 1986;75:158.

^ffInc. s-aC. ELIGARD^® (Leuprolide acetate for injection). Product Monograph. Online document at www.sanofi-aventis.ca/products/en/eligard.pdf Accessed May 31, 2009.

^ggBloedow DC, Ralston DH, Hargrove JC. Lidocaine pharmacokinetics in pregnant and nonpregnant sheep. J Pharm Sci 1980;69:32.

^hhLevy G, Gibaldi M, Jusko WJ. Multicompartment pharmacokinetic models and pharmacologic effects. J Pharm Sci 1969;58:422.

ⁱⁱHoja H, Marquet P, Verneuil B, et al. Determination of LSD and N-demethyl-LSD in urine by liquid chromatography coupled to electrospray ionization mass spectrometry. J Chromatogr B Biomed Sci Appl 1997;692:329.

^jjBredberg U, Paalzow L. Pharmacokinetics of methylergometrine in the rat: Evidence for enterohepatic recirculation by a linked-rat model. Pharm Res 1990;7:14.

^kkSabot C, Debord J, Roullet B, et al. Comparison of 2- and 3-compartment models for the Bayesian estimation of methotrexate pharmacokinetics. Int J Clin Pharmacol Ther 1995;33:164.

^llJordanian Pharmaceutical Manufacturing Co. PLC. Online document at www.jpm.com.jo/products.aspx?product=DOPANORE Accessed June 17, 2009.

^mmReuning RH, Batra VK, Ludden TM, et al. Plasma naltrexone kinetics after intravenous bolus administration in dogs and monkeys. J Pharm Sci 1979;68:411.

ⁿⁿNarcotic antagonists: Naltrexone pharmacochemistry and sustained-release preparations. NIDA Res Monogr 1981;28:1.

^ooKwan KC, Wadke DA, Foltz EL. Pharmacokinetics of phosphonomycin in Man. I. Intravenous administration. J Pharm Sci. May 1971;60:678.

^ppKrekel F, Samland AK, Macheroux P, et al. Determination of the pKa value of C115 in MurA (UDP-N-acetylglucosamine enolpyruvyltransferase) from Enterobacter cloacae. Biochemistry 17 2000;39:12671.

^qqManion CV, Lalka D, Baer DT, et al. Absorption kinetics of procainamide in humans. J Pharm Sci 1977;66:981.

^rrLiedholm H, Wahlin-Boll E, Melander A. Mechanisms and variations in the food effect on propranolol bioavailability. Eur J Clin Pharmacol 1990;38:469.

^ssKaplan SA, Weinfeld RE, Abruzzo CW, et al. Pharmacokinetic profile of sulfisoxazole following intravenous, intramuscular, and oral administration to man. J Pharm Sci 1972;61:773.

^ttBres J, Bressolle F. Pharmacokinetics of sulpiride in humans after intravenous and intramuscular administrations. J Pharm Sci 1991;80:1119.

^uuNiwa T, Inoue S, Shiraga T, et al. No inhibition of cytochrome P450 activities in human liver microsomes by sulpiride, an antipsychotic drug. Biol Pharm Bull 2005;28:188.

^vvGisvold O, Doerge RF, Wilson CO. Wilson and Gisvold's Textbook of Organic Medicinal and Pharmaceutical Chemistry. 8th Edition. Philadelphia: Lippincott, 1982.

^wwKalow W. The influence of pH on the ionization and biological activity of d-tubocurarine. J Pharmacol Exp Ther 1954;110:433.

^xxCassidy SL, Hale A, Buss DC, et al. In vitro drug adsorption to charcoal, silicas, acrylate copolymer and silicone oil with charcoal and with acrylate copolymer. Hum Exp Toxicol 1997;16:25.

FIG. 2.

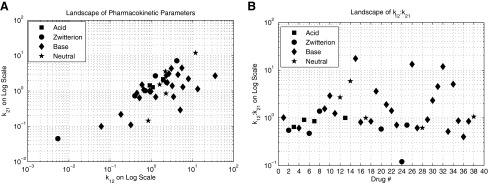
Normal body pharmacokinetics. (A) Landscape and magnitude of k₁₂ and k₂₁ values used in the analysis. (B) Landscape of k₁₂:k₂₁ ratios used in the analysis. Notice that most pharmaceuticals reside between 0 and 2.

To investigate the relationship between physicochemical properties and tumor dose, the tumor PK parameters (k₃₄, k₄₃) were held constant for interpharmaceutical comparison but the normal body parameters (k₂₁, k₁₂) were set according to Table 1. Each pharmaceutical's tumor parameters were fixed to those of Carboplatin (k₃₄ = 1.62, k₄₃ = 0.66)²⁶ because they are well-documented experimental values. The physicochemical properties that were investigated were lipophilicity (log P), acid dissociation constant (pK_a), and fraction unbound (fu).

Results

Relative effectiveness of TRT

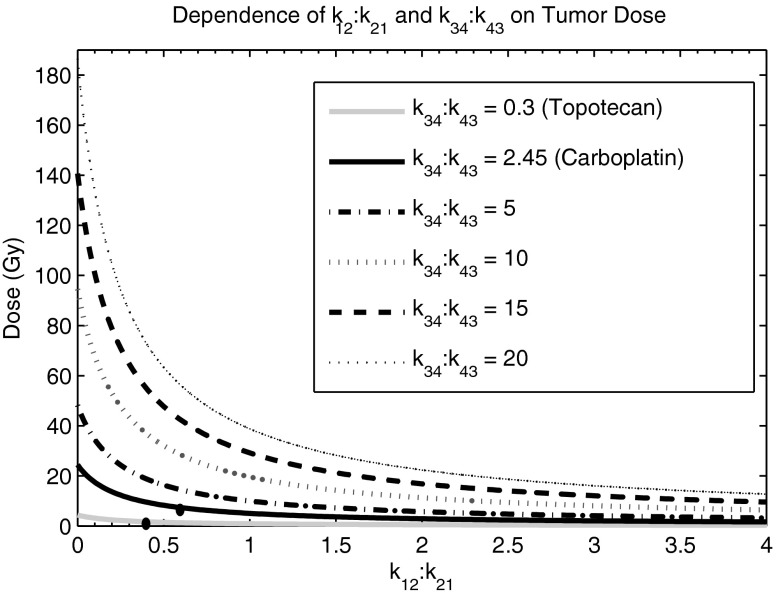
Figure 3 shows the results when the ratio of k₃₄:k₄₃ is held constant and tumor dose is dependent on the k₁₂:k₂₁ ratio. The first two k₃₄:k₄₃ ratios, 0.3 and 2.45, are representative of two common chemotherapy agents, Topotecan and Carboplatin, respectively. As potential TRT agents, it is interesting to notice that neither would be effective at delivering high radiation dose. A TRT agent with a k₃₄:k₄₃ ratio of greater than 5 and a k₁₂:k₂₁ ratio of less than 1 would be effective at delivering high radiation doses to a solid tumor. About half of the pharmaceuticals that were investigated possess a k₁₂:k₂₁ ratio of less than 1, which means that favorable normal body PKs are achievable.

FIG. 3.

Efficacy of targeted radionuclide therapy. The dependence of k₁₂:k₂₁ and k₃₄:k₄₃ on tumor dose. Eq. (5) was used to generate the respective curves. To achieve tumor control, the k₃₄:k₄₃ ratio must be at least 5. The dots on the Topotecan and Carboplatin curves indicate their respective k₁₂:k₂₁ ratios.

PKs landscape of TRT

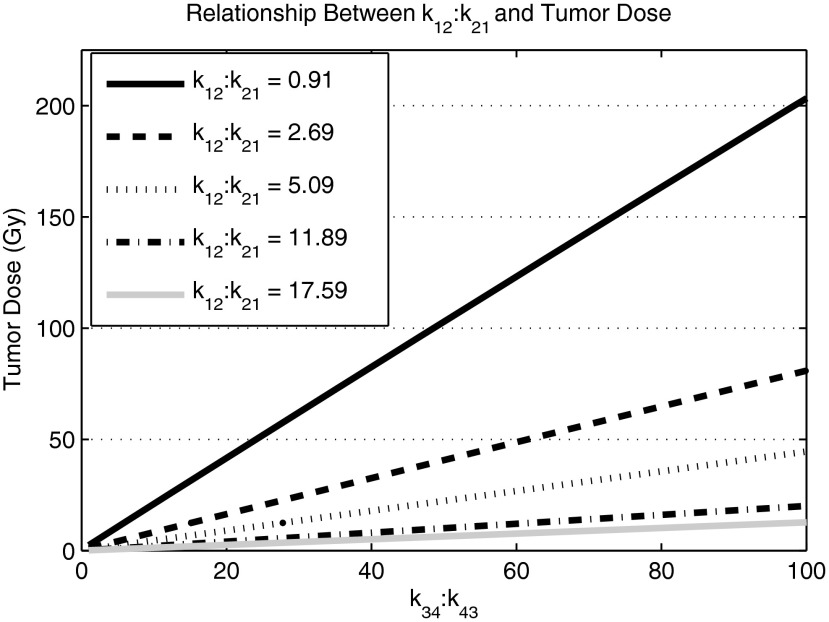
A number of pharmaceuticals that adequately sampled the k₁₂:k₂₁ possibilities of Figure 2B were selected. Examples of tumor doses for varying k₃₄:k₄₃ ratios are shown in Figure 4. The five representative pharmaceuticals that are shown were chosen to show the range of variability within radiopharmaceuticals. Most pharmaceuticals had k₁₂:k₂₁ ratios that were between 0 and 4, which are represented by Cefazolin with a k₁₂:k₂₁ ratio of 0.91 and by Diazepam with a k₁₂:k₂₁ ratio of 2.69. There were three pharmaceuticals between 4 and 6, which are represented by Sulpiride with a k₁₂:k₂₁ of 5.09. The final two k₁₂:k₂₁ values, 11.89 (Quinidine) and 17.59 (Doxorubicin), were selected to show extreme values of k₁₂:k₂₁. The respective slope of each line indicates the sensitivity of each pharmaceutical to a change in k₃₄:k₄₃.

FIG. 4.

Normal body pharmacokinetic and dosimetric efficacy. Each line indicates a different pharmaceutical: cefazolin, k₁₂:k₂₁ = 0.91; diazepam, k₁₂:k₂₁ = 2.69; sulpiride, k₁₂:k₂₁ = 5.09; quinidine, k₁₂:k₂₁ = 11.89; doxorubicin, k₁₂:k₂₁ = 17.59. The slope of each line indicates the sensitivity that each pharmaceutical possesses with respect to k₄₃:k₃₄. The relatively low k₁₂:k₂₁ ratio of cefazonlin, 0.91, is most sensitive to a change in k₄₃:k₃₄ compared with the other pharmaceuticals of interest. Its normal body pharmacokinetics are more conducive to an efficacious targeted radionuclide therapy.

Figure 5 illustrates the results of investigating the correlation of physicochemical properties of a pharmaceutical and tumor dose. Each panel also identifies the possible chemical structures (acid, base, neutral, zwitterions) of a pharmaceutical to assess the possible relationship between structure and tumor dose.

FIG. 5.

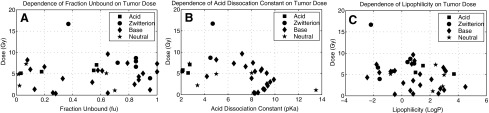
Physicochemical properties and tumor dose. (A) The dependence of fraction unbound (fu) on tumor dose. (B) The dependence of the acid dissociation constant (pK_a) on tumor dose. (C) The dependence of lipophilicity (log P) on tumor dose. The tumor doses in each of these investigations assume the k₃₄:k₄₃ ratio of carboplatin.

Discussion

Based on curves of Figure 3, the k₃₄:k₄₃ ratio must be at least 5 and the k₁₂:k₂₁ ratio needs to be less than 1 to deliver tumor radiation doses (>50 Gy²⁷ is required for local tumor control based on fractionated external radiotherapy) that are high enough to ensure sufficient solid tumor control. It is possible to predict a relative tumor dose using Eq. (4) when both the volumes of the compartments and the PKs of the radiopharmaceutical are known. The difference between the volume-weighted average of Compartment 1, w₁, and Compartment 2, w₂, contributes to tumor dose because it determines the degree of k₁₂:k₂₁ dependence. A large Compartment 2 compared with Compartment 1 amplifies a large k₁₂:k₂₁, which effectively lowers tumor dose according to Eq. (4). Conceptually, Compartment 2 has a greater contribution to total-body dose compared with Compartment 1 because it makes up a larger volume. The differences between w₁ and w₂ within patients will greatly contribute to interpatient variability of TRT. Anatomical imaging, such as afforded by computed tomography (CT), makes it possible to accurately measure a patient's specific volume parameters.

Eq. (4) is used when the half-life of the radionuclide is on the order of hours. When the half-life is on the order of days, λ is negligible, which negates the need for the second part of Eq. (4), resulting in the use of Eq. (5). Most of the clinically useful β-emitting radionuclides such as ⁹⁰Y and ¹³¹I possess half-lives on the order of days.^18,28 This lends itself to the possibility of comparing relative tumor doses of radiopharmaceuticals simply based on their ratios of tumor and normal body PK parameters. In the present study, although the model assumes uniform dose distributions within the decoupled system, it demonstrates the feasibility of simplifying the dosimetry process of TRT into an equation of experimentally derived parameters.

Disregarding the spatial dependencies of the dose scaling factor is a reasonable assumption in most cases because of the limited nature by which one compartment affects another. The only area where one compartment's activity would significantly affect an adjacent compartment is at the border. Because the tumor is so small compared with Compartment 1, which completely encompasses it, its border contribution is negligible compared with the average dose found in Compartment 1. This is the same at the border between Compartment 1 and Compartment 2, because the actual area of the border is negligible compared with the volume of each compartment. In addition, the dose imparted by β-emitters falls off rapidly within the first several millimeters. ¹³¹I, for example, decreases by ∼3.5 orders of magnitude within the first 0.5 cm.²⁹

Qualitatively, as the ratio of k₁₂:k₂₁ increases, the required k₃₄:k₄₃ ratio to reach relatively high tumor doses also increases. This is an intuitive result because an increase in k₁₂ transfers more radiopharmaceutical into Compartment 2, which decreases the availability of the radiopharmaceutical to the tumor because the tumor can only transfer from Compartment 1. To counter this increase, there must be an increase in k₃₄ that competes with k₂₁. Figure 4 is used to predict the therapeutic efficacy of potential TRT agents with known normal body PKs. Each line represents the PK landscape of a particular radiopharmaceutical and the tumor PKs that are necessary for therapeutic efficacy. For normal body PKs similar to Quinidine or Doxorubicin, efficacious TRT is nearly impossible to achieve because of the unfavorable k₁₂:k₂₁ ratios of each pharmaceutical, 11.89 and 17.59, respectively. The relatively low k₁₂:k₂₁ ratio of Cefazonlin, 0.91, is most sensitive to a change in k₄₃:k₃₄ compared with the other pharmaceuticals of interest. Therefore, its normal body PKs is more conducive to an efficacious TRT.

Figure 5A–C shows that tumor dose is not dependent on any individual physicochemical property directly. Interestingly, Obach³⁰ also found no correlation between physicochemical properties that were investigated in this study and PK parameters. PK parameters such as k₁₂, k₂₁, and k_el are directly related to maximum tumor dose but have no direct correlation to fu, pK_a, or log P. It might be true that fraction unbound, acid dissociation constant, and lipophilicity represent only part of the complex pool of variables that affect PKs and thereby tumor dose. In addition, there is no clear relationship between chemical structure and tumor dose.

Scope and limitations

The simplicity of this model does not include the effect of techniques and strategies capable of increasing therapeutic efficacy. For example, there is evidence to suggest that external radiotherapy could influence the vascularity of tumors, thus causing increases in uptake and therapeutic efficacy.³¹ Therapeutic efficacy can also be increased by using catalysts to facilitate tumor uptake³² and radiosensitizers to increase the radiobiological effect of radiation.³³ Myeloablation is often performed prior to TRT³⁴ to increase the whole-body dose beyond the 2 Gy limit. In the present study, the model assumes bone marrow to be the dose-limiting organ because it assumes total-body dose to be a surrogate for bone marrow dose. This is similar to the myeloablative regimens of ¹³¹I-tositumomab and ⁹⁰Y-ibritumomab tiuxetan.^11–13 In contrast, PRRT and mAb therapy are often limited by renal toxicity,¹² which would preclude the use of this model.

Another limitation of this model is that it assumes all tissues to be homogeneous media. Variations in atomic number within the body may influence the distribution of dose delivered by low-energy photons. For example, interfaces between soft tissues, air, and bone have the potential to create inhomogeneous dose distributions. Further, by only considering self-dose within a compartment, cross-dose amongst compartments was neglected, which ultimately reduces the radiation dose absorbed by a compartment. Because of these limitations, the proposed model may not ultimately be relevant for absolute quantification of TRT radiation dosimetry. However, it might be better used as a tool to compare and examine the relative effectiveness of existing and potential TRT agents based on normal body and tumor PKs.

This model suggests that it may be possible to comparatively predict which TRT agents might be better than others. Early measurement of PK parameters of TRT agents may help predict relative effectiveness, which provides means to expedited agent development or rejection. For example, ¹²⁴I-PET/CT is useful for deriving the microrate constants necessary for predicting maximum tumor doses of ¹³¹I-radiolabeled TRT agents. Once a potential TRT agent shows relative effectiveness via the model, three-dimensional dosimetric simulations can be done to further evaluate the effectiveness of the TRT agent. The use of the Zubal phantom³⁵ with dose deposition kernels²⁹ will afford investigations of nonuniform uptake and dose deposition of potential TRT agents. Such a priori information gained from such simulations should provide early insight into the relative effectiveness of TRT agents.

Conclusions

k₁₂ and k₂₁ are global PK parameters that represent the summation of a radiopharmaceutical's physicochemical properties. The data suggest a clear relationship between the ratio of k₁₂ and k₂₁ and tumor radiation dose. A favorable k₁₂:k₂₁ ratio, indicated by a higher k₂₁ in relation to k₁₂, means that there is more radioactivity available in Compartment 1 (Fig. 1), which is available to be transferred into the tumor, determined by k₃₄. In addition, k₁₂ could transfer more activity into Compartment 2 offsetting k₃₄. Therefore, it is the k₁₂:k₂₁ ratio that ultimately contributes to tumor dose. However, k₄₃ transfers the radioactivity out of the tumor, which acts to lower the tumor dose. A favorable k₃₄:k₄₃ ratio—the rate of radioactivity transferred into the tumor is faster than the rate of radioactivity transferred out of the tumor—can be ineffective if the k₁₂:k₂₁ ratio is unfavorable because more radioactivity will be in Compartment 2, which is inaccessible by the tumor.

This study suggests that an efficacious TRT for solid tumors may be difficult to achieve. It is imperative that a good TRT agent has extremely desirable normal body PKs in conjunction with very high tumor retention to achieve the high doses required for local control of solid tumors. Because there are no PK models for TRT agents within the literature that relate normal body and tumor PKs to tumor radiation dose, the scope of this study was to introduce a simple yet comprehensive PK model that would warrant the measurement of compartmental microrate constants of existing and developing TRT agents. By knowing the microrate constants of existing TRT agents, more conclusions might be made about the relationships between PKs and relative effectiveness of TRT. In addition, these PK relationships could suggest criteria for predicting the therapeutic efficacy of potential TRT agents.

Appendix

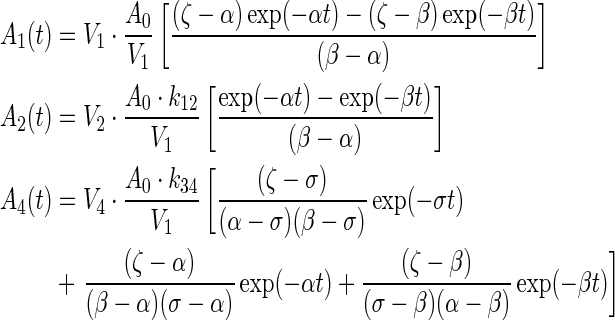(A1)

where A₀ = injected activity, ζ = k₂₁ + λ, σ = k₄₃ + λ, γ =k₁₂ + k_el + λ.

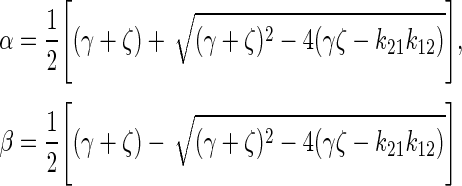A(t) was integrated over all time for each compartment, 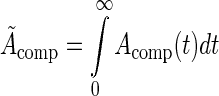, to compute the residence time within each compartment. The residence time equations of each compartment were simplified into analytical solutions:

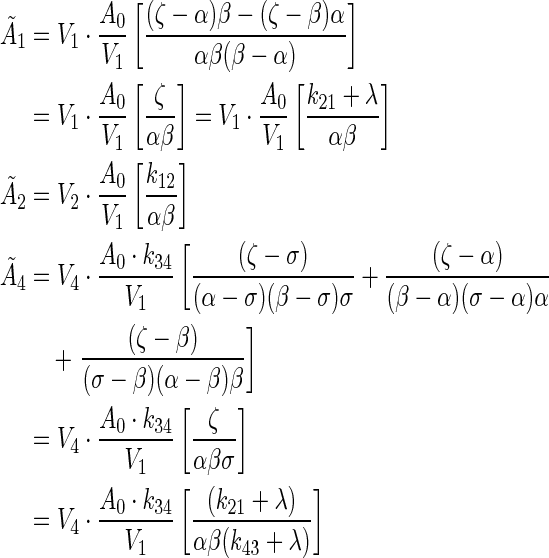(A2)

The average residence time within the normal body was derived using volume-weighted averages according to the two-body compartments:

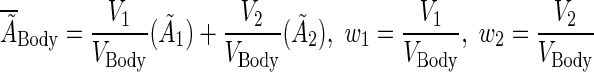(A3)

The average body dose is found by multiplying the body's average residence time by δ, a dose scaling factor that relates residence time to dose:

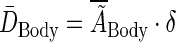(A4)

(A6)

To calculate the maximum permissible activity injected, a whole-body dose threshold can be used, which is a surrogate for bone marrow toxicity:

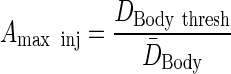(A5)

The maximum permissible activity, tumor residence time, 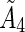, and the linear dose scaling function, δ, are used to create an equation for average tumor dose. The average tumor residence time per unit volume is used.

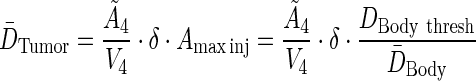(A6)

The expressions for average body dose, 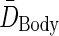, and tumor residence time, 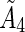, are substituted from above to derive an expression for average tumor dose, 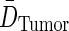. The average residence time per unit volume is used for each body compartment.

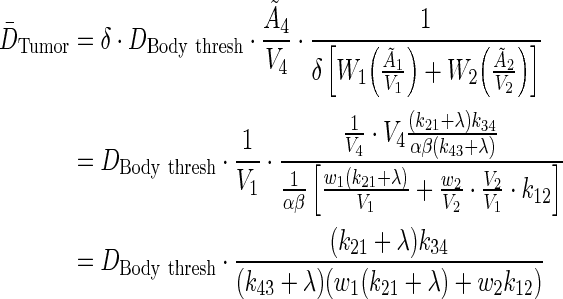(A7)

Notice how the volume dependence is cancelled. To investigate the influence of λ on tumor dose, perturbation theory via Taylor series expansion was implemented:

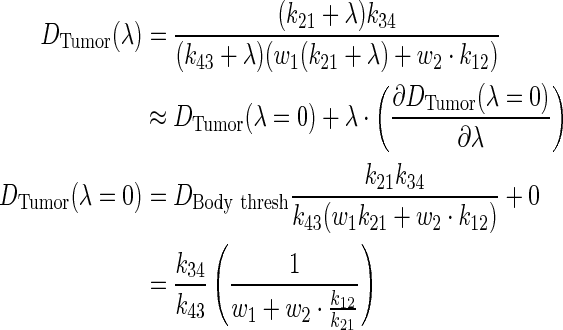(A8)

Through algebraic simplification, a relationship between PK parameters and tumor dose was derived.

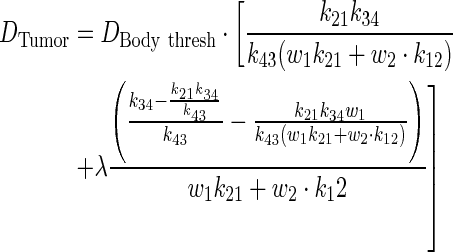(A9)

The above equation is further simplified in terms of PK ratios:

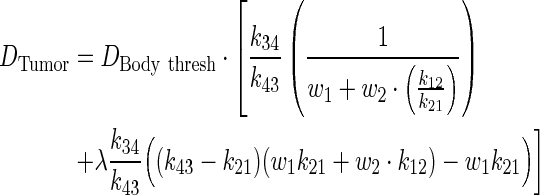(A10)

Disclosure Statement

There is no conflict of interest for any of the authors pertaining to this work.