The control of branching morphogenesis

Abstract

Many organs of higher organisms are heavily branched structures and arise by an apparently similar process of branching morphogenesis. Yet the regulatory components and local interactions that have been identified differ greatly in these organs. It is an open question whether the regulatory processes work according to a common principle and how far physical and geometrical constraints determine the branching process. Here, we review the known regulatory factors and physical constraints in lung, kidney, pancreas, prostate, mammary gland and salivary gland branching morphogenesis, and describe the models that have been formulated to analyse their impacts.

2. Introduction

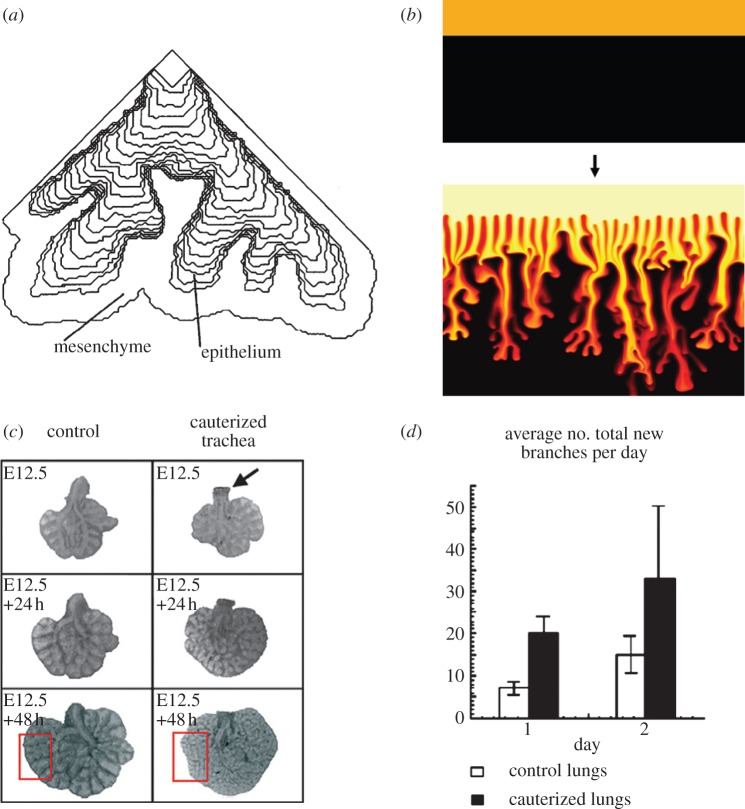
Branching morphogenesis is observed in many organ systems (figure 1) and in many different species. The branching process in the mammalian lung (figure 1a) and in its analogue in flies, the trachea, has been studied in particularly great detail. The bronchial tree arises from the sequential use of three geometrically simple modes of branching: domain branching (figure 2a), planar bifurcation (figure 2b) and orthogonal bifurcation (figure 2c) [2]. Trifurcations (figure 2d) have also been documented in the lung [3], but these are much more prevalent in the ureteric bud of the kidney (figure 1b); in the kidney bifurcations and trifurcations dominate, at the expense of lateral branching [4–6]. Similar modes of branching are observed also in glands (figure 1c–f). In this review, we will focus on branching during mammalian organogenesis, but ignore neuronal and vasculature branching as well as branching observed in plants. For reviews of these branching systems, we refer to [1,7–10].

Figure 1.

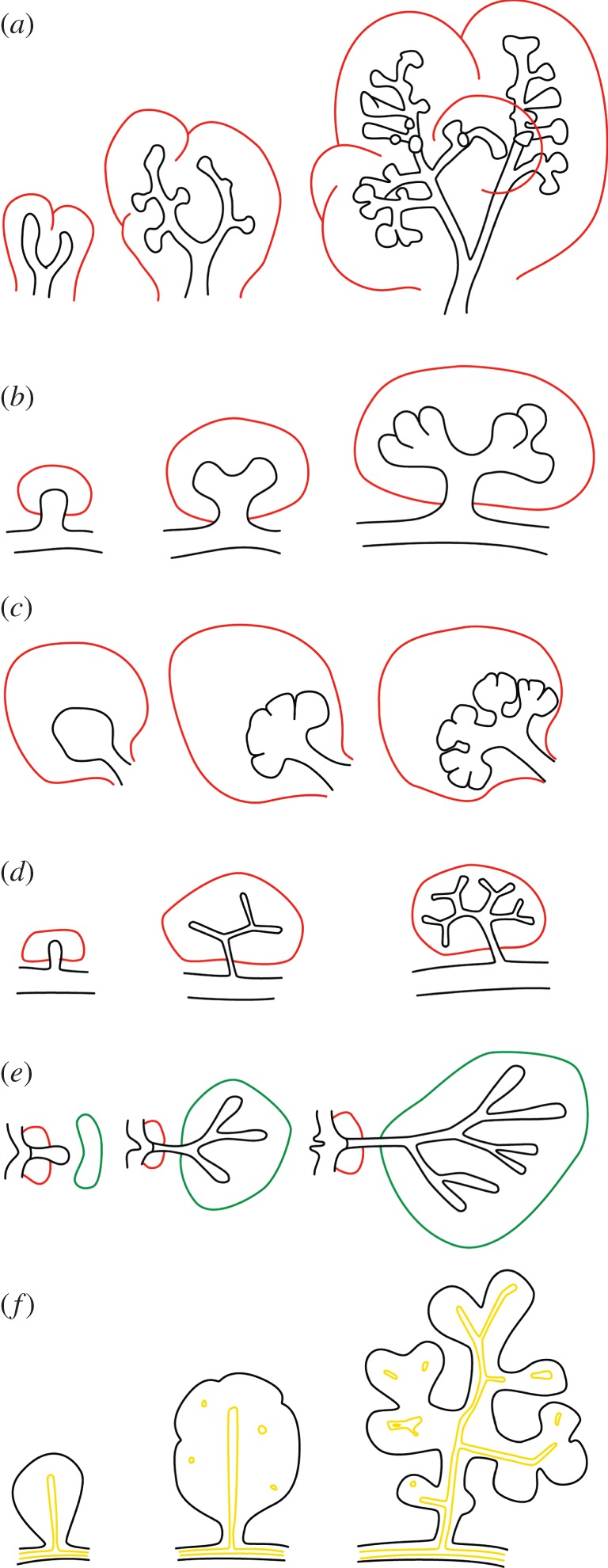
Branching morphogenesis. Typical branching pattern over developmental time in the (a) lung, (b) ureteric bud, (c) salivary gland, (d) prostate, (e) mammary gland and (f) pancreas. The epithelium is shown in black, the mesenchyme in red, the fat pad in the mammary gland in green and the lumen in the pancreas in yellow.

Figure 2.

Modes of branching: (a) lateral branching, (b) planar bifurcation, (c) orthogonal bifurcation and (d) trifurcation. (a–c) Reproduced from [1].

Most processes in higher organisms are intricately regulated by a network of signalling factors. To arrive at a branched structure, these signalling components would have to form a pattern in space that precedes bud outgrowth, as is indeed observed in the case of fibroblastic growth factor (FGF) 10 in the developing lung bud (figure 3a,b). The concentration of FGF10 at the distal tip of the lung bud would then direct elongation (figure 3c), whereas terminal branching would be the result of a split localization of FGF10 (figure 3d), and lateral branching would result from FGF10 signalling being restricted to spots on the side (figure 3e).

Figure 3.

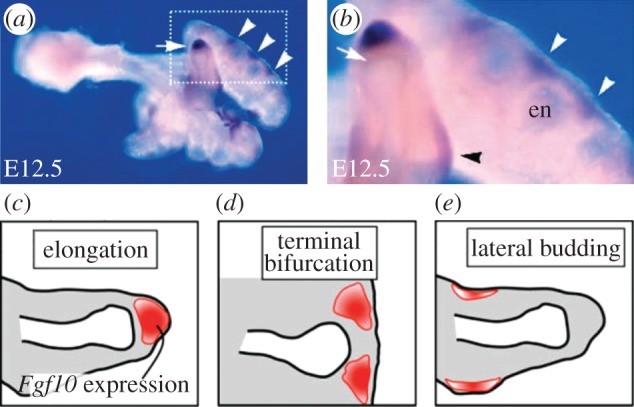
FGF10 in the developing lung. (a,b) Fgf10 expression at embryonic day (E) 12.5. High expression levels of Fgf10 are observed in the distal mesenchyme of the tip (white arrow), as well as on the sides of the tips of a bud (white arrowheads). (b) High magnification of the white dotted box in (a). Note that Fgf10 expression is absent in the mesenchyme adjacent to the endoderm (en) of the tip. Localized Fgf10 expression is also observed in the mesenchyme around the stalk (black arrowhead). (c–e) Schematic of the spatial distributions of Fgf10 expression in (a,b). Fgf10 is expressed in the red region. The white area indicates the lumen, the grey area the mesenchyme, the black line in between the epithelium. The outer black lines mark the mesothelium. The three types of spatial distributions of Fgf10 expression generate different branching modes: (c) elongation, (d) terminal bifurcation and (e) lateral budding. The entire figure is adapted from Hirashimi & Iwasa [11]; (a,b) adapted from the original publication of Bellusci et al. [12].

Such patterns can, in principle, emerge from a pre-pattern that goes back to earlier phases of embryonic development or that arises spontaneously from regulatory interactions. A number of theoretical models have been developed to explain how patterns can emerge and how these are read out in space. We will review these concepts in the context of their use in the models for branching morphogenesis.

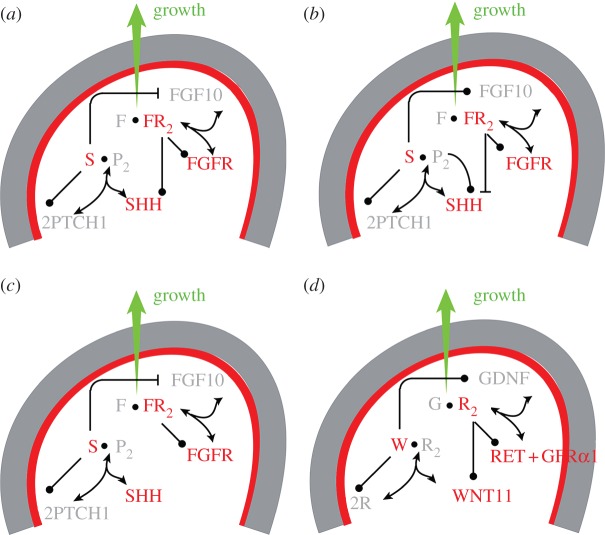
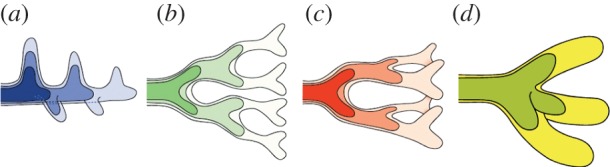
While the branching patterns are similar overall, there are important differences (figure 1), and the signalling proteins that control the branching programme in the different organ systems are not always the same (figure 4). Thus, FGF10 appears to drive outgrowth of lung buds [12], prostate [13] (both figure 4a), salivary glands [14,15] (figure 4b) and pancreatic buds [16,17] (figure 4c), whereas ureteric bud outgrowth is controlled by the transforming growth factor (TGF)-β family ligand glial-derived neurotrophic factor (GDNF; figure 4d) [18–21], and no single growth factor has yet been defined for the mammary gland [7], though FGF receptor 2 is known to be required for ductal elongation in mammary glands [22]. These signalling proteins are controlled by further proteins, and the regulatory networks differ between organs. Given these differences in the signalling networks, mechanisms based on the interplay of physical forces have also been explored.

Figure 4.

Signalling networks in branching morphogenesis. The core signalling networks that have been described to regulate branching morphogenesis in (a) lung and prostate, (b) salivary gland, (c) pancreas and (d) kidney are shown. In the lung, prostate, salivary gland and pancreas FGF10 (F) signalling directs outgrowth of the epithelium. Fgf10 is expressed in the mesenchyme (grey) and binds to its receptor (R) in the epithelium (red). FGF10-bound receptor not only directs outgrowth, but also regulates expression of Shh (S) ((a) upregulation in the lung and prostate, (b) downregulation in the salivary gland, (c) no reported regulation in the pancreas). SHH binds its receptor PTCH1 (P) and the SHH-receptor complex, in turn, regulates Fgf10 expression ((a,c) downregulation in the lung, prostate and pancreas, (b) upregulation in the salivary gland). All ligand–receptor signalling also upregulates the expression of the receptor. (d) In the case of the ureteric bud, GDNF (G) induces bud outgrowth and GDNF-receptor binding stimulates expression of the receptor Ret and of Wnt11 (W) in the epithelium. WNT11, in turn, causes upregulation of Gdnf expression in the mesenchyme.

Key to all such mechanisms is an instability that results in a patterning and/or a symmetry-breaking event. The elongating tube can be regarded as a cylinder with a cap (figure 5). A cylinder with a homogeneous distribution of morphogens on its surface has a cylindrical symmetry, such that if the cylinder is rotated by any angle along the main axis, then the pattern will not change (figure 5). During branching morphogenesis, a symmetry-breaking event must occur, because the outgrowing bud has approximately cylindrical symmetry, whereas the branching events (i.e. bifurcations, trifurcation or lateral branching) change the cylindrical symmetry into a rotational symmetry. Symmetry breaking is a fundamental process, and occurs many times and at various scales during embryo development, as recently reviewed in the collection of Cold Spring Harbor Perspectives in Biology (for the editorial, see [23]).

Figure 5.

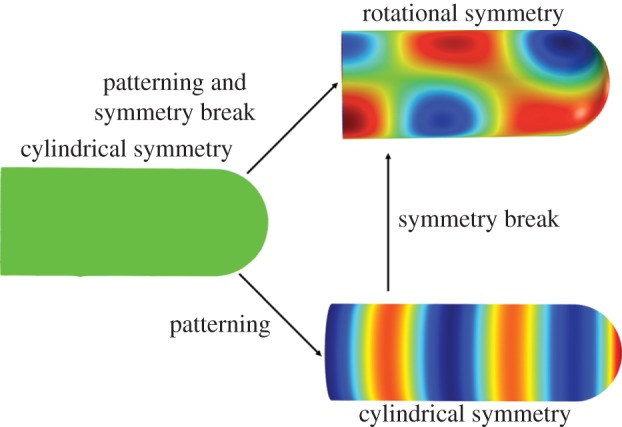
Patterning and symmetry break. A cylinder with a homogeneous morphogen concentration exhibits cylindrical symmetry. Patterning mechanisms may introduce stripes or spots. The spotty cylinder exhibits rotational symmetry, and such pattern would support the outgrowth of defined branches.

Computational models can help us to explore the impact of the signalling interactions, physical forces and domain geometries, and thus discern a minimal set of rules and interactions from which the observed pattern can emerge. In the following, we will discuss the different models that have been applied to branching morphogenesis of various organs. We will be interested, in particular, in how far similar mechanisms can explain branching morphogenesis in different organ systems.

3. Lung branching morphogenesis

Early lung branching morphogenesis is stereotyped, and the lung tree arises from the sequential use of three geometrically simple modes of branching: domain branching, planar bifurcation and orthogonal bifurcation [2]. Transitions from one mode to another are restricted to four routines and lead to three defined sequences that are used to build the entire lung tree [1,2]. In the domain branching mode, the lung bud elongates, and new buds appear first on one side of the stalk in a direction perpendicular to the main axis of the cylinder and subsequently on the another side of the stalk. Planar and orthogonal bifurcations represent two consecutive rounds of bifurcations, and differ in the second round of branching, which occurs in the same plane in the case of planar bifurcations, and orthogonal to the first plane in the case of orthogonal bifurcations [2]. Trifurcations (figure 2d) have also been documented recently [3]. The domain branching mode is used to build the backbone of the respiratory tree, whereas planar bifurcations form the thin edges of the lobes, and orthogonal bifurcations create the lobe surfaces and fill the interior. Only few variations and errors are observed in wild-type littermates [2,3]. The regularity of the process implies that the branching process is not random, but tightly controlled by genetically encoded information. It is an open question how a stereotyped branching architecture with millions of branches can be encoded with only a few genes.

3.1. Fractals

Fractals are complex structures that can be formed by the repetitive application of a set of simple rules. If the lung was a fractal structure, then its complex architecture could result from a set of simple rules, as has been demonstrated in many fractal models of the lung. The most sophisticated and accurate of these models was created by Kitaoka et al. [24], who required nine basic and four complementary rules to fill the three-dimensional thoracic cavity with a branched tree that very much resembled that of the lung (figure 6). So is the lung a fractal-like structure?

Figure 6.

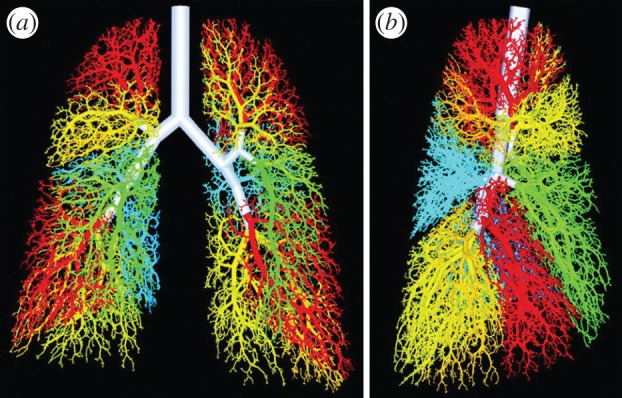
A three-dimensional fractal model of an airway tree with 54 611 branches; branches distal to different segmental bronchi are shown in same colour as segmental bronchus. (a) Anterior view and (b) right lateral view. The figure and legend were adapted from Kitaoka et al. [24].

In the lung, dichotomous branching gives rise to two daughter branches with smaller diameter than the mother branch. To obtain a fractal series, the shrinkage factor would need to be the same in all generations.

Both the length and the diameter of lung branches have been determined for the adult lungs of several mammals [25]. The ratio between diameter and length differs between species, but it is conserved in a given species (i.e. length/diameter ∼ 3 in humans) [26]. We can therefore focus on the diameter. Measurements show that the diameter d_z of the lung branches in generation z decreases exponentially with the branching generations (figure 7). More formally we can write

3.1

where q = exp(–α) < 1 is a constant scaling factor. We can rewrite this equation as

Figure 7.

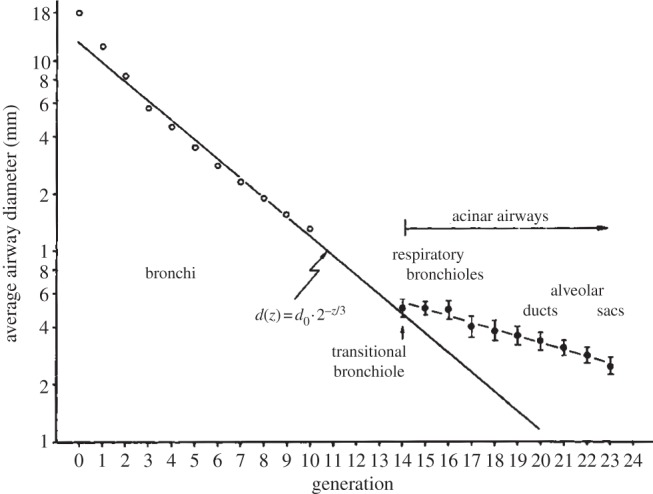
A fractal-like organization of the lung. A logarithmic plot of the airway branch diameter against the branching generation reveals two exponential laws with different scaling factor for conducting and respiratory airways. For the conducting part, the relation d(z) = d(0) × 2^–z/3 was observed for the diameters d in generation z. For such shrinkage factor in the diameter, the total volume of all branches remains constant for dichotomous branching and the entropy generation during breathing is minimal [27]. The plot is adapted from Bleuer [28].

The diameter and length in each subsequent generation thus decreases by a constant factor q < 1. Such constant scaling law reflects the scale invariance of fractal patterns (i.e. the pattern looks the same no matter what scale of the structure we zoom in to). The geometrical figures thus repeat themselves at progressively smaller scales as characteristic for self-similar fractals.

Mathematically, fractals are defined as any series for which the Hausdorff dimension (a continuous function) exceeds the discrete topological dimension. Topologically, dimension corresponds to the number of independent coordinates that are required to describe the position of an object in that particular space. To illustrate the Hausdorff dimension consider a square. If we scale down each side by a scale factor r = 1/2, then we require 2² squares to fill the original square. With r = 1/n, we require n² squares. In three dimensions, we would require n³ cubes. More generally, if we scale down each side by scale factor r = 1/n, then we require 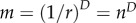elements to fill the original space, where D is the dimension:

Branching in the lung is dichotomous, and from one generation to the next m = 2 elements thus emerge. The diameter is scaled by q = exp(–α) = 2^–1/3 in the first 10–15 generations that generate the conducting airways (i.e. for the airways that do not participate in gas exchange; figure 7). Accordingly, the fractal dimension of the lung airways is

which is greater than the topological dimension of the branching sequence, and which implies that the airway tree fills the entire three-dimensional thoracic space in which it is embedded. Fractal properties in nature have remained controversial because, unlike in mathematical sequences, the geometrical figures are observed over a small, finite scale (number of generations), and fitted scaling factors are therefore not particularly reliable [29]. In fact, a different scaling factor is observed for the lower, respiratory branches (figure 7, acinar airways), and attempts to simultaneously fit both series have led to a different scaling factor [30], and to the suggestion of a power-law relation [25].

There is, however, independent strong support for the fractal-like properties of the branching structure of the conducting airways. Thus, the diameter relation d_z = 2^–z/3 d₀ in the conducting part of the airways has been shown to result in an airway architecture that permits breathing with minimal energy wastage (entropy generation) by minimizing the combined effects of dead volume and resistance [27]. Thus, the upper part of the lung is dead volume because it must be ventilated without contributing to gas exchange with the blood. The larger the diameters in this part of the structure, the larger the dead volume, and thus the more energy is wasted in each breath. However, shrinking these diameters results in an increase in air flow resistance. The diameter relation d_z = 2^–z/3d₀ is the one that minimizes the combined contributions of these two effects. The fractal-like organization of the conducting parts of the bronchial tree thus permits the generation of a space-filling, energy-efficient architecture for ventilation, where all the tips have similar distances from the origin of the airways in the trachea, based on a simple set of rules. While this may explain why such a bronchial tree evolved, it does not reveal the driving force during development, because the embryo does not breathe, and the developing lung is filled with fluid rather than air. Moreover, the diameters and lengths in early lung development do not yet exhibit a fractal-like pattern. So what are the mechanisms that regulate branching morphogenesis?

3.2. Mechanical models

Culture experiments demonstrate that the mesenchymal tissue largely defines the branching pattern when mesenchymal tissue and epithelial tissue of different organs are combined. One striking example came from tissue recombination experiments in which lung mesenchyme induced branching of the ureteric bud with a pattern characteristic of lung epithelium (i.e. with increased lateral branching) [31]. Mesenchymal tissue that either induced or did not induce branching of an epithelial layer in culture was found to differ in its mechanical properties, though the exact differences have not been defined [32]. In line with these observations, lung branching was proposed to be driven by the difference in the viscosity of the luminal/amniotic fluid and the mesenchyme, separated by a ‘skin’ of surface tension, the epithelium [33]. Two fluids with different viscosities exhibit an instability if the more viscous liquid pushes the less viscous one in response to an external force (figure 8a); in physics, this effect is often referred to as viscous fingering (figure 8b) [34,36]. This effect, though physically plausible, has more recently been recognized as biologically incorrect by the authors [37,38], because (i) branching morphogenesis can proceed also without mesenchyme, (ii) branching morphogenesis can proceed without growth (hence without growth pressure), and (iii) the robustness of the branching process suggests that the branching process is highly controlled, which would not be the case for a near-equilibrium instability.

Figure 8.

Branching as a result of mechanical differences. (a) Branching driven by a viscosity difference between the fluid in the lumen and the mesenchyme; adapted from Lubkin & Murray [33]. (b) Viscous fingering is observed in a system with two immiscible fluids of differing viscosities; adapted from Jha et al. [34]. (c,d) The impact of internal pressure on branching; adapted from Unbekandt et al. [35].

In subsequent studies, the authors studied a similar model, but interpreted the two (Stokes) fluids as epithelium and mesenchyme, with surface tension in between and focused on the effects of an external ‘clefting force’, which was assumed to mainly originate from traction forces in the mesenchyme (though epithelial forces were considered as well) [38,39]. The analysis showed that the higher the relative viscosity of epithelium and mesenchyme, the wider the resulting clefts and the faster the clefts emerge [38,39]. How the position of the clefting force would be controlled has not been explored, but this could, of course, be regulated by the signalling networks that control branching morphogenesis.

Signalling factors play a key role in branching morphogenesis, and branching of the epithelium in the absence of mesenchyme is observed only if the appropriate signalling factors (i.e. FGF in the case of the lung) are added to the Matrigel [40]. Similarly, while increased internal pressure is a mechanical effect that leads to an increase of lung branching in in vitro cultures (figure 8c,d), this effect also depends on the activity of FGF signalling, is not observed in FgfR2b null mice and is reduced in Fgf10 hypomorphic lung explants [35]. Signalling networks thus appear to be at the core of the control of branching morphogenesis, and seem to both affect and to be affected by mechanical properties of the tissue. Thus, signalling networks regulate the hydraulic pressure during lung organogenesis [41] as well as the actomyosin-mediated contractility of cells, and local differences in the extracellular matrix (ECM). Inhibition of the actomyosin-mediated contractility in lung explants decreases branching [42], whereas activation of the contractility increases branching [43]. The impact of the ECM structure on branching morphogenesis has previously been reviewed [44].

3.3. Signalling models

The core signalling module that controls branching morphogenesis in the lung comprises the two diffusible proteins, FGF10 and SHH (figure 4a); mutations in both genes and their downstream effectors abrogate branching morphogenesis [45–47], whereas mutations in other genes at most modulate the branching process. FGF10 has been shown to induce the outgrowth of lung buds [12]. FGF10 and SHH engage in a negative feedback loop, in that FGF10 signalling induces Shh expression in the epithelium, whereas SHH signalling represses Fgf10 expression in the mesenchyme.

3.3.1. Diffusion-limited growth

The emergence of branches in cultures of mesenchyme-free lung epithelium has been proposed to be the result of diffusion-limited growth (figure 9a) [48,51,52]. The diffusion-limited regime of growth is observed when the concentration of the growth factor inducing tissue growth is low, and degradation of the growth factor can therefore result in sharp concentration gradients. Small protrusions (which are closer to the source) will then experience higher morphogen concentrations. As a consequence, these protrusions will grow faster and thus get even closer to the source. In the experiment, mesenchyme-free lung explants were placed into a Matrigel-containing FGF. The lung tissue degrades FGF and thus acts as a sink. At sufficiently low FGF concentrations, a gradient of FGF emerges with a minimum concentration of FGF in the proximity of the epithelium and maximum concentration away from the lung explant. For such low concentrations, irregular growth of the explant is indeed observed (figure 9a). In the case of high concentrations of FGF in the Matrigel, no such gradient can emerge, and a uniform expansion of the lung explant was observed [48]. When the conditions of diffusion-limited growth were met, both the model and the experiments show that the mechanical strength of the cytoskeleton can suppress only branching. In the chick lung, a branched structure is formed only dorsally, whereas a cyst structure (air sac) is formed ventrally during development. Miura et al. [53] suggest that this difference can be accounted for by differences in the FGF10 diffusivity that would be sufficiently low only on the dorsal side for branching pattern to emerge by diffusion-limited growth.

Figure 9.

Patterning models based on the local variations in the distance of the epithelium from the source of FGF10. (a) Branching as a result of diffusion-limited growth. Tissue (delimited by white line) that is placed into a solution with a low concentration of an outgrowth-inducing signalling factor (such as FGF10 in the lung) will degrade the signalling factor and thus induce a concentration gradient (red, high; blue, low). As a result of small irregularities in the tissue shape (white line), some part of the tissue will be closer to the higher concentration and accordingly start to grow out faster, thus experiencing even higher (relative) concentrations; adapted from Hartmann & Miura [48]. (b) With FGF10 produced mainly in the submesothelial mesenchyme and its receptor produced only in the epithelium, an FGF10 gradient can be expected to emerge. If the FGF10 concentration is homogeneous close to the mesothelium and on the epithelium, then the gradient would be steeper, the shorter the distance between epithelium and mesothelium. If cells read out gradients rather than concentration, then small differences in the distance could trigger self-avoiding outgrowth of branches; adapted from Clément et al. [49]. (c–e) Distance-based mechanism based on SHH and FGF10. SHH is produced only by the epithelium, and represses Fgf10 expression at high concentrations. Accordingly, Fgf10 expression can be expected to be lower, the closer are epithelium and mesothelium [12]. (c) Assuming that SHH induces Fgf10 expression at low concentrations, the FGF10 concentration is high as long as the bud is sufficiently far away from the boundary, thus supporting bud elongation. (d) As the bud approaches the impermeable boundary, the FGF10 profile splits, thus supporting bifurcating outgrowth. (e) The bifurcation in (d) requires an impermeable boundary and is not observed on an open domain. The FGF10 distribution in (c–e) was calculated according to the model presented by Hirashima & Iwasa [11]. (c–e) Adapted from Menshykau et al. [50].

A further mechanism, similar to the diffusion-limited growth, has been proposed to explain lung branching in vivo. Here, however, the authors assume that the FGF concentration on the epithelium is equal everywhere, because the epithelium efficiently absorbs the growth factor [49,54]. What is assumed to differ is the steady-state FGF10 gradient between mesothelium and epithelium. Assuming that FGF10 is uniformly expressed in the submesothelial mesenchyme and FGF receptors are expressed only in the epithelium (such that there is no FGF degradation in the mesenchyme), then the steepness of the steady-state FGF10 gradient between mesothelium and epithelium would depend only on the distance between these tissue layers. If, similar to in vitro experiments, some part of the bud was closer to the mesothelium than others, then this part of the bud would experience a steeper FGF10 gradient. If cells could sense gradients rather than sense concentrations, then this could, in principle, drive self-avoiding outgrowth of the branch (figure 9b). Moreover, given that the distance between source and sink is key to this mechanism, all buds remain at a comparable distance from the mesothelium during growth. This distance is controlled by the mesenchyme proliferation rate relative to the epithelial proliferation rate. The authors also found that the computed branched tree reproduced multiple morphometric characteristics that have been measured in the adult human lung (i.e. the distribution of branch lengths, diameters and the asymmetry ratio) at least qualitatively. However, in experiments in which FGF10 was added to lung cultures, the mRNA expression of the FGF10 target Sprouty2 was found to be upregulated [55]. This result is consistent with a model in which cells respond to the FGF10 concentration, but is difficult to explain with a gradient-based mechanism, as the homogeneous addition of FGF10 should reduce the gradient and should thus result in a lower expression level.

We note that stereotyped branching could be obtained with diffusion-limited growth only if there was a preceding mechanism in place to generate the same irregularities in the starting geometry for all buds, so that diffusion-limited growth would be initiated always at the same location to obtain the same overall branching pattern.

3.3.2. Distance-based patterning

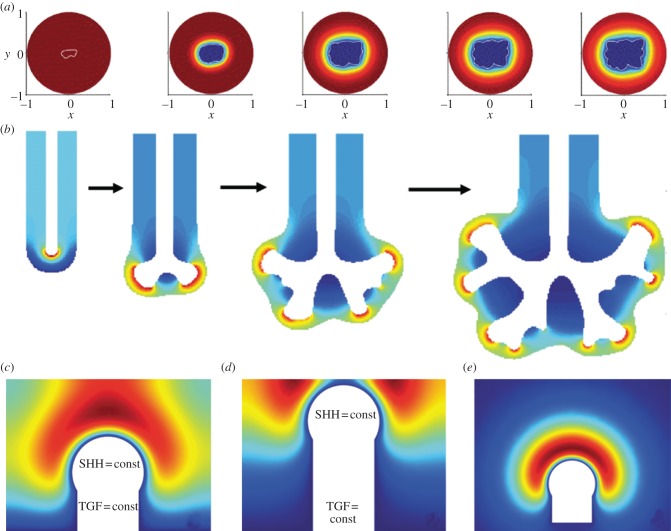
In an alternative model, a different distance-dependent effect has been proposed based on the regulatory interactions between SHH and FGF10 [12]. SHH signalling represses Fgf10 expression, but Shh is expressed only in the epithelium, and Fgf10 is expressed only in the mesenchyme (figure 4a). Accordingly, it has been proposed that the inhibitory effect of SHH on Fgf10 expression will be stronger, the thinner the mesenchyme. Thus, it has been argued that a locally thinner mesenchyme would lead to the local repression of Fgf10 expression, and thus to the accumulation of FGF10 on the sides, thereby triggering bifurcating outgrowth. Hirashima & Iwasa [11] studied a computational implementation of the model on a static two-dimensional domain in the shape of lung bud cross-section. The model focused on the interactions between FGF10, SHH and TGF-β. According to the model, TGF-β is restricted to the stalk and prevents Fgf10 expression, whereas SHH is restricted to the tip, and enhances Fgf10 expression at low concentrations and represses Fgf10 expression at high concentrations. As a result FGF10 is concentrated at the tip as long as the bud is sufficiently far away that the concentration of SHH is low (figure 9c). As the tip grows closer to the impermeable boundary, the local SHH concentration increases and suppresses Fgf10 expression. As a result, the FGF10 profile splits (figure 9d). While the regulatory interactions in the model are plausible, the mesothelium that surrounds the lung bud is unlikely to present a diffusion barrier. In fact, culture experiments show that protein ligands that are added to the lumen of cultured lungs cannot diffuse to the mesenchyme, but protein ligands that are added to the culture medium can pass through the mesothelium to regulate the mesenchyme [56]. Without an impermeable mesothelial boundary, the mechanism does not lead to a bifurcating profile (figure 9e) [50]. We note that this distance-based mechanism would also not explain the lateral branching mode. It is therefore likely that a different mechanism controls branching morphogenesis in the lung.

3.3.3. Diffusion-based geometry effect

In vitro experiments demonstrate that the geometry of the domain can affect its patterning [57]. Thus, as a result of diffusion, more signals are lost at the edges of a domain than in its centre, if a signal-producing domain is embedded in a non-producing domain, and the signal can diffuse. As a result of this geometry effect, signal then concentrates in the centre of the domain (figure 10a). If this factor supports outgrowth of the tissue, then a bud can form. As the bud elongates, more signal is lost at the tip than at the sides, because of the higher curvature, and a bifurcating concentration profile of the signalling factor emerges. Computational studies not only confirm the emergence of a bifurcating profile as a result of a diffusion-based geometry effect, but also show that it does not support bifurcating outgrowth (D. Menshykau & D. Iber 2013, unpublished data). The geometry effect may nonetheless play an important role in branching morphogenesis by inducing an initial pattern that can then be ‘fixed’ by other processes. When three-dimensional shapes of lung bud epithelia were used in a simulation that had been extracted from early developing chicken lungs, simulated secretion of a ligand from the epithelium into a large computational bounding box (that would model the mesenchyme) resulted in a steady-state concentration pattern that approximately coincided with where the authors would expect branching of secondary bronchi to be inhibited (figure 10b,c) [58].

Figure 10.

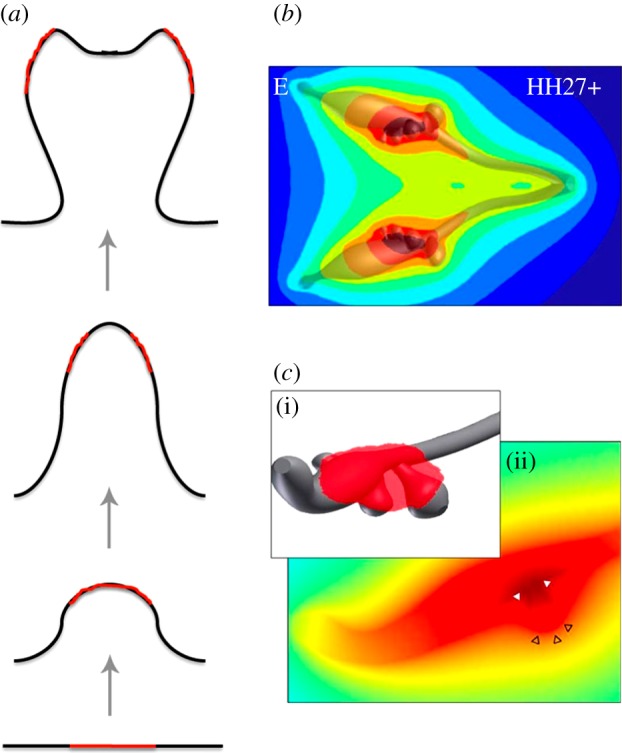
Branching as a result of a diffusion-based geometry effect. (a) A cartoon of the proposed geometry-based branching mechanism. As a result of stronger diffusion-based loss at the edges, the concentration of the signal is highest in the centre of the domain (red line), and drives the outgrowth of a bud. As the bud elongates, more signal is lost at the tip than at the sides, because of the higher curvature, and a bifurcating concentration profile of the signalling factor emerges. Computational studies confirm that the geometry effect results in bifurcating concentration profiles, but reveals that it does not support bifurcating outgrowth (D. Menshykau & D. Iber 2013, unpublished data). (b) The simulated concentration profile of a ligand that is uniformly secreted from the epithelium of extracted three-dimensional chicken lung bud (Hamburger–Hamilton (HH) stage 27+) into a large computational bounding box [58]. The concentration profiles were normalized to the highest value (red, highest relative concentration; blue, lowest). (c) (i) A three-dimensional solid model representation of the region of highest ligand concentration represented by the red shading. (ii) The morphogen concentration in a cross-section through a bud. The bud stalk and branch point have a local maximum (solid white triangles), whereas the bud tip has a local minimum (empty black triangles) in the predicted ligand concentration [58].

3.3.4. Ligand–receptor-based Turing mechanism

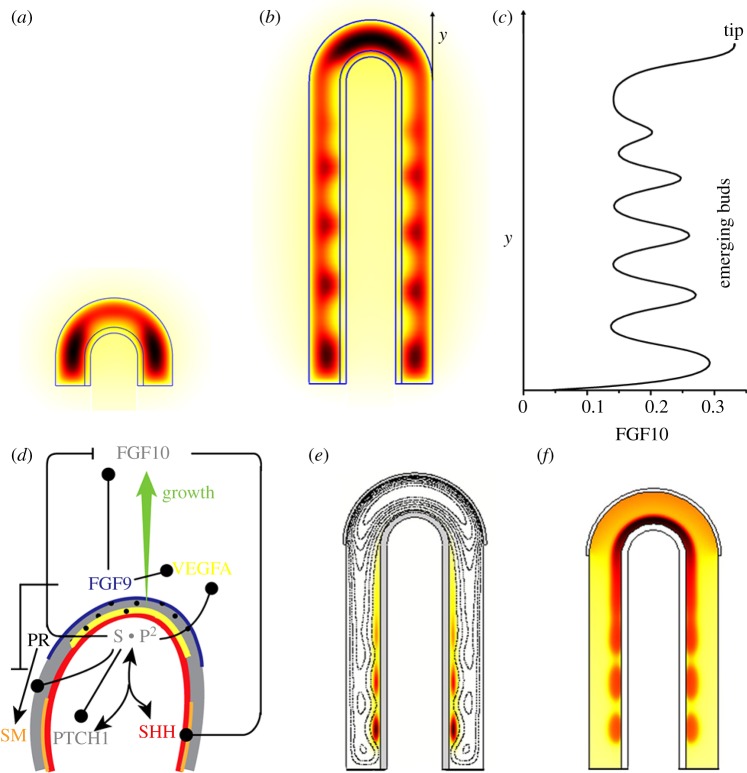
We have recently proposed a ligand–receptor-based Turing mechanism to explain the stereotyped branching processes in the lung [50]. We showed that the reported biochemical interactions between FGF10, SHH and PTCH1 (figure 4a) give rise to a Turing pattern [59] that yields the FGF10 patterns, which represent the two modes of branching in the developing lung: bifurcation and lateral branching (figure 11a,b). The initial model analysis was carried out on a two-dimensional slice of the lung bud. Importantly, the Turing pattern not only permitted the emergence of rings (cylindrical symmetry), but also of spotty patterns on a three-dimensional lung bud shape (rotational symmetry; figure 5). Mutations in genes that are not part of the FGF10/SHH core patterning module have been shown to affect the branching pattern. We find that alterations in almost any parameter value can switch the branching mode in our model. The impact of these other gene products on the branching pattern can thus be explained with indirect effects (i.e. by affecting the parameter values of the core model). Another interesting parameter value is the growth rate. We observed bifurcating patterns at low growth speed and lateral branching patterns at high growth speed. Interestingly, we found that the FGF10 concentration differs in the spots that emerge during lateral branching (figure 11c). If the outgrowth speed depended on the FGF10 concentration, then these different concentrations might explain the different branching sequences observed for different branches.

Figure 11.

A receptor–ligand-based Turing model for lung branching morphogenesis. (a,b) The regulatory network shown in figure 3f gives rise to a Turing pattern and results in distributions of FGF10 (colour code: red, highest; black, lowest) and SHH (black and white contour line plot) on bud-shaped domains as characteristic for (a) bifurcation or (b) lateral branching events. (c) The FGF10 concentration profile along the lung bud. (d) An extended network that includes also FGF9 also reproduces the observed patterns of smooth muscle (SM) formation from progenitors (PR) and Vegfa expression during lung branching morphogenesis. (e) Smooth muscles (colour code) emerge in the clefts between lung buds (contour lines mark FGF10 concentration levels) as the lung bud grows out. (f) Vegfa expression, an inducer of blood vessel formation, emerges in the distal subepithelial mesenchyme. (a–c) Adapted from Menshykau et al. [50]; (d–f) adapted from Celliere et al. [60].

Including FGF9, which is expressed in the distal mesothelium (figure 11d, blue line), and which enhances the expression of Fgf10, promoted lateral branching over the bifurcation mode of branching as observed in the embryo. Further simulations showed that the expanded core regulatory network was capable of controlling the emergence of smooth muscles in the clefts between growing lung buds (figure 11e), and Vegfa expression, an inducer of blood vessel formation, in the distal subepithelial mesenchyme (figure 11f) [60]. How far the vasculature impacts back on the branching pattern is still a matter of investigation. Thus, while ablation of the vasculature impacted on the three-dimensional branching pattern, in that branches formed parallel or at a shallow angle instead of perpendicular to the axis, the authors noted that ‘inhibition of normal branching resulting from vascular loss could be explained in part by perturbing the unique spatial expression pattern of the key branching mediator Fgf10 and by misregulated expression of the branching regulators Shh and Sprouty2’ [61, p. 2359].

Another open question concerns the relative width and length of branches. The proposed Turing mechanism would only explain branch point selection and the choice of the branching mode. How the diameters of the developing bronchial tree are determined relative to the length of each branch element is still an open question. Recent experiments suggest that signalling by extracellular signal-regulated kinase 1 (ERK1) and ERK2, a downstream target of FGF signalling, plays an important role because it affects the cell division plane [62]. A bias in the cell division plane can bias tissue growth in a direction and thus result in either elongation or in a widening of the stalk. Cells that divide parallel to the airway longitudinal axis have lower levels of ERK1/2 signalling, and removal of Sprouty genes, which encode negative regulators of FGF10 signalling, results in the random orientation of cell division planes in the stalk and in airways that are wider and shorter than normal [62].

4. Kidney branching morphogenesis

Similar to the lung, the kidney collecting ducts form via branching of an epithelial cell layer. During kidney development, the ureteric bud invades the metanephric mesenchyme around embryonic day (E) 10.5 [63]. According to culture experiments, most branching events in the kidney are terminal bifurcations and to a lesser extent trifurcations, and only 6% of all branching events are lateral branching events [4–6]. FGF10 is not necessary for branching in the lung as branching is still observed in Fgfr2-mutant mice, though at a reduced rate [64]. Core to the branching mechanism appears to be the TFG-β family protein GDNF. It is expressed in the mesenchyme, and signals via its receptor (RET) and co-receptor GDNF family receptor alpha (Gfrα)1 in the epithelium (figure 4d); Gdnf, Ret and Gfrα1 null mice do not develop kidneys [6,18–20,63,65,66]. FGF and GDNF signalling appear to cooperate, because activation of FGF10-FGFR2 signalling by knocking out the antagonist Sprouty can rescue Gdnf^–/–and Ret^–/– mutants, which otherwise fail to develop kidneys [67]. Moreover, GDNF and FGF10 signalling have, at least in part, the same transcriptional targets [68]. This suggests that the branching mechanisms for lung and kidney are somewhat related in spite of their apparently different molecular nature. An important difference, however, concerns the core feedback structure. While FGF10 and SHH engage in a negative feedback in the lung, GDNF engages in a positive feedback with WNT11 in the ureteric bud [63].

Beads soaked with GDNF induce the outgrowth of extra ureteric buds in kidney culture explants [6,18–20,63,65]. Based on the chemoattractive properties of GDNF [21,69], it was suggested that branching of the ureteric bud is caused by the attraction of the tips towards local sources of GDNF [70]. Accordingly, in early theoretical work, the ureteric bud shape was proposed to be controlled by the interplay of cell proliferation and cell chemotaxis [71]. If chemotaxis towards a source of growth factors (i.e. GDNF) dominates relative to the general growth, then the computed branched structure is kinked, with clearly discernible buds. On the other hand, if growth dominates relative to chemotaxis, then the developing bud is round. The model did not attempt to address the question of how a split expression pattern emerges in the first place. Rather, given the split expression of the signalling protein Gdnf (as hard-coded in the model), the model addressed the different possible bud shapes.

We have recently developed a three-dimensional model for branching morphogenesis in the kidney [72]. Here we noted that, similar to the lung, the reported biochemical interactions between GDNF and its receptors (figure 4d) result in a Turing pattern. Much as reported for the embryo, split concentration patterns, as are characteristic for bifurcations (figure 12b) and trifurcations (figure 12c), dominate in the model for physiological parameter values, whereas elongation (figure 12a) and subsequent lateral branching (figure 12d) are rather rare. The patterning mechanism can also support the invasion of the ureteric bud into the metanephric mesenchyme (figure 13a,b). It is thus possible that the induction and outgrowth of the ureteric bud from the Wolffian duct works by the same mechanism. Interestingly, in the case of thicker mesenchyme, the length of the outgrowing stalk is shorter and branching happens earlier (figure 13c). This is in good agreement with experimental observations in the lung, where side-branching was noted to occur when sufficient space becomes available around the circumference of a parent branch [74].

Figure 12.

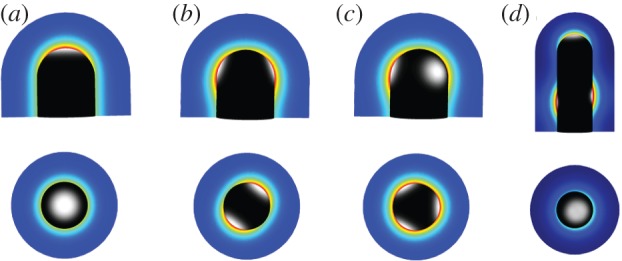
Receptor–ligand-based Turing model for kidney branching morphogenesis. The reported regulatory interactions shown in figure 4d can result in self-emerging patterns of the GDNF-bound RET complex in the epithelium (grey scale: white, highest; black, lowest), and Gdnf expression in the mesenchyme (colour scale: red, highest; blue, lowest), when solved on a three-dimensional idealized bud-shaped domain. The different patterns can, in principle, (a) support elongation, or support the formation of (b) bifurcations, (c) trifurcations or (d) lateral branching. (a–d) Adapted from Menshykau & Iber [72].

Figure 13.

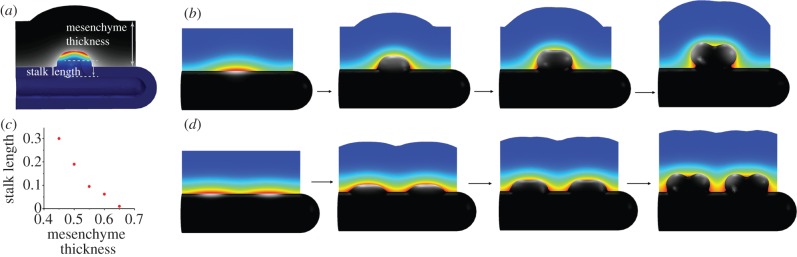
Branching of the ureteric bud into the metanephric mesenchyme. (a) The computational domain for the simulation of an ureteric bud after it has started to branch from the Wolffian duct into the metanephric mesenchyme. The double arrows illustrate the stalk length and the mesenchyme thickness. (b) The branching of the ureteric bud into the metanephric mesenchyme in response to GDNF signalling. Here, the bud grows out normal to its surface and at a speed proportional to the local concentration of the GDNF-receptor complex, as described by Iber et al. [73]. (c) The dependency of the length of the stalk to the first branching point on the thickness of the mesenchyme (both as defined in (a)). (d) The branching of the ureteric bud into the metanephric mesenchyme in a Sprouty^–/– mutant. The concentration of the GDNF-bound RET complex in the epithelium is indicated as a grey scale (white, highest; black, lowest); the strength of Gdnf expression in the mesenchyme is represented by a colour scale (red, highest; blue, lowest). (a–d) Adapted from Menshykau & Iber [72].

Turing mechanisms have been proposed for many other biological patterning phenomena, and reproduce the size- and geometry-dependence of biological patterns of various complexity [59,75]. In spite of the great similarity of simulated and real patterns, it remains to be established whether Turing-type mechanisms rather than alternative mechanisms underlie their establishment [76]. In fact, in several cases, Turing-type mechanisms have been wrongly assigned to patterning processes; for example, to explain the stripy expression pattern of pair-rule genes that emerge during Drosophila development [77]. These failures reveal the importance of a careful and comprehensive analysis of the underlying molecular interactions. That this is still not always carried out is largely due to the lack of sufficient information regarding the chemical properties of the morphoregulatory proteins (half-life, diffusion rates, endogenous concentrations, activities, etc.) and the molecular nature of their interactions (activating, inhibitory, etc.). Mutant phenotypes, if considered comprehensively rather than selectively, can also provide valuable information to challenge Turing models.

In the case of lung and kidney branching morphogenesis, we showed that, for the identified network components, the Turing model reproduces all available mutant phenotypes. In particular, in the case of lung branching morphogenesis allelic sequences of the Fgf10 knockdowns are available. Computational modelling showed that the inter-bud (inter-spot) distance is constant as the Fgf10 expression rate is reduced from 100% to 50%, but it greatly increases as the Fgf10 expression rate decreases below 50% [60]. This is in perfect agreement with the experimental results that show that WT, Fgf10^LacZ/+ and Fgf10^+/– have normal phenotypes and Fgf10 expression between 50% and 100%, whereas Fgf10 expression in Fgf10^LacZ/– mice is reduced to below 50%, and an abnormal phenotype with an increased distance between branching points is observed [78,79]. For kidney branching morphogenesis, a Wnt11/Ret allelic series has been reported [63], and, much as in the simulations, the phenotype of Wnt11 and Ret double mutants become more severe as the expression of both Ret and Wnt11 decreases [72]. Finally, in Sprouty mutants, several ureteric buds branch from the Wolffian duct, as also observed in the simulation (figure 13d).

A receptor–ligand-based Turing mechanism is thus an attractive candidate mechanism for the control of branching morphogenesis in both lung and kidney, in spite of the different proteins involved. In the following, we will compare the core networks that control branching morphogenesis in the glands with those in lung and kidney.

5. Branching morphogenesis in glands

5.1. Salivary glands

The signalling proteins that regulate branching morphogenesis in the salivary gland are well characterized, and FGF signalling is necessary for branching morphogenesis (figure 4b). Thus, transgenic mice lacking FGF8, FGF10, FGFR2b or EGFR do not develop further than the initial bud stage (Fgf8-conditional null mice, Fgf10-null mice and Fgfr2b-null mice), or they have substantially fewer terminal buds (Egfr-null mice) [15]. FGF signalling represses Wnt expression [80]. WNT signalling upregulates the expression of Eda in mesenchymal cells and EDA upregulates Shh expression in epithelial cells via NF-kB signalling [81]. SHH signalling upregulates Fgf8 expression [82], which, in turn, upregulates Fgf10 and Shh expression [83]. Removal of the Eda receptor or Shh results in dysplasia [82]. Knock-out of Bmp7 results in reduced branching, and BMP7 is able to rescue branching in salivary glands treated with the FGFR signalling inhibitor SU5402, suggesting that BMP7 may be downstream of FGFR signalling, or in a parallel pathway [84]. The receptor–ligand interactions are thus very similar to those in the lung (e.g. FGF10-FGFR2b or SHH-PTCH1) and kidney (i.e. WNT and FGF10), and mesenchyme from lung buds can induce a branching of cultured submandibular epithelium [32]. Given these parallels, a similar Turing-based mechanism may also control branching in the salivary gland. Experiments in which the FGF10 diffusivity was modulated by alteration of the binding affinity of FGF10 for heparan sulfate highlight the relevance of a diffusion-based mechanism as they reveal an effect on the branching pattern (elongation versus branching) in the salivary gland [14].

5.2. Pancreas

In contrast to the classical epithelial budding and tube extension observed in other organs, a pancreatic branch takes shape as a multi-lumen tubular plexus, and coordinately extends and remodels into a ramifying, single-lumen ductal system [85]. This initial tube formation takes place from E9.5 to E12.5. During a secondary transition from E13 to birth, branching morphogenesis is observed [86]. In vivo time lapse imaging reveals that the main mode of branching during pancreas branching morphogenesis is lateral branching (86%); terminal bifurcations are also observed, but less often (14%) [87]. The lateral branching mode deployed during pancreas development is simpler than that in the case of lung branching—new buds appear predominantly on one side of the outgrowing tip. However, this might be an artefact of the culture experiment; for example, lung branching patterns are known to be different in vivo and in vitro. Similar to lung branching morphogenesis, both FGF10/FGFR2b [16,17] and SHH/PTCH1 receptor–ligand modules play an important role during pancreas branching morphogenesis, with Hedgehog signalling repressing Fgf10 expression (figure 4c) [88]. Two factors, BMP4 and FGF10, promote pancreatic morphogenesis at the primary stages of the organogenesis. Bmp4 is the first to be expressed and promotes budding formation, whereas Fgf10 is expressed later and promotes (among other things) branching of the pancreatic bud [16]. Ephrin signalling has also been implicated in pancreatic branching as removal of the EphB2 and EphB3 receptors results in shortened branches and smaller pancreata [85]. The developing pancreas displays predictable trends in overall shape and in the elaboration of specific branches [85]. The early stages have been simulated using a fully executable, interactive, visual model for four-dimensional simulation of organogenic development [89]. A computational model of the later developmental stages, including the branching morphogenesis of the exocrine pancreas, is still required, as is a model of the processes that result in the differentiation of the pancreatic tissue into ducts and enzyme secreting acinar cells at the tips of the branches.

5.3. Prostate

Circulating androgens initiate the development of the prostate from the urogenital sinus [13]. The androgen receptor is expressed in the mesenchyme and is necessary for budding of the urethral epithelium [13]. Androgens have been shown to induce the expression of Fgf10 and FGF receptor 2 (Fgfr2)-IIIb in the urethra [90]. FGF7 and FGF10, expressed in the mesenchyme, bind to FGFR2 on epithelial cells, which leads to the induction and maintenance of Shh expression [13]. SHH signalling, in turn, downregulates Fgf expression [13]. Moreover, ductal branching and budding are inhibited by the mesenchymal signalling factors BMP4 and BMP7, and stimulated by the antagonist of these BMPs. The regulatory loop is thus very similar to the one in the lung (figure 4a), and FGF10 has been found to be essential for the development of the fetal prostate [91]. It should be noted that most of the ducts remain unbranched until birth in rodents, but subsequent epithelial–mesenchymal interactions result in further elongation and branching morphogenesis.

5.4. Mammary glands

The development of the mammary proceeds in three stages: a rudimentary gland develops in the embryo and remains quiescent until puberty [92]. During puberty extensive branching occurs, and the mammary glands will undergo further rounds of branching during pregnancy. In male mice, the mesenchyme surrounding the stalk continues to condense until it severs the bud, resulting in a greatly diminished ductal system [93]. Signalling of parathyroid hormone-like hormone (PTHLH) via type 1 PTH/PTHLH receptor (PTH1R) appears to play a key role in the initial process of generating a rudimentary ductal system before birth [94]. Pthlh is expressed in the epithelium and signals through its mesenchymal receptor PTH1R to modulate WNT signalling, and to induce the BMP receptor-1A in the mesenchyme [95]. BMP4 signalling can rescue ductal outgrowth in the cultures of Pthlh^–/– mammary buds [95].

Similar to the lung and the kidney, epithelial–mesenchymal signalling by FGFs, EGFs and WNTs plays an important role in controlling branching morphogenesis [92,96]. FGF receptor 2 is required on epithelial cells for ductal elongation [22], but a unique chemoattractant (such as FGF10 in the lung and salivary gland [97] or GDNF in the kidney [21,69]) has not been identified [7]. TGF-β signalling, on the other hand, has been shown to be important to reduce branching, and thereby restrict branch formation [57,98]. TGF-β signalling has been shown to induce the deposition of ECM [57,98] and to affect basal cell proliferation via roundabout 1, SLIT2 and WNT signalling [99]; the non-canonical WNT signalling member WNT5a is necessary for the effects of TGF-β on branching morphogenesis [100].

Culture experiments support a similar control mechanism for branching morphogenesis as in the other organs, as mesenchyme from the salivary gland induces branching of the mammary gland epithelium, even though the branched structure and lobe then resemble that of the salivary gland [101]. Contrary to the lung and the kidney, branching in the mammary glands is, however, not stereotyped [7,96]. The mechanisms that have been proposed to control branching morphogenesis in the mammary gland have so far mainly focused on mechanical constraints, as provided by interactions with the ECM [44,102], and on diffusion-based geometry effects (figure 10a) [57,103]. Experiments support an influence of mechanical stress on branching morphogenesis in mammary glands [104], but the composition of the ECM is likely to be the result of regulation by signalling networks [57,98].

6. A general mechanism for the control of stereotyped branching

The early branching events differ between the organs (figure 1), but are highly stereotyped (at least in lung and kidney), and must therefore be carefully controlled. A number of mechanisms have been proposed, but most fail to meet all key aspects of such a branching mechanism, which are (i) the production of stereotyped pattern from noisy initial conditions, (ii) pattern stability (or pattern fixation) during outgrowth, such that the pattern can support the outgrowth of the branch, and (iii) the ability to control branching morphogenesis in different organ systems with different signalling networks. The receptor–ligand-based Turing mechanism meets all these conditions [50,60,72]. In particular, it works with a range of signalling networks, because all signalling involves the interaction of secreted ligands with some receptors (figure 4), and any ligand–receptor pair that fulfils the following three conditions can give rise to Turing-type reaction kinetics:

• (i) the ligand must diffuse faster than its receptor, which is generally the case for soluble ligands and membrane receptors [105–108];

• (ii) receptor and ligand must interact cooperatively, which is typically the case when multimeric components bind each other; and

• (iii) receptor–ligand binding must result in increased receptor production. This has been documented in the case of SHH/PTCH1 [109], and GDNF/RET [6,65,68]. In the case of FGF10, both up- and downregulations have been reported [110–113]. BMPs as well as other ligand–receptor systems would also meet the requirements [114,115].

The ligand–receptor-based Turing mechanism is different from the classical activator–inhibitor Turing mechanism, also known as Gierer–Meinhardt Turing mechanism [116], which is the most commonly studied Turing mechanism. Unlike in the activator–inhibitor mechanism, only one ligand is required in the mechanism proposed here, and the two components (ligand and receptor) assume their highest (and lowest) concentrations in different places (figure 14). The ligand–receptor mechanism is based on Schnakenberg-type reaction kinetics [117], which correspond to the activator-depleted substrate Turing mechanism [116].

Figure 14.

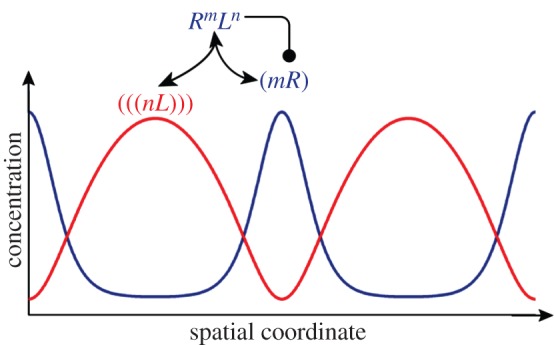
Cooperative receptor–ligand interactions can give rise to Turing patterns. The depicted receptor–ligand interaction can result in spatial patterns via Schnakenberg-type reaction kinetics. Here, m receptors (R) and n ligand molecules (L) (with m + n > 2) need to bind to form the complex R^mLⁿ. The receptor–ligand complex then upregulates the receptor concentration (by increasing its expression, limiting its turn-over or similar). To obtain Turing patterns, ligands must diffuse much faster than their receptors. As is characteristic for Schnakenberg-type Turing pattern, the highest receptor and ligand concentrations are then observed in different places.

Turing mechanisms have been proposed for many systems, and also an alternative Turing-based model has previously been proposed that achieved branching morphogenesis by a combination of patterning and fixation events via cell differentiation [118]. Further experimental studies are now required to carefully test the proposed mechanisms. Turing patterns, much like the other proposed mechanisms, are very sensitive to the geometry of the domain. Simulations of the models on realistic embryonic geometries would therefore present a good test to the model. Developmental sequences of three-dimensional geometries can now be obtained with optical projection tomography (OPT) [119], or two photon or light sheet microscopy [120,121]. Software packages are readily available to construct the four-dimensional geometric series and to efficiently simulate the signalling models on the growing and deforming domains [73,122,123]. The correct mechanism should be able to predict the branch points.

Current models typically consider tissue as a continuum, without cellular resolution. Cell boundaries, however, can have important effects, in particular in the ligand–receptor-based Turing mechanism, where receptor is restricted to the surface of single cells. While we have previously shown that similar patterns can be obtained also on static, cellularized domains [50], it will be important to develop simulation tools that permit the efficient simulation of patterning in three-dimensional cellular systems. In that regard it will be important to include cell growth, diffusion of soluble factors, and diffusion restrictions imposed by cell boundaries to membrane and cytoplasmic proteins.

Finally, it will be important to address the issue that classical Turing models produce patterns only for a tiny parameter space. For such a small parameter space, it is difficult to explain how patterns could emerge in the first place and how they could be preserved during evolution.

7. Conclusion

Branching morphogenesis has long fascinated biologists and theoreticians, and many different effects have been defined that all impact on the branching process. We propose that Turing patterns as a result of receptor–ligand interactions constitute a general core mechanism that controls branching morphogenesis in the different organs, as well as other patterning processes in the various developmental systems. Much as complex fractal patterns can be generated with few rules, a Turing mechanism can, in principle, implement a complex, stereotyped sequence of branching events based on few interacting proteins. It should be noted that fractals and Turing patterns are otherwise very different, and Turing mechanisms do not give rise to fractal patterns.

Many of the other discussed effects are likely to affect the patterning process without being its key controller. One such important effect is likely to be the diffusion-based geometry effect (figure 10) [57], which biases the pattern, but which cannot support bifurcating outgrowth by itself. Moreover, the distance between the Fgf10-expressing distal mesenchyme (close to the mesothelium) and the Shh-expressing epithelium can be expected to affect the exact lung branching pattern without being responsible for the bifurcating concentration profiles per se [12]. Similarly, mechanical differences are clearly affecting the branching process. How these arise and how they are controlled in space and time will be an important direction of future research.

A key open question concerns the mechanism that mediates branch outgrowth once an initial symmetry break in the cellular signalling has defined the branch points. This is likely to be the result of a combination of local changes in the proliferation of cells (in particular, their cell division plane), cell deformation and cell migration [62,124,125]. Similarly, it will be of interest to understand how the diameter of the tubes is defined, and how these diameters are shaped to eventually give rise to a fractal-like sequence in the adult.

Funding statement

The authors acknowledge funding from an SNF Sinergia grant, the SNF SystemsX RTD NeuroStemX, a SystemsX iPhD grant and an ETH Zurich postdoctoral fellowship to D.M.