Abstract
A computational method is developed to allow molecular dynamics simulations of biomembrane systems under realistic ionic gradients and asymmetric salt concentrations while maintaining the conventional periodic boundary conditions required to minimize finite-size effects in an all-atom explicit solvent representation. The method, which consists of introducing a nonperiodic energy step acting on the ionic species at the edge of the simulation cell, is first tested with illustrative applications to a simple membrane slab model and a phospholipid membrane bilayer. The nonperiodic energy-step method is then used to calculate the reversal potential of the bacterial porin OmpF, a large cation-specific β-barrel channel, by simulating the I-V curve under an asymmetric 10:1 KCl concentration gradient. The calculated reversal potential of 28.6 mV is found to be in excellent agreement with the values of 26–27 mV measured from lipid bilayer experiments, thereby demonstrating that the method allows realistic simulations of nonequilibrium membrane transport with quantitative accuracy. As a final example, the pore domain of Kv1.2, a highly selective voltage-activated K+ channel, is simulated in a lipid bilayer under conditions that recreate, for the first time, the physiological K+ and Na+ concentration gradients and the electrostatic potential difference of living cells.
INTRODUCTION
The cell membrane presents a barrier between the cytoplasm and the surrounding environment that is critical to preserving the integrity of the cell. By virtue of this barrier, the differences in ion concentrations across the membrane that are established under the action of various membrane transport proteins can give rise to a difference in electric potential. Although it is relatively straightforward to control both the concentration gradients and membrane potential in experimental biophysical studies, reproducing this set of conditions in computer simulations is nontrivial.
To allow for the simulation of ion channels with a realistic implementation of asymmetric ion concentration and transmembrane potential boundary conditions, a grand canonical Monte Carlo (GCMC)/Brownian dynamics (BD) was implemented previously (Im et al., 2000). In GCMC/BD, asymmetric boundary conditions were imposed on a finite nonperiodic simulated system surrounded by concentration buffer regions (Im et al., 2000). Although this method provided important insight into the factors governing the permeation of wide aqueous pores (Im and Roux, 2002a; Noskov et al., 2004; Egwolf et al., 2010; Lee et al., 2011, 2012), it remained based on fairly crude approximations. For instance, the solvent was represented as a continuum dielectric to enable the GCMC insertion and annihilation of ions on both sides of the membrane. However, imposing asymmetric concentrations in explicit solvent molecular dynamics (MD) simulations introduces special difficulties. Such explicit solvent MD simulations are normally performed with conventional periodic boundary conditions (PBCs), which are critical to reduce finite-size effects. Unavoidably, the PBCs also eliminate the distinction between the two sides of a membrane. Because there is a single continuous bulk solution where ions are free to diffuse and equilibrate, concentration gradients across the membrane cannot be simulated.
One possible avenue for simulating asymmetric ion concentrations in MD simulations with explicit solvent is to use a dual-membranes–dual-volumes strategy (Sachs et al., 2004) in which two spatially separated membranes are included to create two disconnected bulk phases between them (one of the two membranes is replaced by an artificial vacuum separator in the most recent implementation to reduce the computational burden; Delemotte et al., 2008). Manually adjusting the number of cations and anions in the two bulk regions makes it possible to set the effective membrane potential near some pre-chosen value Vm (Delemotte et al., 2011). The latter is related to the charge imbalance across the membrane,
through the linear relation Vm = ΔQ/C, where C is the system’s capacitance. However, frequent manual adjustments are necessary, as the effective membrane potential can shift dramatically by hundreds of millivolts when a single discrete ion is transferred across the membrane because of the small value of C in finite systems (Treptow et al., 2009; Delemotte et al., 2011; Roux, 2011). For example, in previous dual-volume simulations of the voltage-dependent K+ channel, it was necessary to readjust the ion distribution periodically to compensate for the conformational changes of the protein. To avoid the need for these cumbersome manual adjustments, which would preclude simulations under steady-state ion-flux conditions, the dual-volume method was recently extended to allow the ions of the two bulk phases to exchange with water molecules according to a GCMC scheme (Kutzner et al., 2011).
Despite its appeal, a dual-volume strategy remains computationally burdensome, as it doubles the size of the simulated system and the computational cost of carrying out such simulations. Furthermore, the annihilation and reinsertion processes of the particles implemented in the GCMC constitute non-Newtonian stochastic events that interrupt the course of the MD trajectory and add to the overall computational cost. Ideally, it would be desirable to maintain solute concentrations on both sides around chosen values while simulating a single-membrane–single-volume system with conventional PBCs.
In this paper, we show that realistic asymmetric ion concentrations can be realized by introducing a nonperiodic “energy step” at the edge of the simulation cell to maintain a chemical potential difference across the bulk phase. The height of the step can be adjusted dynamically during the simulation to converge to a desired concentration difference between the two phases on either side of the membrane. In addition to the concentration asymmetry, a membrane potential can also be established by applying a constant electric field acting on all charged particles in a direction orthogonal to the membrane (Roux, 2008; Gumbart et al., 2012). The nonperiodic energy-step method is first illustrated by considering a simple system with a fixed nonpolar slab membrane as well as a realistic phospholipid membrane bilayer. The method is then validated by calculating the reversal potential and the conductance of the bacterial porin OmpF under asymmetric conditions. Finally, the method is used to simulate the physiological conditions experienced by the pore domain of the K+ channel Kv1.2, including the negative membrane potential and the asymmetric Na+ and K+ concentrations on either side of the membrane.
THEORY AND METHODS
Theoretical framework
Let us consider a closed system in which the accessible volume is divided into two regions, V1 and V2, along the z axis. The system is described by the potential energy U0(R), where R represents all the atomic coordinates. The equilibrium Boltzmann distribution is
| (1) |
where β = 1/kBT. We focus our attention on one given type of particle in the system and assume that, without any additional energy term, the potential energy U0(R) yields a uniform concentration of the particles. For any configuration R, the instantaneous number of those particles in volume V1 is equal to
where Θ(z) is a step function equal to 1 only when z lies within the volume V1. We wish to enforce that the average of N1(R) will be equal to chosen value i.e.,
| (2) |
If there are N particles of this type in the system, it should be possible to enforce this condition, as long as In practice, a wide range of perturbations could be introduced to impose this condition on the system. However, arbitrary modifications are likely to introduce undesirable and spurious biases. Ideally, one would like to modify the statistical distribution to impose the condition in the least intrusive manner. This goal can be achieved through Jaynes’ maximum entropy method (Jaynes, 1957), whereby one seeks to maximize the excess cross-entropy functional η,
| (3) |
under the constraints that the modified probability distribution ρ(R) is normalized,
| (4) |
and that the average of N1 is known:
| (5) |
The quantity η is a functional of the probability distribution ρ(R), and the constrained optimization problem can be solved using the method of Lagrange multipliers, leading to the form:
| (6) |
where the normalization was implicitly incorporated in the probability distribution, and ε is an unknown coefficient that must be adjusted to match the condition in Eq. 5. The form of ρ(R) in Eq. 6 is consistent with the introduction of a simple energy step, that acts on all the affected particles crossing into the volume V1 along the z axis, with a magnitude of E = kBTε. In principle, determining the magnitude of the energy step may require iterative adjustments until the condition in Eq. 5 is satisfied. In practice, the average number of particles in V1 can be approximated by assuming that the affected particles are nearly independent. In this case, the probability of finding the particles in each volume p1 and p2 and its respective averages can then be written as a function of ε,
| (7) |
and
| (8) |
where p1 + p2 = 1 and V1 + V2 = V is the total volume. For a binomial distribution, the mean number of particles in V1 is Np1, and the variance is Np1(1 − p1). So, to a first approximation, the magnitude of the energy step must be chosen such that The normalized relative root-mean-square (RMS) fluctuations of the number of particles is and for V1 and V2, respectively. It follows that the average concentrations of particles in volumes V1 and V2 are (we drop the brackets for the sake of simplicity)
| (9) |
and
| (10) |
respectively. The concentration ratio is (C1/C2) = e−ε. The relative RMS fluctuation of the concentration in V1 is
| (11) |
and the relative RMS fluctuation of the concentration in V2 is equal to
| (12) |
For the sake of simplicity, let us assume that the two volumes are identical here, i.e., V1 = V2 = V/2. The average concentrations are then
| (13) |
and
| (14) |
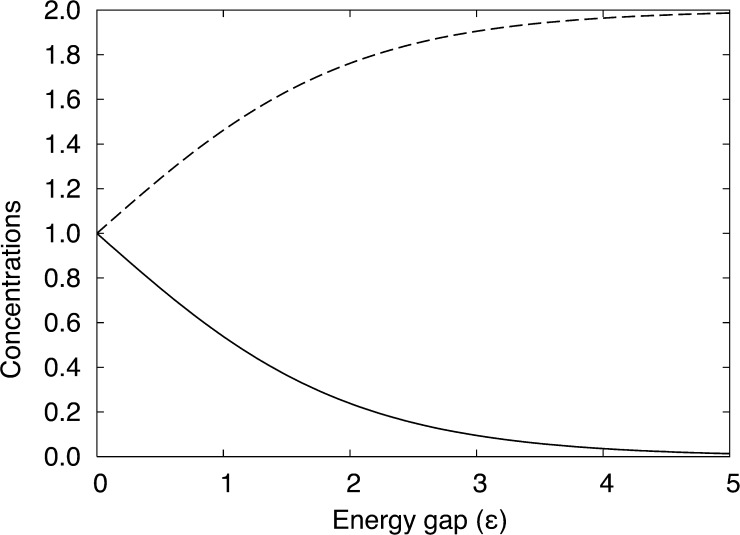
where C = N/V is the overall concentration of the particles in the entire system. Note that the maximum achievable concentration (here 2N/V) occurs when all the particles are forced into one of the two volumes (as shown in Fig. 1). The maximum achievable concentration could be manipulated by either introducing more particles into the system or by choosing a smaller volume for one of the two regions. The range of the concentration ratio achievable is controlled solely by the energy step (in units of kBT), i.e., (C1/C2) = e−ε. However, to achieve a certain concentration C1 in V1, the starting number of solutes should be chosen to build the system such that C1V1 + C2V2 = N, where N is the total number of solute particles in the system.
Figure 1.
Solute concentrations C1 (solid line) and C2 (dashed line) in volumes V1 and V2 as a function of the energy gap ε.
In a practical implementation for MD simulation, it is simpler to avoid the discontinuous energy step by defining a small transition region. Fig. 2 provides a schematic representation for a typical solvated membrane system. PBCs replicate the system in the three dimensions and, thus, connect the two aqueous solutions on the two sides of the membrane along the z direction, defined as the membrane normal. A small transition region of thickness d/2 is defined at each of the edges of the periodic box, over which an external constant force f directed along the z axis acts on all ions. The constant force f over the periodic transition region of thickness d results in a nonperiodic energy step ε = βfd, which alters the chemical potential difference between the ions in the two compartments, generating a concentration ratio of r = (C1/C2) = e−ε.
Figure 2.
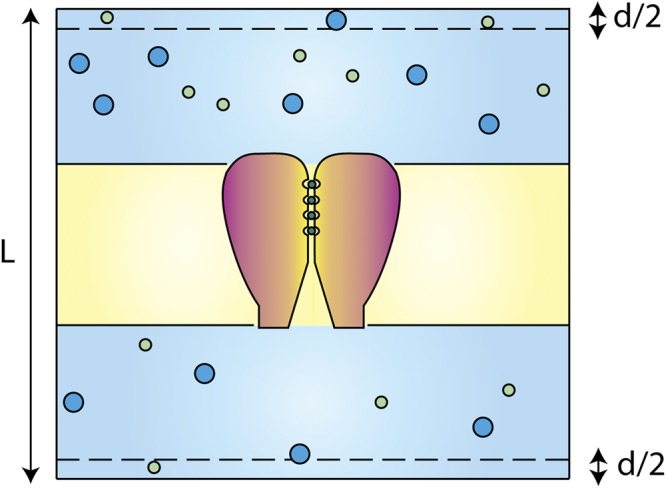
Schematic representation of a typical solvated membrane system. To impose a concentration gradient across the membrane, a constant force is applied to the ions near the boundaries of the periodic box (z > L/2 − d/2 or z < −L/2 + d/2).
It is of interest to point out that the present method is analogous to a previous treatment used to impose hydrostatic pressure differences across a membrane (Zhu et al., 2004), a thermodynamic property that also suffers from the lack of distinct bulk water phases on either side of a membrane in periodic systems. This problem was solved through the application of a small force to water molecules in a region far from the membrane. The resulting chemical potential difference for water between the two sides of the membrane was Δµ = fd, where f was the applied force and d was the size of the region of application in the direction normal to the membrane (Zhu et al., 2004). The method was applied to the study of water transport in aquaporin, permitting calculation of the osmotic permeability, which was found to be in agreement with experimental determinations (Zhu et al., 2004).
Iterative dynamic energy-step adjustment
Although the value of the energy step needed to set a given concentration ratio r can be determined directly as ε = −ln(r) in the ideal case, ion–ion interactions may affect the expected concentration ratio in practice. This deviation from the ideal value determined above requires further adjustment of the energy step as the ionic concentrations change during the simulation. The external force, initially set to f = −kBTln(r)/d, is then adjusted dynamically to reach the proper concentration ratio. Two parameters, τ and α, control the response of the system to the force adjustment. The external force acting on different ionic species is updated according to the following protocol:
| (15) |
and
| (16) |
where C1 and C2 are the estimated ion concentrations in each compartment, and 〈…〉 represents a time average over a period of τ immediately preceding the current time step; ατ determines the response time of the system. Temporal averaging of the concentration ratio over τ is necessary to overcome instantaneous (thermal) fluctuations in the number of ions as they jump between the boundaries of the energy step. The force adjustment follows the initial equilibration of the system and continues for a period of time comparable to the relaxation time of the system, i.e., a few nanoseconds for a system including a single-membrane protein. Ionic concentrations are monitored during the simulation, and the external force is gradually adjusted to reach the ideal concentration over a period of ατ. Convergence of the force is a function of fluctuations in number of ions and, thus, longer simulations might be necessary for smaller systems. To obtain better estimates of ionic concentrations and avoid fluctuations near boundaries, the time-dependent concentrations are calculated for a region of length ΔL, smaller than the length of the entire simulation system L, but large enough to include a finite number of ions at each time. This region should also be located far from the protein/membrane or any discontinuity in the system.
Simulation details
All simulations were performed using the MD program NAMD (Phillips et al., 2005) together with the CHARMM27 or CHARMM36 force field for proteins (MacKerell et al., 1998) and lipids (Feller et al., 1997; Klauda et al., 2010), and TIP3P (Jorgensen et al., 1983) for water. PBCs were used in all simulations, and electrostatic interactions were calculated using the particle-mesh Ewald method (Darden et al., 1993) with a grid spacing of at least 1 per Å. Simulations were performed at constant volume and constant temperature (300 K) with a time step of 1 fs (2 fs for the OmpF simulations). The algorithm described above was implemented in the Tcl interface of NAMD, where external forces were defined and adjusted throughout the simulation.
The membrane slab was constructed of individual carbon atoms arranged in a body-centered cubic lattice with a spacing of 4 Å, similar to the systems simulated in Gumbart et al. (2012). The membrane has six vertical layers and, thus, a thickness of 20 Å, not accounting for the radius of the atoms themselves. In each simulated system, the membrane is fully solvated above and below and ionized with Na+, K+, and Cl− ions at a concentration of either 1 M or 500 mM. The system size for the membrane slab was 44 Å × 44 Å in the membrane plane and 75 Å perpendicular to the membrane. The system consists of ∼11,000 atoms.
The palmitoyl oleoyl phosphatidylcholine (POPC) lipid bilayer system was generated using visual MD (Humphrey et al., 1996). The hydrated system, consisting of 131 lipid and 10,000 water molecules, was ionized with an initial concentration of 55 mM K+, 55 mM Na+, and 110 mM Cl− ions, such that the low concentration and high concentration sides could be maintained at 10 and 100 mM when a concentration ratio of 10:1 was imposed.
The OmpF simulation model consisted of the OmpF trimer embedded in a POPC lipid bilayer, which was constructed using the CHARMM-GUI (Varma et al., 2006; Jo et al., 2008). The structure of the protein was taken from Protein Data Bank accession number 2OMF (Cowan et al., 1995). The protein–membrane system was solvated with explicit waters, and ions were added in visual MD for a total system size of ∼200,000 atoms. Tetragonal PBCs were applied with a distance of 123.5 Å in the xy direction and 127.5 Å in the z direction. A constant electric field Ez corresponding to a transmembrane potential, V, of +150, 0, and −150 mV was applied along the z direction perpendicular to the membrane to all the atoms in the simulation box (Roux, 2008):
| (17) |
where Lz is the length of the system in the z direction. It is worth emphasizing that, although a constant electric field was applied to the system (Roux, 2008), it should be understood that the average electrostatic potential is expected to vary nonlinearly because of the irregular shape of the membrane and of the pore. For illustrative examples, refer to the recent review by Gumbart et al. (2012).
Protein residues E296, D312, and D127 were protonated (Im and Roux, 2002a,b; Varma et al., 2006), and harmonic restraints (with a force constant of 1.0 kcal−1 Å−1) were applied to the Cα atoms at their crystallographic positions to prevent channel closure by the repositioning of L3 under the applied voltage. The Langevin friction was removed for the ions. Pressure control was removed to prevent distortion of the system by the electric field; the virial used in the constant pressure algorithm is no longer well defined in the system when applying an external constant electric field. Simulations were therefore performed at constant volume and temperature (300 K) with a time step of 2 fs. The asymmetric concentration gradient was initially defined with 1 M KCl above the membrane and 0.1 M KCl below, and it was maintained throughout the simulation by imposing an energy step at the edges of the periodic box. Total ionic current was determined by calculating the displacement of all charges across the membrane using (Crozier et al., 2001a,b; Aksimentiev and Schulten, 2005; Pezeshki et al., 2009)
| (18) |
where zi and qi are the z coordinate and charge of ion i, respectively, N is the total number of particles in the system, and Δt is the time step of 100 ps (the results are independent of Δt). Current calculations for individual ions IK and ICl were determined by counting the number of K+ or Cl− that cross the pore over the trajectory. This also allowed the error σi to be calculated for the total ionic currents by assuming a Poisson process (Sotomayor et al., 2007), such that
| (19) |
where N(i) is the number of ion crossing events at the membrane potential Vm(i). Ion conductance G and the reversal potential Vrev were calculated by a least-square fitting of the I-V curves (Fig. 6 B) that minimized
| (20) |
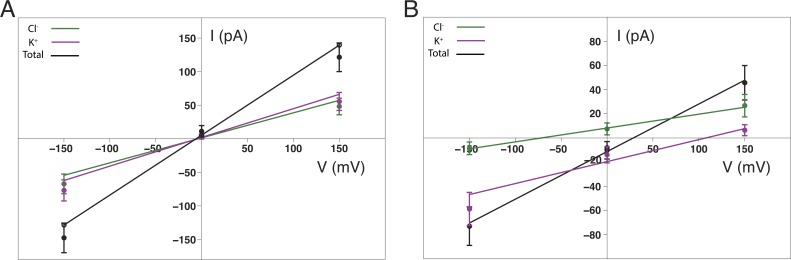
Figure 6.
MD simulation of ion permeation and selectivity of OmpF porin. (A) Ion selectivity of OmpF porin. The I-V curves were calculated in (A) 1 M KCl symmetric solution or (B) 0.1:1 M KCl asymmetric solution from MD trajectories. The total current per monomer (black) is the sum of K+ (purple) and Cl− (green) currents. Error bars are calculated from Eq. 19.
The initial setup of the Kv1.2 system was taken from Khalili-Araghi et al. (2006), in which the pore domain of the voltage-gated potassium channel Kv1.2 has been equilibrated in a patch of POPE lipid bilayer. The structure of the protein was taken from Protein Data Bank accession number 2A79 (Long et al., 2005). The number of ions in the aqueous solution surrounding the membrane–protein system has been adjusted to reach 55-mM concentrations of KCl and NaCl over the entire system. The new configuration was then equilibrated for 10 ns, after which concentration ratios of 10:1 and 1:10 were imposed between Na+ and K+ ions, respectively, on the two sides of the membrane. In addition, a membrane potential of −100 mV was applied via an external electric field Ez = V/Lz (Roux, 2008).
RESULTS AND DISCUSSION
Illustrative examples
To illustrate the effectiveness of the nonperiodic energy-step method, we first simulated a system with a simplified membrane slab surrounded by aqueous KCl or NaCl salt solutions, as shown in Fig. 3 A. The simulations start from a uniform distribution of ions on both sides of the membrane with concentrations C1 and C2 (C1 = C2). External forces are applied to the ions, K+, Na+, and Cl−, as they enter a region 2.5-Å wide at the edges of the periodic box to separate the ions on either side of the membrane. The forces are applied for 20 ns after the initial equilibration, or until the ion concentration on each side of the membrane is stabilized. Fig. 3 (B and C) shows the ratio between the ion concentrations, C1 and C2, on the two sides of the membrane averaged over the last 10 ns of the simulation trajectories as a function of the applied energy step (ε = βfd. The error bars show the standard error in the calculations resulting from the finite number of ions in the system and the finite length of the trajectories.
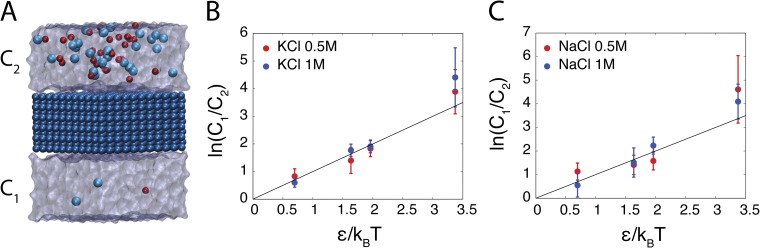
Figure 3.
A membrane slab separated by two ionic solutions with concentrations C1 and C2. (A) Snapshot of the simulation system after application of the energy step. (B and C) The ratio of ionic concentration as a function of the applied force for simulations consisting of (B) KCl or (C) NaCl solutions.
As shown in Fig. 3 (B and C), the concentration ratio increases exponentially with the applied force. The initial concentrations vary between 0.5 and 1 M for each system. Small deviation of the data points obtained from simulation trajectories and the theoretical values (shown as a straight line) indicate the ability of this method to maintain a concentration gradient even at concentrations as high as 2 M. The relative fluctuation in the number of ions increases as the magnitude of the applied force is increased. Imposing a concentration ratio of 10:1 between the two ionic solutions results in a system where only a few ions are left in one solution, assuming a volume of ∼10 nm. Thus, realistic simulations of membrane proteins require a larger volume on each side to allow physiologically relevant concentrations of 100 mM to result in a finite number of ions in the system.
Under physiological conditions, cellular membranes are separated by two ionic solutions. Although the extracellular solution is maintained at concentrations of 100 mM NaCl and 10 mM KCl, the intracellular solution has 10 mM NCl and 100 mM KaCl. Using the method presented in this paper, we have been able to simulate a POPC lipid bilayer in a mixture of NaCl and KCl solutions with an asymmetric distribution around the membrane. The concentration of each ionic species is controlled separately. Two different nonperiodic energy steps are introduced at the edges of the periodic box normal to the plane of membrane, where they act on either Na+ or K+ ions (see Fig. 4 A). The nonperiodic energy steps concentrate K+ ions in the top compartment (z > 0) and Na+ ions in the bottom compartment (z < 0), as shown in Fig. 4 (A and B). The steps are defined such that K+ concentrations are maintained at a ratio of 10:1 (100:10 mM), whereas Na+ concentrations have a ratio of 1:10 (10:100 mM) between the top and bottom compartments. The number of ions in each compartment stabilizes within 20 ns after application of the external force (see Fig. 4, C and D). Additional simulations of a POPC lipid bilayer with a mixture of NaCl and KCl solutions under symmetric concentration condition (without the energy step) yielded density profiles that are consistent with these results (unpublished data).
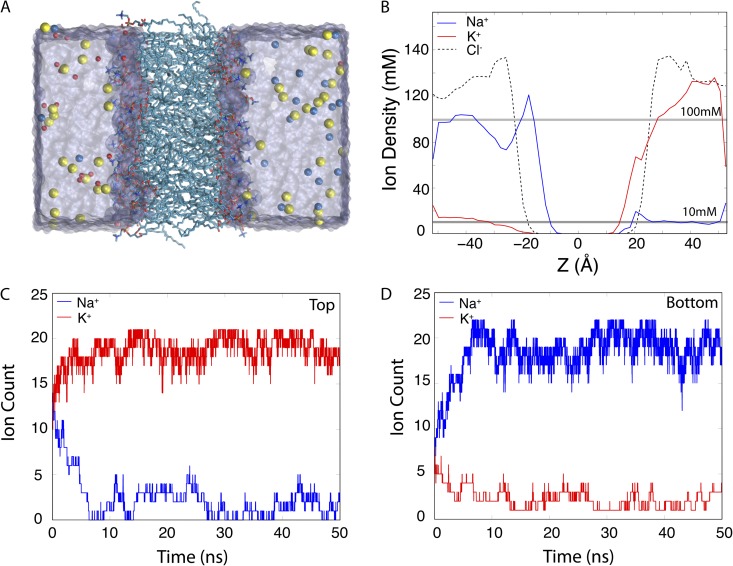
Figure 4.
A POPC lipid bilayer simulated under asymmetric ionic concentrations. (A) Snapshot of a POPC lipid bilayer simulated under asymmetric ionic concentrations. Lipid molecules are shown in licorice representation, and Cl− (yellow), Na+ (red), and K+ (blue) ions are shown as spheres. (B) Average density profile of the ions along the z axis normal to the plane of membrane. (C and D) Number of Na+ and K+ ions in the top and bottom compartments as a function of time.
Fig. 4 B shows the density profile of K+, Na+, and Cl− ions along the z axis, normal to the plane of membrane. As shown in the figure, the ionic concentrations for Na+ and K+ ions drop rapidly over the imposed energy step near the edges of the simulation box (within a region of 5 Å). Cations maintain an average density of 10 mM on the low concentration side, whereas the high concentration side reaches an average density of ∼100 mM. The interaction between negatively charged lipid head groups and cations results in penetration of K+ and Na+ ions inside the membrane, an artifact that has also been observed in previous simulations of membrane proteins (Böckmann et al., 2003; Vácha et al., 2009). During the simulation, the height of the energy step can be adjusted to maintain the proper ratio between average ionic concentrations within a region that excludes the ions that make salt bridges with the lipid head groups.
Reversal potential of OmpF porin
General diffusion porins, such as the OmpF channel from Escherichia coli, are inserted in the outer membrane of Gram-negative bacteria and allow exchange of hydrophilic nutrients with the environment. The crystal structure of OmpF porin reveals a trimer of β barrels, where each monomer is comprised of a separate pore marked by large extracellular and periplasmic pore vestibules that are separated by a constriction zone formed by the insertion of extracellular loop L3 into the pore (Cowan et al., 1992, 1995). Unique factors govern conductance and specificity of these large aqueous pores. Elucidation of these factors is essential for understanding the permeation mechanisms of ion channels in general, as well as for assessing how their cellular regulation is controlled.
Previous computational modeling studies have shown that electrostatic interactions exist between permeating ions and charged porin residues (Im and Roux, 2002a,b), suggesting that ion movement does not follow simple diffusion patterns. Instead, a separation of charged residues over 40 Å from the extracellular to periplasmic vestibules of the OmpF channel leads to the formation of two well-separated average transition pathways for diffusion of cations and anions (Im and Roux, 2002b). Furthermore, ion–ion pairs seem to play an important role in their permeation, especially at high salt concentration. Specifically, Cl− permeation has been observed to require K+ counter ions, whereas K+ permeation can occur independently of Cl− (Im and Roux, 2002b).
Ion conduction through OmpF porin was first examined under symmetric conditions. The OmpF trimer channel embedded in a POPC lipid bilayer (Fig. 5) and surrounded by a symmetric salt solution of 1 M KCl was simulated for 50 ns in the presence of an electrostatic potential of +150, 0, or −150 mV. The resulting ion conductances for a single OmpF pore are 0.81 and 0.98 nS under applied voltages of +150 and −150 mV, respectively. These values are smaller than the experimental conductance of 1.35 nS based on electrophysiological measurements performed for OmpF reconstituted in proteoliposomes (Kreir et al., 2008). A similar reduction in ion current across the OmpF pore was observed previously by all-atom MD with applied electric fields under 1 V using CHARMM force fields (Pezeshki et al., 2009). In fact, a significant decrease in conductivity with salt concentrations around and above 1 M was shown even in bulk water (Pezeshki et al., 2009). However, despite the reduction in total ion conductance, the MD trajectories reproduce the diffusion pathways and selectivity properties of ions across the OmpF pore. Specifically, more current is carried by K+ than Cl− (IK/ICl of 1.16 and 1.14 at +150 and −150 mV, respectively; Fig. 6 A), which reproduces the slight cation selectivity of the OmpF channel and is in agreement with values obtained by previous MD, BD, and Poisson–Nernst–Planck (PNP) simulations (Im and Roux, 2002a; Pezeshki et al., 2009).
Figure 5.
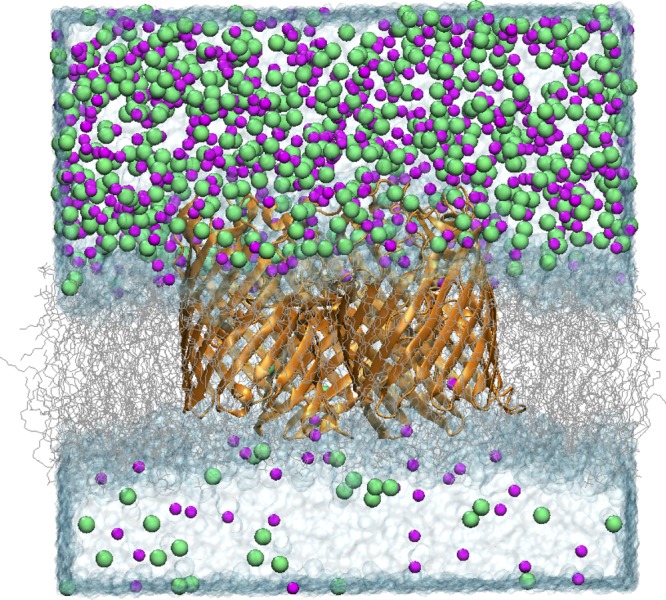
Snapshot of the simulation system consisting of an OmpF trimer embedded in a POPC membrane, fully solvated with 1 M KCl above the membrane and 0.1 M KCl below the membrane, after the application of the energy-step function. K+ (magenta) and Cl− (green) are shown as spheres.
OmpF’s weak specificity for cations is revealed by reversal potential (Vrev) measurements. Vrev is the applied transmembrane voltage that yields zero current in the presence of a concentration gradient across the channel. The advantage of Vrev measurements are in their simplicity, as the sign of Vrev provides a quick estimation of channel selectivity. Additionally, Vrev can be used to calculate the permeability of individual ions by using the well-known Goldman-Hodgkin-Katz equation:
| (21) |
Experimental lipid bilayer measurements report Vrev values of 27 and 26 mV for the OmpF channel from E. coli strains B and K-12, respectively (Benz et al., 1985).
Computational approaches to calculate Vrev have previously been limited to GCMC/BD simulations and three-dimensional PNP electrodiffusion theory, yielding values Vrev of 27.4 and 22.1 mV, respectively (Im and Roux, 2002a). Although those results were in excellent accord with experiments (Benz et al., 1985), they were obtained from simulation models that are based on continuum electrostatic approximations. Using the nonperiodic energy-step method to establish a salt concentration gradient developed here, it becomes possible for the first time to calculate the reversal potential Vrev of OmpF using all-atom MD simulations with explicit solvent molecules.
To calculate Vrev, an asymmetric salt solution across the membrane was constructed with 1 M KCl above (on the extracellular side of) the membrane and 0.1 M KCl below (on the periplasmic side of) the membrane. To maintain the salt gradient, an external force of 0.557 kcal mol−1 Å−1 was applied to the ions as they entered a 2.5-Å wide region at the edges of the periodic box. After convergence, an electrostatic potential of +150, 0, or −150 mV was applied across the membrane to drive current. The ion conductance was monitored over separate 50-ns trajectories. The I-V relationship (Fig. 6 B) shows similar features as those calculated previously using BD and PNP (Im and Roux, 2002a). Calculation of Vrev at zero net current was determined to be 28.6 ± 5.3 mV. This positive value for Vrev, caused by the preferential movement of cations in response to the concentration gradient, is indicative of a cation-selective OmpF channel and is in excellent agreement with previous experimental measurements (Benz et al., 1985).
As a comparison, channel selectivity was determined from the MD simulations by calculating the ratio of permeability coefficients PK/PCl extracted from the Goldman–Hodgkin–Katz equation, or by calculating the current ratio IK/ICl at zero applied voltage in the asymmetric KCl condition. These values (PK/PCl of 4.2 and IK/ICl of 2.4) are in reasonable agreement with each other and correspond to OmpF ion selectivity values calculated previously from experimental data (PK/PCl of 3.9 and 3.6 for the OmpF channel from E. coli strains B and K-12, respectively; Benz et al., 1985), and from BD (PK/PCl of 3.9 and IK/ICl of 3.4) and PNP (PK/PCl of 2.9 and IK/ICl of 2.4) simulations (Im and Roux, 2002a).
Ion selectivity for the OmpF channel has been shown previously to vary dramatically with KCl concentration (Im and Roux, 2002a), preventing accurate calculation of channel selectivity in a symmetric salt solution. Implementation of the developed method therefore allows for channel properties such as ion selectivity to be determined for other molecular pores in the absence of experimental functional data.
Ionic environment of the Kv1.2 channel pore domain
In contrast to the moderate cation specificity of the OmpF porin, the Kv1.2 channel is extremely selective for K+ over Na+. These voltage-gated channels respond to changes in membrane potential by opening (or closing) their highly selective conduction pores to control the flux of ions across the membrane. Upon depolarization of the cell membrane, the ion conduction pore opens and K+ ions flow down their electrochemical gradient across the membrane. Despite a 10-fold concentration gradient, Na+ ions do not pass through the conduction pore. Although K+ ions flow from the intracellular side (high K+) toward the extracellular solution (low K+) through the pore, the smaller Na+ ions face a barrier at the selectivity filter and maintain a high concentration gradient on the extracellular side. Therefore, under physiological conditions, the channel embedded in the cell membrane is exposed to a high concentration of Na+ on the external side and is submitted to a negative membrane potential that could further drive Na+ inward. Understanding how the channel performs under realistic physiological conditions is of great interest. However, all previous MD simulations of K+ channels were constrained by PBCs and assumed a symmetric concentration of K+ on both sides of the channel.
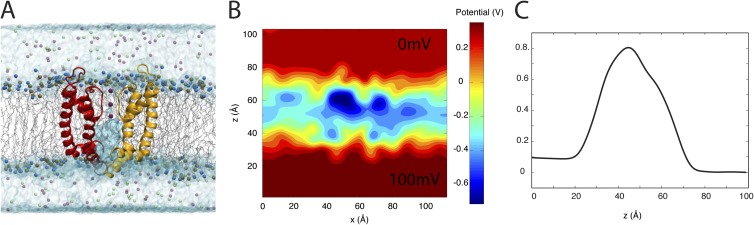
We have simulated the ion conduction pore of Kv1.2 embedded in a POPC lipid bilayer surrounded by NaCl and KCl solutions at physiological ionic concentrations. The intracellular solution is maintained at concentrations of 100 mM KCl and 10 mM NaCl, whereas the extracellular solution is kept at concentrations of 10 mM KCl and 100 mM NaCl. An electrostatic potential of −100 mV is applied across the membrane to mimic the hyperpolarized cellular membrane. A snapshot of the system and the electrostatic potential across a plane passing through the membrane is shown in Fig. 7 (A and B, respectively). The trajectory is obviously too short (50 ns) to obtain an accurate estimate of the channel conductance, although it is sufficiently long to display the average spatial distribution of the different ions around the intracellular and extracellular channel entrances.
Figure 7.
MD simulations of the pore domain of Kv1.2 under physiological conditions. (A) The pore domain of Kv1.2 embedded in a POPC lipid bilayer with asymmetric ionic concentrations. (B) Electrostatic potential map over a cross section of the system normal to the membrane averaged over the last 10 ns of the simulation trajectory. (C) Electrostatic potential normal to the plane of membrane averaged over 1-Å-wide cross sections along the x axis.
Fig. 8 shows the local density profile of K+, Na+, and Cl− ions in a plane normal to the membrane. The density profiles are radially averaged over the symmetry axis of the protein (z axis). Although Cl− ions are distributed uniformly between the two ionic solutions on two sides of the membrane, z > 0 and z < 0, K+ ions are concentrated on the intracellular side (z < 0), and Na+ ions are concentrated on the extracellular side (z > 0) (Fig. 8, A–C). The average density of K+ ions is 10 and 100 mM in the extracellular and intracellular solutions, respectively, whereas the Na+ ions are distributed with an average density of 100 and 10 mM in the extracellular and intracellular compartments. The average Cl− density in each compartment is ∼110 mM, resulting in a solution that is locally neutralized. Fig. 8 A shows the location of two K+ ions in the selectivity filter (high K+ density). On the other hand, Na+ ions (Fig. 8 B) accumulate in excess of 200 mM near the extracellular entrance of the pore, where the selectivity filter prevents Na+ ions from entering the pore and flowing down their electrochemical gradient.
Figure 8.
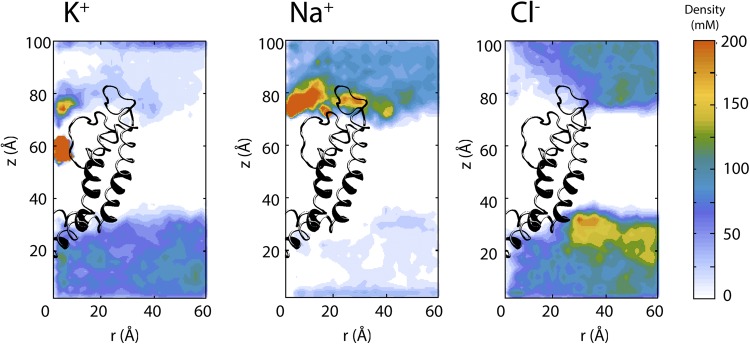
Local density profile of K+, Na+, and Cl− ions obtained from the simulations of Kv1.2. Local densities are plotted as a function of radial distance from the pore axis r and the distance from the bottom of the periodic box z.
In these simulations, the nonperiodic energy steps are applied to Na+ and K+ ions to generate two separate ionic solutions. No energy step is applied to Cl− ions, which are free to move and distribute between the two compartments. However, as shown in Fig. 8 (A–C), each ionic solution remains neutral. In the absence of any external forces, the Cl− ions follow cations, crossing the barrier as part of ion pairs.
Conclusion
A simple method has been developed to permit simulations of biomembrane systems under realistic asymmetric solute concentrations. Introducing an energy step at the boundaries of the periodic cell effectively separates the two solutions and generates a nonuniform distribution of the solute molecules across the cell boundaries. The nonperiodic energy step is implemented through the application of external forces over a thin region near the boundaries of the system. The method allows the ion concentration on each side of the membrane to be controlled separately as long as the total number of ions remains constant. When the total number of solute particles is known, the height of the step directly determines the equilibrium concentration of the solute on each side of the membrane.
In contrast to the alternative dual-membrane–dual-volume approach, in which two bulk regions are constructed to define independent solvent environments on the two sides of a membrane, the present method can be used to simulate a single-membrane system with almost no additional computational cost. In the case of wide membrane pores, such as OmpF, the coarse-grained methodologies that combine BD and PNP theories with a continuum description of the solvent are shown to reproduce conduction properties of the channel successfully (Im and Roux, 2002a). However, describing the selectivity and conduction of more specialized ion channels will require an all-atom description of the system.
It is worth noting that the nonperiodic energy step could also be used to create a net charge imbalance across the membrane, resulting in an effective membrane potential of V = ΔQ/C (Treptow et al., 2009; Delemotte et al., 2011). However, as there is no simple relationship between the energy step, the charge imbalance, and the resulting membrane potential, this procedure would require iterative adjustments until the desired membrane potential is obtained. In contrast, a chosen transmembrane potential can easily be established by applying a constant electric field in the z direction across the system (Roux, 2008; Gumbart et al., 2012). Because the latter method is on solid formal grounds and is more direct, it appears more advantageous (Roux, 2008; Gumbart et al., 2012).
Because the energy step impacts only the probability distribution of the solute and not the absolute number of ions in each solution, it is possible to effectively simulate membrane systems with arbitrarily low ionic concentrations. To achieve physiologically low ionic concentrations in conventional simulations, the solvent volume normally must be expanded such that an integer number of solute particles results in the desired concentration. For a single-membrane system, reaching micromolar concentrations would require a membrane system surrounded by ∼107 water molecules, i.e., 50 times larger than the average size of a typical membrane–protein MD system. In contrast, because the effective concentration is realized as a time average, it can be set to an arbitrarily low value with the nonperiodic energy-step method for a typical-size system.
We have validated the method over a wide range of external forces for the case of a small membrane slab. Next, this method has allowed us to calculate the reversal potential of the current passing through the bacterial porin OmpF from all-atom MD simulations. These simulations replicate the experimental condition under which the reversal potential is measured in electrophysiological experiments, and the quantitative agreement between the two approaches demonstrates the ability of the developed method to accurately reproduce conductance and ion selectivity properties of a complex molecular pore. Finally, we have simulated the Kv1.2 potassium channel under physiologically relevant concentrations of KCl and NaCl by controlling the concentration of each ionic species separately. These simulations provide a realistic representation of the cellular environment in which asymmetric ionic concentrations across the membrane are essential for the proper function of the cell. The simulations reported here are too short (∼50 ns) to reproduce ionic currents passing through the narrow selectivity filter of potassium channels. Extremely long MD simulations of potassium channel under symmetric ion concentration with an external electric field did not succeed previously to reproduce the experimental conductance of K+ channels (Jensen et al., 2010, 2013) because of the limitations of the nonpolarizable atomic force field.
The nonperiodic energy-step method has been implemented in the MD program NAMD; however, its implementation in other simulation packages should be trivial. Although the method was illustrated with two ion channels, it is worth emphasizing that it is completely general and could be used to realistically simulate the asymmetric environment of any membrane protein.
Acknowledgments
This work was supported by grants R01-GM062342 and U54-GM087519 from the National Institutes of Health to B. Roux and K22-AI100927 to J.C. Gumbart.
Edward N. Pugh Jr. served as editor.
Footnotes
Abbreviations used in this paper:
- BD
- Brownian dynamics
- GCMG
- grand canonical Monte Carlo
- MD
- molecular dynamics
- PBC
- periodic boundary condition
- PNP
- Poisson–Nernst–Planck
- POPC
- palmitoyl oleoyl phosphatidylcholine
References
- Aksimentiev A., Schulten K. 2005. Imaging alpha-hemolysin with molecular dynamics: ionic conductance, osmotic permeability, and the electrostatic potential map. Biophys. J. 88:3745–3761 10.1529/biophysj.104.058727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benz R., Schmid A., Hancock R.E. 1985. Ion selectivity of gram-negative bacterial porins. J. Bacteriol. 162:722–727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böckmann R.A., Hac A., Heimburg T., Grubmüller H. 2003. Effect of sodium chloride on a lipid bilayer. Biophys. J. 85:1647–1655 10.1016/S0006-3495(03)74594-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan S.W., Schirmer T., Rummel G., Steiert M., Ghosh R., Pauptit R.A., Jansonius J.N., Rosenbusch J.P. 1992. Crystal structures explain functional properties of two E. coli porins. Nature. 358:727–733 10.1038/358727a0 [DOI] [PubMed] [Google Scholar]
- Cowan S.W., Garavito R.M., Jansonius J.N., Jenkins J.A., Karlsson R., König N., Pai E.F., Pauptit R.A., Rizkallah P.J., Rosenbusch J.P., et al. 1995. The structure of OmpF porin in a tetragonal crystal form. Structure. 3:1041–1050 10.1016/S0969-2126(01)00240-4 [DOI] [PubMed] [Google Scholar]
- Crozier P.S., Henderson D., Rowley R.L., Busath D.D. 2001a. Model channel ion currents in NaCl-extended simple point charge water solution with applied-field molecular dynamics. Biophys. J. 81:3077–3089 10.1016/S0006-3495(01)75946-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crozier P.S., Rowley R.L., Holladay N.B., Henderson D., Busath D.D. 2001b. Molecular dynamics simulation of continuous current flow through a model biological membrane channel. Phys. Rev. Lett. 86:2467–2470 10.1103/PhysRevLett.86.2467 [DOI] [PubMed] [Google Scholar]
- Darden T., York D., Pedersen L. 1993. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092 10.1063/1.464397 [DOI] [Google Scholar]
- Delemotte L., Dehez F., Treptow W., Tarek M. 2008. Modeling membranes under a transmembrane potential. J. Phys. Chem. B. 112:5547–5550 10.1021/jp710846y [DOI] [PubMed] [Google Scholar]
- Delemotte L., Tarek M., Klein M.L., Amaral C., Treptow W. 2011. Intermediate states of the Kv1.2 voltage sensor from atomistic molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 108:6109–6114 10.1073/pnas.1102724108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egwolf B., Luo Y., Walters D.E., Roux B. 2010. Ion selectivity of alpha-hemolysin with beta-cyclodextrin adapter. II. Multi-ion effects studied with grand canonical Monte Carlo/Brownian dynamics simulations. J. Phys. Chem. B. 114:2901–2909 10.1021/jp906791b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feller S.E., Yin D., Pastor R.W., MacKerell A.D., Jr 1997. Molecular dynamics simulation of unsaturated lipid bilayers at low hydration: parameterization and comparison with diffraction studies. Biophys. J. 73:2269–2279 10.1016/S0006-3495(97)78259-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gumbart J., Khalili-Araghi F., Sotomayor M., Roux B. 2012. Constant electric field simulations of the membrane potential illustrated with simple systems. Biochim. Biophys. Acta. 1818:294–302 10.1016/j.bbamem.2011.09.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W., Dalke A., Schulten K. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38 10.1016/0263-7855(96)00018-5 [DOI] [PubMed] [Google Scholar]
- Im W., Roux B. 2002a. Ion permeation and selectivity of OmpF porin: a theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 322:851–869 10.1016/S0022-2836(02)00778-7 [DOI] [PubMed] [Google Scholar]
- Im W., Roux B. 2002b. Ions and counterions in a biological channel: a molecular dynamics simulation of OmpF porin from Escherichia coli in an explicit membrane with 1 M KCl aqueous salt solution. J. Mol. Biol. 319:1177–1197 10.1016/S0022-2836(02)00380-7 [DOI] [PubMed] [Google Scholar]
- Im W., Seefeld S., Roux B. 2000. A Grand Canonical Monte Carlo-Brownian dynamics algorithm for simulating ion channels. Biophys. J. 79:788–801 10.1016/S0006-3495(00)76336-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaynes E.T. 1957. Information theory and statistical mechanics. Phys. Rev. 106:620–630 10.1103/PhysRev.106.620 [DOI] [Google Scholar]
- Jensen M.Ø., Borhani D.W., Lindorff-Larsen K., Maragakis P., Jogini V., Eastwood M.P., Dror R.O., Shaw D.E. 2010. Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. USA. 107:5833–5838 10.1073/pnas.0911691107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen M.Ø., Jogini V., Eastwood M.P., Shaw D.E. 2013. Atomic-level simulation of current–voltage relationships in single-file ion channels. J. Gen. Physiol. 141:619–632 10.1085/jgp.201210820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo S., Kim T., Iyer V.G., Im W. 2008. CHARMM-GUI: a web-based graphical user interface for CHARMM. J. Comput. Chem. 29:1859–1865 10.1002/jcc.20945 [DOI] [PubMed] [Google Scholar]
- Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935 10.1063/1.445869 [DOI] [Google Scholar]
- Khalili-Araghi F., Tajkhorshid E., Schulten K. 2006. Dynamics of K+ ion conduction through Kv1.2. Biophys. J. 91:L72–L74 10.1529/biophysj.106.091926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klauda J.B., Venable R.M., Freites J.A., O’Connor J.W., Tobias D.J., Mondragon-Ramirez C., Vorobyov I., MacKerell A.D., Jr, Pastor R.W. 2010. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 114:7830–7843 10.1021/jp101759q [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreir M., Farre C., Beckler M., George M., Fertig N. 2008. Rapid screening of membrane protein activity: electrophysiological analysis of OmpF reconstituted in proteoliposomes. Lab Chip. 8:587–595 10.1039/b713982a [DOI] [PubMed] [Google Scholar]
- Kutzner C., Grubmüller H., de Groot B.L., Zachariae U. 2011. Computational electrophysiology: the molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 101:809–817 10.1016/j.bpj.2011.06.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K.I., Rui H., Pastor R.W., Im W. 2011. Brownian dynamics simulations of ion transport through the VDAC. Biophys. J. 100:611–619 10.1016/j.bpj.2010.12.3708 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K.I., Jo S., Rui H., Egwolf B., Roux B., Pastor R.W., Im W. 2012. Web interface for Brownian dynamics simulation of ion transport and its applications to beta-barrel pores. J. Comput. Chem. 33:331–339 10.1002/jcc.21952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long S.B., Campbell E.B., Mackinnon R. 2005. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 309:897–903 10.1126/science.1116269 [DOI] [PubMed] [Google Scholar]
- MacKerell A.D., Jr, Bashford D., Bellot M., Dunbrack R.L., Jr, Evanseck J.D., Field M.J., Fischer S., Gao J., Guo H., Ha S., et al. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- Noskov S.Y., Im W., Roux B. 2004. Ion permeation through the alpha-hemolysin channel: theoretical studies based on Brownian dynamics and Poisson-Nernst-Plank electrodiffusion theory. Biophys. J. 87:2299–2309 10.1529/biophysj.104.044008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezeshki S., Chimerel C., Bessonov A.N., Winterhalter M., Kleinekathöfer U. 2009. Understanding ion conductance on a molecular level: an all-atom modeling of the bacterial porin OmpF. Biophys. J. 97:1898–1906 10.1016/j.bpj.2009.07.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R.D., Kalé L., Schulten K. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802 10.1002/jcc.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux B. 2008. The membrane potential and its representation by a constant electric field in computer simulations. Biophys. J. 95:4205–4216 10.1529/biophysj.108.136499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux B. 2011. Computational electrophysiology: the molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 101:755–756 10.1016/j.bpj.2011.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs J.N., Crozier P.S., Woolf T.B. 2004. Atomistic simulations of biologically realistic transmembrane potential gradients. J. Chem. Phys. 121:10847–10851 [DOI] [PubMed] [Google Scholar]
- Sotomayor M., Vásquez V., Perozo E., Schulten K. 2007. Ion conduction through MscS as determined by electrophysiology and simulation. Biophys. J. 92:886–902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treptow W., Tarek M., Klein M.L. 2009. Initial response of the potassium channel voltage sensor to a transmembrane potential. J. Am. Chem. Soc. 131:2107–2109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vácha R., Berkowitz M.L., Jungwirth P. 2009. Molecular model of a cell plasma membrane with an asymmetric multicomponent composition: water permeation and ion effects. Biophys. J. 96:4493–4501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varma S., Chiu S.-W., Jakobsson E. 2006. The influence of amino acid protonation states on molecular dynamics simulations of the bacterial porin OmpF. Biophys. J. 90:112–123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu F., Tajkhorshid E., Schulten K. 2004. Theory and simulation of water permeation in aquaporin-1. Biophys. J. 86:50–57 [DOI] [PMC free article] [PubMed] [Google Scholar]