Location of a Major Susceptibility Locus for Familial Schizophrenia on Chromosome 1q21-q22

Abstract

Schizophrenia is a complex disorder, and there is substantial evidence supporting a genetic etiology. Despite this, prior attempts to localize susceptibility loci have produced predominantly suggestive findings. A genome-wide scan for schizophrenia susceptibility loci in 22 extended families with high rates of schizophrenia provided highly significant evidence of linkage to chromosome 1 (1q21-q22), with a maximum heterogeneity logarithm of the likelihood of linkage (lod) score of 6.50. This linkage result should provide sufficient power to allow the positional cloning of the underlying susceptibility gene.

Schizophrenia is a serious neuropsychiatric illness affecting ~1% of the general population. Family, twin, and adoption studies have demonstrated that schizophrenia is predominantly genetic, with a high heritability (1). Segregation analyses have failed to clearly support a single model of inheritance, with the suggestion of several, possibly interacting, susceptibility loci (2). The existence of a spectrum of related psychiatric disorders has led to uncertainty over the most appropriate phenotype for use in genetic studies. The complex genetics, unclear role of environmental interactions, and phenotypic uncertainty have led to the view that significant genetic linkage will not be easily obtained (3). Of the complete genome scans for schizophrenia susceptibility loci published to date (4 –14), only one (8) has reported a significant linkage result, to chromosome 13q32, which was recently confirmed in our independent sample of families (15). Suggestive (although not significant) results have been obtained to many other chromosomal regions, but the multitude of these findings and the broad regions involved limit their usefulness as starting points for positional cloning.

We conducted a genome-wide search for loci contributing to risk for schizophrenia in a group of 22 families, selected for study because multiple relatives were clinically diagnosed with schizophrenia or schizoaffective disorder. Canadian families of Celtic (n = 21) or German (n = 1) descent were recruited for study if schizophrenic illness appeared to be segregating in a unilineal (one side of the family only), autosomal dominant manner (16, 17). An average of 13.8 individuals per family participated in the study, and five families had 20 to 29 members participating. An average of 3.6 individuals with schizophrenia or schizoaffective disorder participated per family, with 15 individuals with these diagnoses participating in the largest family. On average, two additional participating family members were diagnosed as affected under a broader definition of schizophrenia-related disorders (18). Family members diagnosed as affected spanned three generations in 27% of families. Individuals reported by history to be affected spanned three or four generations in 45% of families. Overall, 304 subjects were evaluated (18), and 288 subjects had DNA samples available. DNA samples were genotyped with 381 simple tandem repeat markers with an average heterozygosity of 0.76 and an average marker density of 9 centimorgans (cM) (19). Parametric linkage analyses were conducted (20), as they are more powerful than nonparametric methods (21, 22) and are robust methods for detecting linkage despite errors or simplifications in the analyzing model, as long as both a dominant and a recessive model are used (21–24). To minimize multiple tests, we selected four genetic models, dominant and recessive for each of a “narrow” and a “broad” diagnostic classification (18, 25). The narrow classification included the diagnoses of schizophrenia and chronic schizoaffective disorder; the broad classification included these and several schizophrenia-spectrum disorders (18). The parameters of the dominant and recessive genetic models were derived from population prevalence and twin concordance rates for schizophrenia and related spectrum disorders (25). Although these parameters are almost certainly not accurate, particularly because they model single-gene inheritance, parametric linkage analysis with single-gene models is a powerful method for detecting linkage to traits controlled by multiple interacting genes, even when certain parameters, such as penetrance, are set to arbitrary values (21–24).

The threshold to declare significance in linkage studies of complex disorders is the subject of debate (26 –28). So as to avoid increasing the number of false-positive results due to multiple testing, statistical corrections are required to account for analysis with multiple markers, multiple inheritance models and diagnostic classifications, and genetic heterogeneity. Unfortunately, the exact appropriate correction may be difficult to determine (26 –28). Alternatively, simulation studies of unlinked “replicates” can empirically determine how frequently any given logarithm of the likelihood of linkage (lod) score will occur in the absence of linkage, accurately accounting for multiple markers and models. Simulation studies with 2500 unlinked replicates were conducted to determine the lod scores corresponding to P = 0.05 (29). This produced a lod score threshold for significance of 3.3 under the hypothesis of homogeneity and 3.5 under the hypothesis of heterogeneity. Simulation studies with linked replicates were also conducted to assess the power of this sample to detect linkage under the four models used in this study (30). These demonstrated good power to detect linkage under all models when 75% or more of families were linked to a given disease locus (31).

A plot of two-point lod scores for the genome-wide scan is shown in Fig. 1. The highest lod score observed was 5.79 [P < 0.0002; (32)] under the narrow definition of illness and a recessive mode of inheritance with marker D1S1679, which maps to chromosome 1q22. Lod scores >2.0 were obtained with five adjacent markers from 1q, spanning a region of approximately 39 cM. Significant linkage was not detected to any other chromosome when two-point analysis was used. All two-point lod scores >1.5 are summarized in Table 1 (33).

Fig. 1.

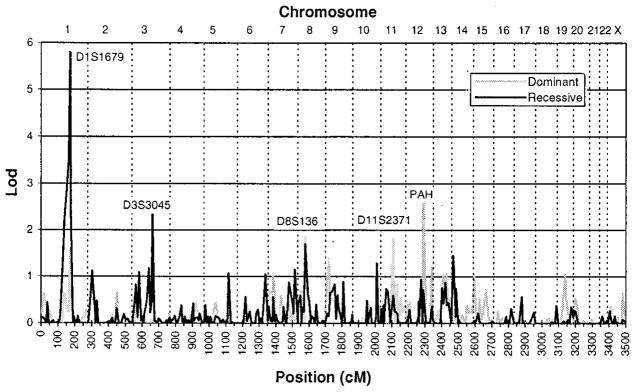
Two-point lod scores for the genome-wide scan. Affected and unaffected individuals in 22 families segregating schizophrenia were genotyped at 381 marker loci throughout the genome. Maximum two-point lod scores under the narrow definition (18) and the assumption of genetic heterogeneity are plotted as a function of marker location in centimorgans for both recessive and dominant models of inheritance. Chromosome number is designated at the top of the plot.

Table 1.

List of all markers with lod scores >1.5. The single phenotype and inheritance model producing the highest lod score is given for each marker. Z_max, maximum lod score; θ, recombination fraction; α, proportion of families linked to a given locus; N, narrow; B, broad; R, recessive; D, dominant.

Marker	Chromosome location	Map location*	Model	Two-point analysis					Three-point analysis
				Homogeneity		Heterogeneity			Heterogeneity
				Zmax	θ	Zmax	θ	α	Zmax	α	Location of Zmax*
Chromosome 1
D1S1631	1p21	137	NR	2.13	0.2	2.19	0.1	0.65	2.57	0.75	147
D1S3723	1p21-p13	141	NR	2.29	0.1	2.39	0.1	0.75	3.65	0.70	148
D1S534	1p13	152	NR	2.90	0.1	2.90	0.1	1	3.65	0.70	147
D1S1653	1q21-q22	164	NR	3.52	0.1	3.52	0.1	1	6.05	0.75	170
D1S1679	1q22	171	NR	5.77	0.05	5.79	0.05	0.95	6.05	0.75	170
D1S1677	1q22-q23	176	NR	2.15	0.1	2.26	0.1	0.80	5.72	0.60	171
Chromosome 2
D2S2952	2p24	18	BR	1.37	0.2	1.97	0.05	0.40	2.00	0.45	28
D2S1400	2p23-p22	28	BR	1.70	0.2	1.98	0.05	0.60	2.42	0.65	18
Chromosome 3
D3S3045	3q13	124	NR	2.11	0.2	2.40	0.1	0.75	1.73	0.65	114
Chromosome 7
D7S1802	7p13	33	ND	0.80	0.2	1.03	0.05	0.55	1.59	1	54
Chromosome 8
D8S1106	8p22	26	BD	1.95	0.2	2.10	0.2	0.75	2.33	0.80	5
D8S136	8p21	44	BD	2.09	0.2	2.16	0.2	0.80	2.80	0.90	65
Chromosome 11
D11S2371	11q13-q23	76	ND	0.56	0.2	1.84	0	0.55	1.88	0.55	76
Chromosome 12
PAH	12q22-q24	109	ND	2.31	0.1	2.60	0	0.70	1.71	0.50	109
Chromosome 13
D13S317	13q22	64	ND	1.02	0.2	1.02	0.2	0.95	1.56	1	85
D13S793	13q31-q32	76	BR	1.44	0.1	1.47	0.1	0.9	3.81	0.65	77
D13S779	13q32	83	BR	1.87	0.1	2.41	0	0.55	2.34	0.45	83
Chromosome 17
D17S784	17p12-p11	117	BR	2.18	0.1	2.19	0.1	0.95	1.54	1	138

^*Distances from pter in centimorgans.

Parametric multipoint analyses of complex disorders must be approached with caution, as incorrect analysis models can exclude a true linked locus from the region between close flanking markers (34). However, multipoint analyses are useful for combating the practical limitations caused by uninformative marker typings, which can either inflate or deflate the lod score. With large, complex pedigrees, simultaneous analysis of multiple highly polymorphic marker loci can be computationally prohibitive, especially when large regions of the genome are scanned for linkage. We therefore conducted three-point analyses with adjacent marker loci and the disease locus for all markers in the genome scan and four-point analyses in the region of significant linkage on 1q. Mul-tipoint analysis with chromosome 1 markers produced a maximum lod score of 6.50 [P < 0.0002; (32)] between the markers D1S1653 and D1S1679, under the recessive-narrow model and with an estimated 75% of families linked to this locus (Fig. 2). Only multipoint analysis on chromosome 13 produced additional significant results, with a maximum lod score of 3.81 [P = 0.02; (32)] under the recessive-broad model at D13S793 with an estimated 65% of families linked to this region, consistent with our previous findings in these same families (15).

Fig. 2.

Multipoint lod scores for the schizophrenia susceptibility locus relative to markers in the 1q21-q23 region. Parametric four-point lod scores were calculated with the narrow defi-nition (18) and the markers D1S1653, D1S1679, and D1S1677 under the recessive model of inheritance. The results are plotted as a function of distance from D1S1653 under the assumption of homogeneity (100% of families linked) and heterogeneity (75% of families linked). In both cases, the maximum lod scores were located within the 12-cM interval between the markers D1S1653 and D1S1679, rising from a value of 5.89 (P < 0.0002) under homogeneity to 6.50 (P < 0.0002) under heterogeneity.

There have been suggestive linkage results for chromosome 1q22-q23 under autosomal recessive inheritance in one published (6), and one preliminary (35), genome scan. Studies showing association of schizophrenia with the Duffy blood group (36), a hetero-chromatin variant (37), a fragile site (38), and a potassium channel gene [KCNN3 (39)], provide further prior evidence for a susceptibility gene in this region. However, most genome scans and association studies have not led to significant results for the 1q21-q23 region or have provided suggestive linkage of major psychotic illness to the more distal regions of 1q25-q32 (40) or 1q32-q41 (14), perhaps due to the genetic heterogeneity of schizophrenia and/or low power of some studies.

This unequivocally significant linkage finding seems somewhat unexpected for schizophrenia, given the multiple challenges of this complex disorder. However, these results confirm the predictions of simulation studies that parametric linkage analysis with simple genetic models, when conducted under both a dominant and recessive mode of inheritance, is a powerful method for detecting linkage to susceptibility loci in complex disorders (21–24). Although nonparametric (NPL) methods as implemented in GENE-HUNTER or affected sibpair analysis are widely used, simulation studies indicate they are not as powerful (21, 22), and sample considerations may limit their utility. As many of the affected-relative pairs in this sample were not within sibships, affected sibpair analysis was not an appropriate choice. The large size of many of the extended families exceeded the capacity of GENE-HUNTER, limiting the utility of that analysis package. Although analysis with multiple other packages could facilitate cross-study comparisons, we have adopted the approach suggested by Risch and Botstein (27) and have reported the power of our study sample to detect linkage under the models tested as well as the significance level of positive results.

This study demonstrates the importance of careful family selection. Because of the time and effort required to identify and collect pedigrees with three or more affected individuals in multiple generations, most studies have focused on gathering large numbers of small nuclear families or pairs of affected siblings, increasing the chance of a clinically and genetically heterogeneous sample. As our simulation studies illustrate (30), power to detect linkage is greatly reduced when a significant proportion of the sample is unlinked to a particular locus. The population selected for study, the inclusion criteria, and fortuitous sample variation may have all combined to produce a group of families with a high proportion linked to the susceptibility locus on 1q21-q22. We are likely to have failed to detect linkage to any contributing loci that are present in less than half of the families we studied (30).

Multiple susceptibility loci are almost certainly involved in the etiology of schizophrenia, with significant evidence for an additional locus on 13q32, even within this set of families. The magnitude of the chromosome 1 linkage finding, coupled with the clear localization to the interval between the markers D1S1653 and D1S1679, should facilitate efforts to positional clone this susceptibility gene. It is hoped that better understanding of the genetic factors involved in this common, devastating disorder will lead to earlier and more effective interventions.