Abstract
Differences in the chemical composition of calcified skeletal structures (e.g. shells, otoliths) have proven useful for reconstructing the environmental history of many marine species. However, the extent to which ambient environmental conditions can be inferred from the elemental signatures within the vertebrae of elasmobranchs (sharks, skates, rays) has not been evaluated. To assess the relationship between water and vertebral elemental composition, we conducted two laboratory studies using round stingrays, Urobatis halleri, as a model species. First, we examined the effects of temperature (16°, 18°, 24°C) on vertebral elemental incorporation (Li/Ca, Mg/Ca, Mn/Ca, Zn/Ca, Sr/Ca, Ba/Ca). Second, we tested the relationship between water and subsequent vertebral elemental composition by manipulating dissolved barium concentrations (1x, 3x, 6x). We also evaluated the influence of natural variation in growth rate on elemental incorporation for both experiments. Finally, we examined the accuracy of classifying individuals to known environmental histories (temperature and barium treatments) using vertebral elemental composition. Temperature had strong, negative effects on the uptake of magnesium (DMg) and barium (DBa) and positively influenced manganese (DMn) incorporation. Temperature-dependent responses were not observed for lithium and strontium. Vertebral Ba/Ca was positively correlated with ambient Ba/Ca. Partition coefficients (DBa) revealed increased discrimination of barium in response to increased dissolved barium concentrations. There were no significant relationships between elemental incorporation and somatic growth or vertebral precipitation rates for any elements except Zn. Relationships between somatic growth rate and DZn were, however, inconsistent and inconclusive. Variation in the vertebral elemental signatures of U. halleri reliably distinguished individual rays from each treatment based on temperature (85%) and Ba exposure (96%) history. These results support the assumption that vertebral elemental composition reflects the environmental conditions during deposition and validates the use of vertebral elemental signatures as natural markers in an elasmobranch. Vertebral elemental analysis is a promising tool for the study of elasmobranch population structure, movement, and habitat use.
Introduction
The trace and minor elemental composition of biomineralized structures can provide insight into the environmental conditions in which the elements were deposited. Elemental assays of coral skeletons and foraminifera tests, for example, have been commonly applied as surrogates of past climatic or oceanographic conditions (paleoproxies) [1–3]. Recently, considerable attention has been directed toward analyses of calcified structures, such as fish otoliths, to gain insight into contemporary ecological processes and inform management and conservation efforts [4–6]. Elements are naturally acquired through respiratory and dietary pathways and assimilated into actively calcifying structures such as scales, shells, and otoliths [7,8]. The elemental composition of these structures can reflect the physical and chemical conditions of the ambient environment. If the calcified material is deposited in a temporally consistent pattern and is not subjected to resorption or reworking, elemental composition can provide permanent chronological records of the environmental conditions experienced over a lifetime.
The most widespread and expanding application of elemental markers in biomineralized structures has occurred using the otoliths of fishes [4,5]. Otoliths are metabolically inert calcium carbonate structures (typically in the form of aragonite) that are used for balance and hearing in teleost fishes. Elements are incorporated into otoliths daily as new aragonite is crystallized onto an organic framework of proteins [8]. The elemental composition of other calcified structures, including vertebrae [9], scales [10], fin rays [11], and bone [12], have been evaluated as potential elemental markers in fishes. However, unlike otoliths, these calcium phosphate structures (in forms of hydroxyapatite) are metabolically active, subject to resorption and provide short-term and unstable chemical records of environmental history [4].
The elemental composition of biogenic calcified structures is not a simple reflection of environmental conditions. A variety of physiological barriers and processes are encountered as elements are taken up from the water through the gills or intestine, transferred through the blood plasma, and eventually incorporated into biomineralized structures [8]. Physiological regulation of internal elemental composition can result in active discrimination or preferential uptake of elements, thus modifying relationships with ambient environmental conditions. Trace metals such as manganese and zinc that are essential for metabolic and cellular transport processes are tightly regulated [13]. Conversely, physiological regulation of elements that do not play critical biological roles or generate toxic effects may be comparatively minimal [8,14]. At the site of calcification, elemental incorporation can be inhibited or promoted by kinetic effects associated with biomineralization. Elemental composition can be further modified by temperature, which has a profound influence on the rates of chemical and metabolic processes [15,16]. Individual variation in growth rates, independent of temperature, can also influence elemental composition [17,18]. Metabolic and kinetic effects on elemental incorporation, however, do not negate the utility of an element as a geochemical marker, providing the degree of regulation is constant or predictable.
Sharks, skates, and rays (elasmobranchs) are cartilaginous fishes that lack otoliths. Elasmobranch skeletons are composed of mineralized cartilage, an impure (non-stochiometric) form of carbonated calcium phosphate (hydroxyapatite) [19]. Like the otoliths of teleost fishes, elasmobranch vertebrae are deposited by the precipitation of elements onto a matrix of proteins and continue to grow throughout the life of the organism [19]. Vertebral growth bands are typically deposited seasonally, allowing individual ages to be determined. Resorption or physiological reworking of vertebrae, as has been observed in scale and bone hydroxyapatite, would alter the elemental composition and severely limit their utility as records of the physiochemical environment. Questions have been raised about the potential for elemental resorption in elasmobranch vertebrae [20], but directed studies have consistently found these structures to be stable [19,21,22]. The function and properties of elasmobranch cartilage, and vertebrae in particular, are fundamentally different than those of other vertebrates [21,23]. Whereas calcified cartilage is usually a transitional tissue that is ultimately replaced by bone, elasmobranch cartilage possesses a permanent mineralized rind that shows no direct evidence of remodeling or resorption [19,24]. Doyle [25] confirmed that mineralization and growth of elasmobranch cartilage is accomplished through surface accretion that proceeds without altering the mineral or protein matrix. Therefore, the elemental composition of elasmobranch vertebrae is unlikely to be modified after deposition and could therefore provide permanent chronological records of the environmental conditions experienced by individuals.
Chemical analyses of elasmobranch vertebrae to date have been predominately directed toward age validation [26,27] and dietary studies [28,29]. The potential use of vertebral elemental composition to delineate elasmobranch populations was first proposed by Edmonds et al. [30] following their analyses of jaw cartilage which revealed spatially explicit patterns of elemental variation. Age-related changes in vertebral elemental composition have recently been examined to discern movement patterns in sharks [31,32]. Although significant temporal and spatial variation in elemental composition have been identified within elasmobranch vertebrae, interpretations of these differences are hindered by a lack of understanding as to how ambient vertebral chemistry relates to environmental conditions. Without an understanding of the factors that influence elemental incorporation and the extent of regulation, it is impossible to know if the elemental composition of a calcified structure presents a reliable record of environmental history. Controlled laboratory validation studies provide a platform for quantifying abiotic and biotic effects on elemental incorporation and identifying those elements that are most likely to serve as useful indicators of the environment in which they were deposited. Incorrect assumptions about elemental relationships and an inadequate understanding of the mechanisms determining incorporation can lead to erroneous interpretations of field data.
Key assumptions regarding vertebral elemental incorporation in relation to the physical and chemical environment must be evaluated before broader ecological questions and hypotheses can be addressed using naturally occurring elemental markers in elasmobranchs. We quantified the effects of temperature and growth rate on vertebral elemental incorporation through controlled laboratory studies using the round stingray, Urobatis halleri, as a model species. We manipulated environmental concentrations of barium (Ba) to determine the extent to which vertebral elemental ratios reflect the ambient environment. Finally, we evaluated the utility of these elemental markers to distinguish the environmental history experienced by individual rays using multivariate classification models. These experiments allowed us to test the following hypotheses: (i) elemental incorporation in vertebrae is mediated by water temperature; (ii) vertebral Ba to calcium ratios (Ba/Ca) reflects water Ba/Ca; (iii) growth rate does not significantly influence vertebral elemental composition; and (iv) vertebral elemental markers can distinguish individuals based on differences in environmental history. This investigation represents the first attempt to evaluate the utility of vertebral chemistry as potential records of environmental history in elasmobranchs.
Materials and Methods
Ethics statement
This investigation was conducted with a permit from the California Department of Fish and Game (803099-01) and in strict accordance with guidelines established by the American Fisheries Society and National Institutes of Health for the use of fishes in research. Experimental protocol was approved by Oregon State University’s Institutional Animal Care and Use Committee (3783).
Specimen collection
The round stingray, Urobatis halleri, is a benthic, live-bearing elasmobranch that occurs in estuaries and nearshore coastal soft bottom habitats from Panama to Eureka, California, USA [33]. The vertebrae of round rays are well-calcified and the annual deposition of a distinctive band pair (one opaque, one translucent growth band) has been validated, making reliable estimates of age and growth rates possible [34]. We selected U. halleri as a model elasmobranch species for vertebral elemental incorporation studies because of their record of hardiness in captivity, relatively small body size (to 31 cm disc width, DW), availability in shallow coastal environments, and validated periodicity of vertebral growth band formation.
Juvenile U. halleri were collected by beach seine at Seal Beach, California (33°44’ N; 118°06’ W) on 6 February 2009 and transported to the Hatfield Marine Science Center (HMSC) in Newport, Oregon. A total of 108 rays were collected, consisting of 67 females and 41 males. Vertebral band counts performed at the end of this study confirmed that these rays were age 0 (i.e. young-of-the-year; n = 104) and age 1 (n = 4) at the time of capture.
Experimental design
We conducted two consecutive laboratory experiments using the same rays to evaluate the effects of: 1) temperature and 2) dissolved barium concentration on the incorporation of elements into the vertebrae of an elasmobranch. Following collection and transport, U. halleri were allowed to acclimate to lab conditions for five weeks. Total weight, DW, and sex were then recorded. Twelve rays were randomly assigned to each of nine 1,700 L independently re-circulating tanks containing a thin layer of sand substrate. Water from each tank circulated through individual wet-dry sumps containing biological filter media to reduce the build-up of potentially harmful nitrogenous waste products. The same combination of squid (Doryteuthis opalescens), herring (Clupea pallasi), or shrimp (Pandalus jordani) was provided daily. Remaining food and waste were removed daily. One-quarter to one-half volume water changes were completed approximately every 1-2 weeks to maintain water quality. Seawater was pumped from Yaquina Bay through HMSC’s seawater system. Tanks were covered with clear plastic lids to reduce evaporation. A 12 hour light:dark photoperiod was established for both experiments. Temperature and salinity were recorded daily and water samples were collected weekly.
Temperature experiment
Following acclimation and initial measurement, all specimens were injected with a 25 mg kg-1 dose of oxytetracycline [35] to provide a visual indicator within the vertebrae that coincided with the start of the experiment. Cooler water from Yaquina Bay was heated and three replicate treatments of 15°C, 18°C, and 24°C were established and maintained, corresponding with the mean winter, summer, and approximate maximum water temperatures at the site of collection [36]. The temperature experiment was conducted for eight months (April-December, 2009) to ensure that adequate vertebral deposition occurred for elemental analysis in all treatments. Three individuals died before the conclusion of the study and were excluded from analysis; praziquantel (Sigma-Aldrich) was subsequently administered to all tanks (10 mg/L) to eliminate parasitic flatworms during two weeks in July and August.
Barium manipulation experiment
The relationship between water chemistry and vertebral elemental composition was evaluated through experimental manipulation of dissolved barium concentrations. Barium was selected because of its utility as a distinctive elemental marker demonstrated in both field [37,38] and laboratory studies [39,40]. Upon conclusion of the temperature experiment, all specimens were weighed, measured, and injected with a 5 mg kg-1 dose of the fluorescent marker calcein to distinguish vertebral deposition between the experiments [41]. Water temperatures were gradually adjusted to 19°C in all tanks over two weeks. Following this acclimation, Ba treatments were systematically assigned to each tank to ensure that one tank from each prior temperature treatment was represented within each Ba treatment. Three tanks were designated as controls that reflected ambient dissolved Ba/Ca ratios (1x). Three tanks were spiked with three times (3x) and three tanks were spiked with six times (6x) the estimated mean local Ba concentration of 4.50 μmol mol-1, providing triplicate treatments of 1x, 3x, and 6x Ba concentrations. These values fall within the naturally occurring regional range for estuaries and coastal waters [40,42]. Elevated Ba treatments were prepared by the addition of BaCl2 (JT Baker) to ambient seawater. Diet, feeding, cleaning, and light regimes were maintained as previously described. Water changes were, however, made from an appropriate supply of 1x, 3x, or 6x Ba/Ca seawater sources. We excluded seven specimens from analysis (five from a single tank, 6x treatment) because of mortality that occurred prior to the completion of the study. All rays were sacrificed after 109 days (December, 2009 – April, 2010) using tricane methanesulfonate (Finquel, MS-222) in accordance with approved Institutional Animal Care and Use protocol. Rays were weighed and measured before vertebrae were excised and stored frozen for analysis.
Vertebral preparation and elemental analysis
Sample preparation for elemental analysis followed procedures typical to age and growth studies of elasmobranchs [43] but incorporated processing methods associated with otolith chemistry studies [44] to minimize contamination. Tissue was removed from vertebrae with acid-washed non-metallic dissecting tools and individual centra were separated and dried in a Class 100 laminar flow bench. Vertebral centra were soaked for 10 minutes in ultrapure 30% hydrogen peroxide (ULTREX, J.T. Baker) to loosen remaining connective tissue, triple rinsed, and ultrasonically cleaned in Nanopure® (18 M Ohm, Barnstead International) water for 45 minutes. Samples were rinsed, dried, embedded in polyester casting resin infused with a spike of indium, and sectioned to a width of ~0.4 mm using a low speed diamond saw (Figure 1a, 1b). Resulting thin-sections were mounted to acid-washed glass slides, polished with lapping film (3MTM; 30, 12, 5, 3, 1 μm), and rinsed. Sectioned centra were randomly attached to acid-washed slides to prevent systematic bias. Sample slides were rinsed with ultrapure 1% nitric acid (HNO3; ULTREX, J.T. Baker), cleaned ultrasonically for 15 minutes, triple rinsed, and dried in Class 100 conditions.
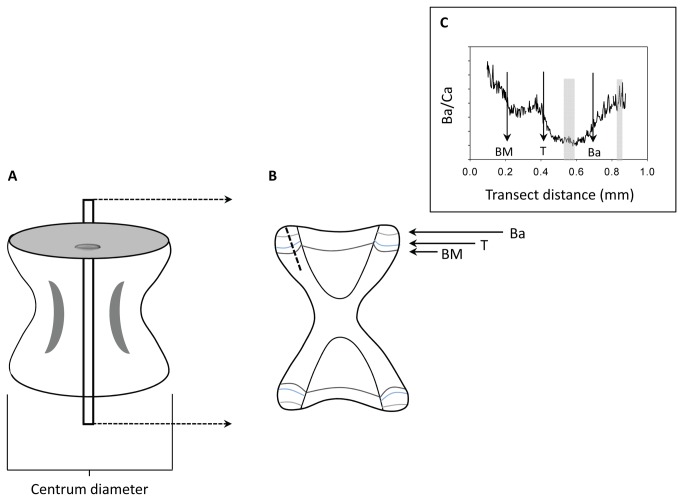
Figure 1. Processing and analysis of vertebral centra.
Depiction of a (A) whole and (B) thin-sectioned vertebral centra and (C) the barium to calcium ratio (Ba/Ca) profile collected along a representative laser transect. The birthmark (BM) provides an intrinsic reference and fluorescent markers injected into round rays (Urobatis halleri) at the beginning of the temperature and barium manipulation experiments provided visual references for identifying specific regions deposited during this study. T represents the beginning of the temperature experiment (indicated by an oxytetracycline mark). Ba represents the beginning of the barium manipulation experiment which was distinguishable by a corresponding calcein mark. The dashed line in (B) exemplifies the transect pathway used for laser ablation. Grey vertical bars within (C) depict the regions integrated for analysis. The example in (C) characterizes the variation in vertebral Ba/Ca of a round ray that was maintained at 18°C and 6x ambient Ba concentration during the temperature and barium manipulation experiments, respectively.
The elemental composition of U. halleri vertebrae was quantified using laser ablation-inductively coupled plasma mass spectrometry (LA-ICPMS). Analyses were conducted at Oregon State University’s WM Keck Collaboratory for Plasma Spectrometry in Corvallis, Oregon using a VG PQ ExCell ICPMS with a DUV193 excimer laser (New Wave Research). The laser was set at a pulse rate of 5 Hz with an ablation spot size of 80 μm and translated across the sample at 5 μm s-1. Laser transects were positioned within the corpus calcareum of the vertebral centrum to collect a time series of elemental composition that included both experimental periods (Figure 1b). Transects were pre-ablated (100μm spot size, 2 Hz, 100 μm s-1) to further reduce potential sample contamination. We collected data on 17 elements: lithium, magnesium, calcium, titanium, vanadium, chromium, manganese, cobalt, copper, zinc, rubidium, strontium, zirconium, cadmium, barium, lanthanum, and lead. However, only magnesium (25Mg), calcium (43Ca), manganese (55Mn), zinc (66Zn), strontium (88Sr), and barium (138Ba) were consistently above detection limits. Lithium (7Li) was often found in concentrations near and occasionally below detection limits but was included in our analyses. Samples with measurements of Li that were not above background levels were dropped from analysis (19% temperature experiment, 29% Ba manipulation experiment). Lead was incorporated into vertebrae at levels exceeding detection limits when specimens were living off Seal Beach, CA. However, Pb/Ca ratios were not consistently above detection limits (≥4.19 μmol mol-1) while rays were maintained at HMSC.
Data processing followed procedures described in Miller & Shanks [44]. To evaluate instrument drift and daily variation in instrument sensitivity, a National Institute of Standards and Technology (NIST) 612 glass standard was run with each sample slide. Background levels of analyte isotopes were measured and subtracted from values determined during vertebral ablation. Mean percent relative standard deviations (%RSD) of the NIST 612 standard were: Li = 5.2%, Mg = 12.6%, Ca = 3.3%, Mn = 4.5%, Zn = 8.3%, Sr = 3.7%, and Ba = 5.0%(n = 21). Time-resolved software (PlasmaLab®) allowed analyte counts to be integrated from specific positions along each vertebral transect. Regions for integration were determined using image analysis (Image ProExpress, Media Cybernetics®). We targeted areas that corresponded with the mid-point of the temperature experiment and the final month of the Ba manipulation experiment for analysis to assure that adequate vertebral precipitation had occurred and to avoid sampling areas associated with the transition between experiments (Figure 1c). Count data were normalized by 43Ca to adjust for variability in instrument sensitivity and the amount of ablated material, then converted to elemental ratios (Me/Ca, where Me represents a metallic element) based on measurements of the NIST 612 standard [45,46]. Elemental ratios are presented in mmol mol-1 (Mg, Sr) or μmol mol-1 (Li, Mn, Zn, Ba).
Water collection and analysis
Dissolved elemental concentrations within and among treatments were evaluated by sampling the water from each tank weekly over the course of both experiments. Samples were collected in acid-washed plastic bottles, filtered with 0.2-μm syringe filters in a Class 100 laminar flow bench, acidified to <2 pH with ultrapure HNO3 (ULTREX, J.T. Baker) and stored refrigerated at ~4°C until analysis. A subset of samples was analyzed to determine the concentrations of Li, Mg, Ca, Mn, Zn, Sr, and Ba during the temperature (n = 11 dates x 9 tanks) and Ba manipulation (n = 7 dates x 9 tanks) experiments. Water samples were selected to provide increased representation during the middle of the temperature experiment (August-October) and the latter half of the Ba manipulation experiment (February-March), the same time period from which vertebral elemental data were targeted.
Elemental concentrations were determined using a Leeman-Teledyne inductively coupled plasma optical emission spectrometer (ICP-OES) (Li at 670.8 nm, Mg at 279.1 nm, Ca at 317.9 nm, Mn at 259.4 nm, Zn at 206.2, Sr at 421.5 nm, and Ba at 493.4 nm). Filtered, acidified samples were diluted 100x for the determination of Mg, Ca, and Sr and 25x for Li, Mn, Zn, and Ba. Matrix-matched standards were created using SPEX Certiprep Group® certified reference materials (CRMs), NIST liquid standard (1643e), and a sodium chloride (NaCl) solution. Matrix-matched NIST standards and HNO3 blanks were introduced throughout analysis to evaluate accuracy. Measured Li, Mg, Ca, Mn, Zn, Sr, and Ba concentrations were within 3%, 2%, 3%, 18%, 8%, 5%, and 3%, respectively, of certified values. A correction factor was applied to those elements that were ≥5% of known values (Mn, Zn and Sr). Repeated measurements of the same CRM calibration standard indicated that precision was within 1.2% for all elements (n = 7). Elemental concentrations are expressed as element to calcium ratios and presented in mmol mol-1 (Mg, Sr) or μmol mol-1 (Li, Mn, Zn, Ba).
Statistical analyses
Partition coefficients (DMe, where the subscript indicates a metallic element of interest) characterize the relationship between the elemental composition of a solution with that of a solid, actively calcifying structure [47]. DMe provide a standardized metric for comparing the effects of temperature, dissolved elemental concentration, and growth rates on elemental incorporation within and among species and calcified structures. We calculated DMe for each element by dividing a given element to calcium ratio (Me/Ca) measured from individual vertebrae by the mean Me/Ca ratio measured from the water of the corresponding tank [47].
Mean salinity, temperature, Me/Cawater, and Me/Cavertebrae were compared among treatments using parametric and non-parametric approaches. Data were screened for outliers and assessed for normality and homogeneity of variance using Shapiro-Wilk’s and Levene’s tests, respectively [48]. Temperature and salinity data did not meet the assumptions of normality following transformation and were analyzed using non-parametric Kruskal-Wallis analysis of variance by ranks [48]. Water (Me/Cawater) and vertebral elemental (Me/Cavertebrae, DMe) data required log10-transformation to conform to the assumptions of parametric statistical analysis.
Data collected from the temperature and Ba manipulation experiments were analyzed separately using the same procedures. As a first step, one-way multivariate analysis of variance (MANOVA) was applied to test for differences in mean Me/Cawater and Me/Cavertebrae among treatments, where treatment (temperature or Ba concentration) was a fixed factor and elemental ratios (Li/Ca, Mg/Ca, Mn/Ca, Zn/Ca, Sr/Ca, Ba/Ca) were the response variables. When significant differences among treatments were identified, Tukey’s Honestly Significant Difference (THSD) tests were conducted to determine which groups accounted for the observed differences [49]. Effects of temperature and Ba concentration on DMe were evaluated in each experiment by ANOVA with tanks nested within treatments as random variables and the corresponding temperature or Ba treatment as a fixed factor. All MANOVAs and nested ANOVAs were completed using JMP (Version 8.0) statistical software.
Effects of growth and precipitation rates
Somatic growth and vertebral precipitation rates were determined to evaluate their influence on elemental incorporation. Because rays were not individually marked, we assumed that sex-specific size ranks were maintained within each tank during the experiments and estimated individual growth rates from these ranks [50]. Somatic growth rates were calculated as the difference in body size (DW) between the start and end of each experiment divided by the number of months that the experiment was conducted, providing an estimate of growth in mm DW month-1. Changes in centrum diameter during each experiment were similarly calculated by subtracting the vertebral diameter at the beginning of a study, as indicated by a fluorescent mark, from that measured at the end of an experiment using Image Pro Plus® (Media Cybernetics). Vertebral deposition/precipitation rates were expressed as mm DW month-1. Mean monthly growth rates were estimated for all tanks (n = 9) and compared among treatments using ANOVA with treatment as a fixed factor. Regression analyses of DMe against somatic growth and vertebral precipitation rates were performed within each treatment.
Classification
The ability to accurately classify individuals based on treatment/environmental history was evaluated with discriminant function analysis (DFA) of the vertebral Me/Ca data (i.e. Mg, Mn, Sr, Ba) generated from our temperature and Ba manipulation experiments. Because Li/Ca measurements were not available for all samples (i.e. below detection limits), Li was not included in these analyses. Group classification accuracy was assessed using a leave-one-out jack-knife procedure [51]. We assumed that prior probabilities of group membership were proportional to group sample sizes. A chance-corrected classification (Cohen’s kappa, κ) was also calculated to determine if predicted group assignments exceeded that of randomly assigning individuals to groups in proportion to their sample sizes [52]. A κ of 0 indicates that no improvement over chance was provided by the DFA and a κ of 1 signifies perfect agreement. SYSTAT (Version 12.0) was used for DFA.
Results
Temperature experiment
Water temperatures differed significantly among treatments, as intended (Kruskal-Wallis, H = 69.96, p < 0.001; Table 1). Salinity varied during the experiment but remained equivalent among and within treatments (Kruskal-Wallis: H = 4.79, p = 0.09; Table 1). Additionally, water elemental ratios did not differ in response to temperature (MANOVA, Pillai’s trace = 0.15, p = 0.74; Table 2). Of the six elemental ratios measured, Zn/Cawater displayed the greatest variation (overall %CV = 47.5) and Sr/Cawater the least (overall %CV = 1.1).
Table 1. Mean experimental conditions by tank and treatment during the temperature experiment.
| Tank | Treament (°C) | n | Mean DW (mm) | Temp (°C) | Salinity | Li/Cawater (μmol mol-1) | Mg/Cawater (mmol mol-1) | Mn/Cawater (μmol mol-1) | Zn/Cawater (μmol mol-1) | Sr/Cawater (mmol mol-1) | Ba/Cawater (μmol mol-1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 15 | 12 | 115.8 (17.4) | 15.4 (1.2) | 31.6 (1.6) | 11.57 (0.26) | 4988 (20.8) | 13.64 (0.76) | 18.88 (7.91) | 8.77 (0.09) | 6.31 (1.52) |
| 6 | 15 | 12 | 117.5 (16.2) | 15.0 (1.2) | 31.6 (1.6) | 11.54 (0.34) | 4963 (61.9) | 13.45 (0.52) | 19.44 (9.55) | 8.74 (0.12) | 5.35 (1.48) |
| 8 | 15 | 11 | 118.0 (20.5) | 15.5 (1.3) | 31.7 (1.6) | 11.43 (0.34) | 4984 (15.3) | 13.45 (0.28) | 27.42 (17.20) | 8.76 (0.09) | 5.14 (1.65) |
| 1 | 18 | 11 | 100.0 (18.0) | 18.8 (0.9) | 32.3 (1.2) | 11.63 (0.27) | 4992 (18.8) | 13.50 (0.24) | 24.37 (10.57) | 8.79 (0.07) | 5.05 (0.95) |
| 4 | 18 | 10 | 121.3 (20.8) | 18.5 (0.8) | 32.2 (1.2) | 11.70 (0.21) | 4990 (12.3) | 13.76 (0.30) | 20.51 (7.78) | 8.79 (0.07) | 5.22 (1.07) |
| 7 | 18 | 12 | 115.9 (16.6) | 18.6 (0.7) | 32.4 (1.2) | 11.64 (0.47) | 4999 (18.5) | 13.64 (0.54) | 22.23 (13.27) | 8.81 (0.08) | 5.39 (1.24) |
| 2 | 24 | 12 | 116.4 (19.6) | 23.9 (0.9) | 32.6 (1.4) | 11.43 (0.64) | 4984 (31.7) | 14.26 (1.08) | 24.10 (6.13) | 8.78 (0.14) | 5.37 (1.52) |
| 5 | 24 | 12 | 119.7 (18.3) | 24.3 (1.2) | 33.0 (1.9) | 11.42 (0.54) | 4987 (17.4) | 13.40 (1.28) | 24.85 (13.90) | 8.78 (0.11) | 5.02 (1.30) |
| 9 | 24 | 13 | 115.6 (14.2) | 24.1 (0.8) | 33.2 (1.4) | 11.44 (0.33) | 4983 (13.1) | 13.68 (0.79) | 28.18 (10.71) | 8.76 (0.08) | 5.63 (1.28) |
The summary includes the number of round rays (Urobatis halleri) per tank (n, their mean size in disc width (DW) at the onset of the study, water temperature (°C), salinity, and dissolved element to calcium (Ca) ratios for lithium (Li), magnesium (Mg), manganese (Mn), zinc (Zn), strontium (Sr), and barium (Ba). Values in parenthesis are ± standard deviation. Untransformed element to calcium ratios are presented below but log10 transformation was necessary to meet the assumptions for parametric statistical analysis.
Table 2. Univariate results from multivariate analysis of variance tests to evaluate the effect of temperature (Temp; 15°C, 18°C, and 24°C) on dissolved element to calcium ratios (Me/Ca) in water and vertebral Me/Ca among treatments.
| Source | Me/Ca | Effect | DF | MSE | F | p |
|---|---|---|---|---|---|---|
| Water | Li | Temp | 2 | < 0.001 | 3.32 | 0.107 |
| (Tank) | 6 | < 0.001 | ||||
| Mg | Temp | 2 | < 0.001 | 1.76 | 0.250 | |
| (Tank) | 6 | < 0.001 | ||||
| Mn | Temp | 2 | < 0.001 | 0.27 | 0.774 | |
| (Tank) | 6 | 0.001 | ||||
| Zn | Temp | 2 | 0.005 | 1.71 | 0.258 | |
| (Tank) | 6 | 0.003 | ||||
| SrSr | Temp | 2 | < 0.001 | 2.98 | 0.126 | |
| (Tank) | 6 | < 0.001 | ||||
| Ba | Temp | 2 | 0.001 | 0.46 | 0.652 | |
| (Tank) | 6 | 0.001 | ||||
| Vertebrae | Li | Temp | 2 | 0.015 | 1.56 | 0.284 |
| (Tank) | 6 | 0.010 | ||||
| Mg | Temp | 2 | 0.002 | 49.81 | < 0.001 | |
| (Tank) | 6 | < 0.001 | ||||
| Mn | Temp | 2 | 0.019 | 8.87 | 0.016 | |
| (Tank) | 6 | 0.002 | ||||
| Zn | Temp | 2 | 0.028 | 12.97 | 0.007 | |
| (Tank) | 6 | 0.002 | ||||
| SrSr | Temp | 2 | < 0.001 | 3.15 | 0.102 | |
| (Tank) | 6 | < 0.001 | ||||
| Ba | Temp | 2 | 0.118 | 91.78 | < 0.001 | |
| (Tank) | 6 | 0.001 |
Significant p-values are indicated by bold font. Data were log10-transformed prior to analysis.
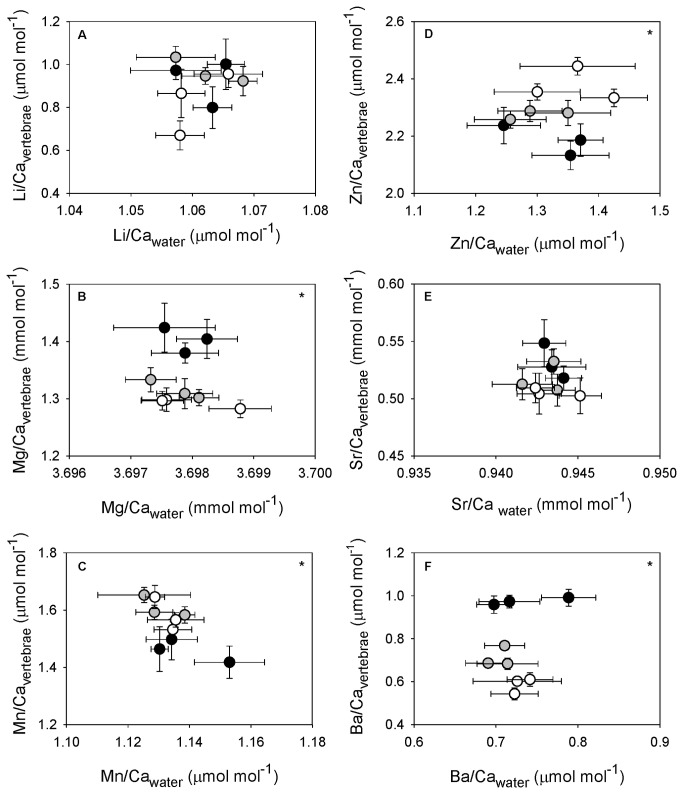
We observed significant and varied responses in vertebral elemental composition among temperature treatments (MANOVA, Pillai’s trace = 10.80, p < 0.001; Table 2). Vertebral Li/Ca and Sr/Ca did not vary among temperatures (Figure 2a, 2e). Vertebral incorporation of Mg/Ca and Ba/Ca was significantly and negatively affected by temperature (Figure 2b, 2f) whereas incorporation of Mn/Ca and Zn/Ca was significantly and positively related to temperature (Figure 2c, 2d). The significant effect of temperature on both Mg/Cavertebrae and Mn/Cavertebrae was attributed to differences in the lowest temperature treatment. Mg/Cavertebrae was elevated at 15°C (THSD, p < 0.001 for 15° v. 18°C and 15° v. 24°C), however, Mn/Cavertebrae at 15°C was significantly less than those measured in U. halleri maintained 18° and 24°C (THSD, p = 0.009 for 15° v. 18°C and p = 0.005 for 15° v. 24°C). Mean Zn/Cavertebrae was significantly greater at 24°C but did not differ between 15 and 18°C treatments (THSD, p < 0.001 for 15 v. 24°C, p = 0.019 for 18 v. 24°C). Significant variation in Ba/Cavertebrae was evident across all treatments, with mean Ba/Cavertebrae decreasing with increasing temperature (Figure 2f; THSD, p < 0.001 for all pair-wise comparisons). Overall mean (± standard deviation, SD) Ba/Cavertebrae was 0.97 ± 0.12, 0.71 ± 0.08, and 0.59 ± 0.09 μmol mol-1 for 15°, 18°, and 24°C treatments, respectively.
Figure 2. Relationships between water and vertebral elemental ratios by temperature treatment.
Mean ± standard error of element to calcium ratios for water and vertebral samples. Black circles represent 15°C treatments, grey circles 18°C treatments, and open circles 24°C treatments. (A) lithium, (B) magnesium, (C) manganese, (D) zinc, (E) strontium, and (F) barium. Element to calcium ratios were log10-transformed. Significant temperature effects are indicated by (*).
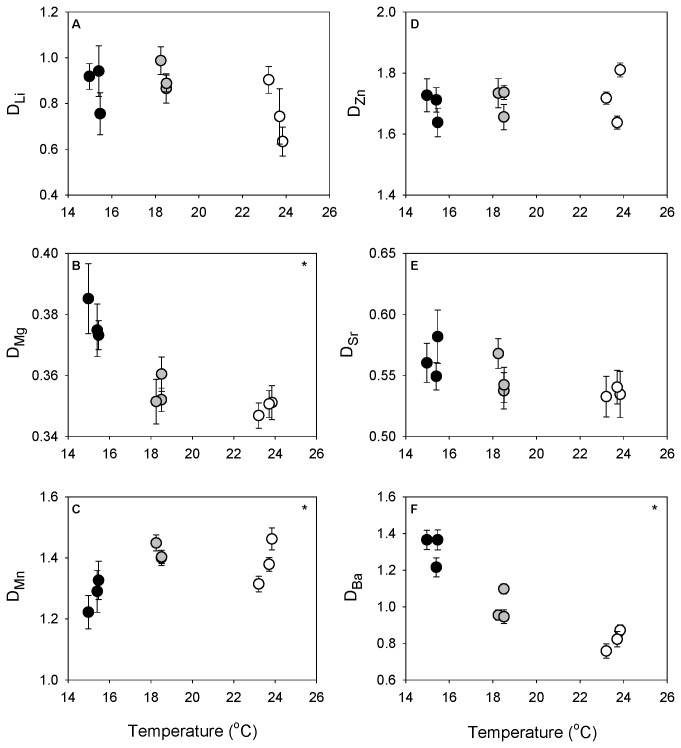
Varied responses to temperature were also observed among the partition coefficients calculated in this study (Table 3, Figure 3). We detected no effect of temperature on Li incorporation. Although a significant temperature effect was associated with Zn/Cavertebrae, DZn indicated no evidence of temperature dependence. DSr values showed a slight decrease with increasing temperatures, but the observed trend was statistically insignificant. Temperature had a significant negative effect on DMg and DBa (Figure 3b, 3f) and positively influenced DMn (Figure 3c). Mean DMg declined with increasing temperature but the observed pattern was driven by differences between the 15°C and warmer treatments (THSD, p < 0.001 for 15° v. 18°C and 15° v. 24°C). A strong, negative effect of temperature on DBa was detected across treatments (THSD, p < 0.001 for all pair-wise comparisons). For DBa, treatment means (± SD) were 1.31 ± 0.18, 0.99 ± 0.12, and 0.81 ± 0.13 at 15°, 18°, and 24°C, respectively. The positive effect of temperature demonstrated by DMn was due to increased discrimination of Mn at 15°C (lower DMn values) compared with 18° and 24°C (THSD, p = 0.017 for 15° v. 18°C and p = 0.001 for 15° v. 24°C).
Table 3. Results of nested analysis of variance to evaluate the effect of temperature (Temp; 15°C, 18°C, and 24°C) and barium ([Ba]; 1x, 3x, and 6x average ambient values) treatments on mean partition coefficients (DMe).
| Experiment | DMe | Effect | DF | MSE | F | p |
|---|---|---|---|---|---|---|
| Temperature | DLi | Temp | 2 | 0.017 | 2.32 | 0.180 |
| (Tank) | 6 | 0.007 | ||||
| DMg | Temp | 2 | 0.001 | 47.86 | < 0.001 | |
| (Tank) | 6 | < 0.001 | ||||
| DMn | Temp | 2 | 0.016 | 5.90 | 0.038 | |
| (Tank) | 6 | 0.003 | ||||
| DZn | Temp | 2 | < 0.001 | 0.17 | 0.850 | |
| (Tank) | 6 | 0.004 | ||||
| DSr | Temp | 2 | < 0.001 | 3.09 | 0.119 | |
| (Tank) | 6 | < 0.001 | ||||
| DBa | Temp | 2 | 0.191 | 31.77 | < 0.001 | |
| (Tank) | 6 | 0.006 | ||||
| Barium | DLi | [Ba] | 2 | 0.003 | 1.50 | 0.297 |
| manipulation | (Tank) | 6 | 0.002 | |||
| DMg | [Ba] | 2 | < 0.001 | 1.69 | 0.261 | |
| (Tank) | 6 | < 0.001 | ||||
| DMn | [Ba] | 2 | 0.002 | 1.96 | 0.221 | |
| (Tank) | 6 | 0.001 | ||||
| DZn | [Ba] | 2 | 0.137 | 0.61 | 0.575 | |
| (Tank) | 6 | 0.023 | ||||
| DSr | [Ba] | 2 | < 0.001 | 0.27 | 0.769 | |
| (Tank) | 6 | 0.001 | ||||
| DBa | [Ba] | 2 | 0.015 | 20.44 | 0.002 | |
| (Tank) | 6 | 0.001 |
Significant p-values are indicated by bold font. Data were log10-transformed prior to analysis.
Figure 3. Influence of temperature treatment on elemental partitioning.
Mean ± standard error of partition coefficients (DMe) for (A) lithium, (B) magnesium, (C) manganese, (D) zinc, (E) strontium, and (F) barium by treatment and mean tank temperature. Black circles represent 15°C treatments, grey circles 18°C treatments, and open circles 24°C treatments. Significant responses of DMe to temperature are indicated by (*).
Ba manipulation experiment
Targeted Ba concentrations of 3x and 6x were successfully attained (Tables 4, 5). Mean Ba/Cawater values differed significantly among treatments (Figure 4; THSD, p < 0.01 for all pair-wise comparisons). Salinity (Kruskal-Wallis, H = 5.71, p = 0.06) and temperature (Kruskal-Wallis, H = 1.18, p = 0.56) did not differ among treatments (Table 4). With the exception of the intended variation in Ba/Cawater, dissolved elemental composition did not differ among treatments (MANOVA, Pillai’s trace = 0.72, p = 0.03; Table 5).
Table 4. Mean experimental conditions by tank and treatment during the barium manipulation experiment.
| Tank | Treament | n | Mean DW (mm) | Temp (°C) | Salinity | Li/Cawater (μmol mol-1) | Mg/Cawater (mmol mol-1) | Mn/Cawater (μmol mol-1) | Zn/Cawater (μmol mol-1) | Sr/Cawater (mmol mol-1) | Ba/Cawater (μmol mol-1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1x | 12 | 162.1 (14.0) | 19.8 (0.2) | 30.0 (0.7) | 11.59 (0.28) | 4988 (8.8) | 14.18 (0.74) | 44.54 (13.22) | 8.76 (0.05) | 4.68 (0.52) |
| 6 | 1x | 12 | 131.8 (15.5) | 19.6 (0.4) | 30.7 (0.6) | 11.87 (0.42) | 4984 (11.0) | 13.77 (0.57) | 24.34 (6.56) | 8.76 (0.07) | 4.85 (0.60) |
| 7 | 1x | 12 | 143.5 (12.6) | 19.5 (0.2) | 29.9 (0.7) | 12.06 (0.64) | 5001 (32.9) | 13.24 (0.67) | 27.08 (9.37) | 8.80 (0.12) | 4.96 (0.50) |
| 3 | 3x | 11 | 132.3 (15.9) | 19.8 (0.4) | 29.5 (1.0) | 11.74 (0.35) | 4996 (26.1) | 13.95 (0.78) | 23.12 (4.72) | 8.78 (0.13) | 10.21 (7.83) |
| 4 | 3x | 10 | 146.6 (15.4) | 19.5 (0.4) | 29.8 (0.9) | 11.73 (0.30) | 4985 (16.1) | 14.54 (1.28) | 25.08 (11.05) | 8.76 (0.09) | 16.94 (14.11) |
| 9 | 3x | 12 | 165.5 (7.7) | 19.4 (0.3) | 29.8 (1.0) | 11.55 (0.37) | 4986 (16.7) | 14.67 (0.56) | 48.99 (20.95) | 8.76 (0.07) | 14.15 (8.30) |
| 1 | 6x | 11 | 148.2 (9.5) | 19.4 (0.3) | 29.8 (0.7) | 11.89 (0.79) | 5005 (39.1) | 14.86 (1.37) | 47.85 (22.22) | 8.74 (0.07) | 31.99 (21.58) |
| 5 | 6x | 7 | 167.4 (9.5) | 19.8 (0.2) | 29.7 (0.8) | 11.81 (0.25) | 4993 (18.9) | 14.80 (1.91) | 35.90 (21.38) | 8.78 (0.11) | 44.22 (3.87) |
| 8 | 6x | 11 | 136.5 (17.9) | 19.7 (0.4) | 29.8 (1.0) | 11.73 (0.22) | 4994 (34.2) | 13.89 (0.59) | 36.10 (15.18) | 8.79 (0.12) | 31.73 (19.23) |
Table 5. Univariate results from multivariate analysis of variance tests to evaluate the effect of barium concentration ([Ba]; 1x, 3x, and 6x local ambient values) on dissolved element to calcium ratios in water and vertebral element to calcium ratios among treatments.
| Source | Me/Ca | Effect | DF | MSE | F | p |
|---|---|---|---|---|---|---|
| Water | Li | [Ba] | 2 | < 0.001 | 1.49 | 0.299 |
| (Tank) | 6 | < 0.001 | ||||
| Mg | [Ba] | 2 | < 0.001 | 0.70 | 0.534 | |
| (Tank) | 6 | < 0.001 | ||||
| Mn | [Ba] | 2 | 0.001 | 5.08 | 0.051 | |
| (Tank) | 6 | < 0.001 | ||||
| Zn | [Ba] | 2 | 0.016 | 0.91 | 0.451 | |
| (Tank) | 6 | 0.017 | ||||
| SrSr | [Ba] | 2 | < 0.001 | 1.08 | 0.398 | |
| (Tank) | 6 | < 0.001 | ||||
| Ba | [Ba] | 2 | 0.424 | 28.19 | < 0.001 | |
| (Tank) | 6 | 0.015 | ||||
| Vertebrae | Li | [Ba] | 2 | 0.004 | 1.14 | 0.382 |
| (Tank) | 6 | 0.004 | ||||
| Mg | [Ba] | 2 | < 0.001 | 0.92 | 0.447 | |
| (Tank) | 6 | < 0.001 | ||||
| Mn | [Ba] | 2 | < 0.001 | 0.16 | 0.858 | |
| (Tank) | 6 | 0.002 | ||||
| Zn | [Ba] | 2 | 0.004 | 0.83 | 0.480 | |
| (Tank) | 6 | 0.002 | ||||
| SrSr | [Ba] | 2 | < 0.001 | 0.19 | 0.829 | |
| (Tank) | 6 | < 0.001 | ||||
| Ba | [Ba] | 2 | 0.145 | 99.59 | < 0.001 | |
| (Tank) | 6 | 0.001 |
Significant p-values are indicated by bold font. data were log10-transformed prior to analysis.
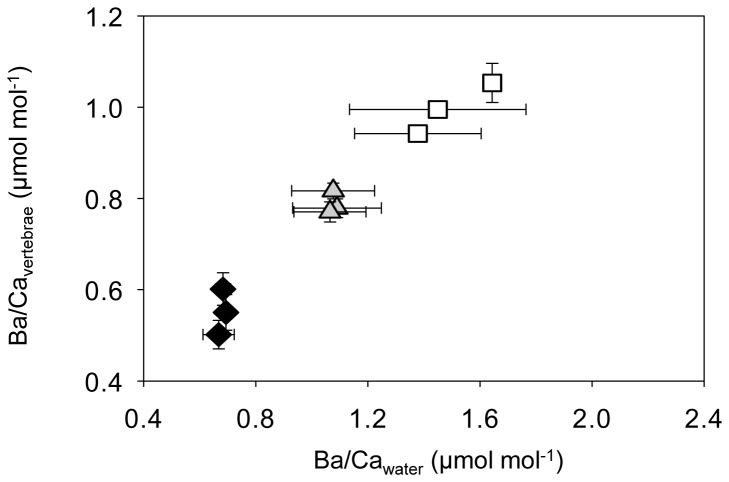
Figure 4. Relationships between water and vertebral barium to calcium ratios by barium treatment.
Mean ± standard error of barium to calcium ratios for water and vertebral samples. Black diamonds represent 1x, grey triangles 3x, and unfilled squares 6x barium treatments. Element to calcium ratios were log10-transformed.
Treatments reflect ambient (1x) barium concentrations and targeted concentrations of three (3x) and six (6x) times the mean ambient value. The summary includes the number of round rays (Urobatis halleri) per tank (n), their mean size in disc width (DW) at the onset of the barium manipulation experiment, water temperature (°C), salinity, and dissolved element to calcium (Ca) for lithium (Li), magnesium (Mg), manganese (Mn), zinc (Zn), strontium (Sr), and barium (Ba). Values in parenthesis are ± standard deviation. Untransformed element to calcium ratios are presented below but log10-transformation of these data was necessary to meet the assumptions for parametric statistical analysis.
Ambient Ba concentration had a positive effect on Ba/Cavertebrae (MANOVA, Pillai’s trace = 0.95, p < 0.001; Table 5). Significant differences were found across treatments (Figure 4; THSD, p < 0.001 for all pair-wise comparisons). Mean (± SD) vertebral Ba/Ca were 0.56 ± 0.11, 0.76 ± 0.05, and 0.99 ± 0.09 μmol mol-1 for 1x, 3x, and 6x treatments, respectively.
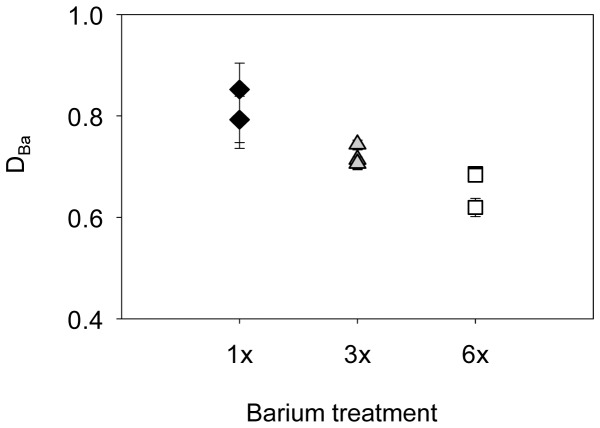
DBa decreased significantly with increasing dissolved Ba concentrations (Table 3, Figure 5). This negative relationship indicates that discrimination of Ba increases (less Ba is incorporated) in response to elevated environmental Ba concentrations. Mean DBa differed significantly among treatments (THSD, p < 0.01 for all pair-wise comparisons). Treatment means (± SD) of DBa were 0.81 ± 0.15 at 1x, 0.72 ± 0.05 at 3x, and 0.67 ± 0.05 at 6x.
Figure 5. Influence of barium treatment on elemental partitioning.
Mean ± standard error of barium partition coefficients (DBa) by barium treatment. Black diamonds represent 1x, grey triangles 3x, and unfilled squares 6x that of average local barium values.
Precipitation and growth rate effects
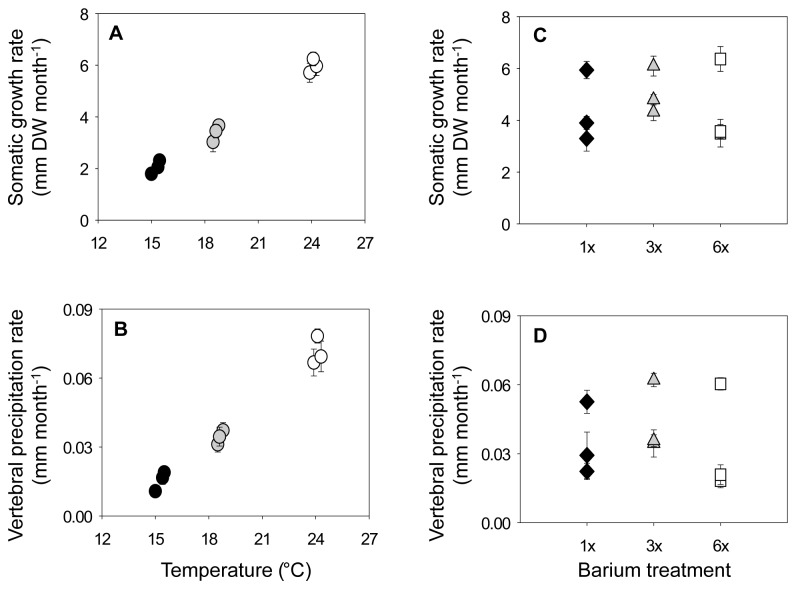
As anticipated, somatic growth (ANOVA, F2,6 = 148.40, p < 0.001) and vertebral precipitation (ANOVA, F2,6 = 115.53, < 0.001) rates were significantly affected by temperature. Mean growth rates increased with increasing temperatures, ranging between 1.8–6.2 mm DW month-1 (Figure 6a, Table S1). Vertebral deposition rates reflected a similar, positive response to temperature (Figure 6b). No significant relationships were identified between DMe and somatic growth (r ≤ 0.30, p ≥ 0.10) or vertebral precipitation rates within temperature treatments (r ≤ 0.41, p ≥ 0.12) (Table S2), indicating that growth rates were not responsible for the variation in elemental composition observed among treatments.
Figure 6. Mean somatic growth and vertebral precipitation rates during temperature and barium manipulation experiments.
Mean (A, C) somatic growth and (B, D) vertebral precipitation rates by tank, treatment, and experiment (± standard error). (A, B) Black circles represent 15°C treatments, grey circles 18°C treatments, and open circles 24°C treatments. (C, D) Black diamonds represent 1x, grey triangles 3x, and unfilled squares 6x that of average local barium values. Temperatures were equivalent among treatments (19°C) during the barium manipulation experiment.
Somatic growth (ANOVA, F2,6 = 0.32, p = 0.80) and vertebral precipitation rates (ANOVA, F2,6 = 1.86, p = 0.23; Figure 6d) did not differ among Ba treatments. Mean somatic growth rates ranged from 3.3–6.4 mm DW month-1 (Figure 6c) and were consistently and significantly elevated in one tank within each treatment (ANOVA, F ≥ 9.4, p ≤ 0.0006 for all comparisons). Tanks with elevated mean growth rates in each treatment represented those that had experienced the least amount of temperature change (1°C) between the temperature and Ba manipulation experiments. Regression analyses indicated DZn was negatively correlated with somatic growth in two of the three Ba treatments (3x, 6x; Table S2). However, there was no detectable influence of vertebral precipitation rate on DZn or the other DMe considered in this study (Table S1, S2).
Classification
The multi-elemental composition of vertebrae successfully distinguished U. halleri based on their environmental (i.e. treatment) history (Table 6). Zinc was excluded from DFA because of the observed potential to vary with growth rate. Therefore, DFAs were conducted using four elemental ratios (Mg/Ca, Mn/Ca, Sr/Ca, and Ba/Ca). For the temperature experiment (15°, 18°, 24°C), overall group classification success was 85%, which was significantly better than expected by chance. Classification of rays based on ambient Ba history (1x, 3x, 6x average local values), was accomplished with 96% success overall, which was also better than random chance. Ba/Ca ratios were the most influential variable used to predict group membership in both DFAs.
Table 6. Group classification success of round rays (Urobatis halleri) determined from discriminant function analysis of vertebral elemental composition of magnesium, manganese, strontium, and barium (expressed as element to calcium ratios).
| Treatment | % Correctly Classified | Overall % Classification Success | κ (± ASE) |
|---|---|---|---|
| Temperature | |||
| 15 | 91 | 85 | 0.77 (0.09) |
| 18 | 86 | ||
| 24 | 76 | ||
| Barium | |||
| 1x | 100 | 96 | 0.94 (0.08) |
| 3x | 97 | ||
| 6x | 91 |
Jack-knife classification success among groups based on known, controlled temperature and dissolved barium concentration histories. Overall percent classification success of groups and chance-corrected classification (κ) ± approximate standard error (ASE) represent independent measures of group classification performance.
Discussion
We demonstrated that the composition of certain minor and trace metal elements in U. halleri vertebrae was related to the physical and chemical properties of the water occupied by the rays. Vertebral incorporation of three of the six elements evaluated demonstrated significant temperature-dependent responses, revealing both positive (DMn) and negative relationships (DMg and DBa) with temperature. Vertebral Ba/Ca ratios in U. halleri were incorporated in proportion to Ba/Cawater, supporting their application as useful intrinsic elemental markers. Elemental incorporation of Li, Mg, Mn, Sr, and Ba did not appear to be mediated by somatic growth or vertebral precipitation rates, indicating that individual variation in growth rates are unlikely to be responsible for observed variation in vertebral elemental composition. Significant relationships between somatic growth rate and Zn incorporation were identified. However, correlations between DZn and somatic growth rate were inconsistent across treatments and between experiments, warranting further investigation. Using DFA, we reliably distinguished the environmental history of individual rays based on differences in vertebral elemental composition. These results indicate that vertebral elemental analysis is a promising tool for the study of elasmobranch populations.
Vertebral elemental composition and influences on incorporation
Lithium
The Li/Ca composition of U. halleri vertebrae was occasionally below detection limits, highly variable, and not affected by temperature. In synthetic (nonbiogenic) hydroxyapatite, Li has been found to directly substitute for Ca and to increase proportionately with ambient dissolved concentrations [53]. The sparse experimental work on temperature effects on Li uptake in biogenic calcified structures provides mixed results. Negative temperature effects of Li/Ca incorporation into calcite and aragonite have been identified experimentally in some foraminifera, brachiopods, and coral [54,55] whereas no effect has been observed in other foraminifera and coral species [56].
Otolith Li/Ca has been used as an elemental marker in freshwater [57], diadromous [58], and marine teleosts [59] as well as an elasmobranch [31]. Fleishman et al. [60] determined that lithium (Li+) concentrations in the blood plasma of elasmobranchs were 5-7 times lower than that of ambient seawater. This marked discrimination against Li+ likely reflects the approach elasmobranchs evolved to maintain internal ionic and osmotic equilibrium (osmoregulation). Because concentrations of NaCl in the plasma of marine elasmobranchs are generally maintained below that of seawater, elasmobranchs experience an osmotic influx of NaCl that must be regulated [60]. Lithium, like Na+, is a monovalent alkali metal that is unlikely to be differentiated from Na+ during osmoregulation [60]. In elasmobranchs, excess Na+, chloride (Cl‾) and Li+ are concentrated in the kidneys and renal gland and excreted with urine and other waste [61]. Discrimination of Li is reflected in the partition coefficients calculated from U. halleri vertebrae in this study (overall DLi: 0.85 ± 0.21 SD). However, elemental partitioning may be underestimated in our analyses because of the exclusion of samples that fell below instrument detection limits. If we include those samples as 0 values, the grand mean decreases (DLi: 0.64 ± 0.39 SD), indicating a greater extent of Li discrimination.
Magnesium
The negative effects of temperature on Mg/Ca incorporation (and DMg) observed in U. halleri have also been reported in marine gastropods [62] and benthic foraminifera [63]. Among marine fishes, significant effects of temperature on otolith Mg/Ca ratios have not been commonly reported. Experimental investigations of elemental incorporation into the otoliths of red drum (Sciaenops ocellatus [64]), spot (Leiostomus xanthurus [16]), gray snapper (Lutjanus griseus [65]), and Pacific cod (Gadus macrocephalus [42]) all concluded that otolith Mg/Ca was not affected by temperature. Increasing temperature has been found to cause an increase in Mg/Ca within the otoliths of Argyrosomus japonicus [66]. In contrast, Mg/Ca ratios in synthetic aragonite show an inverse relationship with temperature similar to that observed within U. halleri vertebrae [67]. These results are likely due to underlying differences in the kinetics of mineralization associated with biogenic aragonite and hydroxyapatite and differences in ionic regulation between teleost fishes and elasmobranchs.
Magnesium partition coefficients were expressed across a narrow range (DMg = 0.32-0.43) and exhibited the strongest discrimination (lowest DMe) among the six elements considered in this investigation (e.g. mean DMg = 0.38, 0.39, 0.39 for 1x, 3x, 6x Ba treatments at 19°C; %CV = 5.6). Magnesium is an essential micronutrient that supports cellular metabolism, immune system function, and skeletal growth, among other physiological processes. In synthetic hydroxyapatites, Mg ions have been found to substitute for and compete with Ca and inhibit mineralization rates [68,69]. Therefore, internal concentrations of Mg are likely subjected to a high degree of physiological regulation that would be reflected in a comparatively consistent pattern of incorporation, as was observed in U. halleri. Despite this regulation, Mg may be a useful indicator temperature history and a valuable geospatial marker in elasmobranchs.
Manganese
Temperature influences on Mn incorporation into biomineralized structures have generally been found to be insignificant [65,70] or negative [40,71], but Mn/Cavertebrae and DMn were positively affected by temperature in U. halleri. The effect was not expressed across temperatures but was driven by significantly lower incorporation of Mn/Ca within the coldest (15°C) treatment. Manganese is an essential micronutrient that is an important cofactor for many enzymes and supports metabolism, protein production, cellular signaling processes, and the activation of reproductive hormones. Though Mn/Ca uptake is proportional to Mn/Cawater in synthetic hydroxyapatite [72], osmotic regulation of Mn ions would alter this direct relationship in biogenic hydroxyapatites. Furthermore, diet represents the primary pathway of Mn uptake in elasmobranchs and other vertebrates [73,74]. In a comparative study of radionuclide accumulation in a teleost and elasmobranch, Pentreath [75] concluded that uptake of Mn radioisotopes solely from water was insufficient to explain internal concentrations of the radionuclide. More recently, Mathews & Fisher [74] experimentally determined that >90% of the Mn accumulated in the soft tissues of lesser spotted dogfish (Scyliorhinus canicula) was derived from dietary sources. The contribution of dietary Mn in addition to uptake from the environment at the gills offers an explanation for the elevated values of Mn/Cavertebrae in comparison to water Mn/Ca in our experiment (Figure 2c).
Considerable variation in DMn has been reported within and among species. DMn ranged between 0.10–1.90 in juvenile black bream (Acanthopagrus butcheri [76]), 0.018–1.02 in grey snapper [65], and 7.67–32.83 in a field-based study of spotted sea trout (Cynoscion nebulosus [77]). Strasser et al. [78] identified ontogenetic differences in DMn between larval (mean ± SD: 1.86 ± 0.19) and juvenile softshell clams (mean ± SD: 0.88 ± 0.13), Mya Arenaria. Our estimates of DMn typically exceeded 1.0 (temperature experiment: 0.9–1.60; Ba manipulation experiment: 1.36–1.69) but fell within the broad range reported among these other investigations. Laboratory studies intended to assess the factors controlling Mn incorporation into otoliths have found no evidence of a relationship between Mn/Cawater and Mn/Caotolith (see review by Miller [40]). However, Limburg et al. [79] hypothesized that cyclical variation of Mn/Caotolith ratios were associated with migrations into deep water hypoxic zones that are characterized by elevated Mn concentrations, providing historic records of hypoxia intensity. Further research on the mechanisms of Mn incorporation is needed to clarify the utility of this element as a geospatial tag or indicator environmental history.
Zinc
Our analyses of Zn incorporation into U. halleri vertebrae revealed a positive influence of temperature on Zn/Cavertebrae, no significant effect of temperature on DZn, and significant influences of somatic growth rates on DZn, providing a somewhat convoluted perspective on the factors influencing Zn incorporation. Few studies have attempted to experimentally validate Zn incorporation into biogenic calcified structures [70,71,80]. Zn is fundamental to a diverse array of physiological processes, including growth, neurotransmission, and cell signaling. It plays a vital role in protein production, structure, and maintenance [81]. Though branchial uptake of Zn is not inconsequential, diet represents the primary source of Zn intake in both elasmobranch and teleost fishes [74,75]. The dietary contribution of Zn in the elasmobranch S. canicula (>80% [74]) is similar to those experimentally estimated for other fishes [82,83]. Given our use of standardized diets, the observed inconsistencies may be the result of the variation in Zn/Cawater values (Tables 1, 4). Alternatively, variation in Zn/Cavertebrae may be influenced by somatic growth rate and kinetic effects.
In synthetic hydroxyapatites, Zn substitution for Ca is minimal and the majority of Zn is incorporated through inclusion into interstitial spaces [84]. Elements incorporated into interstitial spaces can be representative of environmental conditions [8,15], but the pathways and mechanisms of Zn incorporation may differ in biogenic hydroxyapatite. Miller et al. [85] determined that the majority (40-60%) of Zn contained in Atlantic cod (Gadus morhua) otoliths was associated with the protein matrix rather than the mineralized aragonite structure or interstitial spaces. Given the critical role of Zn identified in more than 300 fish proteins [13], it is likely that much of the Zn contained in the biogenic hydroxyapatite of elasmobranch vertebrae is bound within the protein matrix as well. Because it is prevalent in the protein structure of otoliths and is assimilated primarily through dietary sources, Miller et al. [85] concluded that Zn is unlikely to be a reliable proxy of ambient environmental conditions. Zn has been reported to be useful for distinguishing shark populations [30] and movements of sharks between habitats [31]. Based on our results and a review of available literature, we do not anticipate vertebral Zn/Ca ratios and DZn to be commonly representative of ambient conditions.
Strontium
Strontium is one of the most commonly studied elemental markers in biogenic calcified structures. Unlike several of the elements previously considered in this study, a physiological role for Sr has not been identified in fishes [14]. Sr is primarily derived via branchial uptake in fishes and Sr/Ca ratios of otoliths are typically representative of ambient concentrations [86–88]. In synthetic hydroxyapatite and aragonite, Sr is known to compete with and substitute for Ca [89]. Temperature-dependent responses in Sr/Ca incorporation have provided reliable indicators of temperature history in corals [90] and fishes [39], but Sr incorporation was not influenced by temperature in U. halleri. Temperature-independent patterns of Sr/Ca incorporation were also reported in juvenile L. xanthurus scales [91], common cuttlefish statoliths (Sepia officinalis [38]), and the otoliths of European eels (Anguilla anguilla [92]). We anticipate that Sr is likely to be a valuable elemental marker in elasmobranchs, particularly among euryhaline species.
Barium
The strong, negative effect of temperature on Ba incorporation in U. halleri is similar to the pattern observed by Balter & Lécuyer [93] in laboratory studies of synthetic hydroxyapatite. Decreases in Ba/Ca ratios with increasing ambient water temperature have also been found in laboratory studies with synthetic aragonite [67], cephalopods [38], larval gastropods [91,94], juvenile clams [95], and larval fish [42]. However, positive or no effect of temperature on Ba incorporation into otoliths has been much more commonly observed [40]. Studies of Ba incorporation into the hydroxyapatite of fish scales, bone, and teeth have also revealed either positive [12] or no relationship to temperature [91]. Given the inconsistency in temperature effects on Ba incorporation reported within the literature, it is likely that species-specific variation in this temperature response is widespread.
The significant positive relationship between vertebrae and water Ba/Ca supports the utility of Ba/Ca ratios as elemental markers. However, our observation of a negative temperature effect on Ba/Ca incorporation indicates there are likely to be interactive effects of temperature and water concentration on vertebral Ba incorporation. These effects could confound interpretations of field data, particularly in study areas with sharp gradients in both temperature and Ba/Cawater. For example, vertebral Ba/Ca of U. halleri at 15.4°C and exposed to Ba/Cawater of 6.3 μmol mol-1 (Ba/Cavertebrae = 0.96) would be indistinguishable from U. halleri that had resided in water averaging 19.7°C with a mean Ba/Cawater concentration of 31.7 μmol mol-1 (Ba/Cavertebrae = 0.94). This finding highlights the importance of experimental validation studies, the utility of measuring multiple elemental markers, the value of temperature data from study areas, and need for caution when interpreting patterns among elemental signatures from field studies.
Effects of growth and precipitation rates
Variation in growth rates can alter physiological and kinetic processes that directly modify patterns and rates of elemental discrimination and incorporation [47,71]. For example, growth-mediated effects on elemental incorporation could produce significant variability among individuals with inherently different growth rates that occupy the same water mass. Indeed, growth rates have been found to influence the composition of some calcified structures [7,16,18]. In this study, we found no significant relationships between somatic growth or vertebral precipitation rates and DMe for any elements except Zn in U. halleri (Table S1, S2), which supports the premise that growth rates do not generally alter vertebral elemental composition.
In contrast to other elements, DZn, independent of temperature, was significantly but inconsistently correlated with somatic growth. The effect of growth on DZn was restricted to the 3x and 6x Ba treatments (Table S1, Table S2). Vertebral precipitation rates (μm radius month-1), however, were not significantly correlated with DZn. Zn/Cawater values displayed the greatest variance among the six elemental ratios measured in this study (%CV = 47.8). Dissolved Zn concentrations can be highly variable, elevating during periods of increased river discharge and runoff [96]. Water changes that occurred during high flow events could have influenced Zn/Cawater and Zn/Cavertebrae in some tanks. Trace levels of Zn in seawater are also prone to contamination [97]. Given broad environmental variation and the potential for contamination, our sampling frequency may not have been sufficient to adequately characterize the uptake and partitioning of Zn in U. halleri. Further research is needed to clarify the relationships between Zn/Cawater, Zn/Cavertebrae, and somatic growth rates, if this element is to be used as a reliable marker of population structure, habitat use or natal origins.
Ecological applications and future directions
Group classification of U. halleri based on environmental history within the controlled laboratory studies was highly successful (Table 6). Our results indicate that elemental variation in elasmobranch vertebrae can reliably distinguish individuals based on differences in their environmental history or habitat – assuming differences among those habitats or time periods exist. Studies of vertebral elemental chemistry could discern natal origins, biological hotspots, movement patterns, habitat use, and population structure of elasmobranchs, and generate critical information for spatially-explicit conservation and management measures.
The significant temperature effects and the likelihood for interaction between temperature and ambient concentration on Ba incorporation observed in this study emphasize the importance of considering multiple elemental markers when making spatial and temporal inferences regarding environmental history. Measurements of vertebral bulk or compound-specific stable isotopic composition [98,99], mapping of environmental chemical composition/isoscapes [100,101], or molecular analyses [102] used in conjunction with minor and trace elemental assays should provide greater resolution than would be obtained from a single method alone. We anticipate that studies integrating complementary intrinsic markers will generate corroborative and more robust conclusions based on field data.
Our results prompt questions regarding the periodicity of growth band/increment deposition within elasmobranch vertebrae. Increments are deposited daily within fish otoliths and bivalve shells, a phenomenon that has not yet been found in elasmobranchs [4,26]. Yet, microscopic examination of elasmobranch vertebrae typically reveals other increments and checks within the pair of annual growth bands [26,103]. Are growth bands deposited at finer temporal scales within elasmobranch vertebrae? The ability to reconstruct environmental history and assay elemental markers with more refined temporal resolution would enhance the utility of this tool in studies of elasmobranch populations.
Elemental composition of elasmobranch vertebrae may not provide a useful record of environmental history for all species. Vertebral elemental composition could differ due to species-specific environmental tolerances [104,105] or extent of vertebral calcification [24,106]. Additional laboratory or field-based experiments should be pursued to gain insight into the potential differences in elemental incorporation among species. Our validation experiments advance the use of vertebral elemental markers for the study of elasmobranch populations and provide a framework for interpreting the results of future field investigations.
Supporting Information
Correlations (r) between partition coefficients (DMe) and somatic growth rates and vertebral precipitation rates for the temperature (T) experiment. The number (n) of round rays (Urobatis halleri) included in growth rate estimates, observed range of individual somatic growth rates (mm disc width month-1), and vertebral precipitation rates (μm radius month-1) are reported for each treatment. No significant correlations were detected (p ≥ 0.12).
(PDF)
Correlations (r) between partition coefficients (DMe) and somatic growth rates and vertebral precipitation rates for the barium manipulation ([Ba]) experiment. The number (n) of round rays (Urobatis halleri) included in growth rate estimates, observed range of individual somatic growth rates (mm disc width month-1), and vertebral precipitation rates (μm radius month-1) are reported for each treatment. Significant p-values are indicated by bold font.
(PDF)
Acknowledgments
We thank Thomas Farrugia, Chris Lowe, and Chris Mull for assistance with field collection. Neil Allen, Manny Ezcurra, Jeff Landesman, and Polly Rankin provided supplies, support, and valuable advice on specimen transport and maintenance. HMSC’s facilities and maintenance staff provided critical expertise and prompt assistance with electrical and seawater systems. Essential animal care and system maintenance were given by Ashley Metcalfe, Dawn Myers, Rhea Sanders, Jessica Tietjen-Walters, and Scott Walters. Members of the Heppell Lab, Renee Bellinger, Rebecca Hamner, Dylan Heppell, Alexis, Paul, Christine Sislak, Rhea Sanders, and Joshua Kai Smith offered much appreciated assistance with specimen handling and sample processing. Thanks to Andy Ungerer, Adam Kent, and the W.M. Keck Collaboratory for Plasma Spectrometry for guidance and assistance with LA-ICPMS and ICP-OES analyses. We gratefully acknowledge the valuable edits and constructive input on earlier versions of this manuscript by Aaron Carlisle, Zanna Chase, Bruce McCune, and an anonymous reviewer.
Funding Statement
Funding for this research was provided by a National Science Foundation Small Grant for Exploratory Research (OCE 0840860; http://www.nsf.gov/geo/oce/programs/biores.jsp) and Mamie Markham Research Awards (HMSC-OSU). Publication of this paper was supported, in part, by the Thomas G. Scott Publication Fund. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Lowenstam HA (1954) Factors affecting the aragonite: calcite ratios in carbonate-secreting marine organisms. J Geol 62: 284-321. doi:10.1086/626163. [Google Scholar]
- 2. Thompson TG, Chow TJ (1955) The strontium-calcium atom ratios in carbonate- secreting marine organisms. Deep Sea Res 3: 20-39. [Google Scholar]
- 3. Lea DW (2006) Elemental and isotopic proxies of past ocean temperatures. In: Elderfield H. The oceans and marine geochemistry, Treatise on Geochemistry, Vol 6. Elsevier-Pergamon, Oxford. [Google Scholar]
- 4. Campana SE, Thorrold SR (2001) Otoliths, increments, and elements: keys to a comprehensive understanding of fish populations? Can J Fish Aquat Sci 58: 30-38. doi:10.1139/f00-177. [Google Scholar]
- 5. Elsdon TS, Wells BK, Campana SE, Gillanders BM, Jones CM et al. (2008) Otolith chemistry to describe movements and life-history parameters of fishes: hypotheses, assumptions, limitations, and inferences. Oceanogr Mar Biol 46:297-330. [Google Scholar]
- 6. Sponaugle S (2010) Otolith microstructure reveals ecological and oceanographic processes important to ecosystem-based management. Environ Biol Fishes 89: 221-238. doi:10.1007/s10641-010-9676-z. [Google Scholar]
- 7. Stecher HA, Krantz DE, Lord CJ, Luther GW, Bock KW (1996) Profiles of strontium and barium in Mercenaria mercenaria and Spisula solidissima shells. Geochim Cosmochim Acta 60: 3445-3456. doi:10.1016/0016-7037(96)00179-2. [Google Scholar]
- 8. Campana SE (1999) Chemistry and composition of fish otoliths: pathways, mechanisms and applications. Mar Ecol Prog Ser 188: 263-297. doi:10.3354/meps188263. [Google Scholar]
- 9. Mulligan TJ, Lapi L, Kieser R, Yamada SB, Duewer DL (1983) Salmon stock identification based on elemental composition of vertebrae. Can J Fish Aquat Sci 40: 215-229. doi:10.1139/f83-327. [Google Scholar]
- 10. Wells BK, Thorrold SR, Jones CM (2003) Stability of elemental signatures in the scales of spawning weakfish, Cynoscion regalis . Can J Fish Aquat Sci 60: 361-369. doi:10.1139/f03-028. [Google Scholar]
- 11. Veinott GI, Evans RD (1999) An examination of elemental stability in the fin ray of the white sturgeon with laser ablation sampling – inductively coupled plasma-mass spectrometry (LAS-ICP-MS). Trans Am Fish Soc 128: 352-261. doi:10.1577/1548-8659(1999)128. [Google Scholar]
- 12. Balter V, Lécuyer (2010) Determination of Sr and Ba partition coefficients between apatite from fish (Sparus aurata) and seawater: The influence of temperature. Geochim Cosmochim Acta 74: 3449-3458. doi:10.1016/j.gca.2010.03.015. [Google Scholar]
- 13. Watanabe T, Kiron V, Satoh S (1997) Trace minerals in fish nutrition. Aquaculture 151: 185-207. doi:10.1016/S0044-8486(96)01503-7. [Google Scholar]
- 14. Chowdhury MJ, Blust R (2012) Strontium. In: Wood CM, Farrell AP, Brauner CJ. Homeostasis and toxicology of non-essential metals, Fish Physiology Ser Vol 31B. Academic Press, Waltham, MA. [Google Scholar]
- 15. de Vries MC, Gillanders BM, Elsdon TS (2005) Facilitation of barium uptake into fish otoliths: Influence of strontium concentration and salinity. Geochim Cosmochim Acta 69: 4061-4072. doi:10.1016/j.gca.2005.03.052. [Google Scholar]
- 16. Bath-Martin G, Thorrold SR (2005) Temperature and salinity effects on magnesium, manganese, and barium incorporation in otoliths of larval and early juvenile spot Leiostomus xanthurus . Mar Ecol Prog Ser 293: 223-232. doi:10.3354/meps293223. [Google Scholar]
- 17. Kalish JM (1989) Otolith microchemistry: validation of the effects of physiology, age and environment on otolith composition. J Exp Mar Biol Ecol 132: 151-178. doi:10.1016/0022-0981(89)90126-3. [Google Scholar]
- 18. Walther BD, Kingsford MJ, O’Callaghan MD, McCulloch MT (2010) Interactive effects of ontogeny, food ration and temperature on elemental incorporation in otoliths of a coral reef fish. Environ Biol. Fish 89: 441-451. doi:10.1007/s10641-010-9661-6. [Google Scholar]
- 19. Clement JG (1992) Re-examination of the fine structure of endoskeletal mineralization in Chondrichthyans: implications for growth, ageing and calcium homeostasis. Mar Freshw Res 43: 157-181. doi:10.1071/MF9920157. [Google Scholar]
- 20. Welden BA, Cailliet GM, Flegal AR (1987) Comparison of radiometric with vertebral age estimates in four California elasmobranchs. In: Summerfelt RC, Hall GE. The age and growth of fish. The Iowa State University Press, Ames. [Google Scholar]
- 21. Dean MN, Summers AP (2006) Cartilage in the skeleton of cartilaginous fishes. Zoology 109: 164-168. doi:10.1016/j.zool.2006.03.002. PubMed: 16584875. [DOI] [PubMed] [Google Scholar]
- 22. Simkiss K (1974) Calcium metabolism of fish in relation to ageing. In: Bagenal TB. Ageing of fish. Unwin Brother, Ltd., Surrey. [Google Scholar]
- 23. Dean MN, Mull CG, Gorb SN, Summers AP (2009) Ontogeny of the tessellated skeleton: insight from the skeletal growth of the round stingray Urobatis halleri . J Anat 215: 227-239. doi:10.1111/j.1469-7580.2009.01116.x. PubMed: 19627389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Ashhurst DE (2004) The cartilaginous skeleton of an elasmobranch fish does not heal. Matrix Biol 23: 15-22. doi:10.1016/j.matbio.2004.02.001. PubMed: 15172034. [DOI] [PubMed] [Google Scholar]
- 25. Doyle J (1968) Ageing changes in cartilage from Squalus acanthias L. Comp Biochem Physiol 25: 201-206. doi:10.1016/0010-406X(68)90927-4. PubMed: 5657197. [DOI] [PubMed] [Google Scholar]
- 26. Cailliet GM, Goldman KJ (2004) Age determination and validation in chondrichthyan fishes. In: Carrier JC, Musick JA, Heithaus MR. Biology of sharks and their relatives. CRC Press, Boca Raton. [Google Scholar]
- 27. Hale LF, Dudgeon JV, Mason AZ, Lowe CG (2006) Elemental signatures in the vertebral cartilage of the round stingray, Urobatis halleri, from Seal Beach, California. Environ Biol. Fish 77: 317-325. doi:10.1007/s10641-006-9124-2. [Google Scholar]
- 28. MacNeil MA, Skomal GB, Fisk AT (2005) Stable isotopes from multiple tissues reveal diet switching in sharks. Mar Ecol Prog Ser 302: 199-206. doi:10.3354/meps302199. [Google Scholar]
- 29. Kerr LA, Andrews AH, Cailliet GM, Brown TA, Coale KA (2006) Investigations of Δ14C, δ13C, and δ15N in vertebrae of white shark (Carcharodon carcharias) from the eastern North Pacific Ocean. Environ Biol. Fish 77: 337-353. doi:10.1007/s10641-006-9125-1. [Google Scholar]
- 30. Edmonds JS, Shibata Y, Lenanton N, Caputi N, Morita M (1996) Elemental composition of jaw cartilage of gummy shark Mustelus antarcticus Günther. Sci Total Environ 192: 151-161. doi:10.1016/S0048-9697(96)05311-9. [Google Scholar]
- 31. Tillett BJ, Meekan MG, Parry D, Munksgaard N, Field IC et al. (2011) Decoding fingerprints: elemental composition of vertebrae correlates to age-related habitat use in two morphologically similar sharks. Mar Ecol Prog Ser 434: 133-142. doi:10.3354/meps09222. [Google Scholar]
- 32. Werry JM, Lee SY, Otway NM, Hu Y, Sumpton W (2011) A multi-faceted approach for quantifying the estuarine-nearshore transition in the life cycle of the bull shark, Carcharhinus leucas . Mar Freshw Res 62: 1421-1431. doi:10.1071/MF11136. [Google Scholar]
- 33. Babel JS (1967) Reproduction, life history, and ecology of the round stingray, Urolophus halleri Cooper. Calif Fish Game. Bulletin 137: 2–104. [Google Scholar]
- 34. Hale LF, Lowe CG (2008) Age and growth of the round stingray Urobatis halleri at Seal Beach, California. J Fish Biol 7: 510–523. [Google Scholar]
- 35. Simpfendorfer CA (2000) Growth rates of juvenile dusky sharks, Carcharhinus obscurus (Lesuer, 1818) from southwestern Australia estimated from tag-recapture data. Fish Bull 98: 811-822. [Google Scholar]
- 36. Hoisington G, Lowe CG (2005) Abundance and distribution of the round stingray, Urobatis halleri, near a heated effluent outfall. Mar Environ Res 60: 437-453. doi:10.1016/j.marenvres.2005.01.003. PubMed: 15924993. [DOI] [PubMed] [Google Scholar]
- 37. Gillanders BM (2002) Temporal and spatial variability in elemental composition of otoliths: implications for determining stock identity and connectivity of populations. Can J Fish Aquat Sci 59: 669-679. doi:10.1139/f02-040. [Google Scholar]
- 38. Zumholz K, Hanstten TH, Piatkowski U, Croot PL (2007) Influence of temperature and salinity on the trace element incorporation into statoliths of the common cuttlefish (Sepia officinalis). Mar Biol 151: 1321-1330. doi:10.1007/s00227-006-0564-1. [Google Scholar]
- 39. Bath GE, Thorrold SR, Jones CM, Campana SE, McLaren JW et al. (2000) Strontium and barium uptake in aragonitic otoliths of marine fish. Geochim Cosmochim Acta 64: 1707-1714. [Google Scholar]
- 40. Miller JA (2009) The effects of temperature and water concentration on the otolith incorporation of barium and manganese in black rockfish, Sebastes melanops . J Fish Biol 75: 39–60. doi:10.1111/j.1095-8649.2009.02262.x. PubMed: 20738481. [DOI] [PubMed] [Google Scholar]
- 41. Gelsleichter J, Cortés E, Manire CA, Hueter RA, Musick JA (1997) Use of calcein as a fluorescent marker for elasmobranch vertebral cartilage. Trans Am Fish Soc 126: 862-865. doi:10.1577/1548-8659(1997)126. [Google Scholar]
- 42. DiMaria RA, Miller JA, Hurst TP (2010) Temperature and growth effects on otolith elemental composition of larval Pacific cod, Gadus macrocephalus. Environ Biol. Fish 89: 453-462. doi:10.1007/s10641-010-9665-2. [Google Scholar]
- 43. Smith WD, Cailliet GM, Mariano-Melendez E (2007) Maturity and growth characteristics of a commercially exploited stingray, Dasyatis dipterura . Mar Freshw Res 58: 54-66. doi:10.1071/MF06083. [Google Scholar]
- 44. Miller JA, Shanks AL (2004) Evidence for limited larval dispersal in black rockfish (Sebastes melanops): Implications for population structure and marine reserve design. Can J Fish Aquat Sci 61: 1723-1735. doi:10.1139/f04-111. [Google Scholar]
- 45. Dove SG, Gillanders GM, Kingsford MJ (1996) An investigation of chronological differences in the deposition of trace metals in the otoliths of two temperate reef fishes. J Exp Mar Biol Ecol 205: 15-33. doi:10.1016/S0022-0981(96)02610-X. [Google Scholar]
- 46. Kent A, Ungerer C (2006) Analysis of light lithophile elements (Li, Be, B) by laser ablation ICP-MS: comparison between magnetic sector and quadrupole ICP-MS. Am Mineral 91: 1401–1411. doi:10.2138/am.2006.2030. [Google Scholar]
- 47. Morse JW, Bender ML (1990) Partition coefficients in calcite: Examination of factors influencing the validity of experimental results and their application to natural systems. Chem Geol 82: 265-277. doi:10.1016/0009-2541(90)90085-L. [Google Scholar]
- 48. Zar JH (1996) Biostatistical analysis. 3rd ed. Prentice Hall, NJ. [Google Scholar]
- 49. Scheiner SM (2001) MANOVA: Multiple response variables and multispecies interactions. In: Scheiner SM, Gurevitch J. Design and analysis of ecological experiments, 2nd ed. Oxford University Press, Oxford. [Google Scholar]
- 50. Hurst TP, Laurel BJ, Ciannelli L (2010) Ontogentic patterns and temperature-dependent growth rates in early life stages of Pacific cod (Gadus macrocephalus). Fish Bull 108: 382-392. [Google Scholar]
- 51. McGarigal K, Cushman S, Stafford S (2000) Multivariate statistics for wildlife and ecology research. New York: Springer Science + Business Media, Inc. [Google Scholar]
- 52. Titus K, Mosher JA, Williams BK (1984) Chance-corrected classification for use in discriminant analysis: ecological applications. Am Midl Nat 111: 1-7. doi:10.2307/2425535. [Google Scholar]
- 53. Mayer I, Berger U, Markitziu A, Gedalia I (1986) The uptake of lithium by synthetic carbonated hydroxyapatite. Calcif Tissue Int 38: 293-295. doi:10.1007/BF02556609. PubMed: 3087603. [DOI] [PubMed] [Google Scholar]
- 54. Delaney ML, Bé AWH, Boyle EA (1985) Li, Sr, Mg, and Na in foraminiferal calcite shells from laboratory culture, sediment traps, and sediment cores. Geochim Cosmochim Acta 49: 1327-1341. doi:10.1016/0016-7037(85)90284-4. [Google Scholar]
- 55. Marriott CS, Henderson GM, Belshaw NS, Tudhope AW (2004) Temperature dependence of δ7 Li, δ44Ca and Li/Ca during growth of calcium carbonate. Earth Planet Sci Lett 222: 615-624. doi:10.1016/j.epsl.2004.02.031. [Google Scholar]
- 56. Rollion-Bard C, Vigier N, Meibom A, Blamart D, Reynaud S et al. (2009) Effect of environmental conditions and skeletal ultrastructure on the Li isotopic composition of scleractinian corals. Earth Planet Sci Lett 286: 63-70. doi:10.1016/j.epsl.2009.06.015. [Google Scholar]
- 57. Friedrich LA, Halden NM (2008) Alkali element uptake in otoliths: A link between environment and otolith microchemistry. Environ Sci Technol 42: 3514-3518. doi:10.1021/es072093r. PubMed: 18546682. [DOI] [PubMed] [Google Scholar]
- 58. Hicks AS, Closs GP, Swearer SE (2010) Otolith microchemistry of two amphidromous galaxiids across an experimental salinity gradient: A multi-element approach for tracking diadromous migrations. J Exp Mar Biol Ecol 394: 86-97. doi:10.1016/j.jembe.2010.07.018. [Google Scholar]
- 59. Chittaro PM, Usseglio P, Fryer BJ, Sale PF (2006) Spatial variation in otolith chemistry of Lutjanus apodus at Turneffe Atoll, Belize. Estuarine Coast Shelf Sci 67: 673-680. doi:10.1016/j.ecss.2005.12.014. [Google Scholar]
- 60. Fleishman DG, Saulus AA, Vasilieva VF (1986) Lithium in marine elasmobranchs as a natural marker of rectal gland contribution in sodium balance. Comp Biochem Physiol A 84: 643-648. doi:10.1016/0300-9629(86)90379-8. PubMed: 2875828. [DOI] [PubMed] [Google Scholar]
- 61. Evans DH, Piermarini PM, Choe KP (2004) Homeostasis: Osmoregulation, pH regulation, and nitrogen. In: Carrier JC, Musick JA, Heithaus MR. Biology of sharks and their relatives. CRC Press, Boca Raton. [Google Scholar]
- 62. Schifano G (1982) Temperature-magnesium relations in the shell carbonate of some modern marine gastropods. Chem Geol 35: 321-332. doi:10.1016/0009-2541(82)90009-2. [Google Scholar]
- 63. Rosenthal Y, Boyle EA, Slowey N (1997) Temperature control on the incorporation of magnesium, strontium, fluorine, and cadmium into benthic foraminiferal shells from Little Bahama Bank: Prospects for thermocline paleoceanography. Geochim Cosmochim Acta 61: 3633-3643. doi:10.1016/S0016-7037(97)00181-6. [Google Scholar]
- 64. Hoff GR, Fuiman LA (1995) Environmentally induced variation in elemental composition of red drum (Sciaenops ocellatus) otoliths. Bull Mar Sci 56: 578-591. [Google Scholar]
- 65. Bath-Martin G, Wuenschel MJ (2006) Effect of temperature and salinity on otolith element incorporation in juvenile gray snapper Lutjanus griseus . Mar Ecol Prog Ser 324: 229-239. doi:10.3354/meps324229. [Google Scholar]
- 66. Barnes TC, Gillanders BM (2013) Combined effects of extrinsic and intrinsic factors on otolith chemistry: implications for environmental reconstructions. Can J Fish Aquat Sci 70: 1159-1166. doi:10.1139/cjfas-2012-0442. [Google Scholar]
- 67. Gaetani GA, Cohen AL (2006) Element partitioning during precipitation of aragonite from seawater: A framework for understanding paleoproxies. Geochim Cosmochim Acta 70: 4617-4634. doi:10.1016/j.gca.2006.07.008. [Google Scholar]
- 68. Aoba T, Moreno EC, Shimoda S (1992) Competitive adsorption of magnesium and calcium ions onto synthetic and biological apatites. Calcif Tissue Int 51: 143-150. doi:10.1007/BF00298503. PubMed: 1422954. [DOI] [PubMed] [Google Scholar]
- 69. Okamura M, Kitano Y (1986) Coprecipitation of alkali metal ions with calcium carbonate. Geochim Cosmochim Acta 50: 49-58. doi:10.1016/0016-7037(86)90047-5. [Google Scholar]
- 70. Lloyd DC, Zacherl DC, Walker S, Paradis G, Sheehy M et al. (2008) Egg source, temperature and culture seawater affect elemental signatures in Kelletia kelletii larval statoliths. Mar Ecol Prog Ser 353: 115-130. doi:10.3354/meps07172. [Google Scholar]
- 71. Fowler AJ, Campana SE, Jones CM, Thorrold SR (1995) Experimental assessment of the effect of temperature and salinity on elemental composition of otoliths using laser ablation ICPMS. Can J Fish Aquat Sci 52: 1431-1441. doi:10.1139/f95-138. [Google Scholar]
- 72. Mayer I, Jacobsohn O, Niazov T, Werckmann J, Iliescu M et al. (2003) Manganese in precipitated hydroxyapatites. Eur J Inorg Chem 2003: 1445-1451. doi:10.1002/ejic.200390188. [Google Scholar]
- 73. Madejczyk MS, Boyer JL, Ballatori N (2009) Hepatic uptake and biliary excretion of manganese in the little skate, Leucoraja erinacea . Comp Biochem Physiol C 149: 566-571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Mathews T, Fisher NS (2009) Dominance of dietary intake of metals in marine elasmobranch and teleost fish. Sci Total Environ 407: 5156-5161. doi:10.1016/j.scitotenv.2009.06.003. PubMed: 19580992. [DOI] [PubMed] [Google Scholar]
- 75. Pentreath RJ (1973) The accumulation from seawater of 65 Zn, 54Mn, 58Co, and 59Fe by the thornback ray, Raja clavata L. J Exp Mar Biol Ecol 12: 327-334. doi:10.1016/0022-0981(73)90062-2. [Google Scholar]
- 76. Elsdon TS, Gillanders BM (2002) Interactive effects of temperature and salinity on otolith chemistry: challenges for determining environmental histories of fish. Can J Fish Aquat Sci 59: 1796-1808. doi:10.1139/f02-154. [Google Scholar]
- 77. Dorval E, Jones CM, Hannigan R, van Montfrans J (2007) Relating otolith chemistry to surface water in a coastal plain estuary. Can J Fish Aquat Sci 64: 411-424. doi:10.1139/f07-015. [Google Scholar]
- 78. Strasser CA, Mullineaux LS, Walther BD (2008) Growth rate and age effects on Mya Arenaria shell chemistry: Implications for biogeochemical studies. J Exp Mar Biol Ecol 355: 153-163. doi:10.1016/j.jembe.2007.12.022. [Google Scholar]
- 79. Limburg KI, Olson C, Walther Y, Dale D, Slomp CP et al. (2011) Tracking Baltic hypoxia and cod migration over millennia with natural tags. Proc Natl Acad Sci U S A 108: 177-182. doi:10.1073/pnas.1100684108. PubMed: 21518871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Ranaldi MM, Gagnon MM (2010) Trace metal incorporation in otoliths of pink snapper (Pagrus auratus) as an environmental indicator. Comp Biochem Physiol C 152: 248-255. [DOI] [PubMed] [Google Scholar]
- 81. Vallee BL (1983) Zinc in biology and biochemistry. In: Sprio TG. Zinc enzymes, Metal ions in biology Vol 5. John Wiley & Sons, New York. [Google Scholar]
- 82. Milner NJ (1982) The accumulation of zinc by 0-group plaice, Pleuronectes platessa ( L.), from high concentrations in sea water and food. J Fish Biol 21:325-336.. [Google Scholar]
- 83. Willis JN, Sunda WG (1984) Relative contributions of food and water in the accumulation of zinc by two species of marine fish. Mar Biol 80: 273-279. doi:10.1007/BF00392822. [Google Scholar]
- 84. Tang Y, Chappell HF, Dove MT, Reeder RJ, Lee YG (2009) Zinc incorporation into hydroxylapatite. Biomaterials 30: 2864-2872. doi:10.1016/j.biomaterials.2009.01.043. PubMed: 19217156. [DOI] [PubMed] [Google Scholar]
- 85. Miller MB, Clough AM, Batson JN, Vachet RW (2006) Transition metal binding in cod otolith proteins. J Exp Mar Biol Ecol 329: 135-143. doi:10.1016/j.jembe.2005.08.016. [Google Scholar]
- 86. Milton DA, Chenery SR (2001) Sources and uptake of trace metals in otoliths of juvenile barramundi (Lates calcarifer). J Exp Mar Biol Ecol 264: 47-65. doi:10.1016/S0022-0981(01)00301-X. [Google Scholar]
- 87. Webb SD, Woodcock SH, Gillanders BM (2012) Sources of otolith barium and strontium in estuarine fish and the influence of salinity and temperature. Mar Ecol Prog Ser 453: 189-199. doi:10.3354/meps09653. [Google Scholar]
- 88. Walther BD, Thorrold SR (2006) Water, not food, contributes the majority of strontium and barium deposited in the otoliths of a marine fish. Mar Ecol Prog Ser 311: 125-130. doi:10.3354/meps311125. [Google Scholar]
- 89. Schoenberg HP (1963) Extent of strontium substitution for calcium in hydroxyapatite. Biochim Biophys Acta 75: 96-103. doi:10.1016/0006-3002(63)90583-3. PubMed: 14060136. [DOI] [PubMed] [Google Scholar]
- 90. Beck JW, Edwards RL, Ito E, Taylor FW, Recy J et al. (1992) Sea-surface temperature from coral skeletal strontium/calcium ratios. Science 257: 644-647. doi:10.1126/science.257.5070.644. PubMed: 17740731. [DOI] [PubMed] [Google Scholar]
- 91. Wells BK, Bath GE, Thorrold SR, Jones CM (2000) Incorporation of strontium, cadmium, and barium in juvenile spot (Leiostomus xanthurus) scales reflects water chemistry. Can J Fish Aquat Sci 57: 2122-2129. doi:10.1139/f00-178. [Google Scholar]
- 92. Marohn L, Hilge V, Zumholz K, Klügel, Anders H, Hanel R (2011) Temperature dependency of element incorporation into European eel (Anguilla anguilla) otoliths. Anal Bioanal Chem 399: 2175-2184. doi:10.1007/s00216-010-4412-2. PubMed: 21107822. [DOI] [PubMed] [Google Scholar]
- 93. Balter V, Lécuyer (2004) Determination of Sr and Ba partition coefficients and water from 5°C to 60°C: a potential new thermometer for aquatic paleoenvironments. Geochim Cosmochim Acta 68: 423-432. doi:10.1016/S0016-7037(03)00453-8. [Google Scholar]
- 94. Zacherl DC, Paradis G, Lea DW (2003) Barium and strontium uptake into larval protoconchs and statoliths of the marine neogastropod Kelletia kelletii . Geochim Cosmochim Acta 67: 4091-4099. doi:10.1016/S0016-7037(03)00384-3. [Google Scholar]
- 95. Strasser CA, Mullineaux LS, Thorrold SR (2008) Temperature and salinity effects on elemental uptake in the shells of larval and juvenile softshell clams Mya Arenaria . Mar Ecol Prog Ser 370: 155-169. doi:10.3354/meps07658. [Google Scholar]
- 96. Zwolsman JJG, Van Eck BTM, Van Der Weijden CH (1997) Geochemistry of dissolved trace metals (cadmium, copper, zinc) in the Scheldt estuary southwestern Netherlands: Impact of seasonal variability. Geochim Cosmochim Acta 61: 1635-1652. doi:10.1016/S0016-7037(97)00029-X. [Google Scholar]
- 97. Gosnell KJ, Landing WN, Milne A (2012) Fluorometric detection of total dissolved zinc in the southern Indian Ocean. Mar Chem 132-133: 68-76. doi:10.1016/j.marchem.2012.01.004. [Google Scholar]
- 98. Thorrold SR, Campana SE, Jones CM, Swart PK (1997) Factors determining d13C and d18O fractionation in aragonitic otoliths of marine fish. Geochim Cosmochim Acta 61: 2909-2919. doi:10.1016/S0016-7037(97)00141-5. [Google Scholar]
- 99. McMahon KW, Fogel ML, Johnson BJ, Houghton LA, Thorrold SA (2011) A new method to reconstruct fish diet and movement patterns from δ13C values in otolith amino acids. Can J Fish Aquat Sci 68: 1330-1340. doi:10.1139/f2011-070. [Google Scholar]
- 100. Hobson KA, Barnett-Johnson R, Cerling T (2010) Using Isoscapes to Track Animal Migration. In: West JB, Bowen GJ, Dawson TE, Tu KP. Understanding movement, pattern, and process on earth through isotope mapping. Springer Science; +Business Media, NY. [Google Scholar]
- 101. Carlisle AB, Kim SL, Semmens BX, Madigan DJ, Jorgensen SL et al. (2012) Using stable isotope analysis to understand the migration and trophic ecology of northeastern Pacific white sharks (Carcharodon carcharias). PLOS ONE 7(2): e30492. doi:10.1371/journal.pone.003492. PubMed: 22355313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Miller JA, Banks MA, Gomez-Uchida D, Shanks AL (2005) A comparison of population structure in black rockfish (Sebastes melanops) as determined with otolith microchemistry and microsatellite DNA. Can J Fish Aquat Sci 62: 2189-2198. doi:10.1139/f05-133. [Google Scholar]
- 103. Cailliet GM, Smith WD, Mollet HF, Goldman KJ (2006) Age and growth studies of chondrichthyan fishes: the need for consistency in terminology, verification, validation, and growth function fitting. Environ Biol Fishes 77: 211-228. doi:10.1007/s10641-006-9105-5. [Google Scholar]
- 104. Swearer SE, Forrester GE, Steele MA, Brooks AJ, Lea DW (2003) Spatio-temporal and interspecific variation in otolith trace-elemental fingerprints in a temperate estuarine fish assemblage. Estuarine Coast Shelf Sci 56: 1111-1123. doi:10.1016/S0272-7714(02)00317-7. [Google Scholar]
- 105. Hamer PA, Jenkins GP (2007) Comparison of spatial variation in otolith chemistry of two fish species and relationships with water chemistry and otolith growth. J Fish Biol 71: 1035-1055. doi:10.1111/j.1095-8649.2007.01570.x. [Google Scholar]
- 106. Ridewood WG (1921) On the calcification of the vertebral centra in sharks and rays. Philos Trans R Soc Lond B 210: 311-407. doi:10.1098/rstb.1921.0008. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Correlations (r) between partition coefficients (DMe) and somatic growth rates and vertebral precipitation rates for the temperature (T) experiment. The number (n) of round rays (Urobatis halleri) included in growth rate estimates, observed range of individual somatic growth rates (mm disc width month-1), and vertebral precipitation rates (μm radius month-1) are reported for each treatment. No significant correlations were detected (p ≥ 0.12).
(PDF)
Correlations (r) between partition coefficients (DMe) and somatic growth rates and vertebral precipitation rates for the barium manipulation ([Ba]) experiment. The number (n) of round rays (Urobatis halleri) included in growth rate estimates, observed range of individual somatic growth rates (mm disc width month-1), and vertebral precipitation rates (μm radius month-1) are reported for each treatment. Significant p-values are indicated by bold font.
(PDF)