Modeling Clinical Endpoints as a Function of Time of Switch to Second-line ART With Incomplete Data on Switching Times

Summary

Modeling clinical endpoints as a function of change in antiretroviral therapy (ART) attempts to answer one simple but very challenging question: was the change in ART beneficial or not? We conceive a similar scientific question of interest in the current manuscript except that we are interested in modeling the time of ART regimen change rather than a comparison of two or more ART regimens. The answer to this scientific riddle is unknown and has been difficult to address clinically. Naturally, ART regimen change is left to a participant and his or her provider and so the date of change depends on participant characteristics. There exists a vast literature on how to address potential confounding and those techniques are vital to the success of the method here. A more substantial challenge is devising a systematic modeling strategy to overcome the missing time of regimen change for those participants who do not switch to second-line ART within the study period even after failing the initial ART. In this paper, we adopt and apply a statistical method that was originally proposed for modeling infusion trial data, where infusion length may be informatively censored, and argue that the same strategy may be employed here. Our application of this method to therapeutic HIV/AIDS studies is new and interesting. Using data from the AIDS Clinical Trials Group (ACTG) Study A5095, we model immunological endpoints as a polynomial function of a participant’s switching time to second-line ART for 182 participants who already failed the initial ART. In our analysis, we find that participants who switch early have somewhat better sustained suppression of HIV-1 RNA after virological failure than those who switch later. However, we also found that participants who switched very late, possibly censored due to the end of the study, had good HIV-1 RNA suppression, on average. We believe our scientific conclusions contribute to the relevant HIV literature and hope that the basic modeling strategy outlined here would be useful to others contemplating similar analyses with partially missing treatment length data.

1. Introduction

Patients enrolled in therapeutic HIV studies often have opportunity to switch antiretroviral therapies (ARTs), both before and after virological failure on the current ART. In HIV treatment trials conducted by the AIDS Clinical Trials Group (ACTG), for example, study participants may switch ARTs due to toxicity or adverse events, regardless of whether virological failure has occurred or not. In this paper, we address scientific and statistical issues related to switching ARTs after virological failure, a challenging scientific question in the HIV and AIDS literature (cf. Riddler et al., 2007). Although the Department of Health and Human Services (http://www.aidsinfo.nih.gov) currently recommends switching ART early following confirmed virological failure, the recommendation is debatable because it is informed by expert opinion not controlled clinical studies, there is evidence to argue both sides of the issue, and the definition of virologic failure is arbitrary. There exists observational evidence to support delayed switch amidst partial virological suppression (Deeks et al., 2000, 2002) and, on the other hand, arguments that maintaining a failing ART diminishes the chance of success on a future ARTs (Napravnik et al., 2005). It is desirable to assess the benefits of delayed ART regimen change objectively through a controlled clinical study, however, it is difficult to design and enroll such a study. The ACTG designed a randomized, controlled clinical trial (ACTG A5115) to study immediate versus delayed switch for participants on stable ART. However, the study failed to accrue the target enrollment and no definitive conclusions were drawn because the study lacked sufficient power to detect meaningful differences (Riddler et al., 2007). Our contribution here and elsewhere (Li et al., 2012) is to address the same scientific questions as the ones intended by ACTG A5115 but to do so by developing and applying modern statistical tools in secondary analyses of existing ACTG data bases. As we explain below, this paper complements our other work (Li et al., 2012) but others new insight into the problem of how to assess the effect of delayed regimen change and from a completely different perspective.

In Section 3, we conduct a secondary analysis of data from the ACTG A5095 study. The 5095 study was a randomized, multi-center clinical trial of three ARTs: two efavirenz (EFV)-based regimens and one triple nucleoside reverse transcriptase inhibitor (NRTI) regimen. The objective of the study was to suppress and maintain HIV-1 RNA below 200 copies/ml and the primary endpoint was time to first virological failure. At an interim review meeting after a median 32 weeks follow-up, the triple NRTI group was clearly inferior to the combined efavirenz-based group and the data safety and monitoring board recommended that the triple NRTI group be discontinued but continued follow-up for the efavirenz-based group. Detailed summaries of ACTG 5095 appear elsewhere in the literature (Gulick et al., 2004, 2006; Ribaudo et al., 2008).

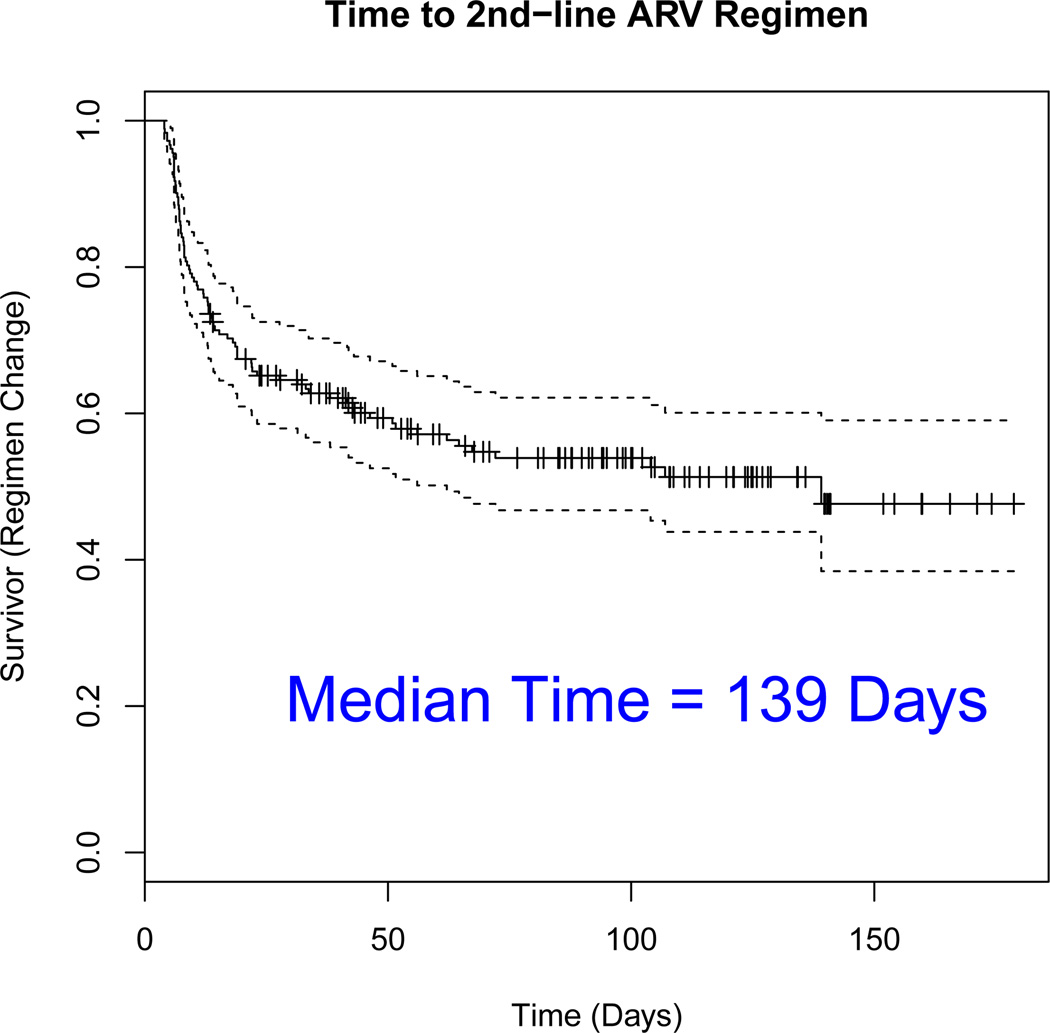
Confirmed virological failure was defined as lab readings from two consecutive visits after at least 16 weeks of study treatment where HIV-1 RNA > 200 copies/ml. In our analysis below, we use data from 182 participants randomized to EFV-based ART who met the protocol definition of confirmed virological failure over the course of the study. After confirmed virological failure on an initial efavirenz-based ART, participants were given opportunity to switch of the initial ART and move to a second-line ART. Unlike ACTG 5115, however, the decision of when to switch to second-line ART was left to the participant and his/her provider. Because factors associated with switching to second-line ART may be associated with immunological response or clinical endpoints, to evaluate the relative benefits of early or delayed switch, we must think carefully of how to address a clear case of confounding. When examining the ACTG A5095 data, a second critical issue arises due to the limited nature of the follow-up window. In Figure 1, we plot the Kaplan-Meier estimate of the time to switch to second-line ART for 182 participants who failed their initial EFV-based ART. Figure 1 tells several intriguing stories. First, it is clear that a subgroup of participants that fail the initial ART switch shortly after confirmed virological failure. Here, we know that 31 participants (17% of 182) switched within eight weeks of confirmed virological failure, which is equivalent to switching at the same clinic visit as the the confirmation lab reading or the following clinic visit.

Figure 1.

Empirical distribution estimate for the time to ARV regimen change for n = 182 participants who failed an initial efavirenz-based regimen.

After eight weeks, switching to second-line ART is far less frequent as the Kaplan-Meier curve flattens out. Next, we notice that a very large proportion of participants do not switch to second-line ART, even nearly five months after confirmed virological failure. To be precise, 100 participants (55% of 182) did not switch within the follow-up period. Of these 100 participants with censored switching times, 42 participants were followed for at least 100 days, 27 participants followed for at least 120 days, and 11 participants followed for at least 140 days. As the text indicates in Figure 1, the median time to switch to second-line ART is 139 days following virologic failure on an initial EFV-based ART. Hence, in addition to addressing the issue of confounding, we must also think critically about how to model data for participants whose outcome may be observed but whose switching time to second-line ART may be unknown.

This paper approaches the data analysis from a completely different perspective compared to another recent work by our group. Li et al. (2012) casts the problem in the context of two-stage designs (Lunceford et al., 2002): a first randomization to initial ART and then a second randomization to immediate or delayed switch to second-line ART if virological failure on the initial ART. They addressed the issues of confounding through a causal framework via propensity scores and a minimum variance estimator for the average causal effect of switching to second-line ART before or after eight weeks of confirmed virological failure. They did not address the issue of censored switching times directly, however, but rather conducted sensitivity analyses to assess the effect on their conclusions depending on whether the participants were included or deleted from the analysis. An interesting and distinguishing feature of the two-stage methodology is how the method uses data from participants who did not fail the initial ART in order to estimate the intent-to-treat causal estimands. Using techniques described in their paper, Li et al. (2012) showed that early switching was modestly associated with lower levels of HIV-1 RNA, higher CD4 cell counts, and a larger proportion of the follow-up period with suppressed levels of HIV-1 RNA.

Although the estimator proposed by Li et al. (2012) has desirable theoretical properties and operating characteristics for their two-stage estimand, some investigators find a two-stage approach awkward for a question directed towards participants who have failed an initial ART. In the two-stage framework, as explained in Li et al. (2012, p. 543), “ … treatment comparisons are made without regard for the success or failure of the initial regimen and, therefore, the estimands reect the combined inuence of initial … regimen and viral load levels.” Identifiability assumptions imposed in their paper are a reflection of the statement above and accommodate a participant that may not, in fact, fail the initial ART. A conditional analysis, on the other hand, foregoes the complexities of the two-stage analysis and simply ignores the first-stage randomization altogether. Here, in this paper, we will model outcomes for n = 182 participants that failed initial ART and whose switch to second-line ART regimen is represented in Figure 1. The methods outlined in Section 2 and the statistical analysis presented in Section 3 will accommodate and model directly censored switching times. Using the methods here and for participants who failed an initial EFV-containing regimen, we estimate linear and nonlinear trends of HIV-1 RNA and CD4 T-cell count outcomes as a function of switching times. Compared with Li et al. (2012), the methods here estimate the entire dose-response curve rather than simply mean outcome for a particular eight-week cutoff. Thus, although the broad objectives of the two statistical analyses are similar, the populations, treatment policies, and causal estimands all differ.

To model the immunological outcomes as a function of switching times, we cast the statistical problem in terms of a dynamic treatment regime: basically, a sequence of decisions over time to continue on initial ART or switch to second-line ART at time t given they are still on initial ART at time t. The problem here is similar to the analysis of infusion trial data, where the treatment decision is whether to stop or continue infusion at time t given the participant has been continuously infused up to time t. Johnson and Tsiatis (2004, 2005) first proposed an estimator in the context of infusion trials for participants undergoing coronary stent implantation. In that application, participants were treated with anticoagulant for an unspecified amount of time after surgery but providers stop infusing participants when it was deemed appropriate to do so or until an infusion-terminating event occurs, whichever came first. To accommodate treatment censoring, they defined a treatment policy which incorporates censoring as part of its definition. Other authors have articulated the causal estimands in terms of targeted treatment lengths or intended treatment lengths (cf. Johnson, 2008; Zhang et al., 2011), arguing that these particular treatment-terminating events led to compulsory treatment discontinuation as opposed to potentially optional treatment-terminating events which could lead to a different set of treatments and more complex treatment assignment mechanism (Zhang et al., 2011). Hence, in the infusion application, an infusion-terminating event censors what would have otherwise been the targeted infusion infusion length.

In this application and extension to therapeutic HIV/AIDS studies, the proposed method accommodates the complexities including sequential decision making, potential for treatment censoring and time-dependent confounding; we make those connections explicit in Section 2. Incidentally, the technique also allows for censoring to be informative but this condition is not necessary for applicability of the method. Although the statistical methods employed below were proposed elsewhere, the application to switching from initial ARTs to second-line ARTs in therapeutic HIV/AIDS studies is new and provides a principled framework for modeling a clinical outcome as a function of a targeted switching time even when some switching times are unobserved.

2. Methods

2.1 Dynamic Regimes

We begin our statistical analysis with notation and assumptions embodied in a theory of dynamic treatment regimes (DTR). A (continuous-time) DTR, say ${\mathrm{\delta ̅}}_T={\{{\delta }_t\}}_{t=0}^T$, is a sequence of decision rules for treatment assignment, or in our application, rules for switching to second-line ART. First, we define treatment assignment,

$$A_t=\{\begin{array}{cc}\hfill 1,\hfill & \hfill \text{switch to second-line ART in}[t,t+\epsilon );\hfill \\ \hfill 0,\hfill & \hfill \text{otherwise},\hfill \end{array}$$

and Ā_t = (A₁, …, A_t) as the history of treatment assignment up to and including time t. Next, we define the treatment assignment rule in the DTR at time t,

$${\delta }_t=\{\begin{array}{cc}\hfill \text{switch to second-line ART in}[t,t+\epsilon )\mathrm{w}/\mathrm{p}.h_{{\mathrm{\delta ̄}}_T}(t)\epsilon ,\hfill & \hfill \text{if}{ℰ}_{t^{-}}=1;\hfill \\ \hfill \text{do not switch},\hfill & \hfill \text{otherwise},\hfill \end{array}$$

where “w/p.” is an abbreviation for “with probability,” ℰ_t is eligibility at time t and ℰ_t⁻ is interpreted to mean that a participant is still on first-line ART just prior to time t. In the DTR, a participant switches in the infinitesimal [t, t + ε) with probability P_δ̄T (A_t = 1|ℰ_t⁻ = 1) ≈ h_δ̄T (t)εI(ℰ_t⁻ = 1), where P_δ̄T (·) denotes probability in the DTR. In the observational study, however, switching to second-line ART depends on participant characteristics. Let X_t denote a time-dependent covariate vector at time t and X̄_t = {X_u, u ≤ t}, the history of co-variate information up to time t. Thus, in the observational study, switch to second-line ART in the interval [t, t + ε) occurs with probability, P(A_t = 1|ℰ_t⁻ = 1, X̄_t) ≈ h(t, X̄_t)εI(ℰ_t⁻ = 1), and P(·) denotes probability in the observational study. The observed outcome is denoted as Y and we elaborate on the clinical outcome measures from 5095 in Section 3.1.

Using results from Johnson and Tsiatis (2005, Appendix) and Lemma 4.1 from Murphy et al. (2001), the marginal mean outcome can be modeled parametrically as a function of target switching times through,

$$E_{{\mathrm{\delta ̄}}_T}(Y)=\mu (t,\mathit{\beta }),$$ (1)

β is vector of parameters, β = (β₁, …, β_p), and estimated through the system of estimating equations,

$$0={\mathbb{P}}_n[{\pi }_{t=0}^T{\left\{\frac{h_{{\mathrm{\delta ̄}}_T}(t)R(t)}{h(t,{\mathbf{X̄}}_t)R(t)}\right\}}^{A_t}\frac{\text{exp}\{-{\int }_0^T{h}_{{\mathrm{\delta ̄}}_T}(t)R(t)dt\}}{\text{exp}\{-{\int }_0^{T}h(t,{\mathbf{X̄}}_t)R(t)dt\}}\mathrm{\mu ̇}(t,\mathit{\beta })\{Y-\mu (t,\mathit{\beta })\}],$$ (2)

where R(t) = I(U ≥ t) and U is the observed time to switch second-line ART or censoring, whichever came first, π is the product integral, μ̇(t, β) is the first derivative of μ(t, β) with respect to β and ℙ_n(·) is the empirical average. To reconcile the at-risk indicator R(t) with earlier notation, note that at-risk is synonymous with eligibility, i.e. R(t) = I(ℰ_t⁻ = 1).

Johnson and Tsiatis (2004, 2005) noted that this dynamic regime has a special structure and that the history of treatment assignment can be viewed as a counting process which takes a jump of size +1 if and when a participant switches to second-line ART and remains zero throughout all time if a participant is censored prior to switching. Without loss of generality, the potential outcomes can be summarized as {Y(t), t ≤ C}, where Y(t) is the outcome if a participant switches to second-line ART at a target of t weeks and C is the time of a potential censoring event. Using their counting process framework leads to a simple expression for the estimator defined by (2). Define the indicator Γ = 1 if a participant switches to second-line ART prior to the end of follow-up and Γ = 0 otherwise. The treatment assignment probability h(t, X̄_t) is the cause-specific hazard function,

$$h(t,{\mathbf{X̄}}_t)=\underset{\epsilon \to 0}{\text{lim}}{\epsilon }^{-1}P(t\le U<t+\epsilon ,\mathrm{\Gamma }=1|U\ge t,{\mathbf{X̄}}_t).$$ (3)

Evaluating the product integral in (2), Johnson and Tsiatis (2005) showed that,

$$(2)={\mathbb{P}}_n[\mathrm{\Gamma }\psi (Y,U,\mathit{\beta })\frac{f_{{\mathrm{\delta ̄}}_T}(U)}{f(U,{\mathbf{X̄}}_U)}+\frac{(1-\mathrm{\Gamma })}{S(U,{\mathbf{X̄}}_U)}{\int }_U^T\psi (Y,s,\mathit{\beta })f_{{\mathrm{\delta ̄}}_T}(s)ds],$$ (4)

where

$$\psi (Y,t,\mathit{\beta })=\mathrm{\mu ̇}(t,\mathit{\beta })\{Y-\mu (t,\mathit{\beta })\},S(t,{\mathbf{X̄}}_t)=\text{exp}\{-{\int }_0^{t}h(s,{\mathbf{X̄}}_s)ds\},f(t,{\mathbf{X̄}}_t)=h(t,{\mathbf{X̄}}_t)S(t,{\mathbf{X̄}}_t),f_{{\mathrm{\delta ̄}}_T}(t)=h_{{\mathrm{\delta ̄}}_T}(t)\text{exp}\{-{\int }_0^t{h}_{{\mathrm{\delta ̄}}_T}(s,{\mathbf{X̄}}_s)ds\}.$$

As with other statistical analyses of observational data, we impose statistical assumptions to help identify the causal estimand and consistently estimate the parameter β using the observed data. We adopt the Rubin causal model (Rubin, 1974) and, in particular, the ‘stable unit treatment value assumption.’ The assumption implies that the observed and potential outcomes are equivalent for the treatment received, that subjects do not contaminate one another and generally satisfied if subjects are independent. We believe such assumption is satisfied in the 5095 study. We also make assumptions about the availability of potential confounders which, in the current analysis, are defined as those factors that affect a participant’s decision to switch to second-line ART and also associated with their subsequent outcome. Namely, we assume the time-dependent data is sufficiently rich such that

$$(3)=\underset{\epsilon \to 0}{\text{lim}}{\epsilon }^{-1}P\{t\le U<t+\epsilon ,\mathrm{\Gamma }=1|U\ge t,{\mathbf{X̄}}_t,C,Y(z),t\le z\le C\}.$$ (5)

In (5), we allow for the possibility that a participant’s decision to switch to second-line ART at any time t may depend on unobserved potential immunological outcomes. But after conditioning on participant’s covariate history up to time t, it is assumed that unobserved potential outcomes provide no additional information on a participant’s treatment decision. This assumption in (3) is also called the sequential randomization assumption. Other technical assumptions are contained in Lemma 4.1 of Murphy et al. (2001) and are omitted because they are tangential to the application here (cf. Johnson and Tsiatis, 2005).

2.2 Modeling Details

We posit first- and second-order polynomial relationships for the marginal mean as a function of target switching times such that the statistical model is written

$$(1)=\mu (t,\mathit{\beta })=\sum _{j=0}^p{\beta }_j{(t-M)}^j,$$ (6)

where β = (β₀, β₁, …, β_p) are the regression coefficients of interest and M is a user-specified centering constant. Consequently, for the continuous outcomes considered below,

$$\psi (Y_i,t,\mathit{\beta })=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill t-M\hfill \\ \hfill ⋮\hfill \\ \hfill {(t-M)}^p\hfill \end{array}\right)\{Y_i-\sum _{j=0}^p{\beta }_j{(t-M)}^j\}.$$

In order to operationalize the estimator in (4), one must model the the cause-specific hazard in (3) and define f_δ̄T (t). We adopt Cox’s proportional hazards model (Cox, 1972) for h(t, X̄_t), i.e.,

$$h(t,{\mathbf{X̄}}_t;\gamma )=h_0(t)\text{exp}({\gamma }^{\mathrm{T}}{\mathbf{X̄}}_t),$$

where h₀(t) is an arbitrary function of time and, hence, allows for much flexibility in modeling the probability of switching to second-line ART. At the same time, the proportional hazards model introduces an infinite-dimensional nuisance parameter h₀(t) that must be estimated to compute f(t, X̄_t) in (4). To overcome this challenge, note that if f_δ̄T (t) ∝ h₀(t), then the expression in (4) simplifies to:

$$0={\mathbb{P}}_n[\frac{\mathrm{\Gamma }\psi (Y,U,\mathit{\beta })}{\text{exp}({\gamma }^{\mathrm{T}}{\mathbf{X̄}}_t)S(U,{\mathbf{X̄}}_U;\gamma )}+\frac{(1-\mathrm{\Gamma })}{S(U,{\mathbf{X̄}}_U;\gamma )}{\int }_U^T\psi (Y,s,\mathit{\beta })h_0(s)ds],$$ (7)

up to some proportionality constant that does not depend on β. Although this eliminates the need to estimate the baseline hazard function h₀(t) in the first expression of (7), the baseline hazard function h₀(t) still persists in the integrand of the second expression. However, under suitable regularity conditions, one can show that

$${\int }_U^T\psi (Y,s,\mathit{\beta })d{Ĥ}_0(s;{\mathrm{\gamma ̂}}_n){\to }_p{\int }_U^T\psi (Y,s,\mathit{\beta })h_0(s)ds,$$

at the nominal root-n rate, where γ̂_n is the maximum partial likelihood estimator, Ĥ₀(t; γ) is the Breslow estimator of the integrated hazard function, i.e.,

$${Ĥ}_0(t;\gamma )={\int }_0^t\frac{dN(s)}{{\sum }_{l=1}^n\text{exp}\left\{{\gamma }^{\mathrm{T}}{\mathbf{X̄}}_l(s)\right\}I(U_l\ge s)},$$

and N(t) is the counting process, $N(t)={\sum }_{i=1}^{n}I(U_i\le t,{\mathrm{\Gamma }}_i=1)$. Johnson and Tsiatis (2005) showed that the β̂, the solution to (7), was root-n consistent and asymptotically normal and proposed a consistent estimator for the asymptotic variance. Their estimator for the asymptotic variance is used to estimate standard errors and construct confidence sets for the point estimates in Section 3.

3. The Effect of Delayed Treatment Switch in ACTG A5095

3.1 Outcome Measures

In Section 3, we present two new statistical analyses of the ACTG A5095 data. The first data analysis in Section 3.2 facilitates comparisons to our earlier work (Li et al., 2012) in that we use the same three clinical endpoints, defined as length-adjusted area-under-the-curve (AUC) outcomes. Briey, the AUCs were computed using a trapezoidal rule (Yeh and Kwan, 1978) for HIV-1 RNA level, CD4 cell count, and days below a limit of detection (LOD). If one does not adjust AUC for length, then the endpoint is a non-decreasing function of follow-up time and has little scientific value in the current analysis (cf. Spritzler et al., 2008). If T* is the follow-up time and H(u) is HIV-1 RNA level or CD4 cell count at time u, then we define the length-adjusted AUC as

$$Y=\frac{{\int }_0^{T^{*}}H(u)du}{T^{*}}.$$ (8)

For the LOD endpoint, Y is simply the average number of days below a limit of detection divided by the entire follow-up period.

In the second analysis in Section 3.3, we consider four new clinical endpoints. The first two endpoints are modifications of the earlier length-adjusted AUCs in (8) but with a start time equal to the date of confirmed virological failure and, thus, could not have been defined for the cohort used in Li et al. (2012) because not all participants experienced virological failure in their analysis. There we define

$$Y=\frac{{\int }_{T_{\mathrm{V}\mathrm{F}}^{*}}^{T^{*}}H(u)du}{T^{*}-T_{\mathrm{V}\mathrm{F}}^{*}},$$

where $T_{\mathrm{V}\mathrm{F}}^{*}$ is the time of virological failure. This modified endpoint is defined for HIV-1 RNA level and the limit of detection (LOD).

The third and fourth endpoints are defined through the final two observed HIV-1 RNA levels in the follow-up period. We consider whether the final two viral load measurements exceed 200 copies/mL, the threshold of virological suppression or failure in 5095, at the end of the follow-up period. We found that 74 participants had both measurements below the LOD, 84 participants had neither measurements below the LOD, and 24 participants had one measurement below the LOD. For simplicity, we ran two analyses labeling the inconclusive 24 participants as suppressed and as non-suppressed. The two new case definitions are made explicit in Table 1 and the analytic results for all four endpoints are displayed in Table 4.

Table 1.

Definition of new outcomes as function of final two HIV-1 RNA measurements in the follow-up period

	Defn. of Y = 1	Y
		0	1
Case 1:	2 Obs. HIV-1 RNA ≤ 200 copies/mL	108	74
Case 2:	1 or 2 Obs. HIV-1 RNA ≤ 200 copies/mL	84	98

Table 4.

Coefficient estimates for the average effect of time of ARV regimen change on new endpoints for n = 182 participants who experience virological failure on an efavirenz-containing regimen. New endpoints are defined as length-adjusted AUCs from the time of virologic failure to the end of study. Time is modeled in weeks and centered at M = 10 weeks.

	Length-adjusted AUC				Last 2 HIV-1 RNA Obs.
Dose	HIV-1 RNA		Days below LOD		Case 1†		Case 2†
Model	Est.	SE	Est.	SE	Est.	SE	Est.	SE
Linear
β0	2.572	0.100	0.356	0.031	−0.507	0.190	−0.012	0.188
β1	0.007	0.013	−0.004	0.004	−0.035	0.024	−0.042	0.023
Quadratic
β0	2.882	0.163	0.267	0.054	−0.972	0.387	−0.581	0.377
β1	0.008	0.010	−0.005	0.003	−0.036	0.020	−0.045	0.020
β2	−0.005	0.002	0.002	0.001	0.008	0.005	0.010	0.005

^†Case 1 uses a binary outcome with success defined as two final HIV-1 RNA measurements below 200 copies/mL. Case 2 uses a binary outcome with success defined as at least one of two final HIV-1 RNA measurements below 200 copies/mL (See also Table 1).

NOTE: Abbreviations used: limit of detection (LOD), coefficient estimate (Est.), standard error estimate (SE).

As a final note on outcome measures, we draw attention to assumptions embedded in the dynamic regime framework as it pertains to our outcomes. In Section 2, we adopt the common assumption that Y = Y(Ā) = Y(ā) and, for this particular dynamic regime, Y(ā) = Y(t)I(C > t)+Y(C)I(C ≤ t). Hence, when Γ = 0, the outcome is Y = Y(C) for any intended or targeted treatmet length t, where t > C. In order for length-adjusted AUC outcomes to remain constant given the already observed HIV-1 RNA levels up to time C, this implies that when as follow-up time increases, the integrated viral load increases proportionally. Constant length-adjusted AUC is quite different than constant AUC given the same history of HIV-1 RNA level up to time C, that latter of which implies HIV-1 RNA is exactly 0 for every t, t > C, and unrealistic even for participants with undetectable viral load. Johnson and Tsiatis (2004, 2005) argued that, in the absence of information to the contrary, assuming that the treatment-censoring event would have occurred at the same moment regardless of the intended treatment length is a reasonable assumption in many studies and we conjecture here as well.

3.2 Different Methods Applied to a Subcohort of Li et al. (2012)

The outcomes used are described in Section 3.1. Next, we model the probability of switching to second-line ART as a function of potential confounders via Cox’s proportional hazard model; in causal inference, this is referred to as a generalized propensity score (PS)- model. We modeled ten potential confounders including HIV-1 RNA (copies/ml) level at baseline, HIV-1 RNA (copies/ml) level at virological failure, time (days) to virological failure, CD4 cell count, CD8 cell count, weight (kg), age (years), gender (1=male), history of drug use (1=yes), and race. The coefficient estimates are presented in Table 2.

Table 2.

Potential risk factors associated with the timing of ARV regimen change, possibly right-censored. Coefficient and associated standard error estimates from four estimators are presented: Weibull, Cox’s proportional hazards model, and log-rank estimators

	Weibull		Cox		Log-rank
Covariable	Est.	SE	Est.	SE	Est.	SE
HIV-1 RNA at BL	−0.271	0.290	0.223	0.200	−0.497	0.330
HIV-1 RNA at VF*	−0.310	0.166	0.218	0.116	−0.419	0.224
Time to VF	−0.300	0.179	0.132	0.124	−0.298	0.192
CD4 cell count	0.663	0.269	−0.414	0.182	0.628	0.274
CD8 cell count	−0.079	0.150	0.069	0.103	−0.024	0.182
Weight	0.043	0.216	−0.050	0.148	0.010	0.270
Age	0.135	0.172	−0.060	0.119	0.111	0.211
Gender	−0.121	0.451	0.037	0.316	0.015	0.565
Drug Use	−0.659	0.449	0.355	0.307	−0.767	0.552
Race
White	–	–	–	–	–	–
Black	−0.846	0.395	0.514	0.272	−1.010	0.437
Hispanic and others	0.052	0.519	−0.002	0.357	0.145	0.594

NOTE: Abbreviations used: baseline (BL), virological failure (VF), coefficient estimate (Est.), standard error estimate (SE). In the case of HIV-1 RNA endpoint, we do not include HIV-1 RNA at VF in the PS model (cf. Li et al., 2012). When HIV-1 RNA is removed from the model, coefficient estimates are similar to those presented above.

Because the validity of our estimator for β in (7) depends on the correct specification of the PS-model for the cause-specific hazard h(t, X̄_t) in (3), we estimated the coefficient parameters γ under three different models to compare the relative contribution of the effects: extreme value distribution (Weibull), Cox model, and rank-based coefficient estimates (Log-rank) in an accelerated failure time model. In Table 2, we see that the two most important covariates associated with switching to second-line ART are CD4 cell count and race. Patients with higher CD4 cell count at baseline tended to wait longer to switch to second-line ART after confirmed virological failure. Furthermore, black participants tend to switch to second-line ART much more quickly compared to white (non-Hispanic) participants, even after adjusting for all the other variables. It is interesting to note that both CD4 cell count and race are the only two strong covariates among the ten across all three statistical models. Although this does not confirm that our PS-model is correct, it does suggest that other models would lead to similar estimates of the participant-specific propensity scores and probably similar conclusions as well.

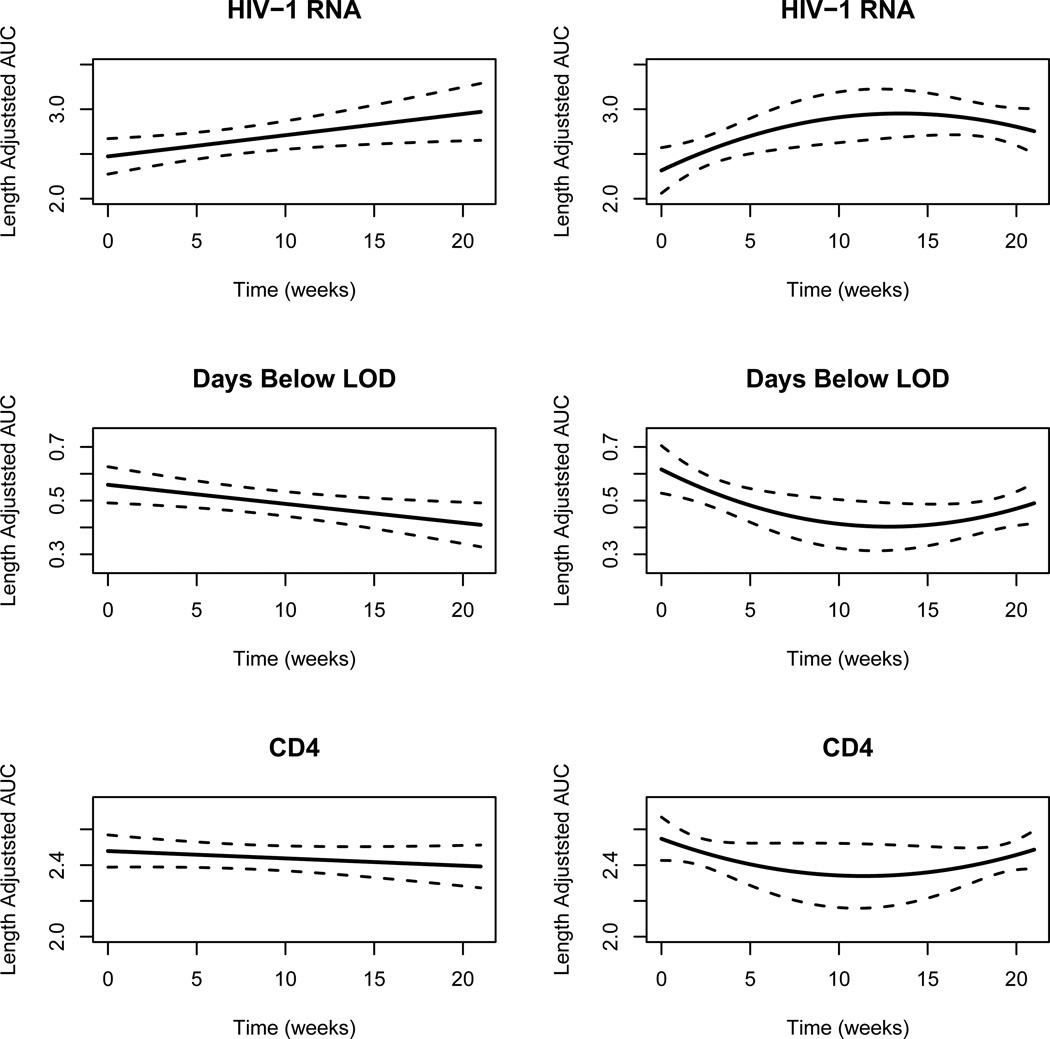
Finally, we estimated the regression coefficients β for two models, linear and quadratic, that parameterizes how the expected length-adjusted AUC changes as a function of target switching time. To compute the estimator in (7), we modeled time in weeks (whereas data presented in Figure 1 is in days) and chose constants T = 21, M = 10 based on the data. The estimated coefficients and their standard errors are presented in Table 3 with an accompanying figure in Figure 2.

Table 3.

Coefficient estimates for the average effect of time of ARV regimen change on outcome for n = 182 participants who experience virological failure on an efavirenz-containing regimen. Time is modeled in weeks and centered at M = 10 weeks.

Dose	HIV-1 RNA		Days below LOD		CD4
Model	Est.	SE	Est.	SE	Est.	SE
Linear
β0	2.7093	0.0809	0.4878	0.0233	2.4376	0.0356
β1	0.0237	0.0102	−0.0071	0.0029	−0.0041	0.0038
Quadratic
β0	2.9102	0.1446	0.4131	0.0462	2.3421	0.091
β1	0.0244	0.0080	−0.0073	0.0027	−0.0045	0.0037
β2	−0.0035	0.0019	0.0013	0.0006	0.0016	0.0011

NOTE: Abbreviations used: limit of detection (LOD), coefficient estimate (Est.), standard error estimate (SE).

Figure 2.

Linear (left-hand side) and quadratic (right-hand side) trends for mean length-adjusted AUC endpoints as a function of switching time to second-line ART. Dashed lines represent 95% pointwise confidence intervals.

From Table 3, one can see that some trends do emerge. First, average HIV-1 RNA level tends to be larger for participants who delay their switch to second-line ART. For this endpoint, the linear term is significant at the nominal level in the linear model and the quadratic term is also moderately significant in the quadratic model. However, the negative coefficient estimate of the quadratic terms suggests that participants who delay their switch to second-line ART have similar HIV-1 RNA profiles (at least approximately in aggregate) to those who switch to second-line ART immediately after failing. A similar story unfolds as we consider average days below LOD. Here, it is clear that participants who switch soon after virological failure tend to spend more days below a limit of detection, 200 copies/ml, during ACTG A5095 follow-up. When we considered the quadratic model, the quadratic term was again moderately significant suggesting that the participants who delay their switch to second-line ART the longest tend to have outcomes more similar to participants that switch soon after confirmed virological failure rather than those participants who switch 3–4 months after failure.

Finally, we failed to find any significant linear or quadratic trends for the CD4 endpoint. The conclusions for the HIV-1 RNA and Days below LOD endpoints agree with Li et al. (2012) while the negative finding about the CD4 endpoint disagrees with the conclusions of Li et al. (2012). In our earlier work, we concluded that there were modest but statistically significant differences in CD4 endpoints between participants that switched to second-line ART before eight weeks of confirmed virological failure compared to those that delayed switch. Two possible explanations emerge for the discrepancy. First, the causal estimands here and in Li et al. (2012) are different and not directly comparable. The two-stage analysis uses data from 562 participants that do not fail initial ART in addition to 182 participants that fail initial ART whereas our analysis here only uses data from the latter 182 participants. Another possible explanation is that our estimates of linear and quadratic trends are global estimates in the sense that we use data across the entire range of time to estimate trend. An alternative approach would be to construct a weighted local regression estimator or use B-spline bases instead of polynomial bases of second-order and see whether this leads to different conclusions than what is presented in Figure 2. However, developing such a statistical method is beyond the scope of the current paper and we leave it for future work.

3.3 New Analysis of New Clinical Endpoints

In this subsection, we use the same statistical method described in Section 2 to analyze four new endpoints described in Section 3.1. For both the length-adjusted AUC endpoints in HIV-1 RNA and days below a LOD, the significant linear trends disappear in the new definition compared to what we found in Table 3. This suggests that participants who had larger HIV-1 RNA before virological failure tended to switch earlier once virological failure actually happened. Interestingly, the quadratic trends were significantly different from zero in the case of HIV-1 RNA, just as it was in Table 3, but not for days below a limit of detection. Finally, when we considered the binary endpoints defined in Table 1, we modeled

$$\text{log}\left\{\frac{P_{{\mathrm{\delta ̄}}_T}(Y=1)}{P_{{\mathrm{\delta ̄}}_T}(Y=0)}\right\}={\beta }_0+{\beta }_1(t-M)+{\beta }_2{(t-M)}^2.$$

In Table 4, we find that delayed switching is associated with lower probability of one or more final HIV-1 RNA observations below a limit of detection. Thus, participants who switched soon after virological failure were more likely to have viral suppression at the end of the follow-up period.

4. Discussion

For persons living with HIV and AIDS, identifying the optimal time to switch from a failing ART regimen to a new ART regimen is an important scientific question with no firm solution. Although current Department of Health and Human Services guidelines (http://www.aidsinfo.nih.gov) recommend that participants switch early after confirmed virologic failure, attempts to collect objective data in controlled clinical studies have been unsuccessful. For example, AIDS Clinical Trials Group (ACTG) A5115 was designed to address such a scientific question but was unable to accrue enough participants to reach target enrollment (Riddler et al., 2007). As a result, study investigators could not conclude whether immediate switch to second-line ART was better or worse than delayed switch. We attempt to answer a similar scientific question as that proposed by Riddler et al. (2007) but do so in a secondary analysis of ACTG A5095 data using semi-parametric methods for missing data problems and causal inference. Although the 5095 study is approximately 10 years old now, optimal switching times for participants failing ARTs are unknown so any data analysis is a contribution to the field. In addition, the methods here could be applied to other studies as that data is made available.

We recast the modeling problem in the context of dynamic treatment regimes with stochastic treatment assignment rules and then adopt an estimator by Johnson and Tsiatis (2004, 2005) to estimate the parameters of interest. This framework allows for sequential treatment decisions, adjusts for the confounding introduced by non-randomized treatment assignment, and accommodates censored switching times as a result of limited follow-up. Our analysis suggests that delayed switch to second-line ART regimen is associated with elevated level of HIV-1 RNA and lowered CD4 cell count, although the latter was not statistically significant. Our results here support a more nuanced conclusion than what we reported in earlier work. Here, and in Li et al. (2012), we conclude that there may some benefit to switching early as opposed to delayed switching. However, our new analysis also suggests that, on average, the worst outcomes are observed for those participants switching to second-line ART regimen 10–13 weeks after confirmed virologic failure, not those participants switching 18–20 weeks post-virological failure. We conjecture that this result may be tied more or less directly to participants who met the 5095 definition of virological failure but then remained on initial ART regimen to the end of the follow-up period. It is conceivable that these participants stopped taking the initial ART for a period of time which resulted in elevated viremia, but then whose viral load levels returned to low levels after they resumed taking their medications. This would explain both their virological failure and subsequent good immunological outcomes. This explanation also begs for an improvement in the current methodology which seems to suggest that all participants who fail virologically must switch to second-line ART. We understand that any recommendation to switch ART regimens will depend on participant adherence to their current ART regimen and, if non-adherence can be corrected, that no such recommendation to switch from initial ART regimen would be necessary.

Presumably, a more dynamic modeling approach could accommodate other subtleties or nuance in the antiretroviral treatments that are not addressed here. In addition to adherence, CD4 cell counts ought to play a role in switching to second-line ART regimen. We recognize that virological failure is not synonymous with a drop in CD4 cell count and that some participants exhibit a robust immune response even in the face of elevated HIV-1 RNA levels. Thus, provider recommendations to switch to second-line ART regimens are more holistic in their rules for treatment assignment. We intend to include more elements in future data analyses that reect what takes place in the clinic but also recognize the need for a larger data set and possibly a different long-term clinical endpoint to realistically estimate treatment effects.

Finally, our analyses here suggest that switching to second-line ART earlier rather than later is preferred. Using two-stage methodology and a related but different causal estimand, Li et al. (2012) reached a similar conclusion. Since mean outcome seems to get better as time to switch is closer to virologic failure, an intriguing question raised by an anonymous referee is whether the optimal switching time lies prior to virological failure. It is our opinion that, except in the case of drug toxicity, no participant with undetectable levels of HIV-1 RNA would be a candidate for switching to second-line ART. So, since the ACTG definition of confirmed virological failure took measurements from two subsequent clinic visits, the only possibility would be that the best time to switch to second-line ART could occur between the first and second clinic visit where an elevated level of HIV-1 RNA is observed. Two consecutive measurements are required because HIV-1 RNA levels may spike for some participants on ART and not indicate whatsoever a failing ART and may, in fact, simply reflect an erroneous lab measurement. Thus, although it may be possible to perform an analysis where the mean outcome is modeled as a function of time-to-switch prior to the confirmatory measurement of HIV-1 RNA level, we feel the results of such analysis will have little impact on the science unless the recommended time to switch occurs after the confirmatory measurement of HIV-1 RNA level.