Abstract
We evaluate the performance of the most widely used wavefunction, density functional theory, and semiempirical methods for the description of noncovalent interactions in a set of larger, mostly dispersion-stabilized noncovalent complexes (the L7 data set). The methods tested include MP2, MP3, SCS-MP2, SCS(MI)-MP2, MP2.5, MP2.X, MP2C, DFT-D, DFT-D3 (B3-LYP-D3, B-LYP-D3, TPSS-D3, PW6B95-D3, M06-2X-D3) and M06-2X, and semiempirical methods augmented with dispersion and hydrogen bonding corrections: SCC-DFTB-D, PM6-D, PM6-DH2 and PM6-D3H4. The test complexes are the octadecane dimer, the guanine trimer, the circumcoronene…adenine dimer, the coronene dimer, the guanine-cytosine dimer, the circumcoronene…guanine-cytosine dimer, and an amyloid fragment trimer containing phenylalanine residues. The best performing method is MP2.5 with relative root mean square deviation (rRMSD) of 4 %. It can thus be recommended as an alternative to the CCSD(T)/CBS (alternatively QCISD(T)/CBS) benchmark for molecular systems which exceed current computational capacity. The second best non-DFT method is MP2C with rRMSD of 8 %. A method with the most favorable “accuracy/cost” ratio belongs to the DFT family: BLYP-D3, with an rRMSD of 8 %. Semiempirical methods deliver less accurate results (the rRMSD exceeds 25 %). Nevertheless, their absolute errors are close to some much more expensive methods such as M06-2X, MP2 or SCS(MI)-MP2, and thus their price/performance ratio is excellent.
Introduction
Noncovalent interactions, such as hydrogen bond, halogen bond, π..π stacking, etc., play an important role in processes like the molecular recognition, crystal packing, protein folding, vapor-liquid condensation, stacking of nucleobases, etc. Although these interactions are at least by an order of magnitude weaker than covalent interactions, they accumulate for larger systems and their impact on structure and function of biomolecules is fundamental.1,2,3
Different binding motifs require different levels of theory to reach a given accuracy. Interactions driven mostly by electrostatics, such as the hydrogen bonding,4,5 are (at least qualitatively) described properly already at the Hartree-Fock (HF) level. However, neither Hartree-Fock theory nor traditional local or semilocal density functional theories include dispersion,6,7,8 and not even highly parametrized exchange-correlation functionals are able to describe dispersion in the asymptotic limit,9 leading to an underestimation of the stability of dispersion dominated complexes at the density functional (DFT) and semi-empirical levels of theory. The simplest method which accounts for dispersion for the right reason, second order Møller-Plesset perturbation theory (MP2), strongly overestimates dispersion for π systems.10 In many cases accurate results are obtained only at the computationally expensive coupled cluster level with the perturbative inclusion of triple excitations in extended basis sets. Two, unfortunately mutually contradictory goals govern the method development. The first one is to achieve maximum accuracy while the second one is the ability to describe large molecular systems efficiently. Significant effort was spent in the past decade to develop methods that strike a reasonable compromise between accuracy and computational cost for dispersion-dominated interactions.11 Some examples are empirical scaling of different contributions in wavefunction-based methods,12,13,14,15 parametrizing exchange-correlation functionals to account for dispersion,16 combining short-range DFT correlation with long-range MP2 (MP2C)17 or RPA18 and adding explicit dispersion terms to conventional DFT.19 Other promising approaches are local electron correlation theories,20 Symmetry-Adapted Perturbation Theory21 based on DFT22,23, modification of the core potentials to mimic dispersion,24,25 and methods aiming at incorporating the physics of dispersion in DFT.26,27,28 Although many of these methods are very promising, we will focus on the following classes of methods: (a) post-HF wavefunction theory (WFT) methods containing empirical parameters, (b) DFT based methods with added dispersion terms, and (c) semiempirical quantum mechanical methods augmented with empirical corrections for noncovalent interactions.
The first group is represented by the SCS-MP2, SCS(MI)-MP2, MP2C, MP2.5 and MP2.X methods.12,14,17,29,30 The formal scaling of these methods is O(N5), for the MP2-based, and O(N6) for MP3-based methods, where N is proportional to the size of the system (assuming constant basis set quality). Perturbational methods such as MPn are non-iterative and are thus about an order of magnitude more efficient than iterative methods, and they are also more readily parallelized.
The most widely used family of quantum chemical methods, local or semilocal density functional theory (DFT) does not account for the dispersion interaction.6,7,8 Dispersion can be included by empirical corrections19,31,32 or by fitting the exchange-correlation functional to reproduce dispersion near the van der Waals minimum33 (note, however, that these methods fail to represent the long-range behavior of dispersion). DFT-based methods have advantages over post-HF methods: smaller basis set superposition error (BSSE) and more favorable scaling. The DFT functionals investigated in this work scale one or two powers lower than post-Hartree-Fock methods, O(N3) - O (N4) versus O(N5) - O(N6).
The third group contains semiempirical methods34 augmented with empirical corrections, such as the dispersion correction of Martin and Clark.35 We focus on the PM6 method36 enhanced with empirical corrections for dispersion and hydrogen bonding.37,38 Empirical corrections used in this group are usually obtained from minimization of the root-mean-square deviation relative to high-quality benchmark data.
The design of reference data is of a crucial importance. They should be obtained by state-of-the-art methods, such as CCSD(T) in extended basis set or even extrapolated to the complete basis set (CBS) limit. They should also be available for a large, balanced set of molecules. Several such benchmark data sets for noncovalent complexes are available. The S22 set,39 developed in Hobza’s group, has become one of the most commonly used data sets for testing and parametrization of methods focused on the noncovalent interactions. This dataset is now being replaced by larger and more balanced data sets such as: S22x5,40 S22+,41 and S66.42 Super databases (databases containing several data sets) such as GMTKN43,44 or NCIE45,46,47,48 are also available.
All the data sets above share the same restriction: only medium-sized systems (less than ~30 atoms) are included. The only exception is the recent study of Risthaus and Grimme49 where the performance of different dispersion-accounting DFT methods is tested with respect to experimental data on the S12L set (set of large molecular clusters). It is a tacit assumption that the accuracy of methods parametrized for small complexes/clusters is preserved for larger ones. This, however, may not be the case if a method works well near the van der Waals minimum but is deficient for distant interactions because larger molecules have more long-range dispersion terms. The potential accumulation of errors with increasing system size is not yet fully understood. Thus there is a need to test the accuracy of recent methods on larger systems. In the present paper we provide benchmark data for noncovalent complexes considerably larger than those in S22 or S66 datasets; this dataset is called L7. We test the performance of WFT, DFT and semiempirical methods on a set of seven large molecular complexes: “CBH”, the octadecane dimer in stacked parallel conformation (representative of aliphatic dispersion-dominated interaction); “GGG”, a stacked guanine trimer arranged as in DNA (representative of the aromatic stacking π…π dispersion interaction with implicit account for the three-body interaction, the binding energy of one of the outer guanine monomers is evaluated); “C3A”, a: stacked circumcoronene…adenine dimer (representative of strong aromatic dispersion interaction with implicit account for three-body interaction); “C3GC”, a stacked circumcoronene and Watson-Crick hydrogen-bonded guanine-cytosine dimer (representative of a strong aromatic dispersion interaction with implicit account for H-bonding-stacking nonadditivity, the binding energy of circumcoronene and guanine-cytosine base pair is calculated); “C2C2PD”: parallel displaced stacked coronene dimer (representative of strong aromatic dispersion interaction); “GCGC”: a stacked Watson-Crick H-bonded guanine-cytosine dimers arranged as in DNA (representative of strong aromatic dispersion interaction with implicit three- and four-body interactions, the binding energy of two guanine-cytosine base pairs is evaluated); “PHE”: an amyloid fragment, a trimer of phenylalanine residues in mixed H-bonded-stacked conformation (representative of “mixed-character” interaction with implicit account for many-body interactions. The binding of one of the “outer” residues is evaluated). Structures of all complexes are shown in Figure 1. The full geometry information of all seven complexes along with explicit specification of interacting subsystems is available in the Supporting Information. Their size ranges from 48 to 112 atoms and they are intentionally selected to be mostly dispersion dominated. The motivation is simple: it is to assemble a set of noncovalent complexes, the accurate description of which is a challenge for the contemporary computational chemistry. The data set includes a representative of aliphatic hydrocarbon dimers, which are, similarly to the π…π stacking complexes, dispersion dominated, but of a different flavor. Aliphatic dispersion interactions are important due to their abundance in proteins48 and membranes but their accurate description is problematic as well.50,51 The dispersion originating from saturated hydrocarbons scales linearly with system size in the asymptotic limit, as opposed to interactions in aromatic systems, because of intrinsically local character of aliphatic hydrocarbons and a significant HOMO-LUMO gap. It still requires high-level ab initio methods to be described accurately. We believe that the complexes included in the data set are representative of the most important motifs dominated by dispersion in biological chemistry.
Figure 1.
Structures of the investigated complexes.
Methods
Geometries
Geometries of the CBH, C3A, C3GC and PHE systems were determined at the TPSS-D/TZVP level32 with no constrains. The structures of GCGC and C2C2PD complexes were taken from Pitoňák et al.52 and Janowski et al.,53 respectively. The GCGC geometry was taken from crystal X-ray data,52 and the C2C2PD structure was optimized at the QCISD(T) level of theory. The cc-pVDZ basis set for all atoms and the corresponding diffuse (aug-cc-pVDZ) basis set for every other, neighboring carbon atom were used. The GGG geometry was extracted from the 1ZF9 structure54 with hydrogen atoms added using xleap,55 one of the Amber software package tools. Subsequently, the coordinates of the hydrogen atoms only were optimized at the TPSS-D/TZVP level.32 Cartesian coordinates of all the complexes studied in this work are included in the supporting information as well as on the www.begdb.com56 web page.
Interaction energy calculations
Interaction energies for all of the complexes investigated were calculated for geometries optimized at lower level (see above) without considering the deformation energy (so called rigid monomer approximation was used). With the exception of semiempirical and DFT results, all calculation used the frozen core approximation and were corrected for BSSE by the counterpoise correction.57
QCISD(T)/CBS as the reference
The QCISD(T)/CBS method was chosen as the reference method, due to an advantage in efficiency over CCSD(T) in the PQS program package58 and the fact that the QCISD(T) results closely agree with “gold standard” CCSD(T) for the noncovalent interactions of closed-shell complexes.59 The hybrid scheme of Sherrill et al.10 and Jurečka and Hobza60 was used to extrapolate the results to the Complete Basis Set limit:
| (1) |
where (E(MP2/CBS)” is a CBS limit estimate of the MP2 interaction energy, obtained as described further, and ΔQCISD(T)|small basis is a QCISD(T) correction term covering the higher-order correlation effects, determined in small sized basis set. The physical basis of this approximation is that the extra correlation energy provided by the large basis originates from highly oscillatory, high-energy basis functions which are well described by low-level perturbation theory. The most time consuming part of the total interaction energy assembly is clearly the calculation of the ΔQCISD(T) correction term. The small basis set is defined as a 6-31G*(0.25) basis set.
| (2) |
The exponents of the diffuse d functions, used in this modified 6-31G* basis set, were changed from their original value of 0.8 to 0.25.61 This basis set, and the 6-31G**(0.25,0.15) basis61 were designed for the treatment of noncovalent interactions. They have been extensively validated for hydrogen bonded and stacked DNA base pairs in Hobza’s group,62 and surprisingly good performance was demonstrated also for more diverse data sets63,64 containing noncovalent interactions. The QCISD(T)/CBS method constructed as described above was used for all complexes with exception of GCGC and C2C2PD ones where slightly different methodology was applied (see later).
The ΔE(MP2/CBS)” term was calculated slightly differently from the routinely used cubic extrapolation of Halkier et al.65,66 Typically, a different two-point extrapolation is performed for the HF and post-HF terms, usually using Dunning’s67,68 aug-cc-pVXZ (aXZ) basis sets with X=2 (D) and 3(T):
| (3) |
and
| (4) |
The use of augmented basis set for extended cluster fragments (or monomers) is problematic, if not impossible. The reason is not so much excessive computational time and storage requirements but numerical instabilities caused by overcompleteness of the atomic basis set. The overcompleteness problem can be overcome in the most straightforward way by excluding the linear dependent basis functions from the basis set. Doing so, the numerical problems usually disappear, but the error with respect to the complete basis set is unpredictable and discontinuities may occur on the potential energy surface. One of the methods of eliminating this problem, as used in this work, is to scale the ΔE(MP2/CBS) term obtained from extrapolation using non-augmented Dunning’s67,68,69 cc-pVXZ (XZ) basis sets, so that the value is close to that obtained from the augmented basis set series. The scaling factors were determined for four model complexes which are simplified representatives of a particular complex category, and for which the ΔE(MP2/CBS) term could be rigorously calculated in both non-augmented and augmented basis sets. The four model complexes were created in accordance with the character of interaction of complexes in the data set: coronene…adenine (C2A) as a representative of C3A, C3CG, GCGC and C2C2PD; guanine…guanine (GG) as a representative of GGG; PHE and octane dimers (C8 dimer) as representatives of PHE trimer and CBH respectively. The structures of the model complexes are shown in Figure 2 and the complete geometry is available in the supporting information. Two ΔE(MP2/CBS) values were calculated for each complex, obtained from two-point aDZ → aTZ and DZ → TZ extrapolation. To our surprise the scaling factors obtained vary only a little, from 1.01 for C8(CBH) to 1.05 for GG(GGG), thus an average value for the scaling coefficient could have been used as well. The values of other two scaling coefficients are 1.02 for C2A model complex and 1.03 for the PHE dimer. The scaled ΔE(MP2/CBS) values, labeled as (E(MP2/CBS)”, are summarized in Table 1.
Figure 2.
Structures of the four simplified (model) complexes.
Table 1.
MP2/CBS interaction energies (in kcal/mol) of the simplified (model) complexes (cf. Figure 2) calculated using non-augmented and augmented Dunning’s (aug-)cc-pVXZ, X=D, T, basis sets
Higher-order correlation correction for the GCGC and C2C2PD complexes were calculated slightly differently than for the other systems, these numbers were taken from our previous publications (Ref. 52 and 53). The GCGC was calculated at the CCSD(T)/6-31G**(0.25,0.15) level.52 The C2C2PD complex at QCISD(T) level with basis set augmented with diffuse functions (aug-cc-pVDZ) on every second carbon atom only, the rest of carbon atoms together with hydrogen atoms were described with non-augmented basis set (cc-VDZ).53 These two levels provide results similar to QCISD(T)/6-31G*(0.25), which was used for the rest of the complexes. This statement is supported by an observation that QCISD(T) and CCSD(T) methods deliver practically identical results for the interaction energies for similar systems,59 as well as by extensive benchmarking of the 6-31G**(0.25,0.15) and 6-31G*(0.25) basis sets.62,64 It is less obvious that the aDZ basis performs similarly to the 6-31G*(0.25) basis. Nevertheless, for larger complexes the results match surprisingly well.63 We did not recalculate these two complexes at QCISD(T) level used for remaining complexes, because of high similarity between QCISD(T) and CCSD(T) techniques.
The presented strategy of obtaining reference binding energy has some limitations that should be mentioned. Firstly, it is the accuracy of the MP2/CBS energies. For such large molecular systems there is not much evidence how effective is the counterpoise correction and whether it should be used or not. Our tests suggest that the CP correction should be applied, for more details see Tables S5 and S6 in the Supporting Information material and the discussion therein. Secondly, the scaling of the resulting MP2/CBS values also brings some degree of uncertainty. Nevertheless, we are convinced that the scaling improves the result, and that it is a legitimate approach since: a) the scaling is based on similar model systems that differ only in size (typically one half or two thirds of the size of the original molecule from the L7 set, octane is used as a model for octadecane, guanine dimer for guanine trimer, coronene for circumcoronene, amyloid chain dimer for amyloid chain trimer); b) the procedure is done separately for each specific molecule from the set. Finally, the calculation of the correction term, where the relatively small 6-31G*(0.25) basis set is used, is another potential source of uncertainty, but we should bear in mind that use of bigger basis set would not be feasible for cluster of presented size and that this basis set has been proven to work well in smaller systems. We may speculate that the same basis set should, in principle, provide better description of larger systems. This opinion is based on the observation that large basis sets which provide satisfactory description in small systems tend to become overcomplete and numerically unstable in larger systems. The same effect should diminish undercompleteness of small basis sets, when applied to large molecules.
Explicitly correlated MP2-F12 methods
The explictly correlated RI-MP2-F12 calculations with cc-pVDZ and cc-pVTZ basis set were utilized in order to estimate error in scaled MP2/CBS values (see above). Because of computational complexity of these calculations along with extended size of the studied complexes explicitly correlated calculations were carried out only for GGG and GCGC complexes. The RI-MP2-F12/CBS values were obtained utilizing the Schwenke general type of extrapolation.70
MP2 and scaled-MP2 methods
MP2 along with its spin component scaled variants SCS-MP2 and SCS(MI)-MP2 were tested. The procedure for obtaining the MP2/CBS values is described in the previous paragraph. For calculation of the CBS value of the spin-component scaled MP2 methods, we refer to DiStasio et al.14 The following scaling coefficients were used for the opposite-spin (os, “singlet”) and same-spin (ss, “triplet”) terms: SCS-MP2: cos=1.20, css= 0.33, SCS(MI)-MP2: cos=0.29, css= 1.46, regardless of the basis set.
Higher order correlation methods
The performance of several methods which go beyond the MP2 level (marked as post-MP2): MP3, MP2.5, MP2.X, MP2C (not exactly a WFT method) and QCISD were investigated. The extrapolation procedure followed for these methods toward the CBS limit was the same as for the QCISD(T) benchmark, eq. (1):
| (5) |
To facilitate the discussion, we group the WFT methods into two categories: “non-empirical”: QCISD, MP3, MP2C and “empirical”: MP2.5 and MP2.X.
Both QCISD and MP3 are traditional methods based on approximating the molecular wavefunction, while the MP2C method of Hesselmann17,71 is slightly different. It combines time-dependent DFT with supramolecular MP2 energy, and therefore it cannot be correctly categorized as a non-empirical WFT method. However, it improves the MP2 results significantly with only a minor computational overhead, thus represents a promising strategy for noncovalent interaction calculations.42,50
The group of “empirical” methods includes methods with the inclusion of the third-order correlation contribution, MP2.X and MP2.5. The MP2.5 method, proposed by Pitoňák et al.,72 takes advantage of the error cancellation between the MP2 (overestimation) and the MP3 (underestimation) binding energies.11 The MP2.5 binding energy is obtained according eq. (6) (the “small size basis set” used in the correction term is consistent with reference QCISD(T) calculation for each complex):
| (6) |
with c=0.5. Riley et al.30 optimized the parameter c for the S66 data set and different basis set. For large basis sets c converges to 0.5 and for extended basis it is almost exactly 0.5. The MP2.X method is analogous to MP2.5, however, the coefficient c is optimized for a specific basis set. Excellent stabilization energies were obtained already for 6-31G*(0.25) basis set with c=0.62.30
DFT methods
In this group the following approaches have been investigated: (a) Grimme’s71 DFT-D3 using the BLYP/def2-QZVP, B3-LYP/def2-QZVP, TPSS/def2-QZVP, PW6B95/def2-QZVP and M06-2X/def2-QZVP combinations of the functional and the basis set.15 These methods were tested with both the “zero” and the “Becke-Johnson” damping73,74,75,76. According to previous studies, these methods provide reasonably accurate description of dispersion interaction.77 (b) Jurecka’s DFT-D method with the TPSS/TZVP combination of the functional/basis set,32 and (c) Truhlar’s M06-2X functional with the def2-QZVP basis set.33
Semi-empirical quantum chemical methods
The PM636 based methods augmented with the empirical correction for the dispersion and the H-bonding interactions (PM6-D,37 PM6-DH278 and PM6-D3H438) as well as the SCC-DFTB-D79,80 method were investigated.
Computational Details
The DFT calculations (with the exception of M06-2X), and MP2 calculations were carried out using TURBOMOLE program package, versions 6.0, 6.1 and 6.4.81 The single point calculations and gradient optimizations were done with a convergence threshold imposed on the change in energy between consecutive SCF iterations, and was set to 10−7 Eh; the geometry convergence criteria were unchanged from default values: energy change of 10−5 Eh and maximum gradient norm of 10−3 Eh/a0. The integral neglect threshold was set by the program automatically: between 10−11 and 10−13 Eh and Turbomole grid m3 was used for all the calculations.
QCISD(T) calculations were done using the PQS program.58 The integral neglect threshold was set to 10−15 Eh. The reason for such a tight threshold was to prevent any numerical problems resulting from possible linear dependencies in the basis set. The QCISD convergence criteria were set to 10−6 Eh for the maximum change in energy and the same threshold was imposed on the largest QCISD residuum element.
MP2C and RI-MP2-F12 calculations were performed using MOLPRO version 2009.82 The integral neglect threshold was set to 10−12 Eh and 10−11 Eh for one-electron and two-electron integrals, respectively. The energy threshold and orbital threshold for the SCF procedure was set to 10−8 Eh. The maximum allowed eigenvalue of the overlap matrix was set to 10−8 Eh. The grid accuracy (per atom) in TDDFT part of MP2C calculation was set to 10−8 Eh. Density fitting approximation in MP2-F12 calculations (RI-MP2-F12) was done with cc-pVD(T)Z/JKFIT and cc-pVD(T)Z/MP2FIT basis sets and the following thresholds: neglect of contracted 3-index integrals in AO basis (10−10 Eh), neglect of half-transformed 3-index integrals (10−9 Eh), Schwarz screening threshold (10−5 Eh), neglect of 2-index integrals in AO basis (10−12 Eh), product screening threshold for first half transformation (10−9 Eh) and screening threshold for F12 integrals (10−8 Eh). Further, the 3C(FIX) Ansatz with geminal Slater exponent set to 1.0 were used.
MP3 calculations were performed using MOLCAS program package.83 The Cholesky decomposition of two-electron integrals84 was applied, with the integral threshold set to 10−5 Eh. The thresholds for the energy change, RMSD of the density matrix and RMSD of the Fock matrix were set to 10−5 Eh, 10−4 Eh and 10−4 Eh, respectively.
The M06-2X calculations were carried out using Gaussian0985 program package with the thresholds for the energy change and RMSD of the density matrix set to 10−5 and 10−7 Eh, respectively. The default grid with 75 radial shells and 302 angular points per shell was used in all the calculations.
PM6 calculations were carried out with MOPAC200986 program, the SCF convergence was set to 1.6x10−7 Eh. SCC-DFTB-D calculations were done via DFTB+79,80 program, here the threshold for self-consistent charge (SCC) procedure was set to 10−5 e.
All the calculations presented in this study, except for the semiempirical ones, were done using spherical basis functions, if not explicitly stated otherwise.
Error analysis
The performance of the studied methods with respect to the benchmark results is measured by the following statistical indicators: Root Mean Square Deviation (RMSD), Mean Unsigned Error (MUE), Mean Signed Error (MSE) and Maximum unsigned error (MAX). RMSD and MUE characterize the overall accuracy of a method. MSE provides information about systematic errors. MAX identifies the worst described entity and thus it measures the robustness of the method. The total binding energies for the noncovalent complexes investigated vary significantly, from 2 to 32 kcal/mol. Hence, the relative (percentage) values marked with prefix “r”, defined as 100×(ΔEmethod - ΔEreference)/ΔEreference are more appropriate for the comparison across the whole data set.
Results and Discussion
Table 1 summarizes the MP2/CBS interaction energies for four model complexes, obtained from extrapolating the augmented and non-augmented cc-pVXZ, X=D, T basis sets to the basis set limit. The extrapolated values of stabilization energies follow the expectations that the former are larger than the later ones, thus leading to the scaling coefficients above one. The variation of the scaling coefficients, as already noted, is surprisingly small, in orders of only few percent (1–5 %). This is most likely the consequence of the basis set saturation already at the non-augmented level due to the extended size of the investigated complexes.
Interaction energies obtained at various levels of theory for all seven complexes are listed in Table 2. Signed errors and the corresponding relative values are shown separately in Table 3. Statistical quantities, i.e. RMSD, MSE, MUE and MAX for the tested methods are summarized in Table 4. In Figure 3 the relative signed errors for the best performing method within the specific subgroup (for more details see Section Error analysis) are visualized, while Figure 4 depicts the relative RMSD for all methods.
Table 2.
Interaction energies in kcal/mol of the investigated complexes at different levels of theory. The CBS limit is obtained according to eqs. 1–6.
| method/bases//complex | CBH | C2C2PD | C3A | C3GC | GCGC | GGG | PHE |
|---|---|---|---|---|---|---|---|
| QCISD(T)/CBS | −11.06 | −24.36a | −18.19 | −31.25 | −14.37b | −2.40 | −25.76 |
| QCISD/CBS | −9.53 | - | −14.52 | −24.79 | - | −1.30 | −24.23 |
| MP2.X/CBS | −10.63 | −22.15 | −15.52 | −26.65 | −12.26 | −1.85 | −25.24 |
| MP2.5/CBS | −10.88 | −22.80 | −17.85 | −30.40 | −13.41 | −2.34 | −25.46 |
| MP2C/CBS | −11.29 | −20.88 | −16.89 | −28.71 | −12.89 | −2.22 | −24.82 |
| MP3/CBS | −9.84 | −6.61 | −8.15 | −14.77 | −8.61 | −0.32 | −24.56 |
| MP2/CBS | −11.92 | −38.98 | −27.54 | −46.02 | −18.21 | −4.36 | −26.36 |
| SCS(MI)-MP2/CBSc | −9.64 | −31.71 | −22.92 | −37.92 | −14.08 | −2.23 | −26.16 |
| SCS-MP2/CBSc | −7.87 | −27.53 | −19.61 | −32.07 | −11.70 | −1.79 | −22.77 |
| B3-LYP-D3/def2-QZVPd | −12.96 | −23.22 | −17.99 | −31.29 | −15.48 | −2.10 | −25.99 |
| BLYP-D3/def2-QZVPd | −14.34 | −22.82 | −18.12 | −31.79 | −16.44 | −2.48 | −25.56 |
| TPSS-D3/def2-QZVPd | −12.35 | −21.19 | −16.71 | −28.58 | −13.38 | −1.87 | −24.23 |
| PW6D95-D3/def2-QZVPd | −10.01 | −19.93 | −16.63 | −29.71 | −12.48 | −1.70 | −24.07 |
| M06-2X-D3/def2-QZVPe | −8.23 | −20.55 | −15.96 | −29.00 | −14.28 | −1.71 | −25.63 |
| M06-2X/def2-QZVP | −4.71 | −16.85 | −12.88 | −23.68 | −11.59 | −0.65 | −23.38 |
| TPSS-D/TZVP | −14.49 | −18.69 | −16.53 | −27.78 | −13.69 | −2.19 | −24.46 |
| PM6-D3H4/SMBf | −9.64 | −17.53 | −16.01 | −26.47 | −19.87 | −3.50 | −25.43 |
| PM6-DH2/SMBf | −9.96 | −21.99 | −18.04 | −30.25 | −22.55 | −4.18 | −24.91 |
| PM6-D/SMBf | −9.96 | −21.99 | −18.04 | −30.03 | −20.99 | −3.85 | −22.80 |
| SCC-DFTB-D/SMBf | −13.26 | −18.7 | −14.52 | −24.41 | −15.57 | −1.08 | −20.17 |
correction term (cf. eq. 2) was determined at QCISD(T) level using cc-pVDZ basis set for all atoms and the corresponding aug-cc-pVDZ basis set for every other, neighboring carbone atom
correction term (cf. eq. 2) was determined at CCSD(T)/6-31G**(0.25,0.15) level of theory
CBS limit calculated using cc-pVDZ and the cc-pVTZ basis sets
Becke Johnson damping of the dispersion correction used
zero damping of the dispersion correction used
SMB stands for “subminimal” basis set
Table 3.
Signed errors (in kcal/mol) and the respective relative values (in %), for the investigated complexes at different level of theory. Negative sign (“-”) indicates overestimation of the interaction energy. The CBS limit is obtained according to eqs. 5–6.
| method/bases//complex | CBH | C2C2PD | C3A | C3GC | GCGC | GGG | PHE |
|---|---|---|---|---|---|---|---|
| QCISD/CBS | 1.53 / 13.8 | - | 3.67 / 20.2 | 6.46 / 20.7 | - | 1.10 / 45.9 | 1.53 / 5.9 |
| MP2.X/CBS | 0.43 / 3.9 | 2.20 / 9.1 | 2.67 / 14.7 | 4.61 / 14.7 | 2.11 / 14.7 | 0.54 / 22.7 | 0.52 / 2.0 |
| MP2.5/CBS | 0.18 / 1.6 | 1.56 / 6.4 | 0.34 / 1.9 | 0.86 / 2.7 | 0.96 / 6.7 | 0.06 / 2.5 | 0.30 / 1.2 |
| MP2C/CBS | −0.24 / −2.1 | 3.48 / 14.3 | 1.30 / 7.2 | 2.54 / 8.1 | 1.48 / 10.3 | 0.17 / 7.2 | 0.94 / 3.7 |
| MP3/CBS | 1.22 / 11.0 | 17.74 / 72.9 | 10.04 / 55.2 | 16.48 / 52.7 | 5.75 / 40.0 | 2.08 / 86.8 | 1.20 / 4.7 |
| MP2/CBS | −0.86 / −7.8 | −14.63 / −60.1 | −9.35 / −51.4 | −14.77 / −47.3 | −3.84 / −26.7 | −1.96 / −81.8 | −0.60 / −2.3 |
| SCS(MI)-MP2/CBSa | 1.41 / 12.8 | −7.35 / −30.2 | −4.73 / −26.0 | −6.67 / −21.4 | 0.29 / 2.0 | 0.16 / 6.8 | −0.40 / −1.6 |
| SCS-MP2/CBSa | 3.18 / 28.8 | −3.17 / −13.0 | −1.42 / −7.8 | −0.82 / −2.6 | 2.67 / 18.6 | 0.60 / 25.2 | 2.99 / 11.6 |
| MP2/CBSa | −0.74 / −6.7 | −13.86 / −56.9 | −8.81 / −48.4 | −13.87 / 44.4 | −3.48 / −24.2 | −1.75 / −73.1 | 0.17 / 0.7 |
| B3-LYP-D3/def2-QZVPb | −1.90 / −17.2 | 1.1 / 4.7 | 0.20 / 1.1 | −0.03 / −0.1 | −1.1 / −7.8 | 0.30 / 12.4 | −0.23 / −0.91 |
| BLYP-D3/def2-QZVPb | −2.35 / −21.3 | −1.05 / −4.3 | −0.61 / −3.3 | −1.91 / −6.1 | −2.14 / −14.9 | −0.16 / −6.8 | 0.80 / 3.1 |
| TPSS-D3/def2-QZVPb | −1.29 / −11.7 | 3.16 / 13.0 | 1.48 / 8.1 | 2.67 / 8.5 | −0.99 / 6.9 | −0.53 / 22.0 | 1.52 / 5.9 |
| PW6D95-D3/def2-QZVPb | 1.04 / 9.5 | 4.42 / 18.2 | 1.56 / 8.6 | 1.55 / 5.0 | 1.89 / 13.2 | −0.70 / 29.1 | −1.68 / 6.5 |
| M06-2X-D3/def2-QZVPc | 2.83 / 25.6 | 3.81 / 15.6 | 2.23 / 12.2 | 2.25 / 7.2 | 0.09 / 0.6 | 0.69 / 28.7 | 0.13 / 0.5 |
| M06-2X/def2-QZVP | 6.35 / 57.4 | 7.51 / 30.8 | 5.31 / 29.2 | 7.57 / 24.2 | 2.80 / 19.5 | 1.75 / 72.9 | 2.38 / 9.2 |
| TPSS-D/TZVP | −3.43 / −31.0 | 5.67 / 23.3 | 1.66 / 9.1 | 3.47 / 11.1 | 0.68 / 4.7 | 0.21 / 8.7 | 1.30 / 5.0 |
| PM6-D3H4/SMBd | 1.42 / 12.8 | 6.83 / 28.0 | 2.18 / 12.0 | 4.78 / 15.3 | −5.50 / −38.3 | −1.10 / −46.0 | 0.33 / 1.3 |
| PM6-DH2/SMBd | 1.10 / 9.9 | 2.37 / 9.7 | 0.15 / 0.8 | 1.00 / 3.2 | −8.18 / −57.0 | −1.78 / −74.4 | 0.85 / 3.3 |
| PM6-D/SMBd | 1.10 / 9.9 | 2.37 / 9.7 | 0.15 / 0.8 | 1.22 / 3.9 | −6.62 / −46.1 | −1.45 / −60.6 | 2.96 / 11.5 |
| SCC-DFTB-D/SMBd | −2.20 / −19.9 | 5.66 / 23.2 | 3.67 / 20.2 | 6.84/ 21.9 | −1.20 / −8.4 | 1.32 / 55.0 | 5.59 / 21.7 |
CBS limit constructed using cc-pVDZ and cc-pVTZ basis sets
Becke Johnson damping of the dispersion correction used
zero damping of the dispersion correction used
SMB stands for “subminimal” basis set
Table 4.
The set of statistical measures (in kcal/mol) calculated with respect to the reference (QCISD(T)/CBS) data for the investigated complexes. The CBS limit is obtained according to eqs. 5–6.
| method/basis set//statis. measure | RMSD | MUE | MSE | MAX |
|---|---|---|---|---|
| QCISD/CBSa | 3.50 | 2.86 | 2.86 | 6.46 |
| MP2.X/CBS | 2.34 | 1.87 | 1.87 | 4.61 |
| MP2.5/CBS | 0.79 | 0.61 | 0.61 | 1.56 |
| MP2C/CBS | 1.83 | 1.45 | 1.38 | 3.48 |
| MP3/CBS | 10.19 | 7.79 | 7.79 | 17.74 |
| MP2/CBS | 8.78 | 6.57 | −6.57 | 14.77 |
| SCS-MP2/CBSb | 2.37 | 2.12 | 0.58 | 3.18 |
| SCS(MI)-MP2/CBSb | 4.20 | 3.00 | −2.47 | 7.35 |
| B3-LYP-D3/def2-QZVPc | 0.95 | 0.70 | −0.24 | 1.90 |
| BLYP-D3/def2-QZVPc | 1.60 | 1.39 | −1.16 | 2.36 |
| TPSS-D3/def2-QZVPc | 1.87 | 1.66 | −1.29 | 3.16 |
| PW6D95-D3/def2-QZVPc | 2.15 | 1.83 | −1.83 | 4.42 |
| M06-2X-D3/def2-QZVPd | 2.17 | 1.72 | 1.72 | 3.81 |
| M06-2X/def2-QZVP | 5.33 | 4.81 | 4.81 | 7.57 |
| TPSS-D/TZVPe | 2.95 | 2.34 | 1.36 | 5.67 |
| PM6-D3H4/SMBf | 3.92 | 3.16 | 1.28 | 6.83 |
| PM6-DH2/SMBf | 3.35 | 2.20 | −0.64 | 8.18 |
| PM6-D/SMBf | 3.00 | 2.27 | 0.04 | 6.62 |
| SCC-DFTB-D/SMBf | 4.33 | 3.78 | 2.81 | 6.84 |
statistical measures are calculated only for five out of seven complexes (C2C2PD and GCGC complexes omitted)
CBS limit constructed using cc-pVDZ and cc-pVTZ basis sets
Becke Johnson damping of the dispersion correction used
zero damping of the dispersion correction used
Jurecka’s dispersion correction
SMB stands for “subminimal” basis set
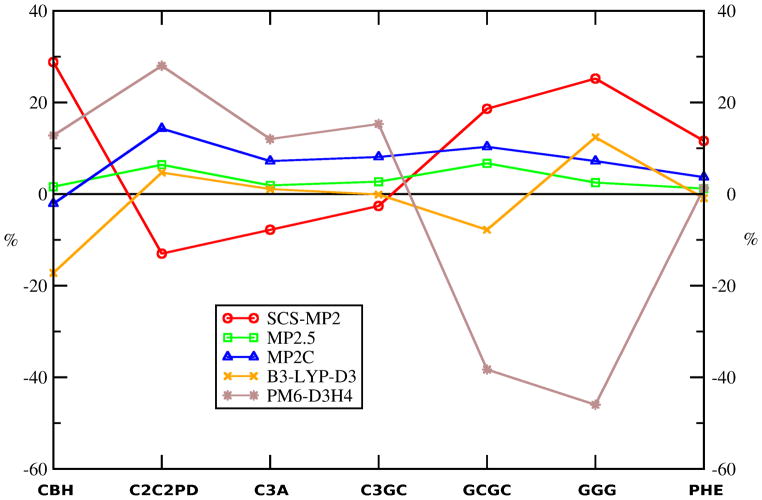
Figure 3.
Relative signed errors (in %) of SCS-MP2, MP2.5, MP2C, BLYP-D3 (Becke-Johnson damping) and PM6-D3H4 methods for the investigated complexes. Negative sign (“-”) indicates overestimation of the interaction energy. Methods listed are the best performing methods within each category of methods: (a) post-HF wavefunction theory (WFT) methods containing empirical parameters (SCS-MP2, MP2.5, MP2C), (b) DFT based methods with added dispersion terms (BLYP-D3 (Becke-Johnson damping)), and (c) semiempirical quantum mechanical methods augmented with empirical corrections for noncovalent interactions (PM6-D3H4).
Figure 4.

Relative RMSD (rRMSD in %) with respect to the reference (QCISD(T)/CBS) for the investigated methods.
Only the results obtained using the largest basis set for a particular complex and theoretical method are discussed below, separately for each group of methods. To emphasize the effect of large cluster size, presented data are compared to results obtained for the S66 data set which contains smaller systems.
QCISD
Comparison of the QCISD values (Table 2) with the reference QCISD(T) data (provided only for 5 complexes cf. Section QCISD(T)/CBS as the reference) confirms the well-known fact that the contribution of the triples is substantial. The RMSD and rRMSD values are rather large, 3.5 kcal/mol and 25%, respectively (cf. Table 4 and Figure 4). For the C3GC complex the error even exceeded 6 kcal/mol (20 %) (cf. Table 3).
MP2
The accuracy of the MP2 method, documented by RMSD value of 8.8 kcal/mol, is poor (cf. Table 4). This is a consequence of the data set being dominated by π…π stacked interactions. The span of relative errors for π…π dispersion dominated complexes is large 27 – 82% (see Table 3). However, signed errors of −0.9 kcal/mol (8%) for the CBH complex and −0.6 kcal/mol (2%) for the PHE trimer (cf. Table 3) confirms that MP2 properly describes the aliphatic dispersion and hydrogen bonding.7,32
The explicitly correlated RI-MP2-F12 calculations with cc-pVDZ and cc-pVTZ basis set were utilized in order to estimate error in scaled MP2/CBS values (cf. Methods; for more information see Table S6 in the Supporting Information material). The absolute (relative) underestimation of scaled MP2/CBS stabilization energy with respect to RI-MP2-F12/CBS values is 0.39 (9%) and 1.57 (9%) kcal/mol for GGG and GCGC complexes, respectively. Based on these values we can estimate the relative error in scaled MP2/CBS values.
Scaled MP2
Empirically scaling the spin components in MP2 improves the description of noncovalent interactions,12 particularly for π stacking. Our RMSD and relative RMSD values for MP2, SCS-MP2 and SCS(MI)-MP252 are 8.8 (48%), 2.4 (18%) and 4.2 (18%), respectively (cf. Table 4 and Figure 4). However, the performance for some dispersion dominated complexes is still inadequate, e.g., the signed error for C2C2PD at the SCS(MI)-MP2 level is −7.4 kcal/mol (−30%) (cf. Table 3). According to the results in Table 4, SCS(MI)-MP2 performs worse than the original SCS-MP2. This is surprising, considering that SCS(MI)-MP2 was, unlike SCS-MP2, parametrized toward the best performance on interaction energies. Comparing the performance of both methods for dispersion dominated complexes in the S66 set, the opposite conclusion in obtained. The relative RMSD of SCS(MI)-MP2 and SCS-MP2 are 18 % and 26 %, respectively,42 which indicates that the size of the investigated molecular cluster has a significant effect. SCS-MP2 underestimates the bonding between aliphatic species.87,51 The relative error, roughly 30 % for the aliphatic CBH complex, is among the largest from all the methods within the group (cf. Table 3 and Figure 3) confirms this observation.
MP3, MP2.5, MP2.X and MP2C
The performance of the plain MP3 method is poor, perhaps comparable with MP2 in the RMSD, MUE and MAX values (cf. Table 4). Typical feature of the MP3 method is underestimation of the aromatic dispersion interaction (MSE about 7.8 kcal/mol, cf. Table 4), contrary to MP2 (MSE about −6.6 kcal/mol, cf. Table 4). However, both MP2 and MP3 describe hydrogen bonded complexes very well. The error cancellation between MP2 and MP3 is responsible for substantially higher accuracy of MP2.5, with RMSD of only about 0.8 kcal/mol (4 %, cf. Table 4 and Figure 4). A statistical evaluation of the MP2.X performance gives 2.3, 1.9, 4.6 kcal/mol and 13 % for RMSD, MUE, MAX and rRMSD, respectively (cf. Table 4), which is quite good. MP2.X outperforms both scaled-MP2 variants. However, its performance is worse than MP2.5, in spite of the optimization of the mixing parameter (cf. Table 3 and 4). This is most likely a consequence of parametrization toward substantially smaller molecular clusters in the S66 data set.
The MP2C method shows a real improvement over MP2. In terms of the relative errors, it is the second best performer among the WFT methods evaluated in this work with an rRMSD of about 8 % (1.8 kcal/mol, cf. Table 4 and Figure 4) and an rMAX of 14 % (3.5 kcal/mol) (for the coronene dimmer, cf. Table 3 and 4).
DFT methods
The performance of the group of functionals augmented with the Grimme’s D3 correction utilizing the Becke-Johnson (B-J) damping is better in comparison with the Zero damping (cf. Table S1–S4 in Supporting Information). These results are consistent with findings of Grimme, where the use of the DFT-D3 methods with B-J damping yield better results for most of the functionals.77 Hence, in this paper we will discuss almost exclusively DFT-D3 methods using B-J damping procedure. The M06-2X-D3 method will be discussed in combination with Zero damping, because there are no B-J damping parameters for the D3 correction. The best performing functional is the B3-LYP followed by the BLYP, TPSS, PW6B95 and M06-2X. Corresponding RMSD in kcal/mol (rRMSD in %) are 1.0 (9), 1.6 (11), 1.9 (12), 2.2 (15) and 2.2 (17), cf. Table 4 and Figure 4. The performance of the PW6B95 and the M06-2X are almost equivalent (cf. Table 4). In Grimme’s study, where different DFT functional were tested against the S66 dataset, the best performing functional for the dispersion bounded subset was B3-LYP.77 This is consistent with our findings. The relative ordering of other functionals in this paper is different compared to Grimme’s study.77 However, the absolute differences in performance of functionals are, in both studies, of order of tenths of kcal/mol. Hence, any definitive conclusions about the general performance based on these results would be questionable.
The M06-2X method in combination with Zero damping form of the D3 correction leads to the RMSD value of 2.2 kcal/mol (17%) as already mentioned. The plain M06-2X functional provides substantially larger value of the RMSD 5.3 kcal/mol or 40% (cf. Table 4). All the statistical indicators are reduced, two to three times, after applying D3 correction (cf. Table 4). This result serves as the proof that functionals which were fitted to reproduce dispersion near van der Waals minimum (for example M06-2X) are not able to cover long-range dispersion interaction. This feature was already demonstrated by Grimme.77
Based on the findings from Grimme’s study, the double-hybrid functionals should provide even better performance than the B3-LYP.88 Moreover, it was shown that double-hybrids as DSD-BLYP-D3 or PWPB95-D3 outperform scaled variants of MP2 such as SCS-MP2, S2-MP2 and SOS-MP2 methods.88 However, we should bear in mind that the computational complexity of the double-hybrids is higher when compared with other groups of functionals. Methods involving double-hybrid functionals include non-local perturbation correction for the correlation part; hence their scaling is equivalent to the regular MP2 method.
The magnitude of the many-body non-additivity term is by an order of magnitude smaller than the interaction energies. 52,89 It is believed that the three-body (Axilrod-Teller-Mutto) correction term is non-negligible for extended molecular systems.19,49. When it is implemented as described in Ref. 19 and is added to the Becke-Johnson and Zero damped dispersion, it weakens the interaction. Because it is not known much about the 3-body correction and its impact on the accuracy of a method, the results are only listed in Supporting Information (cf. Table S1–S4), without any further discussion. In general the accuracy of the DFT-D3 methods after applying the 3-body correction deteriorates. The only exception is the BLYP functional in combination with B-J damping. The RMSD is reduced from 1.6 kcal/mol (11%) to 1.1 kcal/mol (9 %), cf. Table S4 in Supporting Information. The same correction, when added to the zero-damped results, raises the overall error to 2.0 kcal/mol (12%), cf. Table S4 in Supporting Information. In Grimme’s study49 it was shown that the three-body correction is not negligible and it correlates positively with the size of a molecule. In the S12L set, this effect varies between 2 and 15 % of the total stabilization energy. Moreover, the inclusion of three-body correction in the DFT values of binding energies at quadruple-zeta level improves the overall performance of the investigated methods even in smaller systems (for more details see Ref. 49).
The TPSS-D/TZVP method of Jurečka et al.32 performs slightly worse than tested density functionals with D3 correction but clearly better than the M06-2X/def2-QZVP method of Zhao and Truhlar, with RMSD of 3.0 kcal/mol (16 %) and 5.3 kcal/mol (40 %) (cf. Table 4 and Figure 4), respectively. The direct comparison of the TPSS-D/TZVP with the TPSS-D3/def2-QZVP reveals that the latter method is slightly more accurate. However, this comparison is not completely fair because of the unequal quality of the used basis sets. The def2-QZVP basis set is of better quality than TZVP which could be the reason for the higher accuracy. The TPSS-D/TZVP combination of the functional and the basis set was chosen as the best feasible. The use of the TPSS-D/6-311++G(3df, 3pd) method, which should provide best results for dispersion bounded complexes,32 was not possible, due to problems with linear dependences in the basis set in the case of the coronene dimer and circumcoronene. This issue is discussed in the Interaction energy calculation subsection.
DFT methods describe H-bonding (or electrostatic dominated interactions in general) fairly well (see Table 3 and Figure 3), and empirically corrected DFT-D and DFT-D3 methods share a similar feature. Signed errors for the H-bonded PHE complex (ranging from 0.2 to 2.4 kcal/mol, i.e., 1 – 9 %, cf. Table 3) are significantly lower than for other complexes. Dispersion dominated interactions are described less accurately. The largest signed errors of Grimme’s (DFT-D3) methods are: 4.4 kcal/mol (18%) in the case of C2C2PD complex for PW6D95 functional and −2.1 kcal/mol (8%) in the case of GCGC complex for BLYP functional (see Table 3). The latter one is the largest negative error for all DFT methods considered here. Aliphatic dispersion, for instance in the CBH complex, is even worse: the signed errors range from −1.3 kcal/mol up to 6.4 kcal/mol (see Table 3).
Semiempirical methods
The PM6 method,36 corrected for dispersion37 (PM6-D) gives an RMSD of 3.0 kcal/mol, see Table 4. Correction for hydrogen bonding38,78 (PM6-DH2, PM6-D3H4) does not, however, increase of accuracy further (RMSD of 3.4 and 3.9 kcal/mol, respectively) (cf. Table 4). The correction for hydrogen bonding is most likely the source of undesirable errors, and it is responsible for slightly worse correlation with the benchmark data for complexes stabilized by dispersion interaction. On the other hand, errors decrease significantly for the PHE complex upon inclusion of the hydrogen bonding correction: the signed error drops from 3.0 (PM6-D) to 0.9 (PM6-DH2) and 0.3 (PM6-D3H4) kcal/mol, respectively (cf. Table 3). The SCC-DFTB-D method79,80 is comparable with that of PM6-D3H4 (cf. Table 4). In terms of relative RMSD, the ordering of the semiempirical methods we tested is the following: SCC-DFTB-D and PM6-D3H4, roughly equal, are the most accurate, followed by PM6-D and PM6-DH2 (cf. Figure 4). The rRMSD and rMAX values vary between 26–36% and 46–74%, respectively (cf. Table 4). Nevertheless, the absolute errors of the semiempirical methods are comparable with some of more sophisticated methods such as M06-2X/def2-QZVP, MP2/CBS, MP3/CBS or SCS(MI)-MP2 (see Table 4).
Conclusions
Seven extended molecular complexes, stabilized mostly by dispersion interaction, were investigated with a number of modern quantum chemical methods. This set of molecules, called the L7 set, includes the octadecane dimer, the circumcoronene…adenine dimer, the circumcoronene…guanine-cytosine trimer, the coronene dimer, the guanine-cytosine dimer, the guanine trimer and a trimer of amyloid residues containing phenylalanine. These complexes are representative of dispersion-dominated supramolecular associations in biological systems, although a few systems have also significant hydrogen bonding. The methods include wavefunction-based, density functional based and semiempirical methods, spanning a wide range of accuracy and computational cost. We have included both fully nonempirical wavefunction methods, such as MP2, MP3, and QCISD, and methods which contain adjustable parameters. The parametrized methods perform in general better, justifying their use for larger molecular clusters. The performance of the methods was evaluated by comparing them to high-level QCISD(T) (and CCSD(T)) results. These benchmark results, along with the geometries of the L7 complexes, are available online in the BEGDB database (www.begdb.com).
The results of this large-molecule test set differ from earlier results for smaller complexes, most likely because the large molecule test set emphasizes longer-range interactions. The best method in this study in absolute performance is MP2.5, delivering binding energies with an average error of 4% relative to QCISD(T). The performance of the MP2.X method, parametrized towards noncovalent interactions, is surprisingly slightly worse. MP2C provides fairly accurate results, with an average relative error of 8%. It has a clear computational advantage over the MP2.5 by being an order of magnitude faster. The SCS-MP2 and SCS-(MI)-MP2 methods are rather disappointing, although they perform better for this test set than for the S66 data set of medium-sized noncovalent complexes. SCS-MP2 does not resolve fully the overbinding of MP2 for π stacking, while it underestimates dispersion between σ systems.
Among density functional based methods, DFT-D3 is clearly superior to other approaches tested in this work. It represents the best trade-off between the accuracy and computational cost and, at an average relative error of only 11%, it outperforms some more sophisticated methods, such as SCS(MI)-MP2 or M06-2X.
The accuracy of the semiempirical quantum mechanical methods, with empirical corrections for dispersion and/or hydrogen bonding, is less satisfactory. The best are SCC-DFTB-D and PM6-D3H4, and their relative standard deviation exceeds 25%. Nevertheless, the performance of these methods is not much worse than that of dramatically more expensive ones such as M06-2X, MP2 or SCS(MI)-MP2, and thus their price/performance ratio is excellent.
Supplementary Material
Acknowledgments
This work was a part of RVO No. 61388963 of the Institute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic, and was supported by Czech Science Foundation, Project No. P208/12/G016 and the operational program Research and Development for Innovations of European Social Fund (CZ1.05/2.1.00/03/0058). This work was also supported by the Slovak Research and Development Agency, Contract No. APVV-0059-10. Support by the U. S. National Science Foundation (CHE-0911541 and CHE-1213870), by the National Institute of General Medical Sciences of the National Institutes of Health under a COBRE phase III pilot project (P30 GM103450-03), the Arkansas Biosciences Institute, and by the Mildred B. Cooper Chair at the University of Arkansas are gratefully acknowledged. We thank Prof. Jon Baker for implementing DFT-D3 in PQS.
Footnotes
Detailed DFT-D3 results for presented complexes together with their full geometry information are provided. This material is available free of charge via Internet at http://pubs.acs.org/.
Contributor Information
Robert Sedlak, Email: robert.sedlak@uochb.cas.cz.
Tomasz Janowski, Email: janowski@uark.edu.
Pavel Hobza, Email: pavel.hobza@uochb.cas.cz.
References
- 1.Riley KE, Hobza P. Acc Chem Res. 2013;46:927–936. doi: 10.1021/ar300083h. [DOI] [PubMed] [Google Scholar]
- 2.Hohenstein EG, Sherrill CD. Wiley Interdiscip Rev: Comput Mol Sci. 2012;2:304–326. [Google Scholar]
- 3.Vondrášek J, Kubař T, Jenney FE, Adams MWW, Kožíšek M, Černý J, Sklenář V, Hobza P. Chem-Eur J. 2007;13:9022–9027. doi: 10.1002/chem.200700428. [DOI] [PubMed] [Google Scholar]
- 4.Šponer J, Leszczynski J, Hobza P. Biopolymers. 2001;61:3–36. doi: 10.1002/1097-0282(2001)61:1<3::AID-BIP10048>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 5.Šponer J, Leszczynski J, Hobza P. J Mol Struct (THEOCHEM) 2001;573:43–53. [Google Scholar]
- 6.Kristyán S, Pulay P. Chem Phys Lett. 1994;229:175–180. [Google Scholar]
- 7.Perez-Jorda JM, Becke AD. Chem Phys Lett. 1995;233:134–137. [Google Scholar]
- 8.Hobza P, Šponer J, Reschel T. J Comput Chem. 1995;16:1315–1325. [Google Scholar]
- 9.Janowski T, Pulay P. Chem Phys Lett. 2007;447:27–32. [Google Scholar]
- 10.Sinnocrot MO, Valeev EF, Sherrill CD. J Am Chem Soc. 2002;124:10887–10893. doi: 10.1021/ja025896h. [DOI] [PubMed] [Google Scholar]
- 11.Riley KE, Pitoňák M, Jurečka P, Hobza P. Chem Rev. 2010;110:5023–5063. doi: 10.1021/cr1000173. [DOI] [PubMed] [Google Scholar]
- 12.Grimme S. J Chem Phys. 2003;118:9095–9102. [Google Scholar]
- 13.Marchelli O, Werner HJ. J Phys Chem A. 2009;113:11580–11585. doi: 10.1021/jp9059467. [DOI] [PubMed] [Google Scholar]
- 14.Distasio AR, Jr, Head-Gordon M. Mol Phys. 2007;105:1073–1083. [Google Scholar]
- 15.Takatani T, Hohenstein EG, Sherrill CD. J Chem Phys. 2008;128:124111/1–7. doi: 10.1063/1.2883974. [DOI] [PubMed] [Google Scholar]
- 16.Zhao Y, Truhlar DG. Acc Chem Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
- 17.Hesselmann A. J Chem Phys. 2008;128:144112. doi: 10.1063/1.2905808. [DOI] [PubMed] [Google Scholar]
- 18.Chermak E, Mussard B, Angyan JjG, Reinhardt P. Chem Phys Lett. 2012;550:162–169. [Google Scholar]
- 19.Grimme S, Antony J, Ehrlich S, Krieg H. J Chem Phys. 2010;132:154104/1–17. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 20.Schütz M, Werner HJ. Chem Phys Lett. 2000;318:370–378. [Google Scholar]
- 21.Jeziorski B, Moszynski R, Szalewicz K. Chem Rev. 1994;94:1887–1930. [Google Scholar]
- 22.Misquitta AJ, Szalewicz K. Chem Phys Lett. 2002;357:301–306. [Google Scholar]
- 23.Hesselmann A, Jansen G. Chem Phys Lett. 2002;357:464–470. [Google Scholar]
- 24.von Lilienfeld OA, Tavernelli I, Rothlisberger U, Sebastiani D. Phys Rev Lett. 2004;93:153004/1–4. doi: 10.1103/PhysRevLett.93.153004. [DOI] [PubMed] [Google Scholar]
- 25.DiLabio GA. Chem Phys Lett. 2008;455:348–353. [Google Scholar]
- 26.Dion M, Rydberg H, Schröder E, Langreth DC, Lundqvist BI. Phys Rev Lett. 2004;92:246401/1–4. doi: 10.1103/PhysRevLett.92.246401. [DOI] [PubMed] [Google Scholar]
- 27.Dion M, Rydberg H, Schröder E, Langreth DC, Lundqvist BI. Phys Rev Lett. 2005;95:109902/1. doi: 10.1103/PhysRevLett.92.246401. [DOI] [PubMed] [Google Scholar]
- 28.Becke AD, Johnson ER. J Chem Phys. 2007;127:154108/1–6. doi: 10.1063/1.2795701. [DOI] [PubMed] [Google Scholar]
- 29.Pitoňák M, Neogrády P, Černý J, Grimme S, Hobza P. Phys Chem Chem Phys. 2009;10:282–289. doi: 10.1002/cphc.200800718. [DOI] [PubMed] [Google Scholar]
- 30.Riley EK, Řezáč J, Hobza P. Phys Chem Chem Phys. 2011;13:21121–21125. doi: 10.1039/c1cp22525a. [DOI] [PubMed] [Google Scholar]
- 31.Grimme S. J Comput Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- 32.Jurečka P, Černý J, Hobza P, Salahub DR. J Comput Chem. 2007;28:555–569. doi: 10.1002/jcc.20570. [DOI] [PubMed] [Google Scholar]
- 33.Zhao Y, Truhlar DG. Theor Chem Acc. 2008;120:215–241. [Google Scholar]
- 34.Dewar JSM, Thiel W. J Am Chem Soc. 1977;99:4899–4907. [Google Scholar]
- 35.Martin B, Clark T. Int J Quantum Chem. 2006;106:1208–1216. [Google Scholar]
- 36.Stewart JJP. J Mol Model. 2007;13:1173–1213. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Řezáč J, Fanfrlik J, Salahub D, Hobza P. J Chem Theory Comput. 2009;5:1749–1760. doi: 10.1021/ct9000922. [DOI] [PubMed] [Google Scholar]
- 38.Řezáč J, Hobza P. J Chem Theory Comput. 2012;8:141–151. doi: 10.1021/ct200751e. [DOI] [PubMed] [Google Scholar]
- 39.Jurečka P, Šponer J, Černý J, Hobza P. Phys Chem Chem Phys. 2006;8:1985–1993. doi: 10.1039/b600027d. [DOI] [PubMed] [Google Scholar]
- 40.Gráfová L, Pitoňák M, Řezáč J, Hobza P. J Chem Theory Comput. 2010;6:2365–2376. doi: 10.1021/ct1002253. [DOI] [PubMed] [Google Scholar]
- 41.Molnar L, He X, Wang B, Merz K. J Chem Phys. 2009;131:065102/1–16. doi: 10.1063/1.3173809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Řezáč J, Riley KE, Hobza P. J Chem Theory Comput. 2011;7:2427–2438. 3466–3470. doi: 10.1021/ct2002946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Goerigk L, Grimme S. J Chem Theory Comput. 2010;6:107–126. doi: 10.1021/ct900489g. [DOI] [PubMed] [Google Scholar]
- 44.Goerigk L, Grimme S. J Chem Theory Comput. 2011;7:291–309. doi: 10.1021/ct100466k. [DOI] [PubMed] [Google Scholar]
- 45.Zhao Y, Truhlar DG. J Chem Theory Comput. 2005;1:415–432. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]
- 46.Zhao Y, Truhlar DG. J Phys Chem A. 2005;109:5656–5667. doi: 10.1021/jp050536c. [DOI] [PubMed] [Google Scholar]
- 47.Zhao Y, Truhlar DG. J Chem Theory Comput. 2007;3:289–300. doi: 10.1021/ct6002719. [DOI] [PubMed] [Google Scholar]
- 48.Berka K, Laskowski R, Hobza P, Vondrášek J. J Chem Theory Comput. 2010;6:2191–2203. doi: 10.1021/ct100007y. [DOI] [PubMed] [Google Scholar]
- 49.Risthaus T, Grimme S. J Chem Theory Comput. 2013;9:1580–1591. doi: 10.1021/ct301081n. [DOI] [PubMed] [Google Scholar]
- 50.Granatier J, Pitoňák M, Hobza P. J Chem Theory Comput. 2012;7:2282–2292. doi: 10.1021/ct300215p. [DOI] [PubMed] [Google Scholar]
- 51.Janowski T, Pulay P. J Amer Chem Soc. 2012;134:17520–17525. doi: 10.1021/ja303676q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pitoňák M, Neogrády P, Hobza P. Phys Chem Chem Phys. 2010;12:1369–1378. doi: 10.1039/b919354e. [DOI] [PubMed] [Google Scholar]
- 53.Janowski T, Ford AR, Pulay P. Mol Phys. 2010;108:249–257. [Google Scholar]
- 54.Hays FA, Teegarden A, Jones ZJ, Harms M, Raup D, Watson J, Cavaliere E, Ho PS. Proc Natl Acad Sci USA. 2005;102:7157–7162. doi: 10.1073/pnas.0409455102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Case AD, Darden AT, Cheatham ET, III, Simmerling LC, Wang J, Duke ER, Luo R, Merz MK, Pearlman AD, Crowley M, Walker CR, Zhang W, Wang B, Hayik S, Roitberg A, Seabra G, Wong FK, Paesani F, Wu X, Brozell S, Tsui V, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Beroza P, Mathews HD, Schafmeister C, Ross SW, Kollman AP. AMBER 9. University of California; San Francisco: 2006. [Google Scholar]
- 56.Řezáč J, Jurečka P, Riley KE, Černý J, Valdes H, Pluháčková K, Berka K, Řezáč T, Pitoňák M, Vondrášek J, Hobza P. Collect Czech Chem Commun. 2008;73:1261–1270. [Google Scholar]
- 57.Boys SF, Bernardi F. Mol Phys. 1970;19:553–566. [Google Scholar]
- 58.Baker J, Wolinski K, Janowski T, Saebo S, Pulay P. PQS version 4.0. Parallel Quantum Solutions; Fayetteville, Arkansas, USA: 2012. www.pqs-chem.com. [Google Scholar]
- 59.Janowski T, Pulay P. Chem Phys Lett. 2007;447:27–32. [Google Scholar]
- 60.Jurečka P, Hobza P. Chem Phys Lett. 2002;365:89–94. [Google Scholar]
- 61.van Lenthe JH, vanDuijneveldt-van de Rijdt JGCM, van Duijneveldt FB. Adv Chem Phys. 1987;69:521–544. [Google Scholar]
- 62.Hobza P, Šponer J Chem Rev. 1999;99:3247–3276. doi: 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]
- 63.Svozil D, Hobza P, Šponer J. J Phys Chem B. 2010;114:1191–1203. doi: 10.1021/jp910788e. [DOI] [PubMed] [Google Scholar]
- 64.Riley EK, Řezáč J, Hobza P. Phys Chem Chem Phys. 2011;13:21121–21125. doi: 10.1039/c1cp22525a. [DOI] [PubMed] [Google Scholar]
- 65.Halkier A, Helgaker T, Jorgensen P, Klopper W, Koch HJ, Wilson KA. Chem Phys Lett. 1998;286:243–252. [Google Scholar]
- 66.Halkier A, Helgaker T, Jorgensen P, Klopper W, Olsen J. Chem Phys Lett. 1999;302:437–446. [Google Scholar]
- 67.Kendall RA, Dunning TH, Jr, Harrison RJ. J Chem Phys. 1992;96:6796–806. [Google Scholar]
- 68.Woon DE, Dunning TH., Jr J Chem Phys. 1993;98:1358–1371. [Google Scholar]
- 69.Dunning TH., Jr J Chem Phys. 1989;90:1007–1023. [Google Scholar]
- 70.Schwenke DW. J Chem Phys. 2007;122:014107/1–7. [Google Scholar]
- 71.Pitoňák M, Hesselmann A. J Chem Theory Comput. 2010;6:168–178. doi: 10.1021/ct9005882. [DOI] [PubMed] [Google Scholar]
- 72.Pitoňák M, Neogrády P, Černý J, Grimme S, Hobza P. Chem Phys Chem. 2009;10:282–289. doi: 10.1002/cphc.200800718. [DOI] [PubMed] [Google Scholar]
- 73.Grimme S, Ehrlich S, Goerigk L. J Comput Chem. 2011;32:1456–1465. doi: 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- 74.Johnson ER, Becke AD. J Chem Phys. 2005;123:024101/1–7. doi: 10.1063/1.2065267. [DOI] [PubMed] [Google Scholar]
- 75.Becke AD, Johnson ER. J Chem Phys. 2005;123:154101/1–9. doi: 10.1063/1.2065267. [DOI] [PubMed] [Google Scholar]
- 76.Johnson ER, Becke AD. J Chem Phys. 2006;124:174104/1–9. doi: 10.1063/1.2190220. [DOI] [PubMed] [Google Scholar]
- 77.Goerigk L, Kruse H, Grimme S. Chem Phys Chem. 2011;12:3421–3433. doi: 10.1002/cphc.201100826. [DOI] [PubMed] [Google Scholar]
- 78.Korth M, Pitoňák M, Řezáč J, Hobza P. J Chem Theory Comput. 2010;6:168–178. doi: 10.1021/ct900541n. [DOI] [PubMed] [Google Scholar]
- 79.Elstner M, Porezag D, Jungnickel G, Elsner J, Haugk M, Frauenheim T, Suhai S, Seifert G. Phys Rev B. 1998;58:7260–7268. [Google Scholar]
- 80.Elstner M, Hobza P, Frauenheim T, Suhai S, Kaxiras E. J Chem Phys. 2001;114:5149–5155. [Google Scholar]
- 81.Ahlrichs R, Bär M, Häser M, Horn H, Kölmel C. Chem Phys Lett. 1989;162:165–169. [Google Scholar]
- 82.Werner H-J, Knowles PJ, Lindh R, Manby FR, Schütz M, Celani P, Korona T, Mitrushenkov A, Rauhut G, Adler TB, Amos RD, Bernhardsson A, Berning A, Cooper DL, Deegan MJO, Dobbyn AJ, Eckert F, Goll E, Hampel C, Hetzer G, Hrenar T, Knizia G, Köppl C, Liu Y, Lloyd AW, Mata RA, May AJ, McNicholas SJ, Meyer W, Mura ME, Nicklass A, Palmieri P, Pflüger K, Pitzer R, Reiher M, Schumann U, Stoll H, Stone AJ, Tarroni R, Thorsteinsson T, Wang M, Wolf A. MOLPRO, version 2009.1, a package of ab initio programs. see http://www.molpro.net.
- 83.(a) Karlstrom G, Lindh R, Malmqvist PA, Roos BO, Ryde U, Veryazov V, Widmark PO, Cossi M, Schimmelpfennig B, Neogrady P, Seijo L. Comput Mater Sci. 2003;28:222–239. [Google Scholar]; (b) Malmqvist PA, Rendell A, Roos BO. J Phys Chem. 1990;94:5477–5482. [Google Scholar]; (c) Roos BO, Taylor PR. Chem Phys. 1980;48:157–173. [Google Scholar]
- 84.Beebe NHF, Linderberg J. Int J Quantum Chem. 1977;12:683–705. [Google Scholar]
- 85.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam NJ, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09, Revision A.1. Gaussian, Inc; Wallingford CT: 2009. [Google Scholar]
- 86.Stewart JJP. MOPAC2009. Stewart Computational Chemistry. Colorado Springs, CO, USA: 2008. HTTP://OpenMOPAC.net. [Google Scholar]
- 87.Antony J, Grimme S. J Phys Chem, A. 2007;111:4862–4868. doi: 10.1021/jp070589p. [DOI] [PubMed] [Google Scholar]
- 88.Goerigk L, Grimme S. Phys Chem Chem Phys. 2011;13:6670–6688. doi: 10.1039/c0cp02984j. [DOI] [PubMed] [Google Scholar]
- 89.Antony J, Brüske B, Grimme S. Phys Chem Chem Phys. 2009;11:8440–8447. doi: 10.1039/b907260h. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.