Abstract
Proton conduction is essential in biological systems. Oxidative phosphorylation in mitochondria, proton pumping in bacteriorhodopsin, and uncoupling membrane potentials by the antibiotic Gramicidin are examples. In these systems, H+ hop along chains of hydrogen bonds between water molecules and hydrophilic residues – proton wires. These wires also support the transport of OH− as proton holes. Discriminating between H+ and OH− transport has been elusive. Here, H+ and OH− transport is achieved in polysaccharide- based proton wires and devices. A H+- OH− junction with rectifying behaviour and H+-type and OH−-type complementary field effect transistors are demonstrated. We describe these devices with a model that relates H+ and OH− to electron and hole transport in semiconductors. In turn, the model developed for these devices may provide additional insights into proton conduction in biological systems.
Proton (H+) conduction plays a key role in nature1. Examples are oxidative phosphorylation of ATP for biological energy conversion in mitochondria2,3, the light activated proton pumping of bacteriorhodopsin in Archaea4, proton activated bioluminescence in dinoflagellates5, proton activated flagella in bacteria6, the HVCN1 voltage gated proton channel in mammals7, and the antibiotic Gramicidin8. In all of these systems, protons hop along proton wires9,10 formed by networks of hydrogen bonds between water molecules and hydrophilic residues − Grotthuss mechanism11. These proton wires also support the transport of a proton vacancy, or proton hole, as OH−12. Discriminating between H+ and OH− transport with electrophysiological measurements is difficult because H+ and OH− have the same Nernst potential13.
Progress in bioelectronics now includes devices that mimic biological functionality and interface with biological systems14,15,16. Memristors simulate synapses for neuromorphic computing17. Silicon nanowires record and stimulate single cell potential18. Gramicidin and bacteriorhodopsin are integrated with carbon nanotubes19, silicon nanowires20, and organic field effect transistors21 to develop biosensors with increased functionality. Ionic22 and mixed conductivity in biological23 and organic polymers24 are used to record and stimulate physiological functions, and assembled into logic circuits25. Recently, edible batteries to power these devices have been developed26. Following this exciting route, we have previously demonstrated proton conducting field effect transistors (H+-FETs) with polysaccharides that effectively mimic proton wires in ion channels27. Here, we report proton-conducting devices with polysaccharide supported proton wires that are designed to preferentially conduct either H+ or OH−, as proton holes. We describe the conductivity in these devices with a model for proton semiconductivity proposed in 1958 by Eigen and de Maeyer28. We demonstrate an H+ OH− rectifying junction and H+-type and OH−-type complementary FETs. With gate control of the current, these FETs unequivocally discriminate between H+ and OH− conductivity and indeed confirm that proton wires support conduction of OH− as a proton hole.
Results
Device architecture and materials
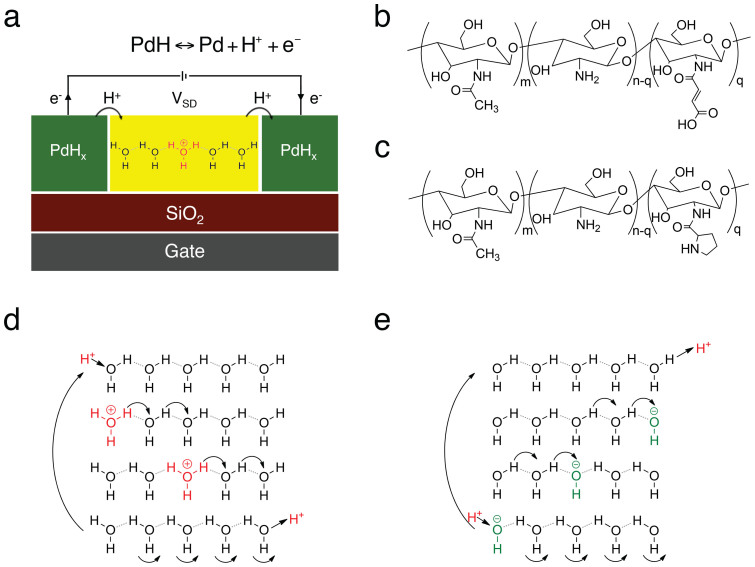
In protonic devices (Fig. 1a), palladium hydride (PdHx) contacts (source and drain) inject and drain protons into and from the proton-conducting channel, effectively serving as protodes27,29,30. For each proton injected into the material, an excess electron is collected by the leads, which complete the circuit. The contacts and the proton-conducting channel are insulated from the back gate with a SiO2 (100 nm) dielectric layer. The proton-conducting channel is either maleic-chitosan (poly (β- (1,4)-N-Maleoyl-D-glucosamine)) (Fig. 1b) or proline-chitosan (poly (β- (1,4)-N-Proline-D-glucosamine)) (Fig. 1c). These biopolymers are both derived from chitin and are of particular interest for developing future devices for bioelectronic applications. Chitin and most of its derivatives are biodegradable, nontoxic, and physiologically inert and are used in bionanotechnologies31,32,33. Maleic-chitosan and proline-chitosan include several hydrophilic groups that participate in hydrogen bonding with water condensed from a humid atmosphere (20% w/w MC and 15% w/w PC at 75% RH) (SI). The resulting chains of hydrogen bonds form proton wires3,9,34 along which protons hop according to the Grotthuss mechanism (Fig. 1d). A proton wire supports H+ conduction via the exchange of a covalent bond on a hydronium ion with the hydrogen bond of a neighbouring water molecule (Fig. 1d). Successive events occurring in the same direction result in the effective transfer of a H+ and the associated positive charge along the chain. The same mechanism also supports the transport of OH− as a proton hole (Fig. 1e). The exact dynamics and the kinetics of H+ and OH− are more complex12 than the simplified description used here. However, this description provides enough insights to further elaborate on the conductivity of proton wires.
Figure 1. Protonic device architecture and proton conductivity mechanism.
(a) Two and three terminal devices with PdHx source and drain. PdHx is created by exposing Pd metal to 5% H2 atmosphere. At this H2 concentration, the Pd metal absorbs H2 to form PdHx with x ≈ 0.5. PdHx is kept under 5% H2 atmosphere throughout the measurements and acts as a H+ reservoir. The PdHx source and drain inject and sink protons into and from the proton wire according to the reversible reaction 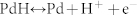 going from left to right at the source and from right to left at the drain. The PdHx source and drain are connected to outside measurement electronics that measure the electronic current and complete the circuit. (b) Molecular structure of the H+-type proton conductor maleic chitosan, (c) Molecular structure of the OH− -type proton conductor proline chitosan. Degree of substitution defined as q/n + m determines the doping level. (d) Hop and turn Grotthuss mechanism for conductivity of H+ as hydronium ion along a proton wire. (e) Equivalent mechanism for OH− conductivity as proton hole along proton wire.
going from left to right at the source and from right to left at the drain. The PdHx source and drain are connected to outside measurement electronics that measure the electronic current and complete the circuit. (b) Molecular structure of the H+-type proton conductor maleic chitosan, (c) Molecular structure of the OH− -type proton conductor proline chitosan. Degree of substitution defined as q/n + m determines the doping level. (d) Hop and turn Grotthuss mechanism for conductivity of H+ as hydronium ion along a proton wire. (e) Equivalent mechanism for OH− conductivity as proton hole along proton wire.
A model for proton (H+) and proton hole (OH−) conductivity
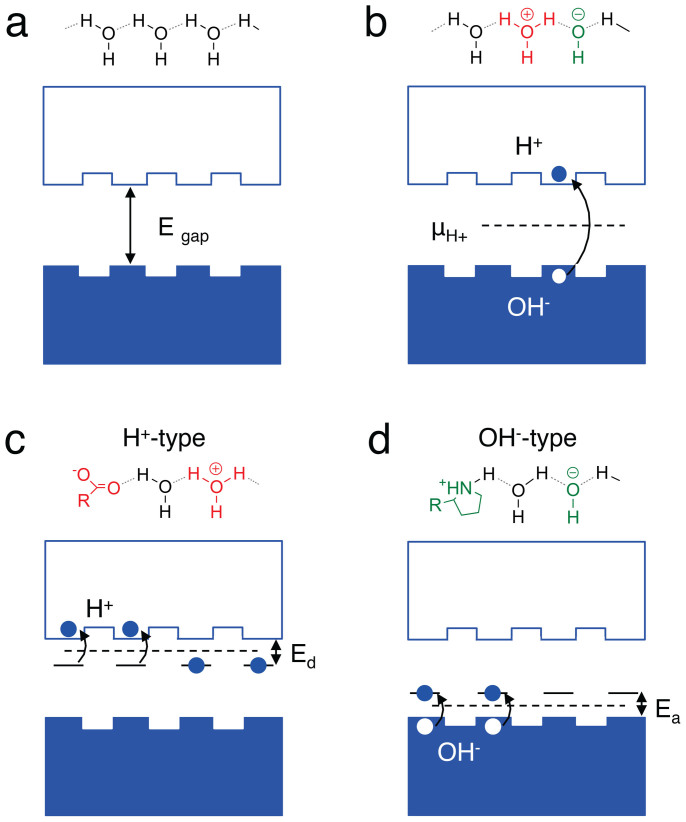
In 1958, Eigen and de Maeyer proposed a phenomenological description of proton conductivity in ice analogous to electron conductivity in a semiconductor28. Ice is a water hydrogen bonded system that is made of proton wires similarly to protein membranes and the hydrated biopolymers used in this work3,9,28,34. A proton wire without any H+ or OH− charged defects does not conduct unless an excess charge is injected from the contacts (Fig. 2a). The charge carriers (protons) are distributed between a “valence band” (H-bonded H2O) and a “conduction band” (excess protons fluctuating in hydrogen bonds). Protons are not delocalized along the proton conduction band, but are separated by potential barriers (Fig. 2a). These barriers represent potential barrier for the proton to transfer from one molecule to the next. The height depends on the precise molecular structure, and is typically of the order of 100 meV. We define the protonic “band gap” as the energy required to create a H+ (proton) and OH− (proton hole) pair in the proton wire (Fig. 2b). We derive this energy from the Gibbs Helmholtz equation and the dissociation constant of water (Kw) as
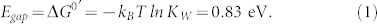 |
This value for the protonic “band gap” is similar to the activation energy measured for proton conducting biopolymers35,36, and remarkably close to the band gap of traditional electronic semiconductors such as Si (1.1 eV) or Ge (0.76 eV). Not unlike Si and Ge, the conductivity of most intrinsic biological protonic conductors at room temperature is low37.
Figure 2. Energy diagram representation of conduction in hydrogen bonded proton wire.
(a) A wire with no H+ or OH− defect does not conduct. The band gap is defined as the energy required to create a H+ OH− pair (proton-proton hole) and is derived from the Egap = ΔG0′ = −kBT ln Kw = 0.83 eV (Gibbs-Helmholtz equation). (b) For an intrinsic proton wire, the protochemical potential uH+ is in the middle of the band-gap. The H+ is not completely delocalized along the conduction quasi band. Hopping barriers of approximately 100 meV (need to be overcome for conduction to occur. (c) An acid donates a H+ into the conduction band of a proton wire to yield a H+-type protonic conductor. Ed = ΔG0a = −kBT ln Ka, Ka is the acid dissociation constant. The maleic acid group pKa (-log Ka) = 3.2, which corresponds to Ed = 0.18 eV. (d) A base accepts a H+ to create a OH− (proton hole) in the valence band of a proton wire to yield a OH−-type protonic conductor. Ea = ΔG0b = −kBT ln Kb, Kb is the base dissociation constant. The proline base pkb (-log Kb = 3.4), which corresponds to Ea = 0.20 eV. For both H+ type and OH− type the protochemical potential is μCH+ = eV0 + µ0+ kBT ln aH+ where aH+ is the activity of H+.
To increase the conductivity of the proton wire, doping is used to introduce H+ and OH− (proton hole) charge carriers. An acidic functionality in the hydrogen bond network (Fig. 2c) donates an H+ to the proton wire “conduction band” in the same way a group V (P, As) impurity donates an electron in the Si conduction band. We derive the position of the H+ donor state respect to the “conduction band” by substituting Kw with Ka (acid dissociation constant) in eq. 1. For maleic-chitosan (pKa 3.2), Ed = 0.18 eV. A basic functionality in the hydrogen bond network (Fig. 2d) accepts a H+ to create an OH− proton hole in the proton “valence band” in the same way a group III (B) impurity creates a hole in the Si valence band. For proline-chitosan we use pKb = 3.4 in (Eq. 1) to calculate Ea = 0.2 eV. The position of the protochemical potential is calculated from the activity of H+, or the pH, and Nernst equation as μCH+ = eV0 + μ0 + kBT ln aH+</emph> (aH+ = activity of H+)10. Qualitatively, μH+ in a protonic semiconductor is affected by doping the same way the Fermi energy in an electronic semiconductor is affected. For an intrinsic material, μH+ is at mid gap. For H+-type material, μH+ is closer to the conduction band and for an OH−-type material μH+ is closer to the valence band. The intrinsic version of maleic chitosan and proline chitosan is unmodified chitin. Chitin does not have functional groups that contribute H+ or OH− dopants to the proton wires. As expected, the protonic conductivity of chitin measured with PdHx contacts is significantly smaller than the protonic conductivity of maleic chitosan or proline chitosan (Fig. S3).
An H+-type and OH−-type junction
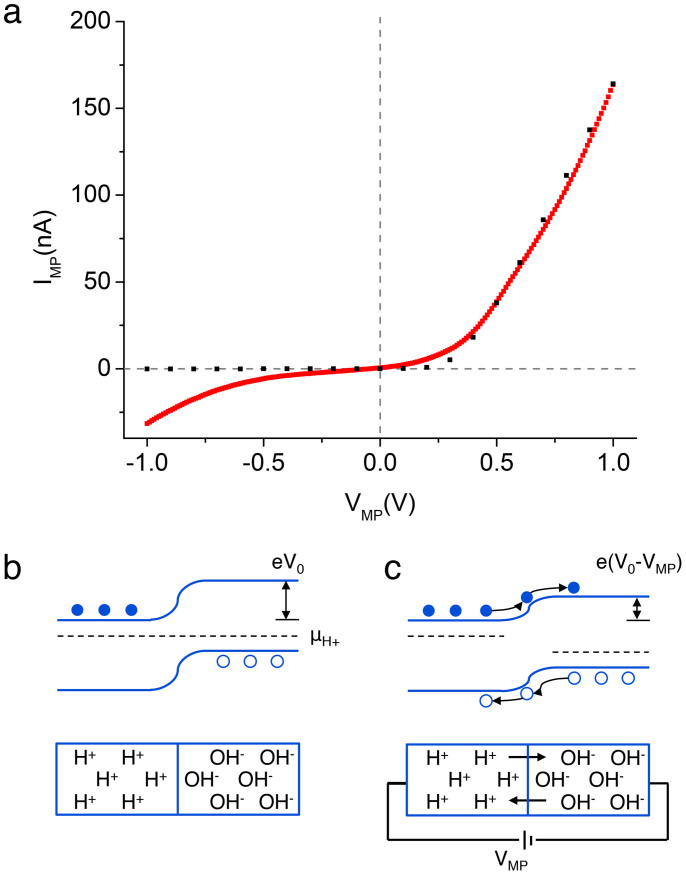
As part of their model that compares H+-type and OH−-type protonic semiconductors with electronic semiconductors, Eigen and de Mayer proposed a H+ - OH− junction in ice with acid and base dopants28. Similarly, here we measure the properties of maleic-chitosan (H+-type) and proline-chitosan (OH−-type) junction devices with proton conducting contacts under 75% RH (Fig. 3). When a potential difference between the contacts is applied (VMP), the measured current (IMP) shows asymmetric characteristics as expected (Fig. 3a). The dependence of IMP on VMP in the H+ - OH− junction is easily described with the semiconductor model (Fig. 3b and 3c). At first contact, the gradient in μH+ drives the diffusion of H+ into the proline-chitosan and OH− into the maleic-chitosan until equilibrium is reached. The charge carriers recombine at the junction as H2O and create a depletion region with an associated contact potential (V0) (Fig. 3b). This H2O generated at the interface does not affect the hydration of the polymers at the interface because the overall concentration of the recombined H+ and OH− is negligible compared to the water already existing in the biopolymers. A positive potential on the H+-type side (forward bias) reduces V0 and results in a net thermally activated current of H+ and OH− across the forward biased junction (Fig. 3c). At the same time, a negative potential on the H+-type side increases the potential barrier and results in very little or no current going across the reverse biased junction. This model is used to simulate the junction characteristics (Fig. 3a). We treat the maleic-chitosan and the proline-chitosan as n-type and p-type electronic semiconductors (switching the sign of the charge carriers) with a band gap of 0.8 eV. The number of H+ donated by the maleic-groups (Fig. 1b) in the proton “conduction band” is derived from the H+-FETs (Fig. 4). In turn, the number of OH− proton holes created by the proline-base in the proton “valence band” (Fig. 1c) is derived from the OH− FETs (Fig. 4). The contribution to the charge carrier doping of the unreacted –NH2 in chitosan (Fig. 1b and c) can be neglected. The dissociation of these amines (pkb = 7.5) is low compared to the dissociation of the proline and the maleic groups. The mobility data for the charge carriers is derived from the H+-FET and OH−-FET devices (Fig. 4). In the forward bias region, the overall shape of the curve matches the shape of the experimental data well for a minority carrier recombination time of 1 μs. This recombination time is remarkably close to the recombination time of H+/OH− in neutral water (35 μs)28 and appropriately smaller because of higher H+/OH− concentration in the devices. Despite the applied voltages being below electrolysis levels, the increased back bias current may be due to field-induced water splitting at the contacts as previously observed in bipolar ion-exchange membranes38. To appropriately simulate the experimental conditions, we scale the current in a 1 × 1 μm2 junction by several fold, but not by the exact amount required to recreate exactly a junction with 1 × 1 cm2 contacts. The H+-type OH−-type junction is assembled from pre-formed components and results in a device with overall poor physical contact. This poor physical contact effectively reduces the area of the junction and the area of the contacts. Despite these shortcomings, the junction devices show the expected rectifying behaviour, which is qualitatively matched by the simulations.
Figure 3. H+- OH− junction.
(a) Red trace- Experimental data for IV characteristics of a H+ OH− junction formed by maleic chitosan and proline chitosan. The curve shows the expected nonlinearity. Black dots - data from simulations for the same junction using the semiconductor model. (b) When a H+ doped and OH− doped material are placed into contact OH− diffuse into the H+ region and H+ diffuse into the OH− region until the μH+ on both sides is the same. H+ and OH− recombine in the depletion region. A contact potential V0 occurs across the junction and is dependent of the difference in μH+ of both sides. (c) A forward bias (+ive on H+ side) applied between source and drain reduces the contact barrier e(V0-VMP) and thermionic emission of H+ into OH− side and vice versa occurs.
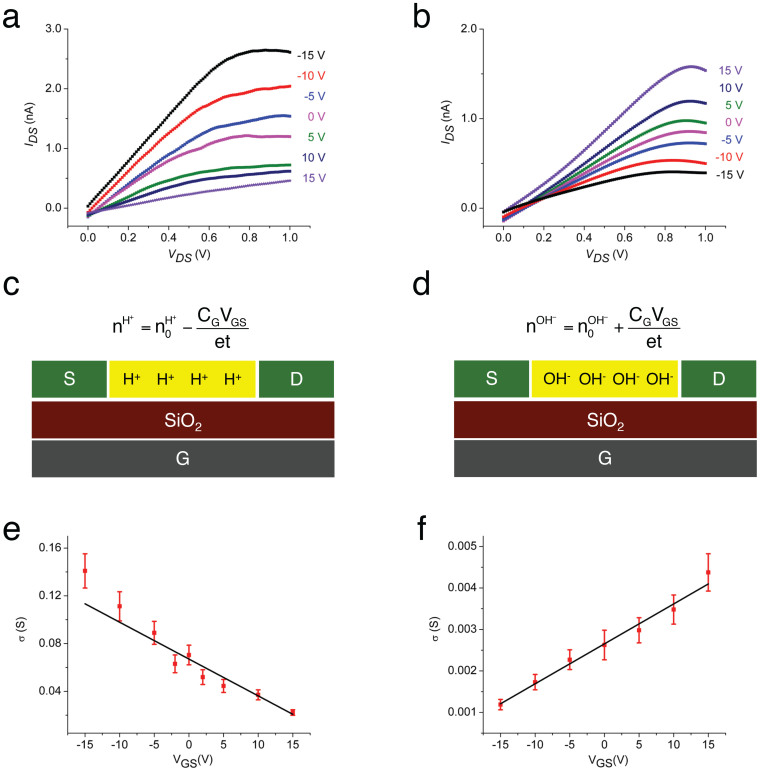
Figure 4. H+ and OH- transistors.
(a) (b) Plots of IDS as a function of VGS for different VDS (RH 75%) for a maleic chitosan H+-FET and a proline chitosan OH−-FET with PdHx contacts. Device dimensions: length 8.6 μm, width 3.5 μm, height 82 nm for (a) and 9.6 μm, width 28 μm, height 200 nm for (b). The small deviation of IDS from zero at VDS = 0 is likely due to hysteresis as previously observed for these types of devices27, (c) (d) Schematics of H+ and OH− transistor capacitative charge carrier nH+ and nOH− modulation. (c) 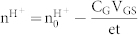 (CG = gate capacitance per unit area, t = device thickness) (d) and
(CG = gate capacitance per unit area, t = device thickness) (d) and 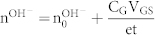 . From simulations of dQ/dVgs, Cg = 3.85 × 10−4 F m−2. (e) (f) Plots of
. From simulations of dQ/dVgs, Cg = 3.85 × 10−4 F m−2. (e) (f) Plots of  as function of VGS and linear fit for the device in (a) and (b) respectively. For cross σ and charge density calculations the cross sectional area of the devices was derived from AFM and the cross sections were approximated to a rectangle with t = 66 nm for (a) and t = 160 nm (b) with the same widths as the actual devices. From the fit,
as function of VGS and linear fit for the device in (a) and (b) respectively. For cross σ and charge density calculations the cross sectional area of the devices was derived from AFM and the cross sections were approximated to a rectangle with t = 66 nm for (a) and t = 160 nm (b) with the same widths as the actual devices. From the fit, 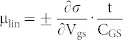 and
and 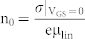 .
.
Complementary bioprotonic field effect transistors
We analyse the output characteristics of complementary protonic-FET devices. In a protonic-FET type device (Fig. 1a), the source-drain protonic current, IDS, recorded as a function of drain-source bias, VDS, is controlled by changing the potential of the back gate electrode, VGS. As previously reported27, for the maleic-chitosan H+-FET (Fig. 4a), a negative VGS results in a higher source-drain current for the same VDS, while a positive VGS almost turns IDS off. This VGS dependence of IDS is consistent with an FET with positive charge carriers (H+). This type of electric field modulation of H+ has also been demonstrated in Nafion based field-effect devices39. In turn, the proline-chitosan OH−-FET shows the opposite VGS dependence. A negative VGS almost turns the device off and a positive VGS results in higher IDS (Fig. 4b). This VGS dependence of IDS is consistent with an FET with negative charge carriers (OH−). Both kinds of devices show current saturation for higher VDS and corresponding IDS. This saturation may be due to charge accumulation at the contacts and the formation of a barrier for higher IDS as previously discussed27. Further investigation of the contact barrier for the devices is required to confirm this hypothesis.
We explain the IDS modulation from VGS in these devices with the gradual channel approximation
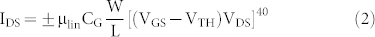 |
(+ for a negative charge carrier and – for a positive charge carrier, μlin = mobility in the linear regime, CG = gate capacitance per unit area, W = device width, L = device length, VTH = threshold gate voltage at which conduction occurs). A few modifications are required to eq. 2 to take into account that in our accumulation mode devices we cannot reach the VTH at which the channel is completely depleted of charge carriers. We first rewrite eq. 2 as
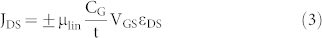 |
(JDS = source drain current density, CGVGS/t = charge carrier per unit volume induced by the gate, εDS = VDS/L = electric field along the device channel) and compare it to
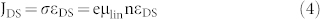 |
(σ = channel conductivity, n = charge carriers per unit volume, e = elementary charge). We then modify n to take into account for the H+ (n0H+) or OH− (n0OH−) from acid and base doping already in the channel at VGS = 0. This modification results in
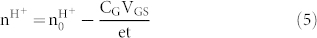 |
for H+-FET and
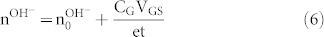 |
for OH−-FET respectively (Fig. 4c and Fig. 4d). For an intrinsic semiconductor, these modifications cannot be used by simply setting n0 = 0. VTH, in this case the voltage at which the protochemical potential of the intrinsic semiconductor is shifted enough to afford injection of charge carriers into one of the bands, should be included back in eq. 2. Using equation 5 and equation 6, equation 3 becomes
 |
for H+-FET and
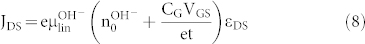 |
for OH−-FET. To calculate 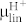 ,
, 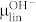 ,
, 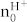 , and
, and 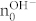 we plot
we plot 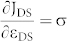 as a function of VGS (Fig. 4e and 4f).
as a function of VGS (Fig. 4e and 4f). 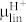 ,
,  are derived from the gradient of the linear fit and
are derived from the gradient of the linear fit and 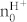 and
and 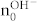 are derived from the intercept (Fig. 4e and 4f)40. From the devices,
are derived from the intercept (Fig. 4e and 4f)40. From the devices, 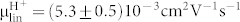 and
and 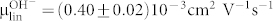 . The mobility for H+ is remarkably close to the mobility for H+ in diluted acidic solutions11 and in hydrated semiconducting polymers41, and is slightly higher than H+ mobility of Nafion (0.87 × 10−3 cm2 V−1s−1) proton exchange membranes widely used in fuel cells42,43. Matching the H+ mobility in water solutions is important for potential future biological applications where the H+ are transferred in liquid. For basic solutions, the mobility of OH− is lower than H+ and reported as 1.96 × 10−3 cm2 V−1 s−1. Our OH−-type devices show a mobility that is in reasonable agreement with this value, but is five-fold lower than expected. A few factors may contribute to the lower than expected OH− mobility. The proline chitosan in the OH− -FET contains less water (15% w/w) than the maleic-chitosan in the H+-FET (20% w/w). This lower water content results in a smaller number of pathways, or proton wires, for the OH− to conduct. Maleic chitosan forms self-assembled nanofibers while proline chitosan forms an amorphous film on the substrate (Fig. S5). The more ordered morphology of the maleic chitosan also likely contributes to the higher proton mobility in the H+-FET respect to the OH−-FET. In our analysis, we have neglected the effects of contacts. It is conceivable that the contact between the PdHx and the proton-conducting channels is affected by the difference in protochemical potentials. From the data for the PdHx reversible electrodes in acidic solutions44, one infers qualitatively that the protochemical potential of the PdHx is closer to the protochemical potential of the H+-type maleic chitosan and is significantly higher than the protochemical potential of the OH−-type proline chitosan. PdHx is thus more likely to form a better protonic contact (Ohmic) with maleic-chitosan, while a potential barrier at the PdHx- proline-chitosan contact may occur. This barrier is similar to a Schottky barrier that occurs between a metal with low work function and a p-type electronic semiconductor. This potential explanation, however, requires further investigation and will be addressed in future work. With the values of the mobility, we extrapolate n0H+ = (8.0±0.4)1017 cm−3 and n0OH− = (4.0±0.1)1017 cm−3 for the devices. Data from the devices confirms that the acid doped maleic chitosan behaves like a H+ doped protonic semiconductor and that the base doped proline chitosan behaves like an OH− doped protonic semiconductor. The semiconductor doping model can be considered a reasonable phenomenological description for proton transport in doped proton wires measured with our devices. It is difficult to quantitatively estimate the expected doping concentration in the materials from the strength and concentration of the maleic acid groups and the proline base groups in the polymers (Fig. 1). Challenges include difficulty in predicting the influence of local dielectric environment in the hydrated solid state and ionic concentration on the strength of acid and base dissociation45. Further work is needed to generalize this model to intrinsic semiconductors to take into account the turn on voltage, VTH. For this work, devices with higher gate capacitance capable of turning on the intrinsic devices at a reasonable VTH are required.
. The mobility for H+ is remarkably close to the mobility for H+ in diluted acidic solutions11 and in hydrated semiconducting polymers41, and is slightly higher than H+ mobility of Nafion (0.87 × 10−3 cm2 V−1s−1) proton exchange membranes widely used in fuel cells42,43. Matching the H+ mobility in water solutions is important for potential future biological applications where the H+ are transferred in liquid. For basic solutions, the mobility of OH− is lower than H+ and reported as 1.96 × 10−3 cm2 V−1 s−1. Our OH−-type devices show a mobility that is in reasonable agreement with this value, but is five-fold lower than expected. A few factors may contribute to the lower than expected OH− mobility. The proline chitosan in the OH− -FET contains less water (15% w/w) than the maleic-chitosan in the H+-FET (20% w/w). This lower water content results in a smaller number of pathways, or proton wires, for the OH− to conduct. Maleic chitosan forms self-assembled nanofibers while proline chitosan forms an amorphous film on the substrate (Fig. S5). The more ordered morphology of the maleic chitosan also likely contributes to the higher proton mobility in the H+-FET respect to the OH−-FET. In our analysis, we have neglected the effects of contacts. It is conceivable that the contact between the PdHx and the proton-conducting channels is affected by the difference in protochemical potentials. From the data for the PdHx reversible electrodes in acidic solutions44, one infers qualitatively that the protochemical potential of the PdHx is closer to the protochemical potential of the H+-type maleic chitosan and is significantly higher than the protochemical potential of the OH−-type proline chitosan. PdHx is thus more likely to form a better protonic contact (Ohmic) with maleic-chitosan, while a potential barrier at the PdHx- proline-chitosan contact may occur. This barrier is similar to a Schottky barrier that occurs between a metal with low work function and a p-type electronic semiconductor. This potential explanation, however, requires further investigation and will be addressed in future work. With the values of the mobility, we extrapolate n0H+ = (8.0±0.4)1017 cm−3 and n0OH− = (4.0±0.1)1017 cm−3 for the devices. Data from the devices confirms that the acid doped maleic chitosan behaves like a H+ doped protonic semiconductor and that the base doped proline chitosan behaves like an OH− doped protonic semiconductor. The semiconductor doping model can be considered a reasonable phenomenological description for proton transport in doped proton wires measured with our devices. It is difficult to quantitatively estimate the expected doping concentration in the materials from the strength and concentration of the maleic acid groups and the proline base groups in the polymers (Fig. 1). Challenges include difficulty in predicting the influence of local dielectric environment in the hydrated solid state and ionic concentration on the strength of acid and base dissociation45. Further work is needed to generalize this model to intrinsic semiconductors to take into account the turn on voltage, VTH. For this work, devices with higher gate capacitance capable of turning on the intrinsic devices at a reasonable VTH are required.
Discussion
In summary, we have demonstrated H+ -OH− rectifying junctions and H+-type and OH−-type complementary field effect transistors with polysaccharide based biomimetic proton wires. These devices confirm that proton wires support the conductivity of OH− as proton holes. We describe the conductivity in these devices with a model in which H+ (protons) and OH− (proton holes) are equivalent to electrons and holes in semiconductors. This model was originally proposed by Eigen and de Maeyer and refined by us to include band gap calculations and effects of doping on the protochemical potential. The mobility for H+ and OH− in our devices 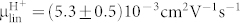 and
and 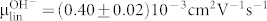 , are in good and reasonable agreement with what has been previously reported for the same species in other hydrogen-bonded systems. The on-off ratio of these devices is low (~3–4). Avenues for improvement include using thinner gate dielectrics and high k gate dielectrics. The field effect manipulation of H+ and OH− currents may be used, in the future, to interface with proton conducting ion channels14. However, for these applications devices that function in physiological conditions need to be developed, given that the current devices are extremely sensitive to the water content in the polysaccharides. The H+ and OH− mobility in our devices are comparable to the mobility of ions in solution, therefore the performance of these polysaccharides does not limit the potential coupling with biological systems. The ability to precisely control the flow and concentration of H+ and OH− may also be used to study the kinetics of acid-base chemical reactions3. Finally, given the importance of protonic conduction in biological energy conversion and electrophysiology in general, insights from the semiconductor model and protonic devices may prove useful at interrogating the conductivity in relevant proton channels from an alternate perspective.
, are in good and reasonable agreement with what has been previously reported for the same species in other hydrogen-bonded systems. The on-off ratio of these devices is low (~3–4). Avenues for improvement include using thinner gate dielectrics and high k gate dielectrics. The field effect manipulation of H+ and OH− currents may be used, in the future, to interface with proton conducting ion channels14. However, for these applications devices that function in physiological conditions need to be developed, given that the current devices are extremely sensitive to the water content in the polysaccharides. The H+ and OH− mobility in our devices are comparable to the mobility of ions in solution, therefore the performance of these polysaccharides does not limit the potential coupling with biological systems. The ability to precisely control the flow and concentration of H+ and OH− may also be used to study the kinetics of acid-base chemical reactions3. Finally, given the importance of protonic conduction in biological energy conversion and electrophysiology in general, insights from the semiconductor model and protonic devices may prove useful at interrogating the conductivity in relevant proton channels from an alternate perspective.
Methods
Maleic chitosan and proline chitosan
Maleic chitosan was prepared following a previously published protocol46. Proline chitosan was synthesized following a well-studied reaction mechanism47 as described in details in the SI. Chitosan powders (medium molecular weight, degree of deacetylation = 0.75 ~ 0.85, Sigma Aldrich) and proline (Sigma Aldrich) were used as received. The maleic chitosan and the proline chitosan hydration level were determined with a thermo gravimetric analyser (TA Instruments, model 2050)26.
H+- OH− junction fabrication and measurement
To fabricate the Pd contacts, a 1 × 1 cm2 Cu plate is used as the base substrate as pure Pd is too soft to be used alone. A 5 nm thick Cr interfacial layer was e-beam evaporated (Balzers PLS 500) on the Cu substrate to promote the adhesion between the Cu and Pd. Then a layer of 50 nm thick Pd was evaporated on top of the Cr. The proline chitosan and maleic chitosan films were prepared from a 2 mL of 3.5 wt% aqueous solutions drop cast onto a Teflon mold. Films were dried in ambient air for 8 hrs and removed carefully from the mold with a pair of tweezer. 100 μm thick maleic chitosan and proline chitosan films were sandwiched by two Pd contacts to form a junction device. The H+- OH− junction device was tested in 75% RH, with 5% H2 gas.
H+ and OH−-FET fabrication
Devices were fabricated on p-type Si (Addison Engineering, B- doped, ρ = 0.001 ohm cm−1) with thermally grown silicon oxide (100 nm). Photolithography and lift-off was used to define the contacts. Pd metal (50 nm) with a 5-nm Cr adhesion layer was deposited via e-beam evaporation (Balzers PLS 500). After dialysis and freeze-drying, maleic chitosan and proline chitosan were dissolved in a DI water solution. This procedure eliminates any salt in the material and thus potential salt effects on the conductivity. To make a polysaccharide-based device, 2 μl polysaccharide solutions of 0.01 mg/mL concentration was carefully drop-cast on top of the patterned silicon wafer and the solution was dried under gentle N2 flow. Devices were mounted on a chip, and wire bonded.
Electrical characterization
Measurements were performed with a semiconductor parameter analyser (Agilent 4155C). An environmental chamber was used (5% H2) with controlled relative humidity (RH) monitored with a traceable hygrometer (Fisher Scientific, ± 0.1% error). During FET measurements at 75% RH and 5% H2, devices with no connections were monitored to have at most noise current. This procedure was done to ensure that the measured device current was from the maleic chitosan and proline chitosan channel and not from water condensed on the top of the SiO2. IDS vs. VDS sweeps were performed at 0.013 V/s, after a 90 s hold, with 0.5 s wait time between points to minimize transient effects.
Simulations
Electrical properties of the H+ -OH− junction were obtained by solving Poisson's equation and the electron (H+) and hole (OH−) continuity equations in a 1 μm square cross section of the 200 μm long junction (100 μm maleic chitosan and 100 μm proline chitosan) using a CAD tool (ATLAS, Silvaco). Pd (Φ = 5.1 eV) source and drain were modelled as Ohmic protonic contacts (no barrier) to the material. We replaced the properties of silicon with those of the channel material: Maleic–chitosan and proline chitosan have εmc = 11.8, and band gap Eg = 0.8 eV. Charge density was estimated from the semiconductor model and mobility was estimated from the H+ and OH− devices. Minority carrier recombination constant was derived from H+ OH− recombination as 1μs, and included in simulations throughout activating Shockley-Read-Hall (SRH) recombination model. The gate capacitance of the H+-FETs was calculated as previously described27. The capacitance was estimated by the simple equation of ΔQ/ΔV, where ΔQ and ΔV represent the variations of the interface charge and gate, respectively.
Author Contributions
M.R. designed the research; Y.D., E.J. and C.Z. performed research (experiments); A.F.R. and M.P.A. designed and performed research (simulations); Y.D., J.J. and B.H. contributed new reagents/analytical tools; Y.D., E.J. and M.R. analysed the data; M.R. wrote the manuscript and all authors read and edited the manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
Support for this research was provided by a National Science Foundation Career Award (DMR-1150630), a 3M Untenured Faculty Award, a University of Washington CGF award, and a Coulter Foundation Grant. Part of the work was performed at the University of Washington Centre for Nanotechnology, which is part of the NSF-Funded NNIN. Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Footnotes
11/01/2013
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
- DeCoursey T. E. Voltage-gated proton channels and other proton transfer pathways (vol 83, pg 475, 2003). Physiol. Rev. 83, 1067–1067 (2003). [DOI] [PubMed] [Google Scholar]
- Mitchell P. Chemiosmotic coupling in oxidative and photosynthetic phosphorylation. Biol. Rev. Camb. Philos. Soc. 41, 445–502 (1966). [DOI] [PubMed] [Google Scholar]
- Morowitz H. J. Proton Semiconductors and Energy Transduction in Biological-Systems. Am. J. Physiol. 235, R99–R114 (1978). [DOI] [PubMed] [Google Scholar]
- Lanyi J. K. Bacteriorhodopsin. Annu. Rev. Physiol. 66, 665–688 (2004). [DOI] [PubMed] [Google Scholar]
- Smith S. M. et al. Voltage-gated proton channel in a dinoflagellate. Proc. Natl. Acad. Sci. USA 108, 18162–18167 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walz D. & Caplan S. R. Bacterial flagellar motor and H+/ATP synthase: two proton-driven rotary molecular devices with different functions. Bioelectrochem. 55, 89–92 (2002). [DOI] [PubMed] [Google Scholar]
- Capasso M., DeCoursey T. E. & Dyer M. J. S. pH regulation and beyond: unanticipated functions for the voltage-gated proton channel, HVCN1. Trends Cell Biol. 21, 20–28 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busath D. & Szabo G. Gramicidin forms multi-state rectifying channels. Nature 294, 371–373 (1981). [DOI] [PubMed] [Google Scholar]
- Nagle J. F., Mille M. & Morowitz H. J. Theory of Hydrogen-Bonded Chains in Bioenergetics. Biophys. J. 25, A48–A48 (1979). [Google Scholar]
- Nagle J. F. & Morowitz H. J. Molecular Mechanisms for Proton Transport in Membranes. Proc. Natl. Acad. Sci. USA 75, 298–302 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cukierman S. Et tu, Grotthuss! and other unfinished stories. Biochim. Biophys. Bioenerg. 1757, 876–885 (2006). [DOI] [PubMed] [Google Scholar]
- Riccardi D. et al. "Proton holes" in long-range proton transfer reactions in solution and enzymes: A theoretical analysis. J. Am. Chem. Soc. 128, 16302–16311 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musset B. et al. Aspartate 112 is the selectivity filter of the human voltage-gated proton channel. Nature 480, 273–U167 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noy A. Bionanoelectronics. Adv. Mater. 23, 807–820 (2011). [DOI] [PubMed] [Google Scholar]
- Richter-Dahlfors A., Svennersten K., Larsson K. C. & Berggren M. Organic bioelectronics in nanomedicine. Biochim. Biophys. 1810, 276–285 (2011). [DOI] [PubMed] [Google Scholar]
- Meredith P., Bettinger C. J., Irimia-Vladu M., Mostert A. B. & Schwenn P. E. Electronic and optoelectronic materials and devices inspired by nature. Rep. Progr. Phys. 76, 034501 (2013). [DOI] [PubMed] [Google Scholar]
- Kim K. H. et al. A Functional Hybrid Memristor Crossbar-Array/CMOS System for Data Storage and Neuromorphic Applications. Nano Lett. 12, 389–395 (2012). [DOI] [PubMed] [Google Scholar]
- Xu L. et al. Design and Synthesis of Diverse Functional Kinked Nanowire Structures for Nanoelectronic Bioprobes. Nano Lett. 13, 746–751 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S.-C. J. et al. Carbon Nanotube Transistor Controlled by a Biological Ion Pump Gate. Nano Lett. 10, 1812–1816 (2010). [DOI] [PubMed] [Google Scholar]
- Misra N. et al. Bioelectronic silicon nanowire devices using functional membrane proteins. Proc. Natl. Acad. Sci. USA 106, 13780–13784 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angione M. D. et al. Interfacial electronic effects in functional biolayers integrated into organic field-effect transistors. Proc. Natl. Acad. Sci. USA 109, 6429–6434 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tybrandt K., Larsson K. C., Richter-Dahlfors A. & Berggren M. Ion bipolar junction transistors. Proc. Natl. Acad. Sci. USA 107, 9929–9932 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostert A. B. et al. Role of semiconductivity and ion transport in the electrical conduction of melanin. Proc. Natl. Acad. Sci. USA 109, 8943–8947 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owens R. M. & Malliaras G. G. Organic Electronics at the Interface with Biology. Mrs Bull. 35, 449–456 (2010). [Google Scholar]
- Tybrandt K., Forchheimer R. & Berggren M. Logic gates based on ion transistors. Nat. Commun. 3 (2012). [DOI] [PubMed] [Google Scholar]
- Kim Y. J., Chun S.-E., Whitacre J. & Bettinger C. J. Self-deployable current sources fabricated from edible materials. J. Mater. Chem. B (2013) 10.1039/C3TB20183J. [DOI] [PubMed] [Google Scholar]
- Zhong C. et al. A polysaccharide bioprotonic field-effect transistor. Nat. Commun. 2, 476 (2011). [DOI] [PubMed] [Google Scholar]
- Eigen M. & Demaeyer L. Self-dissociation and Protonic Charge Transport in Water and Ice. Proc. R. Soc. A 247, 505–533 (1958). [Google Scholar]
- Glasser L. Proton Conduction and Injection in Solids. Chem Rev 75, 21–65 (1975). [Google Scholar]
- Morgan H., Pethig R. & Stevens G. T. A Proton-Injecting Technique for the Measurement of Hydration-Dependent Protonic Conductivity. J. Phys. E 19, 80–82 (1986). [Google Scholar]
- Zhong C., Kapetanovic A., Deng Y. & Rolandi M. Nanofiber Ink: A Chitin Nanofiber Ink for Airbrushing, Replica Molding, and Microcontact Printing of Self-assembled Macro-, Micro-, and Nanostructures. Adv. Mater. 23, 4720–4720 (2011). [DOI] [PubMed] [Google Scholar]
- Cooper A. et al. Self-assembled chitin nanofiber templates for artificial neural networks. J. Mater. Chem. 22 (2012). [Google Scholar]
- Francesko A. & Tzanov T. Chitin, chitosan and derivatives for wound healing and tissue engineering. Adv. Biochem. Eng./Biotechnol. 125, 1–27 (2011). [DOI] [PubMed] [Google Scholar]
- Nagle J. F., Mille M. & Morowitz H. J. Theory of Hydrogen-Bonded Chains in Bioenergetics. J. Chem. Phys. 72, 3959–3971 (1980). [Google Scholar]
- Bardelme G. h. Electrical-Conduction in Hydrated Collagen.1. Conductivity Mechanisms. Biopolymers 12, 2289–2302 (1973). [DOI] [PubMed] [Google Scholar]
- Murphy E. J. Ionic-Conduction in Keratin (Wool). J Coll. Interface Sci. 54, 400–408 (1976). [Google Scholar]
- Christie J. H. & Woodhead I. M. A new model of DC conductivity of hygroscopic solids - Part 1: Cellulosic materials. Textile Research J. 72, 273–278 (2002). [Google Scholar]
- Volgin V. M. & Davydov A. D. Ionic transport through ion-exchange and bipolar membranes. J. Membrane Sci. 259, 110–121 (2005). [Google Scholar]
- Deml A. M., Bunge A. L., Reznikov M. A., Kolessov A. & O'Hayre R. P. Progress toward a solid-state ionic field effect transistor. J. Appl. Phys. 111 (2012). [Google Scholar]
- Sze S. M. Physics of Semiconductor-Devices. (1982).
- Stavrinidou E. et al. Direct Measurement of Ion Mobility in a Conducting Polymer. Adv Mater (2013) 10.1002/adma.201301240. [DOI] [PubMed] [Google Scholar]
- Peckham T. J., Schmeisser J., Rodgers M. & Holdcroft S. Main-chain, statistically sulfonated proton exchange membranes: the relationships of acid concentration and proton mobility to water content and their effect upon proton conductivity. J. Mater. Chem. 17, 3255–3268 (2007). [Google Scholar]
- Yang A. C. C., Narimani R., Zhang Z., Frisken B. J. & Holdcroft S. Controlling Crystallinity in Graft Ionomers, and Its Effect on Morphology, Water Sorption, and Proton Conductivity of Graft Ionomer Membranes. Chem. Mater. 25, 1935–1946 (2013). [Google Scholar]
- Flanagan T. B. & Lewis F. A. Electrode Potentials of the Palladium-Hydrogen System. J Chem Phys 29, 1417–1418 (1958). [Google Scholar]
- Kayser H., Rodriguez-Ropero F., Leitner W., Fioroni M. & Maria P. D. d. Mechanistic comparison of saccharide depolymerization catalyzed by dicarboxylic acids and glycosidases. Rsc Adv 3, 9273–9278 (2013). [Google Scholar]
- Zhong C., Wu J., Reinhart-King C. A. & Chu C. C. Synthesis, characterization and cytotoxicity of photo-crosslinked maleic chitosan-polyethylene glycol diacrylate hybrid hydrogels. Acta Biomater. 6, 3908–3918 (2010). [DOI] [PubMed] [Google Scholar]
- Aytekin A. O., Morimura S. & Kida K. Synthesis of chitosan-caffeic acid derivatives and evaluation of their antioxidant activities. J. Biosci. Bioeng. 111, 212–216 (2011). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information