Incorporating prior knowledge into Gene Network Study

Abstract

Motivation: A major goal in genomic research is to identify genes that may jointly influence a biological response. From many years of intensive biomedical research, a large body of biological knowledge, or pathway information, has accumulated in available databases. There is a strong interest in leveraging these pathways to improve the statistical power and interpretability in studying gene networks associated with complex phenotypes. This prior information is a valuable complement to large-scale genomic data such as gene expression data generated from microarrays. However, it is a non-trivial task to effectively integrate available biological knowledge into gene expression data when reconstructing gene networks.

Results: In this article, we developed and applied a Lasso method from a Bayesian perspective, a method we call prior Lasso (pLasso), for the reconstruction of gene networks. In this method, we partition edges between genes into two subsets: one subset of edges is present in known pathways, whereas the other has no prior information associated. Our method assigns different prior distributions to each subset according to a modified Bayesian information criterion that incorporates prior knowledge on both the network structure and the pathway information. Simulation studies have indicated that the method is more effective in recovering the underlying network than a traditional Lasso method that does not use the prior information. We applied pLasso to microarray gene expression datasets, where we used information from the Pathway Commons (PC) and the Kyoto Encyclopedia of Genes and Genomes (KEGG) as prior information for the network reconstruction, and successfully identified network hub genes associated with clinical outcome in cancer patients.

Availability: The source code is available at http://nba.uth.tmc.edu/homepage/liu/pLasso.

Contact: Yin.Liu@uth.tmc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

A central research focus in genomics is to identify genes and gene networks involved in variety of biological processes. Gaussian graphical models are popular tools for the estimation of gene association networks from microarray data (Dobra et al., 2004; Lauritzen, 1996; Schafer and Strimmer, 2005). These models assume that the available data are generated from a multivariate Gaussian distribution (Whittaker, 1990). As a consequence, the main task for inferring networks is to derive conditional independencies in the joint probability distribution of expression data for multiple genes. In the framework of undirected Gaussian graphical models, conditional independence relationships can be inferred from partial correlations, which are the correlations between pairs of variables given the remaining observed ones. Contrary to the marginal correlation, the partial correlation measures the direct association between two genes in the gene association network. Once a direct gene association network is complete, the knowledge on indirect gene associations can be easily obtained.

The standard estimation of partial correlations involves either the inversion of the sample covariance matrix or the estimation of least square regression problems. Unfortunately, microarray data are typically characterized by a large number of variables with a small number of samples, which makes these traditional approaches inappropriate. To ensure proper estimation capability, suitable alternatives based on regularized estimation of these parameters by sparsity restriction have been proposed. The underlying assumption is the sparsity of biological networks: only a few edges are supposed to be present in the gene regulatory network. A well-known example of these regularization-based techniques is the L1 penalized least square estimator, known as the Lasso technique. The method has been widely adapted to high-dimensional model selection in linear and Gaussian graphical models (Meinshausen and Buhlmann, 2006; Tibshirani, 1996).

One limitation of these approaches is that they focus on computational or algorithmic aspects but neglect prior biological knowledge or information. Many years of intensive biomedical research has deposited a wealth of biological knowledge into databases, including gene–gene regulatory pathway information. One well-known example of these data resources is the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (Kanehisa et al., 2010). It is a collection of comprehensive pathway information derived from experimental results, literature and other databases. Another rich resource is the Pathway Commons (PC) that integrates biological pathway and molecular interaction data from publicly available databases including BioGRID, HPRD, Reactome and others (Cerami et al., 2011). These pathways are often interconnected and can be viewed as a graph of inter-gene regulatory relationships. However, pathway databases represent only the static regulatory relationships between genes or gene products. It is not clear yet to what extent a network in a particular phenotype or cell type aligns with interactions defined in these databases. A recent microarray data analysis of 20 genes involved with the human cell cycle showed that as much as 60–70% of the identified gene regulatory relationships were in agreement with known regulations (Chen et al., 2010). It is expected that integrating a priori pathway information in a gene expression analysis would increase the power of the method to recover biological networks. Recently, several methods have been developed to use pathways or network information, including network-constrained parameter estimation, in the framework of variable selection (Chen et al., 2011; Li and Li, 2008; Tai and Pan, 2007a, b; Wei and Pan, 2008). For example, the prior information was incorporated into a spatially correlated mixture model for selecting targets of one transcription factor (Wei and Pan, 2008). In addition, an Ising model using network knowledge was used to identify differentially expressed genes (Li et al., 2011; Wei and Li, 2007).

In this study, we developed a prior information-dependent Lasso (pLasso) procedure for regularized estimation of large-scale gene association networks. Specifically, we embedded prior network information into the regularized regression, such that it could specify preferences for particular sets of variables in the model. The rationale is derived from a Bayesian perspective of Lasso. A mixture of two Laplacian distributions was conceptually proposed to represent different prior knowledge of two sets of gene interactions: one set is present in known pathways, whereas the other has no known prior information. We first explored the effectiveness of the pLasso using simulation studies, and then applied the pLasso to a breast cancer dataset and an ovarian cancer dataset to evaluate the proposed method. We have demonstrated the effectiveness and power of our pLasso procedure through both simulation studies and real data analysis.

2 METHODS

2.1 Graphical Gaussian model of gene network

Graphical models are a class of statistical models that present direct covariate interactions. These models can be described by means of a graph G = (V, E), where V = {1,….., p} is the vertex set representing variables, and E = (e_ij) is the edge set representing conditional independency relations between vertices. If e_ij = 0, there is no edge between two vertices i and j. The lack of an edge between two vertices corresponds to their conditional independence given all other vertices. Let X = (X₁,…., X_p) be a random vector of vertices states that are real valued and follow a multivariate Gaussian distribution with mean 0 and covariance matrix , so the inverse covariance matrix, Ω = ∑⁻¹ = {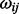} known as the precision matrix, describes the conditional independence structure of X. If e_ij = 0, then 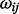= 0. Therefore, it can be easily linked to the partial correlation 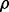in the graphical model through Equation (1).

(1)

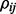is the partial correlation between gene i and gene j conditioned on the values of all the other genes. The pattern of zero entries in the inverse covariance matrix corresponds to conditional independence restrictions between variables.

2.2 Neighborhood selection with the Lasso

In general, a typical genomic dataset has a much smaller number of observations (n arrays) than number of variables (p genes). Under these conditions, inverting the sample covariance matrix as described is inappropriate for estimating the partial correlations. A recent study showed that suitable surrogates based on regularized estimation of the covariance matrix or on regularized high-dimensional regression can lead to practical solutions (Kramer et al., 2009; Meinshausen and Buhlmann, 2006; Parikh et al., 2011). In this study, we will use Meinshausen and Buhlmann’s neighborhood selection method. Basically, Lasso regression is applied to each node in the network, reducing the original problem to multiple sparse linear regression problems.

Formally, let X_\i indicate the p−1 vector of the values of all genes except i. Similarly, let 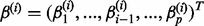represent the regression coefficients where gene i is the response variable and all the other genes are the covariates. The lasso-based estimate of regression coefficients is the solution of the optimization problem:

(2)

where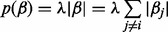

Here λ > 0 is the regularization parameter. This optimization problem can be easily solved by a coordinate descent algorithm (Friedman et al., 2010). Then, the neighborhood estimation of node j is defined by Equation (3).

(3)

Also, based on the relationship between partial correlation coefficients and regression coefficients, the following equation can be derived (Kramer et al., 2009).

(4)

With the L1 penalty, many estimated regression coefficients will shrink to 0. It is not guaranteed that the 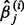and 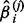always have the same sign for finite sample sizes. In this situation, we applied the ‘max’ symmetrization approach (Parikh et al., 2011), which is defined by Equation (5).

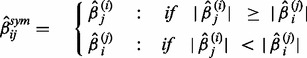(5)

And now by replacing both the 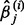and 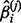in Equation (4) with 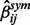, we can define the estimate of the partial correlation coefficients as in Equation (6).

(6)

2.3 Prior dependent lasso estimation of neighborhood

The lasso estimate for linear regression has a Bayesian interpretation. Tibshirani (1996) indicated that the lasso estimate can be viewed as the model of the posterior distribution of β with a double exponential distributed prior (or Laplacian prior). Minimizing Equation (2) can be regarded as maximizing the log posterior distribution of

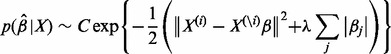(7)

where C is a constant in Equation (7). Thus, the lasso penalty can be regarded as the logarithm of the prior distribution of the parameter β = (β₁,…, β_p)^T, which is a Laplacian prior with mean equal to 0.

Because prior distributions model our prior knowledge of the data, the known network structure can be introduced in a natural way in the form of prior probabilities. A mixture of two Laplacian prior distributions for the regression coefficients is proposed as in Equation (8) with different parameters λ₁ and λ₂.

(8)

Here λ₁ and λ₂ are regularization parameters. β_non-prior and β_prior represent the regression coefficients corresponding to the edges absent and present in the prior knowledge. The prior distribution of regression coefficients for the edges not present in known databases is concentrated. Because of the sparsity assumption, most of these regression coefficients shrink to 0. On the other hand, the prior distribution of regression coefficients corresponding to existing edges in the known databases is diffuse. Their regression coefficient profile is scattered away from zero, as it is preferable to include the regression coefficients representing the known gene interactions from reliable data source. In our proposed pLasso method, we selected different values of the regularized parameter λ (λ₁ and λ₂) in two lasso penalty terms, thus allowing the lasso regression coefficients corresponding to the edges absent and present in the prior knowledge to have different prior distributions.

2.4 A new criterion for regularization parameter selection

Asymptotically, Lasso guarantees both model estimation consistency and selection consistency under certain conditions (Zhao and Yu, 2006). The regularization parameter λ controls the sparsity of the estimated network. Large values of λ lead to sparse networks, whereas small values of λ result in dense networks. Sparse networks have less number of degrees of freedom, but lower log-likelihood. Bayesian information criterion (BIC) is a well-known model selection criterion (Schwarz, 1978). We apply BIC for choosing the regularization parameter λ that is a tradeoff between the data fitting and the model complexity. Taking into account the fact that the degree of freedom of the Lasso equals the number of non-zero entries in the coefficient matrix, we define an average of the BIC score for all genes for neighborhood estimation.

(9)

Here, the first term L(X | β) represents the likelihood of the data. In the second term, n is the sample size; k is the average node degree of the network, calculated by the number of non-zero entries in the estimated coefficient matrix. In the last term, logP(S) is the prior probability of the network model S. A smaller BIC score implies a better model. Usually, the prior probability logP(S) in the BIC score is chosen to be an uninformative uniform prior so that the same prior probability is assigned to all considered models. In this study, we use an informative prior incorporating both our knowledge on network sparsity and the prior information in known databases, defined as the Equations (10) and (11) below.

As an asymptotic result, the original BIC score definition is derived for large samples. In a typical genomic dataset where n << p, we found the original BIC definition often resulted in data underfitting and an over-sparse network. To address this issue, we first define the prior probability that favors the network with an optimal minimum number of edges. In this modified BIC (mBIC) score, q represents the minimum average node degree of the estimated network. When the estimated network has an average node degree of k bigger than q, it has no effect on the score. Otherwise, an extra penalty is imposed into the framework, defined as the following:

(10)

where the third term depicts a form for the prior probability that favors the network S with an average node degree above q.

We also define a second modified BIC (pBIC) score that takes into account the prior pathway information for selecting the optimal value of the regularization parameter λ₂. The rationale underlying the pBIC score is, if the estimated edges are also present in the known databases, a favorable prior distribution will be assigned, leading to a lower BIC score. In the pBIC, η is defined as the average number of estimated edges included in prior information for each node and calculated as η = 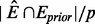, where p is the number of genes, E is the set of edges in the inferred network and E_prior is the set of edges in the prior. We let α represent the precision of the prior knowledge, indicating the proportion of true edges in prior information. To further compensate the false-positive edges in E and E_prior, we use the multiplicity term αη to denote the effective number of true prior edges recovered in the estimated network. Therefore, the complexity of the model in BIC is balanced with respect to the total number of possibly correct prior edges recovered in the estimated network. We have found that this simple prior representation could reflect the information within the prior knowledge, favoring the estimated network models with a large number of edges included in prior information.

(11)

2.5 Evaluate the inferred gene network hubs

To evaluate the performance of the pLasso method, we applied it to two public datasets for network inference. The first dataset was a microarray gene expression study of breast cancer (Wang et al., 2005), measuring gene expression profiles of 286 lymph-node-negative breast cancer patients. Among these patients, 107 patients have developed a distant metastasis, whereas 179 patients are metastasis-free. The second dataset was the serous ovarian cancer data by The Cancer Genome Atlas Research Network (2011). It includes gene expression measurements for 436 patient samples, where 108 patients had remained disease-free and 328 patients experienced disease progression.

We tested whether the gene network hubs inferred from the proposed pLasso method could be used to predict survival outcomes of cancer patients. We also compared their performance with those obtained from other methods that were based on genome-wide expression data alone. The methods for comparison included the differential expression analysis (Significant Analysis of Microarrays, known as SAM) (Storey and Tibshirani, 2003), the partial correlation analysis (GeneNet) (Opgen-Rhein and Strimmer, 2007) and the original Lasso method. The genes were selected if they were among the top genes with most neighbors in the inferred network for patients showing distant metastasis but not in the network for the metastasis-free patients (based on pLasso, Lasso and GeneNet methods) or the most significantly differentiated expressed genes (SAM). We also compared the predictive power of the selected genes with the gene signatures identified previously, including the 76 genes for breast cancer (Wang et al., 2005) and the 193 genes for ovarian cancer (The Cancer Genome Atlas Research Network, 2011). To make a fair comparison, we selected the same number of genes under different methods (76 genes and 193 genes for breast cancer and ovarian cancer analysis, respectively). For breast cancer analysis, we used the 214 patients’ samples from the Wang dataset for training and then applied an independent dataset, including 165 patients who did not receive hormone therapy or chemotherapy, for testing the predictive power of the selected gene signature for survival outcome (van de Vijver et al., 2002). For ovarian cancer analysis, we used a training set of 215 patients from TCGA batches 11–15, and tested in an independent validation set consisting of 253 samples from TCGA batches 17–24. We performed the univariate Cox’s analysis on the selected genes in the training dataset, and used the Cox’s regression coefficients for these genes to calculate the risk score for each sample in the testing dataset as in Creighton et al. (2008). Specifically, the genes with positive Cox’s regression coefficients were considered to be ‘poor prognosis’ genes, whereas others were considered as the ‘good prognosis’ genes. The risk score for each patient in the testing datasets was defined as the t-statistics comparing the average of the poor prognosis genes with the average of the good prognosis genes. Patient samples with risk scores above 0 were predicted to be in the ‘high-risk group’, whereas others were classified in the ‘low-risk group’. The sensitivity and specificity of prediction results based on selected genes from different methods were then compared.

3 SIMULATION RESULTS

To demonstrate the performance of the proposed pLasso method, we conducted simulation studies to empirically compare our method with the traditional Lasso method (Meinshausen and Buhlmann, 2006). In the experiment, we designed two simulation scenarios on different network scales. The first simulated network is a small network with 40 nodes, an average node degree of 4, a maximum degree of 6. The 80 (40*4/2) edges were randomly assigned to the 780 (40*39/2) node pairs with the limit that the maximum node degree is not exceeded. According to this network structure, we simulate its associated gene-expression datasets similar to others (Kramer et al., 2009; Parikh et al., 2011).

Basically, we first constructed a positive definite partial correlation matrix P based on the simulated network. Then the microarray gene expression data were simulated from a standard multivariate normal distribution with correlation structure derived from P with each gene having 10, 100 and 200 replicates so that we could further investigate the effect of sample size on the performance of our method. Our second simulation scenario has a larger network with 300 nodes and 900 edges, an average degree of 6, a maximum degree of 12. Each gene was simulated with 10, 100 and 200 replicates. We first screened the optimal value of λ₁ using both BIC and mBIC criteria to compare their effectiveness on the original Lasso performance. To accommodate the model complexity at different network scales, we set the q value of mBIC score to 2 and 4 in the small and large network scenarios, respectively, and evaluated these estimation results using an F-score, where F = 2*Precision*Recall/(Precision + Recall). Here precision is the proportion of prediction results that are true positives, and recall is the proportion of true positives that are predicted, also known as the true positive rate. The F-score can be interpreted as a weighted average of the precision and recall, and reaches its best value at 1 and worst score at 0. We reported its average and standard error based on 100 simulated datasets for each scenario. As shown in Table 1, if the simulation scenario was in the n > p setting (e.g. p = 40, n = 100 and 200), it possessed the same optimal λ₁ values based on BIC and mBIC screening, and their performance evaluated by the F-score was identical. However, in the p > n setting, Lasso with BIC reached its optimal λ₁ value with severe network sparsity, whereas Lasso with mBIC led to a larger number of true edges in the identified network and a higher F-score. The results demonstrated the effectiveness of our mBIC in addressing the problem of data underfitting, especially in the scenarios of larger networks with smaller sample sizes.

Table 1.

Lasso performance with optimal λ₁ value determined by BIC and mBIC criteria

Nodes	Sample size	Criteria	λ1	F-score	Recovered edges
40	10	BIC	0.51 (0.07)	0.16 (0.05)	10 (3)
		mBIC	0.41 (0.07)	0.19 (0.05)	14 (4)
	100	BIC	0.21 (0.02)	0.69 (0.04)	58 (4)
		mBIC	0.21 (0.01)	0.69 (0.04)	58 (4)
	200	BIC	0.14 (0.01)	0.80 (0.03)	72 (3)
		mBIC	0.14 (0.01)	0.80 (0.03)	72 (3)
300	10	BIC	0.49 (0.07)	0.003 (0.001)	2 (1)
		mBIC	0.39 (0.02)	0.04 (0.01)	33 (5)
	100	BIC	0.46 (0.04)	0.13 (0.02)	90 (5)
		mBIC	0.25 (0.02)	0.30 (0.01)	234 (9)
	200	BIC	0.24 (0.02)	0.39 (0.07)	237 (9)
		mBIC	0.20 (0.01)	0.52 (0.02)	391 (9)

Note: The standard errors in parenthesis are calculated based on 100 simulated datasets. Recovered edges represent the total number of true edges recovered by the method.

In real situations, the true underlying network is only partially known in our prior knowledge and is mixed with spurious edges. To investigate the performance of our pLasso method with imperfect prior information, we have simulated prior information with different precision levels varying from 0.1 to 1.0. The total number of edges in the prior data was set equal to the number of edges in the true underlying network. Therefore, a precision level of 0.1 indicates that 10% of the edges in prior are true edges, whereas the other 90% are spurious ones, and a precision level of 1.0 indicates a perfect prior with all true edges included. To incorporate the prior information, the network recovery method pLasso was implemented to search over a sequence of µ from 0 to 1.2 with an increment of 0.1 to get the optimal λ₂, where λ₂ = μ*λ₁. The optimal λ₂ value was obtained when the minimum pBIC score was achieved. The parameter λ₁ used in pLasso was set the same as that in the original Lasso approach based on the mBIC criterion.

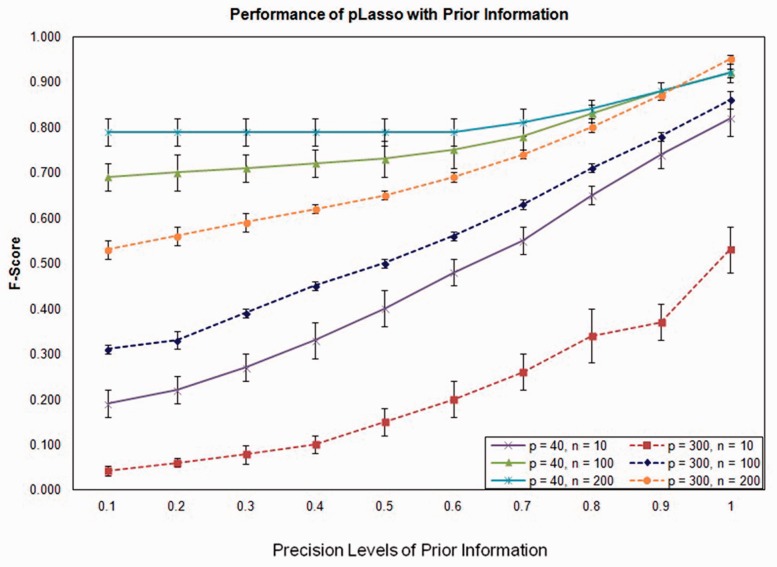
Results in Figure 1 demonstrated that in all simulation scenarios, combining prior knowledge with higher precision in pLasso led to a higher F-score. Nevertheless, we found F-scores from pLasso were consistently higher than those from a traditional Lasso method. Even when the precision of the prior was as low as 0.1, pLasso achieved an F-score comparable with or slightly higher than the Lasso method for all the simulation scenarios. Obviously, the precision of prior knowledge is important in determining the optimal value of λ₂, as defined in the Equation (11), and thus affects the performance of pLasso. As shown in the Supplementary Table S1, the lower precision of prior knowledge, the larger value of λ₂ will be obtained, indicating the penalty on the prior is large. Particularly, when only 10% of edges in the prior were true edges (precision level is 0.1), the optimal µ based on pBIC was close to 1.0 for the simulated network, leading to a large λ₂. This suggested the edges in the prior information get a large penalty, thus reducing the likelihood of including low quality prior knowledge in the network inference process. On the other hand, if the precision of the prior information was high, the corresponding optimal λ₂ (µ) value would be low, indicating that the penalty on the prior knowledge was small. Therefore, even though we often cannot obtain perfect prior information, our approach helps to distinguish the true edges from the spurious ones, and outperforms a traditional Lasso method that neglects prior information.

Fig. 1.

Performance of pLasso with prior information provided at different precision levels

Figure 1 also demonstrated pLasso performance under different simulation scenarios, including different network sizes (p) and sample sizes (n). Performance is affected by both factors. In the simulation scenarios where n > p, the traditional Lasso itself was able to achieve an optimal performance with a high F-score (0.69 and 0.80 for p = 40, n = 100 and 200, respectively). With the pLasso method, a relatively large value of λ₂ (µ) was selected, which restricted the addition of edges present in the prior, and the overall performance did not significantly improve unless the precision of the prior was high (Supplementary Table S1). On the other hand, in the simulation scenarios where p > n, the original Lasso without incorporating prior information performed poorly because of the small sample size effect. In this setting, the advantage of our pLasso method is most obvious, as demonstrated by the performance improvement when the prior information was incorporated even if the prior precision level was low (Fig. 1).

In our simulation studies, the precision (α) of prior used in pBIC score calculation was provided. However, this is often not the case in real data application. Therefore, we can only use an estimated α value in the Equation (9) for choosing the optimal regularization parameter λ₂ and inferring the network. To investigate the effects of α on the performance of our method, we varied the estimated value of α between 0 to 1 for each true value of α (0.1, 0.3, 0.6 and 0.9). It was demonstrated that in the large network of 300 genes with each gene having 100 samples, the performance was affected in the extreme case, if we estimated the precision α to be 1 while the true precision was only 0.1. However, if the estimated α was within a reasonable small range of the true α values, our method performance was relatively robust to the selection of estimated α (Table 2). This conclusion was demonstrated to be valid in other simulation scenarios as well (Supplementary Tables S2 and S3).

Table 2.

The effects of estimated precision level (α) on the method performance

F-score	Estimated precision (α)
	0.1	0.3	0.5	0.6	0.9	1.0
True precision
0.1	0.30 (0.01)	0.30 (0.01)	0.30 (0.01)	0.28 (0.02)	0.26 (0.01)	0.26 (0.01)
0.3	0.36 (0.02)	0.39 (0.01)	0.39 (0.01)	0.40 (0.01)	0.38 (0.01)	0.38 (0.01)
0.6	0.52 (0.03)	0.55 (0.03)	0.56 (0.01)	0.56 (0.01)	0.56 (0.01)	0.56 (0.01)
0.9	0.73 (0.02)	0.75 (0.02)	0.76 (0.05)	0.77 (0.01)	0.78 (0.01)	0.78 (0.01)

Note: The entries in bold represent the F-scores based on the true precision value.

4 APPLICATION TO ANALYSIS OF CANCER GENE EXPRESSION DATA

4.1 Breast cancer data

In the analysis of breast cancer data, our interest is to investigate the gene regulatory networks of two types of breast cancer patients, the metastasis-free group and the group with metastases. Because the performance of Lasso and pLasso are sensitive to the sample size, we only used 107 of 179 metastasis-free patients so that the sample size of the metastasis-free group is the same as that of the patients with metastases. We used a prior gene network compiled from the KEGG database and the PC web resource, which yielded a network with 11 211 genes and 97 128 edges. To make the computation less intensive, we only applied our method to the set of genes included in our prior knowledge. In the experiment, mBIC with a q value of 5 was used to search over the optimal λ₁ value based on the observation that the node degree is on the order of 2 to 10 edges per node (Alon, 2006). With traditional Lasso method, the inferred network from patients with metastases had 21 360 edges. For the pLasso setting, we set the precision of the prior knowledge to 0.6, as we expect that 60–70% of the edges present in the prior knowledge would align with the interactions in the true network corresponding to breast cancer samples (Chen et al., 2010). Both patient groups resulted in networks with similar number of edges. In the groups of patients with metastases, we inferred a network with 5187 genes and 29 821 edges, whereas the metastasis-free patient group yielded a network with 5106 genes and 29 364 edges.

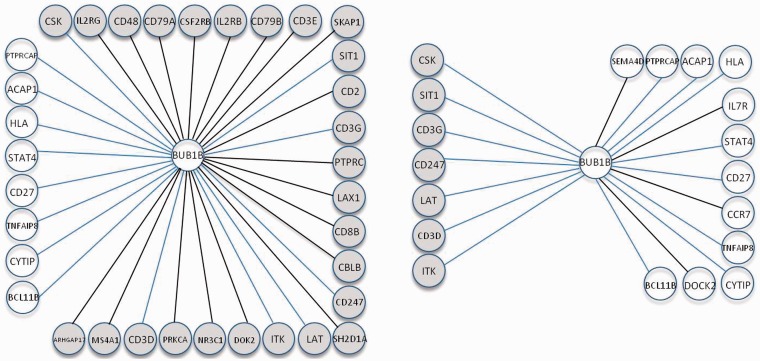
Figure 2 gives an example showing the difference between the inferred networks from the Lasso and pLasso approaches in patients with metastases. The metastatic progression of breast cancer is directly caused by the disregulation of numerous cellular signaling pathways. The mitotic checkpoint serine/threonine protein kinase BUB1 beta (BUB1B), has been known to be essential in the mitotic checkpoint during normal mitosis progression. Recently, an analysis on multiple public datasets of gene expression discovered that BUB1B is associated with early distant metastases in breast cancer (Gusev et al., 2013). Here we took BUB1B and its neighbors to exemplify the inferred network structure difference in breast cancer patients with metastases (Fig. 2). In this group of patients, BUB1B possessed a higher node degree in the pLasso-inferred network (34) than that in the Lasso-inferred network (19). We found 26 of 42 edges present in the prior knowledge were included in the pLasso-inferred network, whereas only 7 edges in the prior were recovered in the Lasso-inferred network. As expected, one effect of incorporating prior knowledge is the inclusion of more edges from the prior. In addition to this effect, because of the nature of Lasso’s linear regression, addition of edges from the prior will yield information on the conditional independence between other edges. This could trigger the elimination of spurious edges in the estimated network, as seen in this application, where we found 4 edges inferred by the Lasso method were not present in the network inferred by the pLasso (Fig. 2).

Fig. 2.

BUB1B and its neighbor genes inferred from pLasso (left) and Lasso (right) methods in patients with metastases. Dark color circles indicated the inferred neighbor genes existed in the prior databases. The edges in bold marked difference between Lasso- and pLasso-inferred networks

To evaluate the performance of our method, we examined the 100 hub genes having most neighbors in the inferred network of patients showing distant metastasis, but not in the other group of metastasis-free patients. Among the 214 lymph–node-negative breast cancer patients we used to construct the gene networks, 107 showed evidence of distant metastasis and were considered as failure in our distant-metastasis-free survival analysis. For each of the hub genes we investigated, we divided the patients into two equal groups based on their expression values of the hub genes: the high-expression group and the low-expression group. We expected that for some of these hubs, the two groups would exhibit significant differences in their distant metastasis-free survival outcome. To test this hypothesis, we used the ‘Survival’ package in R to calculate the Kaplan–Meier survival curves. For each hub, its statistical significance was determined by controlling the false discovery rate at 0.2 with the Benjamini and Hochberg multiple testing procedure for the P-values obtained from log-rank tests (Benjamini and Hochberg, 1995). Based on this significance criterion, we found that the gene expression values of 18% of hubs were significantly associated with breast cancer patient outcomes. For the networks inferred from original Lasso method, the expression values of 13% of hubs showed significant association with breast cancer outcome. As the control, only 8 ± 2% of 100 randomly selected genes demonstrated the significant association between their expression values and the breast cancer patient outcome.

4.2 Ovarian cancer data

As we did with the breast cancer data, we used a prior gene network compiled from the KEGG database and the PC as prior knowledge in our network inference. For the pLasso setting, we also set the precision of the prior knowledge to 0.6. We investigated the gene networks of patients with progressed disease and the disease/progression-free patients. In the group of patients with progressed disease, the inferred network had 4636 genes and 25 836 edges, whereas the disease-free patient group yielded a network with 4630 genes and 25 673 edges. Disease-free survival analysis on the hub genes from the inferred networks was performed. We found 22% of hubs were significantly associated with ovarian cancer disease-free survival outcome (FDR correct q < 0.2). As a comparison, only 18% the hubs obtained from the original Lasso method and 5 ± 2% random genes demonstrated significant association between their expression values and the ovarian cancer survival outcome.

4.3 Comparison with other methods

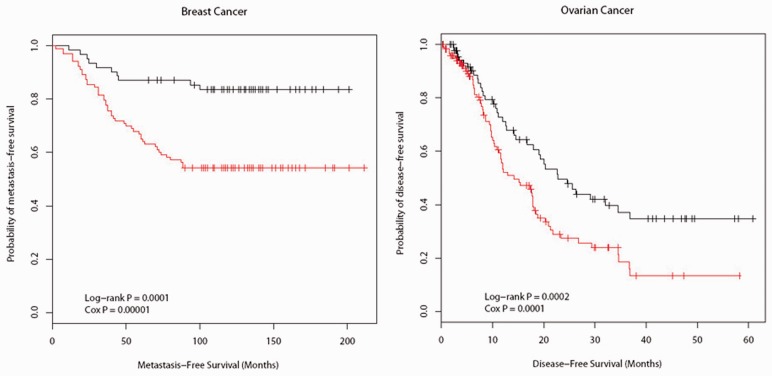
Given the clear association between a subset of inferred network hubs with prognosis for both breast cancer patients and ovarian cancer patients, we further determined if a list of selected gene hubs can be used to predict survival outcome and compared their performance with those obtained from other methods that were based on genome-wide expression data alone. As described in Section 2.5, we calculated the risk score for each patient based on the selected genes. The patients were then divided into two groups based on their risk scores. Kaplan–Meier survival analyses on two patient groups were performed and showed the selected genes from the breast cancer and the ovarian cancer networks inferred by the pLasso method were significantly associated with survival outcome in their corresponding validation datasets (Fig. 3).

Fig. 3.

Kaplan–Meier analysis for metastasis-free survival (breast cancer) and disease-free survival (ovarian cancer) on independent validation datasets. Patients were divided into two groups based on their risk scores: the high-risk group (black) and the low-risk group (red)

The univariate Cox proportional analysis of the gene signatures identified from different methods for survival outcome and the predictive power of these genes in the validation dataset were compared and summarized in Table 3. It was demonstrated that the genes selected from our pLasso method yielded the highest sensitivity (0.81 and 0.69 for breast cancer and ovarian cancer analysis, respectively) among others at a comparable specificity level. We should also note that, whereas the pLasso method effectively identified individual genes with significant predictive power for survival outcome, it also provided information on gene network topology and the relationship among genes. Our pLasso method is effective in inferring clinically significant networks, as demonstrated by the predictive power of the network hubs and their significant association with patients’ prognosis. We also investigated the overlap between the gene signatures from pLasso with those previously identified. We found only 4 and 5 genes overlapped with the 76-gene signature and the 193-gene signature corresponding to breast cancer and ovarian cancer, respectively. It indicated that the pLasso method was effective in identifying novel genes that can serve as potential markers for prognosis prediction.

Table 3.

Univariate Cox analysis and the predictive power of the gene signatures selected from different methods

Methods	Cox analysis		Prediction accuracy
	P	HR (95% CI)	Sensitivity	Specificity
Breast cancer dataset (van de Vijver et al., 2002)
pLasso	0.00001	2.89 (1.68–5.13)	0.81	0.48
Lasso	0.007	1.97 (1.10–2.99)	0.74	0.41
GeneNet	0.003	2.18 (1.14–3.52)	0.71	0.46
SAM	0.007	2.03 (1.21–3.40)	0.76	0.41
76-gene  signature	0.00002	2.23 (1.45–3.43)	0.78	0.47
TCGA ovarian cancer dataset
pLasso	0.0001	1.94 (1.40–2.81)	0.69	0.54
Lasso	0.0009	1.58 (1.28–2.10)	0.63	0.51
GeneNet	0.0006	1.33 (1.15–1.56)	0.58	0.52
SAM	0.0003	1.50 (1.16–2.42)	0.62	0.48
193-gene  signature	0.0009	1.16 (1.11–1.28)	0.60	0.52

Note: The patient samples in the validation datasets were classified into two groups based on the selected genes. P, P-value of Cox analysis. HR, Hazard Ratio.

5 DISCUSSION AND CONCLUSION

Inferring gene networks in a high-dimensional data framework is never a trivial problem. Particularly, the noise inherent in the measurements always dampens the power of making inferences on a genome scale. Therefore, using only gene expression data will not likely be sufficient. Recent techniques attempt to integrate additional data sources or introduce constraints to help guide the inference procedure. Motivated by the application of incorporating prior pathway and network structure information into the analysis of genomic data, we have taken advantage of the Lasso method and its apparent Bayesian perspective in the Gaussian graphic framework. Taking into account that validated gene interactions in prior should occur at a much higher frequency compared with undocumented interactions in real networks, we partition edges in a graphical model into two subsets—a known gene interaction group and an unknown gene interaction group, and then assign the former group with a smaller regularization parameter in Lasso regression compared with the other group. Implemented in neighborhood selection with Lasso, the proposed method was shown to have better performance in recovering network structures compared with the traditional Lasso in our simulated studies and real data analysis.

Lasso is a model selection method shown to be consistent in variable selection under certain conditions (Zhao and Yu, 2006). Its consistency is highly dependent on the right choice of the penalty parameter. In practical implementation, the penalty parameter is typically tuned to achieve optimal prediction accuracy based on cross-validation (CV). However, this procedure was shown not to be consistent in terms of variable selection, with a potential overfitting effect in the resulting model (Meinshausen and Buhlmann, 2006; Wang et al., 2007). This problem will be vastly exaggerated when the sparsity of the network is assumed in the domain of biological network inference. On the other hand, BIC is a well-known model selection criterion, which tends to favor parsimonious models. The comparison of CV and BIC for optimal regularized parameter selection in network inference demonstrated that BIC preferentially resulted in sparse networks and had less overfitting effect than CV (Supplementary Table S4). The results are consistent with those in the previous study (Wang et al., 2007). We also defined a BIC score that incorporated our prior knowledge on network sparsity to address the network over sparsity issue of the original BIC, especially in the setting of large networks with small sample sizes (n < p). mBIC was shown to have less overfitting effect than CV, while consistently outperforming CV in identifying true network edges (Supplementary Table S4). Compared with a CV-based method, the modified form of BIC presents advantages of considering the data fitting during model selection, being more straightforward to compute and more easily to incorporate prior knowledge, and providing better performance in network inference. Therefore, BIC and its modified forms were adopted in our study to select the optimal regularization parameter.

Our proposed pLasso method is conceptually analogous to some other approaches that use a mixture of prior distributions to represent the gene interactions absent and present in the prior knowledge, respectively (Tai and Pan, 2007a, b; Wei and Pan, 2008). However, our approach is different in that we took advantage of the Bayesian perspective of the lasso procedure and modeled the Laplacian prior distributions for the regression coefficients between genes by specifying different values of the regularized parameter in lasso penalty terms. Although the importance of incorporating prior knowledge into analysis has been widely recognized, there seems to be few studies in using the lasso penalty terms to differentiate the gene interactions absent and present in the prior knowledge. Out study is also clearly different from other approaches in terms of its application domain. It is performed in the framework of Gaussian graphical model for inferring a genome-wide gene association network, whereas most other applications incorporating prior information focused on classification analysis (Tai and Pan, 2007a, b), detecting differential gene expression (Li and Li, 2008; Wei and Li, 2007) or identifying transcription factor targets in a small scale (Wei and Pan, 2008).

In our real data analysis, we used the prior knowledge compiled from the KEGG database and the PC web resource. Both KEGG and PC represent an incomplete recapitulation of the true underlying network and may contain some irrelevant interactions. To improve the level of completeness of the prior knowledge, it is natural to combine the information from both resources for network inference. The quality of the prior is another contributing factor to the method performance. Taking into account the relative robustness of our method to the estimated precision level of the prior (Table 2), we used the same precision rates in the application of KEGG and PC prior information. It was demonstrated that using the combined prior information from PC and KEGG yielded a network with more genes and edges than using either the PC or KEGG alone, while achieving better performance in predicting clinical outcome in both the breast cancer and the ovarian cancer datasets (Supplementary Table S5). It was also observed when using KEGG alone as the prior, the performance of the pLasso was not as good as that using PC alone or using the combined prior. These results suggest the coverage of prior knowledge is a more significant contributing factor to the method performance than the quality in this real data application. Based on these results, it is expected the pLasso method lends itself a potential improvement of performance as our knowledge of pathways accumulates over time and an increasing amount of prior knowledge gets incorporated into the analysis.