Abstract
Mediators are intermediate variables in the causal pathway between an exposure and an outcome. Mediation analysis investigates the extent to which exposure effects occur through these variables, thus revealing causal mechanisms. In this paper, we consider the estimation of the mediation effect when the outcome is binary and multiple mediators of different types exist. We give a precise definition of the total mediation effect as well as decomposed mediation effects through individual or sets of mediators using the potential outcomes framework. We formulate a model of joint distribution (probit-normal) using continuous latent variables for any binary mediators to account for correlations among multiple mediators. A mediation formula approach is proposed to estimate the total mediation effect and decomposed mediation effects based on this parametric model. Estimation of mediation effects through individual or subsets of mediators requires an assumption involving the joint distribution of multiple counterfactuals. We conduct a simulation study that demonstrates low bias of mediation effect estimators for two-mediator models with various combinations of mediator types. The results also show that the power to detect a non-zero total mediation effect increases as the correlation coefficient between two mediators increases, while power for individual mediation effects reaches a maximum when the mediators are uncorrelated. We illustrate our approach by applying it to a retrospective cohort study of dental caries in adolescents with low and high socioeconomic status. Sensitivity analysis is performed to assess the robustness of conclusions regarding mediation effects when the assumption of no unmeasured mediator-outcome confounders is violated.
Keywords: mediation analysis, multiple mediators, latent variables, overall mediation effect, decomposed mediation effect, mediation formula, sensitivity analysis
1. INTRODUCTION
Randomized clinical trials and observational studies typically evaluate an overall treatment or exposure effect on a response. Of even greater scientific interest may be to explain by what means the treatment or exposure effect occurs, a goal that invokes the idea of mediation analysis. One way that a researcher can explain the mechanism by which one variable affects another is through the identification of mediating intermediate variables (or mediators). A well-known example of a mediated relationship in psychology is the effect of attitude on behavior which is mediated by intentions [1]. Another example is the mediation of the effect of the apoliprotein E ε4 allele on cognitive impairment through an increase in the likelihood of chronic cerebral infarction [2, 3].
At least a dozen methods have been proposed for testing the simple mediation hypothesis that the effect of an independent variable T on a dependent variable Y is mediated (at least in part) by an intermediate variable M [4]. Traditionally, mediation analysis has been dominated by linear regression (association) model paradigms, and the mediation effect assessed by difference in coefficient [5] or product of coefficient approaches [6]. More recently, causal mediation analysis, namely, methods based on a causal model (usually, potential outcomes) framework, have been developed [7, 8]. In one such causal model approach, Pearl [9] proposed a mediation formula, applicable to nonlinear models for discrete or continuous outcome variables, that permits the evaluation of natural direct and indirect (or mediation) effects. More generally, mediating processes may include multiple mediators. In school-based drug prevention, for example, primary prevention programs target multiple mediators such as resistance skills and social norms to reduce drug use [10]. Reynolds et al. [11] explored knowledge, availability of fruits and vegetables, and parental consumption as mediators of a school-based nutrition intervention to increase healthy food consumption in children.
Models with more than one mediator are straightforward extensions of single-mediator models in the linear case, and the product of coefficients approach can be used for the estimation of multiple mediation effects [12, 13]. With multiple-mediator models, additional questions can be raised. For example, one may investigate the total mediation (or indirect) effect, that is, the extent to which a set of intermediate variables collectively mediate the effect of T to Y. Alternatively, one may wish to assess the extent of mediation through each individual mediator. For inference on mediation effects, Preacher and Hayes [13] advocates the bootstrap – especially bias-corrected bootstrap – over the multivariate delta method [14], since the former provides the most powerful and valid method of obtaining confidence intervals (CIs) for specific indirect effect under most conditions.
For a non-linear response models, a non-standard, for example, mediation formula, approach may be needed. However, such approaches have so far focused on a single mediator. An extension of the mediation formula approach for multiple, and possibly mixed types of mediators, will require modeling of the joint distribution of discrete and continuous outcomes. Such modeling includes three main approaches. The first approach is based on a conditioning argument that allows the joint distribution to be factorized into a marginal and a conditional density [15, 16]. A drawback of the conditioning approach for mixed outcome models is that it does not directly lead to marginal inferences [17]. Also, conditional models do not easily extend to the settings of three or more outcomes, and the correlations between pairs of outcomes cannot be directly estimated. The second approach attempts to specify the joint density of two outcomes directly. Multivariate methods are well established for the modeling of multivariate normally distributed outcomes [18]. To analyze mixed types of outcomes, bivariate (or multivariate) continuous variables are considered with components being either explicitly observed or latent continuous variables underlying the discrete outcomes [19]. The level of an observed discrete outcome is determined according to whether or not the corresponding latent variable exceeds some threshold values. A common example is the probit-type model which assumes an unobservable normally distributed random variable underlying the binary outcome [20]. Instead of using latent variables, the third approach directly specifies the joint distribution via a mixed effects model in which each outcome is modeled conditional on a common random effect or correlated random effects [21]. In this paper, the second approach, which has the advantage of the direct specification of mediator correlation parameters, will be used. This approach is implemented for mixed types of mediators by specifying the joint distribution of the continuous mediators and continuous latent variables underlying binary mediators.
An approach to causal mediation analysis that accommodates multiple mediators is likely to provide a more accurate assessment of mediation effects in many research contexts. A limitation of standard (such as product of coefficients) approaches for multiple mediator analysis is that they rely on linearity of the regression models, a restriction that may be difficult to justify unless the response and mediator are normally distributed. However, in medical research, the outcome or the mediator is often not normally distributed. The mediation formula approach of Albert and Nelson [22] handles sequential mediators, but not ‘contemporaneous’ mediators, for a discrete (count) outcome. Thus, the problem of causal mediation analysis in nonlinear models for multiple (contemporaneous) mediators does not appear to have been previously addressed in the literature. For estimation of the total indirect effect for a dichotomous outcome with mixed types of mediators, we apply the mediation formula approach under a sequential ignorability assumption. In addition, estimation of the mediation effect through an individual mediator or a subset of mediators is possible with additional identifying assumptions.
The remainder of this work proceeds as follows. In Section 2, we define, for multiple-mediator models with a dichotomous outcome, the natural direct, (total) indirect effects, and decomposed mediation effects through individual or sets of mediators. Section 3 presents a mediation formula approach to estimate the total and decomposed mediation effects under given identification assumptions. We introduce the association models and the maximum likelihood estimation methods for multiple mediator models in Section 4. Section 5 proposes a sensitivity analysis that can be implemented by applied researchers to quantify the robustness of their conclusion to the potential violation of sequential ignorability assumptions. Simulation studies are used in Section 6 to examine the statistical properties of the proposed methods. Section 7 describes the application of the proposed method to a dental caries study and presents sensitivity analysis results. Discussion and suggestions for further research are presented in Section 8.
2. DEFINING TOTAL AND DECOMPOSITION OF MEDIATION EFFECTS
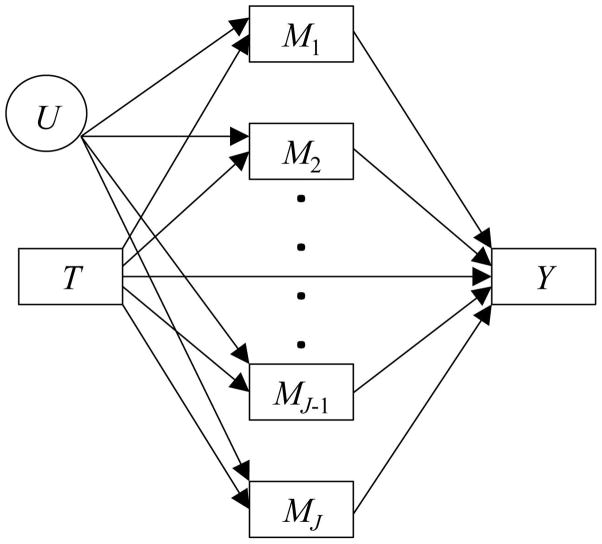
Consider the general causal model including a binary exposure or treatment indicator (T with a specific level represented by t ∈ {0,1}), J mediators (M1, M2, …, MJ) and a dichotomous outcome (Y), where T may affect Y directly and/or T may affect any of the Mj, j = 1 to J, which then affect Y. Figure 1 shows the path diagram. We can define the causal mediation effects of interest using nested potential outcomes [8] within this multiple-mediator model. The total mediation effect (through the set {Mj, j = 1, …, J}) under exposure t is defined as
Figure 1.
Path diagram for a multiple-mediator model with J mediators. T = exposure or treatment; Mj = mediator j, j = 1, …, J; Y = outcome; U = set of unobserved confounders of associations among mediators. T may exert indirect effects on Y through M1, M2, …, MJ, or affect Y directly.
| (1) |
Here, Y(t, M1(t′), M2(t′), …, MJ(t′)) denotes the potential outcome that Y would attain if T was set to t, and each Mj set to the counterfactual value that would be observed if T was set to t′. IE(t) is called the natural indirect effect, and represents the difference between two mean potential outcomes that would result under exposure status t, but where all mediators takes values that would result under two different exposure statuses. Similarly, we can define the natural direct effect and the total causal effect in the potential outcomes framework as
| (2) |
| (3) |
Thus, the natural indirect effect under one exposure status and the natural direct effect under the other exposure status sum to the total causal effect. Here, we consider the decomposition involving IE(1) and DE(0) denoted as IE and DE; for the other decomposition (involving IE(0) and DE(1)) the method will be similar.
In multiple-mediator models, we can further consider mediation effects through an individual mediator or sets of mediators. The total natural indirect effect can be broken into J path effects within a J-mediator model; we use ‘IEj (t0, t1, …, tj−1, tj+1, …, tJ)’ to denote the path (or mediation) effect through the jth mediator (Figure 1) with exposure set to t0 and other mediators except for Mj set to the values attained under exposure levels t1, …, tj−1, tj+1, …, tJ respectively. IEj (t0, t1, …, tj−1, tj+1, …, tJ) can be defined as the difference between two mean potential outcomes as follows,
| (4) |
Mediation effects through sets of mediators can be defined as the sum of mediation effects through the component individual mediators. Note that 2J versions of IEj(t0, t1, …, tj−1, tj+1, …, tJ = 0 or 1), the indirect effect of Mj, can be formulated corresponding to 2J combinations of exposure settings for the outcome and other mediators in a J-mediator model. We use only one of them, IEj (t0 = 1, t1 = 0, …, tj−1 = 0, tj+1 = 1, …, tJ = 1), denoted as IEj for simplicity; the other possible estimands can be handled similarly and thus are not discussed here. Of note, this defined IEj’s provide a proper decomposition of a total (indirect) effect among individual mediators as follows,
| (5) |
3. ANALYSIS OF TOTAL AND DECOMPOSED MEDIATION EFFECTS
3.1. Identification assumptions for causal mediation effects in multiple-mediator models
We present identification results for the (total) indirect and direct effects (defined by (1) and (2)) as well as mediation effects through individual mediators (defined by (4)) using the potential outcomes framework described above. Under a particular version of the sequential ignorability assumption, the mediation effect estimators are identified nonparametrically in the multiple-mediator causal model. We first define our identifying assumption which extends Imai et al.’s version [23].
Assumption 1 (Sequential Ignorability)
| (6) |
| (7) |
for t0, t1, …, tJ = 0, 1, and w ∈ Ω, where Ω denotes the support of the distribution of W.
First, given the observed baseline covariates (W), the exposure or treatment is assumed to be statistically independent of potential outcomes and potential mediators. The second part of Assumption 1 states that all mediators are independent of potential outcomes given the observed exposure or treatment and pretreatment covariates. In addition, we make the consistency assumption throughout, namely, Yi(t) = Yi when Ti = t; that is, for any individual i the potential outcome of Y setting T = t is equal to the observed outcome if the individual happened to receive treatment level t. This assumption provides the connection between potential and observed outcomes.
3.2. Estimation of total and decomposed mediation effects for multiple-mediator models
To demonstrate identifiability of total and decomposed mediation effects for multiple-mediator models, we will examine the identification of the relevant potential outcome means (of the general form E{Y(t0, M1(t1), …, MJ(tJ))}) given baseline covariate W under sequential ignorability (Assumption 1), where conditioning on W is left out of the notation for brevity. Under Assumption 1 (along with the consistency assumption) it can be shown that,
| (8) |
A proof of formula (8) is given in Appendix A. Integration can be replaced with summation in the case of discrete mediators. Formula (8) shows that under sequential ignorability, the expected potential outcomes (left-hand side of the equation), used in the definition of the causal mediation effects, can be expressed as a function of association parameters (in a model for Y) that are directly estimable from the observed data. Estimability of the expected potential outcomes is then attained so long as the joint distribution of the mediator potential outcomes (last term in the expression on the right-hand side of (8)) can be estimated.
The total natural indirect effect, direct effect and total causal effect are identifiable from formula (8) with known or estimated values for the joint distribution of (M1(0), …, MJ(0)) and of (M1(1), …, MJ(1)). However, when assessing mediation effects through individual or sets of mediators we require joint distributions of (M1(t1), …, MJ(tJ)) in which the tj’s are not all equal; such a joint distribution is not estimable because this joint potential outcome cannot be observed for the same subject. For identifiability, we need to make additional assumptions regarding the joint distribution of (M1(t1), …, MJ(tJ)). In fact, the marginal distribution of Mj(tj), j = 1, …, J, is estimable, and if each correlation coefficient ρkl(tk, tl) between Mk(tk) and Ml(tl), k < l, tk ≠ tl is pre-specified, then the mean potential outcome in formula (8) is identifiable and therefore so is the decomposed natural indirect effect through individual or sets of mediators. We use the simplifying assumption of a common correlation for each pair of mediators, that is, ρkl(tk, tl) = ρkl for all tk, tl. In fact, we may allow more general models, but generally a full specification is not needed; in particular, the identification of any specific individual mediation effect needs only one of the two parameters, ρkl(0, 1) and ρkl(1, 0), e. g., the former is needed to identify IEj defined above.
To evaluate the joint integrals, we may also use Monte Carlo integration [24], a numerical integration technique that uses pseudo random numbers generated from a joint distribution of mediator counterfactuals. Suppose (m1n, …, mJn) and (m1n′, …, mJn′) are drawn from the joint distributions fM1(0), …,MJ(0) (m1, …, mJ) and fM1(1), …, MJ(1) (m1′, …, mJ′) respectively. Formula (1) can then be approximated by the following (using Monte Carlo approximations for formula (8)),
| (9) |
The indirect effects through individual mediators (the IEj as defined in formula (4)) can be expressed in a similar way.
4. ASSOCIATION MODELS
Estimation of mediation effects proceeds by estimating the association model parameters in the mediation formula. In this paper we consider models for the joint distribution of binary and normally distributed continuous mediators.
4.1. Regression models
We assume the following regression models for a dichotomous outcome Y and binary and/or continuous, and possibly correlated, mediators Mj, j = 1, …, J,
| (10) |
| (11) |
If Mj is a binary mediator, Mj(*) denote and is a latent variable underlying Mj, such that . In this latent variable model, Var(εj) is not identified, and standard practice assumes that Var(εj) = 1 [25, 26]. Otherwise if Mj is a continuous mediator, Mj(*) denotes Mj and Var(εj) is estimable. In addition, as indicated above, we make the potential outcomes model assumption of a constant unstructured correlation matrix for the J continuous (observed and latent) mediators regardless of the set exposure statuses. The βj′, αj0’s and αj1’s are regression parameters, and W is a baseline covariate vector with corresponding coefficient vectors β′ and αj′.
4.2. Model of the joint distribution for multiple mediators
We will illustrate our estimation approach by formulating the joint distribution of a single continuous mediator and a single binary mediator, which is easily extended to cases with multiple continuous mediators or multiple binary mediators. Let M1i and M2i be two mediators measured on subject i (i = 1, 2, …, N), where M1 denotes the binary mediator and M2 the continuous mediator. Let M1i* be a latent variable underlying M1i, such that M1i = I{M1i* ≥ 0}. For the bivariate response, we assume that the unobserved latent variable M1i* and the observed continuous mediator M2i for individual i together follow a bivariate normal model of the form
where α1 and α2 are fixed effect regression coefficient vectors of the covariate vector Xi for the binary and continuous endpoints, respectively, and Xi may include treatment T and subsets of baseline covariates W. The variance matrix of the residual (mean zero) error vector is assumed to be
Thus, this model specifies an unstructured correlation matrix for the two mediators. The parameter σ1 is not identified as mentioned above and is assumed that σ1 = 1. The specification of a common design vector Xi for two mediators is not necessary, though a reasonable assumption in our application.
4.3. Maximum likelihood estimation
As standard linear or logistic regression models are employed for the marginal models, maximum likelihood estimation for the regression parameters is straightforward. For the joint mediator models, continuing our focus on the case of a single continuous and a single binary mediator, we note that the joint likelihood for the two mediators of subject i can be decomposed as
| (12) |
The first term above is the marginal normal distribution given previously. The conditional density function is given by
Given this formulation, it is easy to then derive the contribution of M1i to the likelihood. Specifically, we have
| (13) |
Therefore, we can write the subject-specific contribution to the joint likelihood for (M1i, M2i) as the product of the marginal normal likelihood for M2i times either the Bernoulli probability (13) or the probability of the complement, depending on whether M1i is 1 or 0 respectively. The log-likelihood for the data is defined by summing the log of the expression in formula (12) over all subjects. Here, model estimation can be implemented in SAS (Version 9.2, SAS Institute Inc., Cary, NC, USA) using either the NLMIXED procedure to specify the likelihood function manually or the QLIM procedure which constructs the likelihood automatically from specified regression models.
5. SENSITIVITY ANALYSIS
Sensitivity analysis explores the impact of departures from untestable assumptions and thus is an important component of our approach. Two sensitivity analyses are provided in this section. The first one assesses the effect of the assumed correlation coefficient ρkl(tk, tl) between Mk(*)(tk) and , k < l, tk ≠ tl on the estimation of decomposed mediation effects, and the second one evaluates the effect of violation of the no unmeasured mediator-outcome confounder assumption (7) on mediation effect estimation. For ease of presentation, we use a two-mediator model with one binary mediator (M1) and one continuous mediator (M2) to illustrate our sensitivity analysis approach in this section. The approach described can be easily extended to models with more than two mediators.
5.1. Effect of assumed correlation coefficient on decomposed mediation effect estimation
As stated in Section 3.2, the correlation coefficient ρ′ (indicating ρ12(0, 1)) between counterfactuals M1*(0) and M2(1) needs to be pre-specified for the estimation of decomposed mediation effects IE1 and IE2. We may examine the robustness of the IE1 and IE2 estimators, thus providing a sensitivity analysis, by varying the specified counterfactual correlation ρ′ over the interval −1 to 1.
5.2. Sensitivity analysis for violation of no unmeasured mediator-outcome confounder assumption
We propose a sensitivity analysis based on the approach of Albert and Nelson [22] and Wang and Albert [27], which applies the Gaussian copula [28], to assess the impact of non-zero correlations between Y(t0, m1, m2) and Mj(tj) (j = 1, 2) on mediation effect estimates, where Y and M1 are binary and M2 is continuous (normally distributed). In order to handle binary variables, corresponding continuous latent variables are introduced, such that the observed binary event is realized if the latent variable exceeds some threshold. Specifically, for the probit-type model, the threshold is 0. Then Y*(t0, m1, m2), M1*(t1) and M2(t2) are assumed to have a trivariate normal distribution with covariance matrix Σ and mean μ. The marginal distributions of Y*(t0, m1, m2), M1*(t1) and M2(t2) are estimable, as is the correlation coefficient ρ between M1*(t1) and M2(t2) under the assumption that the correlation between M1*(t1) and M2(t2) is constant over all t1 and t2. Alternatively, we can use any specified value for ρ as considered in the first sensitivity analysis above. The correlation between Y*(t0, m1, m2) and M1*(t1) is denoted as ρ1 and the correlation between Y*(t0, m1, m2) and M2(t2) as ρ2. Similarly, we assume that ρ1 and ρ2 are constant over all t0, t1, and t2. Nonzero ρ1 (or ρ2) implies that there exists an omitted variable that affects both M1 (or M2) and Y. We propose a sensitivity analysis using Monte Carlo approach to estimate the conditional probability P{Y(t0, m1, m2) = 1} under the assumed ρ1 and ρ2. This approach involves the following algorithm:
Sample the pair of mediator values (m1i*, m2i) ~ fM1*(t1), M2(t2)(m1*, m2), i = 1, 2, …, n. If m1i* > 0 then m1i = 1, otherwise, m1i = 0.
The conditional distribution Y*(t0, m1i, m2i) is obtained based on the trivariate normal distribution of Y*(t0, m1i, m2i), M1*(t1) and M2(t2) with estimated ρ as well as pre-specified ρ1 and ρ2.
Compute P{Y(t0, m1i, m2i) = 1} as P{Y*(t0, m1i, m2i) > 0} based on the distribution in (2).
Repeat steps 1–3 n times and obtain the potential outcome mean E(Y(t0, M1(t1), M2(t2))) as .
This algorithm provides an estimation method for the general expected value of potential outcome Y(t0, M1(t1), M2(t2)) assuming specified correlations (ρ1 and ρ2) between each mediators and the outcome adjusted for the mediators. It thus provides a sensitivity analysis of the total and decomposed natural indirect effect for departures from the sequential ignorability assumption (7).
6. SIMULATION STUDY
In this section, a simulation study was used to assess the empirical bias, coverage probability and power of total and decomposed natural indirect effect estimators from our mediation formula approach for a binary outcome in a two-mediator model. In addition, coverage probabilities were compared for different confidence interval methods. We used SAS/IML for all simulations and statistical analyses.
6.1. Empirical Bias
To assess the empirical bias of mediation effect estimators, we conducted simulations using a 3 × 4 × 3 × 3 factorial design. First of all, we consider two-mediator models with three different combinations of mediator types, two binary, one binary and one continuous, or two continuous mediators. For each two-mediator model, four correlation coefficients values (−0.5, 0, 0.5 and 0.9) between the two mediators (or latent variables underlying any binary mediators) are assumed. The exposure effect is similar for all scenarios (around 0.2). The magnitudes of the total natural indirect effect, IE, (involving parameters β1, β2, α11 and α21) and the natural direct effect, DE, (involving β3) are studied under three cases: dominant IE, dominant DE, and similar magnitude of IE and DE. The last factor, related to the decomposition of the total natural indirect effect, consists of three scenarios: indirect effect exclusively through one mediator, similar mediation effect through each mediator, and substantial mediation effects through each mediator but with different directions. Sample sizes of 200 (100 per exposure group) and 500 (250 per exposure group) were used for each scenario.
The bivariate normal distributed error terms for two mediators (or underlying latent variables corresponding to binary mediators) were generated using the ‘RANDNORMAL’ function in SAS/IML. No baseline covariates were used in our simulation scenarios to simplify the calculations. For each given exposure, the mediator variables or corresponding latent variables were generated using equation (11) with above produced error terms. The response variates were then generated according to the logistic regression model (10) given the individual exposure and observed mediators (possibly from corresponding latent variables). For each dataset, we estimated the total and decomposed natural indirect effects using formulae (1), (4) and (8). The true value is defined by the same function, with true coefficients in place of estimates. In addition, in the calculation of both true and estimated decomposed mediation effects, we assume that the correlation between M1(*)(t1) and M2(*)(t2) (which is estimable only for t1 = t2) is constant over all t1 and t2. We performed 1000 independent datasets and the following statistics for mediation effects estimators (total or individual) were provided: the average estimate; the average percent error (PE, estimate minus true value then divided by true value); the SD of the estimate.
We focus on results for the two-mediator model with one binary mediator and one continuous mediator; results for two-mediator model with either two binary or continuous mediators are similar and therefore not presented. The simulation results are given in Table 1 with total sample size 200. We see that the mediation formula approach generally produces a small bias in its estimation of IE, IE1 and IE2 in most scenarios. However, the proposed approach may provide substantial relative biases in some situations (putting aside cases where the true mediation effect is very small and thus, the average relative bias is unreliable). One such scenario is where the two mediators have mediation effects in different directions (the sixth ‘mixed direction’ scenario in each set); the other scenario has similar mediation effect magnitudes through either mediator but a correlation coefficient between the two mediators of 0.9 (the fifth ‘high mediator correlation’ scenario). In the ‘mixed direction’ scenario, our approach tends to produce high relative bias for the IE (overall) estimator, but low relative bias for the IE1 and IE2 (individual) estimators (less than 4%); on the other hand, high relative bias for individual and low relative bias (less than 2%) for overall mediation effect estimators can be detected in the ‘high mediator correlation’ scenario. When the sample size per group is increased to 250, the proposed approach shows low relative bias for all scenarios (less than 8.9%, data not shown).
Table 1.
Simulation statistics of overall and decomposed mediation effect estimators for a dichotomous outcome model with two mediators (one binary (M1) and one continuous (M2)), n = 100 per group.
| ρ(M1, M2) | True DE | True IE | True IE1 | True IE2 | Est DE | Overall IE
|
IE1
|
IE2
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave Est | Ave PE (%) | SD of Est | Ave Est | Ave PE (%) | SD of Est | Ave Est | Ave PE (%) | SD of Est | ||||||
| −0.5 | 0.185 | 0.024 | 0.024 | 0.000 | 0.184 | 0.025 | 3.66 | 0.034 | 0.025 | 1.66 | 0.017 | 0.000 | - | 0.026 |
| 0.211 | 0.020 | 0.010 | 0.010 | 0.210 | 0.022 | 8.70 | 0.034 | 0.011 | 2.53 | 0.014 | 0.011 | 15.21 | 0.028 | |
| 0.183 | 0.020 | 0.198 | −0.179 | 0.173 | 0.033 | 70.82 | 0.100 | 0.209 | 5.36 | 0.082 | −0.176 | −1.78 | 0.035 | |
| 0.097 | 0.107 | 0.107 | 0.000 | 0.098 | 0.107 | 0.63 | 0.069 | 0.107 | 0.44 | 0.056 | 0.000 | - | 0.024 | |
| 0.099 | 0.113 | 0.056 | 0.056 | 0.097 | 0.116 | 2.74 | 0.095 | 0.057 | 1.81 | 0.054 | 0.058 | 3.67 | 0.061 | |
| 0.092 | 0.101 | 0.309 | −0.208 | 0.106 | 0.090 | −10.89 | 0.124 | 0.297 | −3.94 | 0.107 | −0.207 | −0.57 | 0.036 | |
| 0.023 | 0.179 | 0.179 | 0.000 | 0.022 | 0.178 | −0.53 | 0.087 | 0.177 | −1.58 | 0.056 | 0.002 | - | 0.047 | |
| 0.024 | 0.182 | 0.093 | 0.089 | 0.025 | 0.178 | −2.07 | 0.078 | 0.090 | −3.24 | 0.048 | 0.088 | −0.85 | 0.048 | |
| 0.021 | 0.188 | 0.305 | −0.117 | 0.020 | 0.193 | 2.26 | 0.122 | 0.308 | 0.88 | 0.109 | −0.115 | −1.33 | 0.030 | |
| 0 | 0.185 | 0.024 | 0.024 | 0.000 | 0.184 | 0.025 | 2.99 | 0.031 | 0.025 | 3.82 | 0.017 | −0.000 | - | 0.025 |
| 0.210 | 0.020 | 0.010 | 0.010 | 0.209 | 0.021 | 0.74 | 0.029 | 0.011 | 8.27 | 0.013 | 0.009 | −7.19 | 0.026 | |
| 0.192 | −0.005 | 0.190 | −0.195 | 0.187 | 0.001 | −121.7 | 0.077 | 0.194 | 2.25 | 0.060 | −0.193 | −0.64 | 0.037 | |
| 0.097 | 0.107 | 0.107 | 0.000 | 0.090 | 0.111 | 3.93 | 0.057 | 0.109 | 2.10 | 0.053 | 0.002 | - | 0.021 | |
| 0.098 | 0.112 | 0.056 | 0.056 | 0.097 | 0.115 | 2.12 | 0.075 | 0.056 | 0.19 | 0.049 | 0.058 | 4.04 | 0.057 | |
| 0.095 | 0.083 | 0.303 | −0.220 | 0.084 | 0.095 | 14.03 | 0.122 | 0.312 | 3.12 | 0.107 | −0.217 | −1.02 | 0.038 | |
| 0.023 | 0.179 | 0.179 | 0.000 | 0.022 | 0.180 | 0.27 | 0.071 | 0.178 | −0.79 | 0.053 | 0.002 | - | 0.044 | |
| 0.024 | 0.180 | 0.093 | 0.088 | 0.025 | 0.177 | −2.01 | 0.064 | 0.090 | −2.38 | 0.048 | 0.086 | −1.61 | 0.044 | |
| 0.021 | 0.180 | 0.302 | −0.122 | 0.020 | 0.180 | 0.12 | 0.114 | 0.301 | −0.15 | 0.107 | −0.121 | −0.56 | 0.031 | |
| 0.5 | 0.185 | 0.024 | 0.024 | 0.000 | 0.188 | 0.024 | 1.01 | 0.028 | 0.024 | −0.27 | 0.017 | 0.000 | - | 0.027 |
| 0.210 | 0.020 | 0.010 | 0.010 | 0.206 | 0.021 | 3.72 | 0.026 | 0.011 | 1.66 | 0.015 | 0.010 | 5.89 | 0.027 | |
| 0.207 | −0.019 | 0.185 | −0.204 | 0.204 | −0.012 | −35.22 | 0.063 | 0.189 | 2.10 | 0.056 | −0.202 | −1.38 | 0.035 | |
| 0.097 | 0.107 | 0.107 | 0.000 | 0.096 | 0.108 | 1.28 | 0.053 | 0.108 | 1.07 | 0.055 | 0.000 | - | 0.023 | |
| 0.098 | 0.112 | 0.056 | 0.056 | 0.102 | 0.111 | −0.75 | 0.065 | 0.053 | −6.42 | 0.054 | 0.059 | 4.95 | 0.059 | |
| 0.100 | 0.076 | 0.305 | −0.229 | 0.096 | 0.082 | 8.15 | 0.102 | 0.308 | 1.06 | 0.093 | −0.226 | −1.29 | 0.037 | |
| 0.023 | 0.179 | 0.179 | −0.000 | 0.031 | 0.174 | −2.88 | 0.062 | 0.176 | −1.85 | 0.053 | −0.002 | − | 0.047 | |
| 0.023 | 0.179 | 0.093 | 0.086 | 0.026 | 0.176 | −1.66 | 0.058 | 0.093 | −0.21 | 0.053 | 0.084 | −3.22 | 0.049 | |
| 0.022 | 0.177 | 0.303 | −0.126 | 0.013 | 0.184 | 3.85 | 0.097 | 0.307 | 1.53 | 0.096 | −0.124 | −1.73 | 0.031 | |
| 0.9 | 0.185 | 0.024 | 0.024 | 0.000 | 0.185 | 0.024 | −0.02 | 0.029 | 0.023 | −4.46 | 0.019 | 0.001 | - | 0.034 |
| 0.210 | 0.020 | 0.010 | 0.010 | 0.210 | 0.020 | −1.26 | 0.028 | 0.009 | −13.22 | 0.017 | 0.011 | 11.39 | 0.035 | |
| 0.224 | −0.025 | 0.181 | −0.206 | 0.228 | −0.025 | 2.31 | 0.053 | 0.176 | −2.93 | 0.054 | −0.201 | −2.31 | 0.036 | |
| 0.097 | 0.107 | 0.107 | −0.000 | 0.096 | 0.108 | 1.40 | 0.055 | 0.107 | 0.09 | 0.068 | 0.001 | - | 0.028 | |
| 0.097 | 0.112 | 0.056 | 0.056 | 0.099 | 0.110 | −1.70 | 0.060 | 0.051 | −10.59 | 0.064 | 0.060 | 7.30 | 0.073 | |
| 0.106 | 0.080 | 0.313 | −0.233 | 0.111 | 0.075 | −6.04 | 0.090 | 0.308 | −1.70 | 0.096 | −0.233 | −0.20 | 0.039 | |
| 0.023 | 0.179 | 0.179 | 0.000 | 0.024 | 0.179 | −0.16 | 0.056 | 0.177 | −1.53 | 0.067 | 0.002 | - | 0.059 | |
| 0.023 | 0.179 | 0.094 | 0.085 | 0.018 | 0.181 | 1.18 | 0.051 | 0.092 | −1.64 | 0.060 | 0.089 | 4.28 | 0.059 | |
| 0.023 | 0.180 | 0.307 | −0.128 | 0.024 | 0.180 | 0.18 | 0.096 | 0.306 | −0.45 | 0.103 | −0.126 | −1.33 | 0.033 | |
6.2. Coverage probability and power
In a second simulation study, we compared the coverage probability (CP) of 95% CIs constructed by different methods. Four such methods were evaluated in this section: jackknife [29], percentile bootstrap, bias-corrected bootstrap, and bootstrap-t [30]. The second goal was to assess the power to detect non-zero mediation effects under different correlation coefficients between two mediators. Four correlation coefficients were chosen as before, −0.5, 0, 0.5 and 0.9. For each correlation coefficient, we designed six different simulation scenarios: (1) small indirect effects with different signs for the two mediators; (2) substantial indirect effects with different signs and magnitudes for the two mediators; (3) zero indirect effect through each mediators; (4) zero indirect effect through the binary mediator and small indirect effect through the continuous mediator; (5) zero indirect effect through the continuous mediator and small indirect effect through the binary mediator; (6) small direct effects with the same sign for both mediators. Of note, for power comparison purpose, we adjusted the corresponding parameter β1, β2, α11 and α21 to make the true mediation estimand almost identical (constant up to the fourth decimal) for different specified correlation coefficient values. The CP is calculated as the percent of simulated datasets for which the 95% CIs covered the true value, and the power is calculated as the proportion of these 1000 replicated CIs that do not include zero. The results are summarized in Table 2 and Table 3 respectively.
Table 2.
Coverage probabilities of four confidence interval methods for overall and decomposed mediation effects in a dichotomous outcome model with two mediators (one binary (M1) and one continuous (M2)), n = 100 per group.
| ρ(M1, M2) | True IE | True IE1 | True IE2 | Overall IE
|
IE1
|
IE2
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jack knife | Boot | Bc | Bt | Jack knife | Boot | Bc | Bt | Jack knife | Boot | Bc | Bt | ||||
|
|
|
|
|||||||||||||
| −0.5 | 0.000 | 0.050 | −0.050 | 93.2 | 94.6 | 94.5 | 93.8 | 95.5 | 94.4 | 92.9 | 94.3 | 92.8 | 93.4 | 92.7 | 82.1 |
| 0.200 | 0.300 | −0.100 | 83.8 | 97.3 | 83.1 | 90.4 | 81.5 | 97.7 | 84.4 | 87.5 | 95.2 | 94.9 | 94.3 | 99.9 | |
| 0.000 | 0.000 | 0.000 | 95.2 | 94.7 | 93.7 | 93.5 | 99.7 | 98.0 | 95.1 | 90.8 | 97.0 | 93.1 | 90.6 | 68.0 | |
| 0.051 | 0.000 | 0.051 | 96.3 | 94.8 | 94.7 | 94.9 | 99.5 | 97.3 | 94.6 | 92.0 | 94.9 | 94.3 | 94.9 | 64.2 | |
| 0.050 | 0.050 | 0.000 | 94.2 | 95.1 | 94.9 | 94.5 | 96.0 | 95.3 | 94.6 | 94.4 | 96.8 | 95.6 | 93.0 | 99.2 | |
| 0.100 | 0.050 | 0.050 | 93.6 | 94.7 | 95.1 | 93.2 | 95.4 | 95.0 | 93.4 | 94.3 | 95.0 | 94.9 | 94.0 | 81.8 | |
| 0 | 0.000 | 0.050 | −0.050 | 94.1 | 94.1 | 93.5 | 93.6 | 96.2 | 94.7 | 93.6 | 93.8 | 94.8 | 94.9 | 94.1 | 85.0 |
| 0.200 | 0.300 | −0.100 | 91.4 | 94.8 | 89.7 | 91.9 | 91.5 | 94.5 | 89.0 | 91.6 | 94.4 | 94.0 | 94.6 | 99.9 | |
| 0.000 | 0.000 | 0.000 | 94.7 | 95.2 | 93.1 | 95.0 | 99.7 | 97.9 | 95.2 | 92.3 | 95.8 | 93.7 | 91.1 | 67.5 | |
| 0.051 | 0.000 | 0.051 | 95.2 | 94.8 | 94.1 | 94.9 | 99.7 | 97.4 | 95.4 | 93.0 | 94.0 | 94.2 | 94.1 | 61.7 | |
| 0.050 | 0.050 | 0.000 | 96.8 | 96.2 | 95.6 | 94.8 | 96.8 | 96.5 | 95.5 | 95.3 | 96.8 | 94.5 | 92.9 | 98.7 | |
| 0.100 | 0.050 | 0.050 | 96.1 | 94.4 | 94.3 | 93.9 | 95.3 | 94.1 | 92.6 | 93.9 | 95.8 | 95.3 | 95.1 | 83.9 | |
| 0.5 | 0.000 | 0.050 | −0.050 | 95.2 | 94.6 | 94.6 | 93.9 | 95.8 | 94.4 | 93.7 | 95.0 | 93.2 | 94.2 | 93.9 | 85.8 |
| 0.200 | 0.300 | −0.100 | 92.6 | 95.0 | 94.0 | 93.5 | 92.8 | 94.8 | 93.6 | 93.3 | 94.2 | 93.5 | 94.5 | 100 | |
| 0.000 | 0.000 | 0.000 | 96.7 | 95.2 | 93.0 | 94.3 | 99.1 | 97.8 | 94.7 | 91.2 | 96.0 | 94.1 | 91.0 | 67.5 | |
| 0.051 | 0.000 | 0.051 | 95.5 | 94.7 | 94.5 | 93.9 | 99.4 | 97.9 | 95.3 | 92.4 | 94.9 | 93.1 | 93.1 | 62.5 | |
| 0.050 | 0.050 | 0.000 | 94.3 | 95.9 | 95.0 | 94.8 | 95.4 | 92.8 | 92.2 | 93.5 | 95.6 | 94.7 | 92.7 | 99.3 | |
| 0.100 | 0.050 | 0.050 | 96.2 | 94.4 | 94.1 | 93.6 | 95.5 | 93.9 | 93.0 | 94.7 | 95.2 | 94.0 | 93.4 | 84.2 | |
| 0.9 | 0.000 | 0.050 | −0.050 | 95.9 | 95.1 | 94.2 | 94.5 | 94.8 | 94.7 | 93.4 | 93.5 | 94.7 | 94.7 | 94.4 | 86.5 |
| 0.200 | 0.300 | −0.100 | 95.4 | 93.4 | 93.7 | 94.0 | 94.5 | 93.1 | 93.0 | 93.1 | 95.8 | 93.4 | 94.2 | 100 | |
| 0.000 | 0.000 | 0.000 | 96.4 | 95.3 | 94.5 | 93.9 | 99.2 | 97.6 | 94.4 | 93.6 | 97.1 | 94.7 | 93.0 | 69.2 | |
| 0.051 | 0.000 | 0.051 | 95.8 | 95.3 | 95.0 | 94.6 | 98.8 | 97.6 | 94.1 | 91.4 | 94.7 | 94.7 | 94.1 | 66.3 | |
| 0.050 | 0.050 | 0.000 | 95.6 | 95.2 | 94.8 | 95.0 | 95.1 | 94.8 | 94.3 | 95.3 | 96.7 | 94.6 | 93.8 | 99.1 | |
| 0.100 | 0.050 | 0.050 | 94.6 | 95.1 | 94.8 | 95.4 | 93.5 | 95.2 | 94.3 | 94.1 | 93.7 | 94.8 | 94.6 | 83.4 | |
Jackknife: jackknife CIs; Boot: bootstrap percentile CIs; Bc: bias-corrected bootstrap CIs; Bt: bootstrap-t CIs.
Table 3.
Power of bootstrap percentile CIs to detect non-zero mediation effect for a dichotomous outcome model with two mediators (one binary (M1) and one continuous (M2)), n = 100 and 250 per group.
| ρ(M1, M2) | True IE | True IE1 | True IE2 | Sample Size
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| 100
|
250
|
||||||||
| Overall IE | IE1 | IE2 | Overall IE | IE1 | IE2 | ||||
|
|
|
||||||||
| −0.5 | 0.000 | 0.050 | −0.050 | - | 24.8 | 18.6 | - | 54.8 | 35.0 |
| 0.200 | 0.300 | −0.100 | 36.6 | 91.6 | 95.6 | 74.0 | 100 | 100 | |
| 0.000 | 0.000 | 0.000 | - | - | - | - | - | - | |
| 0.051 | 0.000 | 0.051 | 33.2 | - | 53.0 | 70.2 | - | 89.1 | |
| 0.050 | 0.050 | 0.000 | 14.3 | 26.0 | - | 33.6 | 54.3 | - | |
| 0.100 | 0.050 | 0.050 | 26.1 | 24.4 | 16.0 | 55.0 | 53.0 | 33.8 | |
| 0 | 0.000 | 0.050 | −0.050 | - | 30.9 | 20.4 | - | 59.6 | 41.6 |
| 0.200 | 0.300 | −0.100 | 51.7 | 94.4 | 97.4 | 90.5 | 100 | 100 | |
| 0.000 | 0.000 | 0.000 | - | - | - | - | - | - | |
| 0.051 | 0.000 | 0.051 | 42.4 | - | 57.4 | 86.1 | - | 93.9 | |
| 0.050 | 0.050 | 0.000 | 18.6 | 27.3 | - | 46.0 | 61.8 | - | |
| 0.100 | 0.050 | 0.050 | 38.2 | 30.6 | 16.7 | 75.9 | 63.3 | 37.5 | |
| 0.5 | 0.000 | 0.050 | −0.050 | - | 25.6 | 17.3 | - | 53.5 | 36.4 |
| 0.200 | 0.300 | −0.100 | 62.2 | 94.1 | 96.2 | 94.4 | 100 | 100 | |
| 0.000 | 0.000 | 0.000 | - | - | - | - | - | - | |
| 0.051 | 0.000 | 0.051 | 53.7 | - | 53.9 | 93.0 | - | 88.1 | |
| 0.050 | 0.050 | 0.000 | 25.1 | 27.2 | - | 54.8 | 52.5 | - | |
| 0.100 | 0.050 | 0.050 | 45.3 | 26.7 | 16.1 | 85.6 | 52.0 | 34.0 | |
| 0.9 | 0.000 | 0.050 | −0.050 | - | 17.5 | 12.8 | - | 38.4 | 24.4 |
| 0.200 | 0.300 | −0.100 | 54.9 | 85.7 | 87.9 | 93.9 | 99.9 | 100 | |
| 0.000 | 0.000 | 0.000 | - | - | - | - | - | - | |
| 0.051 | 0.000 | 0.051 | 48.5 | - | 33.7 | 89.9 | - | 71.7 | |
| 0.050 | 0.050 | 0.000 | 30.3 | 19.3 | - | 62.3 | 39.2 | - | |
| 0.100 | 0.050 | 0.050 | 56.5 | 17.8 | 13.3 | 91.2 | 36.8 | 26.2 | |
Table 2 shows the CP of four different methods for total and individual indirect effect estimates with sample size 100 per group. The results indicate that the bootstrap percentile CIs, for which the CP is within 3% of the nominal level for all scenarios, performs best. The coverage for bias-corrected bootstrap and jackknife CIs is only around 85% for the second scenario with correlation coefficient −0.5, and the CP of bootstrap-t CIs for continuous mediator indirect effect, IE2, is unstable in most scenarios. We repeated the simulations with a sample size of 250 per group (data not shown). With the larger sample size, the CP for bootstrap percentile, bias-corrected bootstrap and jackknife CIs gets closer to nominal level while problems for bootstrap-t CIs still exist.
We then compared the power of the bootstrap percentile CI to detect non-zero mediation effects under different values of the correlation between the two mediators. The results, given in Table 3, show that the power to detect non-zero IE increases as the correlation coefficient between two mediators increases, and the power to detect non-zero IE1 and IE2 increases as the absolute value of the correlation coefficient between two mediators gets close to zero for most simulation scenarios. When the sample size per group is increased to 250, the power is larger than that in small sample size scenarios and similar results can be observed.
7. STUDY EXAMPLE
The illustrative example considered here comes from a dental caries study measuring the number of decayed, filled, or missing teeth (#DMFT) at around age of 14 years for a cohort of very low birth weight (VLBW) and a matched group of normal birth weight (NBW) children. The exposure variable of interest is the binary variable, socioeconomic status (SES), coded as SES = 1 for low SES (‘exposed’), SES = 0, for high SES (‘unexposed’). The outcome considered in this example is the dichotomous DMFT variable, DMFT = 0 (#DMFT = 0) versus DMFT = 1 (#DMFT > 0). Baseline covariates adjusted for in the model include birth group (VLBW vs. NBW), sex and race. We also considered the following potential mediators: “Sealant” (a binary variable indicating use of sealants), “AvgOHI” (the average oral hygiene index score with higher values indicating worse oral hygiene status), and “Visit” (a binary variable indicating whether the child received regular (at least once a year) checkups from the dentist or not). We wanted to assess the direct effect of SES on DMFT and its indirect effect through Sealant, AvgOHI and Visit.
The dental dataset we used for the analysis included 129 subjects in the exposed group (SES = 1) and 74 subjects in the unexposed group (SES = 0). 79/129 (61.2%) of subjects in the exposed group and 28/74 (37.8%) of subjects in the unexposed group had at least one DMFT indicating that children from families with low SES may have a higher risk of developing dental caries compared with those from families with high SES. The system of models (including the outcome model (10) and the mediator model (11) for the selected mediators, each of which incorporated the three baseline covariates, birth group, sex and race), were fitted using maximum likelihood estimation. First, we considered the two-mediator model including Sealant and AvgOHI. Estimates of TE, DE, IE, IE1 and IE2 using the mediation formula approach with ‘exact’ integration (SAS, ‘QUAD’ function), and the Monte Carlo approximate integration approach (using 10,000 bivariate samples of M1*(t1) and M2(t2)) are provided in Table 4; 95% CIs for these estimators were computed using bootstrap percentile methodology. The ‘exact’ and Monte Carlo approaches provided almost identical mediation effect estimates as well as CIs. The results indicate that the total natural indirect effect accounts for approximate 25% of the total exposure effect and the mediation effect through AvgOHI predominates among the individual mediation effects. The effect estimates are interpreted as follows. Low (versus high) SES increases the probability of DMFT = 1 by 0.19 (95% CI: 0.04, 0.34), by an estimated 0.04 (−0.00, 0.09) attributable to the two mediators (Sealant and AvgOHI), and an estimated 0.15 (0.00, 0.30) due to the direct effect (or other unknown pathways); we let ‘0.00’ indicate a positive value, and ‘−0.00’ a negative value, less than 0.005 in absolute value. The overall indirect effect (attributable to the two mediators together) can be decomposed into mediation effects through Sealant (−0.00 (−0.02, 0.02)) and through AvgOHI (0.04 (0.01, 0.09)). In summary, we found, using the two-mediator model for the dental data, a significant total exposure effect (TE), direct effect (DE), and indirect effect through AvgOHI (IE2), a marginally significant total indirect effect estimate (IE) and a non-significant indirect effect through Sealant (IE1) (at the 0.05 level based on the CIs). We next included one additional potential mediator, Visit, in the model; the analysis results of this model are shown in Table 5. Similar conclusions were drawn as above. Low (versus high) SES increases the probability of DMFT = 1 by an estimated 0.18 (0.03, 0.34) with an estimated increase of 0.05 (0.00, 0.11) attributable to the set of mediators (with the following individual mediation effects: Sealant 0.00 (−0.02, 0.02), AvgOHI 0.04 (0.00, 0.08) and Visit 0.02 (−0.01, 0.05)) and an estimated increase of 0.13 (−0.03, 0.29) due to the direct effect (that is, any other pathways). Comparing with the results from Table 4, we may conclude that part of the direct effect in the two-mediator model was explained by an indirect effect through the added mediator Visit, although the indirect effect through Visit is not statistically significant.
Table 4.
Estimated causal effects (and 95% bootstrap percentile CIs) based on the mediation formula approach with ‘exact’ integration and Monte Carlo integration in the two-mediator model using dental data.
| Mediation Formula
|
|||
|---|---|---|---|
| ‘Exact’ Integration | Monte Carlo Integration# | ||
| Sealant (binary) and AvgOHI (continuous) | Total TE | 0.19 (0.04, 0.34) | 0.19 (0.04, 0.33) |
| Direct DE | 0.15 (0.00$, 0.30) | 0.15 (0.00, 0.30) | |
| Indirect IE | 0.04 (−0.00$, 0.09) | 0.04 (−0.00, 0.09) | |
| Through Sealant (IE1)* | −0.00 (−0.02, 0.02) | −0.00 (−0.02, 0.02) | |
| Through AvgOHI (IE2)* | 0.04 (0.01, 0.09) | 0.04 (0.01, 0.09) | |
Monte Carlo integration with 10,000 samples was used for estimation of causal effects.
Assumes correlation coefficient (ρ′) between unobserved counterfactual values M1*(0) and M2(1) the same as that between M1*(0) and M2(0) and M1*(1) and M2(1).
‘0.00’ indicates a positive value, and ‘−0.00’ a negative value, less than 0.005 in absolute value.
Table 5.
Estimated causal effects (and 95% bootstrap percentile CIs) based on the mediation formula approach with ‘exact’ integration and Monte Carlo integration in a three-mediator model using dental data.
| Mediation Formula
|
|||
|---|---|---|---|
| ‘Exact’ Integration | Monte Carlo Integration# | ||
| Sealant (binary), AvgOHI (continuous), and Visit (binary) | Total TE | 0.18 (0.03, 0.34) | 0.18 (0.03, 0.34) |
| Direct DE | 0.13 (−0.03, 0.29) | 0.13 (−0.03, 0.29) | |
| Indirect IE | 0.05 (0.00$, 0.11) | 0.05 (0.00, 0.11) | |
| Through Sealant (IE1)* | 0.00 (−0.02, 0.02) | 0.00 (−0.02, 0.02) | |
| Through AvgOHI and Visit (IE23)* | 0.05 (0.01, 0.11) | 0.05 (0.01, 0.11) | |
| Through AvgOHI (IE2)* | 0.04 (0.00, 0.08) | 0.04 (0.00, 0.08) | |
| Through Sealant and Visit (IE13)* | 0.02 (−0.02, 0.05) | 0.02 (−0.02, 0.05) | |
| Through Visit (IE3)* | 0.02 (−0.01, 0.05) | 0.02 (−0.01, 0.05) | |
| Through Sealant and AvgOHI (IE12)* | 0.04 (−0.00, 0.08) | 0.04 (−0.00$, 0.08) | |
Monte Carlo integration with 1,000,000 samples was used for estimation of causal effects.
Assumes correlation between is constant over all ti and tj.
‘0.00’ indicates a positive value, and ‘−0.00’ a negative value, less than 0.005 in absolute value.
We conducted two sensitivity analyses in the two-mediator model for our dental data. In the first sensitivity analysis, we examined the effect on the individual mediation effects, IE1 and IE2, of varying the correlation coefficient ρ′ between M1*(0) and M2(1) from −1 to 1 in increments of 0.01. The change in IE1 and IE2 estimates over ρ′ is shown in Figure 2. The plots indicate that the IE1 estimate increases (Figure 2A) and the IE2 estimate decreases (Figure 2B) as ρ′ increases; the sum of IE1 and IE2 is constant, since ρ′ doesn’t affect the total indirect effect estimate. Based on repeated computations of the confidence intervals, we found a nonsignificant indirect effect through Sealant and a significant indirect effect through AvgOHI over the whole range of ρ′ indicating robustness of the decomposed mediation effect estimates to the correlation between counterfactuals M1*(0) and M2(1).
Figure 2.
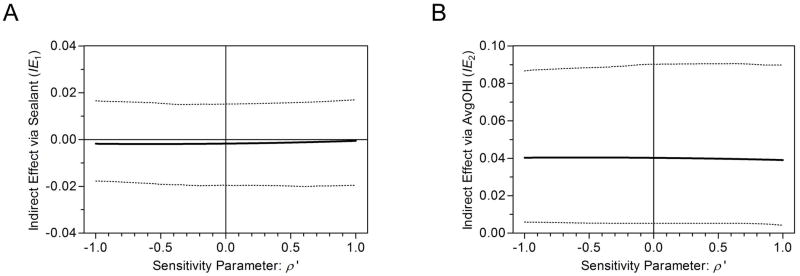
Sensitivity analysis for overall indirect effect decomposition of dental data involving binary ‘Sealant’ and continuous ‘AvgOHI’ mediators. Panels A and B show the estimated indirect effect through ‘Sealant’ and ‘AvgOHI’, respectively, for varying correlation ρ′ between M1*(0) and M2(1). The areas between dotted lines represent the 95% CIs for the decomposed natural indirect effect estimator at each value of ρ′.
In the second sensitivity analysis, we assessed the effect on mediation effect estimates (IE, IE1 and IE2) of possible violation of the no unmeasured mediator-outcome confounding assumption. Since there are two correlation parameters of interest, 3-D graphs (Figure 3) were plotted describing the change of mediation effect estimates over the ranges of the two correlations. Namely, the correlations are those between each of the two mediators (or underlying latent variables) and the latent variable underlying the outcome variable adjusting for the mediators. Of note, when assuming no mediator-outcome confounders (ρ1, ρ2 = 0), a significant positive indirect effect through AvgOHI (IE2, 0.04 (0.01, 0.09)), a positive marginally significant total indirect effect (IE, 0.04 (−0.00, 0.09)) and no significant indirect effect through Sealant (IE1, −0.00 (−0.02, 0.02)) were detected. We find that ρ1 (the correlation between Y*(t0, m1, m2) and M1*(t1)) does not substantially affect estimates of the overall indirect effect (IE), and as ρ2 (the correlation between Y*(t0, m1, m2) and M2(t2)) increases, the IE estimate significantly decreases (Figure 3A). Furthermore, the IE estimate is contained in the bounded interval [−0.14, 0.16], and when ρ2 is greater than 0.56, we find significant negative IE estimate. For the IE1 estimate, it is stable and trivial (bounded by [−0.01, 0.00]) over the range of ρ1 and ρ2 (Figure 3B). The fact that the 95% CIs recalculated over the full bivariate range for the two correlation coefficients always contain zero indicates the robustness of the original conclusion (that there is no evidence for a mediation effect through Sealant). The pattern of the change in the IE2 estimate (over the ranges of ρ1 and ρ2) is similar with that of IE estimate (Figure 3C); IE2 is close to IE in this example since the estimate of IE1 is approximate zero. This result indicates that our original conclusion regarding the significant positive indirect effect through AvgOHI may not hold if unmeasured confounders (explaining a correlation of greater than 0.5) between the mediator and outcome exist.
Figure 3.
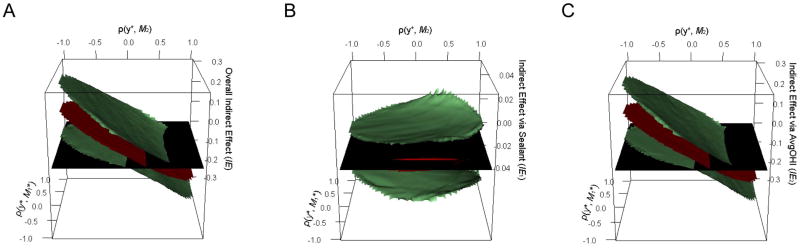
Sensitivity analysis for overall indirect effect estimation and indirect effect decomposition of dental data involving binary ‘Sealant’ (M1) and continuous ‘AvgOHI’ (M2) mediators. Panel A shows the estimated overall indirect effect for varying correlations ρ1 (between Y*(t0, m1, m2) and M1*(t1)) and ρ2 (between Y*(t0, m1, m2) and M2(t2)). Panel B shows indirect effect estimation through ‘Sealant’, and Panel C shows indirect effect estimation through ‘AvgOHI’. Red surface shows the mediation effect estimate, the space between the two green surfaces represents the 95% CIs, and the black surface indicates zero mediation effect reference.
8. DISCUSSION
In this article, we consider multiple-mediator models with binary or continuous mediators and a binary outcome. We model the joint distribution assuming multivariate normality among the latent (if binary) and observed (if continuous) mediators, with marginal probit models for binary mediators and linear models for continuous mediators. Our approach thus accommodates correlations among multiple contemporaneous mediators of different types. The total and individual mediation effects are estimated with a mediation formula approach and proposed sensitivity analyses allow an assessment of the robustness of the results. Mediation effects estimation for two-mediator and three-mediator models described in this paper has been encoded in a SAS macro which is available for downloading from the webpage http://epbiwww.case.edu/index.php/people/faculty/53-albert.
Our simulation study showed good properties (low bias and close-to-nominal confidence interval coverage rates) for the proposed estimators under most scenarios. For the estimation of individual natural indirect effects, there appears to be some bias when there are substantial mediation effects through each mediator and the correlation coefficient between the two mediators is high. This bias, which occurs for n = 200, suggests that our method may have difficulty dissecting the total natural indirect effect accurately in some scenarios when the two mediators are highly correlated and the sample size relatively small. However, in most scenarios low bias for individual mediator indirect effect was obtained even in this case. In addition, we found that our estimators of the total natural indirect effect had low bias in most scenarios, and high mediator correlation appears to be a favorable condition for this estimand.
Based on our simulation study of coverage probabilities from four methods of constructing CIs, we recommend that CIs for mediation effects in our multiple-mediator model context be obtained using the bootstrap percentile method. Preacher and Hayes [13] advocate the bias-corrected bootstrap for CIs of mediation effects estimated with the product of coefficients approach in linear multiple-mediator models. However, we found that CIs from the bias-corrected bootstrap may be biased when there are substantial unbalanced indirect effects through both mediators with different signs and the sample size is 200. An interesting finding is that the power for detecting a total indirect effect increases as the correlation between two mediators increases and the power for individual-mediator indirect effects is maximized when the two mediators are uncorrelated. Therefore it is relatively easy to detect a total mediation effect when the two mediators are highly correlated, whereas individual mediation effects are most easily detected with uncorrelated mediators.
Multiple-mediator models allow us to dissect the total mediation effect and estimate mediation effects through individual or sets of mediators under additional assumptions. Estimation of the decomposed mediation effects involves the joint distribution of counterfactuals that cannot be observed at the same time (namely, M1(0) and M2(1) in our data example). This problem, which may occur when there are more than two stages of mediation, was recognized previously in the literature [22, 27, 31]. The simple identifying assumption of a constant correlation coefficient between counterfactuals M1*(t1) and M2(t2) for all t1, t2 may not always be plausible. Therefore, it may be sensible to make use of bounds for the decomposed mediation effect estimate by considering ρ′ over a plausible range, or even over the entire interval, [−1, 1].
To assess the effect on mediation effect estimates of violations of the no unmeasured mediator-outcome confounders assumption, we use the correlation coefficients between each mediator (or underlying latent variables) and the latent variable underlying the outcome variable (adjusting for the mediators), denoted as ρ1 and ρ2, as our sensitivity analysis parameters. Alternatively, Imai et al. [23] expressed the correlation coefficient between the mediator and the outcome as a function of the coefficients of determination (i.e. R2, which represent the proportion of previously unexplained variance either in the mediator or outcome that is explained by the unobserved confounders), allowing for the sensitivity analysis to be based on the magnitudes of an effect of the omitted confounder. Imai et al. [32] also extended this approach to the case of a binary mediator and/or binary outcome using the pseudo-R2 of McKelvey and Zavoina [33]. This approach may possibly be applied to our model. Although R2 as a sensitivity parameter has an advantage of interpretability, a disadvantage of this approach is that it requires two such R2s instead of a single parameter (ρ). One consequence is that the graphical presentation of the sensitivity analysis results is more difficult, especially for our multiple-mediator models. Imai and Yamamoto [34] (a paper to which an anonymous referee called our attention) also addressed a multiple mediator problem, but where a causal direction between the mediators is specified. They provide an alternative set of identifying assumptions developed for the situation where there is a single mediator of interest that may be causally affected by other mediators.
In conclusion, we have proposed a mediation formula approach for mediation analysis of multiple-mediator models with a dichotomous outcome that allows estimation of the total indirect effect, as well as further decomposition of the total indirect effect through individual mediators. This approach can be easily extended to other types of discrete outcomes (such as a count response). One limitation of the proposed mediation analysis approach is that unbiased mediation effect estimation requires correct specifications of the parametric models for both the mediators and the outcome. This assumption may be violated, for example, if nonzero quadratic terms or treatment-mediator interactions are excluded from the model. However, standard model assessment techniques may be used to test and formulate reasonably correct association models. In addition, the use of the mediation formula (8) involves integration for continuous mediators. Due to the extensive computations required for multivariate integration, the proposed approach may not be feasible with more than three continuous mediators. In such cases, some sort of dimensionality reduction (for example, reducing the number of mediators or using linear combinations) may still allow use of this approach. Future research is needed to find more efficient computational techniques that will allow a larger number of mediators.
Acknowledgments
The authors would like to thank Dr. Lynn Singer for providing access to the longitudinal cohort of VLBW and NBW adolescents, supported by the Maternal and Child Health Program, Health Resources and Services Administration, Department of Health and Human Services [grant numbers MC-390592, MC-00127, MC-00334]. Support for this research was provided in part by the National Institute of Dental and Craniofacial Research, National Institutes of Health Research [grant numbers R01DE022674 (J. Albert), R21-DE16469 (S. Nelson)].
APPENDIX A: PROOF OF FORMULA (8)
In this proof we assume sequential ignorability (6) and (7) and consistency. Note that, the potential outcomes for J mediators in Y(t0, M1(t1), …, MJ(tJ)) are random variables, therefore, to obtain the marginal expected value of Y(t0, M1(t1), …, MJ(tJ)) requires that we integrate over these variables, comprising the endogenous (random) explanatory variables in the model of Y [22], as follows,
So formula (8) holds.
Contributor Information
Wei Wang, Email: wxw28@case.edu, Department of Epidemiology and Biostatistics, School of Medicine WG-37, Case Western Reserve University, 10900 Euclid Ave. Cleveland, OH 44106, Phone: (216) 526-1363, Fax: (216) 368-3970.
Suchitra Nelson, Email: sxn15@case.edu, Department of Community Dentistry, School of Dental Medicine, Case Western Reserve University, 10900 Euclid Ave., Cleveland, Ohio 44106, Phone: (216) 368–3469, Fax: (216) 368-3294.
Jeffrey M. Albert, Email: jma13@case.edu, Department of Epidemiology and Biostatistics, School of Medicine WG-37, Case Western Reserve University, 10900 Euclid Ave., Cleveland, OH 44106, Phone: (216) 368-1968, Fax: (216) 368-3970
References
- 1.Ajzen I, Fishbein M. Understanding attitudes and predicting social behavior. Englewood Cliffs: NJ: Prentice Hall; 1980. [Google Scholar]
- 2.Schneider JA, Bienias JL, Wilson RS, Berry-Kravis E, Evans DA, Bennett DA. The apolipoprotein E epsilon4 allele increases the odds of chronic cerebral infarction detected at autopsy in older persons. Stroke. 2005;36:954–959. doi: 10.1161/01.STR.0000160747.27470.2a. [DOI] [PubMed] [Google Scholar]
- 3.Li Y, Schneider JA, Bennett DA. Estimation of mediation effect with a binary mediator. Statistics in Medicine. 2007;26:3398–3414. doi: 10.1002/sim.2730. [DOI] [PubMed] [Google Scholar]
- 4.MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17:144–158. [Google Scholar]
- 6.MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- 8.Albert JM. Mediation analysis via potential outcomes models. Statistics in Medicine. 2008;27:1282–1304. doi: 10.1002/sim.3016. [DOI] [PubMed] [Google Scholar]
- 9.Pearl J. Technical report R-379. University of California, Los Angeles Computer Science Department; 2011. The causal mediation formula – a guide to the assessment of pathways and mechanisms. [Google Scholar]
- 10.Donaldson SI, Graham JW, Hansen WB. Testing the generalizability of intervening mechanism theories: Understanding the effects of adolescent drug use prevention interventions. Journal of Behavioral Medicine. 1994;17:195–216. doi: 10.1007/BF01858105. [DOI] [PubMed] [Google Scholar]
- 11.Reynolds KD, Bishop DB, Chou CP, Xie B, Nebeling L, Perry CL. Contrasting mediating variables in two 5-a-day nutrition intervention programs. Preventive Medicine. 2004;39:882–893. doi: 10.1016/j.ypmed.2004.03.022. [DOI] [PubMed] [Google Scholar]
- 12.MacKinnon DP. Contrasts in multiple mediator models. Multivariate Applications in Substance Use Research: New Methods for New Questions. 2000:141–160. [Google Scholar]
- 13.Preacher KJ, Hayes AF. Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavior Research Methods. 2008;40:879–891. doi: 10.3758/brm.40.3.879. [DOI] [PubMed] [Google Scholar]
- 14.Bishop YM, Fienberg SE, Holland PW. Discrete multivariate analysis: Theory and practice. Cambridge, MA: MIT Press; [Google Scholar]
- 15.Little RJA, Schluchter MD. Maximum likelihood estimation for mixed continuous and categorical data with missing values. Biometrika. 1985;72:497–512. [Google Scholar]
- 16.Cox DR, Wermuth N. Response models for mixed binary and quantitative variable. Biometrika. 1992;79:441–461. [Google Scholar]
- 17.Geys H, Regan MM, Catalano PJ, Molenberghs G. Two latent variable risk assessment approaches for mixed continuous and discrete outcomes from developmental toxicity data. Journal of Agricultural Biological and Environment Statistics. 2001;6:340–355. [Google Scholar]
- 18.Johnson RA, Wichern DW. Applied Multivariate Statistical Analysis. 5. Prentice-Hall; Englewood Cliffs, NJ: 2002. [Google Scholar]
- 19.Catalano PJ, Ryan LM. Bivariate latent variable models for clustered discrete and continuous outcomes. Journal of the American Statistical Association. 1992;87:651–658. [Google Scholar]
- 20.Regan MM, Catalano PJ. Likelihood models for clustered binary and continuous outcomes: Application to developmental toxicology. Biometrics. 1999;55:760–768. doi: 10.1111/j.0006-341x.1999.00760.x. [DOI] [PubMed] [Google Scholar]
- 21.Molenberghs G, Verbeke G. Models for discrete longitudinal data. Spring; New York: 2005. [Google Scholar]
- 22.Albert JM, Nelson S. Generalized causal mediation analysis. Biometrics. 2011;67:1028–1038. doi: 10.1111/j.1541-0420.2010.01547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science. 2010;25:51–71. [Google Scholar]
- 24.James F. Monte Carlo theory and practice. Reports on Progress in Physics. 1980;43:1145–1189. [Google Scholar]
- 25.Maddala GS. Limited Dependent and Qualitative Variables in Econometrics. Cambridge University Press; Cambridge, UK: 1983. [Google Scholar]
- 26.Edwards YD, Allenby GM. Multivariate analysis of multiple response data. Journal of Marketing Research. 2003;40:321–334. [Google Scholar]
- 27.Wang W, Albert JM. Estimation of mediation effects for zero-inflated regression models. Statistics in Medicine. 2012;31:3118–3132. doi: 10.1002/sim.5380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Song PXK, Li M, Yuan Y. Joint regression analysis of correlated data using Gaussian copulas. Biometrics. 2009;65:60–68. doi: 10.1111/j.1541-0420.2008.01058.x. [DOI] [PubMed] [Google Scholar]
- 29.Mosteller F, Tukey JW. Data analysis and regression: A second course in statistics. Reading, MA: Addison-Wesley; [Google Scholar]
- 30.Efron B, Tibshirani RJ. An introduction to the bootstrap. New York: Chapman & Hall; [Google Scholar]
- 31.Avin C, Shpitser I, Pearl J. Identifiability of path-specific effects. Proceedings of International Joint Conference on Artificial Intelligence. 2005;19:357–363. [Google Scholar]
- 32.Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010;15:309–334. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- 33.McKelvey RD, Zavoina W. A statistical model for the analysis of ordinal level dependent variable. Journal of Mathematical Sociology. 1975;4:103–120. [Google Scholar]
- 34.Imai K, Yamamoto T. Identification and sensitivity analysis for multiple causal mechanisms: revisiting evidence from framing experiments. Political Analysis. 2012 forthcoming. [Google Scholar]