A nuclear F-actin scaffold stabilizes RNP droplets against gravity in large cells

Abstract

The size of a typical eukaryotic cell is on the order of ≈10 μm. However, some cell types grow to very large sizes, including oocytes (immature eggs) of organisms from humans to starfish. For example, oocytes of the frog X. laevis grow to a diameter ≥1 mm. They contain a correspondingly large nucleus (germinal vesicle, GV) of ≈450 μm in diameter, which is similar to smaller somatic nuclei, but contains a significantly higher concentration of actin. The form and structure of this nuclear actin remain controversial, and its potential mechanical role within these large nuclei is unknown. Here, we use a microrheology and quantitative imaging approach to show that GVs contain an elastic F-actin scaffold that mechanically stabilizes these large nuclei against gravitational forces, which are usually considered negligible within cells. We find that upon actin disruption, RNA/protein droplets, including nucleoli and histone locus bodies (HLBs), undergo gravitational sedimentation and fusion. We develop a model that reveals how gravity becomes an increasingly potent force as cells and their nuclei grow larger than ≈10 μm, explaining the requirement for a stabilizing nuclear F-actin scaffold in large X. laevis ooctyes. All life forms are subject to gravity, and our results may have broad implications for cell growth and size control.

Eukaryotic cells are subject to a variety of mechanical forces. These stresses often require structural stabilization by the cytoskeleton, which plays a role analogous to the structural scaffold of a building. However, unlike a building, gravitational forces are typically ignored in cells, because gravity is considered negligible at the small length scales, low Reynolds numbers, and low variation in density characteristic of cells. Rather, attention has focused on forces such as those arising from molecular motor activity in the cytoplasm, where cytoskeletal actin (F-actin) plays a well-characterized mechanical role. Less is known about the mechanical organization of the nucleus. Some studies posit the existence of a nuclear scaffold of uncertain composition, while others suggest that only a nuclear lamina, or chromatin itself, comprises a structural element in the nucleus^1,2. Potential roles of actin in the structural organization of the nucleus have been particularly controversial. Actin in a non-polymeric form is known to be a component of several transcription complexes³, but whether F-actin exists in a typical nucleus⁴, and its structural role, if any, are far from resolved^5,6. In small somatic nuclei, the actin concentration remains low due to a dedicated nuclear export protein factor, Exp6⁷. Large amphibian oocytes, by contrast, have no detectable levels of Exp6 expression⁸, leading to high concentrations of nuclear actin⁹. This actin may play a role in RNA transport¹⁰ or in maintaining the structural stability of the GV⁸. However, whether it is in the form of an F-actin network capable of supporting mechanical loads, and precisely what kinds of mechanical loads such an elastic network would need to bear, remain poorly understood¹¹.

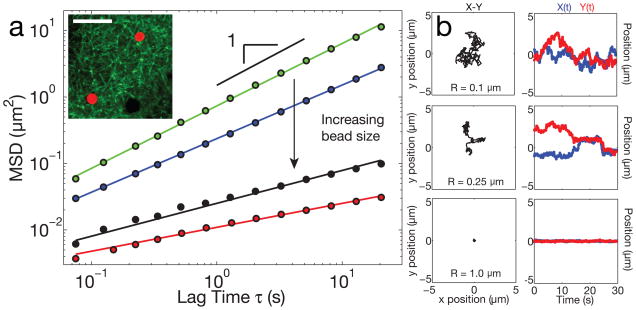
To probe the microstructure of the nucleoplasm in X. laevis GVs, we utilized a microrheology approach to study the fluctuating dynamics of PEG-passivated polystyrene particles microinjected into the GV of stage V–VI oocytes (diameter, L_cell = 1000–1300 μm) (Supplementary Note). The particle mean-squared displacement (MSD) exhibited a power law relationship with lag time, characterized by the diffusive exponent, α. The smallest beads studied, radius R = 0.1 μm, underwent diffusive-like motion through the GV (Fig. 1, A,B, Supplementary Video S1). The MSD of a large ensemble of these beads exhibited α = 0.94 ± 0.04 (Supplementary Note), close to that expected for Brownian motion of a particle within a purely viscous fluid, α = 1 ¹². However, beads with a slightly larger radius, R = 0.25 μm, showed a markedly different behavior. They remained transiently stuck in place, before hopping to a new position and again remaining trapped there for some time (Fig. 1, A,B and Supplementary Video S2). These had a smaller power law exponent, α = 0.81 ± 0.07, as would be expected for such constrained dynamics. This suggests the presence of an elastic meshwork through which intermediate-sized (R = 0.25 μm) beads are hopping. Consistent with this, larger beads, R = 0.5 and 1.0 μm, exhibited highly arrested dynamics; the motion of these large beads exhibited correspondingly lower power law exponents of α = 0.5 ± 0.1 and α = 0.4 ± 0.1, respectively (Fig. 1, A,B, Supplementary Video S3). The decrease in α with increasing bead size suggests that the GV contains an elastic network, which is effective at constraining the mobility of objects greater than its apparent mesh size of ≈0.5 μm (Fig. 2D). Indeed, very similar behavior is observed with in vitro F-actin networks¹³.

Figure 1. Probe particle size-dependent dynamics within the GV.

a, 2D Mean squared displacement of passivated probe particles in GVs from large oocytes (Stage V–VI). Particles of radius R=0.1 μm (green) exhibit diffusive-like motion with a diffusive exponent, α ≈1.0 (24 z-positions from 9 GVs, 10,648 particles identified). For larger bead sizes, the mobility becomes increasingly constrained, with correspondingly smaller values of α. Blue: R=0.25 μm (16 z-positions from 8 GVs, 2,053 particles identified), black: R=0.5 μm (19 z-positions from 6 GVs, 1,867 particles identified), red: R=1.0 μm (35 z-positions from 14 GVs, 3,011 particles identified). Inset shows Lifeact::GFP network (green) and R=1.0 μm probe particles (red); dark spheres are unlabeled RNP bodies; scale bar = 10 μm. b, Left column shows example X-Y trajectories for three different bead sizes. The right column shows corresponding temporal changes in position, X(t) and Y(t).

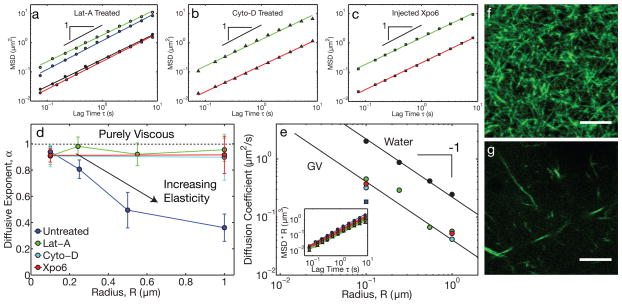
Figure 2. Actin disruption leads to purely viscous nuclear properties.

a, In Lat-A-treated oocytes, the MSD for all bead sizes exhibited diffusive-like behavior. Green: R=0.1 μm (19 z-positions from 9 GVs, 20,224 particles identified), blue: R=0.25 μm (28 z-positions from 15 GVs, 8,950 particles identified), black: R=0.5 μm (23 z-positions from 14 GVs, 3,261 particles identified), red: R=1.0 μm (23 z-positions from 11 GVs, 1,642 particles identified). b, Similar behavior was observed in Cyto-D treated oocytes. Green: R=0.1 μm (13 z-positions from 6 GVs, 7,754 particles identified) and red: R=1.0 μm (9 z-positions from 5 GVs, 382 particles identified). c, Similar behavior was observed in GVs injected with Xpo6 to deplete actin. Green: R=0.1 μm (21 z-positions from 10 GVs, 42,411 particles identified) and red: R=1.0 μm (13 z-positions from 5 GVs, 1,218 particles identified). d, Under actin-disrupting conditions (Lat-A, Cyto-D, and Xpo6), α ≈1 for all bead sizes, while α < 1 for large beads in native GVs. e, The diffusion coefficient, D, of beads in actin-disrupted GVs exhibits a roughly R⁻¹-dependence expected from the Stokes-Einstein equation; small beads in untreated GVs have a comparable value of D (blue square). Solid black symbols are beads diffusing in water. The color scheme is as in d. Inset shows the scaled MSD·R against lag time. f, Lifeact::GFP image showing the native actin network in a live GV. g, Lifeact::GFP image of the fragmented actin network after Lat-A treatment. Scale bars = 5 μm.

To test whether actin is responsible for these constrained dynamics, we treated oocytes with the actin-disrupting drug latrunculin A (Lat-A)¹⁴. These GVs appeared to be more fluid when pipetted into the imaging chamber. Probe particles in GVs from Lat-A treated oocytes were highly mobile, even at the largest bead sizes. The MSD of all bead sizes, R = 0.1–1.0 μm, exhibited diffusive-like motion, with an average exponent of α = 0.94 ± 0.04 (Fig. 2A,D). We also tested another actin-disrupting drug, cytochalasin D (Cyto-D). The MSD of probe particles in GVs from Cyto-D treated oocytes were also highly mobile at all particle sizes, with an average exponent of α = 0.9 ± 0.1 (Fig. 2B,D).

To confirm that these data do not reflect off-target drug effects, we microinjected into the GV high concentrations of a human homologue of the protein Exp6, Xpo6, to decrease the nuclear actin concentration. After ≈1 hour of incubation, we find the same effect as in Lat-A or Cyto-D treated oocytes: both small and large beads exhibited simple diffusive-like motion, with α = 0.91 ± 0.08 (Fig. 2C,D). The data from actin-disrupted GVs exhibited a size-dependence of the diffusion coefficient, D ~ 1/R, consistent with the Stokes-Einstein equation describing Brownian motion in a purely viscous liquid (Fig. 2E, Supplementary Note). We fit this data to the Stokes-Einstein equation to obtain the nucleoplasmic viscosity, η = 0.005 ± 0.002 Pa-s, approximately 5 times more viscous than water (black symbols, Fig. 2E). Interestingly, the diffusion coefficients of small (R=0.1 μm) beads in actin-disrupted GVs were similar to that of small diffusive beads in untreated GVs (blue square, Fig 2E), suggesting the latter are largely probing the background nucleoplasmic fluid.

To visualize the nuclear F-actin network, we constructed a GFP fusion of the small actin-binding peptide Lifeact^15,16. GVs expressing Lifeact::GFP revealed a dense, three-dimensional network of F-actin (inset Fig. 1, Fig. 2F and Fig. 3A,B,C); quantitative image analysis was consistent with our bead microrheology data (Fig. S1). Visualization of the network using a different actin binding construct, Utrophin::GFP⁶ (Supplementary Note), revealed similar structural features (Fig. S2). Microrheological measurements of all bead sizes were unchanged in GVs expressing these constructs (Fig. S3), confirming that these probes do not perturb F-actin structure. Moreover, consistent with our bead microrheology data, GVs treated with either Lat-A, Cyto-D, or Xpo6 exhibited a significantly fragmented actin network (Fig 2G, S1, Supplementary Videos S8 & S9).

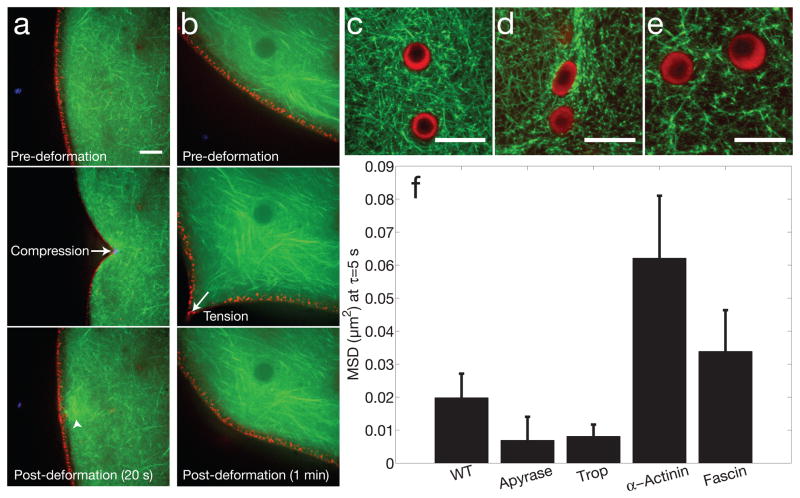
Figure 3. Mechanics, anchoring and structural regulation of nuclear actin.

a, Compressive forces were applied to the GV using a microneedle, demonstrating a coupled elastic response of the actin meshwork (Lifeact::GFP, green) and lamin cortex (RFP::Lamin B3, red). Arrowhead shows increased intensity, suggesting actin polymerization occurs in response to force. b, Tensile forces were applied to the GV using a microneedle, showing a similar coupled elastic response. c, Two nuclear bodies trapped in a dense native actin meshwork. d, Tropomyosin injection leads to a compacted actin meshwork, and the nuclear bodies are often deformed. e, Fascin injection leads to bundling of the actin meshwork. For c–e, nucleoli are labeled with NPM1::RFP (red), and actin is labeled with Lifeact::GFP (green). d, Bar graph showing the MSD of large (R=1 μm) beads at a lag time of 5 sec, under various conditions: untreated (n=35 z-positions from 14 GVs, 3,011 particles identified), apyrase (n=13 z-positions from 4 GVs, 617 particles identified, p-value = 0.22), tropomyosin (n=24 z-positions from 12 GVs, 1,278 particles identified, p-value = 0.16), alpha-actinin (n=18 z-positions from 5 GVs, 1,254 particles identified, p-value = 0.05), and fascin (n=39 z-positions from 18 GVs, 2,123 particles identified, p-value = 0.34). Error bars = s.e.m. Scale bar is 10 μm in all images.

These probes allowed us to visualize the mechanical response of the live actin network. Using a microneedle, we found that the network could withstand repeated compressive deformations, each time elastically recovering after removal of the force (Fig. 3A). We found similar results upon application of tensile forces to the network; each time the network exhibited an elastic response, largely recovering its pre-deformation structural organization (Fig 3B); interestingly, we frequently observed apparent actin polymerization in response to force application (arrowhead, Fig. 3A), suggesting the network architecture is mechano-sensitive. These experiments were conducted at the nuclear periphery, where nuclear lamins are known to assemble a thin cortical shell^17,18. Using an RFP::Lamin B3 construct, we found that the lamin cortex deformed in concert with the actin network. Even under large deformations, we were unable to sever the lamin/actin mechanical connection (Figs. 3A,B), suggesting the actin network is mechanically anchored to the lamin cortex.

Nuclear actin may have structural features that could alter its binding to conventional actin-binding proteins¹⁹. It is thus unclear if this nuclear actin network could be regulated by mechanisms similar to those functioning within the cytoplasm. As a first coarse perturbation, we depleted ATP using the enzyme Apyrase. The particle MSD decreased (Fig. 3F), and the GV appeared stiffer upon dissection, suggesting a possible role for ATP-dependent processes. We next examined the effect of proteins known to regulate cytoplasmic actin. Injecting the actin filament stabilizing protein tropomyosin into the GV led to a decreased particle MSD, comparable to the values seen upon ATP-depletion (Fig. 3F). Visualization of tropomyosin-injected GVs revealed a more dense, compacted actin network structure (Fig. 3D). By contrast, alpha-actinin and fascin, two actin bundling proteins, each led to an increased MSD (Fig. 3F), possibly due to an increased mesh size (Fig. 3E). These data suggest that the structure and mechanics of this nuclear actin network could potentially be regulated by molecular mechanisms similar to those at play in the cytoplasm.

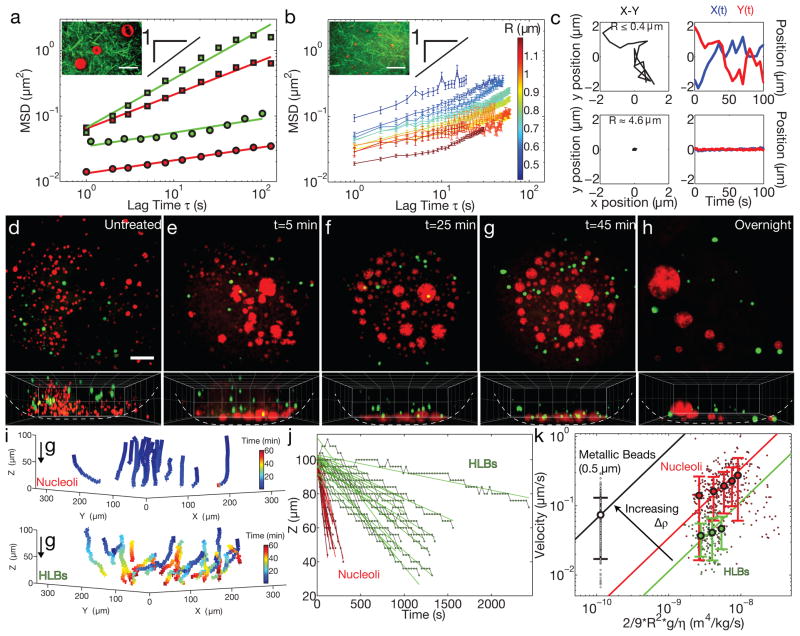
Mature GVs contain over a thousand spherical RNA/protein (RNP) bodies, including many large (>1 μm) extrachromosomal nucleoli and HLBs (closely related to Cajal Bodies, CBs²⁰). Particle tracking of NPM1/Fibrillarin::GFP labeled nucleoli or GFP::Coilin labeled HLBs in untreated GVs revealed constrained motion, with a highly sub-diffusive average exponent of α = 0.2 ± 0.3 (Fig. 4A and Supplementary Note). As seen with the largest probe particles, upon actin disruption, the motion of large nucleoli and HLBs became significantly less constrained, with an average exponent of α = 0.7 ± 0.2 (Fig. 4A). However, a minority population of small “micronucleoli”²¹, of size R ≤ 1 μm, appear to diffuse more freely even in an intact actin meshwork (Fig. 4B); their dynamics are correlated with their size, with the smallest micronucleoli exhibiting nearly freely-diffusive motion (Fig. 4B, Supplementary Video S4), comparable to the microrheology of inert microspheres of similar size (Fig. 1A).

Figure 4. Actin disruption results in sedimentation and fusion of nuclear bodies.

a, 2D MSD of RNP bodies shows highly constrained motion in native GVs (circles). Red: nucleoli (R>2 μm) (11 z-positions from 5 GVs, 320 bodies identified) and green: HLBs (16 z-positions from 10 GVs, 232 bodies identified). In latrunculin-treated GVs (squares) these RNP bodies are more mobile. Red: nucleoli (R>2 μm) (10 z-positions from 6 GVs, 442 bodies identified) and green: HLBs (9 z-positions from 5 GVs, 149 bodies identified). Inset shows a few large nucleoli embedded in an F-actin meshwork visualized by Lifeact::GFP. Scale bar = 10 μm. b, A sub-population of small nucleoli (“micronucleoli,” R<2 μm) are more mobile, and occasionally exhibit intermittent dynamics (“cage hopping”) in native GVs. Inset shows micronucleoli inside a meshwork labeled with Lifeact::GFP. (n=number of displacements at a given lag time per nucleolar size from 11 z-positions from 7 GVs, 240 bodies identified). Error bars = s.e.m. Scale bar = 10 μm. c, Left column shows example X-Y trajectories for a representative micronucleolus (top) and a typical large nucleolus (bottom). The right column shows corresponding temporal changes in position, X(t) and Y(t). For d–h, top images show a maximum intensity projection of a 100-micron thick section of nucleoli labeled with NPM1::RFP (red) and HLBs labeled with GFP::Coilin (green), and bottom images show a 3-D rendering in the X-Z plane. d, Nucleoli and HLBs are suspended in an untreated GV. For e–g, time-lapse images are from the same GV from a Lat-A treated oocyte; time refers to minutes after dissection. h, Large nuclear bodies that form overnight after actin disruption by Lat-A. Scale bar = 50 μm. 3D grid size = 50 μm. i, 3D representation of nucleoli (top) and HLB (bottom) trajectories after actin disruption in the GV shown in e–g. j, The vertical position of nuclear bodies (red: nucleoli R>2 μm, and green: HLBs) from i as a function of time. k, The sedimentation velocity plotted against normalized size. Black: metallic R=0.5 μm beads (n=16 movies of 16 GVs, 237 tracks analyzed), red: nucleoli (R>2 μm) (n=17 movies of 16 GVs, 394 tracks analyzed) and green: HLBs (n=18 movies of 12 GVs, 149 tracks analyzed). Larger circles represent binned data points and solid lines are linear fits of the data, with the slope representing the buoyant density. Error bars = s.d.

In addition to diffusive-like motion within the focal plane, we found that nucleoli and HLBs in Lat-A-treated GVs move to the bottom of the GV; nucleoli moved more quickly, over a timescale of ~5–10 minutes, versus ~30 minutes for HLBs. They were observed to collect at the bottom of the GV and undergo homotypic (nucleoli-nucleoli or HLB-HLB) fusion events upon contact, consistent with a recent study²²; for nucleoli, this ultimately resulted in a small number of large nucleoli of R ≈ 25–50 μm (Figs. 4D–H, S4, Supplementary Videos S5–7). Similar behavior was observed with Cyto-D (Supplementary Video S8) or Xpo6 injected GVs (Fig. S5). This shows that both HLBs and nucleoli exhibit liquid droplet-like behavior previously described for several types of RNP bodies^23–25.

Our protocol for these experiments involved incubation of oocytes in Cyto-D, Lat-A, or injected Xpo6 for 1–2 hours, during which time the oocytes were in a small tube that was gently rotated, such that the gravitational force vector with respect to the animal-vegetal (AV) axis constantly changed, averaging to zero. As soon as the GVs were isolated from the oocyte, and placed on a coverslip in a constant orientation, RNP droplets began settling toward the bottom. By contrast, after overnight incubation of oocytes in a petri dish with a stable orientation, the RNP droplets had undergone massive fusion events, having already settled to the bottom of the stationary GV (Fig 4H).

Unlike RNP droplets, the polystyrene microrheology probe particles (Figs. 1,2), were not observed to sediment to the bottom of the GV, likely due to their relatively low density, ρ ≈ 1.06 g/cc, similar to that of water, and small size. Indeed, we determined the average density of the GV, ρ_GV =1.12 ± 0.03 g/cc (Supplementary Note), which was slightly larger than that of the probe particles. In Lat-A disrupted GVs, when we microinjected metallic beads (R = 0.5 μm) with a significantly higher density, ρ ≈ 1.8 g/cc (Supplementary Note), we observed rapid sedimentation. The velocity, v, of sedimenting spherical particles will be given by a balance between the drag force and the buoyant force, with an expected dependence, v = 2R²Δρg/9η, where Δρ is the density difference between the particle and surrounding fluid, and g is the gravitational acceleration constant²⁶. By measuring the velocity of sedimenting metallic beads, we determined a nucleoplasmic viscosity, η = 0.007±0.002 Pa-s (Fig. 4K, Supplementary Note), consistent with the value from diffusive microrheology data (Supplementary Note).

By tracking the vertical motion of settling RNP droplets, we found that larger RNP droplets settled at higher velocities (Fig. 4K), consistent with the expected R² -dependence of the velocity. Using our measured value for the nucleoplasmic viscosity, we plot the sedimentation velocity, v, as a function of normalized RNP droplet size, 2R²g/9η, to determine Δρ. For HLBs, we find Δρ_HLB = 0.011 ± 0.002 g/cc. For nucleoli, we obtain a higher density, Δρ_NUCLEOLUS = 0.035 ± 0.07 g/cc. HLBs and nucleoli thus have a macromolecular density ≈10% and 40% larger, respectively, than the surrounding nucleoplasm (Supplementary Note). These values are roughly consistent with a previous density measurement using an optical interferometry technique²⁷. Thus, the directed movement of RNP droplets towards the bottom of actin-disrupted GVs agrees quantitatively with a gravitational driving force that arises from the density difference between RNP droplets and the surrounding nucleoplasm.

The need for a nuclear F-actin scaffold to stabilize internal structures can be understood by considering the sedimentation length, ℓ_sed. This defines the length scale beyond which gravitational effects begin to dominate over random, diffusive motion (Supplementary Note). GVs in mature Stage V–VI oocytes are very large, L_GV ≈450 μm. Using our measured value Δρ_NUCLEOLUS, we calculated ℓ_sed for different sized nucleoli, finding that it becomes comparable to L_GV for nucleoli of size, R^* ≈ 0.2 μm. Thus, for nucleoli larger than ≈0.2 μm, ℓ_sed < L_GV, and gravity is no longer negligible. The structure of the nuclear F-actin network, of mesh size ≈0.5 μm, is therefore well-suited to mechanically stabilize sedimentation-prone RNP droplets.

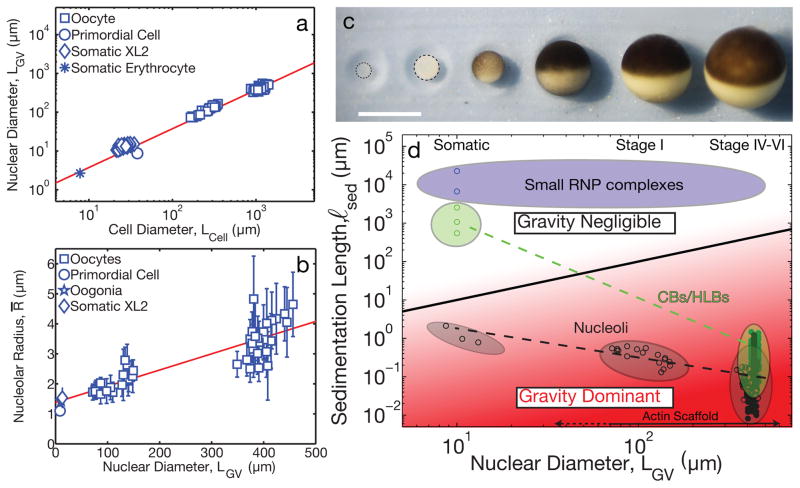
Small somatic cells do not exhibit high actin concentrations in the nucleus⁵, suggesting either gravitational sedimentation is not problematic in somatic nuclei, or that another structure provides a stabilizing scaffold. As cells grow, there is often a concomitant scaling in the size of their organelles²⁸. During oocyte growth from small Stage I oocytes, L_cell ≈ 200 μm, to large mature Stage VI oocytes, L_cell ≈ 1300 μm, the GV grows proportionally, from L_GV ≈ 100 μm to 450 μm²⁹ (Fig. 5, A and C). Since gravity becomes dominant when L_GV > ℓ_sed, gravity becomes increasingly significant as the oocyte and GV grow. Moreover, RNP droplets also scale with cell and GV size, with the average size of nucleoli exhibiting a roughly linear scaling relationship (Fig. 5B); HLBs appear to exhibit similar scaling behavior (Fig. 5D). Since the sedimentation length has an inverse dependence on RNP volume, ℓ_sed ~ R⁻³, this sets a critical GV size, $L_{GV}^{\ast }$, at which gravitational sedimentation becomes significant (Supplementary Note). Using our measured values of these parameters for nucleoli, we estimate a critical size of order, $L_{GV}^{\ast }~10$, similar to the length scale of somatic nuclei. Thus, if a nucleus grows larger than this, nucleoli and other nuclear bodies of comparable density are subject to gravitational sedimentation, requiring a mechanical scaffold for stabilization; the increasing importance of gravity in large nuclei can be visualized directly in the state diagram in Fig. 5D. Interestingly, this shows that gravitational forces may not be completely negligible even in small somatic cells.

Figure 5. Cell size, organelle scaling, and gravity.

a, Linear scaling was observed between nuclear diameter, L_GV, and cell diameter, L_cell from Stage I, IV, V, and VI oocytes and estimated from the literature (Supplementary Note). b, Linear scaling found between average nucleolar radius and nuclear diameter based on measurements in Stage I, IV, V and VI oocytes and estimated from literature (Supplementary Note). Nucleoli were measured from late stage oocytes (n=8 GVs), intermediate stage oocytes (n=17 GVs) and early stage oocytes (n=17 GVs). Error bars = s.d. Red solid line is the weighted best-fit line of the data. c, Cell growth during oogenesis in X. laevis. Each of the six stages is shown. Scale bar = 1 mm. d, State diagram of ℓ_sed vs. L_GV. Black solid line separates region where gravity is negligible (white, ℓ_sed > L_GV) from region where gravity dominates (red, ℓ_sed < L_GV). Measurements (closed circles) and approximations (open circles) (Supplementary Note) are plotted for different nuclear bodies (black: nucleoli, green: HLBs/CBs, blue: small RNP complexes). For nuclear diameters > 10 μm, gravity becomes increasingly dominant for both HLBs and nucleoli, requiring a stabilizing F-actin scaffold.

Our findings reveal a new role for nuclear F-actin, which becomes essential for mechanical stabilization against gravity in large cells. However, even for the largest nucleoli in the X. laevis GV, gravitational forces are relatively small, on the order of ~1 pN (Supplementary Note). Thus, to support these organelles against gravity, the mechanical properties of the actin scaffold must be sufficient to withstand only modest stresses, of order ~0.01 Pa. This nuclear actin network may thus be different from typical cytoplasmic actin networks, in that the elastic modulus is less important than the mesh size. Indeed, the network appears to function as an organelle sieve: large structures prone to gravitational sedimentation are constrained by the network, while smaller macromolecular complexes are free to diffuse throughout the GV.

The key parameter in determining whether gravity plays an important role in the spatial distribution of molecules and organelles is the ratio of the gravitational sedimentation length, ℓ_sed, and the size of the compartment, L (i.e. nucleus size, L_nucleus or cell size L_cell). Our findings show that X. laevis oocytes, and likely other large cells, can be in the regime ℓ_sed/L < 1, where gravitational forces can play a disruptive role in intracellular organization. While oocytes are generally large, and there exist numerous examples of cells of varied size^30,31, eukaryotic cell size is typically on the order of 10 μm, for reasons that are still not well-understood. Our results suggest an intriguing possibility: cells are typically no greater than ~10 um, since beyond this size gravity is increasingly disruptive and additional stabilization mechanisms become necessary.