Abstract
This study compares human walking and running, and places them within the context of other mammalian gaits. We use a collision-based approach to analyse the fundamental dynamics of the centre of mass (CoM) according to three angles derived from the instantaneous force and velocity vectors. These dimensionless angles permit comparisons across gait, species and size. The collision angle Φ, which is equivalent to the dimensionless mechanical cost of transport CoTmech, is found to be three times greater during running than walking of humans. This threefold difference is consistent with previous studies of walking versus trotting of quadrupeds, albeit 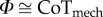 tends to be greater in the gaits of humans and hopping bipeds than in quadrupeds. Plotting the collision angle Φ together with the angles of the CoM force vector Θ and velocity vector Λ results in the functional grouping of bipedal and quadrupedal gaits according to their CoM dynamics—walking, galloping and ambling are distinguished as separate gaits that employ collision reduction, whereas trotting, running and hopping employ little collision reduction and represent more of a continuum that is influenced by dimensionless speed. Comparable with quadrupedal mammals, collision fraction (the ratio of actual to potential collision) is 0.51 during walking and 0.89 during running, indicating substantial collision reduction during walking, but not running, of humans.
tends to be greater in the gaits of humans and hopping bipeds than in quadrupeds. Plotting the collision angle Φ together with the angles of the CoM force vector Θ and velocity vector Λ results in the functional grouping of bipedal and quadrupedal gaits according to their CoM dynamics—walking, galloping and ambling are distinguished as separate gaits that employ collision reduction, whereas trotting, running and hopping employ little collision reduction and represent more of a continuum that is influenced by dimensionless speed. Comparable with quadrupedal mammals, collision fraction (the ratio of actual to potential collision) is 0.51 during walking and 0.89 during running, indicating substantial collision reduction during walking, but not running, of humans.
Keywords: biomechanics, locomotion, bipedal, mammal, mechanical cost
1. Introduction
Quantitative approaches to understanding how the gaits of legged animals compare within and across species have long been sought and each contribution has revealed a subset of similarities and differences. Five decades ago, Hildebrand [1] and others used cine films to distinguish the gaits of terrestrial animals by measuring spatio-temporal metrics such as duty factor and limb contact phase. A later approach revolutionized our understanding of animal locomotion by defining centre of mass (CoM) mechanics using a point-mass model and whole-animal force platform measurements. This influential paradigm for reducing the complexity of gait was introduced by Cavagna et al. [2], who proposed that separate and mutually exclusive mechanisms operate during walking versus running to exchange energy during the gait cycle (i.e. anti-phase versus in-phase kinetic and potential energy fluctuations). This publication galvanized a distinction between walking and running gaits of legged animals, wherein walking is conceptualized as a rigid inverted pendulum and running as a compliant spring-loaded inverted pendulum (SLIP).
The similarity of a given gait to idealized rigid pendular mechanics has long been expressed as percent recovery. In a rigid point-mass pendulum, kinetic and potential energies mirror each other and percent recovery is 100%. Terrestrial gaits have percent recoveries up to 70–80% during walking [2–6], and a percent recovery as low as approximately 20% is typically regarded as the boundary between walking and running or trotting. Compliant SLIP-like gaits including running, trotting and hopping approach a percentage recovery of zero [2,4]. Cavagna recognized that human walking does not fit the mechanics of a rigid inverted pendulum well (50–70% recovery), and several studies have explored leg deflection [7–9] and compliance [10] to explain the low potential relative to kinetic energy fluctuations of human walking. Furthermore, Geyer et al. [11] show that a physics-based simulation of human walking with compliant legs reproduces the force–time pattern of human walking, whereas the rigid inverted pendulum does not.
While percent recovery has been widely used over the past several decades as a key metric to quantify gait, it has two major shortfalls: it does not measure the dynamic interaction of the CoM with the ground in each instance; and, because many terrestrial gaits show percent recoveries broadly distributed between 20 and 60%, it is difficult to ascribe either pendular or SLIP-like mechanisms—for example, the intermediate gaits used by ground-dwelling birds do not fit either model well [12,13], nor do quadrupedal gaits such as the gallop, canter, and amble or tölt [14–18].
Our approach overcomes these deficiencies by capturing the CoM dynamics at each instance of foot contact using metrics that apply across gaits and species [19]. We measure three instantaneous angles, as shown in figure 1 and table 1: the angle of the force vector relative to vertical (force angle θ), the angle of the velocity vector relative to horizontal (velocity angle λ), and the angle of deviation from a perpendicular relationship of the force and velocity vectors (collision angle ϕ). A collision occurs when the collision angle is non-zero. The collision fraction is determined from the instantaneous ratios of the actual collision angle ϕ to the potential collision angle θ + λ (force plus velocity angles)—a smaller fraction indicates reduced collision (table 1). Just as a wheel avoids collisions by maintaining a perpendicular relationship of the force vector (downward) and velocity vector (forward), animals may reduce collisions by adjusting instantaneous orientations of force and velocity vectors, thereby reducing their average collision angle Φ and collision fraction (table 1).
Figure 1.
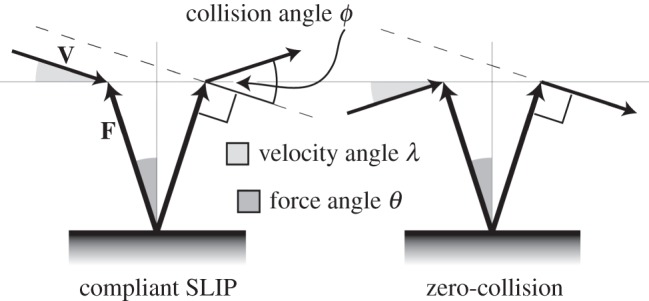
Parameters of a collision-based analysis are determined by the force vector F and velocity vector V of the CoM in each instance of ground contact. Force angle θ is defined as the deviation of F from a vertical axis, velocity angle λ, as the deviation of V from an axis in the direction of travel and collision angle ϕ is defined as the deviation from an orthogonal relationship of F and V. A compliant SLIP results in a full collision wherein F and V deviate in an opposite sense from their respective axes. At the other extreme, F and V may be kept perpendicular throughout stance, representing an idealized zero-collision case. Equations for collision-based parameters are provided in table 1.
Table 1.
Parameters and equations of a collision-based analysis, plus dimensionless speed and individual limbs cost of transport.
| force vector (N), F | 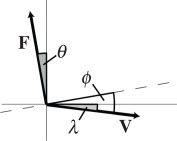 |
|
| velocity vector (ms−1), V | ||
| instantaneous angles (radians): θ denotes force, λ denotes velocity and ϕ denotes collision | ||
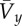 is mean forward velocity; h is hip height; g is acceleration of gravity on the Earth; x is a multiplier of gravity; n is the number of samples in the stride period; m is body mass is mean forward velocity; h is hip height; g is acceleration of gravity on the Earth; x is a multiplier of gravity; n is the number of samples in the stride period; m is body mass | ||
| dimensionless speed (the square root of Froude number) | 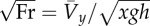 |
equation (1.1) |
| instantaneous force angle, where unit vector a is normal to the substrate and upward | 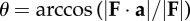 |
equation (1.2) |
| force angle determined by force-averaging over the contact periods of the stride | 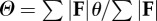 |
equation (1.3) |
| instantaneous velocity angle, where unit vector b is parallel to the substrate and in the direction of travel | 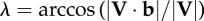 |
equation (1.4) |
| velocity angle determined by velocity-averaging over the contact periods of the stride | 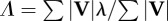 |
equation (1.5) |
instantaneous collision angle determined from the dot product of force on velocity—the arcsine rotates this angle by π/2 such that it quantifies the deviation from 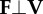
|
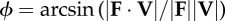 |
equation (1.6) |
| collision angle determined by force- and velocity-averaging over the contact periods of the stride | 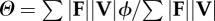 |
equation (1.7) |
mechanical cost of motion is a normalized absolute value of CoM power equivalent to Φ when 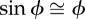 ; the small angle approximation of equation (1.6) is substituted into equation (1.7) ; the small angle approximation of equation (1.6) is substituted into equation (1.7) |
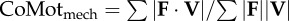 |
equation (1.8) |
| for small vertical and lateral oscillations | 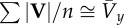 |
equation (1.9) |
| for small fore–aft and lateral forces | 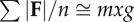 |
equation (1.10) |
individual limbs cost of transport is a normalization of the absolute value of individual limb power [20], where 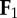 and and 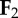 indicate the force vectors of each limb indicate the force vectors of each limb |
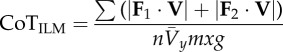 |
equation (1.11) |
mechanical cost of transport is a normalized absolute value of CoM power equivalent to  when the conditions of equations (1.9) and (1.10) are met when the conditions of equations (1.9) and (1.10) are met |
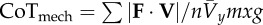 |
equation (1.12) |
| impulse angle for the stride, where I is the impulse vector and unit vector a is normal to the substrate and upward | 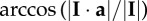 |
equation (1.13) |
| collision fraction determined by force- and velocity-averaging over the contact periods of the stride | 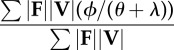 |
equation (1.14) |
Collision fraction, average collision angle Φ, average force angle Θ and average velocity angle Λ (table 1) are non-dimensional, so direct comparisons can be made across gaits, species and gravity conditions. A collision-based approach is compatible with conceptual and explicit musculoskeletal models of locomotor function, and can even be used to verify and bring these higher-level models into sharper focus (figure 2). For example, collision-based parameters could be used to compare the CoM dynamics of simplified mechanistic models [11] or forward dynamic simulations [21] with the CoM dynamics of actual biological gaits.
Figure 2.
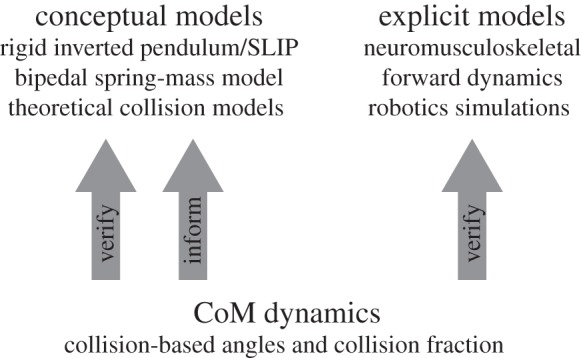
A schematic of collision-based CoM dynamics with respect to higher-level models of locomotion. Collision-based parameters of biological or robotic legged systems can verify conceptual and explicit models of locomotion. A collision-based perspective can also inform simplified mechanistic or conceptual models.
Given the novelty of the collision-based concept, it is helpful to consider examples that compare collision fraction to percent recovery. Recent studies calculate percent recovery and collision fraction side by side for two distinctly different gaits—continuous-contact brachiation of siamangs [22] and galloping of monkeys [18]. Slow brachiation of siamangs has a collision fraction of 0.2 and approximates a point-mass pendulum with percent recovery averaging 70% [22]. Capuchin monkeys similarly reduce collisions during terrestrial galloping, with a collision fraction of 0.36, but show percent recoveries of only 22%. While both gaits employ substantial collision reduction, only brachiation shows kinetic and potential energy fluctuations similar to those of a point-mass pendulum. Hence, a collision-based approach is general enough to capture collision reduction achieved by any pattern of CoM dynamics, whereas percent recovery is only useful in identifying one of the gaits, slow brachiaton, as a more-or-less pendular gait. Galloping monkeys fit neither the pendular nor SLIP-based mechanism well.
As illustrated separately by brachiation and galloping, human bipedal walking comprises collision reduction associated with both pendular and non-pendular CoM dynamics. Percent recovery alone does not capture the CoM dynamics of bipedal walking because it does not model the step-to-step transition, which occurs as the CoM is being redirected from a downward to upward trajectory. However, theoretical models of collision mechanics and experimental results show that this transition can reduce the cost of locomotion [23–28]. Based upon the collision theory, a toe-off impulse prior to heel-strike should reduce the cost of walking by a factor of four [25,26], and separate toe-off and heel-strike impulses could also reduce walking cost in the same manner as additional leg contacts [26]. While percent recovery and the pendular paradigm do not model these cost reductions, the collision fraction quantifies the cost reduction owing to both the pendulum-like vaulting during single support and the smooth redirection of the CoM during step-to-step transition. Both pendulum-like vaulting during single support and opposing braking and propulsive forces during double support promote a perpendicular relationship of the force and velocity vectors of the CoM, thus reducing collisions and cost, as indicated by collision fraction and collision angle, respectively.
While theoretical collision models have abstracted experimental data to a few impulsive collisions per stride, our collision-based approach acknowledges that contact occurs throughout most of the stride as the CoM is redirected by the action of the legs. We analyse the fundamental determinants of CoM dynamics—force and velocity vectors in every instance of ground contact—and quantify their geometries as dimensionless angles and a collision fraction. We test the robustness of these parameters by considering a hypergravity manipulation of walking and running. Here, we apply this novel approach for the first time to human locomotion and place the dynamics of our own locomotion into the larger context of mammalian terrestrial gait.
2. Material and methods
(a). Subjects
Four male and four female subjects volunteered to participate in this study. The project was approved by the institutional review board of Florida State University and all subjects provided fully informed consent. Subjects were healthy adults, 22–27 years of age who were active in recreational sports. Subject data are provided in the electronic supplementary material, table S1. Subjects completed five walking trials at 1.2 m s−1 and five running trials at 1.9 m s−1. The stride that was nearest to steady-speed as indicated by impulse angle (equation (1.13)) was included in our analysis. In an additional set of trials, we simulated hypergravity of 1.35g, as described in the electronic supplementary material, to test the robustness of collision-based CoM dynamics to a hypergravity manipulation.
(b). Force measurement
A series of four force platforms were used to measure vertical and fore–aft forces exerted by each limb during walking and running. These were custom designed for human locomotion analysis and were constructed within the research laboratory following a standard design used elsewhere [29]. Each platform was able to resolve forces in the vertical and two horizontal directions (parallel with and perpendicular to the direction of travel). The front and rear vertical sensors were wired independently so that the centre of applied pressure could be resolved by calibrating the relative output of one to the sum of both. Two of the platforms measured 1.02×1.02 m and the other two measured 0.95×1.02 m. All four platforms were arranged serially and mounted flush in a runway of 10 m in total length. Force platform output was acquired through strain-conditioning amplifiers (SCXI National Instruments, Austin, TX), digitized (DAQCard-AI-16E-4 A-to-D board) and saved in a laptop computer running a custom acquisition routine written in LabVIEW (v. 5.1, National Instruments). Force data from the combined 16 channels of the four force platforms were collected at a rate of 200 Hz.
(c). Selection of strides
Because ground reaction force was measured by one of four force platforms for each footfall, it was possible to select one of two possible strides for analysis. From each trial, we selected the stride that was nearest to steady-speed by initially examining both strides. For consecutive ipsilateral footfalls during running, positive vertical accelerations were integrated to determine the time representing half of the area under the positive acceleration–time curve. For consecutive ipsilateral footfalls during walking, negative vertical accelerations were integrated to determine the time representing half of the area under the negative acceleration–time curve. These times were taken as the beginning and end of each stride.
(d). CoM velocities
Once the stride period was defined, the fore–aft distance between centres of pressure of the ipsilateral footfalls determined the stride length. The mean forward velocity was then computed as the ratio of stride length to stride period. The mean change in fore–aft velocity owing to braking and propulsive acceleration was then subtracted from the mean forward velocity to determine the initial forward velocity for the stride. Because the beginning of the stride represents an inflection point in vertical velocity, the initial vertical velocity was zero. These initial fore–aft and vertical velocities were used as integration constants in the integration of fore–aft and vertical accelerations to determine the instantaneous two-dimensional velocity vector throughout the stride.
Stride parameters: dimensionless stride length was determined relative to standing hip height (measured from the floor to the greater trochanter). Mean forward velocity was made non-dimensional by the square root of Froude number 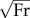 according to hip height and gravity factor (equation (1.1), table 1). Duty factor was determined as the quotient of the support period of the mid-stride footfall (bounded by the two half-footfalls of the contralateral limb) and the stride period.
according to hip height and gravity factor (equation (1.1), table 1). Duty factor was determined as the quotient of the support period of the mid-stride footfall (bounded by the two half-footfalls of the contralateral limb) and the stride period.
(e). Collision-based angles
Force angle Θ, velocity angle Λ and collision angle Φ were determined from the ground reaction force vector F and velocity vector V of the CoM following the equations of Lee et al. [19] and repeated here in table 1. The instantaneous force angle θ is the deviation of the force vector from vertical (equation (1.2)); the instantaneous velocity angle λ is the deviation of the velocity vector from horizontal (equation (1.4)); and the instantaneous collision angle ϕ is the deviation from an orthogonal relationship of the force and velocity vectors (equation (1.6)). It is important to note that these angles of deviation are based upon absolute values, hence magnitudes rather than positive or negative angles are determined in each instance of ground contact.
Force, velocity and collision angles Θ, Λ and Φ (equations (1.3), (1.5) and (1.7)) are determined for the complete stride by force-averaging, velocity-averaging and force × velocity-averaging, respectively, over the contact periods of the stride. Averaging in this manner ascribes less weight to spurious angles that may occur, for example, during initial or final contacts when the force magnitude is small. It is appropriate to consider only ground contact periods because, neglecting air resistance, these are the only physical interactions between the CoM and the environment. The velocity vector is still computed during ballistic flight periods, which provide a correct velocity angle and magnitude to determine CoM dynamics in the subsequent ground contact period.
(f). Collision fraction
In each instance, the potential collision is the sum θ + λ of the instantaneous force angle (equation (1.2)) and instantaneous velocity angle (equation (1.4)), whereas the actual collision is the instantaneous collision angle ϕ (equation (1.6)). Collision fraction is the weighted average of the instantaneous ratio of actual to potential collision ϕ/θ + λ (equation (1.14)).
(g). Mechanical cost of transport
In comparative biomechanics, the mechanical cost of locomotion has traditionally been normalized by body mass and forward distance travelled [30]. However, this quantity has been replaced by a dimensionless mechanical cost of transport CoTmech [31,32], which includes the acceleration of gravity in the denominator (equation (1.12)). This definition of mechanical cost of transport has become a new standard for the robotics and biomechanics communities alike. The inclusion of gravity in the mechanical cost of transport becomes more than just a dimensional convenience when gravity is variable. For example, while mass manipulations would have been accounted for in the traditional normalization of mechanical cost, gravity effects would not. Hence, normalizing by body weight instead of body mass makes CoTmech directly comparable across gravity conditions. As explained by Lee et al. [19], the collision angle Φ is nearly equal to CoTmech (equation (1.12); see electronic supplementary material, figure S1) when vertical undulations and fore–aft forces are small (equations (1.9) and (1.10)). In addition to CoTmech, we determine an individual limb's [20] cost of transport CoTILM based upon the absolute value of individual limb power (equation (1.11); see electronic supplementary material, figure S1).
(h). Statistics
A linear least-squares model (JMP 8.0) included discrete effects of gait and gravity conditions for four trials from each of eight subjects. For the relationship between CoTmech and Φ during walking and running, as well as for the individual limb's cost of transport CoTILM (equation (1.11)) during walking, regression equations were determined by both least-squares and reduced major axis methods.
3. Results
We present the collision-based angles (force Θ, velocity Λ and collision Φ), collision fraction and mechanical cost of transport for human walking and running. The subjects walked at 1.2 m s−1, corresponding to a dimensionless speed (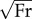 ; equation (1.1)) between 0.38 and 0.41 for normal gravity, and between 0.33 and 0.35 for hypergravity of 1.35 g. The subjects ran at 1.9 m s−1, corresponding to dimensionless speeds between 0.62 and 0.65 for normal gravity, and between 0.54 and 0.56 for hypergravity.
; equation (1.1)) between 0.38 and 0.41 for normal gravity, and between 0.33 and 0.35 for hypergravity of 1.35 g. The subjects ran at 1.9 m s−1, corresponding to dimensionless speeds between 0.62 and 0.65 for normal gravity, and between 0.54 and 0.56 for hypergravity.
(a). Collision-based angles
For human walking and running, force angle Θ is invariant with gait (p = 0.10) at the speeds studied, with values ranging from 0.065 to 0.082 radians (figure 3a). During both running and walking, force angles Θ are significantly (p = 0.02), albeit subtly, reduced in the hypergravity condition (figure 3a). Force angles decrease by about 10% (i.e. become more vertical) during walking and running in hypergravity because the experimental increase in vertical force is not accompanied by a proportional increase in horizontal force.
Figure 3.
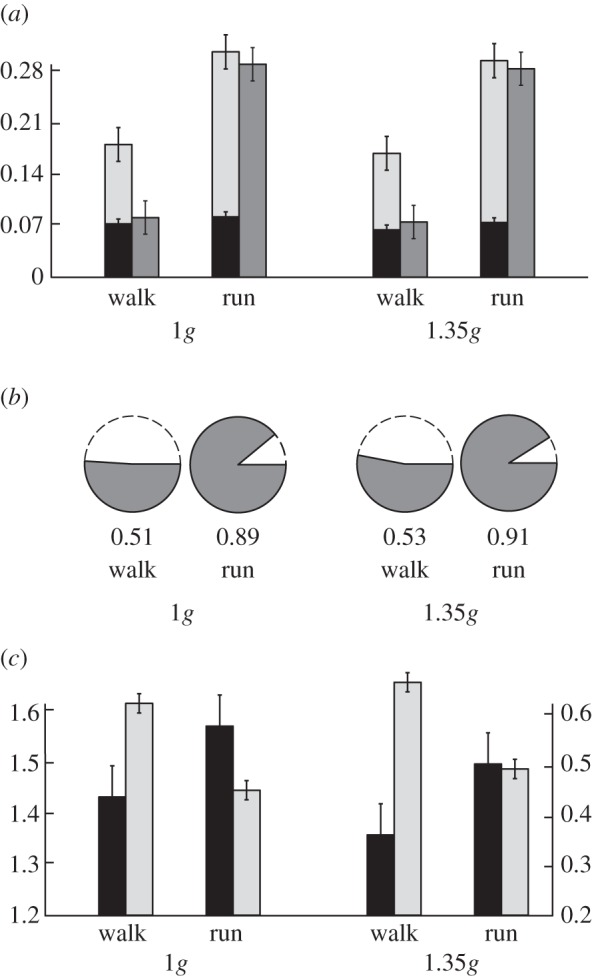
Results of human walking and running analyses comparing normal (1g) and hypergravity (1.35g) conditions. (a) Force angle Θ (black), velocity angle Λ (light grey) and collision angle Φ (dark grey). The scale from 0 to 0.28 radians represents 0–16°. (b) Collision fraction is the ratio of actual to potential collision and is represented by solid areas of the pie charts. (c) Dimensionless stride length (left axis; black bars) and duty factor (right axis; light grey bars). Error bars indicate 95% CIs in all panels. Significant differences (p < 0.05) are found between gaits in all parameters except force angle Θ. Significant differences between 1 and 1.35g (p < 0.05) are found in force angle Θ (a), as well as dimensionless stride length and duty factor (c).
Velocity angle Λ tends to be greater in SLIP-like gaits such as running, hopping or trotting owing to increased vertical oscillations of the CoM during these ‘bouncing gaits’. In contrast to the similarity of Θ during human walking and running, Λ doubles for running (Λ ≈ 0.2) compared with walking (Λ ≈ 0.1; p < 0.0001; figure 3a). Velocity angles Λ are statistically similar (p = 0.76) between normal and hypergravity conditions (figure 3a).
Collision angle Φ is 3.6 times greater during running than walking (p < 0.0001), resulting in a 3.6 times increase in mechanical cost of transport during running versus walking. Collision angles are statistically similar (p = 0.64) between normal and hypergravity conditions (figure 3a).
(b). Collision fraction
Collision fraction is the ratio of the actual collision to the potential collision (equation (1.14))—a smaller fraction indicates reduced collision. During walking and running, collision fractions are, respectively, 0.51 and 0.89 (p < 0.0001; figure 3b). Hence, the dynamics of running reduce the potential collision by only 9–11% compared with 49% during walking, indicating that humans reduce collisions substantially during walking, but not running. There is no significant difference in collision fraction between normal and hypergravity conditions (p = 0.22).
(c). Mechanical cost of transport
The mechanical cost of transport CoTmech (equation (1.12)) is the normalized CoM mechanical power during the contact period of a gait when the limbs redirect the CoM. Humans walk with CoTmech ≈ 0.08 and run with CoTmech ≈ 0.28 (p < 0.0001). There is no significant difference in CoTmech between normal and hypergravity conditions (p = 0.49).
Mechanical cost of transport CoTmech, as well as the individual limbs cost of transport CoTILM (equation (1.11)), are analysed as a function of collision angle Φ (see regressions and statistics in the electronic supplementary material, figure S1). As predicted by equations (1.7)–(1.10) and (1.12), CoTmech is nearly equal to the collision angle Φ.
(d). Spatio-temporal parameters
Spatio-temporal parameters of the stride are determined to evaluate potential gait and gravity effects. As expected, dimensionless stride length and duty factor differ significantly between walking at 1.2 m s−1 and running at 1.9 m s−1 (figure 3c). Dimensionless stride length significantly decreases (p = 0.04) in the hypergravity condition (figure 3c). Duty factor is strongly influenced by hypergravity (p < 0.001)—increasing from 0.62 to 0.66 during walking and from 0.45 to 0.49 during running (figure 3c).
4. Discussion
Our present results, combined with comparative data from a range of species available in recent literature, provide an opportunity to reconsider and reinterpret the similarities and differences across a broad range of terrestrial locomotion strategies. We discuss human walking and running in terms of collision-based angles, collision fraction and cost of transport and place these within the context of other terrestrial gaits used by mammals.
(a). Force Θ, velocity Λ and collision Φ angles
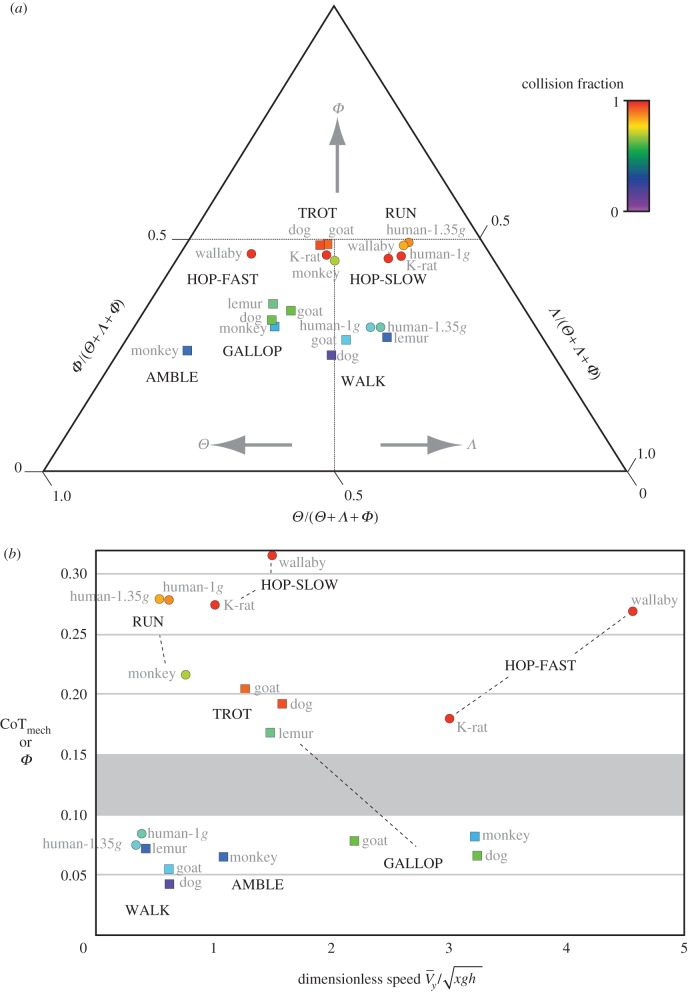
Comparison of collision-based angles reveals patterns across gaits and across species. Figure 4a plots the dynamics of all terrestrial species and gaits for which collision-based angles are available using a ternary representation, and corresponding angles are listed in the electronic supplementary material, table S2. This diagram displays the relative values of force angle Θ, velocity angle Λ and collision angle Φ on three axes, with each angle expressed as a fraction of the sum of all three angles. For example, the relative influence of force angle Θ versus velocity angle Λ is indicated, respectively, as a leftward or rightward shift of the plotted point from the central axis of the triangle. A leftward shift occurs when Θ is greater than Λ and a rightward shift occurs when Λ is greater than Θ (figure 4a). A greater relative value of collision angle Φ is reflected in the altitude on the ternary plot; however, it is important to note that vertical position does not directly correspond to the magnitude of Φ, nor can collision fraction be directly read from a ternary representation. Collision fraction is indicated here via colour coding of the points (figure 4a).
Figure 4.
Collision-based analysis of human locomotion together with gaits of other mammals from the literature. (a) Θ, Λ and Φ as a fraction of their sum plotted on ternary axes. (b) Mechanical cost of transport CoTmech or Φ as a function of dimensionless speed 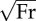 . Filled circles indicate bipedal gaits and filled squares indicate quadrupedal gaits. Colour of data symbols indicates collision fractions with red indicating a collision fraction of one and violet a collision fraction of zero (for spectrum of intermediate colours, see colour scale at right). Collision-based analyses of non-human mammals are for goats and dogs [19], lemurs [17], monkeys [18], kangaroo rats (K-rat) and wallabies [33].
. Filled circles indicate bipedal gaits and filled squares indicate quadrupedal gaits. Colour of data symbols indicates collision fractions with red indicating a collision fraction of one and violet a collision fraction of zero (for spectrum of intermediate colours, see colour scale at right). Collision-based analyses of non-human mammals are for goats and dogs [19], lemurs [17], monkeys [18], kangaroo rats (K-rat) and wallabies [33].
The ternary diagram of collision-based angles visualizes the distinct patterns of CoM dynamics that characterize ambling, galloping, walking and SLIP-like gaits. It is expected that SLIP-like gaits with little collision reduction [19] will appear near the top of the ternary plot and gaits with substantial collision reduction will appear towards the base of the plot. Bearing in mind that relative values determine the position on the ternary plot, it is expected that slower gaits and gaits with greater vertical undulation will tend to appear towards the right of the plot, indicating relatively greater Λ. Conversely, faster gaits and gaits with less vertical undulation will tend to appear towards the left of the plot, indicating relatively smaller Λ.
Examining vertical position on the ternary plot, relative values of Φ reveal distinctions between gaits. Walking, galloping and ambling group into separate, well-delineated regions with low relative magnitudes of Φ and small collision fractions as indicated by colour (figure 4a). On the other hand, trotting, bipedal running and hopping are intermingled along the upper portion of the plot, showing greater relative magnitudes of Φ and large collision fractions as indicated by colour.
Viewing the leftward or rightward shift, relative values of force angle Θ and velocity angle Λ reveal the influences of vertical oscillation and speed. Quadrupedal ambling and galloping appear towards the left side of the ternary plot because they are fast gaits with little vertical oscillation, resulting in relatively small velocity angles Λ. Quadrupedal walking and trotting appear near the centre-line of the ternary plot, indicating roughly equal magnitudes of Θ and Λ. Slow walking and running of humans appear towards the right side of the ternary plot, as does slow bipedal hopping, because these are slow gaits with substantial vertical oscillation, resulting in relatively large velocity angles Λ. However, the data points for faster hopping of kangaroo rats and wallabies shift to the left, as is expected for greater speeds. Hence, it is particularly important to consider dimensionless speed when evaluating the relative magnitudes of Θ and Λ of SLIP-like trotting, running and hopping gaits. A similar leftward shift is expected for faster running of humans, and future studies should address this prediction.
Comparative data suggest that SLIP-like gaits of bipeds have greater vertical oscillations than those of quadrupeds at a given dimensionless speed. Velocity angles of bipedal hoppers are more than twice those of quadrupedal trotters at the same dimensionless speed (see electronic supplementary material, table S2). The collision-based angles measured here for slow running of humans match those of slow bipedal hoppers. Additional comparative data across species and speeds are needed to bolster this empirical observation of greater vertical oscillations in SLIP-like gaits of bipeds than quadrupeds. It is so far unclear whether bipedal walking might also show greater vertical oscillations because dimensionless speed ranges do not overlap in the available data for bipeds and quadrupeds (see electronic supplementary material, table S2).
(b). Collision fraction
The intermediate collision fractions of 0.51 found during human walking compared with the significantly greater collision fractions of 0.89 during running (figure 3b) indicate greater collision reduction during walking than running. If collisions were completely avoided by maintaining a perpendicular relationship between force and velocity vectors throughout the stride, both collision angle Φ and collision fraction would be zero. For example, the collision fraction of a rimless wheel with an infinite number of spokes [26,34] is zero. At the other extreme, if force and velocity vectors deviate in opposite directions such that 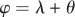 in every instance of the stride, the collision fraction will be unity (figure 1). For example, collision fraction would be unity for a theoretical compliant SLIP [35] in which force and velocity vectors always deviate in opposition—that is, braking force with downward velocity and propulsive force with upward velocity. Biological and engineered legged systems operate between the extremes of zero and unity, hence the collision fraction characterizes the CoM dynamics of any gait, not just the extremes.
in every instance of the stride, the collision fraction will be unity (figure 1). For example, collision fraction would be unity for a theoretical compliant SLIP [35] in which force and velocity vectors always deviate in opposition—that is, braking force with downward velocity and propulsive force with upward velocity. Biological and engineered legged systems operate between the extremes of zero and unity, hence the collision fraction characterizes the CoM dynamics of any gait, not just the extremes.
Collision fractions of human running (0.89) are consistent with the expectations of a compliant SLIP but are somewhat less than those of quadrupedal trotters (0.93) and bipedal hoppers (0.97; see electronic supplementary material, table S2). The lower collision fraction of human running may be due in part to the slow speed considered here. Future studies should examine potential effects of speed on collision fraction.
Collision fractions during human walking (0.51) are somewhat greater than those during quadrupedal walking of goats (0.48), lemurs (0.40) and dogs (0.26). Based upon these comparative data, collision reduction appears to be more complete during quadrupedal walking than bipedal walking. This observation may be explained by the greater number of footfalls used to redirect the CoM during stance, as predicted by theoretical collision models [26,36]. Given that a walking quadruped employs four discrete footfalls and a walking biped employs only two, it is plausible that the collision fraction of a walking dog (0.26) should be half that of a walking human (0.51). Collision fractions from additional bipeds and quadrupeds at the same dimensionless speeds will be needed to further explore theoretical predictions relating collision reduction to the number of foot contacts.
(c). Mechanical cost of transport (CoTmech)
We consider mechanical cost of transport (CoTmech) of human walking and running within a historical context and in comparison to the CoTmech of mammalian and robotic gaits. The collision angle Φ closely approximates CoTmech (equations (1.7)–(1.12)) during human locomotion, as was also previously shown for quadrupedal locomotion [19].
Dimensional mechanical costs of transport from the literature can be easily compared with CoTmech (equation (1.12)) by dividing by gravity (to make it dimensionless) and multiplying by two (to account for negative mechanical power, as explained below). Mechanical cost of transport has historically been considered in light of broad allometric relationships. Alexander [30] predicted that mechanical cost of transport should be independent of body mass and analysis confirmed his prediction, showing a dimensional mechanical cost of transport of approximately 1 J kg−1 m−1 for legged animals across a size range spanning five orders of magnitude [37] (with data of [4]). These mechanical costs of transport were based upon external work, a quantity computed by summing only the positive increments of the potential and kinetic energies of the CoM. While Cavagna and co-workers [2–4] have excluded negative work on the basis that it comprises lower metabolic cost to the organism than does positive work, we count both positive and negative power by summing the absolute value of instantaneous CoM power in the computation of CoTmech (equation (1.12)). This accounting considers generative and absorptive dynamics of the CoM on an equal basis, allowing for separate accountings of mechanical and metabolic cost.
The dimensionless mechanical cost of transport we recalculate from Full & Tu's [37] allometric analysis is approximately 0.2, which is in good agreement with CoTmech for trotting quadrupeds, but overestimates CoTmech of walking and galloping, and underestimates CoTmech of bipedal running and hopping (figure 4b). Based upon data from nearly 20 arthropods, mammals and birds—only one-third of which are bipeds—the allometric prediction of CoTmech ≈ 0.2 represents an average dominated by quadrupedal and hexapedal trotting gaits. The present analysis of CoTmech shows three- to fivefold differences between walking and running gaits (figure 4b). Hence, gait should be considered as a key factor influencing mechanical cost of transport.
Walking quadrupeds show a lower CoTmech than walking bipeds (figure 4b), which agrees with the theoretical prediction that the normalized cost of redirecting the CoM should be inversely proportional to the number of footfalls used in that redirection [26,36]. Quadrupeds tend to walk at greater dimensionless speeds with about half the CoTmech of walking humans (figure 4b). The quadrupedal amble or ‘running walk’, represented here by the amble of monkeys (figure 4b), exploits this effect of cost reduction by multiple footfalls to an even greater extent, achieving nearly twice the dimensionlessspeed of walking dogs and goats at only a slightly greater CoTmech. Galloping dogs, goats and monkeys, similarly, use distributed footfalls to maintain CoTmech on a par with that of walking, despite dimensionless speeds many times greater (figure 4b).
Although they span a range of dimensionless speeds from 0.2 to 3.2, the walking, ambling and galloping gaits discussed so far are achieved with CoTmech < 0.10, apart from a single outlier: the galloping of lemurs (CoTmech = 0.17). Of the species so far surveyed, bipedal hoppers and human runners show the greatest CoTmech ≈ 0.25−0.30. In addition to similarities in absolute (see electronic supplementary material, table S2) and relative (figure 4a) collision-based angles already discussed, CoTmech of humans running at 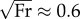 is most similar to that of kangaroo rats hopping at
is most similar to that of kangaroo rats hopping at 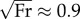 (figure 4b). Compared with walking, bipedal running and quadrupedal trotting show substantially greater CoTmech, with three- and fivefold increases in humans and dogs, respectively. In fact, CoTmech is greater than 0.15 for all trotting, bipedal running and hopping gaits shown in figure 4b.
(figure 4b). Compared with walking, bipedal running and quadrupedal trotting show substantially greater CoTmech, with three- and fivefold increases in humans and dogs, respectively. In fact, CoTmech is greater than 0.15 for all trotting, bipedal running and hopping gaits shown in figure 4b.
The empirical observation that walking, ambling and galloping are characterized by a CoTmech less than 0.10 and that trotting, running and hopping are characterized by a CoTmech greater than 0.15 suggests that an intermediate CoTmech range between 0.10 and 0.15 is generally avoided by mammals. The grey horizontal bar in figure 4b represents this apparent exclusion zone. Importantly, Gaits with CoTmech below this zone typically have collision fractions less than 0.8 and gaits with CoTmech above it typically have collision fractions greater than 0.8. We propose as a general rule that the lower region is occupied by gaits that employ collision reduction strategies and the upper CoTmech region is occupied by gaits that primarily use SLIP-like dynamics.
Bipedal and quadrupedal walking gaits surveyed so far have a CoTmech between 0.04 and 0.08 (figure 4b). Humans walk with a CoTmech of about 0.08 at Earth's gravity and 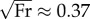 . In comparison with the most economical bipedal walking robots [31], human walkers are both faster and have a greater CoTmech. Such gravity-driven or actuated bipedal robots walk at less than half the speed of our human subjects, with CoTmech ≈ 0.05, yet similar passive dynamic machines would show a CoTmech more like that of humans if they were to walk at faster speeds [38].
. In comparison with the most economical bipedal walking robots [31], human walkers are both faster and have a greater CoTmech. Such gravity-driven or actuated bipedal robots walk at less than half the speed of our human subjects, with CoTmech ≈ 0.05, yet similar passive dynamic machines would show a CoTmech more like that of humans if they were to walk at faster speeds [38].
Like Φ, CoTmech is statistically indistinguishable between normal and hypergravity conditions of 1.35g (figure 4b). This result highlights an advantage of CoTmech—because it is non-dimensional (gravity is in the denominator), CoTmech is directly comparable across gravity conditions. Hence, the CoM dynamics of human walkers and runners are maintained within narrow limits despite an experimental 35% increase in gravity. Further studies will be needed to investigate variance of CoTmech across a range of hypo- and hypergravity conditions.
In the comparison of human running and walking gaits, a threefold increase in mechanical cost of transport CoTmech of human running over walking corresponds to only a 72% increase in metabolic cost of transport, as summarized from the literature [39]. Whereas mechanical cost is based upon CoM energy, metabolic cost is the chemical energy consumed by muscles during locomotion. This discrepancy between mechanical and metabolic costs of transport implicates an elastic mechanism for the storage and return of energy during running [2], wherein some of the mechanical work is done by passive elastic structures, thus mitigating chemical energy consumption by muscles. Humanoid robots running with the same CoM dynamics as their biological counterparts would certainly benefit from elastic mechanisms to mitigate the elevated CoTmech of running versus walking.
5. Conclusion
We provide a unifying context for intra- and interspecific gait comparison by quantifying the CoM dynamics of gaits, including human walking and running, using collision-based force angle Θ, velocity angle Λ and collision angle Φ, and the collision fraction. A collision fraction of approximately 0.50 indicates that human walking employs collision reduction, but not to the extent seen in quadrupedal walking. Human running, bipedal hopping and quadrupedal trotting all show little to no collision reduction with collision fractions approaching unity—as expected for idealized SLIP-like dynamics. Gaits such as walking, ambling and galloping, which employ collision reduction, correspond to a mechanical cost of transport CoTmech less than 0.10, whereas SLIP-like gaits correspond to a CoTmech greater than 0.15, with the intermediate region unoccupied by mammalian gaits surveyed. At the slow speeds considered here, humans walk with a CoTmech of about 0.08 and run with a CoTmech of about 0.28—revealing a threefold increase in collision angle Φ and CoTmech of running versus walking.
Our collision-based approach offers four key advantages in the analysis of terrestrial gait: (i) it considers CoM dynamics in every instance of contact during a stride; (ii) it is dimensionless, allowing comparisons across species of vastly different size and comparisons across gravity conditions; (iii) it is independent of a priori models of CoM mechanics, and therefore applies equally to any gait; and (iv) it explains the mechanical cost of transport from first principles, as opposed to earlier derivations using only dimensional analysis. Furthermore, a collision-based approach is general enough to incorporate modelling at higher levels—from a single axis of leg compliance to detailed musculoskeletal models. In fact, such models may be informed and verified by comparing their collision-based parameters with those of biological or robotic legged systems.
Funding statement
This work was supported in part by a Nevada INBRE Fellowship to T.N.C. (NIH grant no. P20 RR-016464 from the National Center for Research Resources).
References
- 1.Hildebrand M. 1965. Symmetrical gaits of horses. Science 150, 701–708 (doi:10.1126/science.150.3697.701) [DOI] [PubMed] [Google Scholar]
- 2.Cavagna GA, Heglund NC, Taylor CR. 1977. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. 233, R243–R261 [DOI] [PubMed] [Google Scholar]
- 3.Cavagna GA, Thys H, Zamboni A. 1976. The sources of external work in level walking and running. J. Physiol. 262, 639–657 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Heglund NC, Cavagna GA, Taylor CR. 1982. Energetics and mechanics of terrestrial locomotion. III. Energy changes of the centre of mass as a function of speed and body size in birds and mammals. J. Exp. Biol. 97, 41–56 [DOI] [PubMed] [Google Scholar]
- 5.Griffin TM, Main RP, Farley CT. 2004. Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like movements? J. Exp. Biol. 207, 3545–3558 (doi:10.1242/jeb.01177) [DOI] [PubMed] [Google Scholar]
- 6.Griffin TM, Kram R. 2000. Biomechanics: penguin waddling is not wasteful. Nature 408, 929 (doi:10.1038/35050167) [DOI] [PubMed] [Google Scholar]
- 7.Saunders JB, Inman VT, Eberhart HD. 1953. The major determinants in normal and pathological gait. J. Bone Jt Surg. 35, 543–558 [PubMed] [Google Scholar]
- 8.Inman VT. 1966. Human locomotion. Can. Med. Ass. J. 94, 1047–1054 [PMC free article] [PubMed] [Google Scholar]
- 9.Inman VT, Ralston HJ, Todd F. 1994. Human locomotion. In Human Walking (ed. Rose J, Gamble JG.), pp. 2–22 Baltimore, MD: Williams & Wilkins [Google Scholar]
- 10.Lee CR, Farley CT. 1998. Determinants of the center of mass trajectory in human walking and running. J. Exp. Biol. 201, 2935–2944 [DOI] [PubMed] [Google Scholar]
- 11.Geyer H, Seyfarth A, Blickhan R. 2006. Compliant leg behaviour explains dynamics of walking and running . Proc. R. Soc. B 273, 2861–2867 (doi:10.1098/rspb.2006.3637) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gatesy SM, Biewener AA. 1991. Bipedal locomotion: effects of speed, size and limb posture in birds and humans. J. Zool. 224, 127–147 (doi:10.1111/j.1469-7998.1991.tb04794.x) [Google Scholar]
- 13.Usherwood JR. 2010. Inverted pendular running: a novel gait predicted by computer optimization is found between walk and run in birds. Biol. Lett. 6, 765–768 (doi:10.1098/rsbl.2010.0256) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Minetti AE, Ardigo LP, Reinich E, Saibene F. 1999. The relationship between mechanical work and energy expenditure of locomotion in horses. J. Exp. Biol. 202, 2329–2338 [DOI] [PubMed] [Google Scholar]
- 15.Biknevicius AR, Mullineaux DR, Clayton HM. 2006. Locomotor mechanics of the tölt in Icelandic horses. Am. J. Vet. Res. 67, 1505–1510 (doi:10.2460/ajvr.67.9.1505) [DOI] [PubMed] [Google Scholar]
- 16.Starke SD, Robilliard JJ, Weller R, Wilson AM, Pfau T. 2009. Walk–run classification of symmetrical gaits in the horse: a multidimensional approach. J. R. Soc. Interface 6, 335–342 (doi:10.1098/rsif.2008.0238) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.O'Neill MC, Schmitt D. 2012. The gaits of primates: center of mass mechanics in walking, cantering and galloping ring-tailed lemurs, Lemur catta. J. Exp. Biol. 215, 1728–1739 (doi:10.1242/jeb.052340) [DOI] [PubMed] [Google Scholar]
- 18.Demes B, O'Neill MC. 2013. Ground reaction forces and center of mass mechanics of bipedal capuchin monkeys: implications for the evolution of human bipedalism. Am. J. Phys. Anthropol. 150, 76–86 (doi:10.1002/ajpa.22176) [DOI] [PubMed] [Google Scholar]
- 19.Lee DV, Bertram JE, Anttonen JT, Ros IG, Harris SL, Biewener AA. 2011. A collisional perspective on quadrupedal gait dynamics. J. R. Soc. Interface 8, 1480–1486 (doi:10.1098/rsif.2011.0019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Donelan JM, Kram R, Kuo AD. 2002. Simultaneous positive and negative external mechanical work in human walking. J. Biomech. 35, 117–124 (doi:10.1016/S0021-9290(01)00169-5) [DOI] [PubMed] [Google Scholar]
- 21.Neptune RR, McGowan CP, Kautz SA. 2009. Forward dynamics simulations provide insight into muscle mechanical work during human locomotion. Exerc. Sport Sci. Rev. 37, 203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Michilsens F, D'Août K, Vereecke EE, Aerts P. 2012. One step beyond: different step-to-step transitions exist during continuous contact brachiation in siamangs. Biol. Open 1, 411–421 (doi:10.1242/bio.2012588) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kuo AD. 2001. A simple model of bipedal walking predicts the preferred speed–step length relationship. Ann Arbor 1001, 264–269 [DOI] [PubMed] [Google Scholar]
- 24.Donelan JM, Kram R, Kuo AD. 2002. Mechanical work for step-to-step transitions is a major determinant of the metabolic cost of human walking. J. Exp. Biol. 205, 3717–3727 [DOI] [PubMed] [Google Scholar]
- 25.Kuo AD. 2002. Energetics of actively powered locomotion using the simplest walking model. Trans. Am. Soc. Mech. Eng. J. Biomech. Eng. 124, 113–120 (doi:10.1115/1.1427703) [DOI] [PubMed] [Google Scholar]
- 26.Ruina A, Bertram JEA, Srinivasan M. 2005. A collisional model of the energetic cost of support work qualitatively explains leg sequencing in walking and galloping, pseudo-elastic leg behavior in running and the walk-to-run transition. J. Theor. Biol. 237, 170–192 (doi:10.1016/j.jtbi.2005.04.004) [DOI] [PubMed] [Google Scholar]
- 27.Kuo AD, Donelan JM, Ruina A. 2005. Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exerc. Sport Sci. Rev. 33, 88–97 (doi:10.1097/00003677-200504000-00006) [DOI] [PubMed] [Google Scholar]
- 28.Adamczyk PG, Kuo AD. 2009. Redirection of center-of-mass velocity during the step-to-step transition of human walking. J. Exp. Biol. 212, 2668–2678 (doi:10.1242/jeb.027581) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Heglund NC. 1981. Short Communication: a simple design for a force-plate to measure ground reaction forces. J. Exp. Biol. 93, 333–338 [Google Scholar]
- 30.Alexander RM. 1977. Mechanics and scaling of terrestrial locomotion. In Scale effects in animal locomotion (ed. Pedley TJ.), 93–110 London, UK: Academic Press [Google Scholar]
- 31.Collins SH, Ruina A, Wisse M, Tedrake R. 2005. Efficient bipedal robots based on passive-dynamic walkers. Science 307, 1082–1085 (doi:10.1126/science.1107799) [DOI] [PubMed] [Google Scholar]
- 32.Alexander RMcN. 2005. Models and the scaling of energy costs for locomotion. J. Exp. Biol. 208, 1645–1652 (doi:10.1242/jeb.01484) [DOI] [PubMed] [Google Scholar]
- 33.Gutmann AK, Lee DV, McGowan CP. 2013. Collision mechanics of bipedal hopping. Biol. Lett. 9, 20130418 (doi:10.1098/rsbl.2013.0418) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Margaria R. 1976. Biomechanics and energetics of muscular exercise. Oxford, UK: Clarendon Press [Google Scholar]
- 35.Blickhan R. 1989. The spring-mass model for running and hopping . J. Biomech. 22, 1217–1227 (doi:10.1016/0021-9290(89)90224-8) [DOI] [PubMed] [Google Scholar]
- 36.Bertram JEA, Gutmann A. 2009. The running horse and cheetah revisited: fundamental mechanics of two galloping gaits. J. R. Soc. Interface 6, 549–559 (doi:10.1098/rsif.2008.0328) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Full RJ, Tu MS. 1991. Mechanics of rapid running insect: two-, four- and six-legged locomotion. J. Exp. Biol. 156, 215–231 [DOI] [PubMed] [Google Scholar]
- 38.Garcia M, Chatterjee A, Ruina A. 2000. Efficiency, speed, and scaling of two-dimensional passive-dynamic walking. Dyn. Stab. Syst. 15, 75–99 (doi:10.1080/713603737) [Google Scholar]
- 39.Rubenson J, Heliams DB, Maloney SK, Withers PC, Lloyd DG, Fournier PA. 2007. Reappraisal of the comparative cost of human locomotion using gait-specific allometric analyses. J. Exp. Biol. 210, 3513–3524 (doi:10.1242/jeb.000992) [DOI] [PubMed] [Google Scholar]