Quantifying Diagnostic Uncertainty Using Item Response Theory: The Posterior Probability of Diagnosis Index

Abstract

Using traditional Diagnostic and Statistical Manual of Mental Disorders (DSM; American Psychiatric Association, 2000) diagnostic criteria, clinicians are forced to make categorical decisions (diagnosis versus no diagnosis). This forced choice implies that mental and behavioral health disorders are categorical and does not fully characterize varying degrees of uncertainty associated with a particular diagnosis. Using an IRT (latent trait model) framework, we describe the development of the Posterior Probability of Diagnosis (PPOD) Index which answers the question, “What is the likelihood that a patient meets or exceeds the latent trait threshold for a diagnosis.” The PPOD Index is based on the posterior distribution of θ (latent trait score) for each patient’s profile of symptoms. The PPOD Index allows clinicians to quantify and communicate the degree of uncertainty associated with each diagnosis in probabilistic terms. We illustrate the advantages of the PPOD Index in a clinical sample (N = 321) of children and adolescents with Oppositional Defiant Disorder (ODD).

In this study we introduce the Posterior Probability of Diagnosis (PPOD) Index which was developed using item response theory (IRT) to quantify the likelihood that a patient meets or exceeds a latent-trait threshold for a disorder given his or her profile of symptoms. More specifically, the PPOD Index is a Bayesian approach to diagnosis based on the posterior distribution of θ (latent trait score) for an individual patient’s profile of symptoms. Both under-diagnosis and over-diagnosis are significant problems for many disorders, especially disorders for which a diagnosis is based on co-occurrences of symptoms and clinical judgment (e.g., Bruchmüller, Margraf, & Schneider, 2012; Wakefield & First, 2003). The PPOD Index is an attempt to address this issue by providing an empirical means to quantify the likelihood that a patient meets or exceeds the threshold for a disorder in probabilistic terms. As such, the PPOD Index addresses several problems with traditional approaches to psychiatric diagnoses including forced categories, crude symptoms counts, and the sometimes imprecise use of diagnostic labels. We discuss each of these problems briefly before describing the PPOD Index and illustrating its utility with a clinical sample of children and adolescents with Oppositional Defiant Disorder (ODD).

Traditional DSM Diagnostic System

Forced categories

Using traditional diagnostic criteria of the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV; American Psychiatric Association, 2000), clinicians are required to make categorical decisions (diagnosis versus no diagnosis). As a result, a forced choice is made even when there is a great degree of uncertainty about the diagnosis. Such an approach glosses over the varying degrees of uncertainty associated with a particular diagnosis. Compelling arguments have been made that DSM disorders are better conceptualized as dimensional rather than categorical (e.g., Achenbach, 1995; Widiger & Coker, 2003; Widiger & Clark, 2000). Consistent with a dimensional perspective, taxometric methods (see Ruscio & Ruscio, 2004 for a review) are producing substantial evidence that many DSM diagnoses and related constructs represent high levels of continuous latent traits rather than distinct categories, including Posttraumatic Stress Disorder (PTSD; Ruscio, Ruscio, & Keane, 2002) and Attention-Deficit/Hyperactivity Disorder (ADHD; Frazier, Youngstrom, & Naugle, 2007). There is also support for a dimensional structure to ODD (e.g., Achenbach, 1995; Burns, Walsh, Owen, & Snell, 1997; Burns, Walsh, Patterson, Holte, Sommers-Flanagan, & Parker, 1997). Yet clinicians using the DSM are forced to make a diagnostic decision even when a patient is close to diagnostic threshold (e.g. 4 of 8 symptoms) and confidence might be low. Two patients may both be given a diagnosis, even though a clinician is much more confident that one patient has the disorder than the other. The issue is particularly problematic when a clinician is “on the fence” about the diagnosis. For example, a clinician may be uncertain about the clinical impact of a deciding symptom.

Symptom counts

Traditional DSM diagnoses are based on total symptom counts, regardless of which symptoms are endorsed. In order to meet diagnostic criteria for ODD, for example, one must present with at least four of eight symptoms. This means that there are 256 different possible combinations of symptoms, of which 163 result in diagnosis of ODD. In fact, it is even possible for two patients to meet diagnostic criteria for ODD even thought they do not have a single symptom in common. Similar observations have been made for other DSM disorders including Antisocial Personality Disorder (Lykken, 1995, p. 5). The problem is even more pronounced for Conduct Disorder for which there are 32,768 possible combinations of symptoms, of which 32,647 result in a diagnosis (≥3 of 15 symptoms). A symptom count approach does not test and defend the assumption that each symptom should be equally weighted or that each symptom equally discriminates between patients who do and do not have the disorder.

Real world diagnostic practices

Some practitioners have long been dissatisfied with the DSM diagnostic system to varying degrees (e.g., Jensen-Doss, & Hawley, 2011; Miller, Bergstrom, Cross, & Grube, 1981). There is evidence that some practitioners may apply DSM diagnoses inconsistently, unreliably, or perhaps even haphazardly for the purpose of third party reimbursements (Jensen & Weisz, 2002; Jensen-Doss, & Hawley, 2011). This may have a negative impact on patients, given the evidence that diagnostic accuracy leads to better patient engagement and treatment success (Jensen-Doss & Weisz, 2008). There is an increasing call for assessment and diagnostic practices to be evidence-based (e.g., Hunsley & Mash, 2005; Mash & Hunsley, 2005; Pelham, Fabiano, & Massetti, 2005), including diagnoses of childhood conduct problems (McMahon & Frick, 2005). Given the falsifiability of its assumptions, latent-trait models in general, and IRT methods in particular, are consistent with that call.

Item Response Theory

Item response theory (IRT) builds upon and extends many ideas first introduced in classical test theory (CTT; see Lord & Novick, 1968). IRT models and other latent-trait models have both theoretical and practical advantages over CTT including a framework that allows for their assumptions to be tested (see Borsboom, Mellenbergh, & van Heerden, 2003). IRT refers to a class of psychometric techniques in which the probability of choosing each item response category is modeled as a function of a latent trait of interest. By convention, the latent trait is scaled along a dimension called theta (θ), which has a mean of 0 and a standard deviation of 1 (by convenience). In IRT, a person’s responses to a set of items are used to estimate his or her level on a particular latent trait. More specifically, IRT uses each individual’s pattern of item responses (in this case symptom endorsements) in conjunction with estimated item parameters to estimate his or her θ level on the underlying latent-trait continuum. It should be emphasized that in the application of IRT to DSM diagnoses, symptoms are treated as items (e.g., Cole et al., 2011).

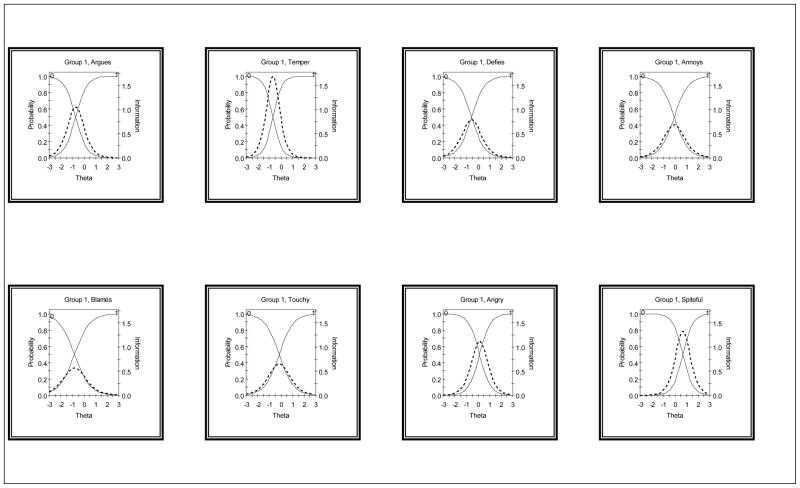
The relationship between the probability of choosing a certain response category (e.g., yes/no) for a specific item and the underlying severity level can be described by a monotonically increasing function (i.e., a sigmoid function) called the item characteristic function (ICF). An ICF can be transformed into an item information curve, indicating the amount of information a single item contains at all points along the severity (θ) scale. See Figure 1 for item information curves for the 8 ODD items. The amount of information provided by an item may vary depending on the level of a respondent’s severity of ODD (θ).

Figure 1.

Item characteristic curves (ICCs) and item information curves (IICs) for each of the eight ODD symptoms. ICCs are represented with solid lines. The probability of endorsing the item (labeled “1”) increases from 0.0 to 1.0 as theta increases. Conversely, the probability of not endorsing the item (labeled “0”) decreases from 1.0 to 0.0 as theta increases. IICs are represented with dotted lines. The peaks of the IICs indicate the level of theta at which each item provides maximum discrimination.

The most basic unidimensional IRT model is the one parameter logistic model (1PL; also known as the Rasch model) for which each item has a severity or threshold parameter β. This threshold parameter is defined as the latent trait level at which a respondent has a .50 chance of endorsing the item. As a result, respondents may differ in the consistency of their response pattern. For example, for 8 dichotomous items (yes/no) there are 256 possible response patterns. Table 1 shows just ten possible response patters for eight items, the first three of which are consistent response patterns. These first three respondents endorsed items with lower threshold parameters but not those with higher threshold parameters. Respondents 4 through 10 have varying degrees of inconsistency in their response patterns (i.e. endorsing some items with higher threshold parameters but not others with lower threshold parameters).

Table 1.

Examples of Hypothetical Response Patters (256 Possible) For Eight Dichotomous Items

Respondent	Items (in order of β)
	1	2	3	4	5	6	7	8
#1	1	1	1	1	1	1	1	0
#2	1	1	1	0	0	0	0	0
#3	1	0	0	0	0	0	0	0
#4	1	1	0	0	1	1	0	0
#5	1	1	1	0	1	0	0	0
#6	0	1	1	1	0	0	1	0
#7	0	1	0	0	0	1	0	1
#8	0	0	1	1	1	0	0	0
#9	0	0	0	1	1	1	1	1
#10	0	1	1	1	1	1	1	1

Two-parameter logistic (2PL) IRT models (first described by Birnbaum [1968]) also have a discrimination parameter α. Conceptually, this is very similar to a point-biserial correlation between an item and the total score in CTT. In IRT models, the discrimination parameter affects the estimate of each patient’s latent trait estimate θ. Items with higher discrimination parameters are “weighted” more heavily than items with lower discrimination parameters. For diagnostics, this takes into account the fact that not all items are equally good at discriminating between those who have the disorder and those who do not. Increasingly, IRT is being applied to clinical measurement (see Reise & Waller, 2009 for a review) including tools such as the Beck Depression Inventory (Bedi, Maraun, & Chrisjohn, 2001). IRT has already been applied to DSM dignostic criteria for depression in both adults (Aggen, Neale, & Kendler, 2005) and youth (Cole et al., 2011). Such applications of IRT have led to insights about the discriminability of particular depression symptoms and the reduction in measurement error. We are aware of one study that has applied IRT to DSM-IV symptoms of ODD (Gomez, Burns, & Walsh, 2008). The study assessed parent ratings of ODD symptoms using the Disruptive Behavior Rating Scale (DBRS; Barkley & Murphy, 1998) in the context of a cross-cultural study.

For our study, we chose the 2PL model because DSM diagnoses are generally unidimensional and symptoms are dichotomous. A 2PL model also allows us to estimate discrimination parameters and thereby test the implicit assumptions in the DSM behind the equal weighting of symptoms. Probably for these same reasons, the 2PL is the model that is most commonly applied to DSM disorders (e.g., Cole et al., 2011).

Current Study

In the current study, we apply IRT to diagnostic assessments to answer the question, “What is the liklihood that patient X has disorder Y?” We use an IRT approach to develop the Posterior Probability of Diagnosis (PPOD) Index to supplement traditional categorical diagnoses. The PPOD Index is based on the posterior distribution for each patient’s response pattern and measures the likelihood that a patient meets or exceeds the latent trait threshold for a diagnosis in Bayesian terms. We demonstrate how an IRT approach solves two problems associated with the more traditional approach to diagnostics in the DSM. These problems are: 1) symptom counts for which all symptoms are weighted equally, and 2) categorical decisions. We demonstrate the utility of an IRT approach to diagnostics with a sample of children who have been referred for clinical services due to disruptive behavior. For this study, we focus on the diagnosis of ODD. To meet diagnostic criteria for ODD, a patient must have four or more of the following eight symptoms: “often loses temper,” “often argues with adults,” “often actively defies or refuses to comply with adults’ requests or rules,” “often deliberately annoys people,” “often blames others for his or her mistakes or misbehaviors,” “is often touch or easily annoyed by others,” “is often angry or resentful,” and “is often spiteful or vindictive” (DSM-IV-TR).

Method

Participants

Participants in this study were parent-child dyads (N = 321) consisting of a clinical sample of boys (n = 207; 65%) and girls (n = 114; 35%) who were referred for services due to disruptive behavior. Children ranged in age from 5 to 12 (M = 8.00; SD = 1.97). Eight (2.5%) children were reported as Hispanic, 67 (21%) Black/African American, 259 (81%) white, and not reported 3 (0.9%) children. None were reported as American Indian/Alaskan Native, Asian, or Native Hawaiian/Pacific Islander. Parent relationship to child was reported as biological mother (n = 291; 91%), biological father (n = 16; 5%), adopted mother (n = 8; 2.5%), adopted father (n = 1; 0.3%), or grandmother (n = 4; 1.3%). Two hundred three (64%) parents were married/remarried and living with their spouse, 70 (22%) were single and never married, 30 (9%) were divorced, 14 (4.4%) were separated from their spouse, and 1 (0.3%) was a widow/widower. Parent education levels were reported as follows: 1 (0.3%) junior high (9th grade); 6 (1.9%) with some high school (10th or 11th grade), 63 (20%) with a high school degree or GED, 62 (19%) with some college (at least 1yr), 52 (16%) with an Associate Degree (2 years), 94 (30%) with 4-year college degree, and 41 (13%) with Graduate/Professional Training. Most parents were employed either full-time (n = 176; 55%) or part-time (n = 48; 15%). Median household income was in the $50,000–$74,999 range. The number of adults in the home ranged from one to five (M = 1.93; SD = 0.63) and the number of children in the home ranged from zero to six (M = 1.60; SD = 1.13).

Measures

Symptoms of ODD were assessed using the Vanderbilt Assessment Scale-Parent Version (VAS-Parent; Wolraich, Hannah, Baumgaertel, & Feurer, 1998). The VAS-Parent was chosen because items 19 through 26 map onto the eight DSM-IV symptoms of ODD. These items are: Item 19) Argues with adults; Item 20) Loses temper; Item 21) Actively deifies or refuses to go along with adults’ requests or rules; Item 22) Deliberately annoys people; Item 23) Blames others for his or her mistakes or misbehaviors; Item 24) Is touchy or easily annoyed by others; Item 25) is angry or resentful; and Item 26) Is spiteful and wants to get even. Each item is rated on 4-point Likert scale (0 = Never; 1 = Sometimes; 2 = Often; 3 = Very Often). To be consistent with DSM diagnostic criteria, each item was recoded as a “symptom” (1 = Often or Very Often) or “not a symptom” (0 = Never or Sometimes). Using this dichotomous variable, Cronbach’s α was high in the current sample (.80). Additional psychometric properties of the VAS-Parent are described in detail in the literature (Wolraich, Lambert, Doffing, Bickman, Simmons, & Worley, 2003). Given that the Oppositional Defiant Disorder (ODD) items on the VAS-P are based on the DSM-IV symptoms, it is not surprising that there is ample evidence of the scale’s validity. Factor analysis of the items supported a four-factor solution with the Oppositional Defiant Disorder (ODD) and Conduct Disorder (CD) items loading onto a separate factor from the inattention, hyperactivity/impulsivity items, and the anxiety-depression items. In addition, scores on these items are significantly associated with the likelihood of being suspended from school and the likelihood of being referred to a mental health provider (Wolraich et al., 2003).

Procedure

Participants were recruited from primary-care offices in the Pittsburgh area. Families who met study criteria were then scheduled for an intake assessment which included a diagnostic interview. Each family met with one of four Masters-level clinicians with additional training in clinical assessments and diagnostics. Parents completed the VAS-Parent during the intake assessment. The total minutes spent with families during the assessment ranged from 105 to 335 minutes (M = 155.48; SD = 29.15).

Data Analyses

Confirmatory factor analysis

A single factor confirmatory model was fitted using Mplus (Muthen & Muthen, 2010) to check the assumption, implicit in the DSM, that ODD is a unidimensional construct. The indicators (items) were treated as categorical variables. The robust weighted least squares (WLSMV) estimator was invoked. Criteria for fit indices were 0.05 for RMSEA and 0.95 for the comparative fit index (CFI) and the Tucker-Lewis index (TLI).

Two-parameter logistic (2PL) IRT model

Data analyses were conducted using IRTPRO (Cai, du Toit, & Thissen, 2011). The data were fit to a two-parameter logistic (2PL) IRT model for dichotomous items. We estimated threshold parameters (βs) and discrimination parameters (αs) for each of the eight ODD symptoms. We also estimated each patient’s IRT trait level θ and standard error of θ. Scoring was based on the expected a posteriori (EAP) estimation method (Bock & Mislevy, 1982) and assuming a standard normal prior distribution.

Posterior Probability of Diagnosis (PPOD) Index

The PPOD Index was developed to answer the following question: “What is the likelihood that patient X meets or exceeds the diagnostic threshold for disorder Y given his/her profile of symptoms (i.e. response pattern). The question is essentially a Bayesian one and is based on the posterior distribution of θ for each response pattern:

$$p(\theta \mid D)=\frac{p(D\mid \theta )p(\theta )}{p(D)},$$ (1)

where D is a response pattern (in this case a symptom profile). In the current study, we defined the PPOD Index as the likelihood that a patient meets or exceeds the threshold on the latent trait θ equivalent to the DSM-IV criteria for ODD of four or more symptoms. This threshold is defined as the lowest θ out of all patients with four of more symptoms. We scored our patients in the current sample using the 2PL model and the θ threshold was −0.38. Thus, the PPOD Index in the current study can be operationalized as the following posterior probability: p(θ ≥ −0.38 | response pattern).

We estimated the PPOD Index using two different methods. The first method (Method A) used the estimates of θ and the SE of θ for each patient from the IRTPRO output to estimate the liklihood that each patient met or exceeded a latent trait θ of −0.38. This was calculated in two steps: 1) calculating the likelihood (Φ) that each patient’s latent trait score (θ) was below −0.38 using the formula,

$$\mathrm{\Phi }=\left[\frac{(-0.38-\theta )}{{SE}_{\theta }}\right]\mathit{cdf},$$ (2)

where cdf is the cumulative distribution function and SE_θ is the standard error of the corresponding θ, and 2) calculating the likelihood (p) that each patient met or exceeded −0.38, where p = 1 − Φ. This method is merely a “short-cut” to avoid having to numerically integrate the posterior distribution of θ (as with Method B). A limitation of this method is the assumption that the posterior distribution of θ is normally distributed. To examine the potential bias resulting from this assumption, we calculated the PPOD Index using a second method. The second method (Method B) used numerical integration to integrate the posterior distribution of θ from −.38 to 2.9 (the maximum quadrature point for IRTPRO). Because IRTPRO does not provide the probability masses of the posterior distribution for each quadrature point for each pattern of responses, we created a program in MATLAB (MathWorks, 2011). The program generates the probability masses for each of discrete values of θ for the posterior distribution for each reponse pattern that is inputted and estimates the PPOD index using numerical integration (see Appendix A). Lines 52−61 of the program generate the probability masses of the posterior distribution of θ using Bayes’ theorem for discrete values of θ :

$$p(\theta \mid D)=\frac{p(D\mid \theta )p(\theta )}{{\sum }_{\theta }p(D\mid \theta )p(\theta )},$$ (3)

where p(θ) is the probability mass at θ and the denominator has been substituted for the denominator in Equation 1 because,

$$p(D)={\sum }_{\theta }p(D\mid \theta )p(\theta ).$$ (4)

The term on the right side of Equation 4 (the new denominator in Equation 3) is sometimes referred to as the normalizing constant. Because IRTPRO uses 60 quadrature points ranging from −3.0 to 2.9 in increments of 0.1, it was necessary to select quadrature points on either side of −.38 which we termed Lower Bound (−.30) and Upper Bound (−.40). Lines 62–66 of the program perform numerical integration the posterior distribution from −.30 to 2.9 (Lower Bound) and −.40 to 2.9 (Upper Bound).

Results

Item Descriptive Statistics

Item frequencies (proportion endorsed) for the sample were as follow: “argues” = .71, “temper” = .72, “defies” = .66, “annoys” = .52, “blame” = .71, “touchy” = .54, “angry” = .46, and spiteful” = .29. Internal consistency for the eight items was good, Cronbach’s alpha = .80. Total symptom counts ranged from 0 to 8 (M = 4.6; SD = 2.5) and were symmetrical (skewness = −0.35; SE = .14) but platykurtic (excess kurtosis = −0.98; SE = .27).

Confirmatory Factor Analysis

Results from the one factor confirmatory factor analysis (CFA) generally supported a one factor solution. Although the chi-square test was significant, χ² (16) = 49.71, p = .00, alternative fit indices were considered acceptable. Although the root mean square error of approximation (RMSEA) was marginal (.08), the comparative fit index (CFI = .96) and Tucker-Lewis Index (TLI = .97) indicated adequate fit.

IRT Calibration

The item parameter estimates for the two-parameter (2PL) model are summarized in Table 2. We see for example that “blames others for his or her mistakes or misbehaviors” had the lowest threshold parameter (β = −0.82). A child would need to exceed this ODD trait level for there is a 50% chance that his or her parent would endorse this item as “often” or “very often”. The item “is spiteful and wants to get even” had the highest threshold parameter (β = .68). A child would therefore need to have a much higher ODD trait level before his or her parent would have a 50% chance of endorsing this item as “often” or “very often.” All eight ODD symptoms had good discrimination parameters (all α parameters above 1.0) and ranged from 1.50 (“blames others for his or her mistakes or misbehaviors”) to 2.59 (“loses temper”). Figure 1 shows the item characteristic curves (ICCs) and item information curves for each of the eight ODD symptoms.

Table 2.

Item Parameters for the Eight Symptoms of Oppositional Defiant Disorder (2PL Model)

Item	Item Parameters		Standard Errors
	α	β	σα	σβ
Argues with adults	2.05	−0.72	0.33	0.12
Loses temper	2.59	−0.69	0.44	0.11
Actively deifies or refuses to go along with adults’ requests or rules	1.77	−0.56	0.29	0.11
Deliberately annoys people	1.65	−0.07	0.26	0.10
Blames others for his or her mistakes or misbehaviors	1.50	−0.82	0.25	0.15
Is touchy or easily annoyed by others	1.61	−0.16	0.26	0.11
Is angry or resentful	2.12	0.14	0.35	0.09
Is spiteful and wants to get even	2.29	0.68	0.43	0.11

The IRT model fit was examined for each item using the IRTFIT macro program (Bjorner et. al, 2006) with an option specified to implement the sum score based method by Orlando and Thissen (2003), which uses the sum score instead of θ for computing the predicted and observed frequencies. The likelihood ratio G-square (S-G²) and the Pearson’s Chi-square (S-X²) fit statistics (Orlando & Thissen, 2000; Orlando & Thissen, 2003) use the sum of score of all items and compare the predicted and observed response frequencies for each level of the sum score. Significance tests are calculated and plots can be produced comparing predicted and observed response probabilities for each level of sum score. Table 3 shows the resulting S-G² and S-X² statistics. All items showed good item fit using the .01 criteria. Just one item (Item 5; “blames”) showed misfit using the .05 criteria. It is worth noting that this item also had the lowest discrimination parameter (α = 1.50). We retained the item for the current study in order to maintain consistency with the DSM criteria for ODD.

Table 3.

Item Fit Statistics

Item	Label	df	S-G2	Prob S-G2	S-X2	Prob S-X2
1	Argues	5	2.60	0.7618	2.56	0.7679
2	Temper	5	2.22	0.8174	2.22	0.8174
3	Defies	5	1.47	0.9165	1.48	0.9155
4	Annoys	6	1.86	0.9325	1.84	0.9337
5	Blames	6	14.25	0.0270	13.48	0.0361
6	Touchy	6	3.38	0.7595	3.38	0.7593
7	Angry	5	9.32	0.0969	9.51	0.0904
8	Spiteful	4	0.61	0.9618	0.61	0.9616

Symptom Counts, Response Patterns, and Latent Trait Scores

There were a total of 97 different response patterns in the sample, out of 256 possible. Most of these response patterns (n = 62) occurred just once or twice. A large proportion of the sample (40%; n = 128) endorsed one of the nine perfectly consistent response patterns (e.g., 1,1,1,1,0,0,0,0). Table 4 summarizes some examples of response patterns and their associated θ estimates. We see for example, that patients # 93 and #244 had the same symptom count (5 symptoms), but different levels of θ due to their different response patterns and the different threshold and discrimination parameters of the items that were endorsed by their parents. Similarly, patients #168, #294, and #113 all had symptoms counts of 4 but different θ estimates. We even see that patient #209 has a higher latent trait ODD level (θ = .251) than patient #23 (θ = .230) despite a lower symptom count (5 symptoms versus 6 symptoms).

Table 4.

Examples (Out of 97 Represented in Our Sample) of Response Patterns, Symptom Counts, Latent Trait (θ) Scores, and PPOD Indices (items in order of β)

ID	Symptom								Symptom Count	θ	S.E.	PPOD Indexa	Lower Boundb	Upper Boundb
	Blames	Argues	Temper	Defies	Touchy	Annoys	Angry	Spiteful
25*	1	1	1	1	1	1	1	1	8	1.373	0.603	> .99	> .99	> .99
46*	1	1	1	1	1	1	1	0	7	0.728	0.473	.99	.99	> .99
59	1	1	1	1	0	1	1	1	7	0.889	0.501	.99	> .99	> .99
30*	1	1	1	1	1	1	0	0	6	0.312	0.419	.95	.95	.97
297	1	1	1	1	1	0	0	1	6	0.428	0.432	.97	.97	.98
23	1	1	0	1	1	1	1	0	6	0.230	0.412	.93	.93	.96
93*	1	1	1	1	1	0	0	0	5	0.037	0.398	.85	.84	.89
244	1	0	1	0	1	0	1	1	5	0.132	0.404	.90	.89	.93
209	0	1	1	1	0	0	1	1	5	0.251	0.414	.94	.93	.96
168*	1	1	1	1	0	0	0	0	4	−0.212	0.388	.67	.64	.73
294	0	1	1	0	0	0	1	1	4	−0.037	0.394	.81	.79	.86
113	1	1	0	0	1	1	0	0	4	−0.376	0.387	.50	.47	.58
285*	1	1	1	0	0	0	0	0	3	−0.477	0.388	.40	.37	.47
34	1	1	0	1	0	0	0	0	3	−0.602	0.392	.28	.26	.35
11*	1	1	0	0	0	0	0	0	2	−0.889	0.415	.11	.09	.14
148	1	0	0	0	0	1	0	0	2	−0.958	0.424	.09	.07	.11
240*	1	0	0	0	0	0	0	0	1	−1.29	0.478	.03	.01	.03
284	0	0	0	1	0	0	0	0	1	−1.23	0.466	.03	.02	.03
71*	0	0	0	0	0	0	0	0	0	−1.693	0.566	.01	< .01	< .01

^*consistent response pattern;

^aestimated using Method A (standard normal cumulative distribution function);

^bestimated using Method B (numerical integration of the posterior distribution)

Posterior Probability of Diagnosis (PPOD) Index

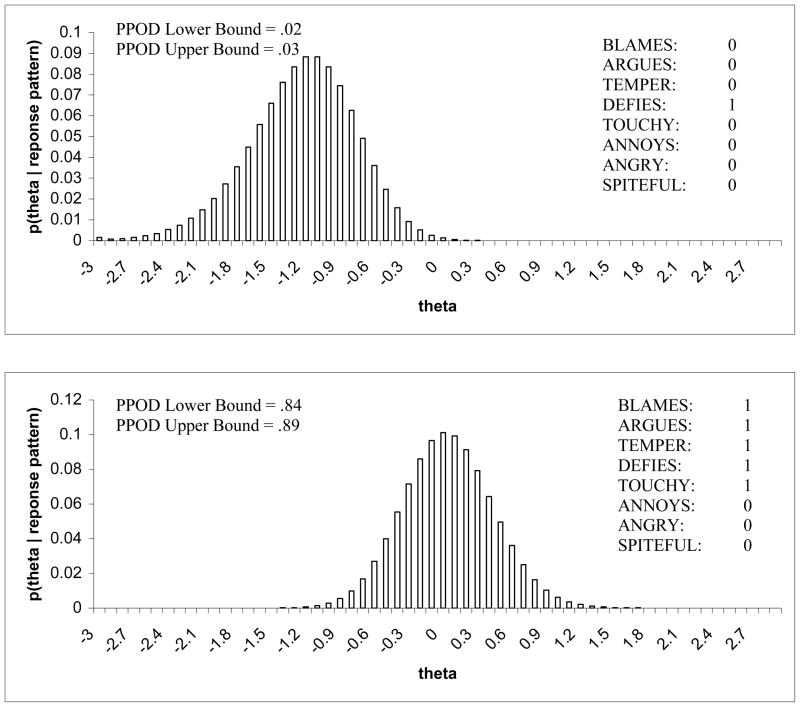
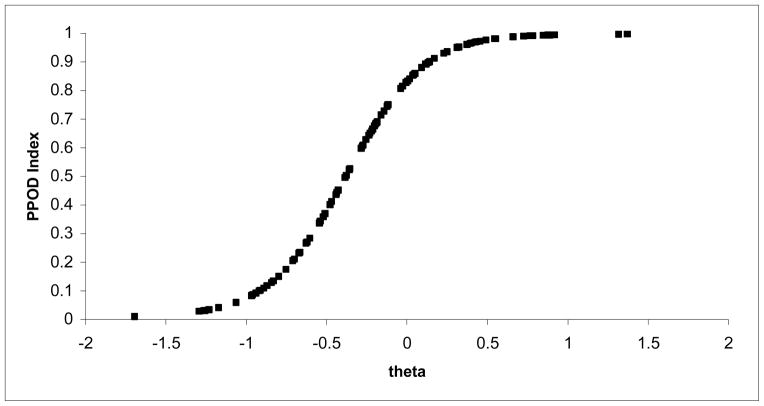
The two methods for estimating the PPOD Index yielded comparable estimates. See Table 4 for examples of PPOD Indices for several response patterns. Specifically, PPOD Indices estimated using Method A (standard normal cumulative distribution function) generally fell between the lower bound and the upper bound for the PPOD Index using Method B (numerical integration of the posterior distribution). Figure 2 shows examples of the posterior distribution of θ for two response patterns estimated using Method B. The graphs provide a visual aid in conceptualizing the PPOD Index, which is the sum of the probability masses (represented by bars) for θ values −.30 to 2.9 (Lower Bound) and −.40 to 2.9 (Upper Bound). Each response pattern (256 possible) has its own posterior distribution of θ although just two examples are shown in the figure. Appendix B shows sample output from the MATLAB program used for Method B for a sample response pattern (1,1,1,1,0,0,0,0). In this example, the lower bound and upper bound were estimated at 64% (.64) and 73% (.73) respectively. Using Method A, the PPOD Index was estimated at 67% (.67) for this same response pattern. Figure 3 depicts a graph with the PPOD index (y-axis) plotted against the θ estimate (x-axis) for each of 97 response patterns represented in our sample. The resulting sigmoid represents the Bayesian estimate of the posterior probability that the latent trait threshold for the diagnosis (in this case −.38) is met or exceeded given a particular estimate of θ.

Figure 2.

Examples of the posterior distribution of theta^a for two response patterns.

^a = estimated using Method B (numerical integration of the posterior distribution)

Figure 3.

This graph plots the PPOD index^a (y-axis) against the theta estimate (x-axis) for each of 97 response patterns represented in our sample. The resulting curve represents the Bayesian estimate of the posterior probability that the latent trait threshold for the diagnosis is met or exceeded given a particular estimate of theta.

^a = estimated using Method A (standard normal cumulative distribution function)

Across patients there was great variability in the PPOD Index, with values ranging from .01 (1% chance that the patient meets or exceeds the diagnostic threshold for ODD) to >.99 (greater than 99% chance the patient meets of exceeds the diagnostic threshold for ODD). Table 5 summarizes the PPOD Index range associated with each symptoms count. Not surprisingly, patients close to the DSM-IV diagnostic threshold of 4 symptoms had the greatest degree of diagnostic uncertainty. Patients with a symptom count of four had PPOD Indices ranging from .50 to .81 depending on their individual response pattern of endorsed and not endorsed items. Patient #168, for example, has a PPOD Index of .67 (see Table 4). This means that he or she has a 67% chance that their true ODD latent trait score meets or exceeds the diagnostic threshold for ODD. Although patient #294 also has a symptom count of four, there is a higher level of certainty (81% chance) that his or her true ODD latent trait score meets or exceeds the diagnostic threshold for ODD.

Table 5.

Symptoms Counts, DSM Diagnostic Categories, Latent Trait (θ) Scores, and PPOD Indices

Symptom Count	DSM Diagnosis	θ Range	PPOD Index Rangea
8 (n = 23)	YES	1.373	> .99
7 (n = 25)	YES	0.662 to 1.318	> .99
6 (n = 25)	YES	0.230 to 0.555	.93 to .98
5 (n = 30)	YES	−0.025 to 0.251	.82 to .94
4 (n = 44)	YES	−0.376 to −0.037	.50 to .81
3 (n = 39)	NO	−0.670 to −0.384	.23 to .50
2 (n = 46)	NO	−0.965 to −0.679	.08 to .21
1 (n = 45)	NO	−1.290 to −1.062	.03 to .06
0 (n = 44)	NO	−1.693	.01

^aestimated using Method A (standard normal cumulative distribution function)

Of the 218 patients who met DSM criteria of ODD (four or more symptoms), the PPOD Index indicated that we could only be 95% confident for 132 or these diagnoses (61%). Similarly, of the 103 who did not meet DSM criteria of ODD (three of fewer symptoms), the PPOD Index indicated that we could only be 95% confident for 41 of these cases (40%). Overall, we could only be confident in the diagnostic status for 173 of the 321 children in the sample (54%) at the 95% level. In other words, there was substantial diagnostic uncertainty for almost half of the sample. For a very small number of patients (n = 4), diagnostic confidence was .50 or equivalent to a coin toss.

Discussion

Using an IRT approach, we see that the eight symptoms of ODD have different severity threshold parameters. In other words, varying levels of the latent trait are required before a parent has a 50% chance of endorsing the item as “often” or “very often.” The item “blames others for his or her mistakes or misbehaviors” had the lowest threshold parameter and the item “is spiteful and wants to get even” had the highest threshold parameter. Although all eight items had good discriminability, some items were marginally better than others. “Loses temper” was found to have the highest discrimination parameter whereas “blames others for his or her mistakes or misbehaviors” had the lowest discrimination parameter. The good discriminability of all eight symptoms is consistent with other research findings for which IRT analyses have been applied to DSM criteria (i.e. symptoms). For example, Cole and colleagues (2011) found that all DSM depression symptoms had good discriminability in several samples of depressed and non-depressed youth.

Response Patterns and Latent Trait θ Scores

Ninety-seven different response patterns were represented in the current study, resulting in far more variability in latent trait scores than traditional DSM symptom counts. Notably, patients with the same symptom count had different latent trait scores depending on individual response patterns of endorsed ODD symptoms. Our results even illustrated that it is possible for a patient with fewer symptoms to have a higher latent trait score than a patient with more symptoms. In other words, which symptoms are endorsed may sometimes matter more than the total number of symptoms endorsed. Indeed, a patient’s profile of symptoms is perhaps more clinically meaningful than a categorical diagnosis. The emphasis of the PPOD approach on symptom profiles draws attention to specific symptoms that might be efficient targets for clinical intervention.

Posterior Probability of Diagnosis (PPOD) Index

Using traditional DSM diagnostic criteria, the clinician is forced to make a categorical decision (diagnosis versus no diagnosis). This approach implies a degree of confidence in the diagnosis that might not be justified. The PPOD Index provides an alternative (perhaps supplemental) method by which the clinician can convey the appropriate degree of certainty (or lack there of) associated with a diagnosis in Bayesian terms. This is especially important when a patient is close to the diagnostic threshold and confidence in the diagnosis is low. A few of the patients in the sample with symptom counts of four even had a PPOD index around .50. By DSM criteria, these patients would meet criteria of ODD, yet the confidence in the diagnoses would be equivalent to flipping a coin.

In the current study, the two methods for estimating the PPOD Index values yielded comparable results. However, it is important to note that Method A (standard normal cumulative distribution function) is a heuristic and should only be used if the posterior distribution of θ is close to a normal distribution. We recommend, therefore, that Method A be used only when there is no significant skewness of symptom counts in the sample dataset. Method B (numerical integration of the posterior distribution), although requiring additional analyses, does not require that the posterior distribution of θ be normally distributed. However, Method B provides only an approximation of PPOD Index values due to a finite number of quadrature points. We recommend that Method B be used when there is significant skewness of symptom counts in the sample dataset.

The sample used to illustrate the PPOD index (i.e. a clinical sample) has the advantage of providing us with a model that is sensitive around the diagnostic threshold. Had we used a normative population to go about building our model, for example, the rates of symptoms would have been much lower, resulting in a less sensitive model around the diagnostic threshold. Given that the PPOD index is intended to be used by mental health professionals to aid in diagnosis (i.e. a patient population), the sample used in this study is a methodological strength.

Implications for Diagnostic Practices

IRT models and the PPOD Index are consistent with the call for the adoption of a dimensional (i.e. continuous) framework for classifying mental health disorders (e.g., Widiger & Coker, 2003; Widiger & Clark, 2000). Studies using taxometric analyses are providing evidence for continuous latent structures of many mental health disorders (e.g., Edens et al., 2006; Frazier et al., 2007; Ruscio, et al., 2002) and therefore latent-trait models seem justifiable. We contend that latent-trait models in general, and PPOD Indices in particular, are consistent with the call for evidence-based assessment practices (e.g., Hunsley & Mach, 2005; Jensen-Doss & Hawley, 2011). We suggest the PPOD Index not replace, but rather supplement, traditional DSM diagnoses based on symptom counts. The PPOD Index provides additional information in the form of an estimate of the likelihood that a patient actually meets or exceeds the diagnostic threshold for the disorder in probabilistic terms. The utility of the PPOD index is in allowing clinicians to communicate the appropriate degree of confidence he or she has in a diagnosis.

Conceptually Related Indices

The PPOD Index is by no means the first attempt to use Bayesian methods to improve diagnostic decisions. In the 1950s, Meehl and Rosen (1955) argued that psychologists should use Bayes’ theorem when making clinical decisions such as establishing cut scores. More recently, stratum-specific likelihood ratios (SSLRs) have been advocated as a means to estimate the post-test probability of a disease (e.g., Furukawa, Andrews, & Goldberg, 2002; Peirce & Cornell, 1993). The SSLR can be multiplied by the prior odds of the disease to estimate the posterior odds of the disease. The posterior odds can then be converted to a probability estimate and interpreted in a similar fashion to the PPOD Index. More recently, Mokros, Schilling, Eher, & Nitschke (2012) related a optimum point of information (obtained through Rasch scaling) to behavioral symptom counts and the probability of a clinical diagnosis. The PPOD Index is also not the first index to use Bayesian methods for estimating the confidence in such probability estimates. For example, Mossman (2000) has proposed a method for establishing 95% confidence intervals around posterior probabilities for malingering tests. The distinction between the PPOD and these other approaches is that the PPOD Index is based on item-level information and patterns of symptoms rather than a summary test result.

Limitations and Future Directions

In the current study we illustrate the PPOD Index with symptoms based on a parent-report measure of DSM symptoms for ODD (VAS-Parent; Wolraich et al., 1998) rather than symptoms based on a structured diagnostic clinical interview. In practice, a single parent report form would rarely be used for diagnostic purposes. A final symptom count would be based on additional information gathered from the child’s teachers and a thorough clinical interview to determine whether or not each symptom endorsed by the parent indeed “occurs more frequently than is typically observed in individuals of comparable age and developmental level” (DSM; American Psychiatric Association, 2000). As a proof-of-concept paper, the VAS-P was merely used to illustrate the potential application of IRT to DSM symptoms and diagnoses. In doing so, we elected to remove clinical judgment from the equation. As a result, this study examined the application of IRT and the PPOD Index to DSM symptoms for ODD as measured by the VAS-P rather than full DSM criteria for ODD. In addition, evidence of clinically significant impairment would also be needed before a clinician would make a diagnosis.

Another potential limitation is that the probability estimates produced by the PPOD Index are influenced by the model parameters and modeling assumptions. For example, 3PL models, generalized partial credit models, or multidimensional models could all be used to estimate the PPOD Index. As a proof-of-concept paper, the 2PL model has reasonable assumptions for the current dataset of ODD symptoms. The 2PL model has also been applied to DSM disorders in the extant literature (e.g., Cole et al., 2011) and is arguably the simplest model with which to illustrate the essential features of the PPOD Index. Probability estimates produced by the PPOD Index could also vary based on different prior distributions, other than the standard normal distribution used in the current study. The extent to which such modeling assumptions influence the probability estimates of the PPOD Index is an important topic for future research on the PPOD Index.

Although not a limitation per se, the PPOD requires some familiarity with Bayesian reasoning. For example, the PPOD Index requires the need to specify a prior distribution. In the current study, our latent trait estimates were based on EAP scoring and assume a standard normal prior distribution. Although this is a reasonable assumption, other prior distributions could have been specified. The adequacy of the prior distribution depends on several things including the intended use of the diagnosis. For example, because ODD is more common in boys than girls, it might be reasonable to assume different prior probability distributions for boys and girls. On the other hand, it could also be reasonable to apply the same prior distribution to boys and girls in order to ensure that the sensitivity and specificity of the diagnosis do not depend on gender. The broader issue of scoring options is not unique to the PPOD Index however. For example, similar options are encountered when scoring the Child Behavior Checklist (CBCL; Achenbach, 1991) for which scoring can be based on gender specific norms or combined norms.

Finally, it should be noted that sum scores such as DSM-IV symptom counts can potentially be a robust alternative to a latent trait estimate based on a 2PL model. Although symptom counts are less precise when discrimination parameters are known, they can potentially be superior if the standard errors of the discrimination parameters are substantial. Follow-up simulation studies are needed to assess whether a 2PL model actually leads to more precise person parameter estimates for moderate sample sizes as with the current study.

Summary and Conclusions

The application of IRT to DSM symptoms of ODD provided more fine-tuned information about each individual patient’s Posterior Probability of Diagnosis than a traditional symptom count. A latent-trait model also allowed for the estimation of the confidence with which each patient could be said to meet or exceed a diagnostic threshold on an ODD latent trait continuum. The PPOD Index allows a clinician to communicate the degree of confidence that he or she has in a diagnosis. The clinical utility of such an index appears to be greatest for patients who are close to diagnostic threshold (i.e. three or four symptoms).

Appendix A

MATLAB program

 1 %Posterior Probability of Diagnosis (PPOD) Index PROGRAM
 2- Blames = input(‘BLAMES: ’);
 3- Argues = input(‘ARGUES: ’);
 4- Temper = input(‘TEMPER: ’);
 5- Defies = input(‘DEFIES: ’);
 6- Touchy = input(‘TOUCHY: ’);
 7- Annoys = input(‘ANNOYS: ’);
 8- Angry = input(‘ANGRY: ’);
 9- Spiteful = input(‘SPITEFUL: ’);
10- %The following vectors (Blames0, Blames1, Argues0, Argues1, Temper0,
11- %Temper1, Defies0, Defies1, Touchy0, Touchy1, Annoys0, Annoys1, Angry0,
12- %Angry1, Spiteful0, Spiteful1
) are based on the output from IRTPRO.
13- if Blames==0
14-   A=Blames0;
15- else
16-   A=Blames1;
17- end
18- if Argues==0
19-   B=Argues0;
20- else
21-   B=Argues1;
22- end
23- if Temper==0
24-   C=Temper0;
25- else
26-   C=Temper1;
27- end
28- if Defies==0
29-    D=Defies0;
30- else
31-    D=Defies1;
32- end
33- if Touchy==0
34-   E=Touchy0;
35- else
36-   E=Touchy1;
36- end
37- if Annoys==0
38-   F=Annoys0;
39- else
40-   F=Annoys1;
41- end
42- if Angry==0
43-   G=Angry0;
44- else
45-   G=Angry1;
46- end
47- if Spiteful==0
48-   H=Spiteful0;
49- else
50-   H=Spiteful1;
51- end
52- P_ResponsePattern_given_Theta = A.*B.*C.*D.*E.*F.*G.*H;
53- % The vector Ptheta reprents the density heights for the normal
54- distribution for
55- % 60 quadrature points (-3.0 to 2.9 in 0.1 increments).
56- P_ResponsePattern_given_Theta_TIMES_P_Theta =
57- P_ResponsePattern_given_Theta.*Ptheta;
58- P_ResponsePattern = sum(P_ResponsePattern_given_Theta_TIMES_P_Theta);
59- %P_ResponsePattern is the NORMALIZING CONSTANT
60- P_Theta_given_ResponsePattern =
61- P_ResponsePattern_given_Theta_TIMES_P_Theta/P_ResponsePattern;
62- Cumulative_sum_of_P_Theta_given_ResponsePattern =
63- cumsum(P_Theta_given_ResponsePattern);
64- PPOD = 1- Cumulative_sum_of_P_Theta_given_ResponsePattern;
65- PPOD_Upper_Bound = PPOD(26,1);
66- PPOD_Lower_Bound = PPOD(27,1);
67- PPOD_Lower_Bound
68- PPOD_Upper_Bound
69- commandwindow
70

Appendix B

Sample Input and Output

BLAMES: 1
ARGUES: 1
TEMPER: 1
DEFIES: 1
TOUCHY: 0
ANNOYS: 0
ANGRY: 0
SPITEFUL: 0
PPOD_Lower_Bound = .6384
PPOD_Upper_Bound = .7314