Modeling spatial population dynamics of stem cell lineage in tissue growth

Abstract

Understanding the dynamics of cell population allows insight into the control mechanism of the growth and development of mammalian tissues. It is well known that the proliferation and differentiation among stem cells (SCs), intermediate progenitor cells (IPCs), and fully differentiated cells (FDCs) are under different activation and inhibition controls. Secreted factors in negative feedback loops have already been identified as major elements in regulating the numbers of different cell types and in maintaining the equilibrium of cell populations. We have developed a novel spatial dynamic model of cells. We can characterize not only overall cell population dynamics, but also details of temporal-spatial relationship of individual cells within a tissue. In our model, the shape, growth, and division of each cell are modeled using a realistic geometric model. Furthermore, the inhibited growth rate, proliferation and differentiation probabilities of individual cells are modeled through feedback loops controlled by secreted factors of neighboring cells within a proper diffusion radius. With specific proliferation and differentiation probabilities, the actual division type that each cell will take is chosen by a Monte Carlo sampling process. With simulations we found that with proper strengths of inhibitions to growth and stem cell divisions, the whole tissue is capable of achieving a homeostatic size control. We discuss our findings on control mechanisms of the stability of the tissue development. Our model can be applied to study broad issues on tissue development and pattern formation in stem cell and cancer research.

I. INTRODUCTION

Precise and robust size control of tissues is a fundamental problem in tissue development and regenerative medicine, which has intrigued developmental biologists for many years. Computational modeling of population dynamics of cells can provide insight into the control process of the growth and development of mammalian tissues.

It is well known that proliferation and differentiation among stem cells (SCs), intermediate progenitor cells (IPCs), and fully differentiated cells (FDCs) are under different activation and inhibition controls [1–4]. Secreted factors in negative feedback loops have already been identified as major elements in regulating the numbers of different cell types and in maintaining the equilibrium of cell populations [1, 5]. For examples, GDF8 of transforming growth factor β (TGFβ) family made by differentiated muscle cells inhibits the production of muscle progenitor cells [1], and GDF11 of the same family can act on self-renewing neural cells [2, 5].

There have been a number of studies on the general dynamics of cell populations for tissue growth and proliferative control involving stem cells [2, 3, 6, 7]. However, spatial information of cells is neglected in these studies, and feedback controls modeled in these studies are based on population average only. This is unrealistic because each feedback factor only acts within a specific spatial range [1].

We have developed a novel spatial dynamic model to study tissue development. We can now characterize not only the overall cell population dynamics, but also details of temporal-spatial relationship of individual cells within a tissue. In our model, the shape, growth, and division of each cell are modeled using a realistic geometric model, and the inhibited growth rate, proliferation and differentiation probabilities of individual cells are modeled through feedback loops controlled by secreted factors of neighboring cells within a proper diffusion radius. With specific proliferation and differentiation probabilities, the actual division type that each cell will take is studied using a Monte Carlo sampling process. With simulations of temporal-spatial population dynamics, we found that with proper strengths of inhibitions to growth and self-renewal of stem cells, the whole tissue is capable of achieving a homeostatic size control. We discuss our findings on control mechanisms of the stability of the tissue development. Our model can be applied to study broad issues on development and pattern formation in stem cell and cancer research.

II. METHODS

In our temporal-spatial cell population dynamics model, the growth, division and decision making about specific division type of each cell are modeled explicitly. Cell growth model is based on the physics of cell growth and division. Cell growth rate and probabilities of three division types depends on the number of differentiated cells within a proper diffusion radius around each cell. The details are described as follows.

A. Cell Growth Model

We use previously developed two-dimensional mechanical vertex model to represent a tissue of contiguous, interacting cells [8]. This model represents accurately the geometric properties of a single cell as well as the collective topological properties of cells in a tissue. Three geometric elements are used to model a biological cell. (1) Cell is a spatial region representing the volume of a biological cell. A cell takes the shape of a disk in isolation, and a disk segment when at the boundary of a tissue. When buried in the tissue interior, it is a polygon connected to neighboring cells. Cells may have different polygonal shapes and sizes. (2) Edge is the cell boundary, modeled as a line segment when inside the tissue or an arc when at the boundary of the tissue. (3) Vertex is the junction point of three edges, at which three cells intersect.

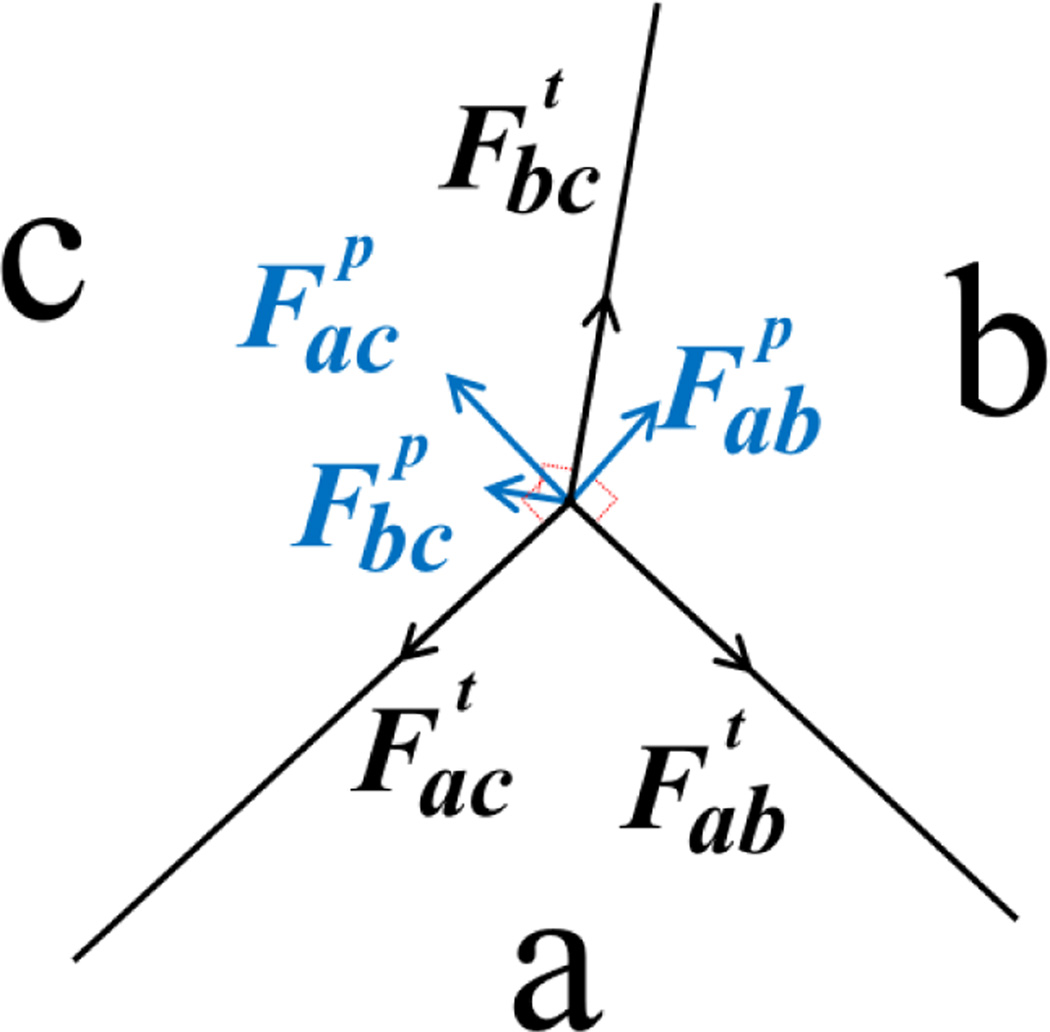
In our model, cell movement and rearrangement within a tissue depend on the mechanical forces a cell experiences. There are two types of forces in our model, tension and pressure. Tension models the compressional forces acting within a cell. These forces arise from cytoskeletal microfilaments, intermediate filaments, and cell membrane. For an edge between cell a and b, the direction of the tension force is tangential to the edge ab (Fig. 1). Pressure represents the forces resisting compression. These forces arise mainly from microtubules and extracellular matrix. In our model, pressure is proportional to the difference in pressure in cell a and b and the length of edge ab. The direction of the pressure force is normal to the edge ab (Fig. 1).

Fig. 1.

The forces at the junction vertex of three cells a, b and c. Tension is tangential to the edge (black). Pressure is normal to the edge (blue). The net force on the junction vertex is obtained by summing tension and pressure acting on the vertex.

The net force on a vertex is obtained by summing all the forces due to tension and pressure acting on the vertex (Fig. 1). The net force over all vertices sums to zero. During the growth process, the forces acting on a vertex change due to the increase in the volume of the cell. Non-zero net force drives a vertex to a new location and the cell shape changes with the vertex movements. Local rearrangements of vertices result in reduction of the stress in the tissue, which lead the system to a lower stress state.

Cell division occurs when the size of the cell is doubled after certain steps of cell growth. A new edge is added that passes through the center of the mother cell. The two resulting daughter cells have half the size of the mother cell. Two new vertices are added at the two ending points of the new edge.

B. Cell Types and Division Types

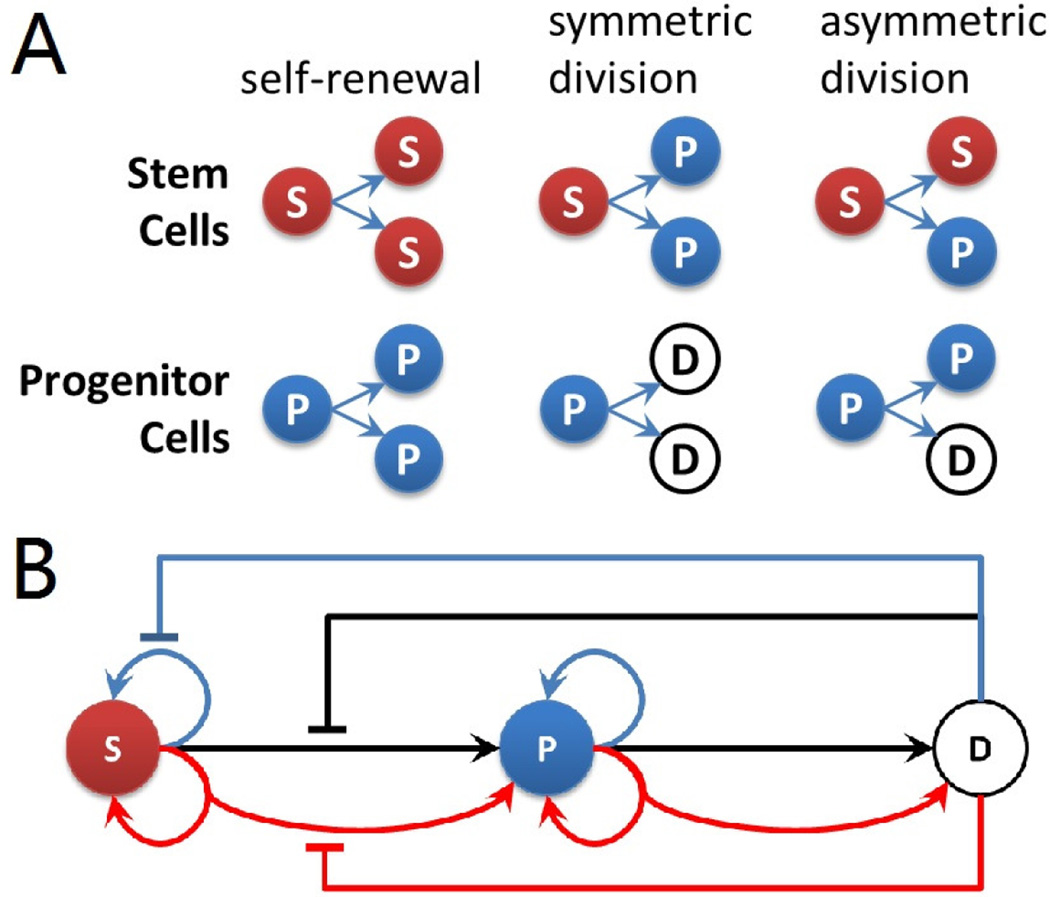
Three different types of cells are modeled in our system: stem cells, progenitor cells and differentiated cells. They have different potentials of cell divisions: stem cells have unlimited power of divisions; intermediate progenitor cells have the potential to divide at most twice; and differentiated cells lose the ability to divide. Divisions of stem cells and progenitor cells can be classified into three categories [2, 9, 10]: (1) self-renewal or proliferation, (2) symmetric division, and (3) asymmetric division. For stem cells, self-renewal division generates two stem daughter cells from one mother stem cell. Asymmetric division generates one stem daughter cell and one progenitor daughter cell. Symmetric division generates two daughter progenitor cells from one stem cell. The same division rules also apply for progenitor cells. All three different types of divisions for stem cells and progenitor cells are illustrated in Fig. 2A. Note that as progenitor cell can maximally divide twice, the type of second division of progenitor cells is then limited to symmetric division.

Fig. 2.

(A) Division types of stem cells and progenitor cells. Red sphere labeled with (S) indicates stem cells, blue sphere (P) indicates progenitor cells, and white sphere (D) indicates differentiated cell. The same color code is used for illustration of resulting tissues. (B) Feedback controls of stem cell model. Blue arrows indicate self-renewal or proliferation divisions. Black arrows indicate symmetric divisions. Red arrows indicate asymmetric divisions. Flat-head arrows extending from differentiated cell with corresponding colors indicate inhibitions to respective type of divisions.

C. Feedback Controls

In our model, the growth rates and different division types of stem cells are inhibited independently by surrounding differentiated cells within a specific diffusion radius. We assume self-renewal, symmetric and asymmetric divisions are inhibited by different negative feedback factors, which are secreted by neighboring differentiated cells through diffusion. Following [2], we use Hill functions shown in Eqn. (1) to calculate the growth rates and division probabilities under inhibitions at each time step. We assume a basal growth rate $v_s^0$ and equal basal probabilities of three division types: $p_r^0=p_s^0=p_a^0=1/3$ for stem cells when without any inhibitions. The growth rate v_S(t) and probabilities of self-renewal p_r(t), symmetric p_s(t) and asymmetric p_a(t) divisions for every stem cell in the tissue at time t are calculated as:

$$v_S(t)=\frac{v_S^0}{1+g_S{N}_D(t)},p_r(t)=\frac{p_r^0}{1+h_r{N}_D(t)}{p}_s(t)=\frac{p_s^0}{1+h_s{N}_D(t)},p_a(t)=\frac{p_a^0}{1+h_a{N}_D(t)},$$ (1)

where N_D(t) is the number of differentiated cells within three layers of neighboring cells, which is calculated from cell growth model described in section II-A, g_S, h_r, h_s and h_a are Hill coefficients for growth rate, probabilities of self-renewal, symmetric and asymmetric divisions of stem cells, respectively. After the new probabilities of division types are calculated, they are normalized to ensure the probabilities of three division types sum to one. Cell division happens when the cell volume doubles. A Monte Carlo sampling step is implemented for selecting the division type based on probabilities for each dividing stem cell and progenitor cell. A uniform random number μ ∈ [0,1] is generated at each step, and the division type is determined by the minimum value of K satisfying inequality: ${\sum }_{i=1}^{K-1}{p}_i(t)<\mu \le {\sum }_{i=1}^K{p}_i(t)$, in which values of i, K ∈ {1,2,3} correspond to division types: self-renewal (i, K = 1), symmetric division (i, K = 2), and asymmetric division (i, K = 3), respectively.

The growth rates and division types obtained from feedback control module are used as input for the cell growth model described in section II-A. The whole system of cells is coupled to model tissue development with stem cells.

All possible negative feedback controls are shown in Fig. 2B. In this paper, we focus on the effects of inhibitions to stem cells, and assume the growth rate and division probabilities of progenitor cells are not affected by neighboring differentiated cells.

III. RESULTS

We first study the fundamental question how the homeostatic tissue size control is achieved through simulations of temporal-spatial dynamics of development of cell population. We study the effects of two different mutations to stem cell inhibitions, and compare results with the normal tissue with proper inhibitions.

A. Size Control of Tissue Development

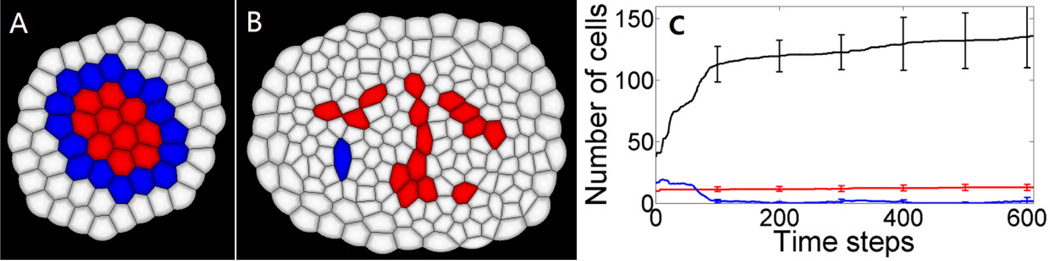
Four independent simulations have been performed starting from a small tissue of 64 cells in total (10 stem cells (red) in the center surrounded by 16 progenitor cells (blue) and 38 differentiated cells (white)), as shown in Fig. 3A. The inhibition to stem cells comes from three layers of neighboring differentiated cells. From Eqn. (1), we found that the tissue is able to achieve size control when inhibition strength parameters are h_r = 0.55, h_s = 1.0, and h_a = 0.55, respectively. Fig. 3B shows the steady state tissue from one simulation result, which contains 15 stem cells, 1 progenitor cell and 158 differentiated cells. The whole tissue automatically stops growing when its size reaches a certain level. The amount of differentiated cells dominates in the developed tissue, showing that this tissue has sufficient amount of differentiated cells to perform normal physiological functions. At the same time, there is still a small amount of stem cells in the center of the tissue, which enables potentials to regenerate. In developed tissue, the inhibitions from surrounding differentiated cells to stem cells are strong enough to prevent stem cells from continued growth and divisions, and the final homeostatic size control of the whole tissue is achieved. The mean and standard deviation of numbers of stem cells (red curve), progenitor cells (blue curve) and differentiated cells (black curve) at each time step have been calculated respectively. Fig. 3C shows the mean trajectories and error bars at 6 points calculated from 4 independent simulations. Although the variance in the number of differentiated cells is larger than that of stem cells and progenitor cells, all simulation results can achieve homeostatic tissue size control over time.

Fig. 3.

Size control of tissue development. (A) Small starting tissue for numerical simulations of the temporal-spatial dynamics model contains 64 cells in total. Stem cells are labeled in red, progenitor cells are in blue, and differentiated cells are in white. (B) One example tissue achieved homeostatic size control. This steady state tissue contains 15 stem cells, 1 progenitor cell and 158 differentiated cells. (C) Dynamics of cell numbers during tissue development. The red curve indicates the change of stem cell numbers, the blue line is for progenitor cells, and the black line is differentiated cells. Error bars show the standard deviations calculated from four simulation results at 100, 200, 300, 400, 500, and 600 time steps, respectively.

Progenitor cells play important roles during the process of tissue development. Fig. 3C shows the amount of progenitor cells has a transient increase at the beginning of tissue development, followed by the large increase of differentiated cells. The amount of stem cells remains roughly constant during the whole process. This result implies that the population of progenitor cells might act as an amplifier to enlarge the size of the whole cell population. This three-level cascade population amplification involving stem cells, progenitor cells and differentiated cells provides an efficient mechanism for cell population development.

B. Effects of Inhibition Mutations

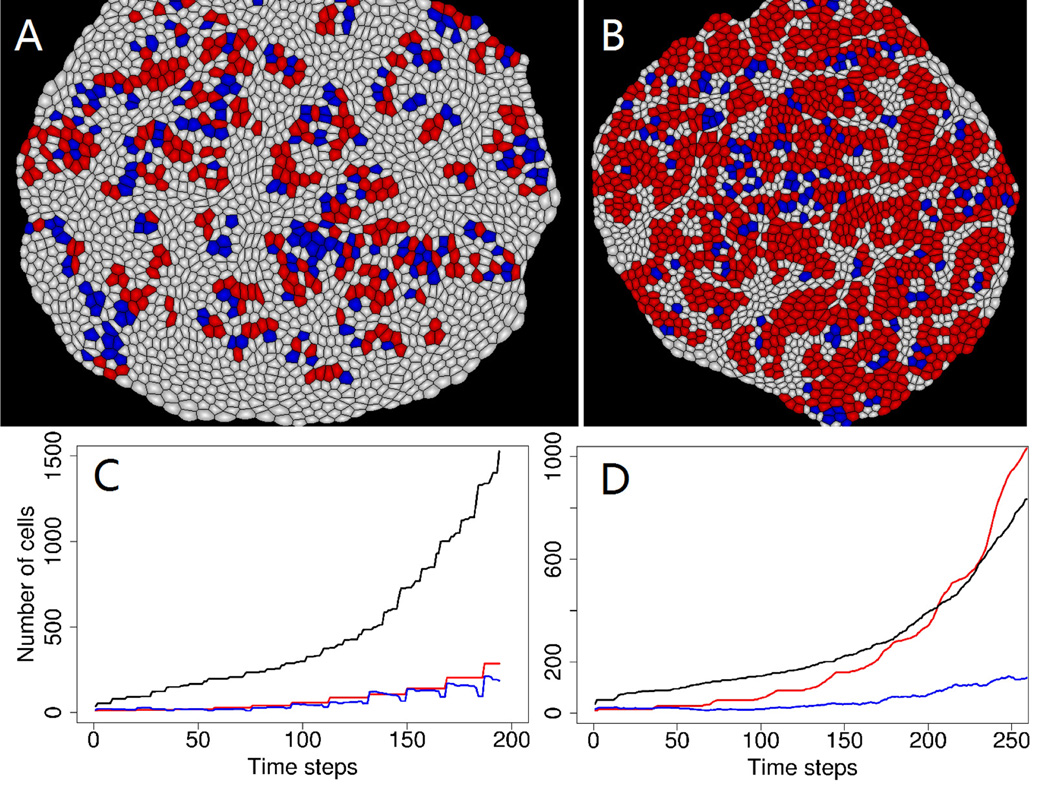
In order to explore the effects of negative feedback controls to tissue development, we first removed all negative feedback controls from the model. In this case, the growth and divisions of different cell types are not correlated with each other. Simulation results of the developed tissue and the dynamic change of cell numbers are shown in Fig. 4A and 4C. We found that the number of all three different types of cells in the tissue increase monotonically with time, and homeostatic tissue size control is not possible in this situation.

Fig. 4.

(A) A snapshot of simulations in tissue without any negative feedback controls. (B) A snapshot of simulations in tissue without inhibition to stem cell self-renewal. (C) Dynamics of cell numbers in tissue without any inhibitions. The red curve indicates the change of stem cell numbers, the blue line is for progenitor cells, and the black line is differentiated cells. (D) Dynamics of cell numbers in tissue without any inhibitions. The red curve indicates the change of stem cell numbers, the blue line is for progenitor cells, and the black line is differentiated cells.

We further explored and evaluated the effect of removing inhibition to stem cell self-renewal division alone. In this case there are more chances for stem cells to self-renew. The result of developed tissue in Fig. 4B shows that stem cells are over-populated in this tissue compared to the normal tissue shown in Fig. 3B. The dynamic change of cell numbers (Fig. 4D) shows that there are more stem cells than differentiated cells in this mutated tissue over time. A low proportion of differentiated cells could impair the normal physiological functions of the tissue, as shown in the example of rodent and primate embryonic cortex [11]. Moreover, there is no tissue size control, because the growth of stem cells is not controlled by less populated differentiated cells.

We also studied the sensitivity of inhibition strength by changing the inhibition range, i.e. the calculation of N_D in Eqn. (1), from 3 layers of neighboring differentiated cells to 2 and 4 layers, respectively. The results show that the stronger inhibition from 4 layers of neighboring cells (larger N_D in Eqn. (1)) will grow a much smaller tissue, whereas weaker inhibition from 2 layers of neighboring cells (smaller N_D in Eqn. (1)) will lose the homeostasis size control (data not shown).

IV. DISCUSSIONS AND CONCLUSIONS

Modeling of cell population dynamics can provide important understandings to the mechanisms of tissue development. However, traditional population dynamics based method ignores the spatial information of cells in real tissues, which makes it unrealistic. A temporal-spatial cell population dynamics model has been developed to realistically model tissue development by combining a realistic cell growth model [8] with negative feedback controls from differentiated cells to stem cells and progenitor cells. The geometries and forces for cell growth and divisions are incorporated in the cell growth model, and the growth rates and division types after receiving inhibitions from surrounding differentiated cells are modeled individually in our negative feedback control model. Specifically, the stochastic choice of division types is modeled through a Monte Carlo sampling process.

Simulation results show that with proper inhibition strengths, the tissue can achieve the homeostatic size control. However, tissue size control becomes impossible without either (1) all inhibitions or (2) inhibition to the probability of stem cell self-renewal. Through these comparisons, we conclude that proper strengths of negative feedback controls are critically important for tissue size control. Different strengths of inhibitions can result in different tissue development outcomes, which could either provide the diversity for physiological functions of different tissues, or be deleterious.

Additional inhibitions and mechanisms of tissue development involving stem cells can be explored in the future studies using this modeling framework. Although all of the negative feedback controls are conceptually modeled with Hill functions, detailed molecular mechanisms can be incorporated in the future [12–14]. This would make our modeling more realistic, and perhaps allowing additional insights to be gained, as previously demonstrated in the study of phage lambda epigenetic switching network [15]. This modeling framework can be used for exploring broad issues in stem cell research, cancer biology and developmental biology.