Abstract
Elasto-inertial turbulence (EIT) is a new state of turbulence found in inertial flows with polymer additives. The dynamics of turbulence generated and controlled by such additives is investigated from the perspective of the coupling between polymer dynamics and flow structures. Direct numerical simulations of channel flow with Reynolds numbers ranging from 1000 to 6000 (based on the bulk and the channel height) are used to study the formation and dynamics of elastic instabilities and their effects on the flow. The flow topology of EIT is found to differ significantly from Newtonian wall-turbulence. Structures identified by positive (rotational flow topology) and negative (extensional/compressional flow topology) second invariant Qa isosurfaces of the velocity gradient are cylindrical and aligned in the spanwise direction. Polymers are significantly stretched in sheet-like regions that extend in the streamwise direction with a small upward tilt. The Qa cylindrical structures emerge from the sheets of high polymer extension, in a mechanism of energy transfer from the fluctuations of the polymer stress work to the turbulent kinetic energy. At subcritical Reynolds numbers, EIT is observed at modest Weissenberg number (Wi, ratio polymer relaxation time to viscous time scale). For supercritical Reynolds numbers, flows approach EIT at large Wi. EIT provides new insights on the nature of the asymptotic state of polymer drag reduction (maximum drag reduction), and explains the phenomenon of early turbulence, or onset of turbulence at lower Reynolds numbers than for Newtonian flows observed in some polymeric flows.
INTRODUCTION
Polymer additives are known to produce upward of 80% of drag reduction in turbulent wall-bounded flows.1 The drag reduction mechanism is now well understood: Polymers interact with quasi-streamwise vortices in the near wall regions by stretching in bi-axial extensional regions.2 This specific flow topology is found in the up- and downwash flows generated by quasi-streamwise vortices where the stretched polymers, extended well above their local mean, produce a stress in opposition to the flow motion.3 The relationship between quasi-streamwise vortices and polymer force was comprehensively illustrated for exact coherent states that mirror the basic structure of near-wall turbulence.4, 5 Recent studies on hairpin vortices originating from the near-wall regions confirmed that polymers effectively apply a negative torque to vortices.6 The drag reduction results from the dramatic damping and reduction in numbers of quasi-streamwise vortices, the very cause of the dramatic increase in skin-friction drag between laminar and turbulent flows.7 Even as the most efficient drag reduction strategies in liquid flows, polymer additives do not lead to flow relaminarization but, at most, to a universal asymptotic state called maximum drag reduction (MDR), the definition of which has been a recent source of debate in the fluid dynamics community. In the present paper, we discuss the possible relationship between a new state of turbulence, elasto-inertial turbulence8 (EIT), and MDR.
EIT is a new state of small-scale turbulence driven by the interaction between elastic instabilities and the flow's inertia. This phenomenon has been observed over a wide range of subcritical Reynolds numbers in channel and pipe flows, both experimentally and numerically.8 EIT exists by either creating its own extensional flow patterns, as we will demonstrate here in subcritical channel flows, or by exploiting extensional flow topologies, as we shall observe in the wake of a hairpin vortex at higher Reynolds numbers. EIT is possibly related to elastic turbulence (ET), a turbulent state known to occur in inertia-less flows with curved streamlines.9, 10 Groisman and Steinberg9 discovered the existence of strong nonlinear mixing supported by elastic turbulence, a state of saturated dynamical interactions between stretched polymer molecules and the base flow that causes the stretching. In inertial flows, EIT has the merit to provide new insights to two interesting phenomena specific to polymer flows. First, EIT is a reasonable explanation for the phenomenon of early turbulence,11 which describes the onset of turbulence in the presence of diluted polymer additives at Reynolds numbers significantly smaller than in the absence of polymers. Second, EIT offers a different perspective on the MDR.
The early quantitative description of MDR12 consisted of a correlation for the friction factor and a fit of measured mean velocity data to the so called Virk log-law mean velocity profile. The basis for a log-law is a matter of recent controversy. Procaccia et al.13 derived a logarithmic mean velocity profile remarkably close to Virk log-law, assuming (a) infinite Weissenberg number (ratio of polymer relaxation time to flow time scale) and infinite Reynolds number, (b) that energy transfer is unilateral (from flow to polymers), and (c) that the action of polymers onto the flow could be modeled as a linear effective turbulent viscosity, to cite the most important, and relevant to the present discussion, hypotheses. Here the polymer relaxation time is the time for a fully stretched solvated polymer to return to its minimum entropic state, coiled, when the mechanical source of stretching suddenly vanishes. Hypothesis (a) renders the verification of the derivation of Procaccia et al. difficult. At the finite, and somewhat low, Reynolds numbers and finite Weissenberg numbers available from experiments and simulations, the existence of a log-law is not verified.14 Hypothesis (b) was motivated by earlier simulations of viscoelastic homogenous turbulence15 and also supported by energetic budgets in channel flows16 at low Weissenberg numbers and minimal flow unit.17 Dallas et al.18 disputed hypothesis (b) on the grounds that their numerical simulations, carried out in a larger computational domain and in larger Weissenberg numbers, show positive contribution of the polymer stress work in the energy budget of turbulent kinetic energy. Our earlier simulations3 discussed the positive contribution of the elastic work to the streamwise velocity fluctuations in the near-wall regions. Another indication of the existence of energy transfer from polymers to flow was found in a numerical experiment.19 This experiment consisted in selectively removing the polymer contribution from either the streamwise component or the transversal components of the momentum transport equations. The absence of polymer contribution in the streamwise direction yielded full relaminarization of the flow. The removal of polymer contribution in the transversal directions lead to a dramatic increase in turbulent kinetic energy and drag, demonstrating that polymers inject energy into the flow. In the present study, we will demonstrate that EIT possesses a mechanism of energy transfer from polymers to flow. The cumulative sum of all observations introduced here supports de Gennes's20 picture that drag reduction derives from two-way energy transfers between turbulent kinetic energy of the flow and elastic energy of polymers at small scales, resulting in the overall modification of the turbulence energy cascade.
Lastly, MDR's dynamics is so far believed to be of Newtonian nature. The most insightful study of MDR so far was performed by Graham's group,21, 22, 23 which defines MDR as a flow that fluctuates between fundamental states: active and hibernating. The former contains the basic dynamical elements of Newtonian near-wall turbulence, vortices, and streaks, and has a higher drag. The latter is devoid of vortices (but streaks are still observable) with negligible polymer dynamic contribution, and its drag is smaller. This description of MDR is certainly valid for low Weissenberg numbers, however we will discuss in this paper that, at larger Weissenberg numbers, EIT is likely to dominate hibernating states and the whole dynamics of MDR.
METHOD
Channel flow simulations are performed at constant flow rate in a Cartesian domain, where x, y, and z are the streamwise, wall-normal, and spanwise directions, respectively. For a polymer solution, the flow transport equations are the conservation of mass, ∇ · u = 0, where u is the velocity vector, and transport of momentum
| (1) |
We define two Reynolds numbers, each based on the bulk velocity Ub, one of the channel height H (Re = UbH/ν), and the other on the channel half-height h (Reh = Ubh/ν = Re/2). The former maintains consistency with the first paper introducing EIT,8 where channel flow simulations were compared with pipe flow experiment using the full diameter as a reference length scale. The latter is the traditionally used Reynolds number in direct numerical simulation. The parameter β is the ratio of solvent viscosity to the zero-shear viscosity of the polymer solution and affects both the viscous stress and polymer stress terms in Eq. 1. The polymer stress tensor T is computed using the FENE-P (Finite Elastic Nonlinear Extensibility-Peterlin) model:24
| (2) |
where the tensor C is the local conformation tensor of the polymer solution and I is the unit tensor. The properties of the polymer solution are β, the maximum polymer extension L, and the Weissenberg number Wi based on the solution relaxation time λ and the flow time scale relevant to the dynamics of interest. Here Wi is based on the wall shear-rate of the initial laminar flow at each Re, hence . The FENE-P model assumes that polymers may be represented by a pair of beads connected by a nonlinear spring defined by the end-to-end vector q. The conformation tensor is the phase-average of the tensorial product of the end-to-end vector q with itself, C = ⟨q⊗q⟩, whose transport equation is
| (3) |
On the right-hand side of Eq. 3, the first two terms are responsible for the stretching of polymers by hydrodynamic forces, whereas the third term models the internal energy that tends to bring stretched polymers to their least energetic state (coiled).
Eqs. 1, 2, 3 are solved using finite differences on a staggered grid and a semi-implicit time advancement scheme described elsewhere.19 A series of simulations was carried out for Reynolds numbers ranging from 1000 to 6000. A thorough resolution study led us to choose a domain size of 10h × 2h × 5h with 256 × 151 × 256 computational nodes. All results discussed here have been verified on domains with a factor 2 in horizontal dimensions and resolution in each directions. The CFL (Courant-Friedrichs-Lewy) number was set to 0.15 to guarantee the boundedness of C.
The protocol for our simulations was designed to mimic the perturbed experimental setup of Samanta et al.8 within the limitation inherent to the DNS (Direct Numerical Simulation) boundary conditions. For any flow, Newtonian or polymeric, the initial flow and polymer fields are first equilibrated to the laminar state corresponding to the desired Reynolds number. A perturbation is then introduced over a short duration, in the form of blowing and suction velocity on both walls, over which white noise of prescribed intensity is introduced. The velocity pattern is periodic in x and z:
| (4) |
where A is the amplitude, Lx and Lz are the horizontal domain dimensions, and ɛ(t) is the random noise. The total duration of the perturbation is 0.5h/Ub, of which the first and last 10% correspond to a gradual increase/decrease through a smooth step function . Choosing A = 0.09Ub and the RMS of ɛ at 0.005Ub causes the Newtonian flow to transition at Re = 6000.
All polymeric simulations are performed with L = 200 and β = 0.9. Two Weissenberg numbers, based on the flow time scale h/Ub are considered, Wih = λUb/h = 8 and 60, chosen on the basis of the highest Reynolds number, Re = 6000. The lowest Weissenberg number matches the one of previous studies of MDR and near-MDR flows,3, 14, 25 when considering the wall shear-normalized Weissenberg number Wi = 96 (see Table 1). The highest is used to investigate the effects of large Weissenberg numbers. Some of the most relevant simulation parameters are compiled in Table 1.
Table 1.
Parameters used in the viscoelastic simulations discussed in the present paper. For all simulations, the FENE-P length and β parameter are fixed at 200 and 0.9, respectively. The Reynolds numbers Re and Reh are both based on the bulk velocity Ub and Newtonian flow viscosity ν, and the channel full height and half-height (h), respectively. Wih and Wi are the Weissenberg numbers based of the integral flow time scale h/Ub and wall shear . h+ defines the channel half-height normalized by the skin-friction velocity ( and ν). DM denotes the drag modification (reduction or increase), which is measured as the relative change of the friction factor with the comparable Newtonian flow friction factor, i.e., vertical difference in Figure 1a between the Newtonian and viscoelastic friction drag factors. The resolution of our simulation is indicated by Δx+, the mesh size in the streamwise direction normalized by the skin-friction velocity of the viscoelastic flow and the Newtonian flow viscosity. The mesh size in the spanwise direction is Δx+/2 and the minimum grid step in the wall normal direction is smaller than 0.1 for all simulations.
| Re | Reh | h+ | Wih | Wi | DM (% ) | Δx+ |
|---|---|---|---|---|---|---|
| 1000 | 500 | 40 | 8 | 24 | +7 | 1.5 |
| 1000 | 500 | 40 | 601 | 180 | +3.5 | 1.4 |
| 6000 | 3000 | 130 | 8 | 96 | −56 | 5 |
| 6000 | 3000 | 120 | 60 | 720 | −61 | 4.6 |
| 6000 | 3000 | 190 | … | … | 0 | 7.5 |
This simulation is not featured in the statistical analysis or in the study of instantaneous snapshots.
STATISTICAL DESCRIPTION OF THE POLYMERIC FLOWS
Velocity statistics
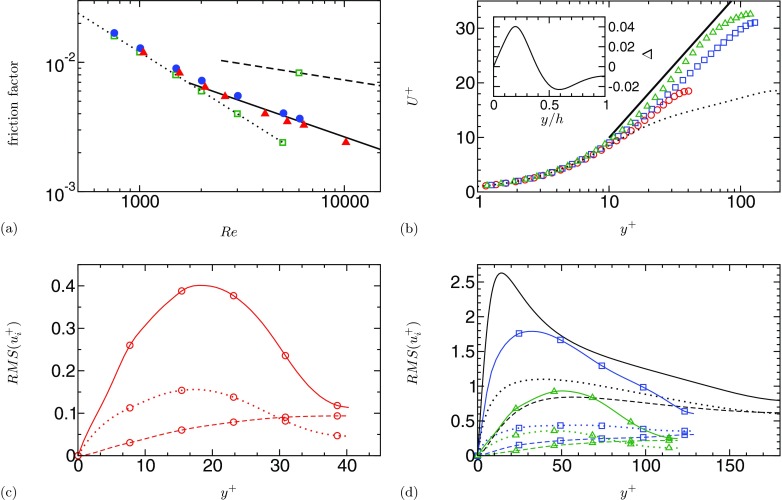
Figure 1 summarizes the main statistical properties of our simulations, which were found to be in excellent agreement with experiments in a pipe flow.8 Figure 1a shows the evolution of the friction factor as a function of the Reynolds number from Re = 1000 to 6000. For viscoelastic simulations, the flow viscosity is corrected for shear thinning effects as in Ptasinski et al.,16 hence the smaller drag increase at Wi = 180 (increased shear thinning) than at Wi = 24 for Re = 1000. Friction drag fluctuates in time between low drag and high drag states in a chaotic manner (not shown). Xi and Graham21 described these states as active (high drag) and hibernating (low drag state). The amplitude and typical wavelength of the drag fluctuations are strongly dependent upon the Weissenberg number and possibly the Reynolds number, which will be the topic of a future investigation. The friction factor of polymeric flows departs from the laminar asymptote, with a slight drag increase, to transition smoothly to the MDR asymptote, where drag is reduced compared to turbulent flow. The effects of increasing elasticity is only noticeable beyond the junction between the laminar and MDR asymptotes of the friction factor at Rec = 1791. The lower Weissenberg number simulations reach a high drag reduced state (HDR3), while the high Weissenberg number simulations slightly overshoot MDR.
Figure 1.
(a) Friction factor as a function of the Reynolds number for two Weissenberg numbers, Wih = 9 (•) and Wih = 60 (▲), with L = 200 and β = 0.9 (see Table 1). Lines indicate correlations for laminar (. . . . . . . ., f = 12/Re) and turbulent (- - - -, f = 0.073Re−1/4) Newtonian channel flow and for MDR (——, f = 0.42Re−0.55); Newtonian solutions are also included (□). (b) Mean velocity profiles normalized by viscous scales; polymer flows: ○, Re = 1000, Wi = 24; □, Re = 6000, Wi = 96; △, Re = 6000, Wi = 720; . . . . . . . ., Newtonian flow at Re = 6000. ——, Virk's MDR velocity profile U+ = 11.7ln (y+) − 17. Inset: Difference, Δ(y) = U(y) − Upois(y), between the analytical Newtonian laminar velocity profile Upois and the velocity profile of polymer flow at Re = 1000, Wi = 24. (c) RMS of velocity fluctuations normalized by viscous scales: ——, streamwise velocity u′; - - - -, wall-normal velocity v′; . . . . . . . ., spanwise velocity w′ for polymer flow at Re = 1000, Wi = 24. (d) Same as (c) for polymer flows at Re = 6000, Wi = 96 and Wi = 720, and for Newtonian flow at Re = 6000 (lines without symbols). For description of symbols see (b).
The increase in drag at subcritical Reynolds numbers (Re ≲ 2000) is consistent with Virk's measurements,12 which shows a similar departure from the laminar friction curve. ET was also shown to augment flow resistance, although more dramatically than the increase in drag observed here, in wall-bounded flows (e.g., curvilinear channels26 and Von-Karman swirling flows9, 10, 27). We remind the reader that the phenomenon of ET requires the mean flow to possess curved streamlines, whereas EIT relies on inertia to sustain locally curved streamlines.8 Interestingly, one of the referees brought to our attention the existence of ET in Kolmogorov flows28 at Reynolds numbers below the critical Reynolds number of for Newtonian flows. Unlike wall-bounded flows, Kolmogorov flows have rectilinear streamlines, which led the referee to suggest a similarity with EIT. In our opinion, this similarity breaks down for two reasons. First, the theoretical work of Bistagnino et al.28 reported a decrease in effective drag (measured as the increase in mean velocity amplitude), at odd with EIT and ET data in wall bounded flows. It is unclear if subsequent simulations29, 30 of 2D ET in Kolmogorov flow support this prediction of drag reduction. Second, it is well known that unstable 2D Kolmogorov flows create wave-like patterns in the instantaneous streamlines and even large scale vortices.31 The viscoelastic case, albeit turbulent at a subcritical Reynolds number, shows such streamlines with regions of quite large curvatures (Fig. 11 in Berti and Boffetta30). There is a commonality though between the viscoelastic Kolomogorov flows at Re ≈ 1 and our channel flow simulations for Re ≲ 2000 in the polymer dynamics' ability to excite flow instabilities at subcritical Reynolds numbers.
Figures 1b, 1c, 1d compare profiles of velocity statistics of the polymeric and Newtonian flows at two Reynolds numbers, Re = 1000 and 6000, representative of the two domains Re < Rec and Re > Rec. At low Reynolds numbers, there is no evidence of logarithmic behavior in the mean velocity profile at HDR or MDR, as discussed in a previous publication.14 The mean velocity profile departs from the Newtonian Poiseuille solution for laminar flow (Figure 1b) by only a few percents. In the second domain (Re > Rec), mean velocity profiles differ significantly from Newtonian turbulence at the same Re. The highest Weissenberg simulation approaches Virk's MDR velocity profile.12 When normalized by viscous flow scales, Figures 1c, 1d, the RMS of velocity fluctuations show a consistent picture at the two Reynolds and Weissenberg numbers considered here, that qualitatively resembles that of Newtonian wall-turbulence. The existence of a maximum in the RMS of streamwise velocity fluctuations suggest the presence of streaks in all flows. The intensity of these streaks and their thickness is obviously modulated by the elasticity of the solution, as obvious at Re = 6000 in Figure 1d from the shift of the maximum of RMS(u+) from y+ ≈ 12 (Newtonian) to y+ ≈ 30 (Wi = 96) and y+ ≈ 50 (Wi = 720). The spatial distributions of spanwise velocity fluctuations for Re = 1000, Wi = 24 and Re = 6000, Wi = 720 are qualitatively similar with a more significant decrease of the centerline RMS relative to its maximum than observed for the Newtonian and Re = 6000, Wi = 720 flows. In all polymer flows the distribution of the wall-normal velocity fluctuations is maximum at the centerline, which is a difference from Newtonian turbulence.
The similarity between Re = 1000, Wi = 24 and Re = 6000, Wi = 720 suggests that the two flows create similar turbulent structures. We will later confirm that Re = 6000, Wi = 720 is indeed dominated by elasto-inertial turbulence. The difference, especially in RMS(w+), with Re = 6000, Wi = 96 indicates the existence of a flow which is still under some influence of typical structures found in Newtonian wall turbulence.
Polymer statistics
Figure 2a shows the profiles of polymer stretch, defined as , for the three simulations of interest. The mean polymer stretch is well below 50% of full extension for the lowest Weissenberg number simulations at Re = 1000 and 6000, indicating that the mechanism at play is not induced by coil-stretch transition, at least from the perspective of time-averaged transport equations. The most elastic solution has significantly larger mean stretch, yet its mean is well below 100%. In a purely laminar flow, i.e., a pure shear flow, the solution for the polymer stretch decreases monotonically and linearly due to the linear behavior of the shear. The emergence of a local maximum away from the wall at our lowest Reynolds number suggests the existence of extensional flow topologies, as such topologies are known to produce the largest polymer extensions in wall turbulence. Indeed, the local maximum of polymer at Re = 6000 arises from the interactions between polymers and turbulent structures in the buffer region, in particular vortices, which produce local extensional flows with dramatic effects on the polymer dynamics.2 The possible existence of extensional flow topology at Re = 1000 is the motivation for Sec. 4.
Figure 2.
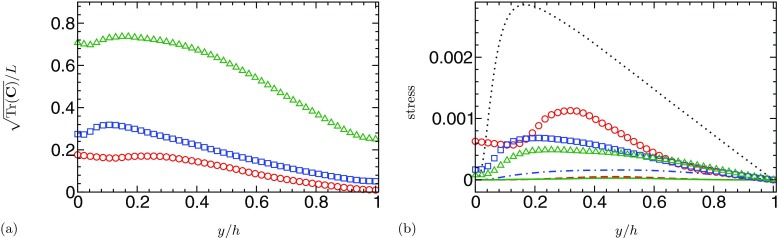
(a) Mean polymer extension: ○, Re = 1000, Wi = 24; □, Re = 6000, Wi = 96; △ Re = 6000, Wi = 720. (b) Polymer (same symbols as in (a)) and Reynolds (lines) shear stresses normalized by the bulk velocity and channel half-height: - - - -, Re = 1000, Wi = 24; – . –, Re = 6000, Wi = 96; ——, Re = 6000, Wi = 720; . . . . . . . ., Re = 6000, no polymers.
Before studying the emergence of extensional flows, the Reynolds shear stress and polymer stress terms are compared (Figure 2b). We remind the reader that the two stresses, with the addition of the viscous stress (not shown), lead for the balance of stresses in a channel flow to
| (5) |
For all simulations, the Reynolds shear stress is very small compared to the polymer shear stress. Supporting the proposition that flows at Re = 1000, Wi = 24 and Re = 6000, Wi = 720 are similar, the Reynolds shear stress is negligible in both cases, indicating the loss of a classical near-wall turbulence structure. The absence of Reynolds shear stress has noticeably been observed in the experiments of Warholic and Hanratty32 for their MDR flow. Even at a slightly lower drag reduction, the polymer shear stress dominates the Reynolds shear stress, which is consistent with HDR flows.3
The statistical analysis of our polymer flow simulations shows turbulent states predominantly supported by polymer stresses. The similarity between the two cases Re = 1000, Wi = 24 and Re = 6000, Wi = 720 indicates that the state, EIT, observed at the lowest Reynolds numbers is likely to exist at higher Reynolds numbers, which suggests that EIT could be the asymptotic structural state of wall-bounded polymer flows.
TOPOLOGY OF EIT
Flow structures
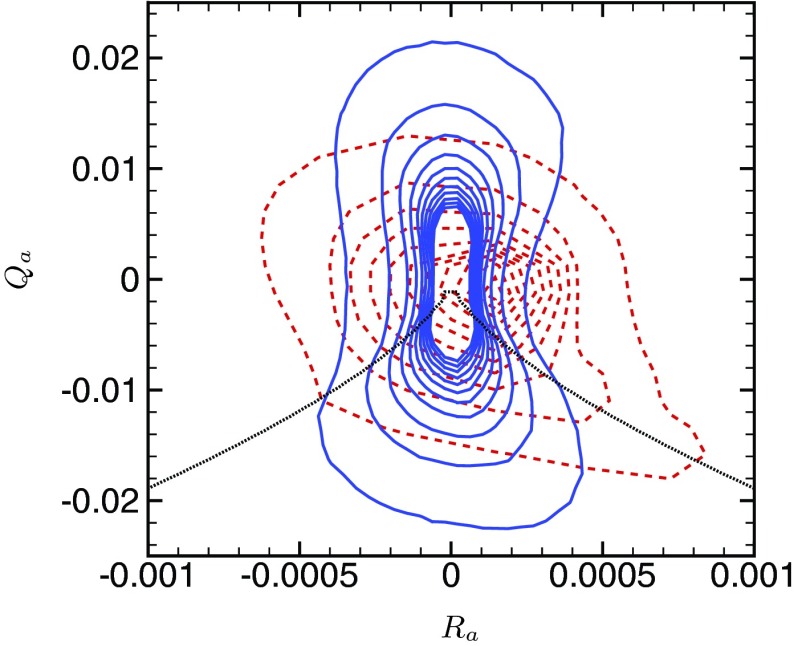
The flow topology is a critical component of the dynamics of polymers,2 since it governs the stretching terms in the transport equation of the conformation tensor, Eq. 3, through the velocity gradient tensor ∇u = ∂jui. We therefore apply the classical reduction of the flow into a joint probability density function (jpdf) of the second Qa = −∂jui∂iuj/2 and third Ra = −∂jui∂kuj∂iuk/3 invariants of ∇u.33, 34 Based on the sign of the discriminant , quadrants I (Ra > 0, D > 0) and II (Ra < 0, D > 0) of Figure 3 define spiraling flows under compression and extension, respectively, and III (Ra < 0, D < 0) and IV (Ra > 0, D < 0) biaxial compressional and extensional flows, respectively. At Re = 6000, the jpdf contours exhibit an inverted teardrop shape common to many turbulent flows, in particular of Newtonian turbulent channel flow. The topology distribution for the lower Reynolds number flow is significantly different with a quasi-symmetry around both Ra = 0 and Qa = 0 and the confirmation of the existence of biaxial extensional events (D < 0).
Figure 3.
Joint probability density functions sampled over the entire channel of flow topology in the (Qa, Ra) phase plot for polymeric flows at Re = 1000, Wi = 24 (——) and Re = 6000, Wi = 96 (- - - -). Line . . . . . . . . describes , the vertical bounds of the four quadrants of flow topology.
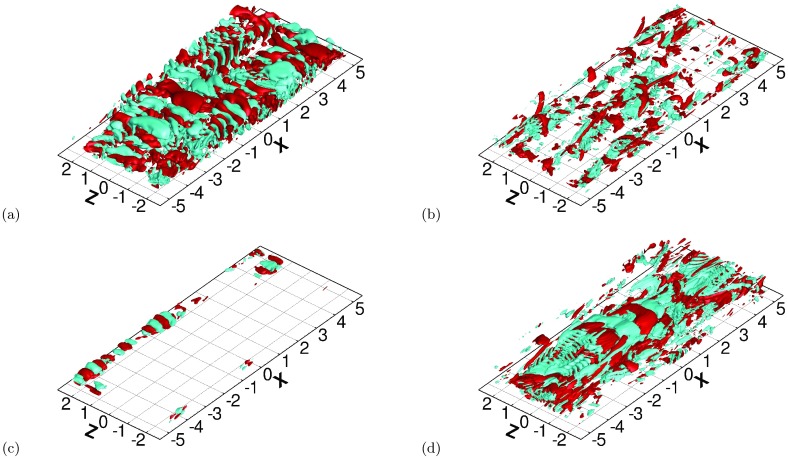
Figure 4 shows the 3D structure of Qa with positive and negative isosurfaces of Qa for Re = 1000 and 6000. At the lower Reynolds number (Figure 4a), the structure of the Qa field is predominantly spanwise with trains of cylindrical structures of various scales. The smallest scale structures depicted by the threshold chosen in this figure are organized in trains of structures of alternating sign. Much larger scales are observed throughout the domain, with typical spanwise dimensions comparable to the small scale structures. The typical streamwise dimension appears to be a couple of wavelength of the structures forming the trains of small scales. At Re = 6000 and moderate elasticity (Wi = 96), we chose the particular instant that is shown in Figure 4b because the structure is characteristic of an active state,21 or state of high drag (thus higher turbulence). No trains of alternating sign cylindrical structures of Qa may be observed. However, these trains reappear during hibernating states21 (not shown for Wi = 96), as evident from Figure 4c for Re = 6000 and Wi = 720. Active states at Wi = 720 (Figure 4d) consist also of hairpin vortices, though much larger than for Wi = 96, and trains of small scale cylindrical structures of alternating sign of Qa. Some of these trains appear in the wake of heads of hairpin vortices and were also observed at higher Reynolds numbers.35 Other train occurrences are also observed in regions of low turbulence, consistent with the hibernating state's picture.
Figure 4.
Instantaneous isosurfaces of the second invariant of the velocity gradient tensor for Qa = ±0.025 at Re = 1000, Wi = 24 (a); Qa = ±0.1 at Re = 6000, Wi = 96 (b); Qa = ±0.1 at Re = 6000, Wi = 720 during hibernating (c) and active (d) state. Red, positive Qa; cyan, negative Qa.
Relation between regions of high polymer extension and flow structures
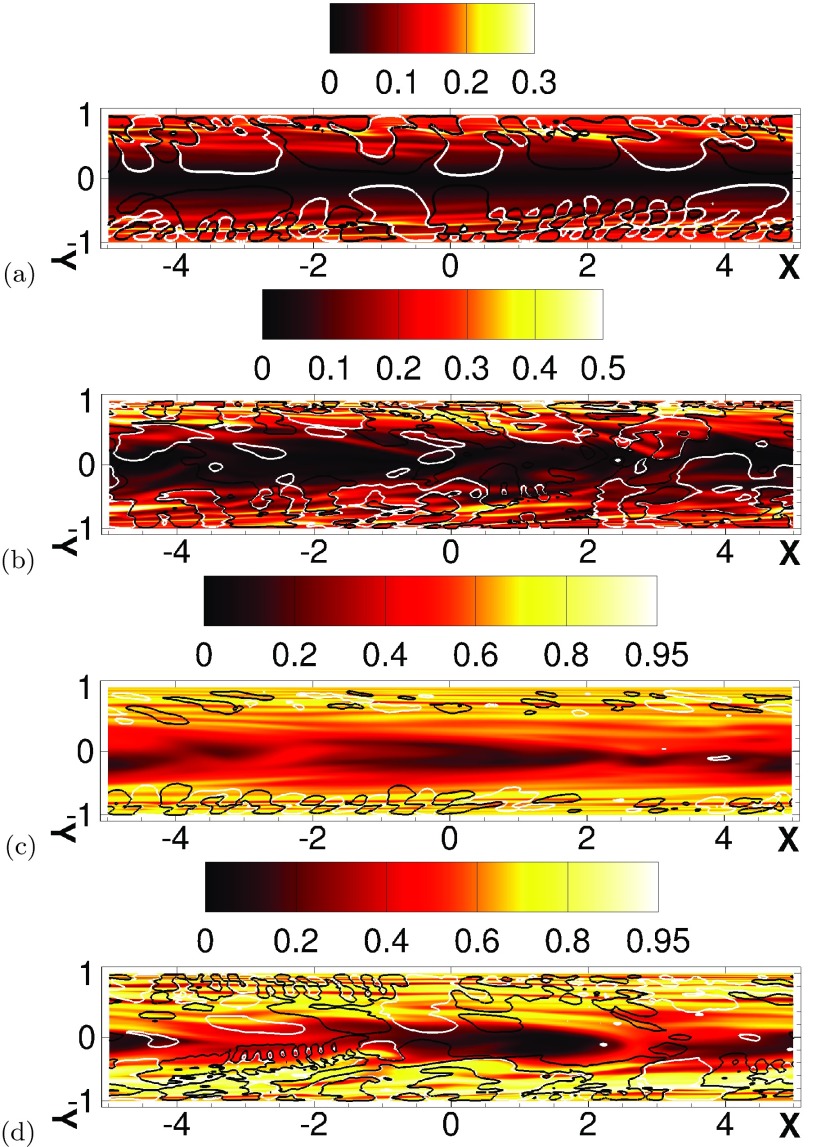
Local extensional flows are captured in contours of polymer stretch (Figure 5) in the form of thin sheets of locally high polymer stretch, tilted upward and elongated in the flow direction. Superimposed to the contours of polymer stretch are the contours of positive and negative Qa, which reveal the existence of trains of circular regions of alternating Qa-sign associated to sheets of large polymer stretch. The intermittence of these sheets is clear for the lowest Weissenberg number (Wih = 8) at both Reynolds numbers, where the sheets of highly stretched polymers are surrounded by large regions of low stretch (Figures 5a, 5b). The smallest scales (cylindrical structures of positive and negative Qa) cluster along the sheets of highly stretched polymers. The cross-section of these cylindrical structures are shaped like the outside contour of a dumbbell, or an ellipsoid squeezed along its shorter radius. The large scales of the Qa field appear also to alternate sign along the streamwise direction. These large scale structures seem to arise from the smallest scales maybe through a merger of the upper head (or most outward head) of the small scale dumbbell structures. This is only a speculation at this point which warrants further investigation but is not critical to the current study.
Figure 5.
Instantaneous contours of polymer extension in an x-y plane showing streamwise sheet-like regions. Re = 1000, Wi = 24 (a); Re = 6000, Wi = 96 (b); and Re = 6000, Wi = 720 for hibernating (c) and active (d) state. The continuous and dashed lines superimposed to the contours of polymer stretch represent isosurfaces of Qa: black, negative; white, positive.
In the active state of the Re = 6000, Wi = 96 simulation (Figure 5b), the trains of small scales are not present, at least in the cross-section considered here. At the highest Weissenberg number, highly stretched polymers occupy most of the domain, yet sheets are still present in the hibernating and active states, Figures 5c, 5d, respectively. During the hibernating state, the structure of Qa exhibits the same dumbbell shape found at Re = 1000. The plane in Figure 5d cuts through a hairpin vortex, illustrating one of the train of small-scale Qa structures spanning over −1 ≲ x/h ≲ 3 in the lower channel half.
One important conclusion of this topological study is that EIT consists of cylindrical structures of Qa of alternating signs at least at two scales, small dumbbell-like cylinders, and larger structures that seem to results from the merging of the dumbbell cylinders. Another important observation is that the features of EIT disappear when the flow is too turbulent or the polymer solution not elastic enough. EIT reappears during hibernation events or even during active events if the Weissenberg number is sufficiently large. This suggests that EIT is an asymptotic state that should occur when the elasticity of the solution can efficiently control and contain the growth of turbulence.
THE ENERGETIC PICTURE OF EIT
Energy spectra
Figure 6a shows longitudinal 1D spectra of turbulent kinetic energy (TKE) at y+ = 15 for all polymeric simulations. The location was chosen for its good approximation of the maximum energy transfer of elastic energy to TKE for the three viscoelastic simulations of interest. In spite of the low Reynolds numbers considered here, a range of wavenumbers, between kx ≈ 4–10 for Re = 1000 and kx ≈ 8–50 for Re = 6000, show a power decay that fits well k−14/3. We checked the robustness of the power law behavior by plotting the exponent derived from α(kx) = (kx/E(kx))(dE/dkx) and confirming the existence of a plateau of α(kx) in the range of wavenumbers of interest (not shown). The −14/3 exponent bears, at this point, no theoretical significance; the best fit was found to be around 4.6. In the two EIT flows, the higher wavenumbers depart from −14/3 and seem closer to −11/3 (not shown). Spectra with similar k−14/3 power decay have recently been simulated in homogoneous turbulence36 and channel flow at higher Reynolds numbers.37 Jun and Steinberg38 also reported k−4 decay in elastic turbulence.
Figure 6.
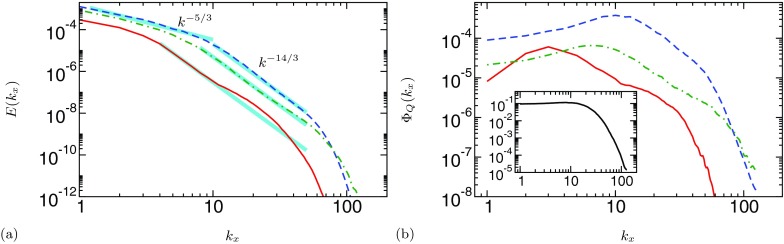
(a) Spectra of turbulent kinetic energy at y+ = 15. (b) Spectra of Qa at the same location. ——, Re = 1000, Wi = 24; - - - -, Re = 6000, Wi = 96; – . –, Re = 6000, Wi = 720. Inset: spectrum of Qa for Newtonian turbulence at Re = 6000, same location.
The interesting peculiarity of Figure 6a is the high wavenumber bump featured only in the two EIT flows (Re = 1000, Wi = 24 and Re = 6000, Wi = 720) and absent from the HDR flow (Re = 6000, Wi = 96) and also from the two simulations cited earlier.36, 37 In other words, consider the approximation E(k) = C(k)k−α(k) for the energy spectra across all wavenumbers. For flows up to high drag reduction, α(k) is an increasing monotonic function, whereas EIT flows appear to experience a reduction in power decay between the −14/3 range and the dissipative range (close to the Kolmogorov scale). The spectral distributions of the fluctuations of the second invariant Qa of the velocity gradient tensor are plotted in Figure 6b for the same flows and locations as in Figure 6a. The second invariant captures the coherent structures of EIT, as shown in Figs. 45. Figure 6b indicates the strong possibility of significant dynamical activity at high wavenumbers in EIT flows, in the range of smallest dumbbell-like structures shown in Figure 5.
We speculate that the high wavenumber structures are more than just signature of EIT; they might be indicative and/or originators of an inverse energy cascade, where the polymer dynamics is feeding into larger flow scales. The inverse energy cascade is a reality of Newtonian turbulence as demonstrated by Biferale et al.39 in 3D isotropic turbulence. Incidentally, Biferale et al. argued that “2D and 3D properties naturally coexist in all flows in nature.” Testing our speculation is beyond the scope of this paper and is left to future investigations. The following focuses only on the study of energy transfer between polymers and flow.
Energy transfer between polymers and turbulence
The only evidence presented so far for the sustainability of EIT through energy transfer from polymers to turbulence is the very existence of EIT at a Reynolds number much lower than the critical Reynolds number for Newtonian flows. At the origin of the mechanism is the transfer of energy from the mean flow to the mean polymer energy, which is a function of polymer stretch.18 The mechanism is universal to polymer flows and only reflects the stretching of polymers by the local mean shear, and obviously exists in laminar flows. The difference between EIT and a purely laminar viscoelastic flow is in the energy transfer between the fluctuations of polymer stress work and TKE. Following Dallas et al.,18 we use the integral of the budget of TKE:
| (6) |
where V is the volume of the channel. The three terms involved are the production of TKE, the dissipation rate of TKE, and the energy transfer between polymers and TKE, or fluctuating polymer stress work, which are respectively defined as
| (7a) |
| (7b) |
| (7c) |
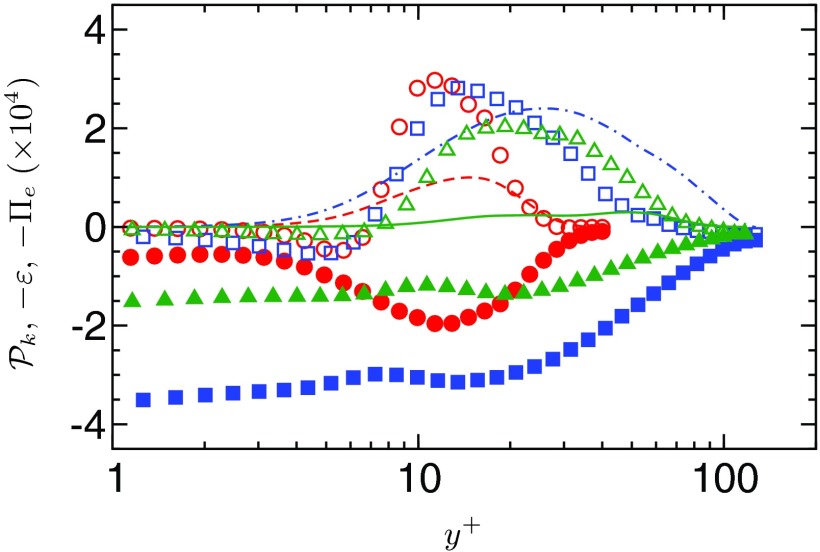
The tensor S′ is the fluctuating strain rate tensor S′ = (∇u′ + ∇u′T)/2 and T′ is the fluctuating polymer stress tensor. Figure 7 shows the profile across one half of the channel of the three terms of interest for polymer flows at Re = 1000 and 6000. The wall-normal coordinate is normalized by viscous scales. In Eq. 6, the production and dissipation rate of TKE terms are always positive. The energy transfer between polymer and turbulence divides the flow in two regions. In a thin region attached to the wall (y+ ≲ 7, polymers supplements the dissipation rate of TKE. Beyond this “polymeric viscous sublayer,” polymers support and even create, for Re = 1000, turbulence with transfers from elastic to turbulent kinetic energy. Lending further credence to our proposition that EIT is the asymptotic state of polymer drag reduction, the production of TKE in the highest Weissenberg and Reynolds number flow is overwhelmingly dominated by −Πe, in a similar fashion as for the Re = 1000 flow.
Figure 7.
Profiles of the production of turbulent kinetic energy, (lines), the negative contribution of dissipation rate of TKE, ε (closed symbols), and transfer of energy between elastic energy and TKE, Πe (open symbols). The sum of the volumetric integral of these term results in the energy balance found in Eq. 6. Re = 1000, Wi = 24 (- - - -, ○ , • ); Re = 6000, Wi = 96 (– . –, □, ■); Re = 6000, Wi = 720 (——, △, ▲).
Dallas et al.18 conducted a sensitivity study of the energetic contribution of polymers to TKE as a function of the Weissenberg number at a Reynolds number (Re = 5666) closed to our highest Re considered here. They found that, at low Wi, the energetic contribution of polymers is predominantly of dissipative nature. For Wi > 100, the contribution to TKE becomes positive, as we observe in Figure 7. The shape of the distribution of −Πe shown in Figure 7 is identical to the distributions obtained by Dallas et al. at Wi ≳ 80. The injection of energy from polymers to TKE through the fluctuating polymer stress work is therefore not an exclusive feature of EIT, rather a general property of highly drag reduced flows, as we observed in earlier work.3, 19 The interesting point nonetheless is that EIT at subcritical Reynolds numbers has the same structure, from the perspective of the energy budget of TKE, as supercritical Reynolds number flows, which suggests that the dynamics at MDR could be driven by the polymer dynamics.
Figure 7 brings further support to de Gennes's theory20 of exchange of energy between elastic energy and TKE; a point also made in other recent studies.18, 40 Our study suggests an extension to the general understanding of MDR: At supercritical Reynolds numbers and large Wi, the dynamics of the flow becomes EIT-like.
An instantaneous picture of transfer between elastic and turbulent kinetic energies
Based on the analysis conducted so far, the energy transfer term between polymers and TKE can be interpreted as follows. TKE is a large scale quantity, whereas the organization of polymers in sheets strongly suggests that polymers are intermediate or small scales, as shown by the Qa structures they create. Indeed the thickness of the sheets of highly stretched polymers appear to govern EIT, as evident from the clustering of Qa structures on these sheets. Defining the volumetric integral as ⟨•⟩ = ∫V•dV, the rate of change of TKE is thus
| (8) |
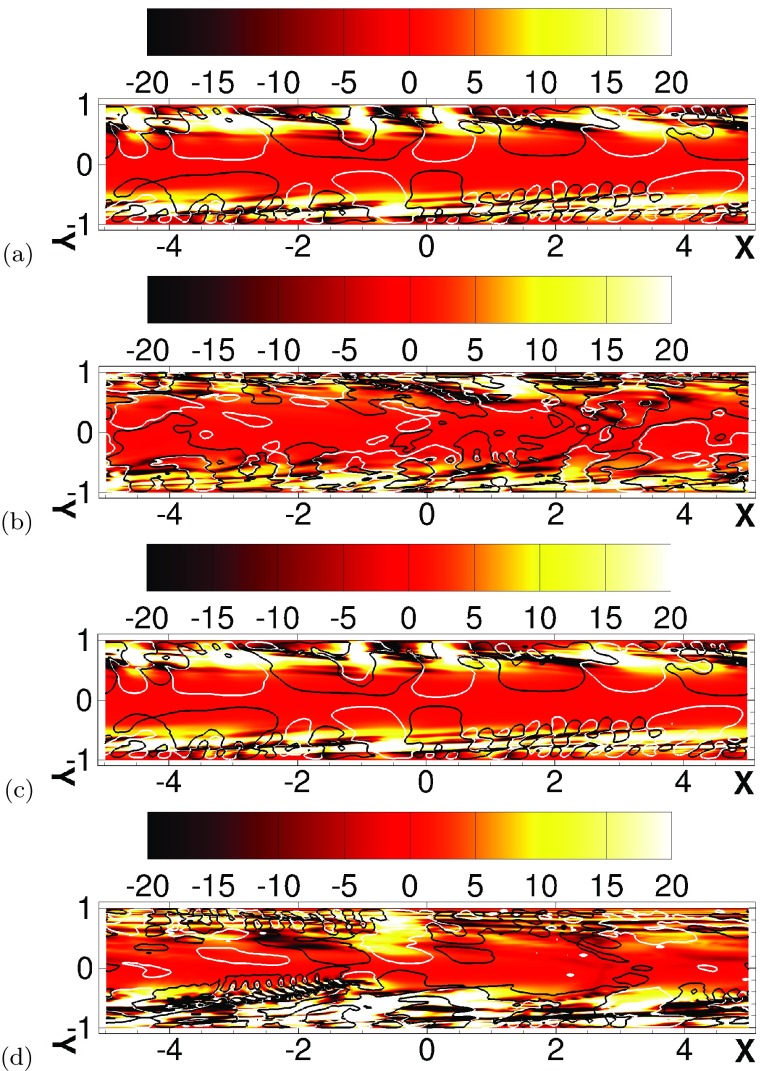
and −⟨ɛ⟩ is always negative, thus a sink of TKE. The scalar product between tensors T′ and S′ is effectively the rate of work done by the strain rate on the polymer stress. When fluctuations of polymer and strain tensors align, T′: S′ > 0, the work is a sink of turbulent kinetic energy, consistent with the increase of polymer stress in sheets (extensional flows) which triggers large increases in extensional viscosity. When polymer stress fluctuations oppose flow deformation fluctuations, −Πe becomes positive and contributes directly to TKE, in the likely form a backward energy cascade. The interplay between −Πe and coherent structures isolated by isosurfaces of Qa is shown in Figure 8. The region of forward cascades are sheets, that one can visually correlate to sheets of highly stretched polymers from Figure 5. These regions also appear to be the cause of the narrow part of the dumbbell shape of the Qa-isosurfaces (Figure 8a for 0 ≲ x/h ≲ 4, for instance). The backward energy cascade surrounds the sheets of forward cascade and contain the largest scales of Qa. Note that in the active state depicted in Figure 8d, one can observe the wake of the head of a hairpin vortex where the flow is extensional and triggers EIT.
Figure 8.
Instantaneous contours of the negative of the fluctuating polymer stress work, −Πe, in an x − y plane showing regions of energy transfer from polymers to flow (white), and from flow to polymer (black). Re = 1000, Wi = 24 (a); Re = 6000, Wi = 96 (b) and Re = 6000, Wi = 720 for hibernating (c) and active (d) state. The continuous and dashed lines superimposed to the contours of polymer stretch represent isosurfaces of Qa: black, negative; white, positive.
PROPOSED MECHANISM OF EIT
The dynamics of EIT was found to be consistent across the two regimes shown in Figure 1a (Re < Rec and Re > Rec), and can be best described by (i) taking the divergence of Eq. 1, which yields the Poisson equation for pressure in a viscoelastic flow:
| (9) |
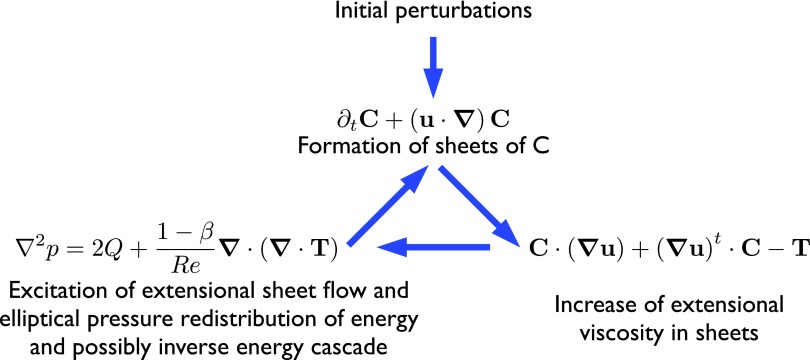
and (ii) considering the hyperbolic nature of the transport equation of the conformation tensor, Eq. 3, caused by the absence of diffusion.19 For Re < Rec, a perfectly laminar flow stretches polymers through the action of shear (stretching term in Eq. 3). The introduction of small perturbations into the flow excites the unstable nature of the nonlinear advection term (u · ∇)C, resulting in the formation of sheets or cliffs of polymer stretch akin to cliffs of scalar concentration observed in the turbulent transport of low-diffusivity passive scalar.41 This behavior is obvious when comparing Figures 3(b) and 3(c) of Somandepalli et al.42 with LIF (Laser Induced Fluorescein) images of fluorescein dye concentration in polymer drag-reduced wall bounded flows. The sheets of high polymer stretch, due to their extensional topological nature, host a significant increase in extensional viscosity. From the perspective of the velocity field, they create a strong local anisotropy, with a formation of local low-speed jet-like flow. The response of the flow is likely to happen through pressure (Eq. 9), whose role is to redistribute energy across components of momentum. The elliptic nature of Figure 9 is a strong candidate to explain the formation of cylindrical waves, or trains of alternating rotational and straining motions as shown by the Qa isosurfaces. The mechanism shares some similarity with the Kelvin-Helmholtz instability, the thickness of these sheets is too close to the Kolmogorov scale (smallest scale of turbulence) for vortices to be created. The perturbations introduced by such trains appear to be sufficient to sustain the formation of extended polymer sheets. Therefore, once triggered, EIT is self-sustained since the elastic instability creates the very velocity fluctuations it feeds upon. Interestingly, Samanta et al.8 and Dubief et al.35 show that the phenomenon of EIT is not confined to low Reynolds numbers, unlike elastic turbulence.9 We also presented circumstantial evidences that EIT shares some interesting similarities with 2D turbulence, which could provide a reasonable framework for further studies. The mechanism of EIT is summarized in Eq. 9.
Figure 9.
Conceptual sketch of the mechanism of EIT.
CONCLUSION
This paper investigates a new turbulent state, elasto-inertial turbulence,8 created by polymers in a channel flow in a range of Reynolds numbers, from sub- to supercritical. EIT shares some properties with another peculiar turbulent state also generated by diluted polymers, elastic turbulence. EIT and ET both operate in a cyclic system where velocity fluctuations induce polymer stress fluctuations, which in turn sustain velocity fluctuations. The difference between EIT and ET is that EIT relies on inertia to feed to create sheet-like regions of high polymer extension, whereas ET requires curved streamlines to occur. EIT has the merit of bringing closure to some unknown phenomena observed in the course of decades of research in polymer drag reduction. Our simulations were able to reproduce the slight drag increase observed by Virk et al.12 in 1970 (and confirmed by the experiments presented in Samanta et al.8). The existence of velocity fluctuations at subcritical Reynolds number also provides an explanation for the observation of early turbulence, or onset of turbulence in flows with polymer additives at smaller Reynolds numbers than in Newtonian flows.11, 43, 44 In our simulations, for the same set of initial flow perturbations, the viscoelastic flow transitions to MDR at around the critical Reynolds number for channel flows, much lower than the transition simulated in our Newtonian flow.
The flow structure of EIT consists of alternating spanwise cylindrical regions of rotational and extensional regions. The regions of rotational flow topology are not intense enough to behave as vortices. These structures appear to emerge from regions of high polymer extension, which are arranged into upward-tilted thin sheets. These sheets bear a strong resemblance with the formation of high-Schmidt number sheets of high concentration of passive scalar in turbulent flows. We argue that they arise from the hyperbolic nature of the polymer conformation tensor transport equation. The large extension of the polymers indicate a local increase of the extensional viscosity of the flow within such sheets. We propose that the anisotropy in polymer stress leads to the formation of the cylindrical flow structures via the elliptic equation for pressure.
Elasto-inertial turbulence offers a new perspective on polymer drag reduction. First, it provides support to de Gennes's20 theory of energy transfers between polymers and flow. Its very existence at subcritical Reynolds numbers highlights a bidirectional energy transfer from polymers to flow. The mean flow stretches polymers, but fluctuations in polymer stress create turbulent kinetic energy. Second, EIT allows us to consider the possible structure of MDR for very large elasticity (Wi → ∞). The energetic picture, as far as the budget of turbulent kinetic energy is concerned, is the same at supercritical Reynolds numbers as at subcritical Reynolds numbers. This suggests that the dynamics of MDR may not be purely of Newtonian nature, rather it may be driven by EIT at increasing Wi. The existence of Newtonian turbulence, specifically active states with dynamically significant vortical structures, depends upon the efficacy of the polymer drag reduction mechanism. During hibernating states, polymer stretching is reduced.22 As vortical structures emerge from flow instabilities, polymers need to extend to a certain magnitude before they can efficiently produce the negative torque that is the essence of the polymer drag reduction mechanism. Now, consider very large Weissenberg numbers. Under such a scenario, the mean flow would maintain the polymers at high extension. As a vortical structure emerges, the drag reduction mechanism would kick in immediately, stop the growth of the vortex before its contribution becomes significant. The flow would therefore remain in a perpetual hibernating state, which would only be sustained by EIT. Much more is to be done to test the validity of this hypothetical scenario.
EIT also offers a different perspective on the form of the velocity profile at MDR. The asymptotic state of polymer drag reduction in the absence, or near absence, of vortices should therefore be driven by the nonlinear transport of polymer stretch, which resembles the transport of a high Schmidt number passive scalar, and the response of the flow to a sheet-like, strongly anisotropic field of effective viscosity governed by the extensional viscosity of polymers. As discussed by Dubief et al.,35 the flow is therefore stuck in a transitional state, specifically the stage of breakdown of nonlinear flow instabilities, which does not support a logarithmic mean velocity profile.45 Unfortunately, a major obstacle in the derivation of a low Reynolds (or possibly high Reynolds) number correction of Virk's log law is the lack of theoretical understanding of high Schmidt number active scalar transport in nonlinear anisotropic flows. We believe that the high wavenumber “bump” in the energy spectra of EIT flows is related to the polymer extension sheet-like structure. We also speculate that there is a backward energy cascade originating from these sheets. These points need to be addressed in order to understand EIT and MDR and will be the focus of future investigations.
ACKNOWLEDGMENTS
This article is dedicated to our mentor, colleague, and friend, Professor Parviz Moin, in honour of his 60th birthday, and without whom this research would have never been undertaken. First, because our interest in polymeric flows started through Parviz's impulsion and guidance more than ten years ago, when research on turbulent drag reduction by polymer additives was initiated at the Center for Turbulence Research (CTR) in Stanford, the project which we had the privilege to be part of. Second, because years later the umbrella of the CTR and its Summer Program gave us the chance to revisit and further deepen this topic. The collaborative and incredibly fertile atmosphere of the CTR, which Parviz created and nurtured, was indeed a major contributor to the results presented here. Finally and foremost, because Parviz's vision and pioneering work in numerical simulations of turbulence paved the way for much more future research in this field. This is very well exemplified by the results presented here, which demonstrate not only the capacity of high-fidelity computations to accurately simulate experimental observations, but also to offer an unparalleled insight into the physics of such complex flows. We are forever in debt to Parviz for his tremendous help, support, and inspiration.
The Vermont Advanced Computing Center is gratefully acknowledged for providing the computing resources necessary for our simulations. Y.D. acknowledges the partial support of Grant No. P01HL46703 (Project 1) from the National Institutes of Health. V.E.T. acknowledges the financial support of a Marie Curie FP7 Career Integration Grant within the 7th European Community Framework Programme (Grant Agreement No. PCIG10-GA-2011-304073). J.S. acknowledges the support of the Australian Research Council. The authors are indebted to the referees whose suggestions and constructive criticisms helped improve this manuscript.
References
- White C. and Mungal M., “Mechanics and prediction of turbulent drag reduction with polymer additives,” Annu. Rev. Fluid Mech. 40, 235–256 (2008). 10.1146/annurev.fluid.40.111406.102156 [DOI] [Google Scholar]
- Terrapon V., Dubief Y., Moin P., Shaqfeh E., and Lele S., “Simulated polymer stretch in a turbulent flow using Brownian dynamics,” J. Fluid Mech. 504, 61–71 (2004). 10.1017/S0022112004008250 [DOI] [Google Scholar]
- Dubief Y., White C., Terrapon V., Shaqfeh E., Moin P., and Lele S., “On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows,” J. Fluid Mech. 514, 271–280 (2004). 10.1017/S0022112004000291 [DOI] [Google Scholar]
- Stone P., Roy A., Larson R., Waleffe F., and Graham M., “Polymer drag reduction in exact coherent structures of plane shear flow,” Phys. Fluids 16, 3470 (2004). 10.1063/1.1775192 [DOI] [Google Scholar]
- Li W. and Graham M. D., “Polymer induced drag reduction in exact coherent structures of plane poiseuille flow,” Phys. Fluids 19, 083101 (2007). 10.1063/1.2748443 [DOI] [Google Scholar]
- Kim K., Li C., Sureshkumar R., Balachandar S., and Adrian R., “Effects of polymer stresses on eddy structures in drag-reduced turbulent channel flow,” J. Fluid Mech. 584, 281–299 (2007). 10.1017/S0022112007006611 [DOI] [Google Scholar]
- Kravchenko A. G., Choi H., and Moin P., “On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers,” Phys. Fluids A 5, 3307 (1993). 10.1063/1.858692 [DOI] [Google Scholar]
- Samanta D., Dubief Y., Holzner M., Schäfer C., Morozov A. N., Wagner C., and Hof B., “Elasto-inertial turbulence,” Proc. Natl. Acad. Sci. U.S.A. 110, 10557–10562 (2013). 10.1073/pnas.1219666110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groisman A. and Steinberg V., “Elastic turbulence in a polymer solution flow,” Nature 405, 53–55 (2000). 10.1038/35011019 [DOI] [PubMed] [Google Scholar]
- Groisman A. and Steinberg V., “Elastic turbulence in curvilinear flows of polymer solutions,” New J. Phys. 6, 29 (2004). 10.1088/1367-2630/6/1/029 [DOI] [Google Scholar]
- Hoyt J., “Laminar-turbulent transition in polymer solutions,” Nature 270, 508–509 (1977). 10.1038/270508a0 [DOI] [Google Scholar]
- Virk P., Mickley H., and Smith K., “The ultimate asymptote and mean flow structure in Toms' phenomenon,” Trans. ASME: J. Appl. Mech. 37, 488–493 (1970). 10.1115/1.3408532 [DOI] [Google Scholar]
- Procaccia I., LÕvov V., and Benzi R., “Colloquium: Theory of drag reduction by polymers in wall-bounded turbulence,” Rev. Mod. Phys. 80, 225 (2008). 10.1103/RevModPhys.80.225 [DOI] [Google Scholar]
- White C., Dubief Y., and Klewicki J., “Re-examining the logarithmic dependence of the mean velocity distribution in polymer drag reduced wall-bounded flow,” Phys. Fluids 24, 021701 (2012). 10.1063/1.3681862 [DOI] [Google Scholar]
- De Angelis E., Casciola C., Benzi R., and Piva R., “Homogeneous isotropic turbulence in dilute polymers,” J. Fluid Mech. 531, 1–10 (2005). 10.1017/S0022112005003666 [DOI] [Google Scholar]
- Ptasinski P., Boersma B., Nieuwstadt F., Hulsen M., Van Den Brule B., and Hunt J., “Turbulent channel flow near maximum drag reduction: simulations, experiments and mechanisms,” J. Fluid Mech. 490, 251–291 (2003). 10.1017/S0022112003005305 [DOI] [Google Scholar]
- Jiménez J. and Moin P., “The minimal flow unit in near-wall turbulence,” J. Fluid Mech. 225, 213–240 (1991); a minimal channel flow unit is a computational domain whose horizontal and spanwise dimensions are minimized to contain a basic set of near-wall turbulence structures, i.e., a pair of vortices and streaks. 10.1017/S0022112091002033 [DOI] [Google Scholar]
- Dallas V., Vassilicos J., and Hewitt G., “Strong polymer-turbulence interactions in viscoelastic turbulent channel flow,” Phys. Rev. E 82, 066303 (2010). 10.1103/PhysRevE.82.066303 [DOI] [PubMed] [Google Scholar]
- Dubief Y., Terrapon V., White C., Shaqfeh E., Moin P., and Lele S., “New answers on the interaction between polymers and vortices in turbulent flows,” Flow, Turbul. Combust. 74, 311–329 (2005). 10.1007/s10494-005-9002-6 [DOI] [Google Scholar]
- de Gennes P., Introduction to Polymer Dynamics (Cambridge University Press, 1990). [Google Scholar]
- Xi L. and Graham M., “Active and hibernating turbulence in minimal channel flow of Newtonian and polymeric fluids,” Phys. Rev. Lett. 104, 218301 (2010). 10.1103/PhysRevLett.104.218301 [DOI] [PubMed] [Google Scholar]
- Xi L. and Graham M. D., “Turbulent drag reduction and multistage transitions in viscoelastic minimal flow units,” J. Fluid Mech. 647, 421 (2010). 10.1017/S0022112010000066 [DOI] [Google Scholar]
- Xi L. and Graham M. D., “Dynamics on the laminar-turbulent boundary and the origin of the maximum drag reduction asymptote,” Phys. Rev. Lett. 108, 028301 (2012). 10.1103/PhysRevLett.108.028301 [DOI] [PubMed] [Google Scholar]
- Bird R., Armstrong R., and Hassager O., Dynamics of Polymeric Liquids. Kinetic Theory (Wiley-Interscience, 1987), Vol. 2. [Google Scholar]
- Li C., Sureshkumar R., and Khomami B., “Influence of rheological parameters on polymer induced turbulent drag reduction,” J. Non-Newtonian Fluid Mech. 140, 23–40 (2006). 10.1016/j.jnnfm.2005.12.012 [DOI] [Google Scholar]
- Burghelea T., Segre E., Bar-Joseph I., Groisman A., and Steinberg V., “Chaotic flow and efficient mixing in a microchannel with a polymer solution,” Phys. Rev. E 69, 066305 (2004). 10.1103/PhysRevE.69.066305 [DOI] [PubMed] [Google Scholar]
- Burghelea T., Segre E., and Steinberg V., “Elastic turbulence in von Karman swirling flow between two disks,” Phys. Fluids 19, 053104 (2007). 10.1063/1.2732234 [DOI] [Google Scholar]
- Bistagnino A., Boffetta G., Celani A., Mazzino A., Puliafito A., and Vergassola M., “Nonlinear dynamics of the viscoelastic Kolmogorov flow,” J. Fluid Mech. 590, 61–80 (2007). 10.1017/S0022112007007859 [DOI] [Google Scholar]
- Berti S., Bistagnino A., Boffetta G., Celani A., and Musacchio S., “Two-dimensional elastic turbulence,” Phys. Rev. E 77, 055306 (2008). 10.1103/PhysRevE.77.055306 [DOI] [PubMed] [Google Scholar]
- Berti S. and Boffetta G., “Elastic waves and transition to elastic turbulence in a two-dimensional viscoelastic Kolmogorov flow,” Phys. Rev. E 82, 036314 (2010). 10.1103/PhysRevE.82.036314 [DOI] [PubMed] [Google Scholar]
- Platt N., Sirovich L., and Fitzmaurice N., “An investigation of chaotic Kolmogorov flows,” Phys. Fluids A 3, 681–696 (1991). 10.1063/1.858074 [DOI] [Google Scholar]
- Warholic M., Massah H., and Hanratty T., “Influence of drag-reducing polymers on turbulence: effects of Reynolds number concentration and mixing,” Exp. Fluids 27, 461–472 (1999). 10.1007/s003480050371 [DOI] [Google Scholar]
- Soria J., Sondergaard R., Cantwell B., Chong M., and Perry A., “A study of the fine-scale motions of incompressible time-developing mixing layers,” Phys. Fluids 6, 871–884 (1994). 10.1063/1.868323 [DOI] [Google Scholar]
- Ooi A., Martin J., Soria J., and Chong M., “A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence,” J. Fluid Mech. 381, 141–174 (1999). 10.1017/S0022112098003681 [DOI] [Google Scholar]
- Dubief Y., White C. M., Shaqfeh E. S. G., and Terrapon V. E., “Polymer maximum drag reduction: A unique transitional state,” in Annual Research Briefs (Center for Turbulence Research, Stanford, CA, 2010), pp. 395–404. [Google Scholar]
- Watanabe T. and Gotoh T., “Hybrid Eulerian–Lagrangian simulations for polymer–turbulence interactions,” J. Fluid Mech. 717, 535–575 (2013). 10.1017/jfm.2012.595 [DOI] [Google Scholar]
- Thais L., Mompean G., and Gatski T. B., “Spectral analysis of turbulent viscoelastic and Newtonian channel flows,” J. Non-Newtonian Fluid Mech. 200, 165–176 (2013). 10.1016/j.jnnfm.2013.04.006 [DOI] [Google Scholar]
- Jun Y. and Steinberg V., “Power and pressure fluctuations in elastic turbulence over a wide range of polymer concentrations,” Phys. Rev. Lett. 102, 124503 (2009). 10.1103/PhysRevLett.102.124503 [DOI] [PubMed] [Google Scholar]
- Biferale L., Musacchio S., and Toschi F., “Inverse energy cascade in three-dimensional isotropic turbulence,” Phys. Rev. Lett. 108, 164501 (2012). 10.1103/PhysRevLett.108.164501 [DOI] [PubMed] [Google Scholar]
- Thais L., Gatski T. B., and Mompean G., “Some dynamical features of the turbulent flow of a viscoelastic fluid for reduced drag,” J. Turbul. 13, N19 (2012). 10.1080/14685248.2012.685522 [DOI] [Google Scholar]
- Schumacher J., Sreenivasan K., and Yeung P., “Very fine structures in scalar mixing,” J. Fluid Mech. 531, 113–122 (2005). 10.1017/S0022112005004040 [DOI] [Google Scholar]
- Somandepalli V., Hou Y., and Mungal M., “Concentration flux measurements in a polymer drag-reduced turbulent boundary layer,” J. Fluid Mech. 644, 281–319 (2010). 10.1017/S0022112009992382 [DOI] [Google Scholar]
- Little R., Hansen R., Hunston D., Kim O., Patterson R., and Ting R., “The drag reduction phenomenon. observed characteristics, improved agents, and proposed mechanisms,” Ind. Eng. Chem. Fundam. 14, 283–296 (1975). 10.1021/i160056a001 [DOI] [Google Scholar]
- Zakin J., Ni C., Hansen R., and Reischman M., “Laser doppler velocimetry studies of early turbulence,” Phys. Fluids 20, S85 (1977). 10.1063/1.861763 [DOI] [Google Scholar]
- Klewicki J., Ebner R., and Wu X., “Mean dynamics of transitional boundary-layer flow,” J. Fluid Mech. 682, 617–651 (2011). 10.1017/jfm.2011.253 [DOI] [Google Scholar]