Evolutionary Fate of an Unstable Human Minisatellite Deduced from Sperm-Mutation Spectra of Individual Alleles

Abstract

Although mutation processes at some human minisatellites have been extensively characterized, the evolutionary fate of these unstable loci is unknown. Minisatellite instability is largely germline specific, with mutation rates up to several percent and with expansion events predominating over contractions. Using allele-specific small-pool polymerase chain reaction, we have determined sperm-mutation spectra of individual alleles of the highly unstable human minisatellite CEB1 (i.e., D2S90). We show that, as allele size increases, the proportion of contractions rises from <5% to 50%, with the average size of deletion increasing and eventually exceeding the average size of expansion. The expected net effect of these trends after many generations is an equilibrium distribution of allele sizes, and allele-frequency data suggest that this equilibrium state has been reached in some contemporary human populations.

Mutation is a major driving force in genome evolution. Tandem repeats are ubiquitous elements that account for a substantial proportion of nuclear DNA and include some of the most unstable elements in eukaryotic genomes. Microsatellites (short tandem repeats) and some AT-rich minisatellites are thought to gain and lose repeat units via replication-slippage errors that escape correction by the mismatch-repair system, particularly when hairpinlike secondary structures could form (Levinson and Gutman 1987; Desmarais et al. 1993; Strand et al. 1993; Gacy et al. 1995; Yu et al. 1997; Schlotterer 2000). In contrast, all GC-rich minisatellites characterized to date mutate via a complex meiotic recombination pathway (reviewed in Buard and Jeffreys 1997 and Jeffreys et al. 1997). However, little is known about the evolutionary fate of these elements. A general picture of microsatellite evolution has recently emerged from analyses of several hundred mutations detected among hundreds of dinucleotide- and tetranucleotide-repeat loci, in the course of large-scale genome mapping and legal paternity testing (Ellegren 2000; Xu et al. 2000). On average, short alleles tend to increase, and longer alleles tend to decrease, resulting in an upper limit on allele length and an apparently stable distribution of microsatellite allele sizes. However, these analyses could be confounded by interlocus variation in the direction of mutation, and the same conclusions could be drawn by pooling data from microsatellites with opposite mutational trends.

The locus-specific analysis of mutation parameters requires the scoring of large numbers of mutants for a given tandem repeat. This is not feasible for microsatellites but is possible for tandem repeats, such as unstable GC-rich human minisatellites (Jeffreys et al. 1988; Vergnaud et al. 1991). Although minisatellite mutation is generally biased toward expansion, little information exists on the net repeat-copy–number change per generation. It is this net change that dictates the evolutionary fate of a locus, whether toward infinite growth, extinction by progressive shortening, or equilibrium. We have therefore analyzed allelic variation in sperm-mutation parameters at human minisatellite CEB1, which mutates almost exclusively in the male germline, at rates up to 21% for some alleles and with most alleles short enough to be analyzed for mutation by small-pool PCR of sperm DNA (Vergnaud et al. 1991; Buard and Vergnaud 1994; Buard et al. 1998). Although minisatellite CEB1 is one of the most unstable minisatellites characterized, most features of its instability (including numerical bias toward expansion, paternal bias for the origin of mutation, and a complex mutation process including intra- and interallelic rearrangements [reviewed in Jeffreys et al. 1997]) are found among other GC-rich minisatellites. Since the vast majority of minisatellite rearrangements are not associated with flanking marker exchange (Wolff et al. 1988, 1989; Vergnaud et al. 1991; Jeffreys et al. 1994), it is possible to use single-nucleotide polymorphisms (SNPs) that flank minisatellite arrays to selectively amplify and score, from diluted aliquots of sperm DNA, new length molecules that arise from one allele (Monckton et al. 1994). Allele-specific small-pool PCR (ASSP-PCR) therefore provides information on the mutation rate and the spectrum of individual alleles, allowing analysis of allele-specific variation in mutation rate and expansion bias. These parameters have, in turn, enabled us to simulate the evolution of this minisatellite over many generations and to compare predicted allele-size distributions with those observed in contemporary human populations.

Sperm-mutation spectra of 22 CEB1 alleles were determined by size fractionation followed by ASSP-PCR, for the two largest alleles (88 and 98 repeats), and by direct ASSP-PCR, for 20 alleles ranging in size from 5 to 69 repeats. Mutation rates of only 12 of these 20 alleles have been described elsewhere (Buard et al. 1998). The number of amplifiable molecules being screened for mutation varies from 20,000, for the shortest (5 repeats) allele tested, to 440, for the longest (>20 repeats) alleles. Although small-pool PCR does not produce PCR artifacts at significant rates (Jeffreys et al. 1994; May et al. 1996; Jeffreys and Neumann 1997; Buard et al. 1998; Tamaki et al. 1999; Buard et al. 2000a, 2000b), pilot experiments on alleles >80 repeats in length produced some very large deletions with weak signal intensities, suggesting that they may not correspond to authentic sperm mutants. We therefore used size fractionation of sperm DNA (Jeffreys and Neumann 1997; Buard et al. 2000b) to validate large deletions for an 88-repeat allele and a 98-repeat allele. Two sperm donors were analyzed; each carried long and short CEB1 alleles (i.e., one donor carried CEB1 alleles of 88 and 20 repeats, and the other donor carried CEB1 alleles of 98 and 11 repeats) and was heterozygous at a flanking SNP located 3′ to the minisatellite. Sperm DNA was digested with restriction endonuclease BglI and was separated by gel electrophoresis, and a size fraction was collected that contained the short allele plus any large deletions that were derived from the longer allele. DNA recovery was estimated by ASSP-PCR amplification of the short progenitor allele from limiting dilutions of the fractionated DNA and by Poisson analysis of the resulting proportion of positive reactions (Jeffreys et al. 1994). By use of the alternative allele-specific primer, large deletions derived from the longer allele and of the correct size range for the DNA fraction were recovered by ASSP-PCR. The internal structures of mutants derived from the 98-repeat allele, determined by minisatellite variant repeat PCR (Jeffreys et al. 1991), showed that most (15/17) had resulted unambiguously from large deletion events of the long progenitor allele, rather than from exchanges with the shorter allele (data not shown). The mutation spectra of each of the two longest alleles (one of which is shown in fig. 1) were thus constructed in part from ASSP-PCR analysis for expansions and relatively small deletions and in part from size-fractionation analysis of larger deletions. Similar frequencies have been found for mutant molecules lying within the size range explored by the two approaches (−20 to −30 repeats), suggesting that no bias has been introduced by pooling together these two kinds of data for constructing the whole mutation spectrum.

Figure 1.

Sperm-mutation spectrum of a 98-repeat CEB1 allele. After PCR amplification of 44 diluted aliquots of sperm DNA (each containing ∼12 CEB1 molecules of the 98-repeat allele) by use of universal 5′-flanking primer P9 and allele-specific 3′-flanking primer 384G (Buard et al. 1998), PCR products were electrophoresed in a 40-cm-long 0.7% agarose (Seakem HGT) gel in 0.5× Tris-borate EDTA buffer, were transferred to a nylon membrane, and were hybridized with a CEB1 probe. One hundred ten mutant molecules >2.8 kb (70 repeats) were detected. Sizes were converted to the number of CEB1 repeats (1 consensus repeat = 40 bp). Large deletions with only 5–80 repeats remaining were detected by size-enrichment ASSP-PCR (see text). The frequencies of mutants 70–80 repeats long (scored in both ASSP-PCR and size-enrichment ASSP-PCR) were similar between the two experiments, suggesting that PCR artifacts do not contribute significantly to losses of ⩽28 repeats for this allele. The mutation frequency for each repeat copy number was deduced and merged from these two experiments.

A total of 777 sperm mutants were detected from these 22 alleles. As described elsewhere, the CEB1 sperm-mutation rate increases with array size (Buard et al. 1998), from <0.05%, for the shortest (5 repeats) allele tested, to 21%, for the longest (98 repeats) allele tested (fig. 2a).

Figure 2.

Influence that array length has on the rate and extent of CEB1 expansions and deletions in sperm. a, Mutation rate versus array length. Sperm-mutation rates of 22 CEB1 alleles ranging from 5 to 98 repeats long were determined from small-pool PCR data. Mutation rate (m) increases with array size (s) as m=s/521 (R²=0.4, t=3.63, P<.01). Different models for mutation rate as a function of array size have been chosen for simulating CEB1 evolution, such as m=s/260 (dashed line) for instance. b, Proportion of deletions versus array length. The proportion of deletions d increases with array length (s) as d=0.5-(3.3/s) (R²=0.63, t=5.8, P<.001). c, Mean size of expansion (triangles) or deletion (circles) per mutation event. Fit for mean size of expansion (dashed line) E=(s/50)+3.54 (R²=0.11, t=1.6, P=.12). Fit for mean size of deletion (solid line) D=s/13 (R²=0.67, t=5.8, P<.001).

The mutant molecules consist of 478 expansion events and 299 deletions. This is consistent with the 2:1 gain:loss ratio previously estimated from pedigree mutants (Vergnaud et al. 1991). However, the ASSP-PCR data showed that there was considerable variation in the gain bias among alleles. The proportion of deletion events increases asymptotically with array size, from <5%, for alleles with <10 repeats, to 50%, for arrays with >70 repeats (fig. 2b). For the shortest alleles, the average size of a deletion event is smaller than the average size of expansion. In contrast, the longest alleles show a mean deletion size that exceeds the mean expansion size. The mean deletion size increases with array length approximately four times more rapidly than does the mean expansion size; the two values achieve equality at ∼62 repeats (fig. 2c).

The following findings resolve the apparent paradox between an overall excess of gain mutation events and the relative rarity of long CEB1 alleles:

• 1. Short alleles show a strong bias toward expansion events, whereas large alleles show equal rates of expansion and contraction.
• 2. The net repeat-copy–number change per mutation event is positive for short alleles, null for a critical array length, and negative for large alleles.

Hence, short CEB1 alleles tend to increase, and long CEB1 alleles tend to decrease.

These mutation parameters also enabled us to investigate the evolutionary fate of this minisatellite. For a given allele size, the allele frequency after one generation is given by the frequency of nonmutated alleles plus the frequency of mutant alleles reaching this size. Using the equations derived from the variable parameters of the mutation spectra (see fig. 2 legend), we built a transition matrix to estimate allele frequencies at generation i+1 from allele frequencies at generation i. Irrespective of the starting allele size, the Markov process specified by the transition matrix produced the same stable and virtually unchanging allele-size distribution after 1,000 generations (∼20,000 years) in an infinite population. The existence of such a robust equilibrium size distribution is to be expected, because of the Perron-Frobenius theorem (Moran 1976; Kingman 1977). At equilibrium, the allele-size distribution is unimodal, with maximum at 49 repeats, and is skewed toward longer alleles, with an average allele size of 63.5 repeats (fig. 3a). The robustness of this mathematical model of CEB1 evolution was further tested by experimentation with various alternative curve-fitting choices (for details, see Appendix A). The alteration of the choice of model for the rate of mutation as a function of array size (fig. 2a) affects the time to equilibrium but has a negligible effect on the equilibrium distribution. Also, regression analysis showed that there was little to choose between the best linear curve fit for the average size of expansion (E) relative to array length (R²=0.11; fig. 2c), and a constant mean size of expansion across all alleles (E=4.2). The latter model reduces the predicted incidence of longer (>80 repeats) alleles, thus modestly reducing the average allele size (by 6 repeats) and the variance at equilibrium. A surprisingly critical aspect of the model, however, is the distribution of deletion amounts about its stipulated mean, which we model with a slower-than-exponential decay. If exponential decay is instead used (as it is for expansions), then nearly all alleles of <20 repeats disappear from the equilibrium population. This suggests that there may be two modes of contraction: one that favors small changes, whose relative proportion may conform to a rule of exponential decay; and another that is a cataclysmic mode that produces small alleles more or less independently of the progenitor size and is responsible for populating the short-allele end of the spectrum.

Figure 3.

Allele-size distributions at CEB1. a, Equilibrium distribution simulated using CEB1 sperm-mutation parameters. The model assumes an infinite population of alleles, with arbitrary initial distribution of sizes and with new alleles generated from old by a modified step model of mutation. A transition matrix was built by use of CEB1 rates and sizes of expansions and deletions relative to array size and was used to estimate allele frequencies at generation i+1 from allele frequencies at generation i in an infinite population (for details, see Appendix A). The equilibrium distribution (mean allele size 63.5 repeats), achieved within 1,000 generations, is shown. b, CEB1 allele-size distributions in contemporary European (thick gray line), Indian (dashed line), African (dotted line), and Japanese (thin black line) human populations, determined by Southern blot sizing of 250, 48, 120, and 110 alleles, respectively. Mean allele sizes are 78, 51, 74, and 80 repeats, respectively, and can be compared with mean allele size of the simulated equilibrium distribution (63.5 repeats). European, Japanese, and, in particular, African allele-size distributions are distinct (Kolmogorov-Smirnoff test; P<.005 for all pairwise comparisons). The smoothed plot of the population distributions is obtained by convolution with a triangular-shaped kernel, which approximately imitates gel-measurement uncertainty.

To see whether this predicted equilibrium distribution is seen in humans, we determined CEB1 allele-size distributions in European (British), African (Zimbabwean), Japanese, and Indian populations (fig. 3b). All populations are similar to the simulated size distribution at equilibrium (fig. 3a) with respect to both mean and variance and in having positive skew. This suggests that mathematical simulation by use of sperm-mutation spectra parameters of CEB1 alleles provides an adequate model of minisatellite evolution. It also implies that these four populations are near mutation equilibrium and that their allele distributions will remain stable in the indefinite future, despite the numerical bias toward mutational expansion at CEB1. By Kolmogorov-Smirnoff tests, most of the populations are found to be distinct both from one another and from the simulated equilibrium (6/10 P values <.01), but this may merely signify that the sample sizes are large enough to reveal the genetic drift that inevitably has occurred, which separated the populations to some extent. However, the Zimbabweans are particularly distinct, with a notable tendency toward shorter allele lengths. Further refinement of the evolutionary model and collection of additional population data are required to see whether deviations from the predicted equilibrium distribution signal the existence of alleles with atypical mutational spectra or, instead, whether such abnormal distributions arise from departures from equilibrium in finite populations—for example, by a recent partial fixation of short alleles via a bottleneck that could lead to a temporary reduction in mean allele size.

These balancing effects of minisatellite expansions and deletions are strikingly reminiscent of the general mutational behavior of microsatellites, with the net repeat-copy–number change being positive, for short alleles, and negative, for long alleles (Ellegren 2000; Xu et al. 2000). This similarity is puzzling, because microsatellites and minisatellites are thought to mutate via very different pathways. However, evidence that microsatellites mutate in the human germline by replication slippage remains indirect and inconclusive and is countered both by difficulties in the explanation of how slippage can result in changes in expansion bias with array size (Xu et al. 2000) and by arguments that microsatellite instability may be influenced by relative array sizes in heterozygotes (Amos et al. 1996). In contrast, there is a high affinity of bacterial RecA protein for CA repeats (Dutreix 1997), in addition to a significant correlation between chromosomal distribution of CA repeats and recombination hotspots along human chromosome 22 (Majewski and Ott 2000). It therefore remains possible that recombination may play a role in microsatellite instability in the germline. Both minisatellite and microsatellite contractions could result from replication-based repair of germline-specific double-strand breaks, with minisatellites also gaining repeats via recombination-based repair of the same initiating lesion.

Appendix A: The Markov Model for CEB1 Evolution

Design of the Model

Our model consists of a transition matrix , where t_sj is the probability that the offspring minisatellite array of a progenitor allele with s repeats will have j repeats. The model is constructed in the following stages:

• 1. m(s) = probability of mutation (fig. 2a);
• 2. d(s) = proportion of mutations that are contractions (fig. 2b);
• 3. D(s) = average extent of contraction, given that contraction occurs (fig. 2c);
• 4. E(s) = average extent of expansion, given that expansion occurs (fig. 2c);
• 5. S(s,a) = probability to contract by a repeat units, given that contraction occurs;
• 6. L(s,a) = probability to expand by a repeat units, given that expansion occurs.

Before giving details of the choices for each of the above functions, we will discuss how T is built from them.

The Transition Matrix

An infinite population of CEB1 alleles is described at generation g by the proportions 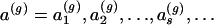with which each allele size, s repeats (s=1,2,…), occurs in the population at that generation. denotes a Markov matrix in which t_sj is the transition probability for an allele of s repeats to mutate to j repeats in one generation. The transition of allele frequencies from one generation to the next is therefore given by 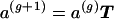. The curves described in figure 2 determine the entries t_sj.

From figure 2a, t_ss=1–m(s). Since d(s) is the probability of deletions under the assumption of mutation, the unconditional probability of deletion is m(s)d(s), which is Σ_j<st_sj. As for the distribution of these deletions as a function of deletion amount, we assume the slower-than-exponential decline that t_sj is proportional to exp[-h(s)(a-1)^0.59], where a=|s-j| is the amount of deletion. Here h(s), h(s)>0, is determined by the condition that the expected deletion amount, given that deletion occurs, is D(s) (see fig. 2c)—that is, that Σ_j<sat_s,(s-a)/[m(s)d(s)]=D(s). Similarly, E(s) and the model assumption that declines exponentially with a-1 determine t_sj for j>s.

In summary, for j<s, t_sj=m(s)d(s)b(s)exp[-h(s)(a-1)^0.59], where b(s) is the normalizing constant 1/{Σ_j<sexp[-h(s)(a-1)^0.59]}, and, for j>s, a function k(s) analogous to h(s) is determined such that , where c(s)=1/{Σ_j<sexp[-k(s)(a-1)]}.

Running the Model

We begin with an arbitrary allele-frequency distribution , such as , 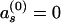for s≠40. The allele distributions at successive generations are given by 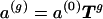. An equilibrium distribution a (such that a=aT), independent of 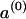, is effectively attained within 1,000 generations.

Determining the Model Parameters

This section explains how the data of observed mutation features for 22 progenitor alleles of various sizes are used to select the form and parameters of each of the six functions that constitute the evolution model.

Mutation rate m(s)

A linear regression m(s)=as+b gives b=1/75, but there is no evidence from the data that b≠0 (P=.45) (fig. 2a). If b=0, then the linear fit becomes m(s)=s/521, with considerable random variation (R²=0.42). A quadratic fit m(s)=(s/303)-(s²/50,000) explains the data only a little better (R²=0.52), at the expense of an extra parameter. A quadratic model is illogical, anyway, since it says that the mutation rate declines for s>82, becomes null for s=165, and is even negative for s>165. Therefore, we choose the simple proportional model m(s)=s/521.

Contraction proportion d(s)

Contractions and expansions approach equal frequency for large sizes, suggesting a model d(s)=0.5-(k/s) for contractions—and e(s)=0.5+(k/s) for expansions (fig. 2b). A linear regression of d(s)-0.5 as a function of 1/s gives a constant term of only 1/130; moreover, a P value of .8, as well as the attraction of symmetry, suggests that we omit the extra constant. Therefore, we obtain d(s)=0.5-(3.28/s), with R²=0.6. For s⩽6, we set d(s)=0.

Average contraction D(s)

A linear regression gives D(s)=0.67+(s/15.4), for which R²=0.71 (fig. 2c). However, the proposition that the constant term is not zero is only weakly supported by the data (P=.17), and D(s)=s/13 explains the data nearly as well (R²=0.67). Therefore, we choose the simpler formula D(s)=s/13.

Average expansion E(s)

We choose the best linear regression E(s)=3.54+(s/50) to model E(s) (fig. 2c). It may (P=.12) be that the linear term is unnecessary; the constant fit E(s)=4.2 fits the data only slightly less well.

Distribution S(s,a) of contraction amounts

From the data, the mutation amount a=|s-j| tends to be small (e.g., we know from sperm-mutation analysis data that >80% of minisatellite mutation events are expansions or contractions of <6 repeats; see, e.g., fig. 1). This suggests a model of the form P(an a-repeat-unitcontraction) proportional to k(s)^a-1, where 0<k<1. However, such a model does not account for the occasional contraction by a large amount; therefore, we choose a more elaborate model, wherein decay of mutation probabilities with a-1 is slower than exponential. One way to accomplish this is to replace a-1 by (a-1)^β for some β<1.

For any given β, for each s, the k(s) value is constrained by the condition that the mean contraction amount must be D(s), and, thus, an expected number of contractions S(s,a) for each s and each a can be computed. The best-fit estimate for β was obtained as that β value that gives the best least-squares fit of S(s,a). The value obtained is β=0.59.

Distribution L(s,a) of expansion amounts

For expansions, any β value in the range 0.9<β<1.2 gives, within two decimal places, an equally good fit to the observed expansion amount. Therefore, by Occam’s razor—and since β>1 seems biologically implausible (since it would suggest an antimutational spring that makes a third step of mutation, given that a second step has occurred, less likely than a second step of mutation, given that a mutation has occurred)—we omit the extra parameter β and assume exponential decline.

Robustness of the Model

In this section, we discuss the relationship between various model assumptions and the equilibrium distribution. Table A1 details the effects that these variations have on the equilibrium.

Table A1.

Main Features of Various Simulated Distributions at Equilibrium and Size Distributions Observed in Populations

							Frequency for s
	Mean	s	Skew	Kurtosis	Peak	Mode	<10	<20
Simulation:
Standard model	63.5	32	1.15	5.4	49	58	.8%	3.4%
m(s)=s/260	63.5	32	1.15	5.4	49	58	.8%	3.4%
m(s)=c(s)(s/521)a	61.5	32.8	.98	5.1	49	57	3.4%	6.8%
β=1	67.3	27.9	1.19	5.5	54	62	…	.3%
m(s)=c(s)(s/521)a and β=1	67.3	27.9	1.19	5.5	54	62	.01%	.3%
β=0.59b	59.7	34	1.18	5.8	45	54	3.7%	7.7%
E(s)=4.2	57	24	.6	3.7	…	…	…	…
d(s)=0.47-(2.96/s)	60	32.3	.99	5.1	47	56	3.5%	7.2%
D(s)=0.67-(s/15.4)	66.3	35	.17	5.4	…	…	…	…
Population:
African	51.4	28.7	.93	4.1	51	48	2.5%	10%
European	78	47.3	1.78	8.6	93	70	1.2%	4%
Indian	80.4	59.7	2.23	8.9	47	72	2.1%	6.3%
Japanese	63.7	29.6	.7	3.9	34	60	1.8%	4.5%

^aWhere c(s)=1/6 if s<3, increasing linearly to c(s)=1 for s>20.

^bThis parameter was introduced for expansions also.

Mutation probability as a function m(s) of progenitor size

The equilibrium distribution is not sensitive to the choice of function m(s). Multiplication of m(s) by a constant affects the time to equilibrium but has no perceptible effect on the distribution. In light of this point, it is also not surprising that the alteration of the shape of m(s) in other ways—for example, by imposing m(s) as m(s)=min[(s/521),0.2]—also has little or no effect on the equilibrium distribution.

Proportion d(s) of mutations that are contractions

Although the process for selecting d(s) that is described above seems compelling, to test the sensitivity of the model to d(s), we test the effect of the model d(s)=0.47-[(constant)/s]. The effect that this has is the slight (counterintuitive) decrease of the mean allele size and the significant increase of the proportion of small alleles (s<20).

Average amount D(s) of contraction, assuming that contraction occurs

Compared to our selected model, the alternate model D(s)=0.67+(s/15.4) slightly increases the mean size (fig. 2c).

Expansion amount E(s), assuming that expansion occurs

Compared to our selected model, the alternate model E(s)=4.2 (fig. 2c) modestly decreases the mean size.

Distribution of contraction amounts

The omission of β from the model (i.e., the choice of a β value equal to 1) slightly increases the mean allele size and considerably reduces the incidence of small alleles. The choice of either a β value <1 or a complicated model of average mutation rate seems necessary to explain the plethora of small alleles that are observed in collected population samples.

Distribution of expansion amounts

For symmetry, we consider introducing the parameter β=0.59 for expansions, as has been introduced for contractions. This change would seem to encourage large expansion events, but, paradoxically, it modestly decreases the mean allele size at equilibrium and significantly increases the number of small alleles.