Abstract
Recent advances in single-cell genomics provide an alternative to largely gene-centric metagenomics studies, enabling whole-genome sequencing of uncultivated bacteria. However, single-cell assembly projects are challenging due to (i) the highly nonuniform read coverage and (ii) a greatly elevated number of chimeric reads and read pairs. While recently developed single-cell assemblers have addressed the former challenge, methods for assembling highly chimeric reads remain poorly explored. We present algorithms for identifying chimeric edges and resolving complex bulges in de Bruijn graphs, which significantly improve single-cell assemblies. We further describe applications of the single-cell assembler SPAdes to a new approach for capturing and sequencing “microbial dark matter” that forms small pools of randomly selected single cells (called a mini-metagenome) and further sequences all genomes from the mini-metagenome at once. On single-cell bacterial datasets, SPAdes improves on the recently developed E+V-SC and IDBA-UD assemblers specifically designed for single-cell sequencing. For standard (cultivated monostrain) datasets, SPAdes also improves on A5, ABySS, CLC, EULER-SR, Ray, SOAPdenovo, and Velvet. Thus, recently developed single-cell assemblers not only enable single-cell sequencing, but also improve on conventional assemblers on their own turf. SPAdes is available for free online download under a GPLv2 license.
Key words: bacterial assembly, chimeric reads, de Bruijn graph, multiple displacement amplification (MDA), single cell
1. Introduction
The standard techniques for next generation sequencing (NGS) require at least a million bacterial cells to sequence a genome. Since most bacteria cannot be cultivated in the laboratory (Rappe and Giovannoni, 2003; Tringe and Rubin, 2005) and thus cannot be sequenced, much of the bacterial diversity remains below the radar of NGS projects. The “microbial dark matter” describes microbes and even entire bacterial phyla that have yet to be cultured and sequenced. For example, only a fraction of the >10,000 bacterial species in the human microbiome have been sequenced (Nelson et al., 2010; Wylie et al., 2012). Single-cell sequencing (Stepanauskas, 2012; Lasken, 2012) has recently emerged as a powerful approach to complement largely genecentric metagenomic data with whole-genome assemblies of uncultivated organisms.
Currently, multiple displacement amplification (MDA), pioneered by Roger Lasken and colleagues (Lasken, 2007), is the dominant approach to whole-genome amplification prior to single-cell sequencing. High throughput single-cell genomics pipelines are well established at various centers including the Single Cell Genomics Center at Bigelow Laboratory, DOE Joint Genome Institute, and J. Craig Venter Institute. The single-cell sequencing pipelines typically generate many random single-cell genomes, then PCR (polymerase chain reaction) and sequence their 16S rRNA genes for identification and target selection for whole-genome sequencing. Genome assembly of reads from MDA-amplified genomes is, however, challenging because of highly nonuniform read coverage, as well as elevated levels of chimeric reads and read pairs. Despite these challenges, recent computational advances (Chitsaz et al., 2011; Peng et al., 2012; Bankevich et al., 2012) have opened the possibility of sequencing the genome of any bacterial cell. In particular, the SPAdes assembler (Bankevich et al., 2012) was recently used to sequence the pathogens Porphyromonas gingivalis (McLean et al., 2013b) and Chlamydia trachomatis (Seth-Smith et al., 2013) from bacterial cells extracted from a hospital environment and clinical samples, respectively.
However, sequencing the vast majority of bacteria in the human microbiome still remains a distant goal. The bottleneck is that it is unclear how to isolate and capture low-abundance cells from a complex sample. While there is a great interest in investigating the rare bacterial species in the human microbiome, currently there is no technology for efficiently and comprehensively capturing very low-abundance cells of such complex samples and for surveying the diversity as a whole. Indeed, capturing and sequencing even 100,000 randomly chosen single cells from the human microbiome is unlikely to comprehensively sample the bacterial diversity, since many of the >10, 000 species in the human microbiome are underrepresented (Huttenhower et al., 2012; Li et al., 2012). Even if a more targeted approach is being applied, sequencing 100,000 single cells is prohibitively expensive. The question thus remains of how to sample bacterial diversity in a more economical way.
McLean et al. (2013a) recently developed a new approach for analyzing the “microbial dark matter” based on forming random pools of single flow-sorted cells and sequencing all cells in the resulting mini-metagenome at once. These pools only contain a small number of cells as opposed to metagenomics samples, which often contain billions of cells from different species. Since the experimentally formed mini-metagenome has lower complexity than the original metagenome, the assembly of individual genomes from such mini-metagenomes may be more feasible than the assembly of entire metagenomes.
Assembly of mini-metagenome MDA reads is even more challenging than for single-cell MDA reads and thus requires additional algorithmic developments. From an algorithmic perspective, mini-metagenome sequencing can be thought of as sequencing an unusually large bacterial genome (formed by all genomes within a mini-metagenome) with extremely nonuniform coverage. Moreover, the elevated number of chimeric reads and read pairs (typical for single-cell sequencing) is likely to present an even more difficult challenge in the case of mini-metagenomes, where intergenomic chimeric reads (resulting from concatenated fragments of different genomes) can be formed.
This article addresses computational challenges arising in single-cell and mini-metagenome sequencing. This includes detection of chimeric edges in de Bruijn graphs (Section 2 and Appendix A), analyzing complex bulges (Section 3 and Appendix B), and estimating genomic distances by aggregating read-pair information (Section 4 and Appendix C). We incorporate these algorithmic developments into the SPAdes assembler (Bankevich et al., 2012) and demonstrate (Section 5) that it improves on existing single-cell sequencing tools E+V-SC (Chitsaz et al., 2011) and IDBA-UD (Peng et al., 2012). SPAdes also performs well on standard (multicell) projects. (We refer to a conventional sequencing project using cultivated strains as multicell sequencing.) In particular, we show that it improves on A5 (Tritt et al., 2012), ABySS (Simpson et al., 2009), CLC,1 EULER-SR (Chaisson et al., 2009), Ray (Boisvert et al., 2010), SOAPdenovo (Li et al., 2010), and Velvet (Zerbino and Birney, 2008) in multicell bacterial assemblies. In Section 5.4, we also benchmark SPAdes on simulated mini-metagenomes obtained by mixing various single-cell read datasets and investigate the computational limits of mini-metagenome sequencing for assessing low-abundance bacterial species.
2. Identifying Chimeric Edges in De Bruijn Graphs
MDA often results in chimeric reads (formed by concatenating fragments from different regions of the genome) and chimeric read pairs (formed by two reads sampled from distant regions of the genome). See Lasken and Stockwell (2007), Chitsaz et al. (2011), and Woyke et al. (2009) for the extent of chimeric reads and read pairs in single-cell projects. Chimeric reads result in chimeric edges in de Bruijn graphs. Single-cell projects often result in a large increase in the number of chimeric edges as compared to standard assembly projects. Most existing assemblers were not designed to cope with this dramatic increase in the number of chimeric edges.
2.1. Double-stranded de Bruijn graphs
Let DB(Genome, k) be the de Bruijn graph (Compeau et al., 2011) of a circular genome, Genome, and its reverse complement, Genome′, where vertices and edges correspond to (k − 1)-mers and k-mers, respectively. Genome and Genome′ each traverse a cycle in this graph; these two cycles form the genome traversal of the graph. If a genome has multiple chromosomes or linear chromosomes, the genome traversal of DB(Genome, k) may consist of multiple paths or cycles. The genomic multiplicity of an edge is the number of times the traversal passes through this edge. We often work with condensed graphs (Bankevich et al., 2012), where each edge is assigned a length (in k-mers), and the length of a path is the sum of its edge lengths (rather than the number of edges).
2.2. Chimeric edges in de Bruijn graphs
Let DB(Reads, k) be the de Bruijn graph constructed from a set of reads, Reads, from Genome and their reverse complements. In the idealized case with full coverage of Genome and no read errors, the graphs DB(Reads, k) and DB(Genome, k) coincide; however, in reality these graphs differ because of coverage gaps and read errors. Edges in DB(Reads, k) may correspond to genome fragments (correct edges) as well as arise either from errors in reads or from chimeric reads (false edges).2
While in DB(Genome, k) the genome traversal consists of a pair of cycles, in DB(Reads, k) these cycles may be broken into multiple paths. The genome traversal defines the genomic multiplicities of edges in DB(Reads, k) (or the condensed graph).3 Since false edges are not traversed by the genome traversal in DB(Reads,k), they have genomic multiplicity zero.
Assemblers use various algorithms to iteratively remove false edges and transform the de Bruijn graph DB(Reads, k) into a smaller assembly graph. In SPAdes (and most other assemblers), all such transformations are done simultaneously on both forward and complementary vertices and edges. We use the notation DB+ (Reads, k) to denote the current assembly graph at any intermediate stage of assembly, and DB*(Reads, k) to denote the final assembly graph.
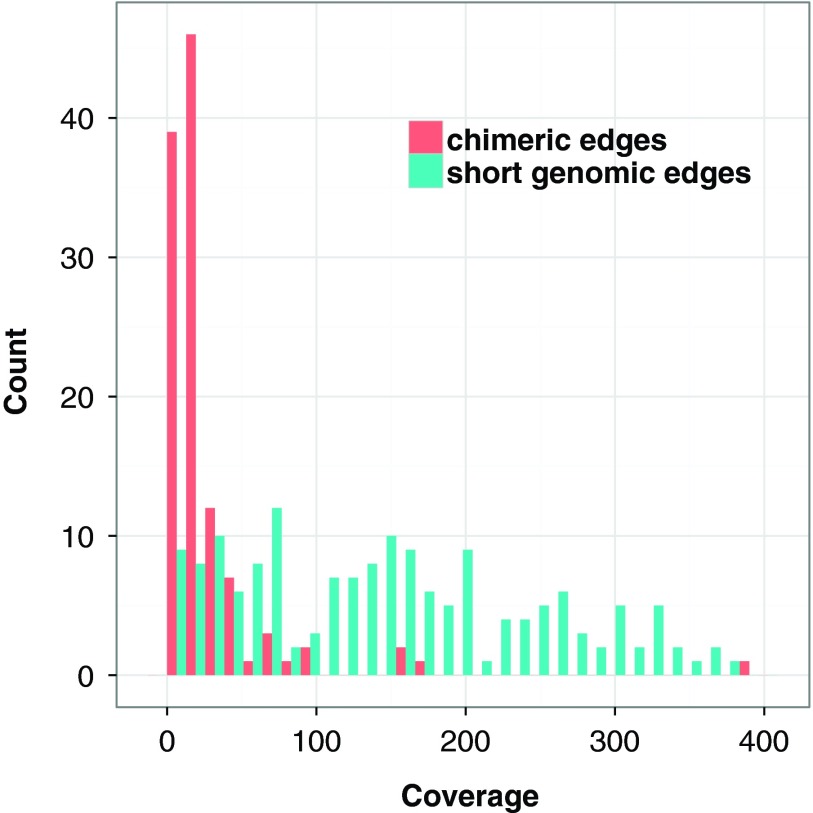
While most false edges correspond to easily detectable subgraphs, called tips and bulges, some form chimeric edges, which are hard to identify. Chimeric edges arise from chimeric reads, which are abundant in single-cell datasets. While chimeric edges in the de Bruijn graph represent a major obstacle to constructing long contigs, in standard (multicell) assembly datasets, chimeric edges usually have low coverage and thus are easily identified as false and removed by the conventional assemblers. However, this approach does not work for single-cell datasets, where coverage is nonuniform and the level of chimerism is high (Lasken and Stockwell, 2007; Chitsaz et al., 2011). For such datasets, low coverage does not characterize false edges since many correct edges also have low coverage (Fig. 1). For example, there are 117 chimeric edges in in the graph DB+ (Reads, 55) constructed for the single-cell E. coli dataset ECOLI-SC, but only 2 chimeric edges in in the graph DB+ (Reads, 55) constructed for the multicell E. coli dataset ECOLI-MC (see Results for the description of the ECOLI-SC and ECOLI-MC datasets).
FIG. 1.
Coverage of chimeric and short genomic edges in the de Bruijn graph of the ECOLI-SC single-cell dataset (described in the Results section). The heights of red columns in the histogram give the number of occurrences of chimeric edges in the graph in each coverage bin. The heights of the blue columns give the number of occurrences of short (length less than n = 250) genomic edges in the graph in each coverage bin.
Our chimeric edge identification procedure is based on the following assumptions for bacterial genomes: (i) since chimeric edges in the condensed de Bruijn graphs are typically short,4 we assume that edges longer than n have genomic multiplicity of at least 1, and (ii) since edges longer than N (referred to as long edges) in the condensed de Bruijn graph tend to have genomic multiplicity 1, we assume that all long edges have genomic multiplicity 1.5 In our experience, the parameters n = 250 and N = 1500 work well across many bacterial genomes we analyzed.
Since genomic multiplicities of edges in DB+ (Reads, k) are unknown, we attempt to bound them. An edge e with genomic multiplicity bounded by clower(e) from below and by cupper(e) from above has capacity (clower(e), cupper(e)).
Ideally, an edge with genomic multiplicity m should be assigned capacity (m, m). In the absence of information about exact genomic multiplicities, we assign capacities to all edges in the condensed graph of DB+(Reads, k) as follows, where the second and third categories are dictated by assumptions (i) and (ii) above:
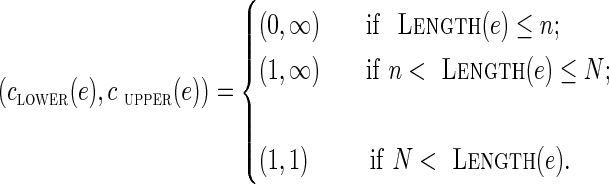 |
To simplify this presentation, we assume that an assembly algorithm successfully removes all (or the vast majority of) bulges and tips, resulting in an intermediate assembly graph DB+ (Reads, k), but fails to remove chimeric edges. Thus, the search for chimeric edges amounts to finding edges of genomic multiplicity zero.
2.3. Chimeric edges and circulations in networks
A graph with capacity constraints on the edges is referred to as a network. Given a vertex v and a function f on edges of a network G, we define 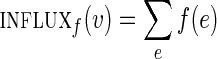 , where the sum is taken over all incoming edges e of the vertex v. We define outfluxf(v) similarly. A function f is called a circulation in the network G if influxf(v) = outfluxf(v) for each vertex v in G, and clower(e) ≤ f (e) ≤ cupper(e) for each edge e in G.
, where the sum is taken over all incoming edges e of the vertex v. We define outfluxf(v) similarly. A function f is called a circulation in the network G if influxf(v) = outfluxf(v) for each vertex v in G, and clower(e) ≤ f (e) ≤ cupper(e) for each edge e in G.
The circulation problem is to find a circulation in a network (Ford and Fulkerson, 1962). Genomic multiplicities define a circulation in the network DB+ (Reads, k) with capacity constraints. There are usually multiple circulations in this network, and we do not know which of them corresponds to the actual genomic multiplicities. However, if an edge e has f (e) = 0 in all circulations, then it must be a false edge and in most cases represents a chimeric edge.6 A polynomial-time algorithm for finding all such edges in the network is described in appendix section 7 a.1. We remark that this strategy is based on the assumption that the genome corresponds to a cycle in the graph, which often fails for real data. Since in DB+ (Reads, k) the genome traversal may be broken into multiple subpaths, a circulation in it may not even exist. To address this complication, we break the network into smaller subnetworks and analyze their subcirculations.
The operation of breaking an edge (v, w) in a graph G removes (v, w) from G; adds two new vertices v* and w* (called the sink and the source, respectively); and adds two new edges (v, v*) and (w*, w) with the same capacity as the edge (v, w). Given a weighted graph G and a positive integer t, we define Gt as the graph obtained from G by breaking all edges longer than t. To break the de Bruijn graph into subnetworks, we break all long edges (Fig. 2).7 After this transformation, the graph DB+ (Reads, k) is typically decomposed into many connected components. For the ECOLI-SC dataset described in the Results section, the graph is decomposed into 114 nontrivial connected components (containing more than one vertex).
FIG. 2.
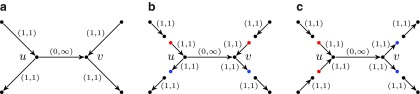
Example of breaking long edges in an assembly graph. (a) Subgraph of assembly graph where the four diagonal edges are long edges, while the horizontal edge in the center is not long. (b) Result of breaking the four long edges contains a connected component (in the center) with two sources (red vertices) and two sinks (blue vertices). The capacities of the edges starting (ending) at the newly formed sources (sinks) are inherited from the capacities of the broken edges. (c) Result of breaking long edges in a subgraph similar to the subgraph in (c) but with different directions on some edges.
A circulation (genome traversal) in DB+ (Genome, k) defines a flow (Ford and Fulkerson, 1962) between sources and sinks of every connected component of 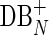 (Genome, k) satisfying the capacity constraints. Similarly to DB(Genome, k), for many components in DB+(Reads, k), the genome traversal also defines a flow satisfying the capacity constrains. Thus, the search for chimeric edges in DB+(Reads, k) can be performed independently in each component.8
(Genome, k) satisfying the capacity constraints. Similarly to DB(Genome, k), for many components in DB+(Reads, k), the genome traversal also defines a flow satisfying the capacity constrains. Thus, the search for chimeric edges in DB+(Reads, k) can be performed independently in each component.8
Many components have a particularly simple structure with two sources and two sinks (Fig. 2b and c). The only flow that satisfies the capacity constraints in Figure 2b (resp., Fig. 2c) assigns flow 0 (resp., flow 2) to the edge (u, v). Thus (u, v) is classified as chimeric in Figure 2b and as correct in Figure 2c.
Unfortunately, the above procedure fails for some connected components (e.g., when the outgoing edge from vertex v in Fig. 2a is missing). Furthermore, such components tend to be large. For example, when assembling reads from a single E. coli cell (the ECOLI-SC dataset), the procedure fails only for 10% of all components, but these components contain most (52%) vertices of the graph. Below we describe an approach to identify chimeric edges in such components.
2.4. Chimeric edges and critical cut-sets
Given a subset U of vertices in the graph, the cut-set, denoted cut(U), is the set of all edges (u, v) in the graph such that 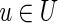 and
and 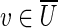 (where
(where 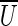 denotes the set of vertices of the graph that do not belong to U). We define clower(U) [resp., cupper(U)] as the sum of lower (resp., upper) capacities of all edges from cut(U). A cut-set cut(U) is balanced if
denotes the set of vertices of the graph that do not belong to U). We define clower(U) [resp., cupper(U)] as the sum of lower (resp., upper) capacities of all edges from cut(U). A cut-set cut(U) is balanced if 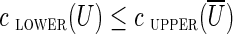 and unbalanced otherwise. According to Hoffman's Circulation Theorem (Ford and Fulkerson, 1962), a circulation exists if and only if every cut-set in the network is balanced.
and unbalanced otherwise. According to Hoffman's Circulation Theorem (Ford and Fulkerson, 1962), a circulation exists if and only if every cut-set in the network is balanced.
A cut-set cut(U) is critical if 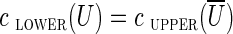 . We remark that if cut(U) is critical, then all edges from
. We remark that if cut(U) is critical, then all edges from 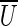 to U should be long, since otherwise
to U should be long, since otherwise 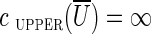 (all edges that are not long have upper capacity
(all edges that are not long have upper capacity  ).
).
It is easy to see that for a critical cut-set cut(U), all edges 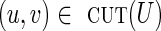 must have genomic multiplicity equal to clower(u, v), while all edges
must have genomic multiplicity equal to clower(u, v), while all edges 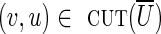 must have genomic multiplicity equal to cupper(v, u). Indeed, if the lower capacity of any edge
must have genomic multiplicity equal to cupper(v, u). Indeed, if the lower capacity of any edge 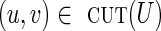 is increased by 1, the cut-set would become unbalanced [as clower(U) + 1 > cupper(U)], implying that no circulation exists. Similarly, the upper capacity of any edge
is increased by 1, the cut-set would become unbalanced [as clower(U) + 1 > cupper(U)], implying that no circulation exists. Similarly, the upper capacity of any edge 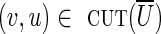 cannot be decreased, implying that the genomic multiplicity of (v, u) must be equal to cupper(v, u). In particular, for a critical cut-set cut(U), all crossing edges
cannot be decreased, implying that the genomic multiplicity of (v, u) must be equal to cupper(v, u). In particular, for a critical cut-set cut(U), all crossing edges 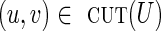 with clower(u, v) = 0 must be chimeric.
with clower(u, v) = 0 must be chimeric.
We apply the same criterion to unbalanced cuts, which also occur in real data. Namely, we identify all edges crossing an unbalanced cut-set as chimeric. Indeed, if such edges had lower capacity larger than 0, the cut-set would be even more unbalanced.
SPAdes analyzes only certain types of critical cut-sets that are common in de Bruijn graphs of reads (see appendix section 7.2).
2.5. Interstrand chimeric edges
For an edge (u, v) connecting genomic (k − 1)-mers u and v at genomic coordinates i and j, respectively, we define the offset as the distance |j − i| between u and v in the genome. An edge is called an interstrand edge if u and v belong to the opposite strands of the genome.
Due to artifacts of MDA (Lasken and Stockwell, 2007), the de Bruijn graph typically contains many interstrand chimeric edges with small offsets (Fig. 3). For example, in graph DB+(Reads, 55) constructed for reads from the ECOLI-SC dataset, after doing initial simplifications including removing condensed edges with average coverage below 10 that satisfy some additional length and topology conditions, there are still 117 chimeric connections. Of those, 113 are interstrand chimeric connections, and 109 of the interstrand chimeric connections have offsets smaller than 50000 bp.
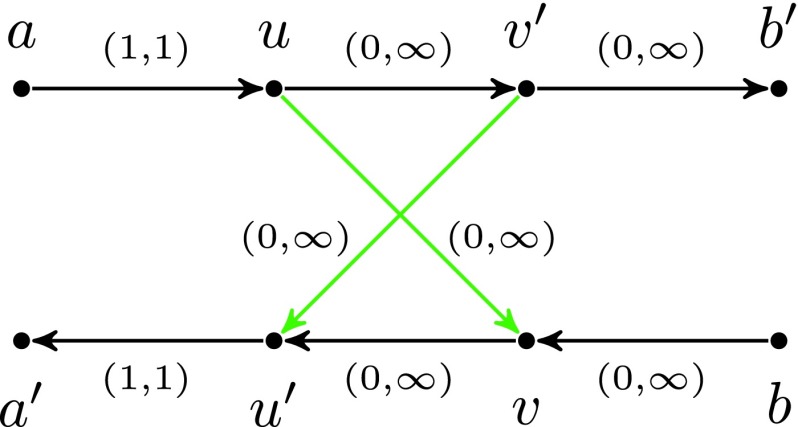
FIG. 3.
Interstrand edge (u, v) and its complementary edge, (v′, u′), both shown in green. The horizontal paths correspond to the two opposite DNA strands in a genome. Capacities are listed on each edge.
For every vertex v in the de Bruijn graph of a doubly stranded genome, there exists a complementary vertex denoted v′. Similarly, for every (condensed) edge (u, v), there exists a complementary edge (v′, u′). Note that the genomic multiplicity of (u, v) is the same as for (v′, u′), and their capacities are also the same since capacities are assigned based on edge lengths.
A cut-set cut(U) is semi-critical if 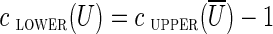 . It is easy to see that if both (u, v) and its complementary edge (v′, u′) have lower capacities 0 and belong to the same semi-critical cut-set cut(U), they can both be classified as chimeric. Indeed, if the lower capacity of these edges increased from 0 to 1, the semi-critical cut would become unbalanced
. It is easy to see that if both (u, v) and its complementary edge (v′, u′) have lower capacities 0 and belong to the same semi-critical cut-set cut(U), they can both be classified as chimeric. Indeed, if the lower capacity of these edges increased from 0 to 1, the semi-critical cut would become unbalanced 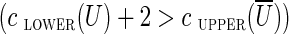 , implying that no circulation exists. Thus, each semi-critical cut identifies each pair of complementary crossing edges as chimeric. We noticed that semi-critical cuts are often triggered by interstrand chimeric edges with small offsets.
, implying that no circulation exists. Thus, each semi-critical cut identifies each pair of complementary crossing edges as chimeric. We noticed that semi-critical cuts are often triggered by interstrand chimeric edges with small offsets.
Consider the situation shown in Figure 3, where edge (a, u) has capacity (1, 1) and edge (v′, b′) has capacity (0, ∞ ). If the edge (u, v′) has lower capacity 1, then the cut-set cut({u}) is critical, implying that the edge (u, v) is chimeric. However, if (u, v′) has lower capacity 0, then the cut-set cut({u}) is not critical and does not provide evidence that the edge (u, v) is chimeric. But, in this case, the cut-set cut({u, v′}) is semi-critical with two complementary crossing edges (green edges in Fig. 3); thus, the two green edges are classified as chimeric.
An additional complication arises if a part of the genome located between chimeric junctions contains repeats. In this case, instead of a single edge (u, v′), the graph may contain a path with multiple edges from u to v′. SPAdes uses a heuristic to resolve such situations: We search for a path from u to v′ and even if the path contains more than one edge, we consider edge (u, v) chimeric and remove it.
3. Removing Complex Bulges
3.1. Bulges and bulge corremoval
Errors in reads often result in two short paths between the same two vertices in the de Bruijn graph, where the two paths have roughly the same length and represent similar sequences. Such pairs of paths may aggregate into larger subgraphs called bulges (see Fig. 4a). Assemblers use various bulge removal algorithms (and additional steps) to transform the de Bruijn graph DB(Reads, k) into a smaller assembly graph DB*(Reads, k). While they remove the vast majority of bulges, they fail to remove some complex bulges. The number of such complex bulges varies widely across various genomes. However, we noticed that even a small number of complex bulges may significantly reduce assembly quality, since such bulges confuse the repeat, resolving algorithms that attempt to increase the contig lengths by using paired reads.
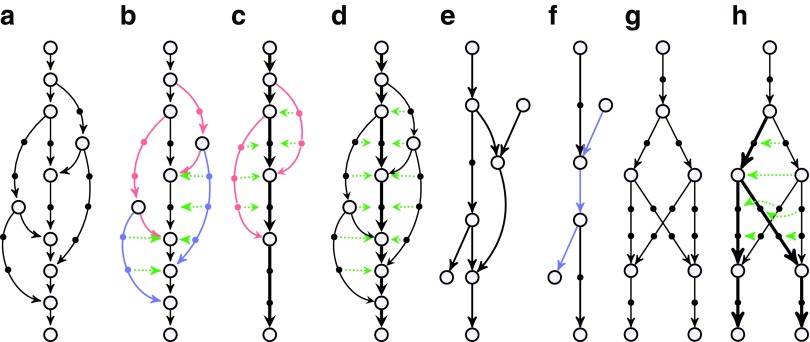
FIG. 4.
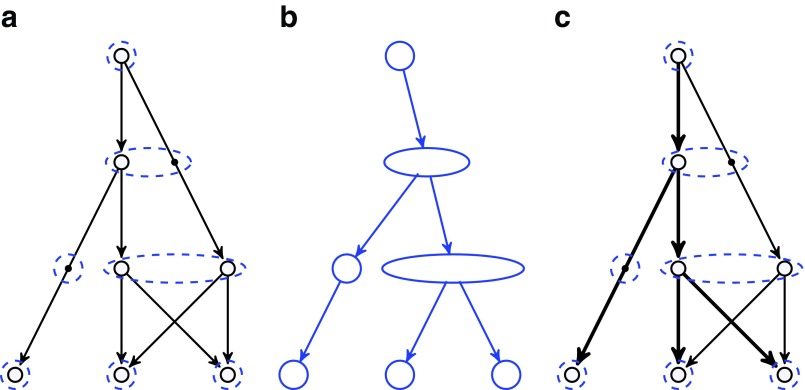
Illustration of bulge removal algorithms. For illustrative purposes, the vertices of the condensed graph are shown in white; the additional vertices present in the uncondensed graph are shown as small solid circles in the color (black, red, or blue) of the condensed edge on which they lie. Dotted green arrows indicate projection operations (not graph edges). (a–c) Algorithm A: The bulge corremoval algorithm from Bankevich et al. (2012). (a) A bulge in the de Bruijn graph. In (b), the blue edges have alternative paths while the red edges do not have alternative paths. After applying the bulge corremoval procedure to the blue edges, graph (b) is transformed into graph (c). There are now alternative paths for red edges in (c), and the graph is further transformed into a single condensed edge representing the bold path in (c). (e–f) Algorithm B: Merging paths instead of projecting paths. Merging two paths in (e) results in a graph (f) with an artificial (blue) path violating condition (ii). (g–h) Algorithm C: Blob corremoval. Complex bulge (g) is not removed by the bulge corremoval procedure from Bankevich et al. (2012). Applying the new “blob corremoval procedure” to blob (g) simplifies it via the projections shown in (h). Thick edges denote the tree to which we project the blob. The blob corremoval procedure may also be applied to (a) to directly simplify it to a single condensed edge in one step via the projections shown in (d); this achieves the same result as bulge corremoval did with two sets of projections, (b) and (c).
In this section, we describe an algorithm for removal of complex bulges that evade the “bulge corremoval” algorithm from Bankevich et al. (2012). One approach to removing bulges is to map the de Bruijn graph onto a smaller graph. SPAdes tries to find a mapping that satisfies the following conditions:
(i) Every path in the de Bruijn graph maps to a path in the assembly graph.
(ii) For every path ρ in the assembly graph, there exists a path in the de Bruijn graph that maps onto ρ.9
Some bulge removal algorithms either do not explicitly map the de Bruijn graph onto the assembly graph or use mappings that may violate conditions (i) and/or (ii). For example, they may find a bulge formed by two paths in the de Bruijn graph and either remove one of the paths or merge these paths into a single one, without considering the impact on other edges incident to these paths. Removing one of the paths may lead to deterioration of assemblies, since important information (along with some correct paths) may be lost. Merging the paths may introduce artificial paths into the assembly graph, violating condition (ii) (see Fig. 4e and f).
SPAdes (Bankevich et al., 2012) introduced the bulge corremoval procedure, which satisfies conditions (i) and (ii). For each edge (u, v) (with length below a threshold) in the condensed de Bruijn graph, SPAdes searches for a path from u to v of length approximately equal to the length of (u, v). If such an alternative path exists, the two paths P and (u, v) form a simple bulge. To remove a simple bulge, the edge (u, v) is projected onto this path and is removed afterward. Applied iteratively,10 the bulge corremoval strategy eliminates the vast majority of bulges. Figure 4a–c illustrates how a bulge with multiple paths is simplified by this strategy. However, for some bulges (such as Fig. 4g), no edge in the bulge has an alternative path, implying that the algorithm from Bankevich et al. (2012) will not be able to remove such bulges. Below we describe an algorithm satisfying conditions (i) and (ii) for removing the majority of the remaining complex bulges.
3.2. Blob corremoval
Let G be a directed acyclic graph (DAG) with vertex set V and edge set E. G may be a multigraph. For vertices v and w in G, we define v ≺ w if there exists a directed path from v to w in G. Every mapping f: V → V induces a mapping f: E → E such that for an edge e = (u, v), we have f (e) = (f (u), f (v)) (though in the case of a multigraph, there may be multiple edges of this form to select). A mapping f: V → V is called a projection if (1) for every vertex 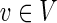 , we have f (f (v)) = f (v), (2) for every pair of vertices v and w, if v ≺ w then f (v) ≺ f (w), and (3) for every edge e, f (f (e)) = f (e).
, we have f (f (v)) = f (v), (2) for every pair of vertices v and w, if v ≺ w then f (v) ≺ f (w), and (3) for every edge e, f (f (e)) = f (e).
A projection f defines the induced DAG Gf on the vertex set Vf = f (V). Clearly, for every path 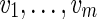 in G, there exists at least one path in Gf that traverses the projected vertices
in G, there exists at least one path in Gf that traverses the projected vertices 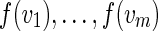 in Gf. We limit our attention to projections of DAGs onto directed trees (i.e., projections f such that Gf is a directed tree) and additionally require that every path and its projection have similar lengths. Figs. 4d and 4h show the directed trees and projections of DAGs shown in Figs. 4a and 4g.
in Gf. We limit our attention to projections of DAGs onto directed trees (i.e., projections f such that Gf is a directed tree) and additionally require that every path and its projection have similar lengths. Figs. 4d and 4h show the directed trees and projections of DAGs shown in Figs. 4a and 4g.
Breaking edges longer than t in the assembly graph DB+(Reads, k) results in a graph 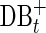 (Reads, k) that typically consists of many connected components. A blob is a component of
(Reads, k) that typically consists of many connected components. A blob is a component of 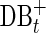 (Reads, k) that is a DAG with a single source and one or more sinks. SPAdes analyzes blobs in DB+(Reads, k) and for each blob, attempts to find a directed tree (with root at the source and leaves at the sinks of the blob) such that there exists a projection of the blob onto this tree.
(Reads, k) that is a DAG with a single source and one or more sinks. SPAdes analyzes blobs in DB+(Reads, k) and for each blob, attempts to find a directed tree (with root at the source and leaves at the sinks of the blob) such that there exists a projection of the blob onto this tree.
This leads to a blob corremoval procedure, which generalizes the bulge corremoval procedure from Bankevich et al. (2012) and satisfies conditions (i)–(ii). A generalized notion of blob and an efficient algorithm to search for trees and projections are described in Appendix B.
4. Estimating Genomic Distances by Aggregating Read-Pair Information
Recently developed assemblers SPAdes and Telescoper emphasized a new approach to aggregating read-pair information (Bankevich et al., 2012; Pham et al., 2013; Vyahhi et al., 2012; Bresler et al., 2012). In order to resolve the repeats, one needs to estimate the (set of) genomic distances between any two edges in the de Bruijn graph. Key features of SPAdes (Bankevich et al., 2012) and Telescoper (Bresler et al., 2012) include algorithms to approximate these distances by aggregating distance estimates obtained from individual read pairs. Below we complement the heuristics for estimating distances between the edges in the de Bruijn graph described in Bankevich et al. (2012); Pham et al. (2013); Vyahhi et al. (2012); and Bresler et al. (2012) by a rigorous likelihood model.
Let g denote the true (but unknown) gap in the genome between the edges A and B of the condensed de Bruijn graph: g is the distance from the end of A to the start of B, measured in k-mers. Denote the lengths of edges A and B in k-mers as ℓA and ℓB.
Let ξil be a random variable representing the insert length in nucleotides. Let Fil denote the insert length probability distribution function and 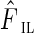 be an estimate obtained by aligning paired-end reads to the edges longer than N50 (see Bankevich et al., 2012).
be an estimate obtained by aligning paired-end reads to the edges longer than N50 (see Bankevich et al., 2012).
Let (l, r) be a pair of reads that aligns to the pair of edges (A, B). Read l maps to edge A at offset pl, while read r maps to edge B at offset pr. Let ℓr denote the length of read r in nucleotides.
Given g, the observed insert length of (l, r) is ξIL* = ℓA−pl + 1 + g + pr + ℓr (see Fig. 5). The likelihood for the single observation can be written as
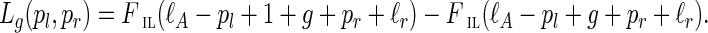 |
(1) |
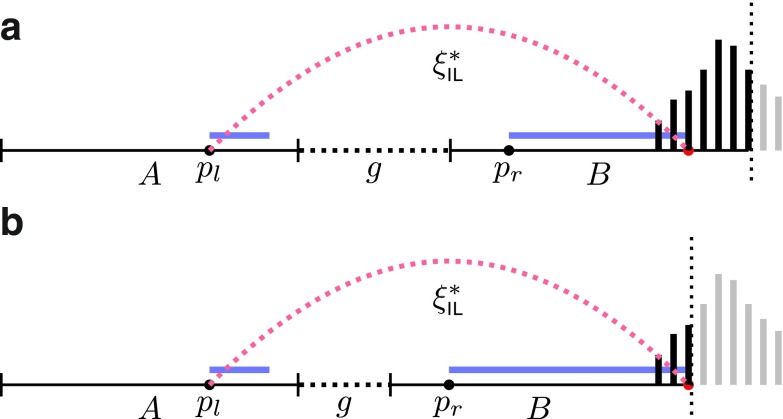
FIG. 5.
Observed insert length distribution between edges A and B of the assembly graph, given alignment positions pl and pr (left-most coordinates of left and right reads) and gap size g. Reads are shown in blue; in general, they can have different lengths, although on the Illumina platform, they have the same length. The insert length of this read pair goes from the start of the left read (pl) to the end of the right read (red point). A histogram of the full insert length distribution is shown on the right end of the figure; the black part of the histogram is observable while the gray part is unobservable due to finite edge length and the particular value of g. Edge B ends at the dotted vertical line, thus truncating the observable part of this histogram. Panels (a) and (b) illustrate different combinations of gap length and edge lengths, resulting in different portions of the distribution being observable.
Given the collection of all alignment positions 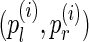 , we can maximize the product of likelihood (1) (or maximize the sum of their logarithms) to get an estimate
, we can maximize the product of likelihood (1) (or maximize the sum of their logarithms) to get an estimate 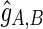 of the gap between the edges (A, B). A similar approach is used by the Telescoper assembler (Bresler et al., 2012). Note, however, that likelihood (1) is not the proper likelihood of the observed insert length
of the gap between the edges (A, B). A similar approach is used by the Telescoper assembler (Bresler et al., 2012). Note, however, that likelihood (1) is not the proper likelihood of the observed insert length 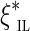 since the edges have finite length (preventing observation of insert sizes above the edge length), and the gap is nonzero (preventing observation of some smaller inserts that fall into the gap). Thus, the distribution of
since the edges have finite length (preventing observation of insert sizes above the edge length), and the gap is nonzero (preventing observation of some smaller inserts that fall into the gap). Thus, the distribution of 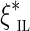 differs from the distribution of ξil. This difference in many cases can be neglected, for example, in the case where the edges are long enough compared to the mean insert length.
differs from the distribution of ξil. This difference in many cases can be neglected, for example, in the case where the edges are long enough compared to the mean insert length.
In general, given the edge gap, g, and the alignment position, pl, of the left read, we “observe” the insert length distribution through the “window” determined by the gap and the lengths of the entities involved (Fig. 5).
The true likelihood of the observed data can be obtained as follows:
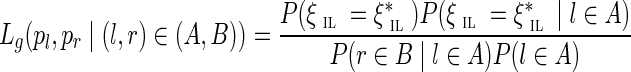 |
As shown in Appendix C, this likelihood can be taken (up to a multiplicative constant that does not depend on g) as
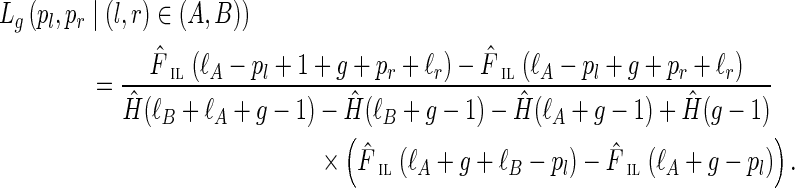 |
where the cumulative insert length distribution is 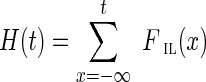 , and its estimate is
, and its estimate is 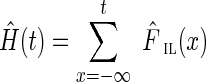 . Given the set of read-pair alignments
. Given the set of read-pair alignments  , we calculate
, we calculate 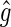 , the maximum likelihood estimate of the gap, as
, the maximum likelihood estimate of the gap, as
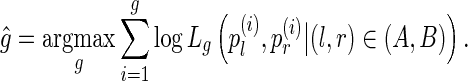 |
5. Results
5.1. Metrics
The N50 (resp., NG50) metric is the maximum contig size such that the total length of contigs of that size or larger represents at least 50% of the assembly length (resp., reference genome length). When assembling a genome with an exact or close reference, NG50 is preferred; when assembling a genome without a reference, N50 is used since NG50 isn't even possible. While N50 and NG50 are in widespread use, they can be artificially increased by improperly concatenating contigs (which introduces misassemblies) or by adding sequences that are not present in the genome.
We use metrics NA50 and NGA50, introduced and justified in Gurevich et al. (2013), instead of the standard N50 or NG50 metrics, to overcome these problems. To compute NA50, contigs are aligned to a reference genome. If a contig has a misassembly or has nonaligning sequences such as large gaps or indels, the contig is broken into blocks that do align. Then we compute N50 using these aligned blocks instead of using the original contigs. Similarly, NGA50 is computed as NG50 applied to these adjusted blocks.
In some of our experiments, the fraction of the genome assembled is below 50%, so NGA50 would be 0 for all assemblers, and thus, we use NA50.
5.2. Benchmarking
We compared a number of single-cell and conventional assemblers on two E. coli paired-end Illumina libraries described in Chitsaz et al. (2011): a single-cell library (ECOLI-SC) and a multicell library (ECOLI-MC). They consist of 100 bp paired-end reads with average insert sizes 266 bp for ECOLI-SC and 215 bp for ECOLI-MC. Both E. coli datasets have 600× coverage. The E. coli K-12 MG1655 reference length is 4639675 bp with 4324 annotated genes.
Tables 1 and 2 present the benchmarking results for various assemblers.11 Table 1 illustrates that single-cell assemblers significantly improve upon the conventional assemblers in single-cell projects. Table 2 shows that recently developed single-cell assemblers IDBA-UD and SPAdes also improve upon the conventional assemblers in standard (multicell) projects by most metrics.
Table 1.
Comparison of Assemblers on ECOLI-SC, a Single-Cell E. coli Dataset
| Assemblera | NGA50 # contigsb | Longest contig | Total length | MAc | MMd | INDe | Nsf | GF (%)g | No. genesh | |
|---|---|---|---|---|---|---|---|---|---|---|
| Conventional (multicell) assemblers | ||||||||||
| A5 | 13310 | 745 | 101584 | 4441145 | 8 | 11.97 | 0.19 | 0.00 | 90.141 | 3453 |
| ABySS | 68534 | 179 | 178720 | 4345617 | 5 | 2.71 | 2.66 | 17.07 | 88.268 | 3704 |
| CLC | 32277 | 503 | 113285 | 4656964 | 3 | 4.76 | 2.87 | 7.40 | 92.378 | 3768 |
| EULER-SR | 26580 | 429 | 140518 | 4248713 | 18 | 9.37 | 218.72 | 58.14 | 85.005 | 3419 |
| Ray | 53903 | 296 | 210612 | 4649552 | 13 | 2.34 | 0.87 | 0.00 | 91.864 | 3838 |
| SOAPdenovo | 16606 | 569 | 87533 | 4098032 | 7 | 114.38 | 11.08 | 1295.26 | 79.861 | 3038 |
| Velvet | 22648 | 261 | 132865 | 3501984 | 2 | 2.07 | 1.23 | 0.00 | 74.254 | 3098 |
| Single-cell assemblers | ||||||||||
| E + V-SC | 32051 | 344 | 132865 | 4540286 | 2 | 1.85 | 0.70 | 0.00 | 92.162 | 3793 |
| IDBA-UD | 98306 | 244 | 284464 | 4814043 | 7 | 2.08 | 0.11 | 0.00 | 95.763 | 4062 |
| SPAdes 2.4 | 110782 | 274 | 268093 | 4929226 | 2 | 3.28 | 0.49 | 2.52 | 96.157 | 4060 |
Comparisons were performed with QUAST 1.2 (Gurevich et al., 2013). In each column, the best assembler by that criteria is indicated in bold.
Only contigs of length ≥500 bp were used.
MA: number of misassemblies. Misassemblies are locations on an assembled contig where the left flanking sequence aligns over 1 kb away from the right flanking sequence on the reference.
MM: Mismatch (substitution) error rate per 100 kb.
IND: number of indels per 100 kb. MM and IND are measured in aligned regions of the contigs.
Ns: Count of undefined bases (Ns) per 100 kb.
GF (%): The genome fraction is the fraction of the genome covered by the contigs. For single-cell projects, the total assembly size often exceeds the genome length due to contaminants and other reasons (see Woyke et al., 2011). The genome fraction filters out these issues.
The number of genes sequenced at full length is out of a list of 4324 annotated genes from www.ecogene.org for E. coli.
Table 2.
Comparison of Assemblers on ECOLI-MC, a Multicell E. coli Dataset
| Assemblera | NGA50 # contigs | Longest contig | Total length | MA | MM | IND | Ns | GF (%) | No genes | |
|---|---|---|---|---|---|---|---|---|---|---|
| Conventional (multicell) assemblers | ||||||||||
| A5 | 43651 | 176 | 181690 | 4551797 | 0 | 0.40 | 0.13 | 0.00 | 98.476 | 4178 |
| ABySS | 105525 | 96 | 221861 | 4619631 | 2 | 2.45 | 0.52 | 3.01 | 99.202 | 4242 |
| CLC | 86964 | 112 | 221549 | 4547925 | 2 | 0.37 | 0.22 | 0.00 | 98.655 | 4239 |
| EULER-SR | 110153 | 100 | 221409 | 4574240 | 8 | 2.98 | 47.15 | 0.37 | 98.438 | 4206 |
| Ray | 83128 | 113 | 221942 | 4563341 | 2 | 2.10 | 0.20 | 0.00 | 98.162 | 4194 |
| SOAPdenovo | 62512 | 141 | 172567 | 4519621 | 1 | 26.56 | 5.58 | 14.03 | 97.405 | 4134 |
| Velvet | 78602 | 120 | 242032 | 4554702 | 3 | 0.70 | 0.20 | 0.00 | 98.824 | 4211 |
| Single-cell assemblers | ||||||||||
| E + V-SC | 54856 | 171 | 166115 | 4539639 | 0 | 1.21 | 0.15 | 0.00 | 98.329 | 4149 |
| IDBA-UD | 106844 | 110 | 221687 | 4565529 | 3 | 1.03 | 0.09 | 0.00 | 98.810 | 4221 |
| SPAdes 2.4 | 134076 | 102 | 285228 | 4642173 | 2 | 2.50 | 0.73 | 2.46 | 99.482 | 4262 |
Comparisons were performed with QUEST 1.2 (Gurevich et al., 2013). In each column, the best assembler by that criteria is indicated in bold.
5.3. Running time of SPAdes
On a 32 CPU (Intel Xeon X7560 2.27GHz) computer with 16 threads, the total run time for SPAdes on ECOLI-SC was 4 hours 55 minutes, while for ECOLI-MC it was 3 hours 23 minutes.
5.4. From genomes to mini-metagenomes
Below we investigate the performance of SPAdes on artificially simulated mini-metagenomes and demonstrate that it is capable of assembling a significant portion of each genome in a mini-metagenome. In addition to simulations, we also applied this assembly algorithm to a real mini-metagenome dataset; details are in McLean et al. (2013a).
We applied SPAdes to a simulated mini-metagenome that consists of four bacterial species with known genomes. We mixed together reads (in various proportions), from four different MDA-amplified single-cell bacterial projects at the DOE Joint Genome Institute and Bigelow Laboratory. The genomes of these bacteria vary in GC content and genome length: Prochlorococcus marinus (Rocap et al., 2003) (31% GC, 1.7 Mb genome length), Pedobacter heparinus (Han et al., 2009) (42% GC, 5.0 Mb genome length), Escherichia coli (Blattner et al., 1997) (51% GC, 4.6 Mb genome length), and Meiothermus ruber (Tindall et al., 2010) (63% GC, 3.0 Mb genome length). Table 3 shows the assembly statistics for each of these datasets. Note that as simulated datasets, these are highly idealized and do not exactly match what would be found in the environment, but they are useful for modeling the ability of the assembler to deal with different mixtures. We expect a significantly higher frequency of misassemblies when analyzing real, environmental metagenomes due to the following reasons: a) the coanalyzed cells may contain similar genome regions that can cross-assemble; b) the coanalyzed cells may have less divergent GC content than the four model strains studied here; and c) intergenomic chimeras may form when MDA is performed on a pool of cells. Analysis of real mini-metagenomes is described in McLean et al. (2013a).
Table 3.
Genome Statistics and SPAdes Assembly Statistics for Each of Four Bacterial Datasets Used to Simulate a Mini-Metagenome
| |
Dataset |
|||
|---|---|---|---|---|
| E. coli | M. ruber | P. heparinus | P. marinus | |
| Genome statistics | ||||
| Genome length (Mb) | 4.6 | 3.0 | 5.0 | 1.7 |
| GC | 51% | 63% | 42% | 31% |
| No. genes annotated | 4324 | 3105 | 4339 | 1732 |
| RefSeq accession | NC_000913.2 | NC_013946.1 | NC_013061.1 | NC_005072.1 |
| Citation | Blattner et al. (1997) | Tindall et al. (2010) | Han et al. (2009) | Rocap et al. (2003) |
| Assembly statistics:a | ||||
| Misassemblies | 3 | 8 | 2 | 2 |
| NA50 (kb)b | 119 | 33 | 149 | 223 |
| Longest contig (kb) | 224 | 113 | 946 | 404 |
| Genome fraction (%) | 99.4 | 75.3 | 97.8 | 94.4 |
| No. genes assembled | 4236 | 2097 | 4136 | 1600 |
The number of reads for these genomes varied from 10 million to 27 million (no normalization was done). In this table, each dataset is assembled separately. Only contigs of length ≥500 contributed to the statistics.
NA50 is N50 of contigs aligned to the reference and broken into blocks at breakpoints from misassemblies, large gaps, or indels.
In the first simulation, we randomly selected a fixed fraction of reads from each genome, mixed them together, and assembled the resulting dataset with SPAdes. This simulation was repeated 10 times, varying the fraction as 1/2m with 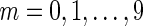 (the same fraction 1/2m applies to all genomes). The assembled contigs were aligned against individual genomes to compute the assembly statistics. (In Table 4 we present statistics for M. ruber and P. heparinus.) In particular, even with a relatively small fraction 1/64 of selected reads, SPAdes assembled 1779 out of 4339 genes for P. heparinus, 1366 out of 4324 genes for E. coli, and 710 out of 3105 genes for M. ruber. This is significantly larger than the number of complete genes captured in a typical metagenomics project. However, for P. marinus, only 55 out of 1732 genes were assembled.
(the same fraction 1/2m applies to all genomes). The assembled contigs were aligned against individual genomes to compute the assembly statistics. (In Table 4 we present statistics for M. ruber and P. heparinus.) In particular, even with a relatively small fraction 1/64 of selected reads, SPAdes assembled 1779 out of 4339 genes for P. heparinus, 1366 out of 4324 genes for E. coli, and 710 out of 3105 genes for M. ruber. This is significantly larger than the number of complete genes captured in a typical metagenomics project. However, for P. marinus, only 55 out of 1732 genes were assembled.
Table 4.
SPAdes Assemblies of a Simulated Mini-Metagenome Consisting of E. coli, M. ruber, P. heparinus, and P. marinus, Using a Fraction of the Reads from all the Genomes
| |
Assemblya |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| All | 1/2 | 1/4 | 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | 1/256 | 1/512 | |
| Assembly statistics | ||||||||||
| No. contigs (≥500 bp)b | 851 | 899 | 928 | 1097 | 1900 | 3095 | 3371 | 2576 | 1693 | 960 |
| Total contigs length (kb) | 13600 | 13047 | 12370 | 11596 | 10722 | 9051 | 6570 | 4098 | 2297 | 1095 |
| N50 (kb) | 112 | 110 | 112 | 64 | 30 | 11 | 4 | 2 | 1 | 1 |
| Multi-species contigsc | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| E. coli | ||||||||||
| Misassemblies | 3 | 4 | 4 | 4 | 4 | 15 | 16 | 27 | 21 | 7 |
| NA50 (kb) | 119 | 127 | 134 | 59 | 25 | 4 | 2 | 1 | 1 | 1 |
| Longest contig (kb) | 269 | 310 | 268 | 222 | 118 | 64 | 46 | 20 | 7 | 3 |
| Genome fraction (%) | 99.4 | 99.2 | 99.2 | 99.1 | 97.0 | 84.1 | 56.1 | 28.4 | 11.3 | 3.0 |
| No. genes (out of 4324) | 4248 | 4238 | 4234 | 4168 | 3707 | 2565 | 1366 | 566 | 176 | 37 |
| M. ruber | ||||||||||
| Misassemblies | 14 | 12 | 5 | 15 | 13 | 10 | 14 | 8 | 8 | 12 |
| NA50 (kb) | 44 | 33 | 39 | 24 | 20 | 14 | 9 | 10 | 8 | 3 |
| Longest contig (kb) | 113 | 133 | 119 | 114 | 108 | 109 | 93 | 61 | 50 | 39 |
| Genome fraction (%) | 76.3 | 69.5 | 62.4 | 56.7 | 49.1 | 39.7 | 29.9 | 22.2 | 15.7 | 10.9 |
| No. genes (out of 3105) | 2160 | 1950 | 1777 | 1533 | 1219 | 939 | 710 | 521 | 357 | 214 |
| P. heparinus | ||||||||||
| Misassemblies | 1 | 2 | 6 | 11 | 11 | 13 | 26 | 27 | 17 | 12 |
| NA50 (kb) | 185 | 207 | 165 | 96 | 70 | 27 | 12 | 4 | 2 | 1 |
| Longest contig (kb) | 946 | 410 | 426 | 307 | 337 | 379 | 225 | 102 | 34 | 32 |
| Genome fraction (%) | 97.8 | 96.6 | 94.3 | 88.4 | 82.5 | 71.3 | 57.6 | 40.4 | 24.9 | 12.1 |
| No. genes (out of 4339) | 4148 | 4038 | 3855 | 3524 | 3133 | 2401 | 1779 | 1125 | 548 | 189 |
| P. marinus | ||||||||||
| Misassemblies | 9 | 9 | 3 | 3 | 5 | 2 | 1 | 0 | 1 | 0 |
| NA50 (kb) | 101 | 63 | 104 | 43 | 21 | 9 | 8 | 12 | 1 | 0 |
| Longest contig (kb) | 215 | 150 | 136 | 74 | 58 | 24 | 19 | 12 | 1 | 0 |
| Genome fraction (%) | 79.6 | 67. | 51.9 | 38.7 | 25.7 | 13.2 | 4.2 | 0.9 | 0.3 | 0.0 |
| No. genes (out of 1732) | 1276 | 1061 | 846 | 646 | 399 | 192 | 55 | 15 | 3 | 0 |
A fraction 1/2m (for 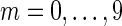 ) of the reads were selected at random from each genome. For each fraction, aggregate assembly statistics are shown in the assembly statistics section, and a breakdown of the same assembly by genome is shown in subsequent sections (using the contigs or blocks that map to that genome).
) of the reads were selected at random from each genome. For each fraction, aggregate assembly statistics are shown in the assembly statistics section, and a breakdown of the same assembly by genome is shown in subsequent sections (using the contigs or blocks that map to that genome).
Only contigs of length ≥500 contributed to the statistics.
A multispecies contig is defined as a contig that aligns to multiple genomes (at least 10% of its length aligns to one of the genomes and at least 10% to another one) but cannot be aligned to a single genome. Such contigs represent assembly errors. This table illustrates that SPAdes generated very few multispecies contigs.
In the second simulation, we formed a mini-metagenome using all reads from three species and varied the coverage for the fourth. For the fourth species, we selected either a genome with high GC content (M. ruber) or low GC content (P. heparinus). Table 5 illustrates that SPAdes recovers a substantial fraction of an underrepresented genome within a mini-metagenome. Even with a small fraction of reads in the underrepresented genome (e.g., 1/256), we recovered a large number of genes (more than 450 genes for M. ruber and P. heparinus). Tables 4 and 5 demonstrate that the assembly quality of an individual genome depends mainly on the coverage of this genome, rather than on what fraction of the mini-metagenome this genome represents. We remark that since all genomes in this simulation differ significantly in GC content, partitioning contigs into four groups by GC content is usually sufficient to attribute the contigs to the various genomes. In the case of genomes with similar GC content, one should use more advanced binning methods developed for metagenomics studies.
Table 5.
SPAdes Assemblies of a Simulated Mini-Metagenome Consisting of E. coli, M. ruber, P. heparinus, and P. marinus, Using all Reads from Three of the Genomes and a Fraction of the Reads from the Fourth
| |
Assemblya |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1/2 | 1/4 | 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | 1/256 | 1/512 | |
| Assemblies using fractions of M. ruberb | |||||||||
| Multi-species contigs | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Misassemblies | 14 | 6 | 8 | 11 | 13 | 14 | 14 | 17 | 11 |
| NA50 (kb) | 47 | 45 | 27 | 15 | 11 | 10 | 7 | 4 | 2 |
| Longest contig (kb) | 137 | 120 | 118 | 106 | 114 | 114 | 62 | 45 | 49 |
| Genome fraction (%) | 70.0 | 63.7 | 58.3 | 52.4 | 43.0 | 34.2 | 27.1 | 21.5 | 16.7 |
| No. genes (out of 3105) | 1973 | 1797 | 1585 | 1327 | 1022 | 822 | 618 | 464 | 330 |
| Assemblies using fractions of P. heparinus | |||||||||
| Multi-species contigs | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 0 | 0 |
| Misassemblies | 2 | 5 | 8 | 12 | 19 | 23 | 14 | 19 | 15 |
| NA50 (kb) | 163 | 165 | 131 | 87 | 33 | 11 | 3 | 2 | 1 |
| Longest contig (kb) | 426 | 439 | 396 | 339 | 333 | 227 | 89 | 40 | 33 |
| Genome fraction (%) | 96.6 | 94.0 | 88.7 | 81.6 | 71.2 | 56.7 | 40.6 | 24.5 | 12.9 |
| No. genes (out of 4339) | 4043 | 3815 | 3527 | 3116 | 2488 | 1752 | 1113 | 534 | 228 |
We used all reads from three of the genomes and a randomly selected fraction 1/2m (for 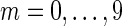 ) of the reads from the fourth (M. ruber or P. heparinus).
) of the reads from the fourth (M. ruber or P. heparinus).
The assemblies using fractions of the M. ruber dataset are separate from the assemblies using fractions of the P. heparinus dataset.
6. Conclusion
Since 2008, when the first NGS assemblers were released, many excellent assemblers have become available. Since most of them use a de Bruijn graph approach, they often generate rather similar assemblies, at least for bacterial projects. Recent developments in single-cell genomics tested the limits of conventional assemblers and demonstrated that they all have room for improvement. Our benchmarking illustrates that single-cell assemblers not only enable single-cell sequencing but also improve upon conventional assemblers on their own turf.
7. Appendix A: Chimeric Edges
7.1. Finding edges with zero flow in all circulations
As was shown in Section 2.3, an edge e such that f (e) = 0 in all circulations is likely to be a false edge. In most cases, e will be chimeric. Thus, one can test if an edge is chimeric by setting its lower capacity to 1 and checking if there exists a circulation in the resulting network. Below, we describe a faster algorithm for finding chimeric edges.
We say that an edge e belongs to a circulation f if f (e) > 0. Let f be a circulation in a network G (with lower and upper capacities on each edge). A function h is also a circulation in G if and only if h − f is a circulation in the residual network of f. (See Cormen et al., 2009, paragraph 26.2, for background on residual networks.) Thus, an edge e belongs to a circulation if and only if either (i) e belongs to circulation f or (ii) e belongs to a circulation in the residual network of f. Since lower capacities in the residual network do not exceed 0, edge e belongs to a circulation in the residual network of f if and only if it belongs to a cycle formed by the edges in this network. The edges that do not belong to any cycle are exactly the ones that connect vertices from different strongly connected components of the residual network of f.
Thus, edges that do not belong to any circulation in network G can be found as follows: (1) Find an arbitrary circulation f. (2) Find the edges that do not belong to f nor to any cycle in the residual network of f. Step 1 requires a single run of a Ford-Fulkerson max-flow search algorithm (Ford and Fulkerson, 1962). Step 2 requires a single run of the Kosaraju-Sharir linear-time algorithm (Aho et al., 1983), which searches for strongly connected components.
With only slight changes, the same algorithm can be applied independently for each component, resulting in the long-edge breaking procedure described in Section 2.3.
The chance of the procedure failing for some component increases with the size of the component. During our experiments, no component with more than 100 vertices could be successfully processed by the algorithm, so we apply this algorithm only for components smaller than this.
It can be shown that in this setting, the max-flow search takes only O(|V||E|2) time, where |E| and |V | respectively are the numbers of edges and vertices in the component rather than in the whole graph. With |V| bounded by 100, this procedure becomes practically linear for the whole graph.
7.2. Examples of chimeric edges and critical cuts
Bankevich et al. (2012) described a simple rule for identification of chimeric edges that we restate as follows: An edge (u, v) with lower capacity 0 is chimeric if (i) u has exactly one incoming edge with upper capacity 1; (ii) u has at least one outgoing edge with lower capacity 1; and (iii) v has at least two incoming edges [including (u, v)]. We remark that under conditions (i) and (ii), the edge (u, v) is a crossing edge for a critical cut-set cut({u}) and thus also satisfies the criteria defined in the main text.
This rule, while useful, identifies only a fraction of chimeric edges. Below we describe some other (more complex) subgraphs of the assembly graph for which the algorithm from Bankevich et al. (2012) fails while the algorithm from the current article succeeds. While condition (iii) is not related to the cut-set criteria defined in the main text, it is still useful to filter false positives in chimeric edges detection: if (u,v) is chimeric, the genome path must enter v through another edge, and thus, v must satisfy (iii). Hence, in each of the cases described below, we also add condition (iii) for vertex v.
Let 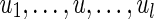 be a path in the assembly graph and (u, v) be an edge with lower multiplicity 0 (Fig. 6a). We require that u ≠ u1, u ≠ ul, and v is not on the path. Consider a cut-set cut(U) with
be a path in the assembly graph and (u, v) be an edge with lower multiplicity 0 (Fig. 6a). We require that u ≠ u1, u ≠ ul, and v is not on the path. Consider a cut-set cut(U) with 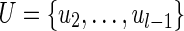 . If (i) the upper capacity of the edge (u1, u2) is 1, (ii) the lower capacity of the edge (ul−1, ul) is 1, and (iii) the edge (u1, u2) is the only incoming edge in U, then
. If (i) the upper capacity of the edge (u1, u2) is 1, (ii) the lower capacity of the edge (ul−1, ul) is 1, and (iii) the edge (u1, u2) is the only incoming edge in U, then 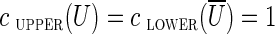 . Thus (u, v) is a crossing edge for a critical cut-set cut(U), implying that (u, v) is chimeric. This approach removes 99 out of 117 chimeric edges in the assembly of the E. coli dataset.
. Thus (u, v) is a crossing edge for a critical cut-set cut(U), implying that (u, v) is chimeric. This approach removes 99 out of 117 chimeric edges in the assembly of the E. coli dataset.
FIG. 6.
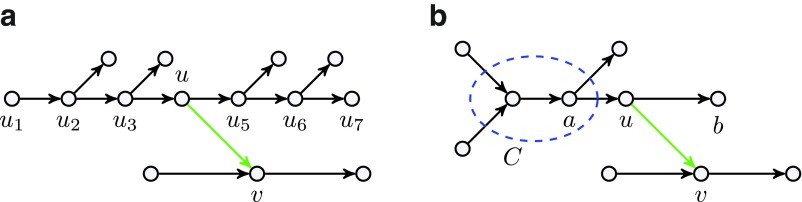
(a) Edge (u, v) is classified as chimeric since it is a crossing edge for a critical cut. (b) Removal of edge (u, v) reveals a connected component C (after breaking long edges) with the number of incoming long edges exceeding the number of outgoing long edges by 1. This component reveals that (u, v) is a crossing edge in a critical cut.
Another common situation is when, for a vertex u, there exists one incoming edge (a, u) and two outgoing edges: (u, v) with lower capacity 0 and (u, b) with lower capacity 1 (Fig. 6b). In this case, we apply the following approach to test whether the edge (u, v) is chimeric. First, we remove the edge (u, v) and condense the edges (a, u) and (u, b) into a single edge (a, b), which we artificially declare as long. Then we break all long edges in the resulting graph and analyze the connected component containing vertex a. Let C be the set of all vertices of the original graph belonging to this component (Fig. 6b). We further define a set U = C ∪ {u} and consider the cut-set cut(U). If it is critical, then (u, v) is chimeric since it is a crossing edge for this cut. This approach removes 78 out of 117 chimeric edges in our E. coli dataset. Combining all our methods removes all but four chimeric connections in our E. coli dataset.
Appendix B: Bulges
8.1. Search for local blobs
Let G be a graph. A subset B of the vertices of G is called well localized if for every  ,
,
(1) Either all incoming edges of x come from vertices of B, or they all come from vertices of
 .
.(2) Either all outgoing edges of x go to vertices of B, or they all go to vertices of
 .
.
A vertex of S whose incoming edges all come from vertices of 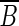 is called a source of a well-localized set B. Similarly, a vertex of B whose outgoing edges all go to vertices of
is called a source of a well-localized set B. Similarly, a vertex of B whose outgoing edges all go to vertices of 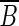 is called a sink of a well-localized set B.
is called a sink of a well-localized set B.
A well-localized set B such that its induced subgraph is a DAG with a single source s can be viewed as a generalization of a blob defined in Section 3. We refer to such sets B as local blobs.
For each vertex 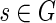 , we are interested in a local blob with source s that satisfies the following two conditions:
, we are interested in a local blob with source s that satisfies the following two conditions:
D1. It contains a bulge (i.e., at least one sink is connected to the source with multiple paths);
D2. It contains a proper skeleton, which is a directed subtree of G satisfying additional properties that will be described in appendix section 8.2.
We define the set D(s) of vertices dominated by vertex s by the following recursive rule: 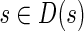 and
and 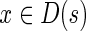 if all the parents of x in G are in D(s), and there is no edge in G from x to s. It is easy to see that the subgraph of G induced by D(s) is a DAG and for any local blob B with source s, we have B ⊂ D(s).
if all the parents of x in G are in D(s), and there is no edge in G from x to s. It is easy to see that the subgraph of G induced by D(s) is a DAG and for any local blob B with source s, we have B ⊂ D(s).
A vertex 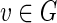 is called interfering with a set of vertices B if
is called interfering with a set of vertices B if 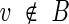 and there exist edges (x, v) and (x, y) with
and there exist edges (x, v) and (x, y) with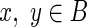 .
.
Let I(B) be the set of all vertices in G interfering with B. It is easy to see that B is a well-localized set if and only if I(B) is empty.
Consider a vertex 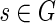 and a set B0 ⊂ D(s) containing s. Let Closure(B0, s) be the minimal local blob with source s that contains B0. It is easy to see that the intersection of two local blobs is also a local blob, so Closure(B0, s) is uniquely defined.
and a set B0 ⊂ D(s) containing s. Let Closure(B0, s) be the minimal local blob with source s that contains B0. It is easy to see that the intersection of two local blobs is also a local blob, so Closure(B0, s) is uniquely defined.
Suppose a vertex u is interfering with B0; then it is easy to see that all local blobs that contain B0 must contain u and also must contain all paths from s to u. Thus one can find Closure(B0, s) (or determine that it does not exist) using the procedure shown in Algorithm 1.
Algorithm 1: Closure
| 1: procedure Closure(B0, s) |
| 2: globalG ▹ Graph G is used implicitly in the operations below. |
| 3: B ← B0 |
| 4: ifI(B) = ∅ then returnB |
| 5: else ifI(B) contains a vertex from outside of D(s) then |
| 6: Closure(B0,s) does not exist and the search terminates. |
| 7: end if |
| 8: Take an arbitrary vertex u from I(B). |
| 9: Add u and vertices that belong to all paths from s to u to B. |
| 10: return Closure(B, s) |
| 11: end procedure |
On each recursive call of the procedure, we have Closure(B) = Closure(B0) and B is a strictly larger set than B0. Thus, the procedure will either stop and report that Closure(B0, s) does not exist, or else I(B) will become empty, in which case B is a minimal local blob with source s that contains B0.
8.2. Construction of skeleton trees
In this section, we give an algorithm for finding a certain directed tree (called a skeleton tree) in a local blob. In most cases, a nontrivial local blob consists of a tree formed by genomic edges, plus a number of erroneous edges. The complex bulge removal algorithm aims to find a tree that could be a tree of genomic edges and to project the rest of the edges of the blob on it. It is convenient to describe this algorithm in terms of conventional (uncondensed) assembly graphs in which each edge has length 1.
We view a complex bulge as an induced subgraph B of the assembly graph such that B is a DAG with a single source s (i.e., a vertex with no incoming edges) and possibly multiple sinks (i.e., vertices with no outgoing edges) such that the length of every path between s and a sink is not greater than n = 250. We say that B is a bulge if it is not a tree, that is, there are multiple paths connecting s with some sink.
For a vertex v, we define height(v) as the length of a longest path in B connecting it to a sink of B. Note that sinks have height 0.
First, we introduce artificial vertices, so that for every vertex v, the length of each path from v to a sink is height(v). To do this, we iterate over all edges (v, u) of B and if height(v) −height(u) = m > 1, we split (v, u) into m subedges: (v, a1), 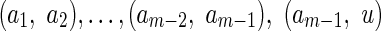 , where
, where 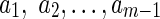 are artificial vertices.
are artificial vertices.
For a DAG D, we define V(D) and E(D) as the sets of vertices and edges of graph D. For a vertex v of D, we define sinksD(v) as the set of sinks reachable from v in D and CD(v) as the set of all children of v in D.
We define composition of functions, g ° f, as (g ° f)(v) = g(f (v)).
We define a skeleton of B (Fig. 7) as a pair (T, f) such that:
FIG. 7.
(a) Graph B. Vertices of the graph are iteratively removed and projected (with mapping g) to form a tree (b). Blue ellipses show groups of vertices that were projected onto the same vertex; g maps each vertex of B to the ellipse that contains it. (b) A representation of all skeleton trees of B. Each skeleton tree is formed by selecting one vertex of B from each ellipse and connecting the selected vertices by the same edges that connect the ellipses; these are not necessarily edges of B, however. (c) Thick edges denote a proper skeleton of graph B; this is a skeleton of B that is also a subtree of B. This was constructed by finding an embedding of panel (b) into graph B.
(1) T is a directed tree. The vertices of T are a subset of the vertices of B. This subset must include the source and all sinks of B. The edges of T are any directed edges formed from these vertices. We do not require that the edges of T be edges of B but if they are (i.e., T is a directed subtree of B), we call the skeleton (T, f) proper.
(2) f: B → T is a projection of vertices of B onto vertices of T (i.e., f is surjective and f ° f = f). In particular, f is the identity when restricted to the vertices of T.
(3) f maps vertices consistently with edges, that is for each edge
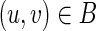 , we have that (f (u), f (v)) is an edge in T. This property allows us to extend f to the set of edges by defining f ((u, v)) = (f (u), f (v)). It further implies that for each vertex v, we have f (CB(v)) ⊂ CT (f (v)).
, we have that (f (u), f (v)) is an edge in T. This property allows us to extend f to the set of edges by defining f ((u, v)) = (f (u), f (v)). It further implies that for each vertex v, we have f (CB(v)) ⊂ CT (f (v)).
Lemma 1. Let (T, f) be a skeleton of B. Then the following properties hold:
(a) f preserves connectivity: if a vertex v is connected to a sink t with a path in B, then f (v) is connected to f (t) = t by a path in T, i.e., sinksB(v) ⊂ sinksT (f (v)) for any vertex v of B.
(b) f preserves heights: height(f (v)) = height(v).
(c) For any two distinct vertices v1 and v2 of the same height in T, we have sinksT (v1) ∩ sinksT (v2) = ∅.
(d) If (T, f) is proper, then for any vertex u of T, we have sinksB(u) = sinksT(u), which further implies that sinksB(f (v)) = sinksT (f (v)) for any vertex v of B.
Proof. Conditions (a) and (b) automatically follow from consistency of mapping of edges and vertices, while (c) is true by virtue of T being a tree.
To prove (d): since T is a subtree of B, for any vertex u of T, we have sinksT (u) ⊂ sinksB(u). On the other hand, (a) implies sinksB(u) ⊂ sinksT (u). Thus, sinksB(u) = sinksT (u). Finally, for any vertex v of B, we have u = f (v) is a vertex of T, so sinksB(f (v)) = sinksT (f (v)).
Eliminating a complex bulge means that we replace B with a proper skeleton. Figure 7 illustrates a graph, all of its skeletons, and a proper skeleton.
We will construct a proper skeleton in two steps. First, in Algorithm 2 (ConstructSkeleton), we construct a skeleton (S, g). Then, in Algorithm 3 (ConstructProperSkeleton), we construct an embedding j of S into B such that (j(S), j ° g) is a proper skeleton.
Algorithm 2: ConstructSkeleton
| 1: procedure ConstructSkeleton(B) |
| 2: S ← B |
3: for all vertices 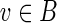 do do
|
| 4: g(v) ← v |
| 5: end for |
| 6: fork ← 1 → height(s) do |
| 7: for all ordered pairs of vertices u ≠ v in S with height(u) = height(v) = kdo |
| 8: ifCS(u) ⊂ CS(v) then |
| 9: Replace every edge (w, u) in S with an edge (w, v). |
| 10: Remove vertex u from S. |
| 11: for all vertices w such that g(w) = udo |
| 12: Redefine g(w) ← v |
| 13: end if |
| 14: end for |
| 15: end for |
| 16: return (S, g) |
| 17: end procedure |
Algorithm 3: ConstructProperSkeleton
| 1: procedure ConstructProperSkeleton(v, B, S, g) |
| 2: j(g(v)) ← v |
| 3: ifv is a sink of Bthen returnj as-is |
| 4: end if |
| 5: for all injective mappings p: CS(g(v)) → CB(v) such that g ° p = idCS(g(v))do |
6: if ConstructProperSkeleton(u, B, S, g) succeeds for each 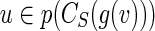 then then
|
| 7: Combine all results of ConstructProperSkeleton calls into a single embedding j of RS(g(v)) into RB(v). |
| 8: return the constructed embedding j |
| 9: end if |
| 10: end for |
| 11: report that a skeleton rooted in vertex v cannot be constructed |
| 12: end procedure |
8.2.1. Constructing a skeleton
In the ConstructSkeleton algorithm, we construct a skeleton of a given DAG B by iteratively compressing B and eventually producing a pair (S, g) where S is a DAG and g is a mapping of B onto S. From the description of the ConstructSkeleton algorithm, it is clear that g maps vertices consistently with edges and thus can be extended to the set of edges by defining g((u, v)) = (g(u), g(v)). Furthermore, g is a height-and connectivity-preserving projection of B onto S. It is also clear that the vertices of S represent a subset of the vertices of B and contain the source and all sinks. In Theorem 4, we will show that if B possesses a proper skeleton, then S is a tree, and thus the constructed pair (S, g) represents a skeleton. Although the constructed pair (S, g) depends on the order in which our algorithms process the pairs of vertices, we prove below in Theorem 4 that the skeletons are isomorphic, that is S is unique up to isomorphism. First we develop some needed additional results.
For the remainder of Appendix B, let (S, g) be the result of ConstructSkeleton(B). The following lemma follows directly from the definition of ConstructSkeleton.
Lemma 2. (a) For any vertex
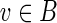 , we have
sinksB(v) ⊂ sinksS(g(v)).
, we have
sinksB(v) ⊂ sinksS(g(v)).
(b) For any vertex
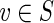 , we also have
sinksS(v) = ∪u: g(u)=vsinksB(u).
, we also have
sinksS(v) = ∪u: g(u)=vsinksB(u).
(c) Since g maps edges and vertices consistently, for any vertex
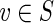 , we have CS(v) = g(CB(v)).
, we have CS(v) = g(CB(v)).
Theorem 3. If B has a proper skeleton (T, f), then (a) f ° g = f and (b) g ° f = g. Thus, (c) the restrictions of f and g from domain B to f′: V (S) → V (T) and g′: V (T) → V (S), are inverses.
Proof. (a) Assume that there is a vertex v of B such that f (g(v)) ≠ f (v) and v has minimum height.
By construction, all sinks of B are also sinks of S, and are fixed points for both f and g. Thus, all sinks t of B satisfy f (g(t)) = t = f (t) and have height 0. Therefore, the height of v is at least 1.
Let w be a vertex of B such that 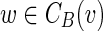 ; then
; then 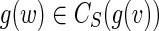 .
.
Since CS(g(v)) = g(CB(g(v))), there exists a vertex 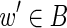 such that g(w′) = g(w) and
such that g(w′) = g(w) and 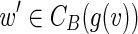 .
.
Since height(w) = height(w′) < height(v), we have f (w) = f (g(w)) = f (g(w′)) = f (w′).
Since f preserves connectivity, we have sinksB(w′) ⊂ sinksB(g(v)) ⊂ sinksB(f (g(v))) = sinksT (f (g(v))) and sinksB(w′) ⊂ sinksB(f (w′)) = sinksB(f (w)) ⊂ sinksB(f (v)) = sinksT(f (v)).
Since f (g(v)) and f (v) are vertices of T that have common sinks, we have f (g(v)) = f (v), a contradiction.
(b) Assume that there is a vertex v of B such that g(f (v)) ≠ g(v) and v has minimum height.
Since vertices g(v) and g(f (v)) produced by the ConstructSkeleton algorithm are distinct and have the same height, we have 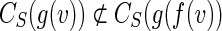 .
.
By Lemma 2(c), we have CS(g(v)) = g(CB(g(v))).
Since all vertices in CB(g(v)) have a smaller height than v, we further have CS(g(v)) = g(CB(g(v))) = g(f (CB(g(v)))).
Since (T, f) is a proper skeleton, we have f (CB(g(v))) ⊂ CT (f (g(v))) = CT (f (v)) ⊂ CB(f (v)).
By Lemma 2(c), we have g(CB(f (v))) = CS(g(f (v)).
Combining these formulas gives
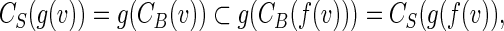 |
a contradiction.
(c) Let 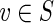 . By (a), g(f (v)) = g(v), and since g is a projection onto S, we have g(v) = v. Thus, g(f (v)) = v.
. By (a), g(f (v)) = g(v), and since g is a projection onto S, we have g(v) = v. Thus, g(f (v)) = v.
Similarly, if 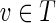 , then f (g(v)) = f (v) = v.
, then f (g(v)) = f (v) = v.
Theorem 4. If B has a proper skeleton (T, f), then S is a tree and the restriction of g to g′: T → S gives an isomorphism of trees.
Proof. Let (v, w) be an edge in T. Since T is a proper skeleton, (v, w) is also an edge in B. Since g: B → S maps vertices and edges consistently, (g(v), g(w)) is an edge in S. Thus, g maps edges of T to edges of S.
Let (v, w) be an edge in S. By construction, there exists an edge 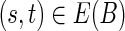 such that (v, w) = (g(s), g(t)). Since
such that (v, w) = (g(s), g(t)). Since 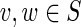 , we have
, we have 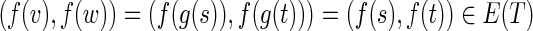 .
.
Let f′: V (S) → V (T) be the restriction of f to V (S) and f′: E(S) → E(T) be defined as f′((v, w)) = (f (v), f (w)). We have just shown this is well defined.
Thus, both f′: S → T and g′: T → S are graph homomorphisms. We show that they are inverse homomorphisms: for 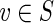 , we have g′(f′(v)) = g(f (v)) = g(v) (by Theorem 3), which equals v (by construction). Conversely, for
, we have g′(f′(v)) = g(f (v)) = g(v) (by Theorem 3), which equals v (by construction). Conversely, for 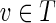 , we have f′(g′(v)) = f (g(v)) = f (v) = v (where f (v) = v follows since T is a skeleton and
, we have f′(g′(v)) = f (g(v)) = f (v) = v (where f (v) = v follows since T is a skeleton and 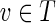 ).
).
Thus, S and T are isomorphic graphs; since T is a tree, so is S.
8.2.2. Construction of a proper skeleton
Given a skeleton (S, g) of B, we describe ConstructProperSkeleton (Algorithm 3), which finds a proper skeleton (T, f) isomorphic to (S, g) if one exists, or reports that no such proper skeleton exists. Note that by Theorem 4, if S is not a tree, then B does not have a proper skeleton, so first we check if S is a tree, and if not, we immediately report that there is no proper skeleton.
For simplicity, we present the algorithm in recursive form, which has exponential complexity due to repetitive recursive calls. This can easily be reduced to polynomial time using dynamic programming.
First we require an additional definition. Let RD(v) be the induced subgraph of a DAG D that consists of all vertices and edges reachable from vertex 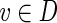 . Note that if (T, f) is a proper skeleton of B, then for each vertex
. Note that if (T, f) is a proper skeleton of B, then for each vertex 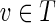 , we have that (RT (v), fv) is a proper skeleton of DAG RB(v) where fv: RB(v) →RT (v) is the restriction of f to domain RB(v). Moreover, for each vertex
, we have that (RT (v), fv) is a proper skeleton of DAG RB(v) where fv: RB(v) →RT (v) is the restriction of f to domain RB(v). Moreover, for each vertex 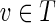 , tree RS(g(v)) is isomorphic to RT(v).
, tree RS(g(v)) is isomorphic to RT(v).
For a vertex 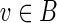 , the algorithm ConstructProperSkeleton(v) determines if it is possible to find a subtree of B rooted at v that is isomorphic to the subtree of S rooted at g(v). Specifically, the algorithm either finds an embedding j of tree RS(g(v)) into DAG RB(v), such that (j(RS(g(v))), j ° g) is a proper skeleton, or reports that no such embedding exists.
, the algorithm ConstructProperSkeleton(v) determines if it is possible to find a subtree of B rooted at v that is isomorphic to the subtree of S rooted at g(v). Specifically, the algorithm either finds an embedding j of tree RS(g(v)) into DAG RB(v), such that (j(RS(g(v))), j ° g) is a proper skeleton, or reports that no such embedding exists.
To find a proper skeleton for B, we invoke ConstructProperSkeleton(s). If it fails, there is no proper skeleton of B. If it succeeds and returns an injective map j: S → B, then T = j(S) is a subtree of B and (T, j ° g) is a proper skeleton of B.
Below we describe technical points of ConstructProperSkeleton.
To see that the domain of j is S, note that Step 2 maps 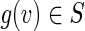 to
to 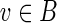 , via j(g(v)) = v. Recursive invocations in Steps 6–7 make assignments j(w′) = v′, where w′ are descendants of g(v) in S and v′ are descendants of v in B.
, via j(g(v)) = v. Recursive invocations in Steps 6–7 make assignments j(w′) = v′, where w′ are descendants of g(v) in S and v′ are descendants of v in B.
Step 5 considers the ways to map children of g(v) in S to distinct children of v in B (with an additional constraint to be described below). Such a map is an injection of the form p: CS(g(v)) → CB(v). Since B is a subgraph of a de Bruijn graph over the 4-letter nucleotide alphabet, CB(v) contains at most 4 vertices. If |CS(g(v))| > |CB(v)|, then no such p exists, and the procedure will fall through to Step 11 and fail. Otherwise, the number of injective maps is |CB(v)|!/(|CB(v)|−|CS(g(v))|)! ≤ 4! = 24; thus, we can easily iterate p through them.
However, there is a constraint that further reduces the candidates for p. If the algorithm succeeds and eventually produces j: S → T, the restriction of f = j ° g from domain B to domain S is j (since g is the identity on S). Thus, by Theorem 3(c), j: S → T and g′: T → S (the restriction of g to T) are inverses. In Step 5, this further limits the choices of p to those satisfying g ° p = idCS(g(v)).]
Theorem 5. If a proper skeleton of B exists, then ConstructProperSkeleton(s) succeeds.
Proof. Let (T, f) be a proper skeleton of B. In Step 5 of ConstructProperSkeleton, if  , one can choose p equal to f restricted to CS(g(v)). Since g ° f = g and g = id on CS(g(v)), we have g ° p = idCS(g(v)). Since all values of f belong to T, the ConstructProperSkeleton procedure succeeds for all
, one can choose p equal to f restricted to CS(g(v)). Since g ° f = g and g = id on CS(g(v)), we have g ° p = idCS(g(v)). Since all values of f belong to T, the ConstructProperSkeleton procedure succeeds for all 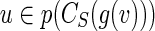 , and thus it also succeeds for v. Hence for each vertex
, and thus it also succeeds for v. Hence for each vertex  , ConstructProperSkeleton(v) successfully finds a proper skeleton in RB(v). Applying this to the source s of B gives a proper skeleton of B.
, ConstructProperSkeleton(v) successfully finds a proper skeleton in RB(v). Applying this to the source s of B gives a proper skeleton of B.
For the rest of this appendix section, assume that ConstructProperSkeleton(s) succeeds and returns some embedding j: S → B and let T = j(S).
Lemma 6. T contains the source and all sinks of B.
Proof. Note that for 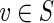 , we have g(v) = v and the assignment j(g(v)) ← v in Step 2 of ConstructProperSkeleton reduces to j(v) ← v.
, we have g(v) = v and the assignment j(g(v)) ← v in Step 2 of ConstructProperSkeleton reduces to j(v) ← v.
Also note that as a skeleton, (S, g) must contain the source and all sinks of B.
Since ConstructProperSkeleton(s) succeeds, its initial invocation assigns j(s) ← s for the source, and recursive invocations include assignments j(v) ← v for each sink.
Thus, the sources and sinks of B will be in the image of j, which is T.
Lemma 7. j ° g is a projection from B to T.
Proof. Note that S = g(G) and T = j(S), so the range of j ° g is T.
Since we constructed j so that g ° j = idS, the restriction g′: T → S is the left inverse of j: S → T, and thus, j ° g′ = idT.
Since j ° g is the identity on its range, it is a projection.
Theorem 8. (j(S), j ° g) is a proper skeleton of B.
Proof. The call ConstructProperSkeleton(s) leads to recursive calls to ConstructProperSkeleton(v) (in Steps 6–7). If ConstructProperSkeleton(s) succeeds, the vertices from the successful recursive invocations form a tree isomorphic to S, and the maps p are combined over all vertices in this tree to give an injection j: S → B for which g ° j = idS. Thus T = j(S) is a subtree of B and j: S → T is a height-preserving isomorphism of trees S and T. By Lemma 6, we have that T contains the source and all sinks of B. By Lemma 7, j ° g is a projection from B to T. Thus, (T,j ° g) is a skeleton of B. Since T is a subtree of B, this is a proper skeleton.
8.3. Removing all complex bulges.
The procedure RemoveComplexBulges (Algorithm 4) presents the whole workflow of bulge removal. We loop over all vertices in graph G. To find a local blob with source s that satisfies conditions (D1) and (D2), we start with a well-localized set B = {s} and iteratively expand it by adding the closest vertex v to s that is outside of B and taking the closure (Steps 6–7). Let G[B] denote the subgraph of G induced by vertex set B; since G is a DAG, so is G[B]. If G[B] is a tree, it is not a bulge, and we continue trying to expand B while possible. If G[B] is not a tree, it is a bulge, and we search for a proper skeleton. If it succeeds, we eliminate the bulge by replacing it with the skeleton found.
Algorithm 4: RemoveComplexBulges
| 1: procedure RemoveComplexBulges |
| 2: globalG |
3: for all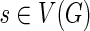 do ▹ s ranges over vertices in the condensed graph do ▹ s ranges over vertices in the condensed graph |
| 4: B ← {s} |
| 5: whileB ⊂ D(s) do |
| 6: Let v be the closest vertex to s that is in D(s) but not in B |
| 7: B = Closure(s, B ∪ {v}) |
| 8: if height of B is larger than 250 orB contains more than 500 vertices then |
| 9: break |
| 10: end if |
| 11: ifG[B] is not a tree then ▹ Condition D1 |
| 12: (S, g) ← ConstructSkeleton(B) |
| 13: ifS is a tree then ▹ Necessary condition for B to have a proper skeleton |
| 14: j ← ConstructProperSkeleton(s, G[B], S, g) |
| 15: if the ConstructProperSkeleton procedure succeeded then ▹ Condition D2 |
| 16: Replace G[B] with a tree j(S) ▹ Project bulge onto a proper skeleton |
| 17: break |
| 18: end if |
| 19: end if |
| 20: end if |
| 21: end while |
| 22: end for |
| 23: end procedure |
To avoid performance issues, the maximum number of vertices in B is additionally bounded by a constant Bmax (set to 500). It is easy to see that the total time spent on expansion of B is O(Bmax). The proper skeleton search procedure can be implemented in almost linear time. Since it might be triggered after each expansion step, the complexity of a blob search from a single vertex is close to O(Bmax2). Finally, we remark that the procedure is heuristic since expansion of B is performed in a greedy manner.
Appendix C: Likelihood Evaluation for Estimating Genomic Distances
This section completes the likelihood evaluation started in Section 4; see that section for notation. The true likelihood of the observed data can be computed as follows:
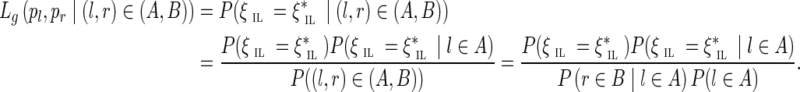 |
Note that 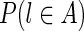 does not depend on the edge gap g and thus can be omitted from the likelihood. The probability
does not depend on the edge gap g and thus can be omitted from the likelihood. The probability 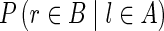 of the right read alignment to the edge B, given that the left read is aligned to the edge A, can be calculated as
of the right read alignment to the edge B, given that the left read is aligned to the edge A, can be calculated as
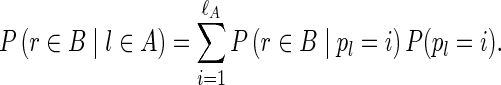 |
(2) |
Here we assume that we can observe the flanking read alignment, when pl and pr take values from 1 to ℓA and from 1 to ℓB, respectively. The probability P(pl = i) is proportional to the coverage ci of the position i of A. If we assume uniform coverage of the edge A, then we can simply put P(pl = i) = 1/ℓA. It is easy to see that
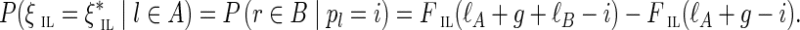 |
This allows us to rewrite (2) as follows:
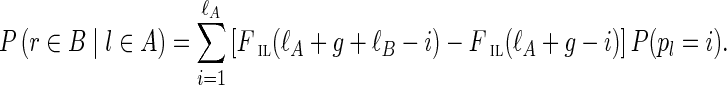 |
From now on, we assume uniform coverage of edge A. We calculate
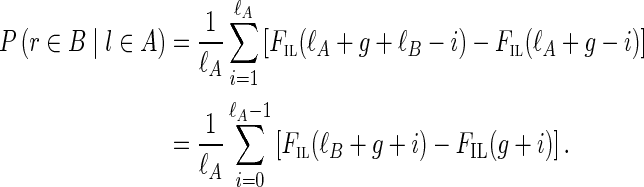 |
(3) |
Introduce 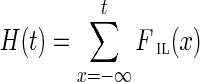 and its estimate
and its estimate 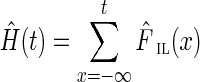 . Then (3) simplifies down to
. Then (3) simplifies down to
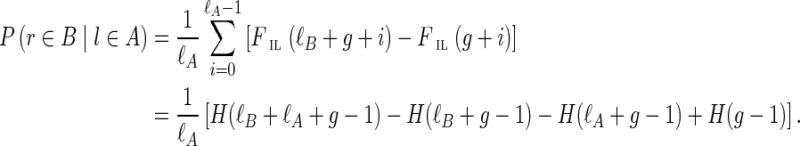 |
Footnotes
CLC Assembly Cell 3.22.55708 (CLC Bio, www.clcbio.com).
Due to uneven coverage in single-cell datasets, contaminants may have coverage comparable to the target genome. Contaminants should be filtered out from the reads before assembly and/or from contigs after assembly; methods for this are beyond the scope of this article. For this article, contaminants with sufficient coverage are regarded as part of Genome and their edges are regarded as “correct edges” rather than “false edges.”
In reality, the genomic multiplicities of edges in DB(Reads, k) are unknown since it is unknown how Genome traverses DB(Reads, k). However, we can estimate some multiplicities even with highly nonuniform coverage, and we can often identify when the multiplicities are zero or nonzero by analyzing the graph structure.
Out of 117 chimeric edges in the graph DB+ (Reads, 55) constructed for the single-cell E. coli dataset ECOLI-SC, 115 have length ≤ n = 250. Here and in further statistics, DB+ (Reads, 55) is the graph that we obtain after doing initial simplifications, including removing condensed edges with average coverage below 10 that satisfy some additional length and topology conditions.
This holds for 97% of long edges in DB(Genome, 55) for the E. coli reference genome. Since this assumption is incorrect for 3% of long edges, it may potentially trigger errors in our chimeric identification procedure. However, it hardly ever triggers errors in practice.
False edges may arise from bulges, tips, chimeric edges, or other errors. This criterion is likely to find false edges due to chimeric edges and tips. False edges in bulges usually are not detected by this criterion, since a circulation through the correct path in a bulge can be rerouted through the incorrect path. False edges in tips potentially can be detected by this criterion, although, tip detection should consider other factors such as edge length. We first eliminate most bulges and tips using algorithms from Bankevich et al. (2012), and thus, when this algorithm is run, most false edges are chimeric.
The graph may also have sources and sinks due to other reasons, e.g., gaps in coverage and chromosome ends.
This component-wise approach is more robust to the failure of the underlying assumption that Genome traverses a cycle in the graph, than the whole-graph circulation approach, since the resulting components are much smaller than the entire de Bruijn graph and failure of the search in one component does not affect the treatment of other components.
In fact, SPAdes creates the assembly graph as a subgraph of the de Bruijn graph so that paths in the assembly graph also represent paths in the de Bruijn graph.
SPAdes (Bankevich et al., 2012) iteratively runs bulge corremoval, tip removal, and chimeric edge removal procedures with gradually changing thresholds. Within each bulge corremoval pass, edges are prioritized in order from lowest to highest coverage.
ABySS 1.3.4, EULER-SR 2.0.1, Ray 2.0.0, Velvet, Velvet-SC, and E+V-SC were run with vertex size 55. A5 and CLC 3.22.55708 were run with default parameters. SOAPdenovo 1.0.4 was run with vertex sizes 27–31. IDBA-UD 1.1.0 was run in its default iterative mode. SPAdes 2.4 was run iteratively with vertex sizes 21, 33, and 55.
Acknowledgments
P.A.P. was supported by the Government of the Russian Federation grant 11.G34.31.0018. P.A.P. and G.T. were supported by the U.S. National Institutes of Health (NIH) grant 3P41RR024851-02S1. G.T. was also supported by the U.S. National Science Foundation (NSF) grant CCF-1115206. R.S. was supported by NSF grants OCE-1148017, OCE-821374, and OCE-1019242. T.W. and S.R.C. were funded by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. R.S.L. and J.S.M. were supported by the Alfred P. Sloan Foundation grant 2007-10-19. J.S.M. was also supported by NIH grant 1R01GM095373. R.S.L. was also supported by NIH grant 2R01HG003647.
Author Disclosure Statement
No competing financial interests exist.
References
- Aho A.V. Hopcroft J.E. Ullman J.D. Data Structures and Algorithms. Addison-Wesley Publishing Company; Boston: 1983. [Google Scholar]
- Bankevich A. Nurk S. Antipov D., et al. SPAdes: A new genome assembly algorithm and its applications to single-cell sequencing. J Comp. Biol. 2012;19:455–477. doi: 10.1089/cmb.2012.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blattner F.R. Plunkett G. Bloch C.A., et al. The complete genome sequence of escherichia coli K-12. Science. 1997;277:1453–1462. doi: 10.1126/science.277.5331.1453. [DOI] [PubMed] [Google Scholar]
- Boisvert S. Laviolette F. Corbeil J. Ray: simultaneous assembly of reads from a mix of high-throughput sequencing technologies. J. of Comp. Biol. 2010;17:1519–1533. doi: 10.1089/cmb.2009.0238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bresler M. Sheehan S. Chan A.H., et al. Telescoper: de novo assembly of highly repetitive regions. Bioinformatics. 2012;28:i311–i317. doi: 10.1093/bioinformatics/bts399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaisson M. Brinza D. Pevzner P. De novo fragment assembly with short mate-paired reads: Does the read length matter? Genome Res. 2009;19:336–346. doi: 10.1101/gr.079053.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chitsaz H. Yee-Greenbaum J. Tesler G., et al. Efficient de novo assembly of single-cell bacterial genomes from short-read data sets. Nat. Biotechnol. 2011;29:915–921. doi: 10.1038/nbt.1966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compeau F. Pevzner P. Tesler G. How to apply de Bruijn graphs to genome assembly. Nat. Biotechnol. 2011;29:987–991. doi: 10.1038/nbt.2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cormen T.H. Leiserson C.E. Rivest R.L., et al. Introduction to Algorithms. 3rd. The MIT Press; Cambridge, Massachusetts: 2009. [Google Scholar]
- Ford L.R. Fulkerson D.R. Flows in Networks. Princeton University Press; Princeton New Jersey: 1962. [Google Scholar]
- Gurevich A. Saveliev V. Vyahhi N., et al. QUAST: quality assessment tool for genome assemblies. Bioinformatics. 2013;29:1072–1075. doi: 10.1093/bioinformatics/btt086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han C. Spring S. Lapidus A., et al. Complete genome sequence of Pedobacter heparinus type strain (HIM 762-3 T) Standards in Genomic Sciences. 2009;1 doi: 10.4056/sigs.22138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huttenhower C. Gevers D. Knight R., et al. Structure, function and diversity of the healthy human microbiome. Nature. 2012;486:207–214. doi: 10.1038/nature11234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasken R. Single-cell genomic sequencing using Multiple Displacement Amplification. Curr. Opin. Microbiol. 2007;10:510–516. doi: 10.1016/j.mib.2007.08.005. [DOI] [PubMed] [Google Scholar]
- Lasken R. Genomic sequencing of uncultured microorganisms from single cells. Nat. Rev. Microbiol. 2012;10:631–640. doi: 10.1038/nrmicro2857. [DOI] [PubMed] [Google Scholar]
- Lasken R. Stockwell T.B. Mechanism of chimera formation during the Multiple Displacement Amplification reaction. BMC Biotechnol. 2007;7:19. doi: 10.1186/1472-6750-7-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li K. Bihan M. Yooseph S. Methe B.A. Analyses of the microbial diversity across the human microbiome. PLoS ONE. 2012;7:e32118. doi: 10.1371/journal.pone.0032118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R. Zhu H. Ruan J., et al. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res. 2010;20:265–272. doi: 10.1101/gr.097261.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean J.S. Lombardo M.-J. Badger J.H., et al. Candidate phylum TM6 genome recovered from a hospital sink biofilm provides genomic insights into this uncultivated phylum. Proc. Natl. Acad. Sci. U. S. A. 2013a;110:E2390–E2399. doi: 10.1073/pnas.1219809110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean J.S. Lombardo M.-J. Ziegler M.G., et al. Genome of the pathogen porphyromonas gingivalis recovered from a biofilm in a hospital sink using a high-throughput single-cell genomics platform. Genome Res. 2013b;23:867–877. doi: 10.1101/gr.150433.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson K. Weinstock G. Highlander S., et al. A catalog of reference genomes from the human microbiome. Science. 2010;328:994–999. doi: 10.1126/science.1183605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nurk S. Bankevich A. Antipov D., et al. Assembling Genomes and Mini-metagenomes from Highly Chimeric Reads. In: Deng M., editor; Jiang R., editor; Sun F., editor; Zhang X., editor. Research in Computational Molecular Biology, Lecture Notes in Computer Science. Vol. 7821. Springer; Berlin Heidelberg: 2013. pp. 158–170. [Google Scholar]
- Peng Y. Leung H.C. Yiu S.-M., et al. IDBA-UD: a de novo assembler for single-cell and metagenomic sequencing data with highly uneven depth. Bioinformatics. 2012;28:1420–1428. doi: 10.1093/bioinformatics/bts174. [DOI] [PubMed] [Google Scholar]
- Pham S.K. Antipov D. Sirotkin A., et al. Pathset graphs: a novel approach for comprehensive utilization of paired reads in genome assembly. J. Comput. Biol. 2013;20:359–371. doi: 10.1089/cmb.2012.0098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rappe M.S. Giovannoni S.J. The uncultured microbial majority. Annu. Rev. Microbiol. 2003;57:369–394. doi: 10.1146/annurev.micro.57.030502.090759. [DOI] [PubMed] [Google Scholar]
- Rocap G. Larimer F. Lamerdin J., et al. Genome divergence in two Prochlorococcus ecotypes reflects oceanic niche differentiation. Nature. 2003;424:1042–1047. doi: 10.1038/nature01947. [DOI] [PubMed] [Google Scholar]
- Seth-Smith H.M. Harris S.R. Skilton R.J., et al. Whole-genome sequences of Chlamydia trachomatis directly from clinical samples without culture. Genome Res. 2013;23:855–866. doi: 10.1101/gr.150037.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson J. Wong K. Jackman S., et al. ABySS: a parallel assembler for short read sequence data. Genome Res. 2009;19:1117–1123. doi: 10.1101/gr.089532.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stepanauskas R. Single cell genomics: an individual look at microbes. Curr. Opin. Microbiol. 2012;15:613–620. doi: 10.1016/j.mib.2012.09.001. [DOI] [PubMed] [Google Scholar]
- Tindall B. Sikorski J. Lucas S., et al. Complete genome sequence of Meiothermus ruber type strain (21T) Standards in Genomic Sciences. 2010;3:26–36. doi: 10.4056/sigs.1032748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tringe S.G. Rubin E.M. Metagenomics: DNA sequencing of environmental samples. Nat. Rev. Genet. 2005;6:805–814. doi: 10.1038/nrg1709. [DOI] [PubMed] [Google Scholar]
- Tritt A. Eisen J.A. Facciotti M.T., et al. An integrated pipeline for de Novo assembly of microbial genomes. PLoS ONE. 2012;7:e42304. doi: 10.1371/journal.pone.0042304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyahhi N. Pyshkin A. Pham S., et al. From de Bruijn graphs to rectangle graphs for genome assembly. WABI. 2012:249–261. [Google Scholar]
- Woyke T. Sczyrba A. Lee J., et al. Decontamination of MDA reagents for single cell whole genome amplification. PLoS ONE. 2011;6:e26161. doi: 10.1371/journal.pone.0026161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woyke T. Xie G. Copeland A., et al. Assembling the marine metagenome, one cell at a time. PLoS ONE. 2009;4:e5299. doi: 10.1371/journal.pone.0005299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie K.M. Truty R.M. Sharpton T.J., et al. Novel bacterial taxa in the human microbiome. PLoS ONE. 2012;7:e35294. doi: 10.1371/journal.pone.0035294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino D. Birney E. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res. 2008;18:821–829. doi: 10.1101/gr.074492.107. [DOI] [PMC free article] [PubMed] [Google Scholar]