Abstract
The problem of inference of family trees, or pedigree reconstruction, for a group of individuals is a fundamental problem in genetics. Various methods have been proposed to automate the process of pedigree reconstruction given the genotypes or haplotypes of a set of individuals. Current methods, unfortunately, are very time-consuming and inaccurate for complicated pedigrees, such as pedigrees with inbreeding. In this work, we propose an efficient algorithm that is able to reconstruct large pedigrees with reasonable accuracy. Our algorithm reconstructs the pedigrees generation by generation, backward in time from the extant generation. We predict the relationships between individuals in the same generation using an inheritance path-based approach implemented with an efficient dynamic programming algorithm. Experiments show that our algorithm runs in linear time with respect to the number of reconstructed generations, and therefore, it can reconstruct pedigrees that have a large number of generations. Indeed it is the first practical method for reconstruction of large pedigrees from genotype data.
Key words: dynamic programming, genotype data, identity by descent, inheritance path, pedigree reconstruction
1. Introduction
Inferring genetic relationships from genotype data is a fundamental problem in genetics and has a long history (Elston and Stewart, 1971; Lander and Green, 1987; Abecasis et al., 2002; Fishelson et al., 2005; Li et al., 2010; Sobel and Lange, 1996). Pedigree reconstruction is a hard problem and even constructing sibling relationships is known to be NP-hard (Kirkpatrick et al., 2011). In this work, we focus on reconstruction methods using genotype data. Various methods have been proposed for automatically reconstructing pedigrees using genotype data, which can be placed into two categories. The first category is methods that reconstruct the haplotypes of the unknown ancestors in the pedigree. Thompson (1986) proposed a machine-learning approach to find the pedigree that maximizes the probability of observing the data. As the method reconstructs both the pedigree graph and the ancestor haplotypes at the same time, it is very time-consuming and can be applied only to small families of 4–8 people. The second category is methods that reconstruct the pedigree directly without reconstructing ancestor haplotypes. Thatte and Steel (2008) proposed an HMM-based model to reconstruct arbitrary pedigree graphs. However, their model, in which every individual passes on a trace of their haplotypes to all of their descendants, is unrealistic. Kirkpatrick et al. (2011) proposed an algorithm to reconstruct pedigrees based on pairwise identity-by-descent (IBD) information without reconstructing the ancestral haplotypes. A generation-by-generation approach is employed, and the pedigree is reconstructed backward in time, one generation at a time. The input of the algorithm is the set of extant individuals with haplotype and IBD information available. At each generation, a compatibility graph is constructed in which the nodes are individuals and the edges indicate the pair of individuals that could be siblings. The edges are defined via a statistical test such that an edge is constructed only when the test score between the pair of individuals is less than a predefined threshold. Sibling sets are identified in the compatibility graph using a Max-clique algorithm iteratively to partition the graph into disjoint sets of vertices. The vertices in the same set have edges connecting to all the other vertices of that set. Both categories of methods encounter difficulties depending on the structure of pedigree. When the individuals are not related through inbreeding, these methods are fast and accurate. However, when inbreeding is present, the reconstruction becomes much more complicated and these methods perform poorly.
In this work, we propose an efficient algorithm, called IPED (Inheritance Path-based Pedigree Reconstruction), which enables the reconstruction of very large pedigrees, with and without the presence of inbreeding. Our algorithm follows the approach of Kirkpatrick et al. (2011), starts from extant individuals, and reconstructs the pedigree generation by generation moving backward in time. For each generation, we predict the pairwise relationships between the individuals at the current generation and create parents for them according to their relationships. When we evaluate the pairwise relationships for a pair of individuals, we consider the pairwise IBD length for their extant descendants, namely the leaf individuals in the pedigree. We then apply a statistical test on the two individuals to determine if they are siblings or not siblings.
A variety of methods have been proposed for pairwise IBD segment detection. Albrechtsen et al. (2009) proposed Relate, which constructs a continuous time Markov model, and the hidden states are the number of alleles shared IBD between pairs of individuals at a given position. Purcell et al. (2007) proposed PLINK, which detects extended chromosomal segmental IBD sharing between pairs of distantly related individuals by using a hidden Markov model (HMM). The underlying hidden IBD state is estimated given the observed identity-by-state (IBS)-sharing and genome-wide level of relatedness between the pair. Gusev et al. (2009) proposed a program GERMLINE based on a dictionary of haplotypes that is used to efficiently discover short exact matches between individuals. These matches are then expanded using dynamic programming to identify long, nearly identical segmental sharing that is indicative of relatedness. Browning and Browning (2010) proposed Beagle, a probabilistic method, to detect IBD with high power. However, the computation time of Beagle IBD scales quadratically with sample size and is impractical for large datasets. It can not be applied to all pairs of individuals in large-scale genome-wide studies. Browning and Browning (2011) further proposed fastIBD specifically for large datasets. FastIBD adopts the same approach with GERMLINE, and the difference is that GERMLINE identifies IBD using shared haplotype length while fastIBD uses haplotype frequency. FastIBD outperforms GERMLINE in accuracy, although, it requires longer computing time.
Recently, Rodriguez et al. (2013) proposed PARENTE, a computationally efficient method to detect related pairs of individuals and shared haplotypic segments within these pairs. PARENTE is based on an embedded likelihood ratio test. It compares the likelihood of the data based on a model that assumes no IBD segment is present versus the likelihood of the data based on a model that assumes IBD segments are present. PARENTE achieves higher accuracy than the current state of the art, especially in detecting short IBD regions. PARENTE assumes that IBD segments are independent of each other along the genome. This assumption is true for distant relatives. However, it may not hold for closely related individuals who share several large IBD segments.
In the meantime, Browning and Browning (2013) incorporated modeling of linkage disequilibrium (LD) into their model and proposed a method called Refined IBD. Refined IBD uses genetic length and a likelihood ratio for an IBD versus non-IBD model to detect the pairwise IBD segments. Refined IBD achieves higher accuracy than fastIBD. However, the gain in power is primarily in the smaller segment sizes, such as 0.5–1 cM. This makes Refined IBD especially useful for analyses in outbred populations.
The statistic test in our approach measures the discrepancy between the observed and the expected pairwise IBD segment lengths for both sibling and non sibling cases. By using any aforementioned pairwise IBD segment detection method, we can identify the average length of IBD segments between any pair of extant individuals. One of the challenges in our approach is to compute the expected IBD length between a pair of extant individuals efficiently in the presence of inbreeding. The CIP and COP methods of Kirkpatrick et al. (2011) are efficient for outbreed pedigrees but very inefficient for inbred pedigrees. This is because for the inbreeding case the alleles from an extant individual can be inherited in an exponential number of ways from his or her ancestors with respect to the number of nodes in the pedigree graph. The CIP algorithm applies a random walk from the ancestor to sample these exponential numbers of ways to estimate the expected IBD length between a pair of extant individuals. In addition, the pedigree needs to be explored multiple times when constructing each generation. Therefore, the algorithm is inefficient even for a relatively small number of generations. In our experiments, CIP can not finish for a family of around 50 individuals with 4 generations.
In order to address this problem, we consider the inheritance paths between the ancestor and the extant individuals, where each inheritance path corresponds to one path in the pedigree from the ancestor to the extant individual. If we know all the inheritance paths from the ancestor to the extant individuals, we can estimate the probability that an allele of the extant individual is inherited from the ancestor. The probability can be further utilized to compute the expected average IBD length between a pair of extant individuals. However, the number of inheritance paths can be exponential, and yet, we observed that their lengths are bounded by the height of the pedigree. Therefore, we use a hash data structure to hash all the inheritance paths of the same length into a bucket, and the number of buckets is bounded by the height of the pedigree and thus is usually small. We save the hash tables for each individual, and we develop a dynamic programming algorithm to populate the hash table of the individuals generation by generation. By doing this, we avoid redundant computation of the inheritance paths where the entire pedigree needs to be explored repeatedly, and thus the dynamic programming algorithm is very efficient. Also, because we avoid the time-consuming sampling step by using the inheritance path, our algorithm IPED is extremely efficient, and it does not need to specify whether or not inbreeding is present, which is a big advantage over COP and CIP. Our experiments show that our algorithm is able to reconstruct the pedigree with inbreeding for a family of 340 individuals with 10 generations in just 14 seconds. To our knowledge, this is the first algorithm that is able to reconstruct such large pedigrees with inbreeding using genotype data.
2. Methods
2.1. Pedigrees
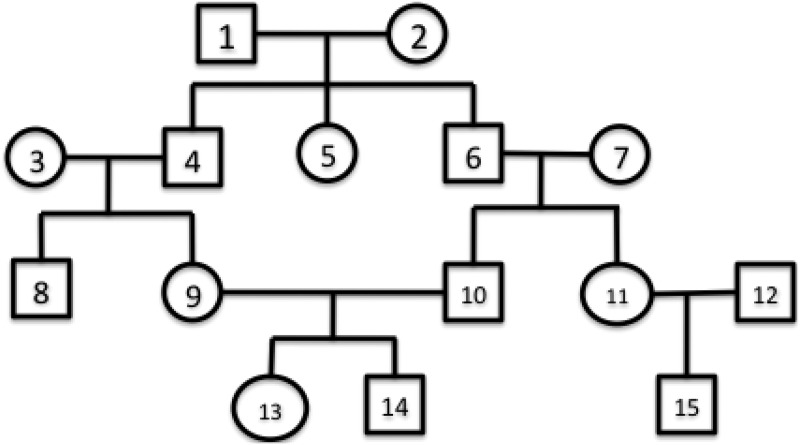
A pedigree graph consists of nodes and edges in which nodes are diploid individuals and edges are between parents and children. Circle nodes are females and boxes are males. An example of a pedigree graph is shown in Figure 1. Parent nodes are also called founders. In the example, individuals 13, 14, 15 are extant individuals, and their founders are individuals 9, 10 and 11, 12, respectively. Outbreeding means an individual mates with another individual from a different family. In the example, 3,4 and 6, 7 are both outbreeding cases. Inbreeding means an individual mates with another individual from the same family. In the example, 9, 10 is an inbreeding case. We can see the inbreeding case is usually more complicated as an individual can inherit from his ancestors in multiple ways. For example, 13, 14 can inherit from 1, 2 in two ways, but 15 can inherit from 1,2 in only one way.
FIG. 1.
An example of a pedigree graph.
As we only have extant individuals and we reconstruct their ancestors, the pedigree is reconstructed backward in time. We use the same notion of generations in Kirkpatrick et al. (2011), namely that generations are numbered backward in time, with larger numbers as older generations. Every individual in the graph is associated with a generation g. All the extant individuals are associated with g = 1, and their direct parents are associated with generation g = 2. The height of a pedigree is the biggest g. We define an inheritance path between a child and his ancestor the same as it is defined in Li et al. (2010), namely as a path between the two corresponding nodes in the pedigree graph. For example, the inheritance path between 1 and 15 consists of nodes 1-6-11-15. There are two inheritance paths between 1 and 13: 1-4-9-13 and 1-6-10-13. Also, we assume the inheritance paths are not directed. In this work, we do not consider pedigrees with half-siblings; we assume an individual only mates with another individual in the same generation.
2.2. Metrics to evaluate the relationship of a pair of individuals
As our algorithm reconstructs the pedigree generation by generation, we need to determine the relationship of any pair of individuals at a generation. We consider two different metrics for extant individuals and ancestral individuals, respectively.
To determine the relationship of a pair of extant individuals, we consider the IBD length of the two individuals. In order to distinguish from IBS, the IBD region needs to be long enough, for example, 1Mb. If we are given the genotypes of the extant individuals, we can compute the IBD regions between a pair of individuals using existing tools such as Beagle (Browning and Browning, 2011). In this work, in our simulation, we assume we are given haplotypes of the extant individuals, and we consider identical regions of length greater than 1Mb between the two individuals as their IBD regions. We consider the average IBD length instead of total IBD length to handle the cases in which IBD regions are unevenly distributed. For simplicity, we use “IBD length” to denote “average IBD length.”
Then, for a pair of extant individuals i, j, we conduct a statistical test and compute a score vi, j as the following:
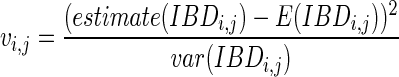 |
(1) |
where estimate(IBDi,j) is the estimated IBD length between individuals i and j, E(IBDi,j) is the expected IBD length between i and j, and var(IBDi,j) is the variance of the IBD length between i and j. Estimate(IBDi,j) can be computed easily given genotypes or haplotypes of individuals i and j. As recombination occurs in meioses, it is shown (Donnelly, 1983) that the length of IBD between i and j follows an exponential distribution exp(Mr), where M is the number of meioses between i and j, and r is the recombination rate that is set as 10−8; in other words, the probability that recombination occurs at any loci is 10−8. Therefore, E(IBDi,j) and var(IBDi,j) are computed as the following:
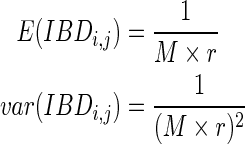 |
(2) |
For the outbreeding case, M = 2(g − 1) where g is the generation. So for extant individuals, as we are constructing the second generation, g = 2. For the inbreeding case, a random walk algorithm whose complexity is exponential is applied. More details will be given in the next section.
As we need to consider both paternal and maternal alleles, our IBD estimation is determined by chromosome by instead of by individual. As i, j both have a pair of chromosomes noted as i1, i2, j1, j2, there are two possible ways to compare them for IBD, namely [(i1, j1), (i2, j2)] and [(i1, j2), (i2, j1)]. We select the way that maximizes the sum of the average IBD length for both chromosomes. Without losing generality, we select [(i1, j1), (i2, j2)]. Then we compute 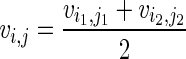 , where
, where 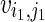 is computed according to Formula 1 by considering the estimated IBD between i1, j1. Notice E(IBDi,j) and var(IBDi,j) don't depend on the chromosomes of i and j.
is computed according to Formula 1 by considering the estimated IBD between i1, j1. Notice E(IBDi,j) and var(IBDi,j) don't depend on the chromosomes of i and j.
In the method of Kirkpatrick et al. (2011), if the test score vi,j is less than a predefined threshold value S, i, j are considered siblings. However, it is not clear how to determine the value S, and the threshold usually varies for individuals of different relatedness. In Kirkpatrick et al. (2011), the threshold is determined empirically by simulating many pedigrees. As we show in our experiments, the performance of the algorithms varies with the threshold.
In our work, we try to avoid using a threshold. As the pair of nodes are either siblings or nonsiblings, we can compute the number of meioses between them for each case. In the case that they are siblings, the number of meioses is 2 and we can compute the length of the expected IBD using Formula 2. For nonsibling cases, we don't know exactly how many meioses there are between the pair of nodes. However, we can compute a lower bound for such a number; namely, the two nodes are first cousins and the number of meioses is 4, which is the minimum number for a pair of nonsibling nodes. Then we can compute the length of the expected IBD for non sibling again using Formula 2. We compare the two test scores and determine the pair of nodes are siblings if the test score for sibling case is lower.
To determine the relationship of a pair of ancestral individuals, we use a similar strategy as the one in Kirkpatrick et al. (2011), assuming individuals k and l are at generation g > 1. The sets of all extant descendants of k and l are K and L, respectively. We compute a score vk,l between k and l as
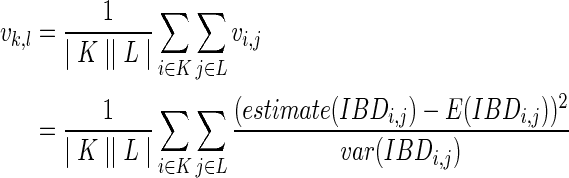 |
(3) |
where |K| is the size of K, the number of extant descendants of k, 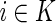 is an extant individual in K, vi,j is computed via Formula 1. Again, we compute vk,l for both sibling case and first-cousin case and determine k, l are siblings if the score for sibling case is lower. More details will be given in the next section on how to compute E(IBDi,j) and var(IBDi,j).
is an extant individual in K, vi,j is computed via Formula 1. Again, we compute vk,l for both sibling case and first-cousin case and determine k, l are siblings if the score for sibling case is lower. More details will be given in the next section on how to compute E(IBDi,j) and var(IBDi,j).
2.3. IPED: Inheritance path-based pedigree reconstruction algorithm
The computation of E(IBDi,j) and var(IBDi,j) is complicated in that the number of possible meioses between i and j can be exponential with respect to the nodes in the pedigree graph. To estimate the expected length of IBD between a pair of extant individuals, we need to consider all possible options for a pair of alleles to inherit from the shared ancestor, which is also exponential to the number of nodes in the pedigree. A random walk algorithm CIP from the founders, with sampling, is applied in Kirkpatrick et al. (2011). However, the sampling is still time-consuming in an exponential search space. What's more, as the reconstruction is generation by generation, from generation 2 to higher generations, the sampling strategy needs to be conducted every time we move from one generation to the next generation backward, which obviously involves redundant computation. Therefore, CIP is not efficient for the inbreeding case. In our experiments, CIP can not finish for a family of around 50 individuals with 4 generations.
To address the two aforementioned problems, we proposed a very efficient algorithm called IPED, which is based on the idea that the probability that a pair of alleles from two individuals are inherited from shared ancestors depends on the number of possible inheritance paths and their corresponding lengths from the shared ancestor. An example of an inheritance path is shown in Figure 1. We can see that the length of inheritance paths determines the number of meioses between the two individuals and thus determines the probability of a pair of alleles from the two extant individuals inherited from the same ancestor. For example, the number of meioses between 8, 9 is 2, as they are siblings, and the distance between them in the pedigree is 2. The number of meioses between 13 and 15 can be either 6 or 4, as there are multiple paths in the pedigree graph between them. In our algorithm, if there are multiple possible numbers of meioses, we used the average value to approximate the IBD length. So for 13 and 15, the average number of meioses is 5.
Therefore, to determine the number of possible distances, or possible meioses between the extant individuals, for any founder in the current generation, we save the number of inheritance paths and the length of these inheritance paths from the founder to all the extant descendant individuals. Notice for inbreeding, there may be an exponential number of inheritance paths with respect to the number of nodes in the pedigree. However, the length of the inheritance paths is finite, which is bounded by the height of the pedigree. Therefore, what we need to save is just a hash table with (length, number) pairs, where the length of the inheritance path is the key and the number of inheritance paths with such length is the value. For example, there are two length-2 paths, five length-3 paths, and six length-4 paths, then we just need to save three pairs (2,2), (3,5), (4,6) instead of saving all nine paths separately. Therefore, we don't need to save exponential numbers of paths. Instead, we must save only a small number of pairs, which are bounded by the height of the pedigree. Notice we need to save such pairs 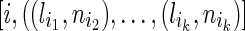 between the founder and every extant descendant of it, where i is the i-th extant descendant, (lik, nik) is the k-th (length, number) pair between the founder and the descendant. We call such pairs inheritance path pair (IPP). Given the number of extant individuals is fixed and usually not a big number, the complexity is bounded by a constant.
between the founder and every extant descendant of it, where i is the i-th extant descendant, (lik, nik) is the k-th (length, number) pair between the founder and the descendant. We call such pairs inheritance path pair (IPP). Given the number of extant individuals is fixed and usually not a big number, the complexity is bounded by a constant.
The inheritance path pairs can be used to compute the possible distances or the average number of meioses of a pair of extant individuals. Assuming a pair of founders G and K with inheritance path pairs 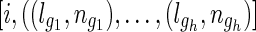 and
and 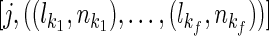 . The average number of meioses between individual i, j can be computed with Algorithm 1, where t is a test option. For the sibling case, t = 1, and for first-cousin case, t = 2. Once the number of meioses is computed, it can be applied to Formula 2 directly to compute the statistic test score.
. The average number of meioses between individual i, j can be computed with Algorithm 1, where t is a test option. For the sibling case, t = 1, and for first-cousin case, t = 2. Once the number of meioses is computed, it can be applied to Formula 2 directly to compute the statistic test score.
Algorithm 1: Calculate the average number of meioses between i, j
Input: t (test option), 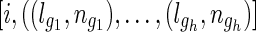 and and 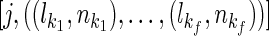
|
| Output: The average number of meioses between i, j |
| Length ← 0 |
| Num ← 0 |
| fora = 1 to h do |
| forb = 1 to f do |
| Num ← Num + nga × nkb |
| Length ← Length + (lga + t + lkb + t) × (nga × nkb) |
| end for |
| end for |
number of meioses ← 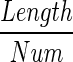
|
Notice some of the inheritance paths may be shared by two extant individuals for the inbreeding case. For example, in Figure 1, the inheritance paths between 1 and 15, 1-6-11-15, and between 1 and 13, 1-6-10-13, share one edge 1-11. Thus, the number of meioses is 4 instead of 6. Using the above algorithm, we will have 6 as the number of meioses. However, as we want to avoid saving the exponential paths explicitly, we just assume the paths do not overlap. Therefore, IPED is not optimal. Instead, it is an approximation algorithm. Another approximation our method is employing is that we approximate the mean and variance of the IBD length by using the average number of meioses (Algorithm 1). In the appendix, we suggest an algorithm that drops this approximation and performs an exact calculation. We also assume that if there are multiple paths between two individuals, it is not possible for the individuals to be IBD through one path at a locus and IBD through another path at the next locus. Such cases should be rare in practice because multiple recombination events should simultaneously occur in the pedigree at one locus. Despite these approximations, our experiments show that IPED achieves good reconstruction accuracy.
Once we save such pairs for each founder at one generation, when we reconstruct the next generation (the parents of the current generation) backward, we need to compute such pairs between all the possible founders in the next generation and all the extant individuals. A naive algorithm is to compute the IPPs between every founder and every extant individual of each generation. However, this requires significant redundant computations since all the nodes of the lower generation will be explored multiple times when computing the inheritance paths. We developed a dynamic programming algorithm in which the IPPs of the current generation can be used to compute the IPPs of the next generation.
The dynamic programming algorithm starts the reconstruction from generation 2 as generation 1 consists of all the known extant individuals. Then at generation 2, assuming we have a founder 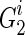 (without losing generality, assuming he is the father) and his k children in generation 1 as
(without losing generality, assuming he is the father) and his k children in generation 1 as 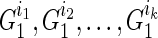 . Then for every paternal allele of each child, obviously we have one possible length-1 inheritance path from the founder. Therefore, we save
. Then for every paternal allele of each child, obviously we have one possible length-1 inheritance path from the founder. Therefore, we save 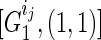 for
for 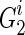 for 1 ≤ j ≤ k. Now let's assume we are at generation T, and we are reconstructing generation T + 1, again, assuming we have a founder
for 1 ≤ j ≤ k. Now let's assume we are at generation T, and we are reconstructing generation T + 1, again, assuming we have a founder 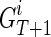 as father and his k children in generation T as
as father and his k children in generation T as 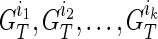 . We then obtain the IPPs for
. We then obtain the IPPs for 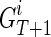 by merging the IPPs for
by merging the IPPs for 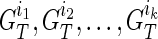 . The recursion is shown below:
. The recursion is shown below:
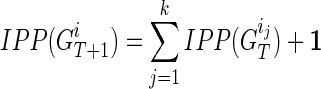 |
where 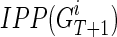 is the set of IPPs for node
is the set of IPPs for node 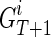 . Assuming for
. Assuming for 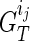 that we have IPPs
that we have IPPs 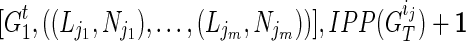 is to update these pairs as
is to update these pairs as 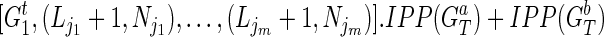 is to merge two sets of IPPs. When we merge two pairs (La, Na) and (Lb, Nb), if La = Lb, we obtain a merged pair (La, Na + Nb). Otherwise we keep the two pairs. Therefore, after the merge, we obtain
is to merge two sets of IPPs. When we merge two pairs (La, Na) and (Lb, Nb), if La = Lb, we obtain a merged pair (La, Na + Nb). Otherwise we keep the two pairs. Therefore, after the merge, we obtain 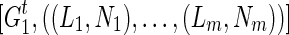 for each extant individual
for each extant individual 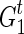 who is the descendant of
who is the descendant of 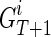 , where
, where 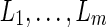 are all unique and m ≤ T + 1. The summation (∑) is similarly defined as the repeated merging operation over multiple sets of IPPs.
are all unique and m ≤ T + 1. The summation (∑) is similarly defined as the repeated merging operation over multiple sets of IPPs.
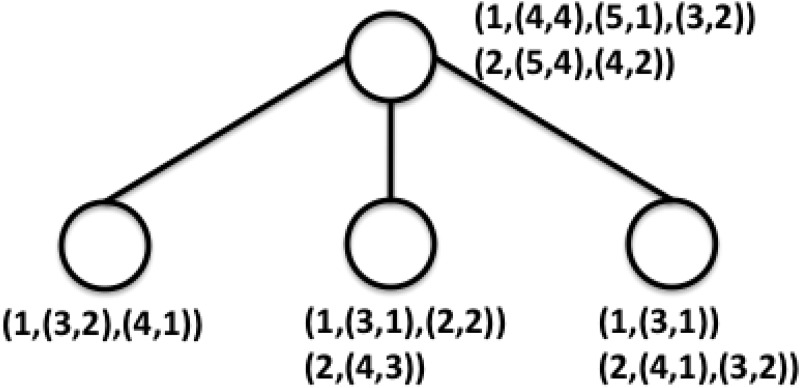
An example of the dynamic programming algorithm is shown in Figure 2. As we can see in the example, when we merge the IPPs, we increase the length of the paths by 1 and add the number for the paths of the same length. The complexity of this dynamic programming algorithm is O(E × k × H), where E is the number of extant individuals, k is the number of direct children for each founder, and H is the height of the pedigree; therefore, it is linear time with respect to the height of the pedigree. Once we compute the inheritance path pairs for each founder, we can calculate the number of meioses of any pair of extant individuals using Algorithm 1 and further compute the test score according to Formula 3.
FIG. 2.
An example of the dynamic programming algorithm.
2.4. Creating parents
Once we determined the relationships of all the individuals of the current generation, we need to create parents for them. In order to guarantee that we create the same parents for all the individuals that are siblings, we create a graph for all the individuals at the current generation. Every individual is a node, and there is an edge between a pair of nodes if they are determined siblings according to the test. We call the graph sibling graph. Then we apply a Max-Clique algorithm (Bron and Kerbosch, 1973) on the sibling graph for the current generation. We select the maximum clique in which all the individuals in the clique are siblings to each other. We then create parents for them and remove them from the sibling graph. We then select the next maximum clique from the remaining sibling graph, and we repeat the procedure until all nodes are selected and all parents are created.
2.5. Performance evaluation
Once we reconstruct the pedigree, we need to evaluate the accuracy of the reconstruction. We can not simply compare the reconstructed pedigree with the true pedigree directly due to graph polymorphism (Kirkpatrick et al., 2010). Therefore, we consider the following metric:
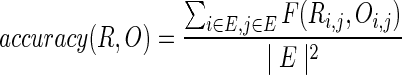 |
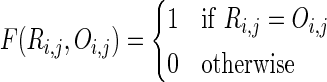 |
where R is the reconstructed pedigree, O is the original pedigree, E is the set of extant individuals, |E| is the number of extant individuals, Ri,j is the distance of individual i and j in pedigree R, and Ri,j = ∞ if i, j are not connected in the pedigree graph. Notice that if there are multiple paths between i and j in R, we select the shortest path. Therefore, in this metric, we only compare the distance of extant individuals. If the distance between a pair of extant individuals in two pedigrees are the same (or two individuals are not connected in both pedigrees as the pedigrees are not high enough), we consider the reconstruction correct for this pair.
3. Experimental Results
We use the simulator from Kirkpatrick et al. (2011) to simulate the pedigrees. Instead of genotype data, we simulate haplotypes directly. The haplotypes of the individuals are generated according to the Wright-Fisher model (Press, 2011) with monogamy. The model takes parameters for a fixed population size, a Poisson number of offspring, and a number of generations (or height of the pedigree). We consider identical regions of length greater than 1Mb as IBD regions. We only compare our algorithm IPED with COP and CIP, as the pedigree size in our simulation is relatively big and can not be handled by other algorithms. All the experiments are done on a 2.4GHz Intel Dual Core machine with 4G memory.
3.1. Outbreeding simulation
We first test the outbreeding case. In the Wright-Fisher simulation, we fix the average number of children of each founder as 3, the individual of each generation as 20, and we vary the height of the pedigree. Notice according to the Wright-Fisher model, the number of individuals simulated in each generation may not be 20. We compare the accuracy of COP and IPED. We randomly simulate 10 pedigrees for each parameter setting and show the averaged accuracy in Table 1. We can see that generally the accuracy drops as the generation and family size increase. IPED achieves slightly better results for outbreeding cases compared to COP. Also IPED is very fast, compared to COP. For all different generations, IPED finishes in less than 1 second.
Table 1.
Outbreeding Accuracy for IPED and COP
| Height | Family size | IPED | COP |
|---|---|---|---|
| g = 3 | 52 | 0.966 | 0.955 |
| g = 4 | 84 | 0.782 | 0.751 |
| g = 5 | 144 | 0.831 | 0.836 |
| g = 6 | 266 | 0.78 | 0.79 |
| g = 7 | 384 | 0.706 | 0.655 |
| g = 8 | 860 | 0.617 | 0.64 |
Average number of children of each founder is 3. The number of individuals for each generation is 20. We vary the height of the pedigree.
IPED, the inheritance Path-based Pedigree Reconstruction Algorithm.
Next, we show that the COP algorithm is affected by the score threshold. As the empirically determined threshold is 0.7 in the work of Kirkpatrick et al. (2011), we vary the score threshold as 0.7 and 0.9. We show the results in Table 2. As we can see, the performance of COP varies with different thresholds. Our algorithm IPED, on the contrary, has the advantage of not relying on any threshold.
Table 2.
Outbreeding Accuracy for COP with Different Test Score Thresholds
| Height | COP (0.7) | COP (0.9) |
|---|---|---|
| g = 4 | 0.905 | 0.89 |
| g = 5 | 0.77 | 0.816 |
| g = 6 | 0.874 | 0.895 |
| g = 7 | 0.684 | 0.605 |
Average number of children in each family is 3. The number of individuals for each generation is 20. We vary the height of the pedigree.
3.2. Inbreeding simulation
Next we test the inbreeding case. As the CIP algorithm is very inefficient for the inbreeding case—even for small pedigrees it takes a long time and most often just simply crashes—we only compare our algorithm with CIP for pedigrees of height 3 and family size 40. IPED achieves an average accuracy of 0.91 while CIP achieves an average accuracy of 0.902 on 10 randomly simulated pedigrees.
Then we compare our algorithm with COP, which is aimed for the outbreeding case, as it is able to finish fast on the simulated datasets. When COP is applied to a pedigree with inbreeding, it simply assumes there is only outbreeding in the pedigree.
We first fix the average number of children as 3 and the individual of each generation as 20, and we vary the height of the pedigree. We show the average accuracy of IPED and COP in Table 3. We can see that for all generations, IPED achieves better results consistently. The accuracy generally drops for both methods. When the generation number is small, such as 3 and 4, the performances of IPED and COP are similar. However, as the pedigree gets bigger and more complicated, our algorithm significantly outperforms COP, which is reasonable as COP doesn't consider inbreeding. The algorithm CIP does consider inbreeding but it is not able to handle pedigrees of this size. IPED, on the contrary, is able to finish in just a few seconds for all parameter settings.
Table 3.
Inbreeding Accuracy of IPED and COP for Different Pedigree Heights
| Height | Family size | IPED | COP | Improvement |
|---|---|---|---|---|
| g = 3 | 50 | 0.93 | 0.924 | 0.6% |
| g = 4 | 62 | 0.722 | 0.715 | 0.9% |
| g = 5 | 74 | 0.689 | 0.605 | 13.9% |
| g = 6 | 88 | 0.65 | 0.446 | 45.7% |
| g = 7 | 94 | 0.599 | 0.335 | 78.8% |
| g = 8 | 110 | 0.533 | 0.297 | 79.5% |
Average number of children in each family is 3. The number of each generation is 20. We vary the height of the pedigree.
Next, we show the performance of both algorithms for different family sizes. We vary the number of individuals in each generation as 20, 40, and 60 and set the generation number as 6. We show the average results from 10 random simulations in Table 4. We can see for all family sizes, our method achieves better accuracies, and the accuracies remain similar to each other, indicating that the performance of our method is very stable with regard to the size of the pedigree. Again, IPED is very fast and finishes in a few seconds for all datasets.
Table 4.
Inbreeding Accuracy of IPED and COP for Different Population Size
| Number of individuals | Family size | IPED | COP |
|---|---|---|---|
| S = 20 | 88 | 0.65 | 0.446 |
| S = 40 | 156 | 0.66 | 0.55 |
| S = 60 | 300 | 0.631 | 0.572 |
Average number of children in each family is 3. We vary the number of individuals for each generation used in the Wright-Fisher model as 20, 40, and 60.
Finally, we simulate a set of deep pedigrees and show the accuracy and running time of our algorithm in Table 5. As we can see, although the accuracy of IPED is relatively low, it is still a few times better than that of COP, which is the only existing algorithm that is able to handle such large pedigrees. In addition, IPED is faster than COP.
Table 5.
Inbreeding Accuracy of IPED and COP for Different Family sizes
| Family size | Generation | IPED | COP | IPED running time (s) | COP running time (s) |
|---|---|---|---|---|---|
| 260 | 10 | 0.365 | 0.125 | 7 | 13 |
| 340 | 10 | 0.227 | 0.08 | 14 | 193 |
Average number of children in each family is 3.
4. Conclusions
We proposed a very efficient algorithm, IPED, for pedigree reconstruction using genotype data. Our method is based on the idea of the inheritance path, where the time-consuming sampling can be avoided. A dynamic programming algorithm is developed to avoid redundant computation during the generation-by-generation reconstruction process. We demonstrate that our method is much more efficient than the state-of-the-art methods, especially when inbreeding is involved in the pedigree. To our knowledge, it is the first algorithm that is able to reconstruct pedigrees with inbreeding containing hundreds of individuals with tens of generations. Our algorithm still does not consider all possible complicated cases in pedigrees, such as half-siblings. Also, it reconstructs pedigree only from the extant individuals. When the genotypes of the internal individuals are known, it is helpful to use all such information. We would like to address these problems in our future work.
5. Appendix
5.1. Exact calculation of the mean and variance of IBD length
An important part of our method is calculating the mean and variance of IBD length between individuals i and j, namely E(IBDi,j) and var(IBDi,j), that are used in Formula 1. To calculate these quantities, we used an approximation that first calculates the average number of meioses (Algorithm 1) and then uses this number in Formula 2. Here we suggest an improved algorithm for obtaining E(IBDi,j) and var(IBDi,j) with an exact calculation.
Suppose that we have q paths between i and j. What are the probabilities that i and j will be IBD through these paths? The probability that an allele is inherited from a parent to a child is 1/2. Thus, the probability that an allele will be IBD through a path with length l is 2-l. This indicates that not all paths are equal; individuals will be more likely IBD through shorter paths than longer paths. Therefore, we can improve the calculation of E(IBDi,j) and var(IBDi,j) by taking into account these unequal probabilities of the paths; particularly, we calculate the weighted average.
Let 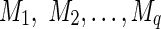 be the lengths of the q paths (or equivalently, the numbers of meioses of the paths). Given the condition that i and j are IBD, the probability of the paths will be proportional to the probability of IBD through the paths (by Bayes' theorem). Thus, the weighted mean of the IBD length will be
be the lengths of the q paths (or equivalently, the numbers of meioses of the paths). Given the condition that i and j are IBD, the probability of the paths will be proportional to the probability of IBD through the paths (by Bayes' theorem). Thus, the weighted mean of the IBD length will be
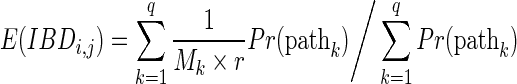 |
where 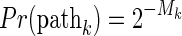 .
.
We can also calculate the variance of the IBD length using the conditional variance formula. Let 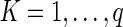 be the indicator variable denoting which path we take. Then, by the standard conditional variance formula,
be the indicator variable denoting which path we take. Then, by the standard conditional variance formula,
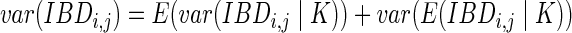 |
The first summand is
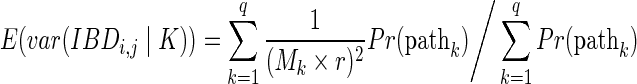 |
The second summand is
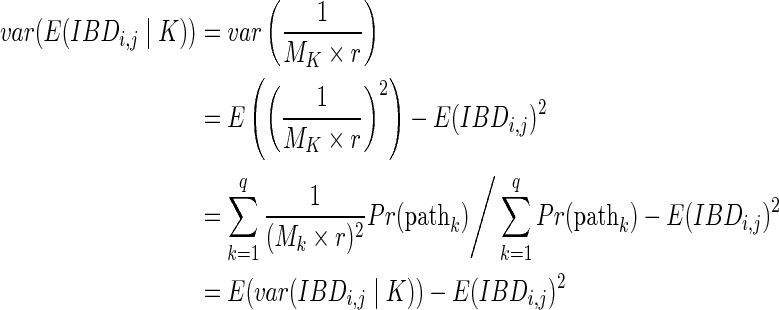 |
Summing the two summands,
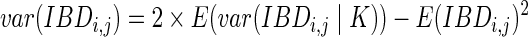 |
Using this observation, we can modify Algorithm 1 resulting in an improved approach described in Algorithm 2.
Algorithm 2: Calculate the exact mean and variance of the IBD length between i, j
Input: t (test option), 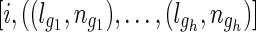 and and 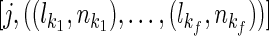
|
| Output: The mean and variance of the IBD length between i, j |
| ProbSum ← 0 |
| Sum1 ← 0 |
| Sum2 ← 0 |
| fora = 1 to h do |
| forb = 1 to f do |
| M ← lga + t + lkb + t |
| P ← 2-M |
| ProbSum ← ProbSum + P × nga × nkb |
| Sum1 ← Sum1 + P × nga × nkb × 1/(M × r) |
| Sum2 ← Sum2 + P × nga × nkb × 1/(M × r)2 |
| end for |
| end for |
| E(IBDi,j) ← Sum1/ProbSum |
| var(IBDi,j) ← 2 × Sum2/ProbSum - E(IBDi,j)2 |
It should be noted that Algorithm 2 still assumes that two inheritance paths do not overlap, which is often not the case as we have already explained. If this assumption holds, Algorithm 2 is an exact calculation for E(IBDi,j) and var(IBDi,j).
Acknowledgments
The authors would like to thank Bonnie Kirkpatrick for her help with the pedigree simulation. Z.W. and E.E. are supported by National Science Foundation grants 0513612, 0731455, 0729049, 0916676, and 1065276, and National Institutes of Health grants K25-HL080079, U01-DA024417, P01-HL30568, and PO1-HL28481. B.H. is supported by National Institutes of Health grant NIH-NIAMS 1R01AR062886-01.
Author Disclosure Statement
No competing financial interests exist.
References
- Abecasis G. Cherny S. Cookson W., et al. Merlin-rapid analysis of dense genetic maps using sparse gene flow trees. Nature Genetics. 2002;30:97–101. doi: 10.1038/ng786. [DOI] [PubMed] [Google Scholar]
- Albrechtsen A. Sand Korneliussen T. Moltke I., et al. Relatedness mapping and tracts of relatedness for genome-wide data in the presence of linkage disequilibrium. Genetic Epidemiology. 2009;33:266–274. doi: 10.1002/gepi.20378. [DOI] [PubMed] [Google Scholar]
- Bron C. Kerbosch J. Algorithm 457: finding all cliques of an undirected graph. Communications of the ACM. 1973;16:575–577. [Google Scholar]
- Browning B. Browning S. A fast, powerful method for detecting identity by descent. The American Journal of Human Genetics. 2011;88:173–182. doi: 10.1016/j.ajhg.2011.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning B.L. Browning S.R. Improving the accuracy and efficiency of identity by descent detection in population data. Genetics. 2013;194:459–471. doi: 10.1534/genetics.113.150029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning S.R. Browning B.L. High-resolution detection of identity by descent in unrelated individuals. The American Journal of Human Genetics. 2010;86:526–539. doi: 10.1016/j.ajhg.2010.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnelly K. The probability that related individuals share some section of genome identical by descent. Theor. Popul. Biol. 1983;23:34–63. doi: 10.1016/0040-5809(83)90004-7. [DOI] [PubMed] [Google Scholar]
- Elston R. Stewart J. A general model for the genetic analysis of pedigree data. Human Heredity. 1971;21:523–542. doi: 10.1159/000152448. [DOI] [PubMed] [Google Scholar]
- Fishelson M. Dovgolevsky N. Geiger D. Maximum likelihood haplotyping for general pedigrees. Human Heredity. 2005;59:41–60. doi: 10.1159/000084736. [DOI] [PubMed] [Google Scholar]
- Gusev A. Lowe J.K. Stoffel M., et al. Whole population, genome-wide mapping of hidden relatedness. Genome Research. 2009;19:318–326. doi: 10.1101/gr.081398.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick B. Li S. Karp R., et al. Pedigree reconstruction using identity by descent. J. Comp. Biol. 2011;18:1181–1193. doi: 10.1089/cmb.2011.0156. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick B. Reshef Y. Finucane H., et al. Comparing pedigree graphs. 2010;arXiv:1009.0909. doi: 10.1089/cmb.2011.0254. [DOI] [PubMed] [Google Scholar]
- Lander E. Green P. Construction of multilocus genetic linkage maps in humans. Proceedings of the National Academy of Sciences. 1987;84:2363. doi: 10.1073/pnas.84.8.2363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X. Yin X. Li J. Efficient identification of identical-by-descent status in pedigrees with many untyped individuals. Bioinformatics. 2010;26:i191–i198. doi: 10.1093/bioinformatics/btq222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press W. Wright-fisher models, approximations, and minimum increments of evolution. 2011. www.nr.com/whp/notes/wrightfisher.pdf www.nr.com/whp/notes/wrightfisher.pdf
- Purcell S. Neale B. Todd-Brown K., et al. Plink: a tool set for whole-genome association and population-based linkage analyses. The American Journal of Human Genetics. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez J.M. Batzoglou S. Bercovici S. An accurate method for inferring relatedness in large datasets of unphased genotypes via an embedded likelihood-ratio test. Proceedings of the 17th International Conference on Research in Computational Molecular Biology, RECOMB’13, 212–229; Berlin, Heidelberg. Springer-Verlag; 2013. [Google Scholar]
- Sobel E. Lange K. Descent graphs in pedigree analysis: applications to haplotyping, location scores, and marker-sharing statistics. American Journal of Human Genetics. 1996;58:1323. [PMC free article] [PubMed] [Google Scholar]
- Thatte B. Steel M. Reconstructing pedigrees: A stochastic perspective. Journal of Theoretical Biology. 2008;251:440–449. doi: 10.1016/j.jtbi.2007.12.004. [DOI] [PubMed] [Google Scholar]
- Thompson E. Pedigree analysis in human genetics. Johns Hopkins University Press; Baltimore, MD: 1986. [Google Scholar]