Abstract
A phylogenetic network is a model for reticulate evolution. A hybridization network is one type of phylogenetic network for a set of discordant gene trees and “displays” each gene tree. A central computational problem on hybridization networks is: given a set of gene trees, reconstruct the minimum (i.e., most parsimonious) hybridization network that displays each given gene tree. This problem is known to be NP-hard, and existing approaches for this problem are either heuristics or making simplifying assumptions (e.g., work with only two input trees or assume some topological properties).
In this article, we develop an exact algorithm (called PIRNC) for inferring the minimum hybridization networks from multiple gene trees. The PIRNC algorithm does not rely on structural assumptions (e.g., the so-called galled networks). To the best of our knowledge, PIRNC is the first exact algorithm implemented for this formulation. When the number of reticulation events is relatively small (say, four or fewer), PIRNC runs reasonably efficient even for moderately large datasets. For building more complex networks, we also develop a heuristic version of PIRNC called PIRNCH. Simulation shows that PIRNCH usually produces networks with fewer reticulation events than those by an existing method.
PIRNC and PIRNCH have been implemented as part of the software package called PIRN and is available online.
Key words: algorithms, hybridization network, parsimony, phylogenetic network, phylogenetics, reticulate evolution
1. Introduction
It is well known that reticulate evolution plays a significant role in shaping the evolutionary history of many species. There are several reticulate evolutionary processes, such as horizontal gene transfer and hybrid specification. To better model the effects of these reticulate evolutionary processes, a network-based model called a phylogenetic network (rather than the traditional phylogenetic tree) is needed. Briefly, a phylogenetic network is a directed acyclic graph, which has nodes (called reticulation nodes) with more than one incoming edge. See Figure 1 for an illustration of phylogenetic networks. The study of phylogenetic networks has received significant attention in recent years. Refer to the recent books by Huson et al. (2010) and Morrison (2011) for more background on phylogenetic networks.
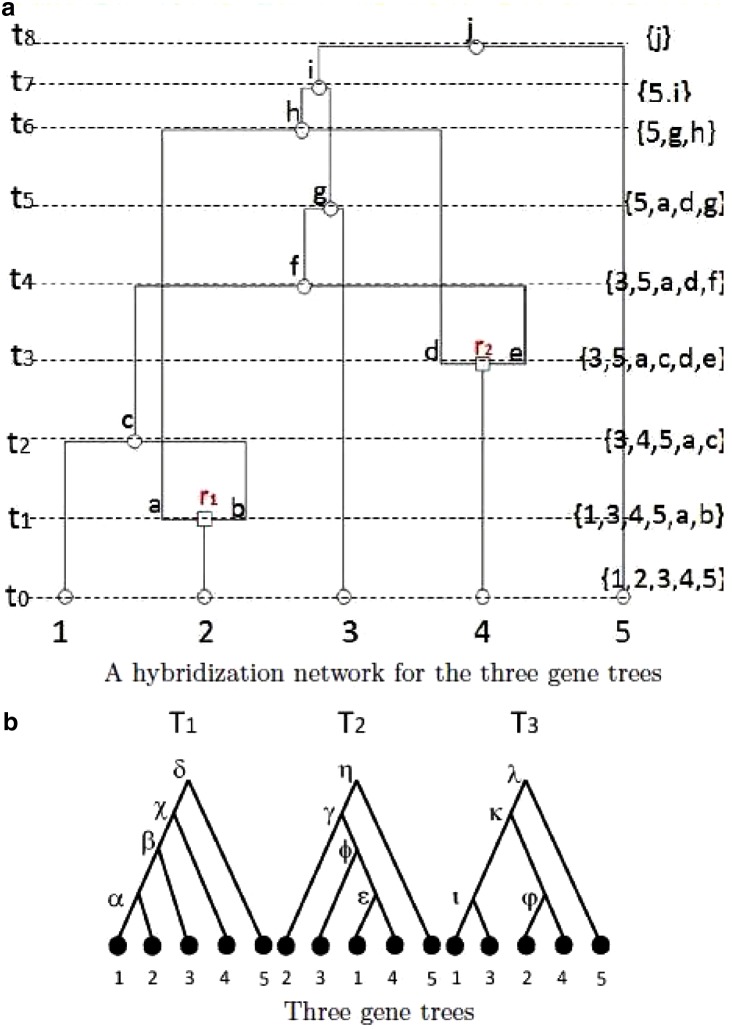
FIG. 1.
An illustration of a hybridization network with two reticulation events for three gene trees T1, T2, and T3. Reticulation: square. Speciation (coalescence): oval. Dotted lines: time. Configurations are shown to the right, one for each time line. Leaf labels: numbers. Internal nodes (subtrees) of gene trees are labeled by Greek letters.
Different models and formulations of phylogenetic networks with various modeling assumptions and different types of input have been proposed and studied. In this article, we focus on one specific formulation of the phylogenetic network, called the “hybridization network” (Semple, 2007; Huson et al., 2010), which takes a set of gene trees as input. Here, a gene tree models the evolutionary history of a gene. Due to reticulate evolution, the gene trees may have different topologies. The goal is to construct a phylogenetic network that “displays” each of the gene trees. We provide more precise definitions in Section 2. Most current approaches for hybridization network inference are based on the parsimony principle (Huson et al., 2010; Morrison, 2011). That is, the goal is to find the hybridization networks with the smallest amount of reticulation events. In this article, we also follow the parsimony principle.
It is often believed that hybridization networks may be useful in studying reticulate evolution. However, hybridization networks have not been widely used by biologists (Morrison, 2011). One obstacle is the computational challenge. Many existing computational formulations for inferring hybridization networks are known to be NP complete. Due to the computational difficulty, most existing approaches are heuristic. Moreover, existing approaches often impose simplifications on the hybridization network formulation. Simplification can be on the modeling of hybridization networks or the types of inputs allowed. For example, phylogenetic networks with structural assumptions such as galled networks (Huson and Klopper, 2007) or the so-called level-k networks as in van Iersel et al. (2008) have been previously studied. There are also approaches for building phylogenetic networks that display not full gene trees but clusters of gene trees (e.g., van Iersel et al., 2010). Another simplification often made in the study of hybridization networks is that only two input gene trees are allowed (e.g., Semple, 2007; Wu and Wang, 2010; Albrecht et al., 2012). Clearly, methods allowing multiple gene trees are likely to be more useful with the more available gene sequence data. Currently, there are only a few heuristic methods (Wu, 2010; Park and Nakhleh, 2012; Chen and Wang, 2012, 2013) on hybridization network construction or reticulation level estimation that allow multiple gene trees and do not rely on structural assumptions.
In this article, we develop an algorithm (called PIRNC) for inferring the parsimonious hybridization networks from multiple gene trees. To the best of our knowledge, PIRNC is the first exact algorithm for this formulation. PIRNC has the following features.
• PIRNC takes a set of rooted binary gene trees as input and constructs a hybridization network that displays each of the gene trees.
• PIRNC is an exact algorithm (i.e., it infers the most parsimonious networks).
• PIRNC allows any number of gene trees in principle, although longer running time and larger amount of memory may be needed for larger input. PIRNC also does not impose any structural constraints (for example, “gall-like” structures as in Huson et al., 2009; Gusfield, 2005) on phylogenetic networks.
• The running time of PIRNC is largely decided by the number of reticulation events in the inferred hybridization networks. When the number of reticulation events is relatively small (say five or fewer), PIRNC runs reasonably fast even for moderately large problems (say, 5 gene trees with 30 taxa). On the other hand, for some larger dataset with, say, 6 or more reticulation events for 5 gene trees with 30 taxa, PIRNC becomes slow.
PIRNC may be best applied for inferring hybridization networks with relatively simple structures (i.e., the number of reticulation events is relatively small). We note that real hybridization networks may indeed have relatively small numbers of reticulation events as suggested in Morrison (2011). Nevertheless, constructing parsimonious hybridization networks with larger number of reticulations is still an interesting problem from the computational perspective. In this article, we also develop a heuristic version of PIRNC, called PIRNCH. PIRNCH does not always find the most parsimonious networks, but simulation shows that PIRNCH usually produces networks with fewer reticulations than an existing method.
2. Definitions and Background
Throughout this article, we assume a phylogenetic tree is rooted, binary, and leaf-labeled by a set of species (called taxa). In-degrees of all vertices (also called nodes) in a tree, except the root, are one. For convenience, for a tree node v, we often call the subtree rooted at v as the subtree v. Our definition of hybridization networks is essentially equivalent to that in Semple (2007) with only some minor differences. A hybridization network (sometimes simply network) is a directed acyclic graph with vertex set V and edge set E, where some nodes in V are labeled by taxa. V can be partitioned into VT (called tree nodes) and VR (called reticulation nodes). E can be partitioned into ET (called tree edges) and ER (called reticulation edges). Moreover,
1. Except the root, each node must have at least one incoming edge.
2. Reticulation nodes have in-degree two. Tree nodes have in-degree one.
3. ER contains edges that go into some reticulation nodes. ET contains edges that go into some tree nodes.
4. A node is labeled by some taxon iff its out-degree is zero (i.e., is a leaf ).
In addition, we have one more restriction:
R1 For a network  , when only one of the incoming edges of each reticulation node is kept and the other is deleted, we always derive a tree T′.
, when only one of the incoming edges of each reticulation node is kept and the other is deleted, we always derive a tree T′.
In this article, we assume the in-degree of reticulation nodes is two. Note that we can always convert a reticulation node with in-degree of three or more to several reticulation nodes with in-degree of two (Wu, 2010). Also a network with only reticulation nodes with in-degree of two may be consolidated when several nodes with in-degree of two is merged into one node with in-degree of three or more. We call a branch of a hybridization network or a tree a “lineage.” Intuitively, a lineage corresponds to some extant or ancestral species modeled in the phylogenetic network. There are two types of lineages: leaf lineages (those originated from the leaves of the network) and internal lineages (which correspond to ancestral species of the network). An internal lineage in a network is created by either a reticulation or a coalescence.
We first consider the derived tree T′ (that is embedded in  ) as stated in R1. When we recursively remove nonlabeled leaves and contract edges to remove degree-two nodes of T′ (called cleanup), we obtain a phylogenetic tree T (for the same set of species as in
) as stated in R1. When we recursively remove nonlabeled leaves and contract edges to remove degree-two nodes of T′ (called cleanup), we obtain a phylogenetic tree T (for the same set of species as in  ). Now suppose we are given a phylogenetic tree T. We say T is displayed in
). Now suppose we are given a phylogenetic tree T. We say T is displayed in  when we can obtain an induced tree T′ from
when we can obtain an induced tree T′ from  by properly choosing a single edge to keep at each reticulation node so that T′ is topologically equivalent to T after cleanup. We denote the induced T′ (if exists) as
by properly choosing a single edge to keep at each reticulation node so that T′ is topologically equivalent to T after cleanup. We denote the induced T′ (if exists) as  . We call the choices of which reticulation edges to keep (and prune) the “display choices.” In Figure 1, each of the three trees is displayed in the network. For example, one possible display choice for T1 (the left-most gene tree) is keeping lineages b and d (and pruning lineages a and e).
. We call the choices of which reticulation edges to keep (and prune) the “display choices.” In Figure 1, each of the three trees is displayed in the network. For example, one possible display choice for T1 (the left-most gene tree) is keeping lineages b and d (and pruning lineages a and e).
For a hybridization network 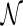 , we define the hybridization number (denoted as
, we define the hybridization number (denoted as  ) as the number of reticulation nodes. Note that this is equivalent to using the summation of in-degree minus one of all reticulation nodes as in Semple (2007), since the in-degree of a reticulation node is assumed to be two. Sometimes
) as the number of reticulation nodes. Note that this is equivalent to using the summation of in-degree minus one of all reticulation nodes as in Semple (2007), since the in-degree of a reticulation node is assumed to be two. Sometimes 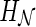 is also called the number of reticulation events in
is also called the number of reticulation events in 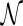 . Recall that the optimal hybridization network is the one with the smallest hybridization number. Now we formulate the central problem in this article.
. Recall that the optimal hybridization network is the one with the smallest hybridization number. Now we formulate the central problem in this article.
The most parsimonious hybridization network problem. Given K rooted and binary gene trees 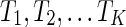 (with the same n taxa), construct the most parsimonious hybridization network
(with the same n taxa), construct the most parsimonious hybridization network  such that (i) each gene tree Ti is displayed in
such that (i) each gene tree Ti is displayed in 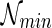 and (ii)
and (ii) 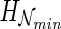 is minimized among all possible such networks. We call
is minimized among all possible such networks. We call 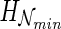 the hybridization number of
the hybridization number of 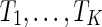 .
.
Constructing parsimonious hybridization networks for a set of K gene trees is a computationally challenging problem. Even the two-gene-tree (i.e., K = 2) case is known to be NP-complete (Bordewich and Semple, 2007). This two-gene-tree case is closely related to computing the subtree prune and regraft (SPR) distance of two trees, a well-studied NP complete problem (Hein, et al., 1996; Bordewich and Semple, 2004) in phylogenetics. Nonetheless, there are several practical algorithms for the SPR distance problem (e.g., Wu, 2009; Whidden and Zeh, 2009). For the two-gene-tree case of the hybridization network problem, there are also several exact methods (Bordewich et al., 2007; Wu and Wang, 2010; Albrecht et al., 2012). Although the worst case running time of these practical methods are exponential, these methods may work reasonably well in practice. A commonly used concept in two-gene-tree case of reticulate networks and the SPR distance problem is the so-called maximum agreement forest (MAF). This is essentially the main formulation used by many existing approaches to these two problems. The divide and conquer approach, developed in Whidden and Zeh (2009), and related approaches (Albrecht et al., 2012; Chen and Wang, 2013) are currently the best performing approaches for these two problems.
It becomes more computationally challenging when there are three or more gene trees. There are currently only a few heuristic methods for either estimating the hybridization number 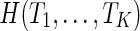 or reconstructing near optimal networks for trees
or reconstructing near optimal networks for trees 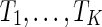 when K ≥ 3 (Wu, 2010; Park and Nakhleh, 2012; Chen and Wang, 2012). There are no existing methods for the exact computation of the hybridization number or reconstructing parsimonious networks with three or more trees.
when K ≥ 3 (Wu, 2010; Park and Nakhleh, 2012; Chen and Wang, 2012). There are no existing methods for the exact computation of the hybridization number or reconstructing parsimonious networks with three or more trees.
3. Constructing Parsimonious Hybridization Networks
Our approach does not follow the commonly used MAF formulation. Rather, it takes a backward-in-time coalescent-style approach.
3.1. The backward/in/time view
The backward/in/time view is the foundation of our method. With a forward/in/time view, a tree node in a hybridization network refers to a speciation event where one lineage splits into two lineages; at a reticulation node a new lineage is created after two incoming lineages are merged. In this article, we take a backward-in-time view instead. In this view of time, a tree node is called a coalescence: two lineages coalesce into a single lineage at a tree node when looking backward in time. Similarly, in this view, two new lineages are created by the reticulation of a lineage at a reticulation node. As an example, we consider the network shown in Figure 1. Lineages 1 and b coalesce at time t2 to form the lineage c, and a reticulation occurs for the lineage 4 at t3 and creates lineages d and e. Recall that a network needs to display gene trees. So when we trace backward in time in the network, we need to ensure the network displays each gene tree T. It is important to note that a lineage created by a reticulation may “vanish” (i.e., be pruned) when we make the display choices for T. For example, to display T2 (the middle tree in Fig. 1), the lineage b vanishes. Displaying a tree T within a network can also be explained with this view of time. Imagine that we “cut” the network with the time line at time t, and we only consider the portion of the network more recent than time t. We say a subtree Ts of T is displayed by time t if Ts can be obtained at the lineage li where li is cut by the time line t. That is, we can obtain Ts by following lineages backward in time to li at t. In this case, we also say Ts is displayed in li or li displays Ts. When we start at the present time, only leaves (i.e., subtrees with singleton taxa) of T are displayed. As the time line moves backward, larger and larger subtrees are displayed. For example, in Figure 1, at time t0, only singleton subtrees of T1 are displayed by t0. When we move the time back, the subtree α is also displayed by t2 (and is displayed in the lineage c). In the end, we reach the root of the network where the entire T is displayed. This simple observation is important for the PIRNC algorithm described here.
3.2. The high-level idea
Here is the high-level idea of the PIRNC algorithm. We take a coalescent-style approach by going backward in time. At a particular time of phylogenetic history, there is a set of lineages that are present at that time. Let us call the snapshot of the phylogenetic history at a particular time the “ancestral configuration” (or simply configuration), which specifies the set of ancestral lineages alive at that time. At present time, there is a single fixed configuration, which contains all the n extant lineages in the given gene trees. When moving backward in time, configuration changes when some genealogical events (namely coalescence and reticulation) occur. Here, we assume there are no two genealogical events occurring at exactly the same time. For example, consider the sample network in Figure 1. The initial configuration (denoted as 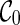 ) contains lineages 1, 2, 3, 4, and 5. The first event backward in time from the present time is the reticulation r1 of lineage 2 at time t1, which creates two new lineages a and b. So right before (i.e., more ancient than) t1, the configuration contains 1, 3, 4, 5, a, and b. When we continue tracing backward, the coalescence between lineage 1 and b happens at time t2, which creates a new lineage c. Then the new configuration right before t2 contains five lineages: 3, 4, 5, a, and c. Eventually we reach the final configuration (denoted as
) contains lineages 1, 2, 3, 4, and 5. The first event backward in time from the present time is the reticulation r1 of lineage 2 at time t1, which creates two new lineages a and b. So right before (i.e., more ancient than) t1, the configuration contains 1, 3, 4, 5, a, and b. When we continue tracing backward, the coalescence between lineage 1 and b happens at time t2, which creates a new lineage c. Then the new configuration right before t2 contains five lineages: 3, 4, 5, a, and c. Eventually we reach the final configuration (denoted as 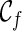 , which contains a single lineage j).
, which contains a single lineage j).
However, when only gene trees are given, we do not know what coalescent and reticulation events will occur nor the series of configurations at the time of genealogical events when tracing backward in time. In fact, if we knew, we would have already found the true hybridization network: configurations at all the genealogical events specify precisely the phylogenetic history. The key for our approach is finding configurations at genealogical events that correspond to the most parsimonious network. Suppose we start with one configuration 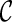 and consider what configurations can be reached from
and consider what configurations can be reached from 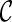 by a single genealogical event backward in time. Here, each pair of lineages in
by a single genealogical event backward in time. Here, each pair of lineages in 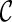 can coalesce and each lineage of
can coalesce and each lineage of 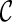 can have a reticulation. New configurations are generated with these genealogical events. If we trace backward long enough, we will reach the final configuration
can have a reticulation. New configurations are generated with these genealogical events. If we trace backward long enough, we will reach the final configuration 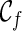 , where the hybridization network corresponding to
, where the hybridization network corresponding to 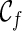 displays each given gene tree. If we also ensure
displays each given gene tree. If we also ensure 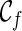 is the one that uses the fewest number of reticulations, we then know the minimum number of reticulations needed for the given input gene trees. Once such a
is the one that uses the fewest number of reticulations, we then know the minimum number of reticulations needed for the given input gene trees. Once such a 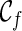 is found, we can then identify the series of genealogical events leading to
is found, we can then identify the series of genealogical events leading to 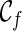 , and this allows us to build the most parsimonious network.
, and this allows us to build the most parsimonious network.
The approach sketched above is a simple strategy. However, a moment of thoughts indicates that its naïve implementation will be too slow: the space of possible configurations is immense. Consider a configuration with n lineages from which we are to search for new configurations. If no restriction is imposed, there are  possible coalescences and n reticulations among the n lineages. Suppose n is 30. Then there are up to 465 new configurations reachable from one configuration with one reticulation or one coalescence. The number of possible configurations to explore quickly becomes prohibitively large shortly after the start of the configuration search. In this article, we show that the basic approach can be made much faster with additional techniques, which allows us to “cut corners” while still ensuring the finding of optimal hybridization networks. The key to our approach is that the search is guided by the given gene trees. That is, our algorithm is based on guided configuration search and configurations that do not lead to parsimonious networks for the given gene trees may be pruned early. We have also developed additional speedup techniques that further improve the efficiency. Together they turn the basic strategy into a practical approach.
possible coalescences and n reticulations among the n lineages. Suppose n is 30. Then there are up to 465 new configurations reachable from one configuration with one reticulation or one coalescence. The number of possible configurations to explore quickly becomes prohibitively large shortly after the start of the configuration search. In this article, we show that the basic approach can be made much faster with additional techniques, which allows us to “cut corners” while still ensuring the finding of optimal hybridization networks. The key to our approach is that the search is guided by the given gene trees. That is, our algorithm is based on guided configuration search and configurations that do not lead to parsimonious networks for the given gene trees may be pruned early. We have also developed additional speedup techniques that further improve the efficiency. Together they turn the basic strategy into a practical approach.
3.3. The guided search for the parsimonious configurations
Ancestral configuration is the basic data structure used in our algorithm. An ancestral configuration 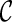 contains a set of lineages
contains a set of lineages 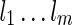 . Recall that each subtree Ts of T is also displayed in some lineage li of the network. Initially,
. Recall that each subtree Ts of T is also displayed in some lineage li of the network. Initially, 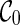 only displays the singleton subtrees. As we explore the configuration space backward in time, we may find configurations where increasingly larger input subtrees are displayed within their lineages. The search stops when each whole gene tree is displayed in the single lineage of the final configuration
only displays the singleton subtrees. As we explore the configuration space backward in time, we may find configurations where increasingly larger input subtrees are displayed within their lineages. The search stops when each whole gene tree is displayed in the single lineage of the final configuration 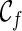 . Therefore, the set of subtrees displayed in a configuration measures the progress made from
. Therefore, the set of subtrees displayed in a configuration measures the progress made from 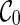 to the current configuration: the more large subtrees displayed in a configuration, the closer we are in finishing the construction of hybridization networks. For example, in Figure 1, the lineage 2 only displays singleton subtrees with taxon 2. And so do the lineages a and b. The lineage c is created by the coalescence of lineages 1 and b. Thus, the lineage c displays the subtree α. Note that b is created by a reticulation and thus b can vanish (i.e. b may be pruned in displaying a subtree). Thus, c also displays the singleton subtree with taxon 1 (in case b vanishes).
to the current configuration: the more large subtrees displayed in a configuration, the closer we are in finishing the construction of hybridization networks. For example, in Figure 1, the lineage 2 only displays singleton subtrees with taxon 2. And so do the lineages a and b. The lineage c is created by the coalescence of lineages 1 and b. Thus, the lineage c displays the subtree α. Note that b is created by a reticulation and thus b can vanish (i.e. b may be pruned in displaying a subtree). Thus, c also displays the singleton subtree with taxon 1 (in case b vanishes).
The above discussion suggests the set of displayed subtrees of a lineage is key to configuration search. We let a lineage li maintain the set of input subtrees, denoted as T(li), which are displayed in li. For convenience, we sometimes use T(li) to represent the lineage li (as in Figure 2). For a leaf lineage li that is labeled with taxon x, T(li) contains the singleton subtrees labeled by x (which appears in each gene tree). When the lineage li is an internal lineage, T(li) is determined when li is created by genealogical events as follows.
FIG. 2.
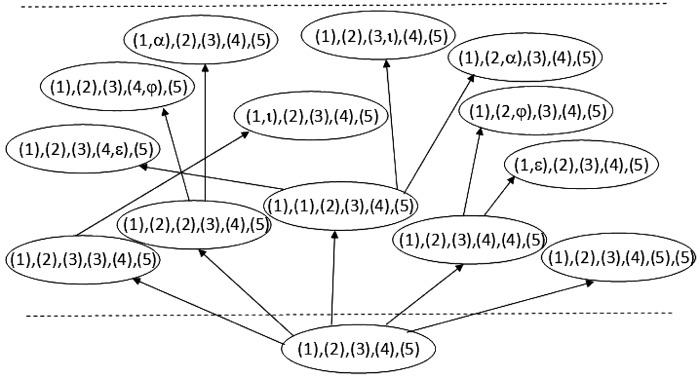
The list of configurations of stages 0 and 1 for the example in Figure 1. A configuration (ellipse) contains a set of lineages, where each lineage is represented by its set of displayed subtrees (in numerical taxa form and Greek letters as in Figure 1).
1. If li is created by a reticulation of the lineage
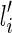 , then
, then 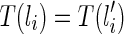 .
.2. If li is created by a coalescence of the lineages
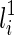 and
and 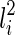 , then T(li) contains new subtrees formed by coalescing one subtree displayed in
, then T(li) contains new subtrees formed by coalescing one subtree displayed in 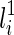 and another subtree displayed in
and another subtree displayed in 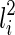 . More specifically, T(li) contains p(s1, s2) (if exists), where
. More specifically, T(li) contains p(s1, s2) (if exists), where  . Here, p(s1, s2) refers to the subtree in some input gene tree that has subtrees s1 and s2 as children; if s1 and s2 do not form a subtree in a gene tree, then p(s1, s2) does not exist. For example, in Figure 1, p(α, 3) = β, p(φ, ι) = κ, but p(α, 4) does not exist.
. Here, p(s1, s2) refers to the subtree in some input gene tree that has subtrees s1 and s2 as children; if s1 and s2 do not form a subtree in a gene tree, then p(s1, s2) does not exist. For example, in Figure 1, p(α, 3) = β, p(φ, ι) = κ, but p(α, 4) does not exist.
As alluded before, when determining T(li) formed by coalescing 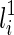 and
and 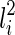 , we also need to consider whether
, we also need to consider whether 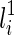 or
or  is vanishable. We say a lineage li is vanishable if either li is created by a reticulation or li is created by a coalescence between two lineages, where both of them are vanishable. Intuitively, a vanishable lineage means that the lineage may vanish and thus does not involve forming new displayed subtrees with the other lineage if certain display choices are made. For example, in Figure 1, the lineages a, b, d, and e (and also h since both of its children a and d are vanishable) are vanishable while the lineages 1, 2, 3, 4, 5, c, f, g, i, and j are not. Suppose one coalescing lineage (say
is vanishable. We say a lineage li is vanishable if either li is created by a reticulation or li is created by a coalescence between two lineages, where both of them are vanishable. Intuitively, a vanishable lineage means that the lineage may vanish and thus does not involve forming new displayed subtrees with the other lineage if certain display choices are made. For example, in Figure 1, the lineages a, b, d, and e (and also h since both of its children a and d are vanishable) are vanishable while the lineages 1, 2, 3, 4, 5, c, f, g, i, and j are not. Suppose one coalescing lineage (say 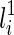 ) is vanishable. Then T(li) also contains each
) is vanishable. Then T(li) also contains each 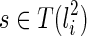 . For example, in Figure 1, the lineage f is created by the coalescence of c and e, where T(c) = {1, α} and T(e) = {4}. Then, subtrees 1 and 4 form the subtree
. For example, in Figure 1, the lineage f is created by the coalescence of c and e, where T(c) = {1, α} and T(e) = {4}. Then, subtrees 1 and 4 form the subtree 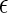 of T2, and thus
of T2, and thus  . Moreover, since e is vanishable,
. Moreover, since e is vanishable, 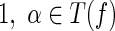 . Also, c is not vanishable. Thus, T( f) = {1, α, ε}.
. Also, c is not vanishable. Thus, T( f) = {1, α, ε}.
A subtle issue for displayed subtrees. Occasionally, when a subtree is formed by a coalescence of lineages l1 and l2, conflicts in the display choices of l1 and l2 may occur. This happens when displaying l1 and l2 relies on some shared reticulation. In this case, l1 and l2 can not both be displayed at the same time, and thus they can not coalesce. To avoid such conflict, additional constraints in forming displayed subtrees need to be imposed. In particular, we require two coalescing subtrees l1 and l2 do not share reticulations. That is, if l1 and l2 share some reticulation, no coalesced subtree is formed. This is because if there are shared reticulations within l1 and l2, l1 and l2 can not both be displayed at the same time. To enforce this constraint, we maintain a set of reticulations R(s) for each displayed subtree s such that s is displayed when display choices are made on reticulations in R. For the leaf lineage, its set of reticulation is empty. When a subtree s is created by a coalescence of two displayed subtrees s1 and s2, R(s) = R(s1) ∪ R(s2), where R(s1) and R(s2) do not intersect. When a reticulation r occurs at a lineage, then for each displayed subtree s on this lineage, R(s) = R(s) ∪ {r}. Our experience shows that such conflicts in displayed subtrees only occur rarely when the number of reticulation is small (where PIRNC is designed to handle). However, when the network becomes more complex, it becomes more common to observe such phenomenon, and when this occurs, the network does not display some gene trees. Thus, we implement this additional check in PIRNC.
The configuration search algorithm. The basic algorithm for constructing parsimonious hybridization networks explores configurations in a breadth-first search style. The algorithm runs in stages, where at each stage the algorithm constructs a set of configurations in the following way. First, new configurations are added to this stage with one reticulation performed upon configurations found during the previous stage. Then, we perform as many coalescences on these newly formed configurations and obtain additional configurations for this stage. That is, configurations on one stage are obtained from the same number of reticulations from the initial configuration 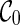 . More specifically, in this algorithm, R refers to the breath-first search level and is equal to the number of reticulations performed so far from
. More specifically, in this algorithm, R refers to the breath-first search level and is equal to the number of reticulations performed so far from 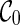 . LC(R) is the list of configurations found at level R. Rmax is the user-defined maximum of reticulations allowed.
. LC(R) is the list of configurations found at level R. Rmax is the user-defined maximum of reticulations allowed.
1. R ← 0. 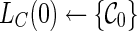 . . |
| 2. While R < Rmax |
3. For each 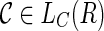
|
4. Perform one reticulation on each lineage of 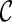 and obtain new configurations and obtain new configurations 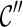 . . |
5. For each  , recursively try all ways of coalescences of two lineages in , recursively try all ways of coalescences of two lineages in 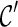 to create new configurations to create new configurations 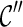 ; then discard ; then discard  if it is incompatible (defined later in this section); otherwise, if it is incompatible (defined later in this section); otherwise, 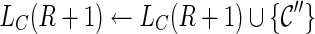 . . |
| 6. If a final configuration is found, construct the optimal network by trace-back and stop. |
| 7. R ← R + 1 |
| 8. Report there is no solution with less than Rmax reticulations. |
See Figure 2 for an example of executing the configuration search algorithm on the trees shown in Figure 1 for the first two levels. At level 0, we start with a single configuration 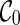 . With proper preprocessing (see below), we do not need to perform coalescences on
. With proper preprocessing (see below), we do not need to perform coalescences on 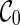 . At level 1, a single reticulation is performed on
. At level 1, a single reticulation is performed on 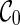 to obtain new configurations
to obtain new configurations 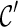 ; then all possible coalescences are performed on each
; then all possible coalescences are performed on each  . We find thirteen configurations in total at level 1.
. We find thirteen configurations in total at level 1.
Optimality. The PIRNC algorithm examines configurations with nondecreasing reticulation distance from 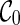 . Since no configurations that lead to the final configuration are discarded, the found network is the most parsimonious hybridization network.
. Since no configurations that lead to the final configuration are discarded, the found network is the most parsimonious hybridization network.
Incompatible configurations. In principle, every pair of lineages in a configuration can coalesce to create a new configuration. However, some coalescence will lead to a configuration 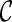 that is incompatible: the final configuration
that is incompatible: the final configuration 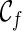 can not be obtained from
can not be obtained from 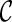 . Early removal of incompatible configurations can significantly speed up the search for optimal networks. Here is a simple test for finding incompatible configurations. Given a set of displayed subtrees
. Early removal of incompatible configurations can significantly speed up the search for optimal networks. Here is a simple test for finding incompatible configurations. Given a set of displayed subtrees 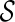 within a gene tree T, we say T is displayable from
within a gene tree T, we say T is displayable from 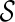 if each leaf of T is “covered” by some subtree in
if each leaf of T is “covered” by some subtree in 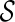 . Otherwise, we say T is not displayable from
. Otherwise, we say T is not displayable from 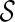 . A leaf is covered by a subtree if the subtree contains the leaf. Intuitively, if subtrees in
. A leaf is covered by a subtree if the subtree contains the leaf. Intuitively, if subtrees in  can not cover each leaf of T, then T can not be displayed by
can not cover each leaf of T, then T can not be displayed by 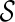 . Checking whether a tree T is displayable from
. Checking whether a tree T is displayable from 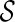 can be easily done by a traversal of T. A configuration
can be easily done by a traversal of T. A configuration 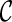 is incompatible if some input gene tree is not displayable from the set of displayed subtrees of all the lineages in
is incompatible if some input gene tree is not displayable from the set of displayed subtrees of all the lineages in 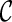 .
.
We illustrate the concept of incompatible configurations through an example as shown in Figure 3. Suppose we start with the initial configurations 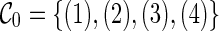 with four leaf lineages. There are different ways of coalescence from
with four leaf lineages. There are different ways of coalescence from 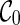 . Suppose we coalesce lineages 1 and 2 first. This creates a configuration
. Suppose we coalesce lineages 1 and 2 first. This creates a configuration 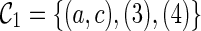 (noting that lineages 1 and 2 coalesce to create subtrees a and c in T1 and T2 respectively).
(noting that lineages 1 and 2 coalesce to create subtrees a and c in T1 and T2 respectively). 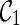 is compatible because each leaf in T1 and T2 is covered by some lineage in
is compatible because each leaf in T1 and T2 is covered by some lineage in 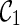 . To see this, first note that the leaf lineages 3 and 4 appear in each input tree and thus leaves 3 in T1 and T2 are covered by lineage 3 in
. To see this, first note that the leaf lineages 3 and 4 appear in each input tree and thus leaves 3 in T1 and T2 are covered by lineage 3 in 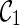 . So do leaves 4. Leaves 1 and 2 of T1 are covered by the subtree a of lineage (a, c). Leaves 1 and 2 of T2 are covered by the subtree c of lineage (a, c). If, however, we first coalesce lineages 3 and 4 from
. So do leaves 4. Leaves 1 and 2 of T1 are covered by the subtree a of lineage (a, c). Leaves 1 and 2 of T2 are covered by the subtree c of lineage (a, c). If, however, we first coalesce lineages 3 and 4 from 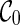 , we get a different configuration
, we get a different configuration 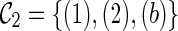 (noting that coalescing lineages 3 and 4 only forms a subtree b in T1 but not in T2). Now,
(noting that coalescing lineages 3 and 4 only forms a subtree b in T1 but not in T2). Now, 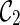 is incompatible because leaves 3 and 4 are not covered by any of the three lineages in
is incompatible because leaves 3 and 4 are not covered by any of the three lineages in  . One can verify that if we first reticulate the lineage 3 and then coalesce a copy of the lineage 3 and the lineage 4, the resulting configurations are compatible. This example shows that we can speed up the configuration search by pruning the incompatible configurations.
. One can verify that if we first reticulate the lineage 3 and then coalesce a copy of the lineage 3 and the lineage 4, the resulting configurations are compatible. This example shows that we can speed up the configuration search by pruning the incompatible configurations.
FIG. 3.
An illustration of compatible and incompatible configurations for the two gene trees T1 and T2.
3.4. Other techniques for speed up
We now describe several other speed-up techniques that help to make the configuration search algorithm practical while still ensuring the optimality of the approach.
3.4.1. Avoiding redundant coalescences
Note that there are usually more possible coalescences than reticulations: for a configuration with n lineages, there are O(n2) possible coalescences and only O(n) reticulations. Some coalescences are redundant in the sense that optimal networks can still be found even when these coalescences are not allowed. To speed up the configuration search, it is important to identify these redundant coalescences. There are several cases in which a coalescence can be determined to be redundant. First, sometimes a coalescence creates a lineage that has no displayed subtrees. In this case, the coalescence is clearly redundant and can be ignored. Similarly, if the new lineage l of a coalescence contains exactly the same displayed subtrees as one of the coalesced lineages l′, this coalescence is redundant since we can always use l′ instead of l in all future operations.
Preprocessing of input gene trees can be used for avoiding redundant coalescences. Preprocessing is a common technique for algorithms for hybridization network construction. Similar to Semple (2007) and Wu (2009), we first preprocess the input gene trees by contracting common subtrees into a single taxon. A common subtree is a subtree that appears in each input gene tree. Contracting common subtrees is known to preserve optimal solutions (Semple, 2007). After common subtrees are contracted, the initial stage contains only 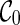 and thus search time is reduced by directly moving to the next stage. That is, no coalescences can be performed on
and thus search time is reduced by directly moving to the next stage. That is, no coalescences can be performed on 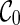 . This is because each lineage in
. This is because each lineage in 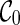 is always present, and thus coalescing two lineages labeling with taxa a and b in
is always present, and thus coalescing two lineages labeling with taxa a and b in 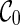 implies that there is a common subtree of a and b (while preprocessing should have already removed such common subtrees).
implies that there is a common subtree of a and b (while preprocessing should have already removed such common subtrees).
3.4.2. Comparing configurations and symmetry
We have also implemented several other speed-up techniques. First, suppose we obtain two configurations 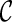 and
and 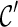 at one stage. Normally, we need to explore new configurations from both
at one stage. Normally, we need to explore new configurations from both 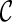 and
and  . Sometimes we can infer
. Sometimes we can infer 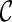 is “beaten” by
is “beaten” by 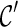 , and in this case we only explore new configurations from
, and in this case we only explore new configurations from 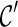 and remove
and remove 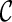 from consideration. We say a lineage l is beaten by another lineage l′ if the set of the displayed subtrees of l is a subset of the displayed subtrees of l′. For example, if T(l) = {α, φ} and T(l′) = {α, φ, ι}, then l is beaten by l′. We say
from consideration. We say a lineage l is beaten by another lineage l′ if the set of the displayed subtrees of l is a subset of the displayed subtrees of l′. For example, if T(l) = {α, φ} and T(l′) = {α, φ, ι}, then l is beaten by l′. We say 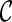 is beaten by
is beaten by 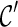 if each lineage in
if each lineage in 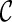 is “beaten” by some distinct lineage in
is “beaten” by some distinct lineage in 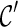 . Intuitively, if
. Intuitively, if 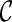 is beaten by
is beaten by  ,
, 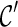 can be used in place of
can be used in place of 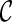 : if
: if 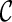 leads to an optimal network,
leads to an optimal network, 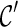 can also lead to an optimal network and thus it is safe to remove
can also lead to an optimal network and thus it is safe to remove 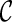 from consideration. Thus, when a new configuration
from consideration. Thus, when a new configuration 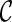 is created, we remove
is created, we remove 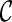 from consideration if
from consideration if 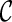 is beaten by some existing configurations at the same stage. At the same time, an existing configuration beaten by
is beaten by some existing configurations at the same stage. At the same time, an existing configuration beaten by 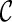 is also removed from consideration. This sometimes reduces the number of configurations to explore in the next stage significantly.
is also removed from consideration. This sometimes reduces the number of configurations to explore in the next stage significantly.
Another speed-up technique is avoiding symmetry in exploring new configurations. Suppose there are four lineages l1, l2, l3, and l4 in a configuration 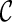 , where a new configuration
, where a new configuration 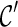 are created when l1 coalesces with l2, followed by l3 coalescing with l4. Since we allow all pairs of lineages to coalesce, the first coalescence from
are created when l1 coalesces with l2, followed by l3 coalescing with l4. Since we allow all pairs of lineages to coalesce, the first coalescence from 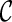 can be either between l1 and l2 or between l3 and l4, and both will lead to the same
can be either between l1 and l2 or between l3 and l4, and both will lead to the same 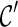 when the remaining pair of lineages coalesce. Such symmetry leads to redundant efforts by reaching the same configurations multiple times. To break symmetry, each lineage in
when the remaining pair of lineages coalesce. Such symmetry leads to redundant efforts by reaching the same configurations multiple times. To break symmetry, each lineage in 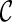 is arbitrarily assigned an integer as its rank. Coalescences are required to be performed at lineages in nondecreasing order. For example, if the last coalescence is performed between lineages 10 and 11, then a coalescence involving lineage 7 and 8 are not allowed.
is arbitrarily assigned an integer as its rank. Coalescences are required to be performed at lineages in nondecreasing order. For example, if the last coalescence is performed between lineages 10 and 11, then a coalescence involving lineage 7 and 8 are not allowed.
Sometimes, some reticulation can be deferred and thus reduce the time spent on performing searches from this reticulation. As an example, consider the initial configuration 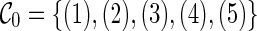 in Figure 2. The reticulation of lineage 5 can be deferred because the reticulation at lineage 5 alone does not start the coalescence; taxon 5 does not directly coalesce with any other leaf lineages in the gene trees. Thus reticulation must also occur at some other lineage and the reticulation of lineage 5 can thus be deferred.
in Figure 2. The reticulation of lineage 5 can be deferred because the reticulation at lineage 5 alone does not start the coalescence; taxon 5 does not directly coalesce with any other leaf lineages in the gene trees. Thus reticulation must also occur at some other lineage and the reticulation of lineage 5 can thus be deferred.
3.5. PIRNCH: a heuristic
PIRNC becomes slow when the number of reticulations increases. In order to construct more complex networks, we develop a heuristic called PIRNCH, which is based on the same principle of PIRNC but has more aggressive approaches to trim the search space of configurations.
PIRNCH uses a scoring scheme to rank configurations so that lower-ranked configurations may be pruned. The score of a configuration 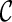 is based upon the progress made by the configuration toward the final configuration. The progress of the configuration
is based upon the progress made by the configuration toward the final configuration. The progress of the configuration 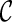 is measured by
is measured by 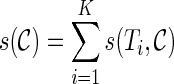 . Here
. Here 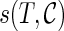 is the score for gene tree T and
is the score for gene tree T and  and is equal to the smallest number of disjoint subtrees displayed in
and is equal to the smallest number of disjoint subtrees displayed in  whose union contains all the taxa in T. For example,
whose union contains all the taxa in T. For example, 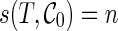 since only singleton leaves are displayed in
since only singleton leaves are displayed in 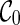 . In Figure 2, for the configuration
. In Figure 2, for the configuration 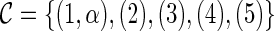 ,
, 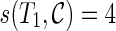 since the displayed subtrees α, 3, 4, and 5 together cover all the leaves in T1. The smaller the score is of a configuration, the higher ranked it is. Then we can keep the top Nc ranked configurations and prune the rest at each stage. The value of Nc is chosen by the user. There is a trade-off between accuracy and efficiency in choosing the value of Nc. Note that it is possible that configurations leading to good networks may be dropped since these configurations may appear to be less promising than others at an earlier stage. When this happens, either the heuristic runs very slow (by exploring the wrong portion of the configuration space) or the constructed networks are far from the optimum. However, this happens very rarely in our simulation.
since the displayed subtrees α, 3, 4, and 5 together cover all the leaves in T1. The smaller the score is of a configuration, the higher ranked it is. Then we can keep the top Nc ranked configurations and prune the rest at each stage. The value of Nc is chosen by the user. There is a trade-off between accuracy and efficiency in choosing the value of Nc. Note that it is possible that configurations leading to good networks may be dropped since these configurations may appear to be less promising than others at an earlier stage. When this happens, either the heuristic runs very slow (by exploring the wrong portion of the configuration space) or the constructed networks are far from the optimum. However, this happens very rarely in our simulation.
PIRNCH also implements several other rules to further trim the search space. For example, PIRNCH does not consider a coalescence of two lineages where no new displayed subtrees are generated after the coalescence. With these heuristic rules, PIRNCH can not ensure always finding the optimal networks. Nonetheless, PIRNCH can construct more complex networks and seems to perform reasonably well in practice (see Section 4).
4. Results
4.1. Implementation
We have implemented both PIRNC and PIRNCH for building the parsimonious network as part of the software package PIRN. It is available online for download. PIRNC can find optimal networks for multiple gene trees. It runs reasonably well for gene trees with relatively small reticulation numbers (say five or less). PIRNC can handle larger gene trees (say with 30 taxa). PIRNCH takes a heuristic approach and can find networks with larger hybridization number. When a proper setting is chosen, PIRNCH can find good networks for gene trees with hybridization numbers of up to 10. Both PIRNC and PIRNCH output the found network in the extended Newick format (see, e.g., Huson et al., 2010).
4.2. Simulation results
We test our new algorithms with simulated data on a 3192 MHz Intel Xeon workstation. We use the same simulation data generated by a two-stage approach, as in Wu (2010). Since PIRNC is designed to build networks with relatively small numbers of reticulation, we use the datasets generated in Wu (2010) with lower reticulation level. We test for several settings of n (the number of taxa) and K (the number of gene trees).
To test PIRNC, we compare the bounds computed by the program PIRN (Wu, 2010). PIRN provides a lower bound (called the RH bound) and an upper bound (called the SIT bound). Note that when the RH bound matches the SIT bound, PIRN finds the optimal network. When the two bounds do not match, we only know the range of hybridization number but not the true hybridization number, and this is a major weakness of the PIRN approach (Wu, 2010). Wu (2010) shows that the lower and upper bounds match often for lower reticulation level and smaller number of gene trees, but diverge more for higher reticulation level and larger number of gene trees. The reason for comparing with PIRN is that PIRN appears to infer networks that, in practice, are close to the optimum (Wu, 2010; Park and Nakhleh, 2012). In our simulation, we restrict our attention to datasets whose hybridization number is at most 4 since PIRNC is designed for data with a smaller hybridization number. For datasets with a higher hybridization number, PIRNC simply reports that their hybridization number is larger than 4 and no network is constructed. Table 1 shows the results of our simulation. The “#Data ≤ 4” refers to the percentage of datasets that have a hybridization number of 4 or less, and we only give results for these datasets (i.e., PIRNC does not give results for some datasets). Table 1 shows that PIRNC can find optimal networks where PIRN does not: for example, for n = 10 and K = 4 case, PIRNC finds the true optimum for 6 out of 98 datasets, where the bounds of PIRN do not match (and thus PIRN does not know whether its solutions are optimal or not) for these datasets. For some other settings, PIRNC gives the same results as PIRN does. Still, it may be useful to have a method that always finds optimal solutions. The ability to find optimal networks is the key advantage of PIRNC when compared with existing methods like PIRN. The running time of PIRNC is more influenced by the hybridization number than by n or K. The case of hybridization number being 4 (or even 5) or smaller is usually practically solvable by PIRNC.
Table 1.
Average Performance of PIRNC over 100 Datasets for Each Setting on Simulated Data
| |
n = 10 |
n = 20 |
n = 30 |
||||||
|---|---|---|---|---|---|---|---|---|---|
| K = 3 | K = 4 | K = 5 | K = 3 | K = 4 | K = 5 | K = 3 | K = 4 | K = 5 | |
| #Data ≤ 4 | 98 | 98 | 93 | 88 | 77 | 65 | 84 | 76 | 65 |
| PIRNC = RH | 96 | 93 | 90 | 88 | 74 | 63 | 84 | 75 | 61 |
| PIRNC > RH | 2 | 5 | 3 | 0 | 3 | 2 | 0 | 1 | 4 |
| PIRNC < SIT | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| PIRNC = SIT | 98 | 97 | 93 | 88 | 76 | 65 | 84 | 75 | 65 |
| PIRNC > SIT | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| #Data not optimal by SIT | 2 | 6 | 3 | 0 | 4 | 2 | 0 | 1 | 4 |
| Time | 13.4 | 49.9 | 92.6 | 276.8 | 705.8 | 1686.6 | 606.7 | 2227.1 | 2811.5 |
RH, lower bound; SIT, upper bound.
Results are only for those datasets with a hybridization number of 4 or less (i.e., datasets with a hybridization number of 5 or more are excluded). #Data ≤ 4: percentage of datasets with the hybridization number of 4 or less (where PIRNC constructs the optimal networks). PIRNC = RH (resp. PIRNC > RH): among the datasets where PIRNC gives optimal results, the percentage of datasets PIRNC gives the same (resp. larger) hybridization number as given by the RH lower bound. PIRNC < SIT (the other two are straightforward): percentage of datasets PIRNC gives the smaller hybridization number as given by the SIT upper bound. #Data not optimal by SIT: percentage of data where the RH bound and SIT bounds do not match (and thus the optimality is not determined by the two bounds) while PIRNC gives optimal solution. Time: average run time of PIRNC in seconds.
For handling more complex networks, we also test our heuristic PIRNCH on datasets with higher hybridization numbers. Note that the choices of PIRNCH parameters (e.g., Nc, the maximum number of configurations kept at each search level) have a large impact on the accuracy and efficiency. For this simulation, we set Nc to be 100,000. Results are shown in Table 2. The coarse mode of the SIT bound is used for larger data (when n = 40 and 50) as in Wu (2010). As shown in Table 2, PIRNCH performs well against PIRN: there is only one out of 900 datasets in which PIRNCH constructs a network using more reticulation than PIRN; and PIRNCH finds optimal networks (when its reticulation number matches the RH bound) for 82% of data with 50 taxa and 5 gene trees, while the SIT bound can only do the same for 58%. Also the gap between the results of PIRNCH and the SIT bound increases for larger and more complex data.
Table 2.
Performance of PIRNCH on 100 Simulated Datasets Per Setting
| |
n = 30 |
n = 40* |
n = 50* |
||||||
|---|---|---|---|---|---|---|---|---|---|
| K = 3 | K = 4 | K = 5 | K = 3 | K = 4 | K = 5 | K = 3 | K = 4 | K = 5 | |
| = RH | 98 | 93 | 77 | 97 | 90 | 83 | 98 | 89 | 82 |
| SIT = RH | 97 | 92 | 78 | 92 | 73 | 55 | 96 | 75 | 58 |
| Gap(RH) | 0.02 | 0.08 | 0.25 | 0.03 | 0.11 | 0.18 | 0.02 | 0.10 | 0.18 |
| <SIT | 1 | 3 | 3 | 5 | 22 | 37 | 2 | 16 | 34 |
| =SIT | 99 | 97 | 96 | 95 | 78 | 63 | 98 | 84 | 66 |
| >SIT | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Gap(SIT) | 0.01 | 0.03 | 0.02 | 0.06 | 0.25 | 0.54 | 0.02 | 0.17 | 0.39 |
| Time | 850.6 | 3,321.3 | 6,453.6 | 2,942.7 | 5,299.8 | 16,384.3 | 2073.7 | 8,204.7 | 13,846.64 |
= RH (resp. SIT = RH): the number of datasets PIRNCH (resp. SIT bound) gives the same results as the RH lower bound (and thus optimal networks are found). *: coarse mode of the SIT bound is used for n = 40 and 50. Gap(RH): average gap between PIRNCH results and the RH bound. < SIT (the other two are straightforward): the number of datasets PIRNCH gives the smaller hybridization number as given by the SIT upper bound. Gap(SIT): average gap between PIRNCH results and the SIT bound. Gap of two values a and b is defined as a − b. Time: the time of PIRNCH in seconds.
5. Discussion
Simulation shows that PIRNC and PIRNCH perform reasonably well compared to PIRN (previously the best approach for building hybridization networks of multiple trees). Our approach is based on the concept of ancestral configuration. This is different from most existing approaches to this subject, which mainly use the maximum agreement forest (MAF) formulation or its variation. One advantage of the ancestral configuration approach is its flexibility and its potential application to other evolutionary processes. A similar data structure has been used in studying the discordance of gene trees caused by the so-called incomplete lineage sorting (another important evolutionary process for the so-called gene tree and species tree problem) (Wu, 2012). Ancestral configurations may be useful in developing new algorithms for studying multiple evolutionary processes together (e.g., reticulate evolution and incomplete lineage sorting) on a proper model. We expect more research will be conducted along these lines in the near future.
Constructing optimal hybridization networks is still challenging computationally. We expect the study of the hybridization network with multiple trees is likely to continue (see, e.g., van Iersel and Linz, 2013). More theoretical observations for revealing properties of hybridization networks may be obtained. On the other hand, an important issue is finding more biological applications of the hybridization network model. So far, there have been a number of computational tools that may allow the solving of hard optimization problems on hybridization networks of realistic biological datasets. It will be interesting to see more applications of these tools for the hybridization network model.
Acknowledgments
This work is partly supported by U.S. National Science Foundation grants IIS-0803440 and CCF-1116175.
Author Disclosure Statement
No competing financial interests exist.
References
- Albrecht B. Scornavacca C. Cenci A. Huson D.H. Fast computation of minimum hybridization networks. Bioinformatics. 2012;28:191–197. doi: 10.1093/bioinformatics/btr618. [DOI] [PubMed] [Google Scholar]
- Bordewich M. Semple C. On the computational complexity of the rooted subtree prune and regraft distance. Annals of Combinatorics. 2004;8:409–423. 2004. [Google Scholar]
- Bordewich M. Semple C. Computing the minimum number of hybridization events for a consistent evolutionary history. Discrete Applied Mathematics. 2007;155:914–928. [Google Scholar]
- Bordewich M. Linz S. John K.S. Semple C. A reduction algorithm for computing the hybridization number of two trees. Evolutionary Bioinformatics. 2007;3:86–98. [PMC free article] [PubMed] [Google Scholar]
- Chen Z. Wang L. Algorithms for reticulate networks of multiple phylogenetic trees. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2012;9:372–384. doi: 10.1109/TCBB.2011.137. [DOI] [PubMed] [Google Scholar]
- Chen Z. Wang L. An ultrafast tool for minimum reticulate networks. J. of Comp. Biol. 2013;20:38–41. doi: 10.1089/cmb.2012.0240. [DOI] [PubMed] [Google Scholar]
- Gusfield D. Optimal, efficient reconstruction of Root-Unknown phylogenetic networks with constrained and structured recombination. J. Comp. Sys. Sci. 2005;70:381–398. [Google Scholar]
- Hein J. Jiang T. Wang L. Zhang K. On the complexity of comparing evolutionary trees. Discrete Appl. Math. 1996;71:153–169. [Google Scholar]
- Huson D. Klopper T. Beyond galled trees - decomposition and computation of galled networks, 211–225. In: Speed T., editor; Huang H., editor. Proc. of RECOMB; The 11th Ann. International Conference Research in Computational Molecular Biology; New York: Springer; 2007. 2007. [Google Scholar]
- Huson D. Rupp R. Gambette P. Paul C. Computing galled networks from real data. Bioinformatics. 2009;25:i85–i93. doi: 10.1093/bioinformatics/btp217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huson D.H. Rupp R. Scornavacca C. Phylogenetic Networks: Concepts, Algorithms and Applications. Cambridge University Press; Cambridge, U.K: 2010. [Google Scholar]
- Morrison D.A. Introduction to Phylogenetic Networks. RJR Productions; Uppsala, Sweden: 2011. [Google Scholar]
- Park H.J. Nakhleh L. Proc. of Bioinformatics Research and Applications (ISBRA 2012) Vol. 7292. Springer: LNCS; 2012. Murpar: A fast heuristic for inferring parsimonious phylogenetic networks from multiple gene trees, 213–224; p. 2012. [Google Scholar]
- Semple C. Hybridization networks, 277–309. In: Gascuel O., editor; Steel M., editor. Reconstructing Evolution. New Mathematical and Computational Advances; Oxford: 2007. [Google Scholar]
- van Iersel L. Linz S. A quadratic kernel for computing the hybridization number of multiple trees. Information Processing Letters. 2013;113:318–323. [Google Scholar]
- van Iersel L. Keijsper J. Kelk S., et al. Constructing level-2 phylogenetic networks from triplets, 450–462. In: Vingron M., editor; Wong L., editor. Proc. of RECOMB; The 12th Ann. International Conference Research in Computational Molecular Biology(RECOMB 08); New York: Springer; 2008. 2008. [DOI] [PubMed] [Google Scholar]
- van Iersel L. Kelk S. Rupp R. Huson D. Phylogenetic networks do not need to be complex: using fewer reticulations to represent conflicting clusters. Bioinformatics (supplement issue for ISMB 2010 proceedings) 2010;26:i124–i131. doi: 10.1093/bioinformatics/btq202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whidden C. Zeh N. In Proc. of Algorithms in Bioinformatics (WABI 2009) Springer; New York: 2009. A unifying view on approximation and fpt of agreement forests, 390–402. [Google Scholar]
- Wu Y. A practical method for exact computation of subtree prune and regraft distance. Bioinformatics. 2009;25:190–196. doi: 10.1093/bioinformatics/btn606. [DOI] [PubMed] [Google Scholar]
- Wu Y. Close lower and upper bounds for the minimum reticulate network of multiple phylogenetic trees. Bioinformatics (supplement issue for ISMB 2010 proceedings) 2010;26:140–148. doi: 10.1093/bioinformatics/btq198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y. Coalescent-based species tree inference from gene tree topologies under incomplete lineage sorting by maximum likelihood. Evolution. 2012;66:763–775. doi: 10.1111/j.1558-5646.2011.01476.x. [DOI] [PubMed] [Google Scholar]
- Wu Y. Wang J. Fast computation of the exact hybridization number of two phylogenetic trees, 203–214. In Proceedings of International Symposium on Bioinforamtics Research and Applications (ISBRA) 2010; Springer-Verlag, Berlin, Germany. 2010. [Google Scholar]