Efficiently Identifying Significant Associations in Genome-wide Association Studies

Abstract

Over the past several years, genome-wide association studies (GWAS) have implicated hundreds of genes in common disease. More recently, the GWAS approach has been utilized to identify regions of the genome that harbor variation affecting gene expression or expression quantitative trait loci (eQTLs). Unlike GWAS applied to clinical traits, where only a handful of phenotypes are analyzed per study, in eQTL studies, tens of thousands of gene expression levels are measured, and the GWAS approach is applied to each gene expression level. This leads to computing billions of statistical tests and requires substantial computational resources, particularly when applying novel statistical methods such as mixed models. We introduce a novel two-stage testing procedure that identifies all of the significant associations more efficiently than testing all the single nucleotide polymorphisms (SNPs). In the first stage, a small number of informative SNPs, or proxies, across the genome are tested. Based on their observed associations, our approach locates the regions that may contain significant SNPs and only tests additional SNPs from those regions. We show through simulations and analysis of real GWAS datasets that the proposed two-stage procedure increases the computational speed by a factor of 10. Additionally, efficient implementation of our software increases the computational speed relative to the state-of-the-art testing approaches by a factor of 75.

1. Introduction

Research in complex diseases has progressed rapidly in the last decade with the advent of genomic technologies (Devlin and Risch, 1995; Risch and Merikangas, 1996; International HapMap Consortium, 2005; Hardy and Singleton, 2009). In genome-wide association studies (GWAS), information on millions of single nucleotide polymorphisms (SNPs) across the genome is collected from thousands of case and control individuals. Typically, each SNP is statistically tested for disease association by comparing the minor allele frequency (MAF) between the cases and controls. The significant associations are used to gain insight into the genetic basis of disease, and hundreds of GWASs have been performed on dozens of complex diseases and successfully discovered many novel loci involved in disease susceptibility (Hindorff et al., 2009).

More recently, there has been great interest in applying the GWAS approach to genomic data such as gene expression. In these studies, the goal is to identify regions of the genome harboring genetic variation that affect gene expression levels or expression quantitative trait loci (eQTL) (Bochner, 2003; Rockman and Kruglyak, 2006; Cookson et al., 2009). A challenge in applying GWAS to genomic data is that these technologies typically obtain tens of thousands of measurements for each sample resulting in a tremendous computational burden when performing the analysis, including computing billions of tests, and requires substantial computational resources. This challenge is compounded for novel statistical approaches such as linear mixed models, which account for population structure (Kang et al., 2010; Lippert et al., 2011; Zhou and Stephens, 2012), yet themselves are computationally intensive.

eQTL studies are already very popular (Brem et al., 2002; Brem and Kruglyak, 2005; Keurentjes et al., 2007) and with rapidly decreasing costs of RNA-seq technologies (Wang et al., 2009; Majewski and Pastinen, 2011) will likely become more popular in the future. These include several major efforts collecting expression from multiple-tissues in humans (Cheung et al., 2005; Stranger et al., 2007; Emilsson et al., 2008; Spielman et al., 2007; Baker, 2012) and mice (Chesler et al., 2005; Bystrykh et al., 2005). More broadly, application of the GWAS approach to phenotypes measured by other genomic technologies such as those reported by the ENCODE consortium (The ENCODE Project Consortium, 2004, 2007, 2011, 2012) will face similar computational challenges.

In this article, we introduce a novel two-stage method that can be applied to reduce the computational burden of a wide range of association studies including those that employ case-control, quantitative trait, and mixed-model statistical testing methodologies. In each trait, typically only a small percentage of the SNPs are significantly associated and the SNPs neighboring a significant association have elevated statistics. Intuitively, one can first test an informative subset of the SNPs, termed proxy SNPs, across the genome to quickly locate these regions and test the SNPs therein. This way, many of the regions with no associations can be discarded from the analysis to reduce the computational burden.

Our novel method for genome-wide rapid association testing (GRAT) guarantees to identify all of the significant associations with high probability while reducing the total number of tests. The proposed method chooses the proxy SNPs and determines which additional SNPs to test based on the observed proxy SNP statistics and the patterns of linkage disequilibrium (LD) in the region. The key insight underlying GRAT is that by taking advantage of how the statistics at SNPs in LD with each other behave, we can estimate the probability that an untested SNP has a significant association and use this probability to only eliminate SNPs from consideration if they are highly unlikely to have significant associations. We have selected a set of proxy SNPs for the 1000 Genomes Project, and any study that imputes to the 1000 Genomes Project SNPs can readily use our approach. We also provide our method for choosing proxy SNPs, which can be applied to any reference dataset. We show through simulations and analysis of real eQTL datasets that the proposed two-stage procedure identifies the significant associations while only testing approximately 10% of the SNPs. GRAT's efficient software implementation reduces the computational time for computing large-scale association studies by a factor of 30 compared to currently used state of the art methods. When our method is applied to association studies that utilize linear mixed models, the speed-up is cumulative with recent efforts that decrease the computational burden of computing the actual association statistic such as EMMAX, FaST-LMM, and GEMMA (Kang et al., 2010; Lippert et al., 2011; Zhou and Stephens, 2012).

2. Methods

2.1. Genome-wide association studies

Old version: For the simplicity of description, we consider a balanced case-control genome-wide association study (GWAS) with N/2 individuals (N copies of each chromosome) per panel. For our actual experiments, we will use association statistics for quantitative phenotypes, but the approach assuming case-control phenotypes is equivalent. 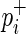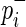For SNP m_i, p_i denotes its population minor allele frequency (MAF); and denote its population case and control MAFs; 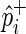and 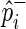denote its observed case and control MAFs in the GWAS. Given the relative risk of the SNP, γ_i, in the disease and the prevalence of the disease, F, in the population, it can be shown that the case and control MAFs of the SNP follows,

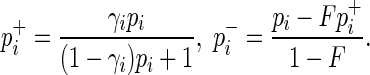(1)

An SNP is defined as not associated if .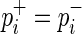

In case-control GWASs the following statistic is widely used, which is normally distributed for large N with mean 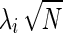(the noncentrality parameter), and unit variance,

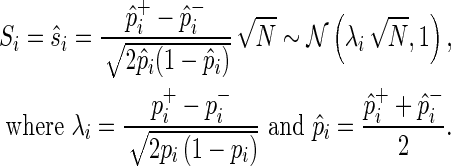(2)

Given the significance level α and the observed value of the test statistic 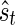, the SNP is deemed as significant, or statistically associated, if 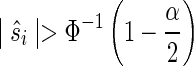, where Φ⁻¹(.) is the quantile function of the standard normal distribution. For simplicity, we use the notation: 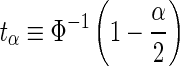. Typically, in a GWAS, the significance level is chosen as α = 10⁻⁸.

2.2. A two-stage approach for identifying the significant associations

We propose the following two-stage testing procedure for dentifying the significant associations within a set of SNPs 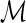. Given a subset of the SNPs 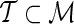, referred to as the proxy SNPs, for each proxy SNP, 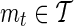, its association statistic, ŝ_t, is computed. In the second stage, a decision rule is exercised for each of the remainder SNP, 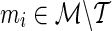, in order to determine whether or not to compute the association statistic of the remainder SNP. The decision rule for a remainder SNP m_i is defined using a proxy SNP, 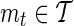, and a threshold, 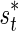, for its observed statistic ŝ_t. If the observed statistic of the proxy SNP is more extreme than the threshold value, 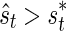, the remainder SNP is tested.

2.3. Performance of the two-stage approach

In a GWAS, the performance of the two-stage approach can be summarized by the total number of SNPs tested (NT), and the percentage of the significant SNPs identified, or the recall rate (RR). The total number of tests is the sum of the tests performed on the proxy SNPs, plus the remainder SNPs that are tested as a result of the decision rules. We use a standard GWAS simulation model (Kostem et al., 2011) to evaluate a given set of proxy SNPs and decision rules based on their expected performance within the simulated data.

The simulation model considers the probability of each SNP being causal, c_i, and the noncentrality parameter (NCP) of the causal SNP, 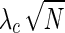. For simplicity, we give a brief explanation of the simulation procedure for a single causal SNP using a genomic reference dataset such as the HapMap. Using the given probabilities of each SNP being causal, at most a single causal SNP is randomly selected. Given the disease prevalence F and the NCP of the causal SNP 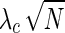, the case and control MAFs, 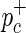and 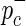are determined. Next, the HapMap haplotypes are divided into two pools according to the minor and major allele of the causal SNP, and case-control panels are sampled using 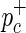and .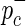

For each simulation dataset, each association statistic is computed to identify which SNPs are significant in the dataset. We then apply the two-stage method to observe the NT and RR. The expected recall rate (ERR) and the expected number of SNPs to be tested (ENT) then can be computed by repeatedly simulating datasets, applying the two-stage approach and averaging the observed NT and RR value.

2.4. Finding the optimal decision rules for given proxy SNPs

For a given set of proxy SNPs, one can determine the decision rules empirically by evaluating the performance of using different threshold values on the remainder SNPs in the simulated data. The empirical approach can be cumbersome, and instead we derive an analytical framework for estimating the expected performance, which eliminates the need for generating simulated data and saves time. Furthermore, using this analytical framework we show how to determine the optimal decision rules for the remainder SNPs given a set of proxy SNPs.

An SNP that is disease-associated can be either causal in the disease or in LD with the causal SNP. Given that SNP m_i is the causal SNP, the noncentrality parameter (NCP) of a correlated SNP m_t, 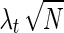, is proportional to the NCP of the causal SNP, 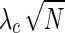, by their correlation coefficient, r, where λ_t = rλ_c. It can be shown that the joint distribution of the association statistics of the causal SNP m_i and the noncausal SNP m_t follows a bivariate normal distribution (Han et al., 2009). In addition to case-control studies, these principles can also be applied to quantitative traits (Schaid et al., 2002).

We follow a conservative approach in which each remainder SNP m_i is paired with the proxy SNP that is most strongly correlated, referred to as the best-proxy and denoted by m_b(i). For each remainder SNP m_i, we denote the association statistic of its best-proxy m_b(i) with s_b(i) and test SNP m_i if its best-proxy SNP association statistic is more extreme than a given threshold, 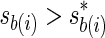. For simplicity, we assume only the remainder SNP can be causal and express the density function of the joint distribution, f (s_i, s_b(i)),

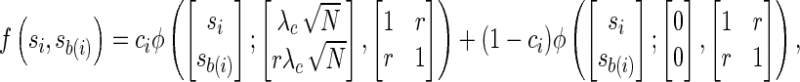(3)

where ϕ(x; μ, Σ) denotes the density of a multivariate normal distribution with mean vector μ and covariance matrix Σ. The first term corresponds to having the remainder SNP as causal, with probability c_i, and the second term to not causal with probability 1 − c_i.

Assume we are given K proxy SNPs, where 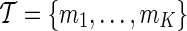. The ENT can be expressed as the fixed cost of testing K proxy SNPs, plus the expected number of decision rules that are triggered,

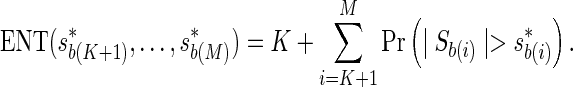(4)

We approximate the ERR as the ratio of the expected number of significant SNPs that the two-stage approach discovers, to the expected number of significant SNPs in a GWAS,

(5)

where the first and the second terms in the numerator correspond to the expected number of significant SNPs obtained from testing the proxy SNPs and the remainder SNPs, respectively. Further, we refer to the second term as the expected recall function, which can be computed using the joint distribution,

(6)

where .

We are interested in determining the decision rules that lead to the lowest ENT, while the expected recall rate (ERR) satisfies a given target value, ρ, which can be expressed as an optimization problem,

(7)

We show the problem is convex and outline an efficient iterative solution in the Appendix.

2.5. Choosing the optimal proxy SNPs

The expected number of SNPs to be tested (ENT) in the two-stage approach depends on the number of proxy SNPs and which SNPs are chosen as proxies. It can be shown that the problem of finding the optimal set of proxy SNPs, among all possible sets of proxy SNPs, the set that gives the minimum ENT, is an NP-Hard problem (Bafna et al., 2003). Therefore, we propose a heuristic algorithm for choosing the proxy SNPs using a greedy approach, which incrementally builds the set of proxy SNPs.

Starting with an empty set, let 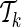denote the current set of proxy SNPs with size k, where ENT_k and ERR_k denote the values of its ENT and ERR. (ENT₀ = +∞ and ERR₀ =−∞). Each remainder SNP m_i is a candidate to extend the current set of proxy SNPs to become 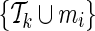, which performs 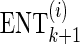. The remainder SNP with the least 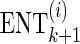is chosen for extending the current set of proxy SNPs:

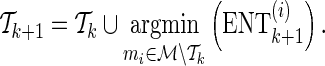(8)

While the extended set 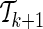improves the ENT, that is, ENT_k+1<ENT_k, the algorithm continues.

For each candidate set of proxy SNPs, the algorithm solves the optimization problem (7) to compute 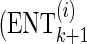. This leads to a quadratic computational complexity in the order of the number of the collected SNPs and in practice makes it hard to scale to large numbers. We further introduce a heuristic extension to the above greedy approach to reduce this complexity. While extending the current set of proxy SNPs 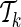to 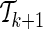, the optimization problem (7) is solved M − k times. In particular, solving the optimization problem (7) corresponds to finding the gradient, g*, at which the ENT function is minimized while satisfying the constraints (see Appendix). We assume that for 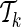and 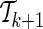the gradient values of their ENT functions are close enough, 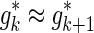. Therefore, while extending the current proxy set, we compute the ENT of each candidate set, 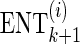, using the gradient value from the previous step, 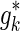. This way, rather than solving the optimization problem M − k times for each possible proxy SNP at each step k, the gradient is updated once after the new set 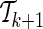is determined. Using this approach, the optimization problem (7) is solved a total of K times, where K is the size of the final set of proxy SNPs.

2.6. Updating the remainder SNP thresholds in linear mixed models

We consider the following linear mixed model (LMM) formulation,

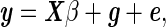(9)

where y is the (n × 1) vector of phenotypic values, X is the (n × p) matrix of fixed effects, which includes the mean, covariates, and the SNP to be tested, β is the (p × 1) vector of fixed effect weights, g is the variance component accounting for the population structure, and e is the iid noise. We assume the random effects, g and e, follow multivariate normal distribution, 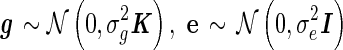, where K is the known (n × n) genetic similarity matrix, I is the (n × n) identity matrix with unknown magnitudes 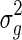and 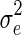. We follow the approach taken in EMMAX (Kang et al., 2010) and estimate 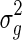and 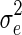in the null model, with no SNP effect, and use these parameters while testing the SNPs. That is, when each SNP is tested, the covariance of y is kept fixed, 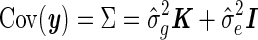, where 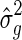and 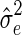are the restricted log likelihood (REML) estimates (Kang et al., 2010; Lippert et al., 2011).

In GRAT, the threshold value for each remainder SNP is computed after the covariance matrix Σ is estimated, and the alternate model is transformed by the inverse square root of this matrix,

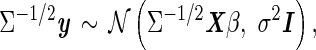(10)

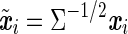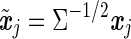where the residuals are iid. For two SNPs m_i and m_j, let x_i and x_j be their (n × 1) allelic indicator vectors. When the SNPs are tested individually in the above model, the same transformation is applied to the genotype vectors, which may moderately change the pairwise correlation between the SNPs. The transformed genotype vectors are and , and their correlation coefficient is,

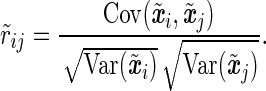(11)

3. Results

3.1. Genome-wide rapid association testing (GRAT)

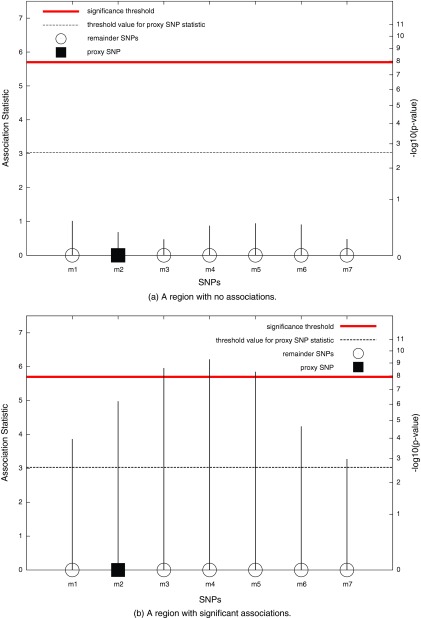
In Figure 1, we consider two possible scenarios for a genomic region in a GWAS. In (a), the region contains no significant associations, and in (b), the region contains a causal SNP. In (a) and (b), the statistics for each SNP are shown, denoting what could have been observed in each scenario had all the SNPs in the region been tested. Let m₂ be the proxy SNP for this region to decide whether or not to test the rest of the SNPs. We refer to the SNPs other than the proxy SNP (m₁, m₃, m₄, m₅, m₆, and m₇) as the “remainder SNPs.” If the observed statistic of the proxy SNP is stronger than a threshold value, which in this example is 3.0, the remainder SNPs are tested.

FIG. 1.

An example of applying GRAT in two hypothetical regions. First, the proxy SNP (rectangle) is tested and its statistics are compared to the threshold (dashed line). If the statistic is above the threshold, the remaining SNPs in the region are tested. SNP, single nucleotide polymorphism.

In the first stage, only the proxy SNP is tested, and its association statistic is observed. In (a), where the region contains no associations, the statistic of the proxy SNP is 0.7. The observed statistic of the proxy is less than the threshold value (0.7 < 3.0), and hence none of the remainder SNPs within the region are tested. In (b), the region contains associations and the proxy SNP captures this information. The observed statistic of the proxy SNP is stronger than the threshold value (5.0 > 3.0), which leads to testing each of the remainder SNPs in the region. This results in identifying all the significant SNPs (m₃, m₄, and m₅).

In the Methods section, we introduce a novel approach for choosing the proxy SNPs and the threshold values, which provide guarantees that all statistically significant associations will be discovered while computing the least amount of association tests. Due to the complexity of linkage disequilibrium (LD) across the genome, we use a separate threshold value for each remainder SNP rather than using a common threshold value for all the remainders SNPs in an LD region. This is performed by pairing each remainder SNP with its most strongly correlated proxy SNP, and a threshold value is used for the pair to decide whether or not to test the remainder SNP. We have precomputed the proxy SNPs for the 1000 Genomes Project, and studies imputing to SNPs in this reference can benefit from our method. Even though the LD structure among the SNPs in the study and the reference dataset may be different, our method guarantees to discover all significant associations with high probability. This is achieved by updating the threshold values using the LD structure observed in the study. We term our novel two-stage testing procedure as genome-wide rapid association testing (GRAT).

GRAT can be applied to a wide range of statistical models, such as case-control studies, quantitative traits, and LMM. In particular, the LMM approach has recently become popular due to its effective control of population structure. Computing the LMM association statistic is computationally expensive, and recently, its efficient computation has attracted great interest (Kang et al., 2010; Lippert et al., 2011; Zhou and Stephens, 2012). The speed-up due to GRAT is cumulative with these efforts.

3.2. Application of a large-scale eQTL study

We compared the performance of GRAT to the standard approach of testing all the SNPs using a large-scale eQTL study (Stranger et al., 2012) that contains 47, 292 gene expression traits on 80 HapMap ASN (East Asian ancestry) individuals that are fully sequenced in the 1000 Genomes Project. We obtained the genotype data from the MACH web site (Li et al., 2010) and retained approximately 5.9 million SNPs that are filtered for Hardy-Weinberg equilibrium (HWE) and minor allele frequency (MAF) greater than 5%. We eliminated SNPs with lower MAF frequency since they could not be genome-wide significant due to the sample size.

We performed the standard analysis using PLINK (Purcell et al., 2007), which took approximately 2600 hours. We used a conservative genome-wide significance threshold level, α = 10⁻⁸, to label the significant SNPs and observed 85,219 significant associations. We repeated the association analysis by applying GRAT using the proxy SNPs precomputed for the 1000 Genomes Project ASN population SNPs. The number of proxies is 276,702, which means GRAT tests approximately 5% of the SNPs in the first stage.

Applying GRAT to the whole eQTL dataset took 35 hours using the same computational resources (single core of an Opteron CPU). In addition to the proxies, GRAT tested 8.5% of the SNPs in the second stage, reducing the computational cost down to analyzing 13.5% of all the SNPs with the rest of the speedup coming from a faster implementation compared to PLINK. GRAT identified all of the significant associations and speeded up the computation by a factor of 75.

3.3. GRAT applied to linear mixed model association

We applied GRAT to a linear mixed model (LMM) association of the eQTL dataset. A challenge in applying GRAT to LMMs is that GRAT utilizes the fact that the joint distribution of traditional association statistics for correlated markers is directly dependent on the correlation between the markers as shown in Pritchard and Przeworski (2001). Unfortunately, when applying LMMs, this relation no longer holds. We derive an analogous relationship between LMM statistics that takes into account both the correlation between the markers and the kinship matrix. Utilizing this relationship, we apply GRAT to LMMs using an efficient implementation (Lippert et al., 2011).

We performed the standard analysis, testing each SNP in each expression trait, which identified 66,818 significant associations (α = 10⁻⁸). We applied GRAT using the proxy SNPs precomputed for the 1000 Genomes Project ASN population. In two stages, GRAT statistically tested a total of 9.1% of the SNPs, identifying all of the significant associations and demonstrating that GRAT can speed up LMM association by a factor of 10.

3.4. Simulations using the 1000 Genomes Project

To obtain a more robust estimate of the performance, we applied GRAT to thousands of simulated GWAS studies. We simulated the studies using common SNPs (minor allele frequency  >5%) available from the 1000 Genomes Project (The 1000 Genomes Project Consortium, 2010) using the phased SNP genotypes obtained from the MACH web site (Li et al., 2010) on four populations: African (AFR), East Asian (ASN), admixed American (AMR), and European (EUR) ancestries.

We divided each chromosome into panels of 1000 SNPs and simulated case-control GWASs by randomly selecting 5% of the panels as alternates, in which we simulated a causal SNP, and the remaining panels as the null panels, without any causal SNPs. In each alternate panel, we randomly selected the causal SNP and set its statistical power to be 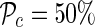at the significance level α = 10⁻⁸. Using this procedure, we simulated 500 GWASs in each population.

We applied GRAT to each simulated GWAS and recorded the recall rate of the significant SNPs and total number of tests performed. In Table 1, we show the performance of GRAT in each population averaged over the simulations. GRAT practically identified all significant associations and reduced the number of tests by 10-fold. Across the simulations, from the total 3,718,126 significant associations, GRAT only missed 1052 significant associations.

Table 1.

Performance in Simulations

Population	Number of SNPs	Recall Rate	Reduction
AFR	8.5 × 106	>99.9%	88.2%
AMR	6.7 × 106	>99.9%	92.4%
ASN	6.1 × 106	>99.9%	92.8%
EUR	6.6 × 106	>99.9%	92.6%

The average performance of GRAT in 500 simulated GWASs using 1000 Genomes Project data in four populations. GRAT identified practically all significant associations by only testing 10% of the SNPs.

GRAT, genome-wide rapid association testing; GWAS, genome-wide association studies; SNPs, single nucleotide polymorphisms.

3.5. Comparison to traditional tag-SNP–based association testing

Choosing an informative subset of SNPs, termed tag-SNPs, under various criteria has been extensively investigated (Stram, 2004; de Bakker et al., 2005; Stram, 2005; Cousin et al., 2003, 2006; Halperin et al., 2005; Lin and Altman, 2004; Pardi et al., 2005; Qin et al., 2006; Saccone et al., 2006; Carlson et al., 2004; Santana et al., 2010). The main goal of these methods is to reduce the cost of GWASs by genotyping a subset of the SNPs yet collect as much information as possible on the remaining SNPs.

We mimic a two-stage association testing approach using a traditional tag-SNP selection method and compare its performance to GRAT. In the first stage, we test all the tag-SNPs and use a p-value threshold, α_tag, to choose which of the tag-SNPs to follow. If the p-value of a tag-SNP is stronger than the threshold, the remainder SNPs tagged by this tag-SNP are tested.

We simulated association studies using the 10 HapMap ENCODE regions, which are densely genotyped for four HapMap populations (The ENCODE Project Consortium, 2004). In each simulation study, we used the ENCODE regions to generate null regions that harbor no causal SNPs and alternate regions each harboring a causal SNP with 50% statistical power at the genome-wide significance level of α = 10⁻⁸. Following this approach, we generated 500 association studies in each population.

In each region and in each population, we identified the tag-SNPs with the widely utilized tag-SNP selection method Tagger (de Bakker et al., 2005). Given a set of SNPs and information on their minor allele frequencies and pairwise correlation coefficients, Tagger selects the minimum number of tag-SNPs such that each of the remaining SNPs correlates to a tag-SNP with a minimum r² pairwise correlation value. In our evaluations, we have used the default value of r² = 0.8. In order to perform a comparison, we also applied GRAT to identify the proxy SNPs and the statistic threshold rules for testing the remainder SNPs to achieve 99% target recall rate on the significant associations. The number of tagging SNPs chosen by Tagger and the number of proxy SNPs chosen by GRAT are summarized in Table 3. On average, Tagger chose more than 4 times the number of proxy SNPs chosen by GRAT.

Table 3.

Performance of GRAT and Tagger in ENCODE Simulations

Method	Recall	ReductionCEU	Speedup	Recall	ReductionCHB	Speedup
GRAT	99.89%	89.7%	9.7×	99.73%	89.6%	9.6×
Taggerαtag = 1e-8	86.25%	78.9%	4.7×	87.78%	79.7%	4.9×
Taggerαtag = 1e-7	95.74%	78.6%	4.7×	97.70%	79.4%	4.8×
Taggerαtag = 1e-6	98.40%	78.3%	4.5×	99.62%	79.0%	4.8×
Taggerαtag = 1e-5	99.30%	77.8%	4.5×	99.97%	78.4%	4.6×

Method	JPT			YRI
GRAT	99.63%	90.2%	10.2×	99.72%	88.4%	8.6×
Taggerαtag = 1e-8	88.53%	80.5%	5.1×	87.62%	65.3%	2.9×
Taggerαtag = 1e-7	98.10%	80.1%	5.0×	97.55%	65.3%	2.9×
Taggerαtag = 1e-6	99.52%	79.6%	4.9×	99.39%	65.1%	2.9×
Taggerαtag = 1e-5	99.92%	79.1%	4.8×	99.94%	65.0%	2.9×

In each HapMap population, the average performance of GRAT and Tagger in 500 simulated GWASs are shown. GRAT guarantees to achieve the 99% target recall rate, while reducing the number of tests by 90%. Using Tagger, we test the remainder SNPs that are tagged by the tag-SNPs that exceed a p-value cut-off threshold, α_tag. GRAT outperforms the traditional tag-SNPs in all populations.

Table 2.

The Average Number of Tagging SNPs Chosen by Each Method and the Total Number of SNPs in Each Population

Population	GRAT	Tagger	Number of SNPs
CEU	55.0	234.0	1138.6
CHB	45.7	201.2	1024.3
JPT	42.7	198.7	1058.5
YRI	89.1	486.3	1410.1

In each HapMap population, the average number of tagging SNPs chosen by GRAT and Tagger are shown. The fourth column indicates the average number of SNPs across the ENCODE regions. On average, Tagger chooses 4.7 times more tagging SNPs than GRAT.

In Table 3, the performance of GRAT is compared to Tagger in four HapMap populations using various p-value threshold values, α_tag = {10⁻⁸, 10⁻⁷, 10⁻⁶, 10⁻⁵}. In each population, GRAT achieved more than 99% recall rate while testing approximately 10% of all SNPs. Among all the p-value threshold values used, the traditional tag-SNPs led to testing more than twice the number of SNPs tested by GRAT and only achieved the target recall rate in all populations when the p-value threshold value was α_tag = 10⁻⁵. Unfortunately, Tagger, unlike GRAT, does not guarantee a recall rate, so it is not clear how to set the threshold and be certain that no associations are missed. Because Tagger selects the tagging SNPs to maintain a particular correlation between the tagging and the nontagging SNPs and using a uniform threshold value, α_tag, to choose which SNPs to test; this does not guarantee any sensitivity on the discovery of the significantly associated SNPs.

4. Discussion

In the genome-wide association study (GWAS), information on SNPs across the genome is collected from thousands of case and control individuals. Typically, each SNP is tested individually for disease association, and the significant SNPs provide insight into the genetics of the disease. Association studies attempt to collect information on as many SNPs as possible to cover the whole genome. However, as the number of collected SNPs increases so does the computational burden to identify the significant associations.

We introduced a novel method, GRAT, for genome-wide rapid association testing to identify all significant associations by testing a small subset of SNPs. Due to the correlation, or LD, testing an SNP provides information about the associations of its neighboring SNPs. Using this intuition, the procedure first tests a subset of SNPs, referred to as the proxy SNPs, across the genome to locate the regions that may contain the significant associations. Once located, additional SNPs are tested from those regions to identify the significant SNPs. Each unobserved, or remainder, SNP is paired with its most strongly correlated proxy SNP, termed best-proxy, and a threshold value is used for the best-proxy's statistic to decide whether or not to test the unobserved SNP. We introduced a novel approach to choose the proxy SNPs and determine the threshold values for each best-proxy SNP. Through simulations and real GWAS data, we showed that the proposed approach can identify more than 99% of the significant SNPs by reducing the number of tests by a factor of 10. Furthermore, GRAT can also be applied to association studies that utilize linear mixed models, where the speed-up is cumulative with recent efforts that decrease the computational burden of computing the actual association statistic. GRAT is implemented in C++ for high performance and is available online.

4. Appendix

4.1. Derivatives of the expected number of tests and the expected recall functions

The derivative of the expected number of tests from a single remainder SNP with respect to the decision threshold follows,

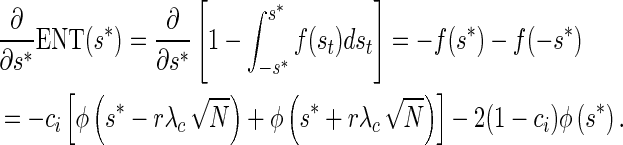(12)

Note that the second derivative is negative, hence convex. Therefore, the expected number of SNPs to be tested (ENT) is the sum of convex functions and is also convex. Let us denote the expected recall function by 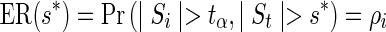. Its derivative follows,

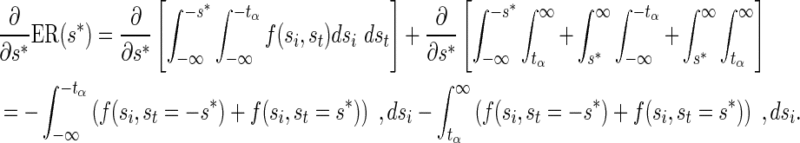(13)

Note that given,

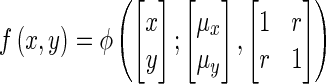(14)

it can be shown that a cross-section of the joint distribution at y = a follows,

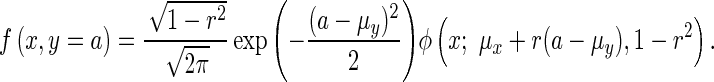(15)

Therefore, using the joint distribution of the statistics of a remainder SNP and its best-proxy, Equation (13) can be expressed as,

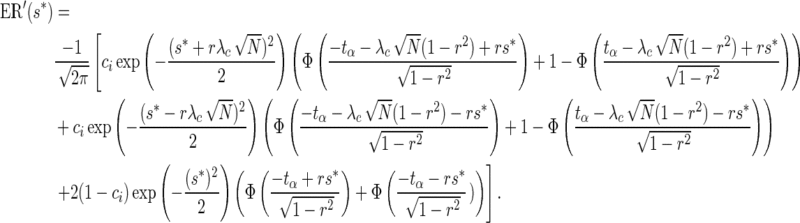(16)

It can be shown that ER(.) is a monotonic function of the best-proxy statistic threshold, s*. Therefore, there exists a unique ρ_i such that ER⁻¹(ρ_i) = s*, where ER⁻¹(.) is the inverse of the expected recall function. Using this property, the problem can be simplified by linearizing the constraint function, which reads

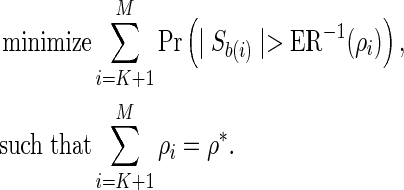(17)

Note that , hence the derivative of the expected number of tests from a single remainder SNP with respect to ρ follows,

(18)

Using the method of Lagrange multipliers, it can be shown that at the optimum solution the expected number of tests from each remainder SNP has the same derivative value, g*. In GRAT, we determine g* by using binary-search such that for each remainder SNP m_i, g* uniquely maps to , where .

4.2. Performance on a single SNP pair

We apply the proposed method to a pair of SNPs, a causal SNP and noncausal proxy SNP, to verify whether or not the target sensitivity is reached for any value of the pairwise correlation. For each value of the correlation, we sampled thousands of joint statistics for the SNP pair and recorded how many times the causal SNP is significant. The power at the causal SNP is set to 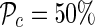using a genome-wide significance level of α = 10⁻⁸.

We computed the threshold of the proxy SNP statistic for different target sensitivities in each pairwise correlation using a small prior probability for the causal SNP, c_i = 10⁻⁵. In each correlation value, we applied the decision rules to the samples and recorded the recall rate of significant causal SNPs in each target sensitivity.

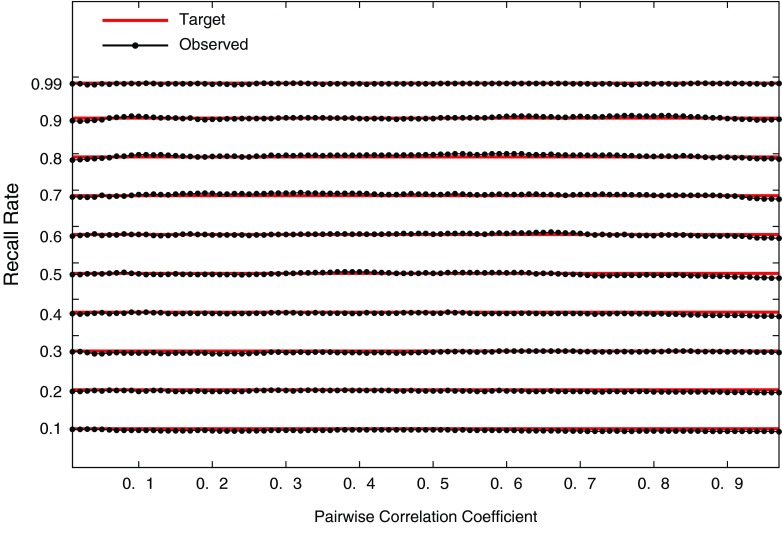
In Figure 2, the observed recall rates are shown for different values of target sensitivity and pairwise correlation. The target sensitivities are shown as horizontal lines and are followed closely by the observed recall rates. The variation around a target value is due to the asymptotic distribution of the test statistic and diminishes as the sample size increases.

FIG. 2.

Performance of the method using a single pair of SNPs. The observed recall rate of the significant causal SNP is shown for different target sensitivity and pairwise correlation values.

Acknowledgments

E.K. is supported by training grant 2T32NS048004-06A1. E.K. and E.E. are supported by National Science Foundation grants 0513612, 0731455, 0729049, 0916676, and 1065276, and National Institutes of Health grants K25-HL080079, U01-DA024417, P01-HL30568, and PO1-HL28481.

Author Disclosure Statement

No competing financial interests exist.