Real-time control of walking using recordings from dorsal root ganglia

Abstract

Objective

The goal of this study was to decode sensory information from the dorsal root ganglia (DRG) in real time, and to use this information to adapt the control of unilateral stepping with a state-based control algorithm consisting of both feed-forward and feedback components.

Approach

In five anesthetized cats, hind limb stepping on a walkway or treadmill was produced by patterned electrical stimulation of the spinal cord through implanted microwire arrays, while neuronal activity was recorded from the dorsal root ganglia. Different parameters, including distance and tilt of the vector between hip and limb endpoint, integrated gyroscope and ground reaction force were modeled from recorded neural firing rates. These models were then used for closed-loop feedback.

Main Results

Overall, firing-rate based predictions of kinematic sensors (limb endpoint, integrated gyroscope) were the most accurate with variance accounted for >60% on average. Force prediction had the lowest prediction accuracy (48±13%) but produced the greatest percentage of successful rule activations (96.3%) for stepping under closed-loop feedback control. The prediction of all sensor modalities degraded over time, with the exception of tilt.

Significance

Sensory feedback from moving limbs would be a desirable component of any neuroprosthetic device designed to restore walking in people after a spinal cord injury. This study provides a proof-of-principle that real-time feedback from the DRG is possible and could form part of a fully implantable neuroprosthetic device with further development.

1. Introduction

Many people with paraplegia due to a traumatic spinal cord injury (SCI) have a strong desire to walk again (Widerstrom-Noga et al., 1999; Brown-Triolo et al., 2002). Neuroprostheses can restore some walking function by activating parts of the nervous system. Devices such as the Parastep that electrically activate motor nerves to produce contractions in paralyzed muscles can restore limited walking function (Graupe and Kohn, 1998). However, neuroprostheses have not replaced the wheelchair for mobility purposes in part due to high energy costs (Ragnarsson, 2008; Stein et al., 2005; Thrasher and Popovic, 2008). Another limitation of the Parastep is its inability to adapt to perturbations in the environment through sensory feedback. The control of natural walking within the spinal cord utilizes a combination of descending control, sensory feedback and intrinsic timing all of which are modulated by a central pattern generator (Pearson, 1995; McCrea and Rybak, 2008; Prochazka et al., 2002a; Rossignol et al., 2006). Mimicking the control mechanisms within the spinal cord has been the most successful approach to restore walking and has highlighted the importance of sensory feedback (Yakovenko, 2011; Mazurek et al., 2012; Guevremont et al., 2007; Yakovenko et al., 2004).

A neuroprosthetic system for restoring walking may require a larger number of sensors to control the coordinated action of many joints. Recent advances in sensor manufacturing have resulted in the creation of small, low power, and accurate sensors for a variety of sensing modalities (e.g., accelerometers, gyroscopes). Even with their small size, the external sensors may be cumbersome to don and difficult to place correctly for accurate measurements (Webster, 1992).

Although rudimentary walking can be produced with minimal or no sensory input, robust natural control of walking requires large amounts of accurate sensory information (Rossignol et al., 2006). Sensory afferents convey information about a variety of modalities (e.g., position, pressure) to the locomotor networks in the spinal cord. The cell bodies from these sensory afferents are located in the dorsal root ganglia (DRG) just outside the spinal cord for each spinal level. Action potentials from these afferents can be recorded extracellularly from the DRG and decoded to provide an approximation of natural sensory information (Loeb and Duysens, 1979; Stein et al., 2004a; Stein et al., 2004b; Cordo et al., 2002). Many algorithms are available for decoding sensory information, such as linear decoding, Kalman filters or Bayesian-modified Kalman filters (Carmena et al., 2005; Stein et al., 2004b; Li et al., 2009; Li et al., 2011). As early as the 1970s, recordings of single sensory cells from chronically implanted electrodes in awake, walking cats were decoded (Prochazka et al., 1976; Loeb et al., 1977).

The recent development of high density silicon recording arrays (e.g., Utah electrode arrays) has enabled the simultaneous extracellular recording from up to 100 electrodes (Nordhausen et al., 1996; Branner and Normann, 2000). The ability to record simultaneously from populations of neurons has allowed new decoding methods to extract a wide range of neural information, from the motor commands in the cerebral cortex to bladder pressure levels in the spinal cord (Velliste et al., 2008; Patil et al., 2004; Bruns et al., 2011).

Stein et al. (2004b) performed the first implantation of a Utah array into the DRG to record simultaneously from many sensory afferents in anaesthetized cats. Recordings were made during passive limb movements and the signals were processed offline to decode hind limb position from collections of neurons in the DRG. To implement DRG feedback in a walking device, decoded predictions of hind limb state must be calculated in real time. Recently, limb locations were predicted from DRG recordings in real time and used to control intramuscular stimulation patterns in cats (Bauman et al., 2011; Bruns et al., 2013). The algorithm moved the leg sequentially to one of four quadrants based on predicted limb location.

The present study used a novel form of functional electrical stimulation (FES) called intraspinal microstimulation (ISMS) to elicit walking-like movements. ISMS does not fatigue the muscles as quickly as intramuscular stimulation, and is, therefore, a better candidate for implementation in an eventual neuroprosthesis (Lau et al., 2007; Bamford et al., 2005; Mushahwar and Horch, 1998). ISMS uses an array of fine wires to stimulate motor neuron pools electrically in the ventral horn of the lumbar spinal cord to activate individual muscles selectively (Mushahwar and Horch, 1997, 2000). Interneurons link motor neuron pools to activate synergistic muscles producing multi-joint movements (Mushahwar and Horch, 2000; Prochazka et al., 2002b; Saigal et al., 2004; Mushahwar et al., 2002).

The electrodes required for ISMS and DRG feedback can be implanted in the lower lumbar spinal cord via one surgical opening. Unfortunately, the close proximity of the intraspinal stimulation electrodes (within 2 cm) to the recording arrays can cause stimulation artifacts that overwhelm the action potentials (Weber et al., 2007). Recording in the DRG during peripheral stimulation (e.g., intramuscular stimulation) is less susceptible to artifacts due to a greater distance between the stimulation site and the recording arrays. However, the smaller current amplitude levels required for ISMS may allow for closer proximity of the stimulation and recording sites. Additionally, contamination of recordings by biopotentials (such as electromyographic activity) can be prevented by placing shielding around the recording array (Clark et al., 2011).

This study provides a proof-of-principle for using continuous real-time predictions of limb state based on sensory afferent firing in the DRG to control walking. Combining this form of internally derived feedback with a form of stimulation that is delivered through the spinal cord could eventually lead to a fully implantable neuroprosthetic system for walking. The system was tested by using the limb state predictions in combination with a previously developed walking control algorithm, to limit backward extension in response to varying perturbations (Mazurek et al., 2012). We also tested a number of factors affecting prediction quality, including the type of external sensor used for training, the frequency of retraining, and the effect of stimulation artifacts on prediction quality.

2. Methods

2.1 Implantation

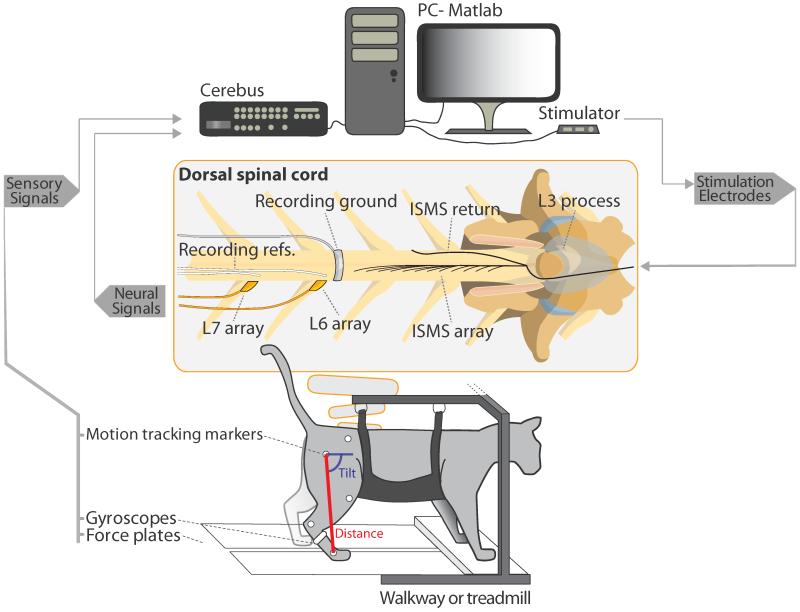
All experimental procedures were approved by the University of Alberta’s Animal Care and Use committee. A total of 5 intact cats (3.6-5.7 kg) were used in acute, non-recovery experiments lasting 24 to 36 hours. Anesthesia was induced with isoflurane (5%), and subsequently replaced with sodium pentobarbital to maintain the animals throughout the implantation procedures and data collection (induction: 25mg/kg intravenously; maintenance: 1 in 10 dilutions of the anesthetic). A laminectomy was performed to expose spinal cord segments L4-S1 and the right L6 and L7 DRG (figure 1). A fine-wire array consisting of 12 electrodes (Pt-Ir 80-20%, 50 μm diameter, 4 μm polyimide insulation, <1 mm deinsulated tip) was implanted in the right side of the spinal cord for stimulation. The fine-wire array was fixed to the L3 spinous process using dental acrylic. The electrode tips targeted motor neuron pools in the ventral horn of the gray matter. Maps of the cat motor neuron pools facilitated the implant (Saigal et al., 2004; Yakovenko et al., 2002; Vanderhorst and Holstege, 1997). The electrodes were implanted in regions that produced 4 distinct functions: hip flexion, ankle flexion, knee extension and a full limb extensor synergy. Two to three electrodes were implanted per function. The stimulation return electrode was a 9-strand stainless steel wire (AS632, Cooner Wire Inc., Chatsworth, CA, USA) deinsulated for approximately 2 cm at its tip. To fix the return wire in place, the end of the wire was tucked along the left side of the spinal cord between the cord and the spinal canal in the center of the stimulation array (figure 1, center). Utah electrode recording arrays were implanted into the right L6, L7 or both DRGs with a high speed pneumatic inserter. Each Utah array consisted of either 4×10 (L6) or 5×10 (L7) electrodes with an electrode shank length of 1.5 mm (Blackrock Microsystems, Salt Lake City, UT, USA). The recording ground electrode was a deinsulated band of braided stainless steel wire approximately 3 mm wide that was curved around the dorsal spinal cord between the stimulation and recording locations. The recording reference wires were placed proximally and as close as possible to their respective arrays (figure 1, center).

Figure 1.

Experimental overview. Sensory signals recorded from video recordings of the hind limb and from gyroscopes and force plates are recorded by the Cerebus system. Within the spinal cord, Utah arrays are implanted in the dorsal root ganglia and an ISMS array is implanted. Sensory recordings from the Utah arrays are sorted and recorded by the Cerebus. Training and real-time prediction was done in Matlab from streaming recordings from the Cerebus. The Matlab algorithm controlled an ISMS stimulator to produce unilateral stepping-like movements.

2.2 Electrical Stimulation

The 8 electrodes producing the best response to ISMS in the ipsilateral limb were selected and connected to a custom 16 channel, current-controlled stimulator that delivered trains of charge-balanced, biphasic pulses (up to 120 μA, 290 μs pulse width, 62 Hz). The 4 remaining electrodes were disabled. This provided 2 stimulation channels for each of the 4 functions mentioned above. The stimulation controller addressed the channels individually or combined during 4 sequential controller states. A flexion state (F) produces the swing phase, and is followed by 3 extension states. In the first extension state (E1), the knee is extended with the hip flexed to prepare for paw touch down. In E2, the ankle and knee are extended for weight support during mid-stance, and in E3, hip extension is added to provide propulsion. Each state accounted for respectively 20%, 20%, 20%, and 40% of the step cycle which had a duration of 1.5 s (Mazurek et al., 2012). Stimulation was modified in real-time on a pulse-by-pulse basis, and the controller was capable of adapting the intrinsic timing cycle using sensory feedback. The stimulator was only capable of sequentially delivering stimulation pulses across the electrodes. Therefore, the proportion of the recording time contaminated with stimulation artefacts was higher than it would be with synchronous stimulation across electrodes

2.3 External sensors

Testing of walking was performed on an instrumented walkway (Cats A, B, C) or split-belt treadmill (Cats D, E). Markers were fixed to the right hind limb to record two-dimensional kinematics using a camcorder with lens parallel to the walking plane (120 fps, JVC Americas Corp., Wayne, NJ, USA). Markers were placed on the iliac crest, and the hip, knee, ankle and metatarsophalangeal (MTP) joints. Marker positions were digitized with custom Matlab software written by Dr. Douglas Weber (University of Pittsburgh, Pittsburgh, PA, USA). Hind limb segment length was defined as the distance between the hip and MTP marker (referred to as: distance). Hind limb segment angle was defined as the angle between the hip-MTP segment and horizontal (referred to as: tilt) (figure 1, bottom). Force transducers mounted within the walkway and treadmill captured supportive (vertical) forces of the right hind limb. A gyroscope was fixed to the right foot and was continuously integrated to provide a measure of angle of the foot with respect to horizontal. The gyroscope was reset during the end of the flexion phase to eliminate the build-up of error due to drift. Force and gyroscope signals were sampled using a Cerebus data acquisition system (Blackrock Microsystems, Salt Lake City, UT, USA) at 1 kHz and filtered in Matlab (The MathWorks Inc., Natick, MA, USA) with a moving average filter of 120 ms. Each sensor modality provided a unique means to train the prediction models (see Section 2.6) and was evaluated separately to determine which model would result in the best prediction accuracy and closed-loop stepping performance. For instance, an approximation of limb tilt was provided by both video recordings and the integrated gyroscope. If the gyroscope was adequate for training the prediction model, it would be easier to implement clinically than a motion tracking system.

2.4 Neural signals

The neural signals from the DRG were also recorded and processed with the Cerebus system and Central software (v. 6.01.00.00). After filtering with a high-pass digital filter (250Hz) and a low-pass Butterworth filter (3^rd order, 7.5 kHz), the signals that crossed a manually-set amplitude threshold were identified as action potentials of interest or “spikes”. Spike-sorting based on time-voltage windows was used to distinguish the signals of multiple neurons on one recording electrode (channel). Signals identified as coming from one source (typically from 1 neuron) are further referred to as a unit. The time-voltage windows for all channels were set during passive manipulation of the hind limb at the beginning and midpoint of the experiment. All sensor data and timestamps of action potentials were streamed into Matlab.

2.5 Artifact Rejection

Artifact rejection ensured that information recorded from the DRG consisted of natural sensory afferent signals rather than waveforms artificially created by the electrical stimulation in the spinal cord. Artifacts were rejected using two software filters, one based on the timing and the other on the amplitude of the artifact. Unlike action potentials that may appear on one or a few neighboring channels, a stimulation artifact appeared across almost all recording channels concurrently. Therefore, if a synchronous event was detected across at least 60% of the channels, the following 1 ms window of data was rejected to discard the artifact. The majority of artifacts were discarded using the timing filter. Additionally, some artifacts were discarded based on their amplitudes. Often artifacts were much larger in amplitude than action potentials (sometimes by an order of magnitude). When either the positive or negative phase of a waveform exceeded ± 600 μV, it was assumed to be an artifact and was discarded.

2.6 Prediction Algorithm

Models were developed for real-time predictions of external sensor signals using neural recordings from the DRG. The first phase, called the training phase, compared signals from external sensors (distance and tilt from video recordings, foot angle from gyroscope signal, and forces) with the firing rates of DRG neurons after a recorded trial. The result of the training phase was a set of multivariate linear equations that used the firing rates of selected units to predict the signal of an external sensor. During the second phase, the testing phase, the model was used to create a real-time prediction of an external sensor signal and in some trials, use that prediction for closed-loop control.

2.6.1 Training

The objective of the training process was to build a multivariate linear model to predict the signals from external sensors based on the weighted firing rates of selected units within the DRG. Although Kalman or Wiener filters might provide better predictions, this study used a simple linear filter. Our goal was to show that such a filter can work in real time, not that a simple linear filter is the best method. Prediction models could be created using any recorded external signals. Training was performed on 20 s of stepping produced by ISMS under open loop control, during which neural signals and external sensor signals were simultaneously captured. Although the entire 20 s of data were available to process continuously, the data were processed discretely in 31 ms snippets (based on the frequency of the controller) to simulate the processing used during real-time prediction. Video recordings required processing before they could be used for training. The marker locations were digitized and the tilt and distance of the vector connecting the hip to the limb endpoint was calculated. The first derivatives for all external sensory variables were also calculated. The methods were similar to the offline training algorithm described previously (Stein et al., 2004b; Weber et al., 2007).

First, the discrete timestamps were converted into a continuous firing rate (f_i) for each unit:

$$f_i=\frac{1}{\Delta t}{\Sigma }_j\left(1-\frac{\mid t_i-t_j\mid }{\Delta t}\right)$$ (1)

where Δt is the sampling interval (1/120s), t_i is the current simple time indexed by i, t_j is the time of the jth spike in the interval between the preceding and the following samples [t_i − Δt, t_i + Δt]. This process was similar to the standard method of binning; however, our method weighted each spike by the latency between the current time t_i and the spike-event time t_j to preserve the exact timing of each spike. Both the firing rates and the external sensor signals were then filtered with a critically damped, 2^nd order, low-pass filter with a time constant of 50 ms to prevent any time shifting (Stein et al., 2004a).

Next, the firing rate of each unit was correlated with an external sensor signal and its derivative. The units were ranked according to correlation and two separate groups of units, those best correlated with the signal and those best correlated with the derivative, were selected. The groups could contain any combination of different or similar units. A pre-determined number (selected by the operator) of the most highly correlated units were included in the prediction model (10 units was the default). Then the linear model was trained using least squares regression to find an optimal set of coefficients (c_k) to relate the firing rates to the external sensory signal:

$${\widehat{q}}_i=c_0+{\Sigma }_{k=1}^N(c_k\cdot f_{i,k})$$ (2)

where ${\widehat{q}}_i$ is the estimated value of state variable q at time i. The estimate is derived from a weighted summation of firing rates of N neurons and f_i,k is the firing rate of neuron k at time i. c₀ is a bias term in the regression model.

After the model was generated, the firing rates (previously used to generate the model) were used as inputs to create a prediction of the external sensor signal. The error between signal and prediction (expressed as percent variance accounted for (VAF), see below) served as a measure of the training quality. The final stage in the training process optimally weighted the prediction of the signal with its prediction of the derivative to best match the external sensory signal. The idea was to mimic sensory afferents like muscle spindles, which sense both position its first derivative, velocity. For the weighting, a number (w) between 0 and 1 was created representing the proportion of the signal weighted to the derivative. The algorithm systematically combined the signal and derivative at 0.01 proportional increments from w=0 to w=1 according to:

$${\tilde{q}}_i=w\cdot \left({\widehat{q}}_{i-1}+\frac{d{\widehat{q}}_i}{dt}\cdot \Delta t\right)+(1-w)\cdot {\widehat{q}}_i$$ (3)

where ${\tilde{q}}_i$ is the new estimate using a weight of w for the ith sample time. The first derivative $\frac{d{\widehat{q}}_i}{dt}$ was integrated to provide an independent estimate of the prediction. The optimal weight maximized the VAF between the weighted prediction and the external sensor signal. This procedure was repeated for all selected external sensors and resulted in an independent model to predict each external sensor signal.

2.6.2 Testing (Real-Time Implementation)

The testing phase used the model weightings created during the training phase to predict external sensor signals in real time using only streaming neural recordings. The real-time implementation was coded into the controller and ran from Matlab m-files using a timer function. Every 31 ms (the period of the controller), the timestamps of all neural channels were downloaded into Matlab from Cerebus using software provided by Blackrock Microsystems. Only timestamps from the lists of highly correlated units selected by the models were processed. The timestamps (which occurred since the previous prediction) were converted into continuous filtered firing rates using the same calculations from the training phase. By solving equation (2), the prediction of both the external sensor signals and its first derivative (${\widehat{\mathit{q}}}_{\mathit{i}}$) were calculated from the firing rates (f_i,k) using the trained model.

Then the predictions of the external sensor signal and its first derivative were proportionally combined according to the weighting coefficient in equation (3). The final weighted prediction (${\tilde{q}}_i$) was then recorded and fed into the IF-THEN rule base for closed loop control. The IF-THEN rule base compared (${\tilde{q}}_i$) for each predicted external sensor signal against a pre-set threshold for a rule. If the threshold was exceeded, a state change occurred during the next controller period and the stimulation patterns changed accordingly. Several external sensor signals can be simultaneously processed due to the low computational demand of the prediction models. For Cats A, B and C, tilt and distance were predicted. For Cats D and E gyroscope and force plate predictions were added. All data were saved at the end of every controller period (31ms) and were used to initialize the filters for the following controller period. Predictions were calculated within the first ~5ms of the controller period and the remaining time was used to deliver asynchronous stimulation pulses. Optimal time lags were calculated during post-hoc analysis and were not found to improve prediction accuracy and, therefore, were not used.

2.7 Experimental Procedure and Test Protocol

After implantation of ISMS microwires and DRG recording arrays, the cats were transferred to an instrumented walkway (Cats A, B, C) or a split-belt treadmill (Cats D, E) and partially suspended in a sling and maintained under anaesthesia. The walkway had a cart that supported the sling (which in turn supported the head, fore limbs, trunk and abdomen) while the hind limbs freely stepped on the two tracks with embedded force transducers. The distance walked over the walkway was 2.9 m. During initial setup trials, appropriate ISMS amplitudes were established for each of the 4 controller states (flexion and 3 extension states) in order to produce adequate limb movement in that state. Because unilateral stepping did not produce continuous propulsion, the cart was pulled forward at constant velocity. During treadmill walking the belt speed was set to match the step cycle (about 0.15 m/s). All walking trials were 25 s long.

At set intervals open loop trials were conducted to retrain the prediction algorithm. No more than four consecutive test trials were performed without retraining (except during the “longevity test”, which tested the stability of predictions over time). Frequent retraining was used to eliminate the instability (i.e., changes in firing rates) of units observed over the duration of the longevity test (see below). Frequent retraining erred on the side of caution and was used to ensure that prediction accuracy was not affected by the instability of the units. Our goal was to verify the feasibility of real-time closed-loop performance while minimizing confounding factors such as unit instability. Halfway through the experiment, the thresholds and time-voltage windows for spike sorting were adjusted to account for larger variations in waveform shape and amplitudes that gradually built-up during the experiment and that could not be eliminated with retraining. Ideally, optimization of the thresholds and time-voltage windows should have been done every few trials, but due to time required to manually adjust these parameters, it was only performed halfway through the experiment. The sensory afferents were characterized according to their modality (e.g. muscle spindles, skin receptors, etc.) by passively manipulating the leg following the methods described in Aoyagi et al. (2003). Briefly, the leg was manipulated throughout its passive range of motion for hip, knee and ankle joints and tapped over muscles bellies and tendons to identify muscle receptors. Palpation (touch, pressure, and pinch) and gentle blowing were used to identify cutaneous and hair receptors. Waveform snippets (approximately 1.6 ms duration, sampled at 30 kHz) of action potentials were collected during manual stimulation of the receptor to compare with the units used in the prediction models (for Cats D and E only).

Three types of trials were studied: manual stepping and stepping produced by ISMS with open loop control and closed loop control. During passive stepping trials, an operator moved the foot of the cat in a stepping-like pattern and applied force against the walking surface during the stance phase. The operator minimized contact with the foot during passive movements. During open loop trials the progression of controller states was based on timing only. The stability of the predictions over time was tested in longevity tests, during which 8 consecutive testing trials were performed without retraining the model. The total duration of the longevity test was approximately 30 minutes (including the time between each trial, 2-3 minutes). Stability of units over longer durations was not tested. To evaluate the effect of ISMS stimulation frequency on prediction accuracy, the number of channels and stimulation frequency were reduced from the standard of 8 channels at 62 Hz to 4 channels at 31 Hz. The stimulation frequency of 62 Hz through 8 electrodes resulted in the greatest number of artifacts that would possibly be encountered in an ISMS-based neuroprosthesis. Four channels of stimulation at a reduced frequency of 31 Hz is the minimal number of channels and the minimal frequency needed to produce walking in one leg. With the lower rate and number of channels the stimulation amplitudes were increased by ~ 80% to maintain a similar walking pattern. During closed loop trials, the effect of activating a stance-to-swing phase transition was tested. Swing was initiated if the hind limb segment angle crossed a threshold (rotation clockwise with respect to forward horizontal) to limit backward hyperextension. Rule activation was tested by walking at different belt speeds (0.10, 0.15, and 0.20 m/s) during the training and testing trials.

2.8 Data Analysis

Data analysis was performed on the middle 15 s of the trial (between 5-20 s) to reduce the effects of starting and stopping of the cart on the walkway. For consistency, analysis of the treadmill trials was also limited to the middle 15 seconds of a trial. The trials were parsed into steps by taking the touchdown of the foot on the force plate as the beginning of each step. Stepping parameters were averaged across a trial.

Rule triggering during closed loop trials was evaluated offline. As the controller was state-based, the rule could only be activated during a subset of the total states (activation window). A rule triggering was successful when both the prediction and the recorded external sensor signal crossed the threshold within the activation window or neither crossed. When both signals crossed, the time delay was measured between the crossing of the prediction and the recorded sensor signal. A false positive was reported if the prediction crossed the threshold but the recorded sensor signal did not. Conversely, false negatives were reported when the recorded sensor signal crossed the threshold but the prediction did not.

The accuracy of the predictions against their simultaneously recorded external sensor signals was evaluated with VAF, a measure of the percent of explained variance between the external sensor signal and the predicted values. VAF was calculated by: where

$$VAF=100\left(1-\frac{variance(q-\tilde{q})}{variance\left(q\right)}\right)$$ (4)

where q and $\tilde{q}$ are, respectively, the actual and estimated state variables.

A Chi-Square goodness of fit test was used to test the differences in frequencies of the identified unit types. T-tests and one-way ANOVAs were used to test differences between group means. A value p≤0.05 was considered significant. All values are shown as mean ± standard deviation.

3. Results

3.1 Open loop stepping

Five experiments produced a total of 72 open loop trials and 71 closed loop trials with default parameters (62 Hz stimulation, 10 units selected for training and trained within 4 trials; see table 1). Table 1 shows the average kinematic variables and vertical forces per cat across unilateral stepping trials produced with ISMS using open loop control. The mean peak distance was greater for the cats tested on the treadmill (224 - 235 mm) than for those on the walkway (191 - 206 mm, p<0.001); similarly mean peak tilt was greater on the treadmill (129 - 134 °) than on the walkway (110 - 118 °, p<0.001). The moving belt of the treadmill probably resulted in greater backward extension of the hind leg. The mean peak ground reaction forces (%body weight) were not different for the cats tested on the walkway (6 - 8.2%) and those tested on the treadmill (6.4 - 8.9%, p=0.53).

Table 1.

Summary of experimental parameters and average stepping parameters for each cat.

	Cat A	Cat B	Cat C	Cat D	CatE
Sex a	M	M	M	F	M
Weight (kg)	5.7	5.0	3.6	4.8	5.0
Surface b	W	W	W	T	T
Trials
OL	9	10	11	22	20
CL	4	7	6	20	34
Kinematics c
Peak Distance d (mm)	191 ± 4.1	206 ± 9.0	205 ± 7.5	224 ± 2.9	235 ± 3.9
Peak Tilt d (°)	110 ± 2.4	118 ± 5.3	118 ± 4.3	129 ± 1.7	134 ± 2.2
Hip Range (°)	19 ± 1.2	29 ± 2.5	26 ± 5.5	21 ± 2.3	40 ± 5.5
Knee Range (°)	12 ± 0.9	26 ± 2.8	18 ± 6.8	22 ± 3.3	47 ± 3.9
Ankle Range (°)	32 ± 5.5	16 ± 2.9	19 ± 6.1	59 ± 4.2	77 ± 11.1
Kinetics c
Peak Force (%BW)	8.2 ± 2.5	7.9 ± 1.4	6.0 ± 1.2	6.4 ± 1.8	8.9 ± 1.5

^aM=male, F=female

^bW= walkway, T=treadmill

^cKinematic ranges and kinetics are shown as: mean ± standard deviation.

^dPeak: the maximum value per trial averaged across trials for each cat.

3.2 Afferents used in prediction

A Utah electrode array was implanted in the L7 DRG in cats A and B, in the L6 DRG in cat D, and in L6 and L7 DRG in cat C and E (table 2). The arrays recorded from a total of 158 afferents during passive manipulation of the hind limb in the 5 cats. For the majority of these afferents (89%), the location (e.g., skin, muscle) and sensory modality (e.g., pressure, touch, stretch) could be identified. The number of recordable units per array was variable, ranging from 17 to 37, and depended on the success of the array injection procedure in the DRG. There was no significant difference between the number of cutaneous (41%) and muscle (48%) afferents identified (p=0.31). The average number of the different types of units (e.g., skin, muscle, unknown) selected as predictors (out of 10) during training are shown in table 2. During stimulation, some new units would appear while others were not activated. Therefore, many of the units used as predictors were not identified during the passive movements (45%). All predictions (regardless of sensor type) used more muscle units than cutaneous units (p<0.01, chi-square test).

Table 2.

Recorded sensory afferents used in predictions. Cats were implanted with either one or two recording arrays in dorsal root ganglia (DRG) locations L6 and/or L7. Count shows the total number of each unit type identified and total of all units identified per cat. Predictor units show the average number of each sensory afferent type used by each sensor. Unclassified units were units found during identification but their function could not be ascertained. Unknown units were not found during identification. A total of 10 units were used for each prediction.

	DRG	Units identified			Predictor Units
			Count	Distance	Tilt	Gyro	Force
Cat A	L7	Muscle	7	1.3	1.0
		Cutaneous	10	1.0	0.8
		Unclassified	9	1.3	2.5
		Unknown		6.5	5.75
		Total	26	10	10
CatB	L7	Muscle	9	2.6	2.9
		Cutaneous	8	2.1	2.2
		Unclassified	0	0.0	0.0
		Unknown		5.3	4.9
		Total	17	10	10
Cat C	L6, L7	Muscle	28	5.7	0.8
		Cutaneous	15	0.4	0.4
		Unclassified	5	0.5	0.2
		Unknown		3.4	8.6
		Total	48	10	10
CatD	L6	Muscle	15	4.3	4.8	4.4	4.2
		Cutaneous	20	1.7	3.5	2.2	2.1
		Unclassified	2	0.5	0.1	0.0	0.0
		Unknown		3.4	1.5	3.4	3.7
		Total	37	10	10	10	10
CatE	L6, L7	Muscle	17	5.3	7.3	0.5	6.6
		Cutaneous	11	1.4	1.3	0.7	1.2
		Unclassified	2	0.0	0.0	0.0	0.0
		Unknown		3.3	1.3	8.8	2.2
		Total	30	10	10	10	10

3.3 Prediction during Passive Movements

Real-time predictions of all external sensor signals during a single trial are shown in figure 2. During this trial, the limb was passively moved in a stepping-like pattern with realistic levels of force applied during the stance phase. Therefore, it illustrates the capabilities of the real-time prediction algorithm without the presence of stimulation artifacts.

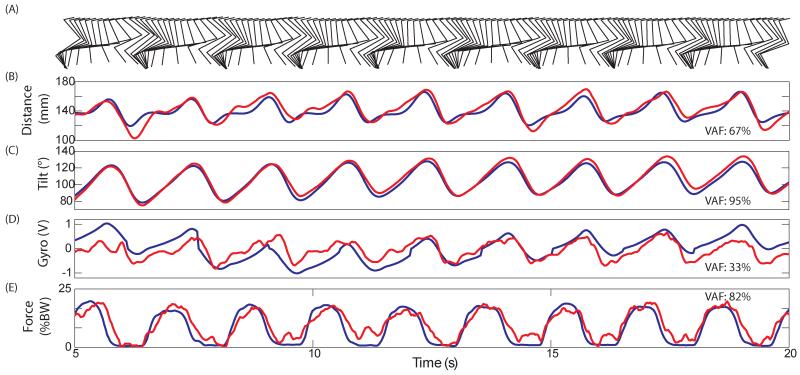
Figure 2.

Single trial predictions during passive stepping-like movement in Cat E. Recorded signals are in blue and real-time predictions of the signal are in red. A) Motion capture of the right hind limb every 120 ms. B) Distance from the hip to the limb endpoint. C) Angle of the vector connecting hip to limb endpoint (measured clockwise from horizontal forward). D) Integrated gyroscope signal. E) Supportive force in % body weight. Predictions of external sensor signals are possible using recordings from the dorsal root ganglia.

The prediction of tilt (VAF: 95%) was more accurate than the prediction of distance (VAF: 67%). The gyroscope did not provide a usable signal during passive movements because the resets were pre-set in the controller and not synchronized with the passive movements. Force prediction was the second most accurate with a VAF of 82%. The force (artificially applied pressure to mimic the stance phase) reached an average peak value of 18±0.9% body weight (BW) across steps. This was higher than forces produced during ISMS stepping in our experimental setup.

3.4 Artifact Rejection

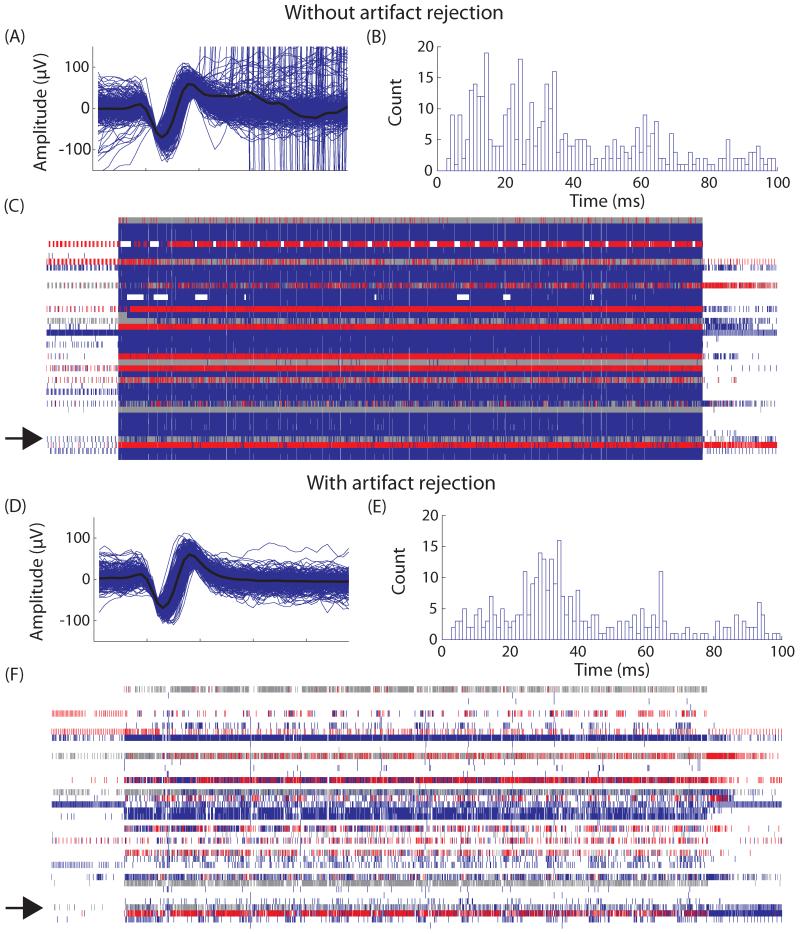
Stimulation artifacts contaminated recordings of neural signals and degraded the accuracy of the prediction based on those signals. Figure 3 shows neural recordings before and after the implementation of artifact rejection filters on a single trial. The first section shows neural recordings during an ISMS-driven stepping trial without any artifact rejection. The patterned stimulation was applied from approximately 3 to 23 s into the trial. In addition to the identified unit (panel A), large magnitude artifacts were also misidentified as the same unit. Based on a stimulation frequency of 62 Hz, the intervals between stimulation artifacts was approximately 16 ms (panel B). In the interspike interval histogram, defined peaks were visible at the stimulation frequency and its harmonics (32 ms, 48 ms, etc.), indicating that the detected spikes were likely caused by stimulation artifacts instead of neural signals. During stimulation, large numbers of events were continuously detected on all electrodes and appeared as a solid block in the raster plot (panel C). All of these stimulation artifacts, which were recorded across all electrodes, were identified as neural signals because their waveforms crossed the time-amplitude window(s). In panels D-F, artifact rejection filters were activated during recording of an otherwise similar stepping trial (recorded consecutively). Even with the same stimulation parameters, clean neural signals were recorded with few visible artifacts on the same electrodes. The waveform of the identified unit shown in panel D did not contain any large amplitude artifacts and the ISI histogram (panel E) did not have the characteristic peaks at the stimulation frequencies. In the raster plot (panel F), the solid block of stimulation events was mostly eliminated by the artifact rejection code and phasic firing of spikes was distinguishable. With artifact rejection during an ISMS stepping trial, the average number of spikes per recording electrode was reduced from over 1800 to approximately 250 spikes.

Figure 3.

Single neuron recordings without and with artifact rejection in Cat D. Without artifact rejection: A) Multiple waveforms identified as a single unit are overlaid with the average waveform shown in black. Large amplitude stimulation artifacts are also erroneously identified as the single unit. B) A histogram of interspike intervals (ISI) shows large numbers of events occurring at harmonics of the stimulation frequency (16 ms). C) A raster plot of all channels with neural data. Each channel is plotted on a separate horizontal line. Each small vertical line represents detection of an action potential on an electrode. Gray lines are unsorted units while colored lines represented signals accepted for processing. Due to stimulation artifacts so many events are accepted that it appears as a blue block. The channel of the single unit shown is A) and B) is highlighted with an arrow. D), E), and F) are similar except they show the same single unit with artifact rejection. Artifacts have been successfully removed from the waveform, ISI histogram and the raster plot and are not accepted into the prediction algorithm.

3.5 Prediction during ISMS

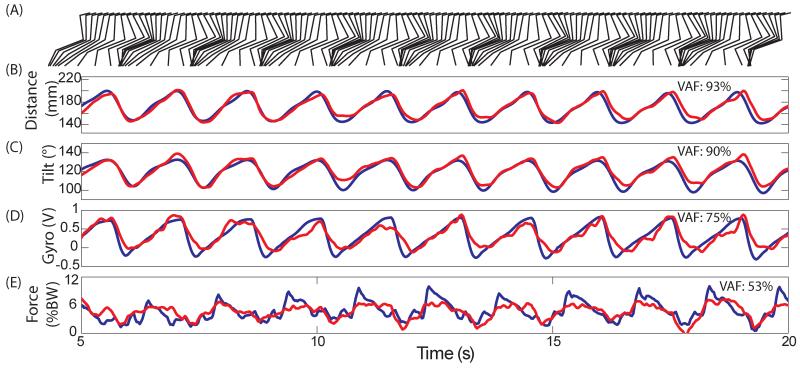
Figure 4 shows one of the best examples of real-time predictions generated during a single trial of ISMS stepping with artifact rejection enabled. The layout is similar to figure 2. The prediction accuracy was again high for both distance (VAF: 93%) and tilt (VAF: 90%). The average backward tilt was 132±0.6 ° and was slightly more than during passive manipulations (126±2.5 °). The gyroscope prediction of foot angle was much better (VAF: 75%) than during the passive trial. Force profiles displayed a steep decrease during the stance phase due to some backward slipping caused by the moving treadmill belt. However, peak force was less (9±1.8 %BW) than in the passive trial and the prediction was less accurate (VAF: 53%). Overall, by rejecting stimulation artifacts, the controller predicted kinematics and kinetics accurately based on streaming neural signals.

Figure 4.

Single trial predictions during ISMS stepping in Cat E. Recorded signals are in blue and real-time predictions of the signal are in red (similar format to Figure 2). All external sensor signals can be predicted in the presence of ISMS.

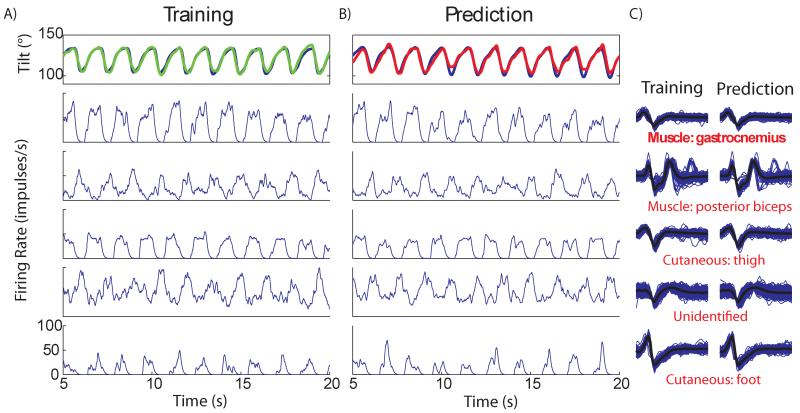
Figure 5 shows the 5 most correlated units used to predict tilt during the above mentioned trial and their consistency between training and testing trials. Panel A shows the overlap between the measured and calculated tilt (VAF: 96%). Real-time prediction using the trained model had a VAF of 90% (panel B). The firing rates were well modulated to the stepping pattern during training. During testing, the firing rates had similar magnitudes and were still well modulated. Waveform plots recorded during the training and testing trials for each corresponding unit are shown in panel C. The waveform shapes did not change appreciably, indicating that they were recorded from the same neuron in both trials. Two units that were best correlated with tilt during the training phase were muscle spindles located in the gastrocnemius and posterior biceps. Two units were identified as cutaneous afferents and one was unknown.

Figure 5.

The individual single units used in a prediction of limb tilt in Cat E. The training column (panel A) shows the recorded tilt during the training trial (blue) and the training fit (green). Below are the firing rates of the five most correlated units used in the prediction. The testing column (panel B) shows the recorded tilt (blue) and the real-time prediction (red) from the same trial as Figure 4. Again, firing rates for the same units are shown for the prediction trial. The waveforms during training and prediction of the selected units are shown in panel C, respectively for each unit during training and testing. Functionality of each unit is listed under the waveform and was determined during a separate identification process. From training to prediction waveforms and firing rates are stable.

3.6 Effects of system settings

3.6.1 Sensor type

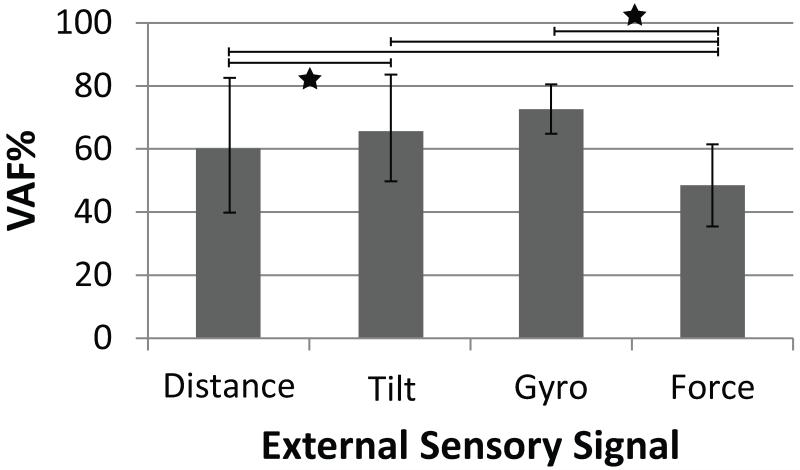
We first evaluated which external sensor signal could be predicted most accurately. Figure 6 shows a bar graph of the average VAF for each external sensor signal for all stepping trials with open loop ISMS. Distance models (VAF: 60±21%) had significantly lower prediction accuracy than tilt models (VAF: 66±17%, p<0.001). The VAF was highest for the gyroscope model (73±8%) and lowest for the force model (48±13%). Prediction accuracy for force was significantly lower than for distance, tilt and gyroscope (p<0.001).

Figure 6.

The average VAF when predicting each external sensor signal during open loop trials. Error bars represent the standard deviation of the predictions. Significance differences in means between sensor types are shown with a star (P<0.001). N: distance, tilt=47; gyro, force=34.

3.6.2 Time duration

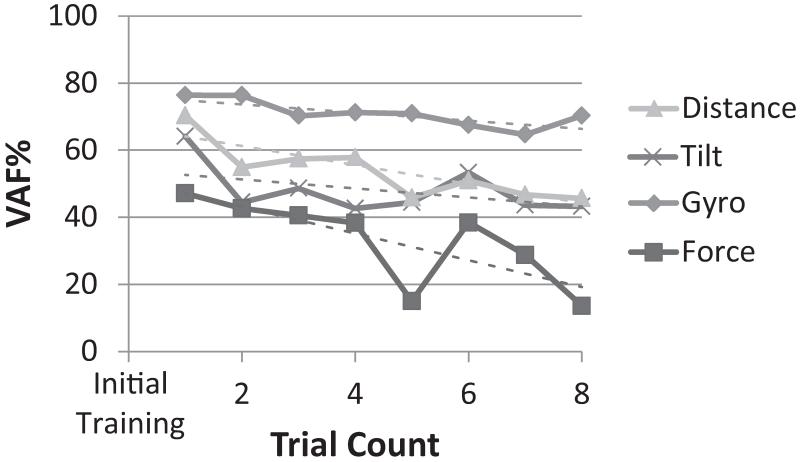
Another factor influencing prediction quality was the time elapsed after the training phase. Figure 7 shows the prediction accuracy averaged across cats (Cat B was not included due to technical issues) for up to 8 successive walking trials without retraining. The time elapsed between the walking trials 1 and 8 was typically about 30 minutes. Linear regressions performed on the mean values showed a significant negative correlation with time for all sensors, except for tilt (r²=0.03, p=0.18,). Prediction accuracy for distance decreased from 70% in trial 1 to 46% in trial 8 (r²=0.73, p=.007). The gyroscope prediction accuracy decreased by only 8% over 8 trials (r²=0.65, p=.016). Force prediction was more variable over time but still showed a significant negative relationship with trial number (r²=0.06, p=.026). The linear trend lines indicated that the rate of decay in VAF was highest for force prediction (4.0%/trial), and lowest for gyroscope prediction (1.3%/trial). Figure 7 shows that the VAF for Tilt and Distance shows a sharp drop after trial 1. Secondary analyses eliminating trial 1 showed that the overall picture of trend lines did not change; however the trends over time were not significant for Gyroscope and Force.

Figure 7.

The prediction quality (VAF%) of each external sensor signal over time after initial training. Each sensor signal is shown in a different shade of gray (from 1 to 8 trials after training). Linear trend lines are dashed and matched to their respective sensor signal.

3.6.3 Stimulation frequency

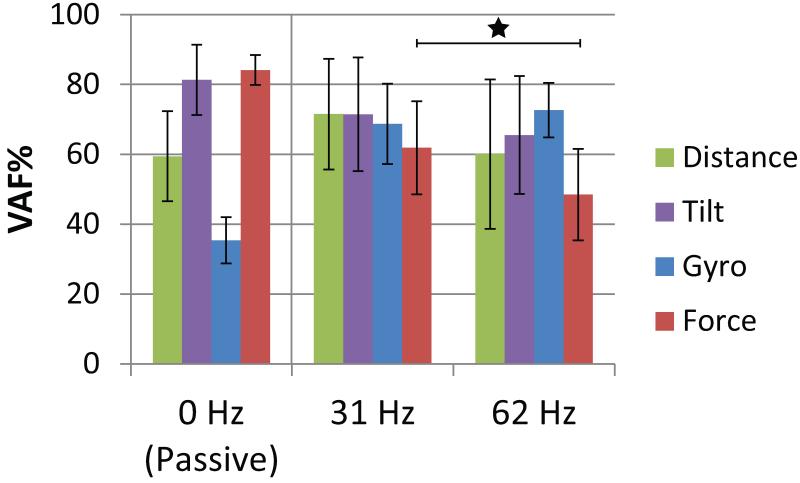
Figure 8 shows the prediction accuracy for each external sensor (averaged across cats during open loop trials) for passive, 31 Hz and 62 Hz ISMS conditions. An unpaired t-test (when all statistical assumptions were met) showed that the mean VAF for gyroscope prediction was higher for ISMS stepping (respectively, 31Hz: 69±11%, p<0.001; 62Hz: 73±8%, p<0.001) than for manual stepping (35±7%), because the resetting was synchronized to the step cycle, as mentioned above. Tilt and force prediction accuracy was the highest during passive movements (VAF, respectively: 81±10%, 84±4%). For force, the prediction accuracy for 31 Hz was significantly higher than 62 Hz (p<0.001). For distance and tilt, the difference between 31 Hz and 62 Hz was not significant, p=0.11 and p=0.22, respectively.

Figure 8.

The effect of stimulation frequency on prediction quality (VAF%) for each sensory signal during open loop trials. Bars represent the standard deviation of the predictions. Significant differences in mean VAF% between stimulation frequencies for each sensor are shown with a star (P<0.001). 0 Hz is passive movement of the hind limb, 31 Hz is the lower stimulation frequency tested and 62 Hz is the higher stimulation frequency. Passive distance and tilt: N=16, gyro: 7, force: 11; 31 Hz distance and tilt: N=13, gyro and force= 15; 62 Hz distance and tilt: N=47, gyro and force= 34.

3.6.4 Closed loop performance

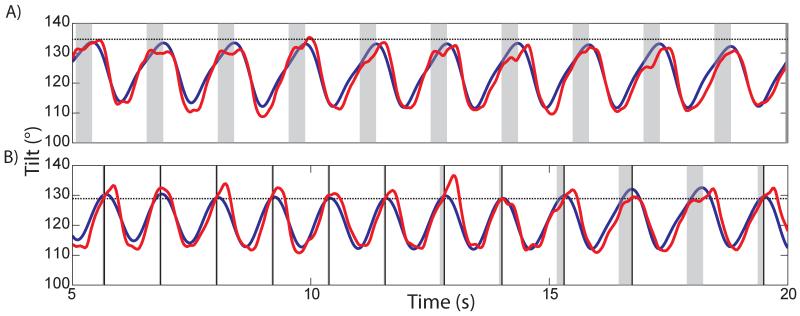
The predictions of external sensor signals were used for triggering a closed loop rule to modify stepping produced by the controller. When a prediction crossed a rule activation threshold within the activation window, an IF-THEN rule was activated immediately. This initiated another walking state to reduce undesirable stepping behaviour. During the closed loop trials shown in figure 9, a single rule designed to limit backward hyperextension (by changing from E3 (propulsion) to F (swing)) was triggered based on real-time predictions of hind limb segment angle.

Figure 9.

Activation based on predicted sensory input of a closed loop rule to limit backward hyperextension in Cat E. Recorded hind limb tilt is shown in blue and the real-time predicted tilt is shown in red. The activation threshold of the rule is shown with a black horizontal dotted line. Gray vertical regions represent times within the step cycle (corresponding to the underlying state system of the controller) when a rule can activate if the threshold is exceeded (activation windows). In panel A, the prediction (red) did not exceed the threshold during the activation windows. Panel B shows that a lower threshold causes many activations of the rule. The solid vertical line marks a rule activation and subsequent state transition to swing. Due to the underlying state transition, the activation window is truncated based on sensory feedback and appears irregular across steps.

The activations of the E3-F transition rule are shown in figure 9 during two consecutive trials with different thresholds. If the prediction of tilt exceeded the threshold within the activation window, the rule was activated (shown by a vertical black line at time of triggering) and the controller immediately entered the swing phase. In panel A, the threshold was set at 135 °. As the prediction did not reach threshold, the rule was not activated. In panel B, all settings were the same but the threshold was lowered to 129 °. As the prediction already exceeded the threshold at the onset of the activation window during the first 5 steps, the rule was activated immediately. During the next 4 steps, the triggering occurred when the prediction crossed threshold. In the next to last step, the rule was not triggered because the prediction did not cross the threshold within the activation window. By causing an earlier transition to the swing phase, the rule decreased the step duration by an average of 180 ms and consequently sped up the stepping. Tilt was reduced from 133±0.6 ° to 131±1 °, indicating that unwanted backward hyperextension was reduced or eliminated. The rule also reduced the range of motion in hip, knee and ankle joints from 33±2, 43±4, 58±2 to 27±2, 31±3, 40±8 °, respectively.

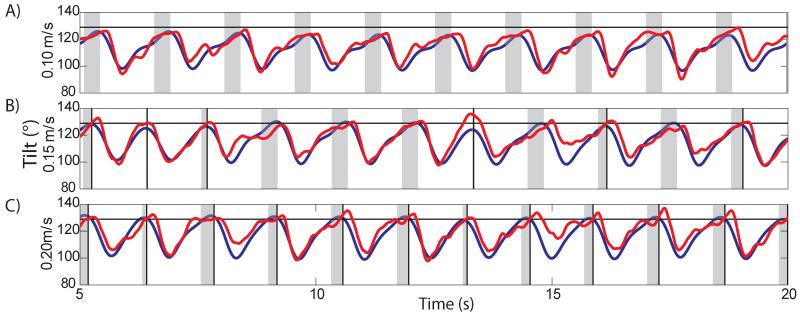
3.6.5 Adaptation to Treadmill Belt Speed

Next we showed how the E3-F transition rule adapted the stepping to different treadmill belt speeds. The transition threshold was held constant at 129° across three trials with various treadmill belt speeds: the normal speed used for all experiments, 0.15 m/s, and 0.10 m/s and 0.20 m/s. Tilt prediction models were retrained at each speed to ensure that prediction quality was controlled and only treadmill speed was variable. Figure 10 shows the three trials plotted with a similar format to figure 9. During walking on the slow belt (0.10 m/s), the E3-F rule was not activated as the leg did not hyperextend before the swing phase began (panel A). The average measured backward tilt was 124±1.1°. Panel B shows that six steps triggered rule activation with normal belt speed (0.15 m/s), which limited the measured backward tilt to 128±2.1°. Walking on the fast belt (0.20 m/s) triggered rule activation in all 12 steps (panel C). The measured tilt was 130±1.5 °. As the belt speed increased, the leg was extended farther backwards (increased tilt) during the stance phase, which increased the chance of triggering the rule.

Figure 10.

The effect of treadmill speed on activating the rule for backward hyperextension in Cat D (format similar to Figure 9). Each panel shows a trial at a different belt speed: 0.1 m/s (panel A, slow), 0.15 m/s (panel B, medium), 0.20 m/s (panel C, fast). The faster the belt speed the more the limb hyperextends and the more likely the rule will activate and begin the swing phase (thus truncating the activation window with the state transition). The threshold levels (horizontal black lines) were constant between belt speeds.

3.6.6 Rule Triggering Performance

Rule triggering performance based on a real-time prediction was compared to the hypothetical triggering based on the recorded external sensor signal for each step (table 3). Tilt and gyroscope prediction models were successful for a similar proportion of steps (59.7% and 60.9%, respectively). When successful, the tilt sensor had the lowest timing error (29.9±56.3 ms). The gyroscope prediction model had the highest timing error (57.6±80 ms). The force prediction model produced the highest number of successful activations (96.3% of the 108 total steps), and the lowest average timing error (15.3±65.6 ms). All sensors produced more false positives than false negatives.

Table 3.

Rule triggering performance for each external sensor signal. Total number of closed loop trials and steps are shown. Number and percentage of successful steps are shown for each sensor. Jitter represents the mean ± standard deviation of time delay between the recorded and predicted signal threshold crossings. FP=false positive (prediction crossed the threshold but recorded signal did not), FN= false negative (recorded signal crossed the threshold but prediction did not).

	Trials	Steps	Successful	%	Jitter (ms)	FP	FP%	FN	FN%
Tilt	43	464	277	59.7	29.9 ± 56.3	141	30.4	46	9.9
Gyroscope	11	115	70	60.9	57.6 ± 80.0	24	20.9	21	18.3
Force	9	108	104	96.3	15.3 ± 65.6	3	2.8	1	0.9

4. Discussion

The main objective of the study was to develop an algorithm that could process sensory information from neurons within the DRG in real time to use as feedback in a future neuroprosthetic walking device. Overall, the real-time prediction accuracy was similar to previous work from our lab using offline prediction algorithms for distance and tilt (Weber et al., 2007).

Although the approach is invasive, it offers a number of advantages over external sensors. In particular, multiple sensory modalities (limb position, force, etc.) are accessed from a single location. While we recognize that presently the risks and difficulties of this implanted system outweigh the benefits, this study demonstrates that it is feasible to combine DRG feedback and ISMS stepping.

4.1 Artifact rejection

Stimulation artifacts from ISMS electrode sites in close proximity to the recording sites degrade prediction performance by masking action potentials. Artifact rejection methods previously used offline (Weber et al., 2007), were successfully applied in real time during ISMS stepping. Recorded artifacts were rejected using two forms of software filters: detection of synchronous events and rejection based on signal amplitude. Signals from antidromic activation of DRG neurons would also have been eliminated by the 1 ms rejection window following a stimulation artifact.

4.2 Sensor Type

Overall, the best predicted sensor model for the closed loop unilateral stepping approach used in this study was tilt. It was the only prediction that did not show a significant negative correlation with time (trial number), thus requiring less retraining. Video-based prediction of tilt had less timing error than gyroscope-based foot angle prediction (gyroscope) during successful closed loop rule activations (while maintaining a similar percentage of successful activations). The main limitation to training a tilt prediction model would be the space required for a video recording system and its lack of portability. Potentially, a complementary filter combining an accelerometer and gyroscope to accurately measure leg tilt (Lovse et al., 2012) could be used to train a prediction model in a smaller space while still providing reasonable prediction accuracy.

Force prediction had the lowest accuracy, possibly due to the relative lack of recordings from force or pressure sensory afferents. We expected force prediction to utilize the pressure receptors in the foot. Instead, based on identified units, force prediction was being trained with muscle afferents correlating to limb position rather than cutaneous pressure and force. Cutaneous afferents sometimes provide information from a very localized area (e.g., pressure only on the 4^th toe pad). With such spatially specific activation areas, step-to-step variations in paw placement or loading may result in drastic changes in firing behaviour. Furthermore, while numerous Golgi tendon organs may be available in the muscles, each one only monitors the force of a few motor units in a particular muscle. The correlations between the total weight supported by the paw and either of these single unit recordings may not be very high. Perhaps larger ensembles of these units would provide better force predictions. Force prediction provided the highest percentage of successful activations of the closed loop rule. Its success may be partially attributed to the large change in signal during hyperextension (the change from full load-bearing to almost nothing). Other signals had smaller variations at the point of threshold crossing, which made it more difficult to correctly trigger the rule.

4.3 Changes over Time

Some firing rates and waveform shapes of sensory action potentials gradually changed during the course of an experiment. Gradual changes in ISMS activated movements and/or body posture in the support sling may also result in stepping variations during the course of an experiment. These variations in the stepping pattern can unpredictably change the firing rates of afferents with highly specific receptor fields. For instance, a pressure sensor in the lateral border of the paw may no longer fire if changes in paw placement result in a more medial loading.

Over time, changes in the distances between electrodes and neurons can cause gradual variation in neural waveforms (Cham et al., 2005). Chronic implants may result in greater mechanical stability of the recording arrays. Over a period of several weeks, a connective tissue capsule develops over the arrays, which secures the array to the DRG. Previous work in our lab has shown that chronic implants in cats can produce stable recordings for 21 days (Weber et al., 2006, 2007) and up to 110 (Stein, unpublished data). Furthermore, with online adaptive sorting, minor changes in waveform amplitude or shape would not affect unit sorting and prediction quality (Franke et al., 2010).

4.4 Stimulation Frequency

Action potentials coinciding with stimulation artifacts cannot be recorded, which results in erroneous calculations of firing rate, which in turn results in a degrading the prediction quality. During passive movements with no stimulation artifacts, predictions of distance and tilt were more accurate than during ISMS-driven stepping. The higher prediction performance during passive movements may partially result from a higher sensory activation from manipulating the limb and the greater ground reaction forces compared to ISMS-driven stepping. A reduction in stimulation frequency, which reduces the number of stimulation artifacts, resulted in a higher prediction quality, but the trend was only significant for force.

The prediction algorithm was tested using stimulation conditions in terms of number of stimulation pulses that are similar to those we typically use to produce bilateral walking; i.e., 8 channels and 62Hz (Holinski et al., 2012). Under these conditions, over half of the recording time has to be discarded, assuming an artifact duration of about 1 ms. Synchronous stimulation cannot be used for ISMS, as current spread through network activation would sum within the motor pools causing unintended movements. Therefore, an ISMS-based neuroprosthetic device with DRG feedback should use the lowest possible asynchronous stimulation frequency with the fewest number of stimulation channels possible to generate walking. We have previously shown that ISMS can generate bilateral walking with as few as 4 channels per side stimulated at 31 Hz (Holinski et al., 2012).

4.5 Closed loop Performance

The controller used timed transitions between states to produce stereotyped stepping. In response to perturbations, stepping speed was modified using a simple closed loop rule that responded to limb position or force production. Specifically, the predictions activated an IF-THEN rule to transition from stance into the swing phase to reduce backward hyperextension as treadmill belt speed changed. As treadmill belt speed increased, the frequency of rule triggering increased as well, limiting backward hyperextension. All sensor predictions were capable of triggering a rule within the appropriate activation window during the walking cycle with varying performance. Setting rule activation thresholds appropriately was critical for proper operation of the rules. Adaptive thresholding might perform better (Mazurek et al., 2012). Interestingly, prediction accuracy was not correlated to the number of successful activations of the transition rule. This implies factors other than prediction quality, such as threshold location, rule design and sensor behaviour, may be important as well.

Many degrees of freedom are used in the biological system and we could try to predict 3 or 4 joint angles per leg to produce realistic locomotion. However, one advantage of ISMS is that it produces synergies that span several joints. We show in this paper for the first time that the orientation (tilt) of the hind limb can be controlled during locomotion in real time using ISMS and DRG feedback.

5. Issues and improvements

Prediction accuracy may be improved with advanced decoding models. Kalman or Wiener filters might provide better real-time predictions than a simple linear filter. Prediction gains can be made by using a second-order model; however, higher order models show minimal further benefits (Stein et al., 2004a). Other models have used individual representations of each sensory afferent resulting in an increased performance when decoding certain parameters such as limb distance but could not improve prediction of limb tilt (Weber et al., 2011). These models require more computational effort and predictions were made offline. With increasing computational power in small devices, more complex models could become feasible for real-time prediction.

6. Future directions

In the future, the algorithms should be tested with bilateral over ground walking. Although substantial ground reaction forces were produced during both walkway and treadmill stepping, better prediction accuracy might occur during self-propulsion. If biocompatibility issues can be overcome, a chronic implantation might also increase the recording stability of the units over time, which could lead to less retraining and better prediction accuracy over a longer duration.