Haplotype Estimation Using Sequencing Reads

Abstract

High-throughput sequencing technologies produce short sequence reads that can contain phase information if they span two or more heterozygote genotypes. This information is not routinely used by current methods that infer haplotypes from genotype data. We have extended the SHAPEIT2 method to use phase-informative sequencing reads to improve phasing accuracy. Our model incorporates the read information in a probabilistic model through base quality scores within each read. The method is primarily designed for high-coverage sequence data or data sets that already have genotypes called. One important application is phasing of single samples sequenced at high coverage for use in medical sequencing and studies of rare diseases. Our method can also use existing panels of reference haplotypes. We tested the method by using a mother-father-child trio sequenced at high-coverage by Illumina together with the low-coverage sequence data from the 1000 Genomes Project (1000GP). We found that use of phase-informative reads increases the mean distance between switch errors by 22% from 274.4 kb to 328.6 kb. We also used male chromosome X haplotypes from the 1000GP samples to simulate sequencing reads with varying insert size, read length, and base error rate. When using short 100 bp paired-end reads, we found that using mixtures of insert sizes produced the best results. When using longer reads with high error rates (5–20 kb read with 4%–15% error per base), phasing performance was substantially improved.

Introduction

Haplotype estimation is often one of the first stages in any genetic study of populations, traits, or diseases. The precise sequence (phase) of alleles on each homologous copy of a chromosome is not directly observed by genotyping and must be inferred by statistical methods. Once estimated, haplotypes can be used to infer ancestry¹ or demographic history,² impute unobserved genotypes,³ or detect selection or detect causal variants.⁴ The literature on phasing methods is extensive.⁵ Most methods were designed to work on SNP genotypes derived from microarray genotyping chips. These methods take advantage of linkage disequilibrium (LD) between SNPs and local haplotype sharing between individuals to borrow information across samples when estimating phase.

High-throughput sequencing is becoming widely used in all aspects of human disease genetics and population genetics. Obtaining haplotypes from sequencing data, rather than genotypes from SNP microarrays, is more challenging for several reasons. First, the density of polymorphic sites being phased is much higher and contains many more low-frequency sites⁶ than on typical SNP microarrays. Low-frequency sites can be harder to phase and impute⁷ and the increased SNP density increases the necessary computation. Second, if sequencing coverage is low, then genotypes are only partially observed, with each genotype having some level of uncertainty depending on the number of reads that cover the site. It has become the norm to represent this uncertainty in a genotype likelihood (GL) at each site in each individual. These GLs take the form $P\left(\text{Reads}|G\right)$, where $G\in \left\{0,1,2\right\}$ is one of the three possible genotypes.⁸ Several existing phasing methods (Thunder,⁹ Beagle,¹⁰ Impute2,^3,11 and SNPtools¹²) can now process genotype likelihoods to impute genotypes and infer the underlying haplotypes.

Until now, no linkage disequilibrium (LD)-based phasing method has attempted to take advantage of phase information present in the sequence reads. Sequence reads are effectively mini haplotypes, and when enough reads span two heterozygote sites the reads can help resolve the phase of the two sites. In real sequencing data sets, there can be a large number of phase informative reads (PIRs). For example, in 379 European samples from the 1000 Genomes Project (1000GP) sequenced at ∼4× coverage, when we considered all heterozygous genotypes in the samples, we found that 33.8% were covered by a sequence read that also covered another heterozygous site in the same individual. This is a striking statistic and highlights the potential for using sequencing reads in haplotype estimation.

In this paper, we present a method that can use the partial phase information in sequence reads to increase the accuracy of haplotypes estimated from genotype data. Our method builds on the SHAPEIT2 method of haplotype estimation.¹³ SHAPEIT2 outperforms the leading methods when applied to GWAS scale data sets, can simultaneously handle unrelated individuals, mother-father-child trios, and parent-child duos, and can phase whole chromosomes at once. A key feature of the method is that the hidden Markov model calculations involved are linear in the number of haplotypes being estimated, whereas some other methods scale quadratically. The method uses a unique approach that represents the space of all possible haplotypes consistent with an individual’s genotype data in a graphical model. A pair of haplotypes consistent with an individual’s genotypes are represented as a pair of paths through this graph, with constraints to ensure consistency that are easy to apply as a result of the model structure.

Our new approach uses the phase information in sequencing reads as further constraints in this model. The method is primarily designed for use on high-coverage sequence data or on data sets that have already had genotypes called. Because sequencing reads contain errors, it might be that different reads disagree on phasing of sites, so we implement the constraints probabilistically by using information about base quality of the reads. This feature is especially important when using sequencing technologies that produce high error rates because it allows our method to down-weight (but not disallow) haplotypes that are inconsistent with observed reads (see Material and Methods for more details).

We have used this method to investigate three questions that will be of interest to the field. First, we have assessed whether our method can improve haplotype estimation when using data from current sequencing technologies. For this we have used data from a mother-father-child trio sequenced at high coverage by Illumina and have combined this with low-coverage sequencing data from the 1000GP.¹⁴ Second, we have assessed the impact of read coverage, read length, paired-read insert size, and base-error rate on phasing performance by using simulated sequencing data. We have used the properties of existing sequencing technologies to guide these experiments. The results allow us to make suggestions about how different combinations of these factors can be used to increase phasing performance. Finally, we have investigated the utility of the method for phasing single samples. Single-sample phasing could be of great value in clinical applications or when analyzing rare cases of a particular disease. For example, if compound heterozygote effects are an important factor in disease risk, then determination of accurate phase might be important.^15,16 Our method takes advantage of existing panels of haplotypes to phase sites in each single sample that are in common with the haplotype panel and utilizes phase-informative reads to phase variants that are singletons in the individual.

Material and Methods

Notation

We wish to estimate the haplotypes of N unrelated individuals with sequence data at L biallelic SNPs. We assume that sequence coverage is high enough that genotypes can be called at the L sites independently of the phasing process. Like several other accurate haplotype estimation methods, the algorithm we use is a Gibbs sampling scheme in which each individual’s haplotypes are sampled conditionally upon the sequence reads of the individual and the current estimates of all other individuals. Thus it is sufficient for us to consider the details of a single iteration in which we update the haplotypes of the i^th individual.

We denote a single individual’s genotype vector as $G=\left\{G_1,\dots ,G_L\right\}$, where $G_l\in \left\{0,1,2\right\}$ is the genotype at the l^th SNP and the two alleles at each SNP are arbitrarily coded as 0 and 1. We use $H=\left\{H_1,\dots ,H_K\right\}$ to denote the K current haplotype estimates of other individuals being used in the iteration.

We want to sample a pair of haplotypes $\left(g_1,g_2\right)$ that are compatible with G so that the sum of the alleles is equal to G, denoted $G=g_1+g_2$. To obtain a parsimonious representation of the possible haplotypes, we partition the vector G into a number, C, of consecutive nonoverlapping segments such that each segment contains B heterozygous genotypes. This segmentation is carried out on an individual basis so that the boundaries of the segments will vary between individuals. We use $S_l\in \left\{1,\dots ,C\right\}$ to denote the segment that contains the l^th SNP and $b_s$ and $e_s$ to denote the first SNPs and last SNPs included in the s^th segment, respectively.

A consequence of this segmentation is that there only are $2^B$ possible haplotypes and thus $2^{B-1}$ possible pairs of haplotypes that are consistent with G within each segment. We use $A_{lb}$ to denote the allele carried at the lth site by the b^th consistent haplotype. We can now represent a haplotype consistent with G as a vector of labels $X=\left\{X_1,\dots ,X_L\right\}$, where $X_l$ denotes the label of the haplotype at the l^th site in the $S_l$ th segment. The segmentation implies that the labels are identical within each segment so that we always have $X_l=X_{l-1}$ when $S_l=S_{l-1}$. We use $X_{\left\{s\right\}}$ to define the label of the haplotype across all sites residing in the s^th segment. Moreover, we represent a pair of haplotypes for G as a pair of vectors of labels $\left(X^1,X^2\right)$ with the restriction that the underlying pair of haplotypes is consistent with G. We use notation $X_{b,e}$ to denote the subset of $e-b+1$ labels going from the b^th site to the e^th. We use the notation $H^i$ to denote the haplotypes that span the sites within the i^th segment.

Additionally, we have a set of M single-end or paired-end sequencing reads that have been mapped to a reference genome, so we know which sites that each read overlaps. Let R be a matrix of M rows and L columns where $R_{ml}\in \left\{0,1,-\right\}$ is the allele carried by the m^th read at the l^th site. The value $-$ encodes either a site that is not covered by the corresponding read or a site that is homozygous in G. We discard sequencing information at homozygous sites because we are only interested in sites that need phasing, i.e., that are heterozygous. We use another matrix Q of the same dimension as R, where $Q_{ml}$ gives the error probability that the base at the l^th site in the m^th read is wrong. We treat Q as a fixed parameter and R as data. We also partition the reads into groups associated with each segment. We let $R^i$ be the rows of R that contain reads spanning the $\left(i-1\right)$ th and i^th segments. Then $R_j^i$ is the j^th read in the i^th partition.

We have written a standalone program to extract the PIRs from the BAM files available for G in order to build the matrices R and Q. Specifically, we use the samtools API to parse the sequencing reads in the BAM files and identify those that span at least two heterozygous genotypes in G. The new version of SHAPEIT2 then reads R and Q.

The Model

Given the segment representation described above, sampling a diplotype for G given a set of known haplotypes and a set of sequencing reads involves sampling from the posterior distribution $P\left(X^1,X^2|H,R,Q\right)$. By assuming first that the reads for the individual we are updating, R, are conditionally independent of the haplotypes in other individuals, H, given the pair of haplotypes $\left(X^1,X^2\right)$, we can write

$$P\left(X^1,X^2|H,R\right)\propto P\left(X^1,X^2,R,H\right)$$ (Equation 1)

$$\propto P\left(R|X^1,X^2\right)P\left(X^1,X^2|H\right)$$ (Equation 2)

$$\propto P\left(X^1,X^2|R\right)P\left(X^1,X^2|H\right),$$ (Equation 3)

where Equation 3 follows by assuming a uniform prior distribution $P\left(X^1,X^2\right)\propto 1$.

This factorization involves a model of the diplotype given the observed haplotypes, $P\left(X^1,X^2|H\right)$, which we refer to as the “haplotype model,” and a model of the diplotype given the observed reads, $P\left(X^1,X^2|R\right)$, which we call the “read model.” The haplotype model involves assumptions about the molecular and demographic mechanisms that have shaped the linkage disequilibrium patterns in the study population. For this, we use the previously described SHAPEIT2 model.¹³ This model has the simultaneous advantages of better performance than competitive methods and only linear complexity in $\left|H\right|$. The read model captures the features of the sequencing reads.

Based on the segmentation of the chromosome into C segments, our haplotype model is the same as the Markov model used in the SHAPEIT2 method¹³ and can be written as

$$P\left(X^1,X^2|H\right)=P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|H^1\right)\prod _{s=2}^{C}P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2|X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2,H^s\right).$$ (Equation 4)

We use a forward-backward algorithm to calculate the marginal distribution of the first segment, $P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|H\right)$, and the joint distributions between successive segments,

$P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2,X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2,H\right)$, given the set of haplotypes H. Note that the difference between these quantities and those in Equation 4 is that they are conditional upon the haplotypes across all segments H. Precise details of the forward-backward algorithm used to calculate this model can be found in the Supplemental Data of Delaneau et al.¹³.

For the read model, we use a similar Markov model that can be written as

$$P\left(X^1,X^2|R\right)=P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|R^1\right)\prod _{s=2}^{C}P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2|X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2,R^s\right).$$ (Equation 5)

The distribution of the first segment can be written as

$$P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|R^1\right)\propto P\left(R^1|X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2\right)=\prod _{i=1}^{\left|R^1\right|}P\left(R_i^1|X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2\right).$$

We assume that the two copies of each homologous chromosome are sequenced with equal probability. Therefore, the i^th read is generated from one randomly drawn haplotype among the two possible ones underlying G, allowing us to write

$$P\left(R_i^1|X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2\right)=\frac{P\left(R_i^1|X_{\left\{1\right\}}^1\right)+P\left(R_i^1|X_{\left\{1\right\}}^2\right)}{2}=\frac{P\left(R_i^1|X_{b_1,e_1}^1\right)+P\left(R_i^1|X_{b_1,e_1}^2\right)}{2}.$$

Similarly, the transition distribution between the $\left(s-1\right)$ ^th and the s^th segment conditional upon the reads that span that segment boundary can be written as

$$P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2|X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2,R^s\right)\propto P\left(R^s|X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2,X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2\right)\propto \prod _{i=1}^{\left|R^s\right|}P\left(R_i^s|X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2,X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2\right)\propto \prod _{i=1}^{\left|R^s\right|}\frac{P\left(R_i^s|X_{b_{s-1},e_s}^1\right)+P\left(R_i^s|X_{b_{s-1},e_s}^2\right)}{2}.$$

We model the probability that a read $R_i^j$ is produced from a given haplotype X by using an independence assumption between the sites we are trying to phase as follows:

$$P\left(R_i^j|X_{b,e}\right)=\prod _{l=b}^{e}P\left(R_{i,l}^j|X_l\right).$$

It might be the case that errors within a given read are correlated, but the SNP sites will tend not to be close to each other in a read.

The specification of the model is completed by assuming that the error probabilities Q are well calibrated, allowing us to model the probability that the l^th allele of the i^th sequencing read is observed from the l^th allele of the k^th haplotype by using the base error probabilities in Q as follows:

$$P\left(R_{i,l}^j|X_l=k\right)=\{\begin{array}{ll}1\hfill & R_{i,l}^j=-\hfill \\ 1-Q_{i,l}^j\hfill & R_{i,l}^j=A_{lk}\hfill \\ Q_{i,l}^j\hfill & R_{i,l}^j\ne A_{lk}\hfill \end{array}.$$

We then use a forward-backward algorithm to calculate the marginal distribution of the first segment $P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|R\right)$ and the joint distributions between successive segments $P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2,X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2|R\right)$ given the set of reads R. Note that the difference between these quantities and those in Equation 5 is that they are conditional upon all the reads in R.

By using Equation 3, we can calculate the marginal distribution of the first segment as

$$P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|H,R\right)\propto P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|R\right)P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|H\right).$$ (Equation 6)

Similarly, the transition matrices can be calculated via the joint distributions across segment boundaries as

$$P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2|X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2,H,R\right)\propto P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2,X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2|H,R\right)$$ (Equation 7)

$$\propto P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2,X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2|R\right)\times P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2\left|X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2\right|H\right).$$ (Equation 8)

MCMC Algorithm

Our algorithm starts by building the graphs of possible haplotypes for each sample to be phased. Then, for each sample in turn, we calculate the marginal distribution of the first segment $P\left(X_{\left\{1\right\}}^1,X_{\left\{1\right\}}^2|R,Q\right)$ and the conditional distributions between successive segments $P\left(X_{\left\{s\right\}}^1,X_{\left\{s\right\}}^2|X_{\left\{s-1\right\}}^1,X_{\left\{s-1\right\}}^2,R,Q\right)$. The calculations only need to be done once at the start because they do not depend upon the underlying haplotypes and R and Q are fixed. Once done, haplotypes for each sample are randomly initialized and the MCMC algorithm starts. Each MCMC iteration consists of updating the haplotypes of each sample conditional upon a set of other haplotypes with the Markov model described above. The scheme we use to sample consistent haplotypes is described by the following steps:

(1) A pair of consistent haplotypes in the first segment with labels $\left(i,j\right)$ is sampled with probability proportional to $P\left(X_1^1=i,X_1^2=j|H,R\right)$. Note that only pairs of labels $\left(i,j\right)$ consistent with G are considered.

(2) A pair of consistent haplotypes $\left(d,f\right)$ for the s^th segment is sampled given the previously sampled pair $\left(i,j\right)$ for the $\left(s-1\right)$^th segment with probability proportional to $P\left(X_{\left\{s\right\}}^1=d,X_{\left\{s\right\}}^2=f|X_{\left\{s-1\right\}}^1=i,X_{\left\{s-1\right\}}^2=j,H,R\right)$.

(3) Set $s=s+1$.

(4) If $s=C+1$ then stop, else go to Step 2.

The result is a pair of vectors of consistent haplotype labels, $X^1$ and $X^2$, that label the whole region being phased, and these can be turned into new haplotype estimates, $\left(g_1,g_2\right)$, by using $g_{il}=A_{l{X}_l^i}$ for $i\in \left\{1,2\right\}$. These haplotype estimates can then be added back into the haplotype set H and the next individual’s haplotypes can be estimated, although their current haplotype estimates must be removed from H first.

Our MCMC algorithm follows the same scheme as SHAPEIT2. We carry out a number of burn in iterations and then a number of pruning and merging iterations. The pruning iterations are used to remove unlikely states and transitions from the Markov model that describes the space of haplotypes consistent with each individual. When enough transitions are pruned, we merge adjacent segments together. This simplifies the space of possible haplotypes so that a final set of sampling iterations can be carried out more efficiently. In practice, we find that after the pruning and merging steps the segments usually include ∼50 SNPs, which corresponds roughly to a segment length of 5 kb. Thus two adjacent segments span ∼10 kb, which can allow phase information in long inserts to be utilized in the latest stages of the algorithm.

In addition, we only use a subset of all available haplotypes when updating each individual. We use a carefully chosen subset of K haplotypes that most closely match the haplotypes of the individual being updated.³ The haplotype matching is carried out on overlapping windows of size W. When processing genotypes derived from sequence data, our experience is that setting $W=0.5$ Mb produces the most accurate results.¹³

The first step of the algorithm, extracting the PIRs, has a complexity linear in the sequence coverage, whereas the second step, the MCMC iterations, is linear with the product of the number of sites L to be phased and the number K of conditioning haplotypes used to build the HMM. Combined running times of these two steps on real data sets are shown in Table S1 available online.

Application to the High-Coverage Sequencing Data

To assess the utility of the method on real data, we obtained Illumina sequencing data on a mother-father-child trio of European ancestry at high-coverage (∼130× in total of 100 bp paired end reads in 300 bp inserts). We only used data from chromosome 20. We also used SNP genotypes called from Phase I of the 1000GP on 379 European samples.¹⁴

We used samtools (v0.1.17) to make genotype calls in the trio samples at all of the SNP sites called as polymorphic in the European samples of the 1000GP data set. This produced an initial list of 345,331 candidate SNPs. We then used VCFtools (v0.1.10) to perform QC on the trio genotypes at these sites. Specifically, we filtered out sites (1) with a calling quality below 30, (2) with a per-site depth of coverage below 60× and above 200×, and (3) with a per-genotype depth of coverage below 10× (n = 28,929). We then combined the Illumina trio with the 379 1000GP European samples and removed (1) all singletons in the resulting data set (n = 72,977), (2) all sites with Mendel inconsistencies (n = 25), and (3) all SNPs too close to the centromere (25.7 Mb to 30.1 Mb) (n = 2,809). We finally removed the trio child to produce a data set with 381 unrelated European samples at 240,591 non-singleton SNPs.

We then estimated haplotypes in these 381 samples by using different methods. We applied Beagle and SHAPEIT2, both without any use of the sequencing reads on any of the samples, and our new method that utilizes the phase-informative reads. We ran several versions of this analysis in which we subsampled the reads on these parental trio samples to vary the amount of sequence data used. The subsampling preserved the paired read structure of the data set.

Currently our method is primarily designed for use on high-coverage sequence data or on data sets that have already had genotypes called. Our experiments that use lower levels of sequencing reads allow us to investigate how performance scales with increasing levels of phase-informative reads and indicates the potential value of using read-aware phasing methods on low-coverage sequencing.

In these experiments, we kept the genotypes fixed to those called from the high-coverage sequencing to assess the value of increasing levels of phase-informative reads in isolation. We could have recalled the genotypes from subsampled sequence data, but when comparing the haplotypes to the “truth” haplotypes derived from the high coverage trio we would need to exclude sites with genotype errors. This would cause the results to be on different sets of sites for each level of coverage.

We also reran our experiments with the phase-informative reads on all of the 379 1000GP samples in addition to the reads on the trio parents. We assessed performance by comparing the estimated haplotypes in the two trio parents to the haplotypes estimated by using the family information. All of our experiments were run three times by using different random seeds, and the results we report are the average across the three runs. We calculated the switch error rate (SER) and the mean switch distance (MSD), which is the mean of all the distances between switches.

Simulations

We used simulated data to investigate the performance of read-aware phasing when varying properties of the sequencing such as read length, insert size, base error rates, and coverage. These experiments are designed to assess the future utility of read-aware phasing as sequencing technology evolves. For example, it might soon be possible to obtain much longer sequence reads, albeit with higher base error rates.¹⁷ Longer reads will capture extensive phase information. If this information can be harnessed, it might be possible to estimate haplotypes much more accurately than is presently possible.

We used haplotypes called from chromosome X in 1000GP male samples as the basis for our simulations. We extracted the haplotypes in 40 Mb of the nonpseudo autosomal region of chromosome X and paired haplotypes randomly to create phase-known genotype data in 262 samples at 328,122 polymorphic SNPs. The advantage of using real data sets as the basis of the simulations is that we do not have to make choices about the demographic scenarios required to simulate realistic data sets using existing simulation tools.

We then simulated sequencing reads from these sequences of varying read length, coverage, and, for paired-end reads, insert size. The next two subsections give the details of these simulations. We assigned base qualities of reads by sampling from an empirical distribution of base qualities from the 1000GP Illumina sequence data. The base qualities were used to simulate sequencing errors.

Paired-End Reads

We simulated paired-end 100 bp reads by using different mean $\left(m\right)$ insert sizes (300 bp, 500 bp, 1,000 bp). We simulated insert sizes from a normal distribution with mean m and variance $m/10$. We also considered several strategies that use mixtures of insert sizes. The first strategy we tried was an equal mix of 300 bp, 500 bp and 1,000 bp mean insert sizes. We also tried two strategies that mixed mean insert sizes of 500 bp and 6 kb, one with a 90/10 mix and one with a 50/50 mix. Finally, we considered a strategy with insert sizes drawn from a distribution derived from the empirical distribution of distances between flanking heterozygous genotypes in an individual. This strategy was designed so that increasing coverage increases the chance of observing a read that is informative about any pair of flanking heterozygous genotypes. To all these data sets we applied Beagle and SHAPEIT2. SHAPEIT2 was run with varying levels of coverage of sequence reads from 0×–20×. Accuracy of the inferred haplotypes was compared to the true chromosome X haplotypes in terms of Mean Switch Distance (MSD).

We also measured two other statistics: first, the proportion of heterozygous genotypes spanned by PIRs, which quantifies the potential of using read information in each setting; and second, a switch error rate focused only on rare sites because these are the most challenging to phase. For the latter, we classified all heterozygous genotypes into two categories: rare when the minor allele count at the SNP is $\le 10$ and common otherwise. Then, we calculated the switch error rate between the rare heterozygote and their closest flanking common heterozygote. We stratified the results by minor allele count.

Long Sequence Reads

We also investigated the performance of very long sequencing reads. Such reads might become more common as sequencing technologies such as those from PacBio¹⁸ and Nanopore¹⁷ become more widely used. We simulated reads from the chromosome X data set with lengths of 5 kb, 10 kb and 20 kb. We simulated two sets of reads with base error rates fixed uniformly at 4% and 15%. We varied coverage from 0× to 20×. We also measured the proportion of heterozygous genotypes spanned by PIRs and the switch error rates at rare sites, as described above.

Single Sample Phasing

One of the main motivations for developing a read-aware phasing method was to estimate haplotypes in single samples sequenced at high coverage. High-coverage sequencing allows the genotypes at each polymorphic site to be determined with near certainty. Our method proceeds in two stages. First, we focus on phasing the genotypes at sites that exist in publicly available reference panels such as the 1000GP. At these sites, our method takes advantage of LD information in the haplotype reference panel and the phase information in the sequencing reads. In the second step, we phase the remaining sites. These sites will not exist in the reference panel and will be polymorphic for the nonreference allele in the sample being phased. The vast majority of these genotypes will be heterozygotes and we refer to these as singleton sites.

The HMM we use to take advantage of the LD in the reference panel has no information to phase such singletons. However, if the site is covered by a phase informative read, then the site can be phased. We carried out two experiments to investigate the phasing performance on high coverage sequencing from single samples. The first experiment examines the performance of various versions of our method when phasing polymorphic sites that exist in the reference panel. The second experiment focuses on the phasing of singleton sites.

In the first experiment, we phased the genotypes of the parents from the high-coverage Illumina trio together with the haplotypes from 379 1000GP European samples as the reference set on the same set of 240,591 sites described before. We carried out several versions of this experiment where we varied whether the reference panel was phased and whether we used phase-informative reads in the single sample. When phasing without using any phase informative reads (PIRs) and using genotypes from the 1000GP European samples, we ran the standard version of SHAPEIT2, which phases all 381 samples by using parameters $W=0.5Mb$ and $K=100$. This method uses multiple MCMC iterations to refine the phase of all 381 individuals.

When phasing without using any PIRs and using haplotypes from the 1000GP European samples, we used a modified version of SHAPEIT2 that uses just a small number of iterations (1 burn-in iteration, 1 pruning iteration, and 1 main iteration) to phase single samples by using all the 758 reference haplotypes $\left(K=758\right)$ in a single window that spans the whole chromosome $\left(W=63Mb\right)$. We found this approach was ∼80 times faster than the version that used the 379 1000GP samples as unphased (Table S1), although this includes the time taken to extract the PIRs from the BAM files, which accounts for the majority of the time taken to phase when using a phased reference panel.

We repeated this experiment by using two different versions of the 1000GP Phase 1 haplotypes. The first version was the official release version described in the most recent 1000GP publication.¹⁴ The second version was our own version of the Phase 1 haplotypes which was estimated by using SHAPEIT2 and utilized microarray genotypes available on the same samples (https://mathgen.stats.ox.ac.uk/impute/data_download_1000G_phase1_integrated_SHAPEIT2.html). When phasing by using both the PIRs and the 1000GP haplotypes, we used $K=758$ and $W=63Mb$. The resulting haplotypes were compared to those derived from trio phasing the high-coverage genotypes. We analyzed each parental set of genotypes and averaged the results. Note that no singleton sites are included in this experiment, as before.

In the second experiment, we assessed how many of the singleton sites could be phased by using PIRs. We defined a singleton to be a polymorphic site with an allele count of 1 in the trio parents that is not polymorphic in 1000GP samples. To do this, we first phased the 240,591 nonsingleton sites by using official 1000GP haplotypes and PIRs. We then phased the singleton sites onto these haplotypes.

To assess the accuracy of their phase, we generated a highly accurate set of phased singleton sites for each of the trio parents by using the family information in the full trio. To do this, we ran samtools v0.1.17 (r973:277) on all three of the individuals in the trio to detect and call genotypes at all possible polymorphic sites (SNPs + short indels). This resulted in a total of 135,169 candidate sites. To extract a list of SNP singletons from this, we first removed all indels (n = 19,262), then all SNPs polymorphic in 1000GP European samples (n = 81,876), and finally all SNPs that are not singletons in the trio parents, that is, with a nonreference allele count different than 1 in the parents (n = 22,212). We ended up with a total of 11,819 candidate singletons.

The trio information allows us to phase all these sites. However, if genotypes are miss-called in this process, it can introduce errors in phasing. We have found that such errors can seriously confound an analysis of whether phase-informative reads can help to phase singleton sites, so we applied an additional set of stringent filters to remove as many miscalled genotypes as possible. First, we removed all singletons located less than 10 bp away from an indel because they are likely to be artifacts as a result of misalignment (n = 6,790). Then, we filtered out all singletons that failed the following QC criteria by using VCFtools v0.1.10: a per-site calling quality score below 30, a per-genotype calling quality below 30, a per-site depth of coverage below 60 or above 200, or a per-genotype depth of coverage below 10 (n = 1,311). Finally, we removed all singletons near the centromere (25.7 Mb to 30.1 Mb) and miss-called genotypes due to large deletions (n = 1,347). Specifically, for the large deletion filter we took each individual in turn and calculated the median (and robust SD) of the insert sizes of all the paired reads and removed all sites where the mean insert size of the reads spanning the site was more than two SDs away from the chromosomal median.

After applying all these filters, we were left with 2,371 highly accurate singleton sites out of the 11,819 candidates. Then, we phased all these singletons onto the haplotypes generated in the previous experiment by using different coverage of sequencing reads (5×, 10×, and 20×). These haplotypes were compared to those derived from trio phasing the high-coverage genotypes at the 1000GP sites and the singleton sites.

We note that this method of deriving haplotypes is expected to be highly accurate, but it only estimates the transmitted and untransmitted haplotypes in the parents, so that real recombination events that occur in the meioses between parents and child are not properly detected. This means that we would expect to observe a handful of errors when comparing our haplotypes to trio-derived haplotypes. To do this comparison, we took each singleton in turn, combined it with the nearest 1000GP site with a heterozygote genotype to create pairs of two SNP haplotypes, and compared these haplotypes to the trio-phased haplotypes. We only considered those singleton sites that had a heterozygote genotype at a 1000GP site within 300 bp of the singleton sites.

Results

Application to the 1000 Genome Project Data

The results of our methods comparison with the 1000GP samples are presented in Figure 1. There are three clear results from this analysis. First, SHAPEIT2 (MSD = 270.1 kb, SER = 0.747%) outperforms Beagle (MSD = 163.2 kb, SER = 1.239%) when no read information is used, as expected.¹³ These results purely reflect the quality of the LD models used by these approaches. Second, the use of phase-informative reads on the trio parents improves performance. For example, performance improves noticeably (MSD = 295.3kb, SER = 0.686%) when using 5× coverage sequencing on the trio samples. However, although increasing coverage above 5× does produce further gains in accuracy, there does seem to be a diminishing return. Finally, the additional use of phase-informative reads from the 1000GP samples further increases accuracy. With 20× coverage we obtain MSD = 328.6 kb and SER = 0.616%.

Figure 1.

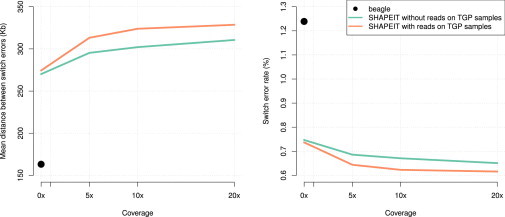
Phasing Accuracy on the High-Coverage Trio Parents’ Genotypes Phased Together with the 1000GP Genotypes

The x axes show the amount of sequencing reads on the trio parents that was used by SHAPEIT2. The y axes show the accuracy measured on the trio parents by MSD on the left and SER on the right. Results of Beagle are shown with black dots. SHAPEIT2 was run with (orange line) and without (green line) use of the $\sim 4x$ sequencing reads on the 1000GP samples.

Simulations

The results of our simulations of paired-end reads as we vary insert sizes and coverage are shown in Figure 2. The MSD results for the 300bp insert size paired-end reads are in good agreement with our results on real 1000GP autosomal data shown in Figure 1. The MSD is improved by the use of sequence reads, but increasing coverage above 5× does not lead to large increases in performance. As insert size increases there is more of a benefit of going above 5× coverage. We find that the strategies that mix 500 bp and 6 kb inserts outperform the use of just using 500 bp inserts. Interestingly, the strategy of using a mixture of 300 bp, 500 bp, and 1 kb inserts outperforms the two strategies that mix 500 bp and 6 kb inserts. The strategy of using a heterozygote distance distribution for insert sizes further increases performance, especially at 20× coverage.

Figure 2.

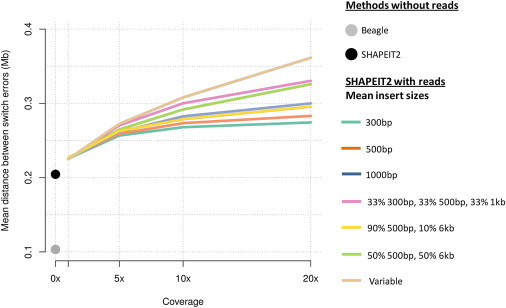
Results of Simulations by using Paired-End Reads with Varying Insert Size Distribution

The x axis shows the sequence coverage and the y axis shows the mean switch distance. Beagle and SHAPEIT2 were run without any phase informative reads, and these results are plotted as gray and black points, respectively. The results are shown for different mean insert sizes: 300 bp insert (green), 500 bp insert (orange), 1,000 bp insert (blue), a mixture of 300/500/1,000 bp inserts (pink), 90% 500 bp and 10% 6 kb (yellow), 50% 500 bp and 50% 6 kb (light green), and distribution of insert sizes matched to the distribution of distances between heterozygote SNPs (light brown).

The results of our simulations of long reads with higher base error rates and varying coverage are shown in Figure 3. For reference, Figure 3 also includes the results from the 300 bp insert size paired-end reads from Figure 2 (green line). Using long reads, even with high base error rates, substantially increases the MSD compared to methods that do not use phase-informative reads. Using 5× of 5 kb reads with a 4% base error rate in SHAPEIT2 results in MSD = 584 kb. Without using phase-informative reads, SHAPEIT2 and Beagle have MSD equal to 204 kb and 103 kb, respectively.

Figure 3.

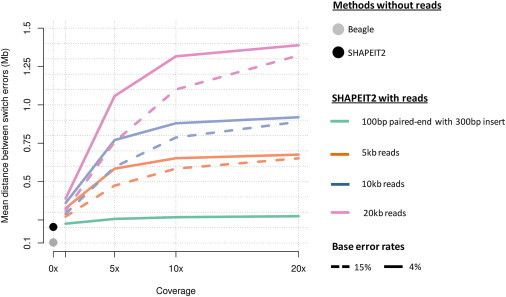
Results of Simulations by using Long Reads with High Error Rates

The x axis shows the sequence coverage and the y axis shows the mean switch distance. Beagle and SHAPEIT2 were run without any phase informative reads (0×) and these results are plotted as gray and black points respectively. The results are shown for different lengths of reads: 100 bp reads with 300 bp insert (green), 5 kb single reads (orange), 10 kb single reads (blue), and 20 kb single reads (pink). Two different base error rates were used in the simulations: 15% (dashed line) and 4% (solid line).

We also looked at phasing accuracy at rare variants for both sets of simulations. Results for some of the 20× simulations are shown in Figure 4 and clearly show that the decrease in error rate is mainly driven by improved performance at rare variants. For instance, we observe switch error rates of 19.3%, 8.7%, 6.1%, and 0.7% at sites with a minor allele count of 2 (doubletons) and 4.9%, 2.2%, 1.7%, and 0.3% at sites with a minor allele count of 8 with Beagle, SHAPEIT2 without using reads, SHAPEIT2 using 100 bp reads in 300 bp inserts, and SHAPEIT2 using 20 kb reads, respectively. Concerning singleton sites (minor allele count of 1), we get switch-error rates of 49.3% for both Beagle and SHAPEIT2 without using any reads, which makes sense because no LD information is available to phase these sites. When using 20× 100 bp reads in 300 bp inserts and 20 kb single reads, the switch errors drop to 37.1% and 2.9%, respectively.

Figure 4.

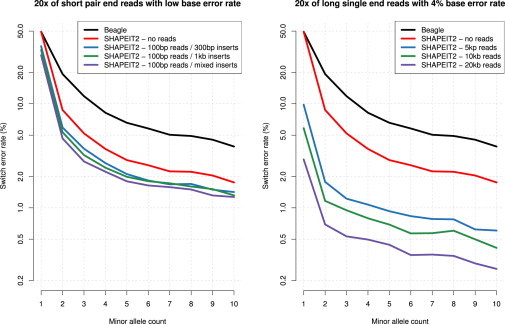
Phasing Accuracy at Rare Variants by using Simulated Data

The left panel shows the results for the short paired-end reads with varying insert sizes. The right panel shows the results for the long reads with 4% error rates. The x axis shows the minor allele count ranging form 1 (singleton) to 10. The y axis shows the SER relative to the closest heterozygous genotype taken at a site with a minor allele count greater than 10. Results for Beagle and SHAPEIT2 without using any reads are plotted as black and red lines respectively. The legends in the two panels provide details of the different simulations.

Finally, we looked at the proportion of heterozygous genotypes covered by PIRs in the simulations. Results are shown in Figure 5. As expected, for the short paired-end read simulations, this proportion increases with sequence coverage, which increases phasing accuracy in turn. For instance, the heterozygote coverage goes from 17% at 1× to 50% and 70% at 20× for 100 bp reads with 300 bp and mixed inserts, respectively. Note that the proportions of covered heterozygous genotypes change very similarly to the MSD as the coverage increases. This can be seen by comparing Figures 2 and 5. For the long single end reads (Figure 3), it seems that most of the heterozygous genotypes are covered with just 5× of sequence while accuracy keeps increasing beyond 5×. This phenomenon is explained by the fact that additional reads above 5× allow to connect more heterozygous genotypes to an already covered heterozygous genotype.

Figure 5.

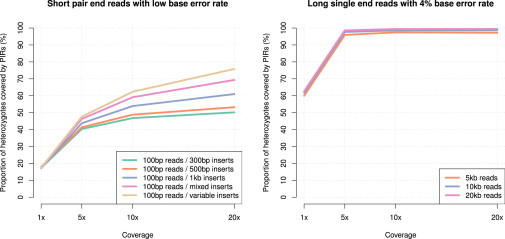
Proportion of Heterozygous Genotypes Covered by Phase Informative Reads (PIRs) in Simulated Data

The x axis shows the sequence coverage while the y axis gives the proportion of heterozygous SNPs covered by PIRs. Results for short pair-end reads are shown on the left plot with read length of 100 bp and various insert sizes: 300 bp insert (green), 500 bp insert (orange), 1,000 bp insert (blue), a mixture of 300/500/1000 bp inserts (pink), and distribution of insert sizes matched to the distribution of distances between heterozygote SNPs (light brown). Results for long reads are shown on the right plot with various read lengths: 5 kb single reads (orange), 10 kb single reads (blue), and 20 kb single reads (pink).

Single-Sample Phasing

The results of the first experiment to assess phasing accuracy at 1000GP sites and the value of using a phased or unphased reference set and the use of PIRs are shown in Figure 6. These results show that the best SHAPEIT2 strategy involves using an unphased 1000GP reference panel. Also, the use of our own version of the Phase 1 haplotypes produces better results than using the official 1000GP Phase 1 haplotypes. Interestingly, using an unphased 1000GP panel with 0× coverage of reads on the single sample gives almost the same results (SER = 0.747, MSD = 270.1 kb) as using our own version of the Phase 1 haplotypes with 20× coverage of reads on the single sample (SER = 0.741, MSD = 272.6 kb). Similarly, using our own version of the Phase 1 haplotypes with 0× coverage of reads on the single sample gives almost the same results (SER = 0.873, MSD = 231.9 kb). The results of Beagle are worse (SER = 1.239, MSD = 163.2 kb). The best performance we achieve by using our method (20× coverage and using the unphased 1000GP) (SER = 0.651, MSD = 310.6 kb) is almost a factor of 2 better than the Beagle results.

Figure 6.

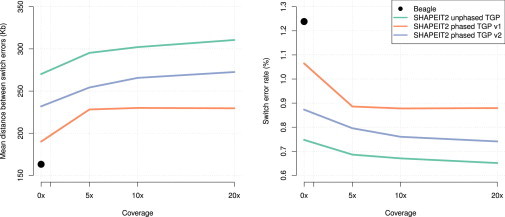
Comparison of Methods for Single Sample Phasing by using a Reference Panel

The plots show the performance of several experiments in which single samples were phased in terms of SER (left panel) and MSD (right panel) on the y axis. The x axis shows the coverage of the sequencing reads used on the single samples. The results of using SHAPEIT2 with an unphased 1000GP reference panel are shown as a blue line. The results of using SHAPEIT2 with the official 1000GP Phase 1 phased reference panel (denoted v1) are shown as a red line. The results of using SHAPEIT2 with our own version of the 1000GP Phase 1 phased reference panel (denoted v2) are shown as a green line. The use of Beagle is shown a black dot.

In our second experiment focusing exclusively on singleton sites, we found that there were 2,371 highly confident singletons on chromosome 20 in the two parental samples combined that are not reported in the 1000 Genomes Project. The results are shown in Table 1. When we use 5× coverage of sequencing reads, we find that 625 of the singletons are covered by PIRs and our model is confident in its ability to phase 615 of these the singletons $\left(p>0.99\right)$. This means we have a chance of phasing 26% of the singletons using PIRs that would otherwise be phased at random by LD part of our HMM. When comparing the phase of these 615 singletons, we find just five discrepancies when compared to the trio-derived haplotypes. This number of errors is consistent with the number of recombination events that we might expect to observe in two parents of a trio over a whole chromosome. When we increase the coverage to 10× and 20×, we observe a higher number of singletons that are covered by PIRs: 33% and 37%, respectively. The number of errors reduces slightly, to four. When we examined the location of these errors, we found that the same four errors occurred for all three levels of coverage. Also, we found that these errors were closer to recombination hotspots than you might expect by chance (empirical p value = ∼0.005) as illustrated in Figure S1.

Table 1.

Performance of Singleton Phasing in the Illumina Trio Parents

Read coverage of the trio	5×	10×	20×
Singletons covered by PIRs	625	775	869
Singletons covered by PIRs and $p>0.99$	615	768	862
Number of errors	5	4	4
Error rate	0.93%	0.61%	0.55%

The table shows the number of singletons that are phased incorrectly (row 4) using different read coverage (5×, 10×, and 20×) and the corresponding switch error rates (row 5). Row 2 gives the number singletons that are covered by PIRs. Row 3 gives the number singletons that are covered by PIRs for which our model is confident of the phase of the singleton $\left(p>0.99\right)$. Note that the reported switch error rate is measured for singletons close enough (<300 bp) to heterozygous genotypes at 1000GP sites that can be trio phased.

Discussion

In this paper we have presented a method that uses the phase information inherent in sequencing reads to aid the estimation of haplotypes. Our method builds upon the SHAPEIT2 phasing method, which has previously been shown to outperform other popular phasing methods.¹³ The phase information in the sequence reads is used to constrain the estimated haplotypes via a probabilistic model.

On the basis of our analyses, we are able to make a number of conclusions. First, all of our analyses show that using PIRs does help to reduce switch error rate and increase the mean switch distance. By using real data from the 1000GP we found that using PIRs from 5× coverage sequencing could decrease switch error substantially. Interestingly, we found that while increasing coverage beyond 5× did lead to further reductions in SER, there was a diminishing return. One explanation of this could be that some switch errors will occur between SNPs that are too far part to be covered by a PIR, and so no amount of increase in coverage will help to resolve them. Therefore, we might reasonably expect switch error rate to plateau with increasing coverage. These conclusions were further validated by performance on simulated data.

Second, our simulations allowed us to investigate how changes in the read length, insert size, and base error rate affect performance. For short 100 bp paired-end reads, we found that using a sequencing design in which insert sizes are approximately matched to the distribution between heterozygote sites gave the best results. Similar approaches in which mixtures of a small number of insert sizes also worked well. We were able to demonstrate that the addition of some long (6 kb) reads increased performance. Structural variants can be detected by examining the inferred insert size of mapped pair-end reads, so in practice the strategy of using a mixture of a small number of insert sizes might be more prudent than designs in which insert sizes are more randomly distributed. We also examined the performance of much longer reads and we found excellent phasing performance when using long reads from 5–20 kb with base error rates ranging up to 15% per base.

At present, the method is primarily designed for use on high-coverage sequence data or on data sets that have already had genotypes called. With high coverage, very accurate genotypes can be obtained one sample at a time without the need for imputation-based genotype calling. For low-coverage sequencing projects, a two-step process would be needed where genotypes are first called by using imputation-based methods^3,9–12 and then our method would be used to add in the phase informative read information to create a set of haplotypes. It would of course be advantageous to carry out the genotype calling and phasing by using the phase informative reads in one step, and this is a possible future direction of research.

Genotypes called from low-coverage sequence data will contain some errors. Experience from the 1000 Genomes Project suggests that the accuracy of individual genotype calls at heterozygous sites is more than 99% for common SNPs and 95% for SNPs at a frequency of 0.5%. Our model has a component that allows for errors in the reads and our haplotype model allows for mutation and imperfect copying. Both these parts of the model can soak up the effect of genotyping error, but we do not attempt to correct the errors. Genotyping errors will tend to flip homozygotes to heterozygotes and vice versa. If the former, then any reads that link this site to a flanking heterozygote will contain some ambiguity about the true phase. In this case, it would be likely that the LD part of the model will have most weight when phasing the site to a flanking heterozygote. If the latter, and a heterozygote is called as a homozygote, then the phase will be fixed and any phase informative reads spanning this site and a flanking site will not be used.

A major focus of our analysis was the scenario of phasing single-sequenced samples. As sequencing costs are reduced, high coverage sequencing of single samples will become even more routine, especially in clinical and diagnostic settings. At the same time, panels of reference haplotypes from world-wide populations will increase in size, especially as more and more groups work together to share sequencing data sets. Our approach is designed to take advantage of both these developments. Phasing of single high-coverage samples with reference to a haplotype panel could be a useful tool for many groups. We found that our approach was able to take advantage of PIRs and LD when phasing SNPs that were present in the 1000GP reference haplotypes. Interestingly, we found that the best approach involved taking haplotype uncertainty in the reference panel into account when phasing each single sample. A quicker approach, which uses a fixed haplotype panel, was shown to perform less well, and our own version of the 1000GP haplotypes, estimated using SHAPEIT2, outperformed the official 1000GP haplotypes. In general, we found that a conservative set of filters was needed when selecting which genotypes we should attempt to phase using PIRs.

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://browser.1000genomes.org

• BEAGLE, http://faculty.washington.edu/browning/beagle/beagle.html

• SAMtools, http://samtools.sourceforge.net/

• SHAPEIT2, http://www.stats.ox.ac.uk/∼marchini/#software

• VCFtools, http://vcftools.sourceforge.net/