Fast Sampling of A-to-B Protein Global Conformational Transitions: From Galileo Galilei to Monte Carlo Anisotropic Network Modeling

Local and global conformational transitions underlie protein function. Local changes include induced-fit effects such as the reorientation of residues. Global motions may involve interdomain motion, allosteric switches, and the dynamics of secondary structure elements several nanometers distant from each other (1). Global conformational changes are activated processes, thus particularly challenging for traditional atomistic simulation, because sampling can be prohibitively slow or activated by rare events. The easiest simulation scenario arises when at least knowledge of two states of interest, A and B, is available; these states can be assumed the most relevant and the problem is reduced to two key questions: what are the most convenient pathways connecting A to B, and vice versa? Does one unique, most favorable pathway exist?

These questions are long-standing, intriguing problems of general relevance in science. Four-hundred years ago, Galileo Galilei noted during his studies on the brachistochrone curve (2):

“From the preceding it is possible to infer that the fastest path of all, from one point to another, is not the shortest path, namely, a straight line, but the arc of a circle.”

Derivations of the brachistochrone curve problem are still challenging nowadays when the two points to be connected are locations on macromolecular phase spaces, with the complication that numerous pathways with similar minimal free energies—not only a unique solution—are generally available at standard conditions. The typical case is that the shortest A-B path is the least likely, thus various methods were recently proposed to allow the initial reaction coordinate guesses to relax during the search for convenient sampling paths. A remarkable example is the string method proposed by Maragliano et al. (3). Because a reaction coordinate guess is adapted to the landscape before or while walking over a free energy surface, pathways that are more favorable can be accurately identified. However, robust approaches of this type can still be prohibitively expensive when applied to large conformational transitions in biomolecular systems of large size. To address these issues, a multitude of more approximate, yet faster approaches have also been proposed, relying on diverse fundamental assumptions, and generally on smoother simplified potentials. These faster methods do not attempt to reproduce physical time and/or spatial scales, neither to determine the details of the free energy pathway. Instead, they aim to rapidly explore the most dominant global motions involved, such as interdomain conformational changes. Fast approaches can be generally distinguished considering whether 1), they involve topological simplification of the model, e.g., coarse-grained approaches; 2), they simplify molecular dynamics (MD) sampling by considering only the most dominant, low-frequency motions in the system, as obtained by analysis of the system atomistic fluctuations; or 3), they combine points 1) and 2).

Principal component analysis (4) or normal mode analysis (5,6) are typical choices to find the lowest frequency, largest amplitude motions in proteins. To some extent, these principal components can also be used as input to run efficient simulations of protein dynamics, such as in the essential dynamics approach (7). However, it remains a general issue to choose which pool of the mode spectrum to actually pick for sampling, as the lowest frequency modes have to be fed as input from an initial simulation guess (point 2 above). Gur et al. (8) presented in Biophysical Journal a new and notable method named collective MD (coMD) belonging to the class depicted in point 3 above. The coMD method uses two important ingredients for the initial guess. First, the collective motions are rapidly estimated using an anisotropic network model (ANM) (9), an elastic network approach that resolves the low-resolution collective modes based on a coarse-grained mapping to the structure (10). These low-resolution ANM modes are conveniently selected using a Monte Carlo Metropolis scheme that allows the system to diverge from the shortest path strictly identified by the chosen mode, thus circumventing free energy barriers by following the gradient of this low-resolution free energy surface (8). In details, the algorithm uses the probability of square displacement along a given mode for this selection, and is independently applied starting from two endpoints A and B of choice. Explicit solvent atomistic MD runs are used after each step of ANM dynamic propagation to obtain relaxed atomic level structures along the path.

Validation of the coMD was presented on the test case system adenylate kinase (see Fig. 1), which is a well-characterized prototype for investigating protein global transitions because it coverts between closed and open states that are remarkably different. coMD generates ensembles of transition pathways that closely map atomistic simulations (8) and it is well suited for distributed computing (∼3 ns MD runs and 30 short Monte Carlo simulations).

Figure 1.

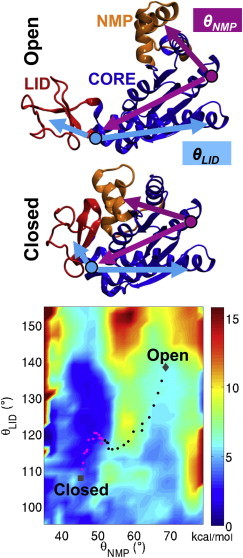
Models of the open and closed states of adenylate kinase. Angles θ_NMP and θ_LID are used to compare fast coMD path sampling by Gur et al. (8) with the two-dimensional potential of mean force by Beckstein et al. (11) obtained through more dynamic importance sampling. Conformers from independent coMD simulations starting from closed (magenta) or open (black) substates lead to a well-defined pathway of the landscape. The free energy is color-coded with reference to the lowest energy points on the surface. See Gur et al. (8) for computational details. To see this figure in color, go online.

Fig. 1 summarizes a validation example, in which coMD sampling of two alternative pathways over the free energy surface closely maps the free energy surface independently generated at the atomistic level by Beckstein et al. (11) using efficient dynamic importance sampling. This is a particularly relevant validation case, because dynamic importance sampling allowed thus far the most effective sampling of adenylate kinase in explicit solvent (a statistically relevant number of transitions are sampled within the 85–135-ps simulation timescales). coMD also captures the three-step mechanism interconverting close-to-open states proposed by Matsunaga et al. (12) by means of a rigorous, yet computationally more expensive simulation using the string method (3). The latter allows accurate free energy estimation, as shown by a committor test. The robustness of coMD for the system investigated was also tested by running simulations initiated from both the closed and the open states. In both cases, the least-work-expensive path was consistently predicted.

Future applications of coMD will explore global transitions in larger systems. Validation of this approach will likely be extended against a broader spectrum of macromolecules, including systems that might display more complex, multistate transition pathways. The work by Gur et al. (8) also opens new endeavors on the methodological viewpoint. This implementation of coMD makes use of ANM typically performed in terms of Cartesian coordinates that rely on evaluating and diagonalizing the mass-weighted Hessian matrix associated with a single structure (usually corresponding to a stationary point on the potential-energy surface). Like normal-mode analysis, ANM probes the vibrational modes associated with this single structure, i.e., a local region of the configurational space along the guessed pathway. On the contrary, quasi-harmonic and principal component analyses aim at characterizing the global extent of the configurational space accessible to the system at a given temperature (13). Could more efficient mapping be obtained using quasiharmonic or principal component, low-resolution modes? Alternative network models may be explored to produce input anisotropic modes, by using optimal networking partitioning methods such as the one proposed in 2008 by Li and Vanden-Ejinden (14). coMD will surely prompt new exciting routes to rapidly connect A to B, and vice versa.