Trends in Gender Segregation in the Choice of Science and Engineering Majors

Abstract

Numerous theories have been put forward for the high and continuing levels of gender segregation in science, technology, engineering, and mathematics (STEM) fields, but research has not systematically examined the extent to which these theories for the gender gap are consistent with actual trends. Using both administrative data and four separate longitudinal studies sponsored by the U.S. Department of Education’s National Center for Education Statistics (NCES), we evaluate several prominent explanations for the persisting gender gap in STEM fields related to mathematics performance and background and general life goals, and find that none of them are empirically satisfactory. Instead, we suggest that the structure of majors and their linkages to professional training and careers may combine with gender differences in educational goals to influence the persisting gender gap in STEM fields. An analysis of gendered career aspirations, course-taking patterns, and pathways to medical and law school supports this explanation.

1. Introduction

Women now surpass men in college completion (Buchmann and DiPrete 2006; DiPrete and Buchmann 2013) and attain bachelors, masters and doctoral degrees at rates that exceed those of men (Snyder and Dillow 2010). Yet horizontal gender segregation in fields of study, which had decreased somewhat in the 1970s and 1980s, has been stagnant for the past 20 years (Alon and Gelbsiger 2011; Charles and Bradley 2002). In particular, the literature has emphasized the slow gender integration in the pursuit of science, technology, engineering, and mathematics (STEM) majors (Turner and Bowen 1999; Xie and Shauman 2003). Given concerns about an undersupply of STEM graduates and a continuing gap in wages between male and female college graduates, the female shortfall in the pursuit of STEM majors is an important social policy issue (U.S. Department of Commerce 2012; Xie and Killewald 2012).

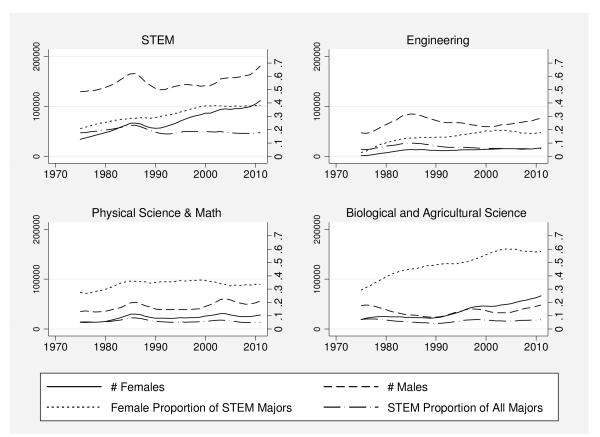
Recent evidence could support an impression that the gender gap in the attainment of STEM bachelor’s degrees is narrowing. Although only 25 percent of STEM bachelor’s degrees were awarded to women in 1977, women received 40 percent of STEM bachelor’s degrees as of 2000 and, as figure 1 shows, they continue to receive STEM bachelor’s degrees in increasing numbers.

Figure 1. Bachelor’s Degrees Awarded to Men and Women in STEM Fields of Study, 1977-2011.

Source: National Science Foundation WebCASPAR Database

Note: The first graphic displays the number of male and female STEM bachelor’s degree recipients from four-year colleges over the period 1975 to 2011, along with a dotted line showing the female proportion of STEM degree recipients in each year. The second-fourth graphics display the same information broken down for the subfields of engineering, physical science, and biological and agricultural science.

Aggregate data about the share of STEM degrees by gender, however, conceal several related trends. First, more women than men enroll in higher education and receive bachelor’s degrees, and the female lead has increased since women achieved parity in the number of bachelor’s degrees in 1982. Yet, women continue to prefer non-STEM degrees to STEM degrees; the increased share of STEM degrees awarded to women coexists with a continuing disproportionate female preference for non-STEM majors.¹ Second, the number of male students receiving STEM degrees has oscillated since 1980; the number of male STEM degrees decreased noticeably in the late 1980s before rising again in the 2000s.² The male trend suggests that there are external factors bearing on the attractiveness of STEM majors. Third, the biological sciences became more popular in the early 1990s for both males and females.³ During the past two decades, women who choose STEM majors disproportionately pursue biological science degrees. The combined consequence of these trends is that the share of biological science degrees awarded to women has increased from 40 to 60 percent over the last 30 years. At the same time, however, the shares of physical science and engineering degrees awarded to women have fallen in the last decade. The gender disparity is sharpest in engineering, where the share of degrees awarded to women has never reached 25 percent. In other words, any female advantage in STEM degrees is confined to the biological sciences; the male advantage persists in the physical sciences and engineering (at least in aggregate) (Figure 1).⁴

Numerous theories have been proposed for the high and continuing levels of gender segregation, but research has not systematically examined the extent to which these theories for the gender gap are consistent with actual trends. The question that motivates our study is how the gender gap in STEM fields of study has remained relatively stable in the face of both the changing gender distribution in higher education enrollment and trends in gender-specific factors that bear directly on the attractiveness of STEM fields of study, including especially test scores, life goals, expectations about work-family compatibility, and desires for extrinsic or intrinsic satisfaction. To address this question, we revisit arguments from prior research to see how they hold up to different analytical strategies with better and more recent data. Turner and Bowen (1999) analyzed the College and Beyond data (which are drawn from 12 elite colleges and universities), and attributed between one-third and one-half of the gender gap in STEM majors in 1989 to a gender discrepancy in SAT test scores, with even larger effects in preceding years. Using nationally representative data, a more inclusive set of test score measures, as well as a more robust set of math performance measures, we find, in contrast, that gender differences in math performance explain only a small fraction of the gap and play even less of a role in accounting for gender-specific trends in the pursuit of STEM majors. Second, using survey questions about twelfth graders’ life goals, we find that gender differences in life goals contribute little to understanding the disparity in fields of study (Hakim 2002; Shu and Marini 1998). We then present a set of counterfactual analyses to demonstrate the continuing and substantial role of preferences (net of test scores) in predicting the major choices of women and men and how these changing preferences are greatly increasing the number of women in STEM fields but in the direction of biological sciences, not physical sciences or engineering. Finally, we develop a relatively unexplored and potentially promising explanation for the continuing gender gap in STEM majors, namely, that women and men in four-year colleges differ in the way they link college majors to post-bachelor training, occupations, and their broader educational goals while in school. We find support for our hypothesis by examining gender differences in career aspirations, in course-taking patterns, and in the distribution of majors among the set of students who apply to law school or medical school. These results suggest that there are important consequences for choices of major in the constraints associated with majors such as engineering that limit curricular flexibility during the undergraduate years.

2. Trends in Gender Segregation in Fields of Study

The literature on gender and higher education has documented a substantial decline in gender segregation in fields of study through the 1970s, followed by a period in the 1980s in which the declines subsided (Barone 2011; Bradley 2000; England and Li 2006; Jacobs 1989b, 1995, 1996; Turner and Bowen 1999). Much of the decrease in gender segregation was attributed to progress during the 1960s and 1970s toward gender parity in the fields of education and business. The reasons for the stabilization at still-high levels of segregation are less settled, although it has been noted that few men have entered female-dominated fields (England 2010; England and Li 2006; Jacobs 1995) and that the arts and sciences have been particularly resistant to gender convergence (Turner and Bowen 1999).

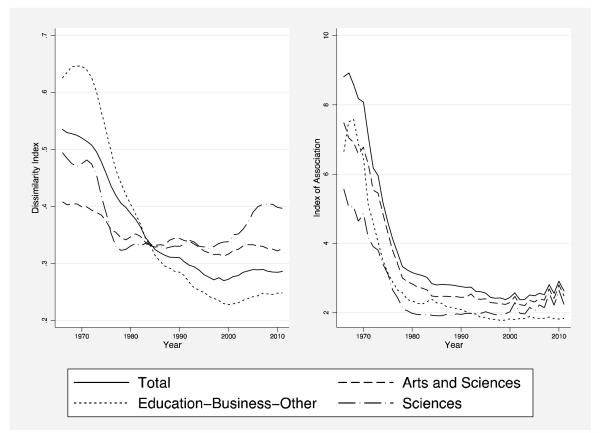
Figure 2 illustrates the continuation of the slowdown in gender integration identified a decade ago by Jacobs (1995) and Turner and Bowen (1999). The first panel of Figure 2 displays an all-inclusive index of dissimilarity based on 53 field-of-study categories in the National Science Foundation’s WebCASPAR database,⁵ as well as several indices based on subsets of the data.⁶ The index shows a pronounced decline in gender segregation through the mid-1990s, at which point the declining segregation trend began to stagnate. In 1970, about 52 percent of all women would have needed to change college majors for women to be distributed in the same manner as men; by the mid-1990s, this number reached a low of about 28 percent. Since that time, however, the dissimilarity index has risen slightly.⁷ The education-business-other index suggests that much of the overall decline in gender segregation through the mid-1980s was situated within those areas. Gender segregation within the arts and sciences has been more uneven, but the overall level of segregation in sciences has been much higher and appears to be rising.⁸

Figure 2. Measures of Gender Segregation Over Time, for Bachelor’s Degree Recipients.

Source: National Science Foundation WebCASPAR Database

Note: The first graphic displays the index of dissimilarity from years 1966-2011 for bachelor’s degree recipients from four-year colleges. The second graphic displays the index of association for the same years. Each graphic contains an all-fields index in addition to subindices broken down by field.

The second panel of Figure 2 displays trends in the index of association. The index of association measures the factor by which women are underrepresented in the average field of study and is not affected by changes in the share of students in particular fields (Charles and Grusky 1995), which is important because of the changes in the overall attractiveness of many STEM fields, shown in Figure 1. With this measure, the gender segregation trends seem more pronounced. We detect a large decrease in the all-fields index before 1980 (dropping from more than 8 in the late 1960s to about 3 in 1980), which is consistent with our findings using the dissimilarity index. Looking at broader subfields, we find that the sciences have experienced increasing levels of segregation in the past ten years.

3. Explanations for Gender Segregation in Fields of Study

Much of the earlier decrease in gender segregation (shown in Figure 2) has been attributed to improved opportunities for women in the labor market and consequent changes in the attractiveness of particular majors. The growing opportunities for women in the labor market would suggest comparable progress in gender integration in fields of study. Thus, even in engineering, which is the most segregated STEM field, women made steady progress until recently: the number of engineering and computer science degrees for women increased by a factor of six and raised the female share of engineering degrees from 5 percent in 1977 to a peak of 21 percent in 2002 (see Figure 1). Still, the striking persistence of segregation in fields of study is difficult to reconcile with gender parity in labor market participation along with the female advantage in pursuit of higher education (Charles 2011); the juxtaposition of these trends suggests increases in the numbers of female students who enter traditional female majors and occupations (Alon and Gelbgiser 2011).

It has been suggested that gender segregation in STEM fields of study is highly resistant to change, with a prominent explanation being gender discrepancies in average and high-end mathematics performance (Boli, Allen and Payne 1985; Ceci and Williams 2010; Ceci, Williams and Barnett 2009; Halpern et al. 2007; Turner and Bowen 1999; Wilson and Boldizar 1990; Xie and Shauman 2003).⁹ Although gender disparities in math performance, as measured by standardized tests, are well documented (Ceci and Williams 2010; Ellison and Swanson 2010; Halpern et al. 2007; Hedges and Nowell 1995; Hyde and Mertz 2009; Hyde et al. 2008; Kane and Mertz 2012; Lohman and Lakin 2009; Machin and Pekkarinen 2008; National Center for Education Statistics 2010; Penner 2008; Wai et al. 2010), gender differences in average math achievement are now too small to explain any substantial portion of the gender segregation in STEM fields or occupations (Hyde et al. 2008; Xie and Shauman 2003). Similarly, the disparity in high-end performance, albeit more pronounced, has diminished since 1970 (Ceci and Williams 2010; Wai et al. 2010), and it is unclear the extent to which the remaining gender differential in test scores might be responsible for the gender gap in STEM majors and occupations (Ceci and Williams 2010; Halpern et al. 2007; Hyde et al. 2008; Spelke 2005; Xie and Shauman 2003).

Although the gender gap in average math achievement has diminished, at least in the United States, there is a gap in verbal test scores that continues to favor females. Furthermore, women with high math scores are disproportionately likely to have high verbal scores (Ceci et al. 2009). If individuals choosing between two fields of study will choose the one where they have a comparative advantage (Jonnson 1999), then high achieving females on average might be more likely to choose fields of study that reward verbal abilities (such as the humanities or social sciences).¹⁰ The relative advantage explanation for gender segregation in STEM fields warrants study.

In addition, Jacobs (1989, 1995) observes that gender segregation in field of study is attributable not only to gender socialization or differences in math ability but also to various mechanisms of social control that exist throughout the educational and career exploration processes. These can take the form of differences in course-taking patterns that influence subsequent major and occupational choices; Jacobs (1989a), for example, suggests that curricular tracking in high schools might be part of a social control system that explains sex segregation in occupation.

Aside from mathematics ability alone, some researchers have focused on the undervaluation by women of their competencies in mathematics, which discourages women from pursuing quantitative majors even when they have strong mathematics backgrounds (Correll 2001, 2004). Although there is some empirical support for the relation between math attitudes and fields of study (Correll 2001, 2004), the contribution of gender differences in math attitudes to the gender gap in quantitative fields of study has not been examined.

The other general category of explanations for the continuing gender gap in STEM fields has focused on the notion that women are less interested in math-intensive majors and occupations because they do not conform to traditional gender roles (Bradley 2000; Ceci and Williams 2010; Cotter, Hermsen and Vanneman 2011; England and Li 2006). Cotter, Hermsen, and Vanneman (2011) documented the fact that, after liberalizing for decades, gender role attitudes leveled off in the 1990s in a way that seems to be consistent with a separate but equal frame (Cotter et al. 2011). Persistence in gender essentialist beliefs about educational and occupational opportunities thus might explain gender differences in choice of college majors and careers (Charles and Bradley 2009), and the apparent stagnation in such beliefs could be associated with a continuing gender disparity in the internalized decisions of women about whether to pursue STEM majors and occupations. The coincidence of this trend with a stagnation in major choice bears closer examination.

The literature includes several explanations for the way in which gender differences in values and preferences relate to the female tendency to choose non-STEM majors. Hakim’s (2002) theory argues that women and men frequently differ in the centrality of work-centered, home-centered, or adaptive lifestyles to the respondent’s identity (see also England 2005; Frehill 1997). Similarly, Bobbitt-Zeher (2007) suggests that gender differences in the perceived importance of having lots of money produce gender differences in decisions regarding higher education and occupation. And using job-values survey questions, Marini et al. (1996) suggest that the sexes attach different values to extrinsic and intrinsic rewards associated with work (see also Beutel and Marini 1995; Bobbitt-Zeher 2007; Bridges 1989; Davies and Guppy 1997; Frehill 1997; Konrad et al. 2000; Johnson 2001; Marini et al. 1996). Although men once attached greater value to extrinsic rewards, women and men now do so to the same extent; conversely, although both sexes attach importance to the intrinsic rewards of work, women have consistently attached greater value than men to intrinsic rewards (Marini et al. 1996).¹¹ And, finally, men and women are said to have different interests in working with people as opposed to physical objects and abstract concepts (Barone 2011; Eccles 2007; Hansen et al. 1993; Lippa 1998).

This research, however, has not established that aspirations, values, and identities have a strong influence on the gender gap in field of study, occupation, or pay (Frehill 1997; Hakim 2002, 2003; Polachek 1978). For example, Hakim finds that most men are work-centered, compared to only a minority of women; yet lifestyle preferences have little impact on women’s choice of occupation (Hakim 2000, 2002, 2003). Similarly, Bobbitt-Zeher (2007) finds that aspirations for earning lots of money have only a modest effect on the gender income gap. Using High School and Beyond data, Frehill (1997) finds that gender differences in high school preparation and work-related values explain 30 and 2 percent, respectively, of the gender gap in engineering.

Although values explanations linked with family/work conflicts have superficial appeal, they are undermined by the substantial gender integration that has occurred in medicine, law, and business professions, which all are demanding in the number of hours they require (England 2010; Wilson and Boldizar 1990). There is no obvious difference in the level of work flexibility between STEM careers and law, medicine or business. Boulis and Jacobs (2008) specifically consider the explanation that differences in work flexibility account for gender segregation in medical specialties and find it wanting. Growing opportunities for women in these fields may be related to the slower rates of women’s progress in physical science and engineering, but prior research has not addressed this issue empirically. Indeed, no existing studies directly test the matrix of existing explanations against comprehensive trend data on the gender pattern in STEM fields. This limitation is significant: trend studies are necessary to investigate dynamic theories about changes in either the broader opportunity structure or in the gender-specific distribution of values and skills across cohorts.

In the sections that follow, we test several existing theories to see how well they explain the trends in the gender gap in STEM fields of study, and we use more recent and comprehensive data than prior studies. We examine math and reading test scores and related performance measures to see how much of the gender gap they explain, and to determine whether there is evidence of a trend in female major choices when holding performance measures constant. We also examine the life goals and attitudes of male and female adolescents to see how well they explain the gender disparity in major choice.

We then develop an alternative theory that combines gender differences in preferences with structural differences in the organization of college majors. Studies that focus exclusively on the attractiveness of STEM fields to women without considering competing opportunities in other elite fields cannot address the broader environment in which women make choices about their college majors. To remedy this gap, we consider whether the slow rates of women’s progress in the physical sciences and engineering is connected with women’s growing opportunities for pursuing non-STEM degrees and careers that are equally prestigious and socially important. We suggest a complex relationship between college major and post-baccalaureate choices in which high-achieving women are more likely than high-achieving men to prefer elite careers that are flexible regarding the requisite undergraduate majors (particularly majors that are structured to be less specialized).

4. Data and Methods

To evaluate the contributions that mathematics performance and life goals have made to the persisting gender gap in STEM fields over the past forty years, we use data from four NCES (National Center for Education Statistics) longitudinal surveys conducted since 1972. Collectively, the studies permit us to analyze and compare the educational pathways of high school students who graduated in the spring of 1972, 1982, 1992, and 2004. The oldest, the National Longitudinal Study of the High School Class of 1972 (NLS-72), is a national probability sample of about 19,000 high school seniors, nested within about 1060 schools, and is designed to represent all twelfth graders enrolled in public or private American high schools in the spring of 1972 (Ingels et al. 2012); we use data from the spring of 1972, and data from the 1973 follow-up study.¹² The second of the four studies, High School and Beyond Longitudinal Study of 1980 (HSB), is a nationally representative sample of approximately 30,000 high school sophomores nested within about 1120 high schools, with follow-ups in 1982, 1984, 1986, and 1992. We use the 1982 and 1984 follow-ups. The third of the four studies, the National Education Longitudinal Study of 1988 (NELS), began with a sample of 25,000 eighth grade students in 1988 within about 1000 schools, with follow-ups in 1990, 1992, and 1994. For each in-school follow-up, the student sample was freshened to obtain a representative, cross-sectional grade-cohort (i.e., 10th-graders in 1990 and 12th-graders in 1992). We use the 1992 “freshened” sample, which was nationally representative of high school seniors, and the 1994 follow-up. The most recent panel survey is the Education Longitudinal Study of 2002 (ELS), which began with a sample of about 15,000 sophomores in 2002 that were followed up in 2004 when they were high school seniors and in 2006 when they were typically two years past high school graduation. We use the 2004 freshened sample and the 2006 follow-up.

For this study, we use data from student and parent surveys conducted during the students’ 12^th grade year of high school and from follow-up student surveys conducted two years later. With this restriction, the NLS72 sample includes approximately 15,640 students that answered the questionnaire and participated in the first follow-up study. The HSB sample has approximately 13,260 students. The NELS sample contains approximately 12,400 students. And the ELS sample is restricted to approximately 12,530 students. We use panel weights to tabulate findings for the population of 12th graders. These weights allow us to adjust for unequal selection probabilities and to more accurately represent the field of study decisions of a national population of 12th graders.

For some analyses, we limit the sample to students enrolled in a 4-year degree-granting institution who are college sophomores during the follow-up study. For HSB, NELS, and ELS, the follow-up is conducted in the spring follow-up study; for NLS72, we use the 1973 follow-up (conducted in the fall of the second year of college). We define college sophomores as those who graduate from high school on or before July 31 of their senior year, enroll in college before January 1 of their graduating year, and remain enrolled through the interview date of their second year in college. With these restrictions, the sample sizes are reduced to approximately 2680, 3570, 4070, and 4650 for NLS72, HSB, NELS, and ELS, respectively.

Our analysis explores STEM fields of study across four cohorts. The dependent variable for most of the analyses is a dichotomous indicator of whether the student was a STEM major in the follow-up study. Following NCES (2009), we define a STEM major as a major in the biological sciences, agricultural sciences, computer sciences, engineering, engineering or science technologies, math and statistics, or physical sciences subfields; non-STEM majors are architecture, business, communications, education, fine arts, health professions, law, psychology, social sciences, or other, unknown or undecided majors (see Appendix). Some analyses use a categorical indicator of particular STEM subfields – engineering; physical sciences, math, statistics, and computer science (combined); or biological or agricultural sciences (combined) – as opposed to non-STEM majors. The appendix explains the procedures we use to make the field-of-study variables comparable across the datasets.¹³

Our focal explanatory variables measure performance in high school in the subjects of mathematics and reading, coursework and grades. A significant proportion of the samples contain missing data for the performance measures (nearly 40 percent of the observations in NELS). To address this problem, we use multiple imputations (by gender) based on the multivariate normal model approach with a large number of auxiliary variables.

We use 12^th grade test scores to compare students from representative samples of high school students, including students who do not take college entrance examinations. The test scores come from cognitive test batteries given to the respondents of each survey during the spring of their 10^th grade and 12^th grade years, and are standardized by cohort. The tests are similar but not identical across surveys. The ELS did not include a reading test in the 12^th grade year, so we use 10^th grade reading test scores for the ELS cohort.

In addition to examining the relationship between math test scores and STEM major, we wish to test the relative strength theory that suggests that females are more likely to choose non-STEM majors because they are more likely than males to have relative strength in reading. At the same time, we wish to account for nonlinearities in the effects of test scores on major choice. To do so, we re-express the specification for the full second-order polynomial as the absolute math score, the difference between math and reading scores, and interactions between this difference and both math and reading scores.¹⁴ In the regression decomposition models, we use this formulation; in the trend analysis we use a simpler formulation based simply on standardized math and reading scores.

It can be argued that test scores measure math and science performance incompletely, and therefore that measures of math and science courses taken and course grades should be included in the model. On the other hand, it is also possible that choices of high school courses are the consequence rather than the cause of growing interest in science.¹⁵ Nonetheless, we include measures of curricular choice and course performance to assess whether trends in these variables or in their effects can plausibly be implicated in gender trends in STEM fields of study in college. We use measures of grades and coursework from the transcript studies for the surveys where this information was available.¹⁶ For HSB, NELS and ELS, we use transcript data to obtain high school grades and coursework in specific quantitative subjects. We standardize grades on a scale of 4 being high (As) and 1 being low (Ds). We include a measure coded 0 to 3, indicating whether a student took calculus, physics or chemistry during high school in the regression decomposition analysis; a 3 indicates that a student took all of those courses, a 0 indicates that a student took none of those courses, and a 1 or 2 indicates that a student took 1 or 2 of the courses.

We use survey questions about respondent life goals from the NCES panel studies to consider whether males see their life goals as more compatible with STEM careers than do females. Because our main focus is on the relevance of changing gender attitudes on the choice of STEM majors, we develop a set of indices using only survey questions that were asked in all four surveys. The survey questions we use are intended to capture respondent life goals as of twelfth grade. We constructed three indices to measure three latent concepts of relevance in the literature. The first is based on the mean of responses to four questions representing the respondent’s aspirations regarding a family. The second is based on the mean of responses to four questions about the importance of money and success. The third is based on the mean of responses to two questions regarding the importance of helping others. We use the first as a measure of concern about work-family compatibility. The second and third reflect the potential attribution of significance to extrinsic and intrinsic rewards, respectively.¹⁷

The four panel studies do not have comparable questions about attitudes that would allow us to conduct trend studies of changes in the effects of attitudes on choice of STEM majors. We therefore focus on the ELS dataset to create an index for attitudes about math abilities, and use this index in a decomposition analysis to assess the contributions of attitudes to choice of STEM majors for a single cohort. Math self-assessment is based on a factor analysis of responses to 5 questions representing the respondent’s attitudes about mathematics; the attitude questions loaded primarily on one factor.¹⁸

In addition to the above-described variables and gender (coded female=1), we include controls for socioeconomic status (a continuous measure), race (with categories for white, black, Hispanic, Native American, and Asian), and parent’s highest education (categorized as less than college degree, college degree, or advanced degree). For simplicity, we refer to this set of variables as the “demographic” variables in the discussion below. We follow Ingels et al. (2012) in constructing comparable measures across the four datasets.

We generally use the term “gender gap” to refer to differences in the probability that a young woman or young man who was enrolled in a four-year college (or who graduated from college) would have majored in a STEM field. However, we also sometimes pay attention to the “gender share” of STEM fields. Because women transitioned from being a minority to being a majority of college enrollees and college graduates, their share of STEM majors would rise even if their relative propensity to major in a STEM field had not changed. In other words, changing both relative propensities and changing relative shares of college enrollees and graduates have affected the trend in the gender share of STEM fields.

We estimate two sets of models to examine the explanatory power of performance and life goals and attitudes for the gender gap in STEM fields of study and trends in the returns to those measures. In the first, we present a nonlinear regression decomposition analysis of the gender gap in STEM fields for each cohort using the performance measures outlined above. In the second set of models, we construct a pooled dataset of the three most recent cohorts. Then, using a logistic regression model with interaction terms, we examine changes in the returns to performance measures across cohorts. Table 1 contains descriptive statistics for the students in the four-year college sophomore and the full samples on the relevant performance metrics.

Table 1. Descriptive Statistics for Variables Used in Regression and Decomposition Models.

	NLS		HSB		NELS		ELS
Sophomores at Four-Year Schools	Female	Male	Female	Male	Female	Male	Female	Male
Grade Point Average	3.35	3.14	3.18	2.97	3.22	3.06	3.37	3.19
English Coursework	6.48	6.40
Math Coursework	4.55	5.40
Adv. Science Coursework			0.97	1.19	1.48	1.66	1.56	1.73
Std. Math Test Score	0.62	0.90	0.71	0.96	0.51	0.69	0.43	0.72
Math-Reading Diff.	−0.04	0.28	0.04	0.24	−0.08	0.30	−0.08	0.22
Importance of Family	2.38	2.35	2.50	2.50	2.53	2.47	2.61	2.54
Extrinsic Values	2.42	2.54	2.59	2.69	2.64	2.69	2.68	2.68
Intrinsic Values	1.96	1.90	1.73	1.74	2.25	2.05	2.24	2.05
Math Self Assessment							0.123	0.367
STEM Major (%)	9.81	20.34	14.48	32.98	12.75	27.87	12.47	27.17
All High School Seniors
Grade Point Average	2.96	2.65	2.67	2.43	2.82	2.60	2.93	2.68
English Coursework	6.26	6.26
Math Coursework	3.53	4.29
Adv. Science Coursework			0.38	0.47	0.89	0.92	1.03	1.02
Std. Math Test Score	−0.04	0.22	−0.10	0.03	−0.11	−0.01	−0.17	−0.02
Math-Reading Diff.	−0.14	0.15	−0.04	0.05	−0.19	0.14	−0.16	0.09
Importance of Family	2.39	2.36	2.49	2.47	2.51	2.45	2.58	2.54
Extrinsic Values	2.49	2.59	2.60	2.69	2.66	2.70	2.69	2.72
Intrinsic Values	1.87	1.86	1.62	1.69	2.20	2.01	2.21	2.06
Math Self Assessment							−0.142	0.054
STEM Major (%)	5.80	8.44	5.55	12.28	7.37	15.78	5.95	11.73

Note: All performance and values variables are measured in twelfth grade, with the exception of ELS, where the reading test score is from tenth grade. The estimates are weighted (using full sample weights) to reflect the population of 12th graders in the respective year. The conditional sample (first panel) is restricted to students who attend four-year institutions during the spring of their sophomore (HSB, NELS, ELS) years or during the fall of their sophomore year (NLS72). The unconditional panel (second panel) is representative of all high school seniors.

5. Results

5.1 Decomposition of the Gender Gap in STEM Majors

A widely discussed determinant of college field of study is math ability. While gender differences in average math test scores have always been small and have converged in recent decades (Hyde et al. 2008; National Center for Education Statistics 2010), males at all relevant times have received a disproportionate share of the very best math scores. Yet if the relative scarcity of women with high math achievement were the primary cause of the gender gap in the STEM fields, we would expect the propensity for high scoring students to major in STEM fields to be nearly identical for men and women. But this expectation is not accurate, as others have observed (Ceci and Williams 2010; Ceci et al. 2009; Hyde et al. 2008). For each of the four surveys, men with high math scores have a higher propensity to major in STEM fields than their female counterparts, although it should be noted that there is a decline in the proportion of high-scoring students who major in STEM fields for more recent cohorts, possibly reflecting both competitive opportunities in other fields and declining interest in STEM fields among U.S. students. Similarly, although taking advanced science and math courses increases the odds of becoming a STEM major across cohorts, of the students who take calculus, chemistry or physics in high school, a declining proportion become STEM majors.

To explore the separate effects of test scores and coursework on the decision to major in STEM fields, we estimate a logistic regression model and then compute a regression decomposition. We present in Table 2 the results of a logistic regression for all male and female sophomores in four-year colleges in the NLS, HSB, NELS and ELS, of STEM major on gender, absolute and relative test score measures, other performance variables, life goals, SES, race, and parental education; we conduct a comparable analysis for all high school seniors (Table 2A).

Table 2. Logistic Regression of Sophomore STEM Major on Demographic Variables,Academic Performance, and Life Goals (Four-Year Schools Only).

	NLS		HSB		NELS		ELS
	O.R.	Std.Err.	O.R.	Std.Err.	O.R.	Std.Err.	O.R.	Std.Err.
Female	0.497***	0.060	0.352***	0.060	0.384***	0.053	0.398***	0.044
Race:
Asian	1.113	0.355	2.477**	0.771	1.473*	0.266	1.247	0.190
Black	1.224	0.297	1.817*	0.513	2.448***	0.618	2.208***	0.424
Hispanic	0.543	0.266	1.446	0.392	1.393	0.327	1.109	0.228
Nat. Amer.	1.700	1.691	0.948	0.621	1.384	0.793	0.544	0.524
Parents Education
College degree	0.939	0.183	1.078	0.266	1.298	0.265	1.034	0.158
Advanced degree	1.070	0.244	0.877	0.251	1.379	0.320	1.240	0.242
SES	0.926	0.122	0.687**	0.096	0.669***	0.082	0.770*	0.094
12th Grade Performance
Math Score	1.431**	0.178	1.678**	0.306	1.467*	0.209	1.225+	0.127
Math – Reading Score	1.091	0.173	1.225	0.273	1.028	0.148	1.210+	0.133
MR Diff * Math	0.741*	0.104	0.925	0.169	1.097	0.179	1.044	0.090
MR Diff * Reading	1.026	0.096	1.213	0.157	1.083	0.120	1.090	0.077
Total Semesters English Coursework	0.840***	0.042
Total Semesters Math Coursework	1.205***	0.048
Adv. Science Coursework			1.840***	0.182	1.499***	0.167	1.505***	0.115
High School G.P.A.	1.300*	0.154	1.549**	0.263	1.163	0.199	1.927***	0.252
Life Goals:
Importance of Family	0.801	0.134	1.016	0.283	0.750	0.164	0.837	0.156
Extrinsic Values	1.116	0.174	1.168	0.361	0.743	0.145	1.208	0.221
Intrinsic Values	0.766**	0.078	0.889	0.147	1.172	0.148	0.960	0.101
Constant	0.199*	0.126	0.029***	0.030	0.247+	0.185	0.016+++	0.011
# Students	3570		2090		4070		4650

Note: The sample is restricted to students who attend four-year institutions during the spring of their sophomore (HSB, NELS,ELS) years or during the fall of their sophomore year (NLS72).

⁺p ≤0.10;

^*p ≤.05;

^**p ≤.01;

^***p ≤.001 (two-tailed tests).

Table 2A. Logistic Regression of Sophomore STEM Major on Demographic Variables, Academic Performance, and Life Goals (All High School Seniors).

	NLS		HSB		NELS		ELS
	O.R.	Std.Err.	O.R.	Std.Err.	O.R.	Std.Err.	O.R.	Std.Err.
Female	0.739***	0.061	0.412***	0.041	0.421***	0.040	0.420***	0.038
Race:
Asian	1.273	0.357	1.846**	0.358	1.395*	0.208	1.431**	0.175
Black	1 759***	0.255	1.982***	0.308	2.082***	0.341	2.391***	0.340
Hispanic	1.510*	0.307	1.369*	0.193	1.446**	0.204	1.023	0.163
Nat. Amer.	1.484	0.800	0.430*	0.178	0.964	0.363	0.538	0.372
Parents Education
College degree	0.943	0.125	1.098	0.171	1.043	0.150	1.078	0.133
Advanced degree	0.958	0.144	0.828	0.162	0.978	0.162	1.305+	0.204
SES	1.264**	0.104	1.104	0.096	1.032	0.088	0.994	0.095
12th Grade Performance
Math Score	1.459***	0.104	1 781***	0.139	1.552***	0.158	1.397***	0.109
Math – Reading Score	0.889+	0.056	1.033	0.100	1.044	0.098	1.159+	0.088
MR Diff * Math	1.003	0.061	1.102	0.094	1.027	0.089	1.059	0.067
MR Diff * Reading	1.078	0.060	1.078	0.071	1.107	0.109	1.026	0.056
Total Semesters English Coursework	0.914**	0.030
Total Semesters Math Coursework	1.185***	0.030
Adv. Science Coursework			1.799***	0.110	1.555***	0.116	1.528***	0.091
G.P.A.	1.546***	0.110	1.815***	0.163	1.094	0.107	2.485***	0.241
Life Goals:
Importance of Family	1.003	0.119	0.739*	0.102	0.854	0.120	0.816	0.112
Extrinsic Values	1.135	0.129	1.254	0.200	1.033	0.139	1.343*	0.200
Intrinsic Values	0.781***	0.055	0.912	0.085	1.107	0.098	0.965	0.083
Constant	0.019***	0.007	0.017***	0.009	0.075***	0.035	0.003***	0.001
# Students	14420		13260		12400		12530

Note: The sample includes all high school seniors.

⁺p ≤0.10;

^*p ≤.05;

^**p ≤.01;

^***p ≤.001 (two-tailed tests).

The estimated odds ratios from the logistic regression for college sophomores in four-year schools show that higher math scores increased the odds of majoring in STEM fields in each cohort; math and science coursework increased the odds of becoming a STEM major in all cohorts and high school grades increased the odds of becoming a STEM major in most cohorts. Students who rated the importance of intrinsic values highest had the lower odds of becoming a STEM major in NLS. The logistic regression results imply a large female shortfall in STEM majors net of test scores, life goals, and other performance measures and other covariates in each cohort. The analysis of the larger sample of high school seniors produced comparable results (Table 2A), although the importance of family significantly reduced the odds of becoming a STEM major in the HSB full sample and the importance of extrinsic rewards significantly increased the odds of becoming a STEM major in the ELS full sample.

Next, to show how the gender gap has been influenced by math and reading test scores (and other factors), we use estimates from parallel logistic regression models for men and women to estimate how much the gender gap would be reduced if these factors were the same for boys and girls. We use Fairlie’s (2005) nonlinear decomposition technique to identify the extent to which gender differences in math performance contribute to the gender gap in being a STEM major (a binary outcome). Table 3 shows the results for each cohort for six different sets of measures: demographic variables alone, demographic variables and test scores, demographics with test scores and life goals, and the full model of demographics, test scores, life goals, and grades and coursework (using both samples). We use coefficients from the regression equation for males and the actual test scores of women; an even smaller portion of the gender gap would be explained by the included covariates if we use coefficients for females and test scores for males.

Table 3. Percentage of the Gender Gap in Sophomore STEM Majors that is Explained by Demographic Variables, Academic Performance, and Life Goals.

	Descriptive Data					% Explained
	% Male STEM	% Female STEM	Difference	Demographics	Plus Test Scores	Plus Life Goals	Plus Grades and Coursework	Plus Math Self Concept
Sophomores in 4-year schools
NLS72	20.3%	9.81%	0.105	4.22%	20.92%	25.56%	34.87%
HSB	32.98%	14.48%	0.185	−0.23%	23.06%	24.35%	19.12%
NELS	27.87%	12.75%	0.151	2.41%	15.83%	7.93%	7.37%
ELS	27.17%	12.47%	0.147	0.97%	32.34%	32.70%	13.82%	24.23%
Senior Sample
NLS72	8.44%	5.80%	0.026	16.00%	54.38%	56.51%	40.43%
HSB	12.28%	5.55%	0.067	7.94%	31.25%	34.21%	14.82%
NELS	15.78%	7.37%	0.084	6.10%	15.14%	10.37%	8.07%
ELS	11.73%	5.95%	0.058	4.57%	38.02%	39.50%	−1.17%	1.77%

Notes: Calculations are based on logistic regression estimations parallel to those shown in Table 2 (without gender as a variable).The second and third columns show the percentages of men and women in STEM majors in the respective sample, and the fourth column shows the observed difference in the share of men in STEM fields and the share of women in STEM fields. The fifth through eighth columns show the percentage of the difference attributable to different combinations of variables, using the coefficients from the estimation for men. Standard errors are adjusted for school clusters. Full sample weights were used for the test score estimates. The sample in the first panel is restricted to students who attend four-year institutions during the spring of their sophomore (HSB, NELS, ELS) years or during the fall of their sophomore year (NLS72). Demog. (demographic variables) consist of race and ethnicity, socioeconomic status, and parents’ education level.

Using the full model and looking at the sample of sophomores in four-year schools, we see that demographic variables, academic performance, and life goals can explain roughly 35 percent of the observed gender difference in NLS and roughly 20 percent in HSB. However, in the two more recent studies (NELS and ELS), less than 15 percent of the observed gender difference can be explained by these variables. Although some of the demographic measures had statistically significant effects on major choice (see Table 2), these effects have almost no bearing on the gender gap in STEM majors in any of the cohorts. Group differences in coursework and test scores do contribute in significant ways to the gender gap in STEM fields of study across cohorts, although it should be noted that coursework had diminishing power to account for the gender gap in STEM fields as the coursework patterns became more similar in recent cohorts for male and female students.¹⁹ Finally, gender differences in life goals make only small contributions to the gender gap in STEM fields even though these differences can be observed across cohorts.²⁰ In the senior sample, we see that the gender gap can no longer be explained by the factors in the model by the time of the ELS cohort. Although men appear to have a continuing advantage in test scores and this advantage explains part of the gap, this advantage is completely offset by female advantage in college entry and grades and by the closing of the gap in high school coursework.

Self-assessed math ability may also be related to major choice. Because these assessment measures vary by dataset, we do not include these factors in our basic trend models. However, to provide a better understanding of how social comparison processes and biased self-assessments might relate to the decision about college field of study, we have included a math self assessment index in the ELS model to estimate the portion of the gender gap that remains unexplained after all identified individual-level factors are introduced. With the inclusion of these measures, only a small fraction of the gender gap in STEM fields is explained. Most of the gender gap in STEM majors is unexplained by any of the factors discussed above, at least in the form that they are measured in the education cohort studies.

5.2 Trends in the Returns to Performance and Life Goals

To evaluate whether the relationship between test scores, life goals and the gender gap in STEM majors has changed in the past 30 years, we constructed a pooled dataset of the three most recent panel studies.²¹ We then estimated a logistic regression of STEM major on gender, cohort (or survey), math and reading scores, grades, science coursework, and life goals, with two-way and three-way interactions involving gender, cohort, and performance measures – all of which are comparable across the three datasets. Table 4 displays the results, using the HSB cohort as the reference category.

Table 4. Logistic Regression of STEM Major on Covariates with Cohort Interactions (Four-year Sample).

	O.R.	Std Err.
Race (White ref)
Asian	1.404***	0.117
Black	2.256***	0.224
Hispanic	1.327**	0.133
Nat. Amer.	0.954	0.413
Parent’s Education (no degree ref)
College degree	1.094	0.092
Advanced degree	1.194+	0.123
SES	0.777***	0.047
Survey
HSB (ref.)
NELS	2.460	3.006
ELS	0.30	0.374
Female	0.077	0.130
Std. Math Score	1.571**	0.239
Std. Read Score	0.830+	0.092
Adv. Science Courses	1.719***	0.151
High School GPA	1.790***	0.267
Importance of family	0.875	0.225
Extrinsic values	1.322	0.393
Intrinsic values	0.797	0.123
Interactions:
Female × Math	1.696*	0.433
Female × Read	0.777	0.143
Female × ASC	0.973	0.134
Female × GPA	1.043	0.277
Female × Family	1.110	0.451
Female × E.V.	1.321	0.635
Female × I.V.	1.011	0.253
NELS × Female	26.22	54.65
ELS × Female	14.10	29.00
NELS × Math	1.150	0.231
ELS × Math	0.969	0.178
NELS × Read	1.031	0.147
ELS × Read	0.926	0.126
NELS × ASC	0.852	0.105
ELS × ASC	0.886	0.102
NELS × GPA	0.639*	0.138
ELS × GPA	1.266	0.253
NELS × Family	1.059	0.339
ELS × Family	1.120	0.357
NELS × E.V.	0.781	0.282
ELS × E.V.	0.831	0.290
NELS × I.V.	1.406+	0.273
ELS × I.V.	1.065	0.201
NELS × Female × Math	0.554+	0.183
ELS × Female × Math	0.611+	0.183
NELS × Female × Read	1.303	0.319
ELS × Female × Read	1.619*	0.358
NELS × Female × ASC	1.333	0.258
ELS × Female × ASC	0.931	0.165
NELS × Female × GPA	0.832	0.315
ELS × Female × GPA	0.673	0.231
NELS × Female × Family	0.627	0.313
ELS × Female × Family	0.654	0.323
NELS × Female × E.V.	0.684	0.400
ELS × Female × E.V.	0.906	0.516
NELS × Female × I.V.	0.814	0.256
ELS × Female × I.V.	1.324	0.400
Constant	0.028***	0.028
Observations	10800

Note: The logistic regression estimations use a combined dataset from HSB, NELS, and ELS. Major choice was standardized across surveys as explained in the Appendix. In each model, the reference category is non-STEM majors. Math and reading test scores are based on standardization of the senior test data for each survey. .

⁺p ≤0.10;

^*p ≤.05;

^**p ≤.01;

^***p ≤.001 (two-tailed tests).

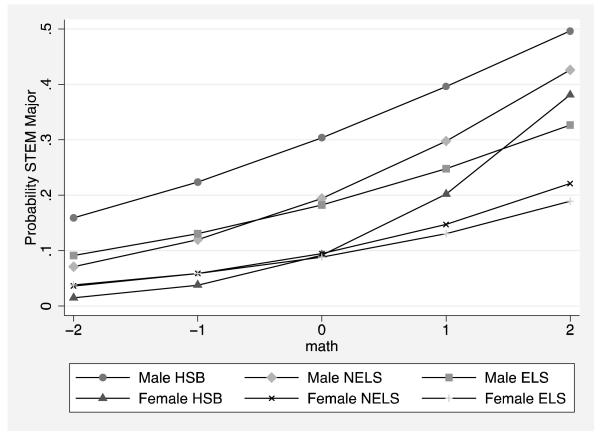
To provide a more direct assessment of how academic performance in high school influences the gender gap over time, we present estimates of the marginal effects of the academic performance regressors -- test scores, grades, and coursework -- by gender and cohort (Appendix Table A3); we also present estimates of the marginal effects of these same variables from a multinomial logistic regression model predicting STEM category. The predictive margin for a gender cohort represents the average of the predicted probabilities of being a STEM major if the entire sample had been in that gender and cohort. Figure 3 plots these predictive margins of majoring in STEM for each gender cohort at different levels of math achievement. In general, women received greater returns than men to math scores in the HSB cohort, but this pattern reversed in NELS and ELS; men have always received greater returns to coursework and grades. The second panel shows that the effects are concentrated in engineering and the physical sciences rather than in the biological sciences.

Figure 3. Predictive Margins of Being STEM Major by Gender and Survey at Different Levels of Math.

Source: HSB, NELS, ELS

Note: The analysis is restricted to sophomores in four-year colleges.

Applying HSB effects to the actual distribution in ELS, we isolated the probabilities of being a STEM major for women and men in ELS assuming that they received the returns on the factors in the model that women and men received in HSB but that the composition of the sample stayed the same. The predictive margins for men in this scenario are 27 percent when treated as men and 12 percent when treated as women; the predictive margins for women were 11 percent when treated as women and 26 percent when treated as men. Then, we isolated probabilities of being a STEM major for women and men in ELS assuming the same distribution of covariates as women and men in HSB but that the importance of the factors in the model did not change. The predictive margins for men in this scenario are 11 percent when treated as men and 6 percent when treated as women; the predictive margins for women are 6 percent when treated as women and 12 percent when treated as men. Distributional differences in the covariates thus have only a modest effect on gender differences in the probability of being a STEM major. Across cohorts, differences in the effects produce somewhat larger differences in the probabilities of being a STEM major. However, the large difference in the probabilities of being a STEM major when comparing males as females to males as males, for example, confirms that gender preferences are a substantial factor in producing the gender gap in STEM majors.

The conclusion drawn from these models is that men are more likely to choose a STEM major, without regard to performance or life goals. We find no substantial gender difference in the translation of test scores or life goals into STEM majors, and we find only limited evidence that the relation between test scores or life goals and STEM fields of study has changed over the course of the study. Women, in short, had a substantial preference for non-STEM majors throughout the study period. The reason for this preference, however, is not explainable in terms of the academic or life-course goals variables that are measured in the education panel datasets.

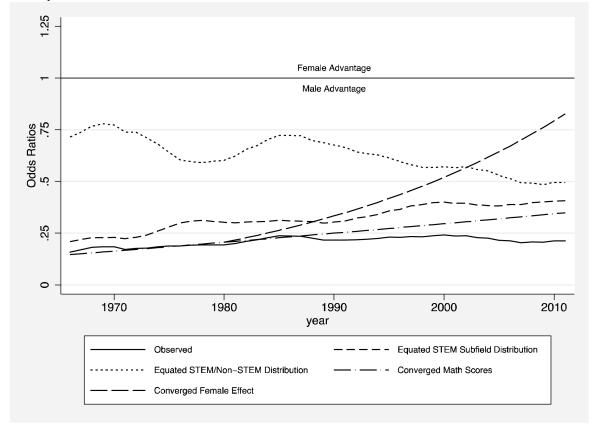
To further explore the implications of the multinomial models for gender trends in STEM majors, we compare actual and three counterfactual trend lines constructed using data on bachelor’s degrees in STEM fields from WebCASPAR and the coefficients from a model predicting choice of STEM majors. The “Observed” line in Figure 4 uses aggregate data on bachelor’s degree recipients to depict the actual trends in the female-to-male odds of receiving bachelor’s degrees in the physical sciences, mathematics, or engineering, with all other fields of study as the reference category. The “Equated STEM/Non-STEM Distribution” line is a counterfactual trend line constructed by assigning the male propensity to major in STEM fields²² to females,²³ but retaining the actual female preference for life sciences, conditional on majoring in a STEM field.²⁴ The “Equated STEM Subfield Distribution” counterfactual line was constructed by assigning to females the male propensity to major in the hard sciences, conditional on majoring in a STEM field but retaining the actual female propensity to major in STEM. The third counterfactual line in Figure 4 explores the importance of the gender difference in math test scores on STEM majors by imposing a convergence in male and female math scores over a thirty-year period.²⁵

Figure 4. Counterfactual Odds Ratios for Physical Science, Engineering, and Math Majors.

Source: National Science Foundation WebCASPAR Database

Note: The solid line represents a trend line for the observed female to male odds of receiving a bachelor’s degree from a four-year college in the physical science, engineering, or mathematics subff elds from the late 1960s through 2011. The broken lines each represent a different counterfactual trend line, as described in the text.

Figure 4 shows that the observed trend in the female-male odds ratios peaked at about 0.25 in the late 1980s, but fell back to early 1970s levels (about 0.20) around 2007. In the counterfactual trend that equates the gender preferences for STEM vs. non-STEM distributions, the female-male odds ratio approached 0.75 in the early 1980s but dropped to below 0.50 in more recent years. Conversely, in the past 30 years, the counterfactual trend that equates the gender preference for physical sciences and engineering, conditional on being a STEM major, increases from less than 0.25 to nearly 0.40. Clearly, the choice of subfields within STEM fields—and specifically, the choice of biological science as opposed to physical science, mathematics, or engineering—has become increasingly important to understanding the gender gap in the physical sciences and engineering, and gender differences in the within-STEM distribution have become almost as important as the overall gender gap in choosing a STEM major in explaining the female shortfall in physical sciences, mathematics, and engineering.²⁶

Using the third counterfactual, we find that there would have been no substantial effect on the gender gap if average male and female math scores converged over time from the level found in HSB. As a comparison, we then constructed a fourth counterfactual. Using the same logistic regression as for the third counterfactual, we imposed a thirty year convergence of the residual effect of gender rather than of the gender difference in math test scores. Our results demonstrated that the residual effect of gender is a much stronger producer of STEM differences than is the gender difference in math scores. If females had developed the same residual preferences over time as males, we would see the gender gap narrowing, with the odds ratio rising above 0.75 by 2009. These data document the statistical importance of otherwise unexplained female “preference” in comparison with the observed variables in our multinomial logistic regressions.

6. Competition Among Majors and the Gender Gap

Taken together, the preceding analyses establish that preferences (what we earlier referred to as “preferences, all things considered”) are important – both in the form of preference for biological sciences compared with physical sciences and engineering, and preferences for STEM majors compared to non-STEM majors. One obvious possibility – though difficult to assess empirically – is that the female preference for non-STEM majors or non-physical science majors within the STEM group arises not from the greater value they place on non-career life goals but rather on the extent to which they (correctly or incorrectly) perceive certain STEM fields as being inhospitable to their desired work-family balance. A second possibility is that they avoid certain fields not because they would not like them under other circumstances, but rather because they perceive them to have “chilly” climates towards women. Neither of these possibilities can be explored satisfactorily with the education panel data sets and so we do not pursue them further here even though we view them as potentially important explanations. Instead, we explore a third possibility, namely that women college students are more likely than men to value the humanistic as well as vocational aspects of education, that they on average have stronger preferences for a liberal arts curriculum than men, and that they are therefore more likely than men to perceive their broader educational goals to be in conflict with the curricular requirements of certain STEM majors and occupations. We address this possibility next.

When specific majors are requirements for entry into specific occupations, then gendered socialization affects major choice via the consequences of gender differences in occupational preferences. But when linkages between majors and occupations are flexible, then gender differences in major selection can arise from gender differences in curricular goals. The implications of choosing a specific major for the prospects of taking elective courses to achieve a student’s broader curricular goals will also produce gender differences in major choice if curricular goals differ by gender. While some college majors such as education and engineering have at least symbolically tight linkages to particular careers (Carnevale, Smith and Melton 2011; Shauman 2006, 2009),²⁷ other majors have more flexible linkages that encourage the pursuit of a variety of occupational goals from the same major. Similarly, while some occupations require specific vocational preparation, other (including some highly skilled) occupations are accessible from a variety of college majors. The link between major and occupation is also likely to differ by gender, including the tendency to see tight linkages between specific ostensibly vocationally-oriented majors and the careers to which they are symbolically linked. For example, Shauman (2009) finds that among graduates from female-dominated majors (such as education and social work), women are more likely to utilize their education by entering an occupation that is substantively related to their major; conversely among graduates from male-dominated majors (such as agriculture and computer science), men are more likely to enter a substantively-related occupation.²⁸ The factors driving choice of major, in other words, are not identical with the factors driving choice of occupation. Or, to put it differently, educational utilization varies by gender and major (Shauman 2009).

These differences have potential implications for differences in the gender distribution of both majors and occupations. Curricular constraints in majors may enhance gender differences in these majors and, correspondingly, gender differences in the occupations linked to these majors. Greater curricular flexibility may have the opposite effect. Similarly, occupational pathways that allow relative freedom in curricular choices at the undergraduate level may reduce gender differences in the occupation relative to occupational pathways that reduce freedom in curricular choice at the undergraduate level in a way that differentially disadvantages one gender relative to the other with respect to their broader educational preferences.

The contrast between engineering, on the one hand, and the humanities or social sciences, on the other, is a useful illustration of how differently structured curriculums can affect the gender distribution of majors. Upon completion of a bachelor’s degree in engineering, a graduate might have options to take a job in the engineering field (making the time spent in postsecondary education shorter than that for other professions), to pursue graduate studies in many STEM disciplines, or to enter professional school (law school, medical school, or business school). This degree field thus would appear to open multiple career pathways. However, the engineering degree is associated with vocationally oriented coursework and involves a relatively large number of required undergraduate courses (Frehill 1997). It is thought to have strong linkages to engineering occupations (Shauman 2009). Engineering is also unusual in typically requiring a commitment in the first or second semester of college (Frehill 1997). Students who do not select engineering in the first few semesters but decide to move into engineering later in their college career will spend more time before graduation than those that committed earlier. At the same time, the structure of most engineering degree programs requires that engineering majors be relatively restricted in their ability to pursue coursework in other fields of interest. The engineering major thus comes at the expense of curricular flexibility, in general, and a liberal arts curriculum, in particular; the result is that some gender segregation in engineering is associated with major field and some is associated with intended occupation.

In contrast to engineering, a humanities or social sciences student typically has the opportunity to select a major relatively late in the undergraduate career and pursue a broad range of coursework, because the major requirements are fewer, and because the courses are not hierarchically organized to the same extent as in engineering. Upon completing the degree, s/he can enter any of a variety of occupations that do not require specific technical skills upon entry, or enter graduate school in a field related to their major. However, the humanities student also has the opportunity to attend professional school, including in the relatively technical fields of medicine or law where much or all of the technical training is reserved for post-undergraduate education. It is much more difficult to indulge a preference for humanities or social science courses if one’s goal is to become a professional engineer.

Gender differences in the linkages between majors and expected occupations can be seen using data from the Baccalaureate and Beyond Longitudinal Study (B&B) 1993-2003 on the career aspirations of graduates in particular majors.²⁹ The B&B collects data about respondents’ bachelors degree field of study and their expected long-term occupation. Consistent with the definitions used in Sections 4 and 5, STEM fields include engineering, biological sciences, and mathematics and physical sciences. Non-STEM fields include business and management, education, health professions, public affairs/social services, social science, history, humanities, psychology, and other majors.

To examine the contributions of gender to career aspirations directly and through STEM subfields for respondents with STEM degrees, we use Buis’ (2010) nonlinear decomposition method. The dependent variable in these models is whether a respondent aspired to a particular occupation at the time of college graduation; here, we confine our analysis to the occupations most closely associated with STEM degrees -- engineers, physicians, teachers, managers or entrepreneurs, and other professionals (including lawyers, medical professionals, professionals in the arts, entertainment, and media industries, and other professionals). We calculate the indirect effects of gender on career aspirations that relate to STEM subfield distribution (engineering, biological sciences, or physical sciences) by giving a counterfactual group of boys the subfield distributions of girls, and then comparing the boys to the counterfactual. The direct effects are the effects of gender on career aspirations that cannot be explained by subfield distributions; we calculate this by comparing the counterfactual group with the girls (which keeps subfield distributions constant).

As shown in Table 5, the unadjusted odds of aspiring to managerial and engineering occupations for boys are more than 2 times as large as the odds for girls; conversely, the unadjusted odds of aspiring to teaching and professional occupations for girls are more than 2 times as large as are the odds for boys. Looking at the indirect effects running through the distribution of subfield, most of the male advantage in aspiring to engineering occupations is related to STEM subfield choices, and the direct effects of male, net of major choice are smaller than the total effects and are not statistically significant in the B&B data. However, the direct effects are statistically significant and more substantial than the indirect effects for most other career aspirations. The aspiration to become a physician is striking in that girls have somewhat higher unadjusted odds than boys of aspiring to the occupation of physician, and this is related to their STEM subfield choices; however, net of the distribution of subfields, male STEM majors have higher odds than female STEM majors of aspiring to careers as physicians.

Table 5. Male-Female Odds of Expecting Certain Long-Term Occupations for STEM Bachelor’s Degree Recipients.

	Male-Female Odds Ratios
Expected Occupation	Total Effect	Indirect Effect	Direct Effect
Engineer	2 49***	2.08***	1.20
Manager/proprietor	217***	1 34***	1.63**
Other professional	0 43***	0.63***	0.68***
Physician	0.74+	0.52***	1.43*
Teacher	0.35***	0.73***	0.48***

Source: B&B 93/03. Table shows odds ratios. Each row compares males and females. Indirect effects are mediated through

STEM subfield distribution, using the Stata command ldecomp (Buis 2010). The analysis is restricted to degree recipients in

STEM fields from four-year colleges.

⁺p ≤0.10;

^*p ≤.05;

^**p ≤.01;

^***p ≤.001 (two-tailed tests).

These data show that STEM major choice or subfield choice does not necessarily reflect expected STEM occupation; accordingly, gender differences in “persistence” rates from STEM major to STEM occupation do not necessarily reflect gender differences in the rate of change of career orientations, because the initial distribution of career orientations may have differed by gender for those in the same major. In other words, it is not simply the case that women and men pursue degrees in particular major fields and subsequently decide to use those degrees in different ways, it may also be the case that women and men sometimes plan to pursue major fields to different ends from the start. These data also shed light on a different issue – that men are more likely to have entrepreneurial aspirations that motivate their choices to pursue STEM degrees.³⁰ This is consistent with the fact that nearly one-third of male STEM majors do not expect to pursue advanced degrees.³¹

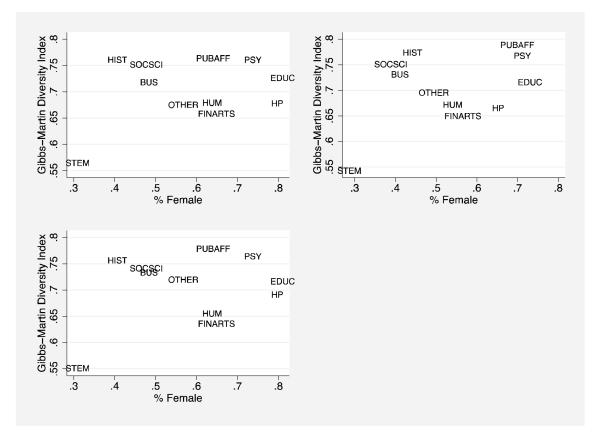
To test the curricular choice hypothesis more directly, we used B&B transcript data with the major categories listed above to examine the number of humanities and social science courses women and men take in the path to a bachelor’s degree.³² We also use the Gibbs-Martin diversity measure to examine the diversity of coursework taken by women and men within different majors (Gibbs and Martin 1962).³³ Figure 5 displays the relationship between the proportion of females within each major and the average Gibbs-Martin diversity index for students in that major. We find that students obtaining STEM degrees take more courses within their field than any other group of students; consequently these students as a group experience less curricular diversity than do non-STEM majors. These students, moreover, are disproportionately male. However, when STEM majors are omitted, there is not a strong positive relation between the proportion of females within a major and the curricular diversity of students’ coursework within that major. The absence of any strong relation becomes even clearer when we restrict the analysis to high-achieving students and when we remove post-secondary institution variability (Figure 5, second and third panels). Thus, these data provide little support for the notion that men prefer specialization in general. Yet we note that this measure of specialization is imprecise because it does not account for the size of different major groups or their internal heterogeneity.

Figure 5. Coursework Heterogeneity by Proportion Female, Within Major.

Source: B&B (1993/2003).

Note: The first panel depicts percent female within major (weighted) on the x-axis and the Gibbs-Martin diversity index for each major. The second panel restricts the analysis to the top quartile of students as measured by the SAT/ACT. The third panel builds on the second by adding school fixed effects.

Among STEM majors, however, gender differences in curricular preferences are more clearly visible. To show this, we estimate regression models of different curricular choices on female, using postsecondary institution fixed effects to account for differences in degree requirements between schools (Table 6). In the first model, we regress the Gibbs-Martin index on female, conditional on being a STEM major. In the second and third models, we use Poisson regression to examine whether female STEM majors take more credits in humanities or the social sciences. Consistent with our expectations, we find that female STEM majors take a more diverse set of courses than male STEM majors (Table 6). In addition, female STEM majors take more humanities and social science courses than male STEM majors. These results are not sensitive to the definition of STEM in the sense that if we reach similar conclusions with a definition of STEM that excludes the biological sciences. Although we cannot observe the majors that students would have pursued but for curricular restraints, we suggest that these data are consistent with a curricular motivation for avoiding STEM majors.

Table 6. College Coursework, by Gender and Major.

	Gibbs-Martin Index (Female Coef.)	Humanities Credits (Female IRR)	Social Science Credits (Female IRR)
STEM Majors	.052 (.006)	1.10 (.039)	1.11 (.040)
STEM Majors (Top Quartile SAT/ACT)	.046 (.012)	1.15 (.085)	1.11 (.065)

Source: B&B (1993/2003). Note: We use postsecondary institution fixed effects to account for unobservable differences in degree requirements between schools. Robust standard errors. Fixed-effects regression of Gibbs on female. Fixed-effects Poisson regression of credits on female. The analysis is restricted to degree recipients in STEM fields from four-year colleges.

Our final inquiry examines the different choices that women and men make in college, conditional on their enrolling in professional school. We obtained data on medical school applicants from the American Association of Medical Schools. The data include the number of applicants and matriculates coming from each undergraduate major by sex. These data suggest that women are less likely than men to enroll in medical school with a primary undergraduate degree in a STEM field: in 2009, 40 percent of women matriculated into medical schools with a non-STEM undergraduate degree, but only one-third of males did so, and the results are similar when the broader group of medical school applicants is considered. Female enrollees and applicants had higher odds of coming from the humanities (1.37 for applicants and 1.47 for matriculates) and the social sciences (1.18 for applicants and 1.24 for matriculates) than did males.³⁴ These data suggest that women are able to attend medical school and reach a high-status profession without compromising their gendered preferences for a more humanistic undergraduate education.³⁵ Female enrollees and applicants had about the same odds as males of coming from the biological sciences fields, and substantially lower odds than males of coming from the physical sciences (0.58) and mathematics (0.80). Further, the data suggest that a STEM undergraduate education has become less important to medical school entry during the last 30 years: in 1981, 75 percent of matriculates had undergraduate degrees in STEM fields, compared to only 63 percent in 2009. This coincides with the dramatic increase in female enrollment in medical schools during that time.³⁶

Because of medicine’s close connection to STEM fields, medical school entrants are probably the most interesting case for understanding the implications that constraints on undergraduate curricular choices have for the gender gap in STEM fields of study. Nonetheless, an examination of pathways to law school is also illuminating. We obtained data from the Law School Admissions Council on the undergraduate majors of law school applicants during the past 5 years. These data suggest that in 2009 female law school applicants had higher odds of coming from the humanities and arts (1.25), the social sciences (1.05), and other non-STEM fields (1.37), but lower odds of coming from the natural sciences (0.83), engineering and computer sciences (0.26), and business (0.67). Law school applicant data also suggest that women pursue a broader set of pathways to law school than males. Looking to some of the largest “feeder” majors, 19 percent of men major in political science, 17 percent in business, and 7 percent in history (collectively 43 percent). For women, by contrast, those numbers are 17 percent, 11 percent, and 4 percent, respectively (collectively 32 percent). Women also are much more likely to major in fields that are not traditional pathways to law school; thus, 7 percent of women major in English, and 7 percent of women major in psychology (compared to 5 percent and 4 percent, respectively, for males).

The data on law school and medical school applicants affirm that a substantial group of women follow the traditional pathways both to law school (political science) and to medical school (biology). Nonetheless, it is more common for women to pursue nontraditional pathways than it is for men. Women are more likely than men to apply or enter medical school or law school from non-STEM majors, and, although it is less clear what the expected feeder routes might be for law school applicants, women tend to pursue a different set of pathways. Thus, these data support the hypothesis that women contemplating a professional career are able to pursue female-dominated majors.³⁷

Some might argue that it is not surprising that fewer women in professional school come from STEM majors, as they are less likely to receive STEM degrees in the first place. The data we present arguably are also consistent with increased female representation associated with recent policy interventions (such as the revisions to the MCAT), and do not necessarily imply a choice related to occupational aspirations. We agree that differential selection into STEM majors is relevant to interpreting the results regarding medical and law schools. Indeed, it is likely that professional schools have increased gender parity, in part, by expanding the undergraduate fields of study from which they accept applicants. This is consistent with the declining proportion of STEM majors in medical schools from 1980 to 2010. Even so, we suggest that selection into or out of STEM majors should not be considered exogenous to the pursuit of a seat in law school and medical school.

If students make choices about major with career aspirations in mind, then we can assume that students are aware of the flexibility offered by these pathways, and that they act, in part, on the basis of that understanding. While we do not assume that sophomores are always strategic in making major choices with a view to occupational entry, we think it would be remiss to assume that they act in complete disregard of this element of the career path. Moreover, if women were increasingly attracted to medical professions, and if STEM majors were a nearly essential path to those professions, we would expect to see an increasing share of female medical school matriculates from undergraduate STEM majors. The fact that we do not, suggests that women who aspire to be doctors do not perceive a necessity to sacrifice their academic preferences for their chosen career.

7. Discussion

Although women have closed much of the gender gap in the pursuit of STEM majors in the last 30 years, their progress has been uneven outside of the biological sciences. Despite some moderate success in chemistry and mathematics, the share of women obtaining math and physical science degrees is not markedly higher than it was 30 years ago. Moreover, women have made virtually no progress in engineering fields since the mid 1990s, and they earn fewer degrees in engineering than they do in the physical sciences, math, and computer sciences. Indeed, the gender gap in subfields other than life sciences is wider now than it was ten years ago.

Conventional narratives explain little of the continuing (and, in some ways, worsening) gender gap. Although a gender differential in top mathematics test scores remains, this gap has been narrowing and thus would not explain a widening gender gap in quantitative-based fields like computer science and engineering. Further, the success of women in some strongly quantitative science fields (such as chemistry) undercuts the math ability rationale.³⁸ Our decomposition analysis buttresses those points; contrary to earlier work, we show that (at least since the 1980s) the gap in math performance explains less than one-third of the variation in field of study choices. Similarly, the increasing female representation in four-year institutions is consequential for the absolute numbers of female students majoring in STEM fields, but is not closing the gender gap in rates of majoring in STEM fields; the increased numbers of women in postsecondary education are equally if not more likely to pursue non-STEM fields of study. Finally, although research into life goals appears to be a relevant and important line of inquiry for future research into how males and females choose majors, our analyses suggest that values or life goals alone will contribute little to understanding gender disparities in undergraduate major choice, because they do not account for the different ways that majors fit into life plans.

Recognizing the limited explanatory power of math ability and life goals, we instead suggest a greater focus on curriculum and the vertical as well as horizontal structure of the educational pathways to alternative elite careers. In Part 6, we highlight three related phenomena. First, we emphasize the gendering of the pathways from major to occupation; we suggest that both the perceived necessity for a substantive link and the determination of whether particular links are substantive might differ for men and women. We also show that occupational expectations within major fields differ for men and women, so that transition rates from major to occupation should not be interpreted as pure “leakage.”

Second, we show that women are more likely than men to prefer a liberal arts education, by which we mean that women are more likely to take electives in the humanities and social science fields and more likely to continue to pursue traditionally female-dominated majors. This preference applies to the subsets of high-achieving students and STEM majors. Further, using a crude measure of diversity of coursework, we also show that women in STEM fields take a more diverse set of courses than men in STEM fields.

Third, we show that the growing opportunities for women in law and medicine have allowed women to construct separate pathways and pursue curricular preferences. Although it has become more likely for women to follow what have been traditionally “male” pathways into higher education, they have not altered their underlying preferences for STEM majors to a significant extent. At the same time, with more choices among elite occupations, women also tend disproportionately to enter new occupations that permit greater diversification in undergraduate majors. We cannot be sure why women enter these fields, but we observe that the women that do so come from a different set of undergraduate majors than the males that do so. Men, in contrast, appear more bound to traditional, more vocationally oriented pathways; this is consistent with Shauman (2009), which finds that among graduates from male-dominated majors (including STEM majors) men are more likely than women to utilize their educations by entering related occupations.

We cannot show what effect the changing opportunity structure in medicine and law has had on the trend in the gender gap in STEM fields, but we can suggest that it coincided with the point at which gender integration in fields of study halted. Even if other factors have contributed to the continuing gender segregation in fields of study, our results suggest the possibility that if engineering professions were organized like medicine with some training in the undergraduate years followed by intensive training in graduate school, the fraction of engineers who were women would be higher than is currently the case.

The data we use about degree and occupational aspirations, coursework, and professional school applicants offer an interesting glimpse of a much larger puzzle and provide an indication that the gender gap in STEM fields cannot be explained by focusing on individual-level determinants such as test scores, or job values and life goals as expressed in current survey data. We need a better way to model competition among majors and between STEM careers and other elite professional careers including especially law, medicine, and business (which remains gender imbalanced). Such a model also needs to incorporate the gendered nature of selection into these schools; thus, future trends in the gender gap in STEM fields could be affected if professional schools enforce a gender-parity policy and increasingly become more selective for female students than they are for male students.

In sum, the analyses in this paper suggest that the contribution to the gender gap of competition among majors is a promising avenue for further research. They imply that the curricular structure of undergraduate and professional education and the differing constraints they place on curricular choice may play a role in gender segregation in STEM fields that is as important as the factors implicated in the existing theories we test in this paper. This is a conjecture that merits additional investigation.

HIGHLIGHTS.

• ■This trend study tests prominent theories for the gender gap in STEM fields.
• ■Gender differences in test scores explain little of the gender gap in STEM fields.
• ■Gender differences in life goals and self-concepts also explain little of the gap.
• ■These factors also fail to account for the gender-specific trends in STEM majors.
• ■Women and men link college majors to jobs and curricular goals in different ways.

Appendix

Field of Study Definition – Longitudinal Datasets

All four studies asked in slightly different ways about students’ field of study. In each follow-up, NLS-72 respondents were asked to report their actual or intended fields of study if they were attending postsecondary school. The answers were coded into six-digit numerical codes. From the 1972 base year and the 1973 follow-up, NLS-72 used a coding system described by A Taxonomy of Instructional Programs in Higher Education (HEGIS). We convert the HEGIS codes to CIP codes.

Field of study is reported in the other three datasets using the CIP taxonomy. The CIP originally was developed by the NCES in 1980 and was revised in 1985 and 1990. The 2000 edition (CIP-2000) is the third and current revision of the taxonomy and has 53 general categories and more than 2000 specific categories. The CIP categorizes fields at the most granular level under six-digit codes of the form xx.yyzz. Fields of study can be further aggregated according to two- and four-digit prefixes of the code. For example, “Organic Chemistry” has the six-digit code 40.0504, which places it in “Chemistry” (40.05) and “Physical Sciences” (40).

Beginning in the second follow-up, HSB classified field of study information using six-digit CIP codes (High School and Beyond Fourth Follow-up Methodology Report p.78), a list of which can be found in High School and Beyond, 1980: Sophomore Cohort Second Follow-up (1984) (ICPSR 8443). This is the most detailed information we have about field of study in any of the datasets. Consistent with the CIP taxonomy, “Organic Chemistry” has the code 40.0504 in the HSB.

NELS uses a 3-digit field of study coding system. The first two digits and associated titles appear to follow the CIP coding system. The third digit provides additional detail, but not necessarily in a way that is parallel to the specific categories in CIP. For example, NELS 400 represents chemistry, but the final digit does not map to the CIP coding system. Moreover, we are not able to distinguish organic chemistry from other chemistry subfields.

ELS uses a classification system that is “largely” based on CIP-2000, but with 33 general categories and 192 specific categories (ELS: 2002 Base-Year to Second Follow-up Data File Documentation, p. 117). In the restricted dataset, F2MAJOR4 is a four-digit code, with the first two digits (equivalent to F2MAJOR2 in the public dataset) indicating one of the 33 general categories, and the last two digits indicating a subcategory. Unfortunately, the numerical designations do not track the CIP coding system; thus, we had to rely on the titles of the major groups to construct major variables. For example, in the two-digit codes, physical sciences are categorized with code 25; in the four-digit codes, the chemistry subfield is separately designated as code 2503. However, it appears that ELS merely aggregated CIP general categories in a few cases (presumably those with small enrollment) and then renumbered the resulting categories. For this paper, the more granular categories in HSB and NELS were collapsed into the 2-digit codes found in ELS.

A related issue is the source of the field of study information. The field-of-study variables for college sophomores are all based on self-report, but the treatment of undecided or undeclared majors varies across datasets. This produces substantial variation in the proportion that report a particular field of study across datasets; thus, in ELS, about 22 percent of college enrollees have undeclared majors, but the proportion declining to identify a field of study is much lower in the other datasets. The data are consistent with an increase in college sophomores with undecided majors over time. However, the form of the survey question might influence the apparent trend. In HSB, college sophomores are asked: “(During the last month enrolled), what was your actual or intended field of study or training (for example…)?” Similarly, in NELS: “(During your last month of attendance,) what is(was) your actual or intended major field of study at ÌNSTNAME’?” However, in ELS, students first were asked: “Now in 2006, have you declared a major yet at [spring 2006 school]?” Then, students who answered yes were asked, “What is your major or field of study?”

There is no substantial gender variation in the proportion of unknown or undecided majors in any of the surveys.

Field of Study Categorization—NSF WebCASPAR Data

The WebCASPAR database used in Figures 1-3 includes 53 field of study categories that can be mapped to the CIP codes used in the longitudinal studies. We group the 53 field of study categories as follows:

1. STEM

   1. Engineering

      1. Aerospace
      2. Chemical
      3. Civil
      4. Electrical
      5. Mechanical
      6. Materials
      7. Industrial
      8. Other engineering
   2. Physical sciences

      1. Astronomy
      2. Chemistry
      3. Physics
      4. Other physical sciences
      5. Atmospheric sciences
      6. Earth sciences
      7. Oceanography
      8. Mathematics and statistics
      9. Computer science
   3. Biological sciences

      1. Agricultural science
      2. Biological science
2. Non-STEM

   1. Non-Stem Arts and Sciences

      1. Psychology
      2. Economics
      3. Political science and public administration
      4. Sociology
      5. Anthropology
      6. Linguistics
      7. History of science
      8. Area and ethnic studies
      9. Other social sciences
      10. History
      11. English and literature
      12. Foreign languages
      13. Other humanities
      14. Religion and theology
      15. Arts and music
      16. Architecture and environmental design
   2. Other

      1. Science technologies
      2. Engineering technologies
      3. Health technologies
      4. Other science and engineering technologies
      5. Interdisciplinary or other sciences
      6. Communication and librarianship
      7. Law
      8. Social service professions
      9. Vocational studies and home economics
      10. Other non-sciences or unknown
      11. Medical sciences
      12. Other life sciences
   3. Education

      1. Science education
      2. Mathematics education
      3. Social science education
      4. Other science/technical education
      5. Non-science education
   4. Business and management

Table A1. Life Goals Survey Questions.

Family Aspirations

Finding the right person to marry and having a happy family life

Having strong friendships

Living close to parents/relatives

Having children

Extrinsic Motivation

Being successful in my line of work

Having lots of money

Being able to find steady work

Giving children better opportunities

Intrinsic Motivation

Helping others in the community

Working to correct inequalities

Note: These questions are based on a single survey stem that takes the form: “How important is each of the following to you in your life? (Not important; Somewhat important; Very important)”. The three indexes are represented along with the questions that comprise the index. Each index has a range of 1-3.

Table A2. Mathematics Self Assessment: Survey Questions.

I’m confident that I can do an excellent job on my math tests.

I’m certain I can understand the most difficult material presented in my math textbooks.

I’m confident I can understand the most complex material presented by my math teacher.

I’m confident I can do an excellent job on my math assignments.

I’m certain I can master the skills being taught in my math class.

Note: These questions are based on a single survey stem that takes the form: “In your current or most recent math class, how often do/did the following statements apply to you?”, with response categories “almost never”, “sometimes”, “often”, “almost always.”A high self-assessment is associated with a higher numeric value.

Table A3. Marginal Effects of Academic Performance on STEM Major, from Logistic Regression of STEM Major on Demographics, Measures of Math and ReadingAchievement and Life Goals.

	HSB-Female	HSB-Male	NELS-Female	NELS-Male	ELS-Female	ELS-Male
Math	0.107***	0.087**	0.055***	0.112***	0.047***	0.071
Reading	−0.048**	−0.036+	−0.015	−0.029+	−0.003	−0.045***
Sci. CW	0.056***	0.105***	0.067***	0.072***	0.033***	0.071***
GPA	0.068**	0.113***	−0.001	0.025	0.048**	0.139***

Marginal Effects from Multinomial Logistic Regression of STEM Major Categories on Demographics, Measures of Math and Reading Achievement and Life Goals
	HSB-Female	HSB-Male	NELS-Female	NELS-Male	ELS-Female	ELS-Male
Biol. Sci.
Math	0.017	−0.009	−0.010	0.020	0.009	−0.007
Reading	−0.001	0.009	0.019+	−0.006	0.007	0.007
Sci. CW	0.013*	0.007	0.032***	0.007	0.005	0.012
GPA	0.018	0.016	0.005	0.025	0.045**	0.056***
Phys. Sci.
Math	0.052**	0.033	0.028**	0.030*	0.019**	0.023*
Reading	−0.036**	−0.015	−0.018*	−0.003	−0.005	−0.017*
Sci. CW	0.027**	0.029*	0.025***	0.012	0.013**	0.010
GPA	0.025	0.023	−0.0014	0.000	0.004	0.042**
Eng’g
Math	0.041**	0.071**	0.039***	0.065***	0.015**	0.057***
Reading	−0.010	−0.031+	−0.015*	−0.021+	−0.006	−0.034***
Sci. CW	0.015*	0.069***	0.009	0.061***	0.016***	0.052***
GPA	0.027+	0.075***	−0.001	0.001	−0.003	0.041*

Notes: The analysis is restricted to sophomores in four-year colleges.

Notes: The analysis is restricted to sophomores in four-year colleges. The reference category is non-STEM majors.