Abstract
This article presents a six-rule algorithm for the reconstruction of multiple minimum-recombinant haplotype configurations in pedigrees. The algorithm has three major features: First, it allows exhaustive search of all possible haplotype configurations under the criterion that there are minimum recombinants between markers. Second, its computational requirement is on the order of O(J2L3) in current implementation, where J is the family size and L is the number of marker loci under analysis. Third, it applies to various pedigree structures, with and without consanguinity relationship, and allows missing alleles to be imputed, during the haplotyping process, from their identical-by-descent copies. Haplotyping examples are provided using both published and simulated data sets.
Introduction
Haplotyping analysis in pedigrees refers to the reconstruction of haplotypes from phase-unknown genotype data within each pedigree. Haplotype data are extremely valuable in the mapping of disease-susceptibility genes, particularly in the identification of genes related to complex diseases. The technique for experimentally derived whole-genome haplotypes is becoming available (Douglas et al. 2001), and such exact haplotype data are expected to have significant impact on future gene-mapping studies, especially in unrelated individuals. However, the reconstruction of haplotypes from conventional genotype data are still the major choice in most haplotype-based studies, because of both the lower cost of genotyping and the availability of fast and accurate haplotyping algorithms.
Haplotyping analysis in a pedigree involves the consideration of the whole space H of all possible distinct haplotype configurations. The whole space H can be partitioned into subsets Hr, where r⩾0 and Hr is the space of haplotype configurations with r recombinants. We denote Hmin as the space of all possible minimum-recombinant haplotype configurations (MRHCs). Tapadar et al. (2000) proposed a minimum-recombinant haplotyping (MRH) algorithm that is based on certain evolutionary principles, to reconstruct at least one MRHC in each run, but their method seems difficult to extend to the handling of missing genotypes and is not expected to find all MRHCs in limited computations. We have successfully utilized the MRHCs reconstructed by their evolution-based algorithm in several haplotype-based analyses (Qian and Thomas 2001), although the rationale for and pitfalls of ignoring haplotype configurations in the space H-Hmin require further investigation. Wijsman (1987) proposed a 20-rule algorithm, and O'Connell (2000) described a genotype-elimination algorithm; both can be used for the reconstruction of zero-recombinant haplotypes in large pedigrees. These two methods are designed to reconstruct haplotypes without recombinants and can be used to analyze SNP data in a region that is small enough that the expected number of recombinants in the pedigree is very close to 0. Likelihood-based haplotyping methods are often flexible enough to tackle large and complex pedigrees (Sobel et al. 1996; Lin and Speed 1997; Thomas et al. 2000), but the price of this flexibility is complexity and slowness in computation. The present article presents a six-rule MRH algorithm that exhaustively searches all possible MRHCs in large pedigrees with many markers and allows missing genotype data to be imputed from the identical-by-descent (IBD) alleles during the haplotyping process. Haplotyping results of data for a published pedigree (Litt et al. 1994) are compared with those reported in other articles. Results in simulated data sets are compared between our rule-based MRH method and Tapadar's evolution-based MRH method.
Methods
Definitions, Notation, and Assumptions
To describe the haplotyping algorithm, we consider a pedigree of J family members and a set of L linked marker loci, and we define several terms under consideration: A “parent” is a family member with at least one child, a “founder” is a parent without his or her own parent, an “offspring” is a family member with at least one parent, and an “individual” is any family member. An individual is defined as “genotyped” at locus l if the genotype data at locus l either are experimentally derived from the DNA sample or can be determined from the first-degree relatives. A genotyped parent is defined as “informative” if the individual has at least one genotyped offspring. An ungenotyped parent is defined as “informative” if the individual has a genotyped spouse and has transmitted both haplotypes to multiple offspring. An ungenotyped parent is defined as “partially informative” if the individual has a genotyped spouse and has transmitted one haplotype to an offspring. A genotyped offspring is defined as “informative” if the individual has at least one genotyped parent.
Parental source (PS) and grandparental source (GS) are the two types of information identified for the two constituent alleles at each locus in each family member in the haplotyping analysis. “PS” refers to the allele that is paternally or maternally inherited, and “GS” refers to the PS of each parental allele. An individual is haplotyped at locus l if the PS of the two constituent alleles at locus l has been assigned.
For a nuclear family or a parent-offspring trio, with both parents (j=1,2) and N offspring (j=3,…,N+2) at locus l, we use the following definitions:
al,bl denote the two constituent alleles of parent 1;
cl,dl denote the two constituent alleles of parent 2;
ej,l,fj,l denote the two constituent alleles of offspring j;
Al,Bl denote the paternal and maternal alleles of parent 1;
Cl,Dl denote the paternal and maternal alleles of parent 2;
Ej,l,Fj,l denote the paternal and maternal alleles of offspring j;
sj,1,l,sj,2,l denote the GS of paternal and maternal alleles of individual j.
For simplicity of presentation, we will drop the subscripts “j” and “l” completely or partially in most of the descriptions below unless such an omission would cause confusion.
We use the following notation to express alleles, genotypes, haplotypes, and their relationships:
amin,amax denote the minimum and the maximum allele values, respectively, in sampled population (typically, amin=1,amax=2 for SNP alleles, and amin=1,amax⩾10 for highly polymorphic microsatellite alleles);
(ab) denotes PS-unknown genotype with alleles a and b;
AB denotes PS-known haplotype with paternal allele A and maternal allele B;
(ab)=(cd) denotes that genotypes (ab) and (cd) are equal—that is, (a=c, b=d) or (a=d, b=c);
(ab)≠(cd) denotes that genotypes (ab) and (cd) are not equal—that is, (a≠c or b≠d) and (a≠d or b≠c);
c∈(ab) denotes that allele c is a constituent allele of genotype (ab)—that is, c=a, or c=b;
c∉(ab) denotes that allele c is not a constituent allele of genotype (ab)—that is, c≠a, and c≠b.
We define three types of flexible locus that require a different treatment in the haplotyping process: First, if genotypes at locus l in a parent-offspring trio are identical heterozygotes—that is, a≠b, c≠d, e≠f, and (ab)=(cd)=(ef)—and if at least one parent and the offspring have not been haplotyped at locus l, then locus l is considered as a flexible locus in each of these unhaplotyped individuals. Second, if two alternative haplotype assignments at locus l in a founder result in equal number of recombinants in offspring, then locus l is considered as a flexible locus of the founder. Third, if two alternative haplotype assignments at locus l in an offspring result in equal number of recombinants, then locus l is considered as a flexible locus of the offspring.
Our haplotyping algorithm required data on pedigree structure (i.e., the parentage of each offspring), marker order, and genotype in family members. Missing alleles are imputed from their IBD copies whenever possible. Between-marker distances, locus-specific allele frequencies, and the assumption of Hardy-Weinberg equilibrium on genotype frequencies are not required. We have made four basic assumptions in our haplotyping approach: first, only informative and partially informative individuals are included in analysis; second, marker orders are known; third, genotypes in all family members are consistent with Mendelian inheritance; and, fourth, all family members are related as stated (i.e., there was no incorrect parentage, adoption, or mistake in DNA samples).
Rules
A pedigree of any size is haplotyped by the sequential and repeated application of each rule to each nuclear family or parent-offspring trio until all individuals are haplotyped at all loci or until no individual can be further haplotyped at any locus. Each rule makes some inference about missing genotype, PS, and GS at a marker locus in parents and/or offspring within a pedigree. Without loss of generality, we describe the rules by assuming that the haplotyping process is started at locus 1 and is ended at locus L.
Rule 1. Impute a missing genotype at each unambiguous locus in each parent, conditional on genotypes in spouse and offspring in each parent-offspring trio.—Rule 1 is applied before any other rules in each parent-offspring trio at each locus with genotype data missing in one parent and known in the other parent and the offspring, and it can be subdivided into 16 imputation strategies that are based on the Mendelian law of inheritance (table 1). These strategies are used to impute the missing allele(s) in a parent (i.e., alleles a and/or b in parent) conditional on available alleles in trio members (i.e., alleles c–f in a spouse and an offspring). We note that an unknown allele in a missing genotype is imputable only if the allele has been inherited by at least one offspring. In other words, for a missing genotype with two unknown alleles in a parent, there is a 100% probability for the imputation of one allele if the parent has at least one genotyped offspring, and there is a 50% or 75% probability for the imputation of both alleles if the parent has two or three genotyped offspring.
Table 1.
Strategies for Imputation of a Missing Genotype at an Unambiguous Locus in a Parent, Conditional on Genotypes in Spouse and Offspring, in a Parent-Offspring Trio
| Conditionsa | AlleleImputation |
| c=d, e=f: | |
| a Missing, b ≠ e | a=e |
| b Missing, a≠e | b=e |
| c=d, e≠f: | |
| e=c, a Missing, b≠f | a=f |
| e=c, b Missing, a≠f | b=f |
| f=c, a Missing, b≠e | a=e |
| f=c, b Missing, a≠e | b=e |
| c≠d, e=f: | |
| a Missing, b≠e | a=e |
| b Missing, a≠e | b=e |
| c≠d, e≠f, (cd)≠(ef): | |
| e∈(cd), a Missing, b≠f | a=f |
| e∈(cd), b Missing, a≠f | b=f |
| f∈(cd), a Missing, b≠e | a=e |
| f∈(cd), b Missing, a≠e | b=e |
| e Missing, f≠c, f≠d: | |
| a Missing, b≠f | a=f |
| b Missing, a≠f | b=f |
| f Missing, e≠c, e≠d: | |
| a Missing, b≠e | a=e |
| b Missing, a≠e | b=e |
The conditions of allele imputation in a parent are the conditions on genotypes in spouse and offspring and the conditions on alleles in parent-offspring trio members.
Rule 2. Assign a haplotype at each unambiguous locus in each offspring, conditional on genotypes in parents in each parent-offspring trio.—Rule 2 is applied to each parent-offspring trio at each locus when the offspring has not been fully haplotyped at all the loci, and it can be subdivided into 30 haplotyping strategies that are based on the Mendelian law of inheritance (table 2). Paternal and maternal PSs both are inferred by 22 of these strategies and only one parental PS is inferred by the remaining 8 strategies. Once an individual has been haplotyped at locus l, we determine his or her own GS, and we update the GS in all corresponding offspring (if any), by 12 strategies conditional on parental haplotypes at locus l, on own GS at previous locus l-1, and on the criterion of minimum recombinants (table 3). For example, the first strategy in table 3 indicates that, if the father is homozygous and is haplotyped at locus l (i.e., A=B) and if his offspring has an unknown paternal GS at previous locus l-1 (i.e., s1,(l-1)=-1), then a flexible paternal GS is assigned to the offspring at locus l (i.e., s1,l=0).
Table 2.
Strategies for Haplotype Assignment at an Unambiguous Locus in Offspring, Conditional on Genotypes in Parents, in a Parent-Offspring Trio
| Conditionsa | Haplotype Assignment |
| a=b, c=d: | |
| e=a, f=c | E=e, F=f |
| e=c, f=a | E=f, F=e |
| a=b, c≠d: | |
| e=a, f∈(cd) | E=e, F=f |
| f=a, e∈(cd) | E=f, F=e |
| a≠b, c=d: | |
| f∈(ab), e=c | E=f, F=e |
| e∈(ab), f=c | E=e, F=f |
| a≠b, c≠d, not (ab)=(cd)=(ef): | |
| e∈(ab), f∈(cd) | E=e, F=f |
| f∈(ab), e∈(cd) | E=f, F=e |
| a And/or b missing: | |
| e=f | E=F=e |
| e≠f, e∉(cd) | E=e, F=f |
| e≠f, f∉(cd) | E=f, F=e |
| c Missing and/or d missing: | |
| e=f | E=F=e |
| e≠f, e∉(ab) | E=f, F=e |
| e≠f, f∉(ab) | E=e, F=f |
| e Missing, a=b, c=d: | |
| f=a | E=f, F=c |
| f=c | E=a, F=f |
| e Missing, a=b, c≠d: | |
| f=a | E=f |
| f≠a, f∈(cd) | E=a, F=f |
| e Missing, a≠b, c=d: | |
| f=c | F=f |
| f∈(ab), f≠c | E=f, F=c |
| e Missing, a≠b, c≠d: | |
| f∈(ab), f∉(cd) | E=f |
| f∉(ab), f∈(cd) | F=f |
| f Missing, a=b, c=d: | |
| e=a | E=e, F=c |
| e=c | E=a, F=e |
| f Missing, a=b, c≠d: | |
| e=a | E=e |
| e≠a, e∈(cd) | E=a, F=e |
| f Missing, a≠b, c=d: | |
| e=c | F=e |
| e∈(ab), e≠c | E=e, F=c |
| f Missing, a≠b, c≠d: | |
| e∈(ab), e∉(cd) | E=e |
| e∉(ab), e∈(cd) | F=e |
The conditions of haplotype assignment in offspring are the conditions on genotypes in both parents and the conditions on alleles in parent-offspring trio members.
Table 3.
Strategies for GS Assignments in Haplotyped Offspring, Conditional on Parental Haplotypes and Own GS at a Previous Locus, in a Parent-Offspring Trio
| Conditionsa | GS Assignment |
| A=B: | |
| s1,l-1=-1 | s1,l=0 |
| s1,l-1⩾0 | s1,l=s1,l-1 |
| A≠B: | |
| E=A | s1,l=1 |
| E=B | s1,l=2 |
| C=D: | |
| s2,l-1=-1 | s2,l=0 |
| s2,l-1⩾0 | s2,l=s2,l-1 |
| C≠D: | |
| F=C | s2,l=1 |
| F=D | s2,l=2 |
| A≠B, C≠D, not AB=CD=EF: | |
| E=A, F=C | s1,l=1, s2,l=1 |
| E=A, F=D | s1,l=1, s2,l=2 |
| E=B, F=C | s1,l=2, s2,l=1 |
| E=B, F=D | s1,l=2, s2,l=2 |
The conditions of GS assignment in haplotyped offspring are the conditions on parental haplotypes at current locus l, on own haplotypes at locus l, and on own GS at previous locus l-1 in a parent-offspring trio. s=-1 represents GS unknown; s=0 indicates that the GS assignment to either grandfather or grandmother is consistent with Mendelian inheritance but that the assignment cannot be made under the criterion of minimum recombinants; s=1 represents parental allele from grandfather, and s=2 represents parental allele from grandmother. For starting locus l=1, apply the strategies corresponding to conditions of s1,0=-1 and s2,0=-1.
Rule 3. Assign haplotypes at each unambiguous locus in each founder, conditional on haplotypes in offspring and the criterion of minimum recombinants in each nuclear family.—The haplotype assignment in a founder with genotype (ab) at locus l is based on the two alternative assignment—that is, (A=a, B=b) or (A=b, B=a)—that will result in fewer recombinants in all offspring within the nuclear family. The strategies of such assignment are different under four different conditions. First, if a=b, then A=B=a is the easiest case. Second, if a≠b and no heterozygous locus has been haplotyped at previous loci (i.e., at loci 1 to l – 1), then the haplotype assignment is arbitrary and could be conventionally assigned as A=min(a,b), B=max(a,b). Third, if a≠b and if at least one heterozygous locus has been haplotyped at previous loci and the founder is flexible at locus l, then no action is taken under rule 3. Forth, if a≠b and if at least one heterozygous locus has been haplotyped at previous loci and the founder is not flexible at locus l, then the haplotype assignment depends on which of the two alternative assignments gives fewer recombinants in offspring. To do this, we count the recombination sites under each of the two alternative assignments at immediate left and right marker intervals in all offspring within the nuclear family. If recombinants are equal under the two assignments or incalculable under at least one assignment, then no action is taken under rule 3, otherwise the one with fewer recombinants is accepted.
Rule 4. Assign haplotypes at each unambiguous locus in each offspring, conditional on haplotypes in parents and the criterion of minimum recombinants in each parent-offspring trio.—The haplotype assignment in an offspring with genotype (ef) at locus l is based on whether assignment (E=e, F=f) or (E=f, F=e) gives fewer recombinants at immediate left and right marker intervals in the offspring. If recombinants are equal under the two assignments or incalculable under at least one assignment, then no action is taken under rule 4, otherwise the assignment with fewer recombinants is accepted.
Rule 5. Impute a missing genotype at each unambiguous locus in each parent, conditional on haplotypes in offspring and the criterion of minimum recombinants in each nuclear family.—Rule 5 is a tool for the imputation of missing genotypes that are unable to be imputed unambiguously by rule 1. The typical situation is that several candidate alleles are consistent with Mendelian inheritance, but one allele may give fewer recombinants than all the others when the haplotypes in offspring have already been assigned. Specifically, a missing allele in a parental genotype is imputed as follows. First, each allele value from amin to amax is checked and only those showing Mendelian consistency are retained as candidate alleles for the missing genotype. Second, each candidate genotype (a′b′) with the missing allele(s) replaced by its corresponding candidate allele is evaluated and the number of recombinants at the two flanking marker intervals in all offspring within the nuclear family is recorded as n1 under the assignment (A=a′, B=b′) and n2 under the assignment (A=b′, B=a′). The number of recombinants under candidate genotype (a′b′) is defined as min(n1,n2). Third, if the number of recombinants under some candidate genotype is not calculable or at least two candidate genotypes have the same minimum recombinants, then no action is taken under rule 5, otherwise the allele corresponding to the fewest recombinants is accepted.
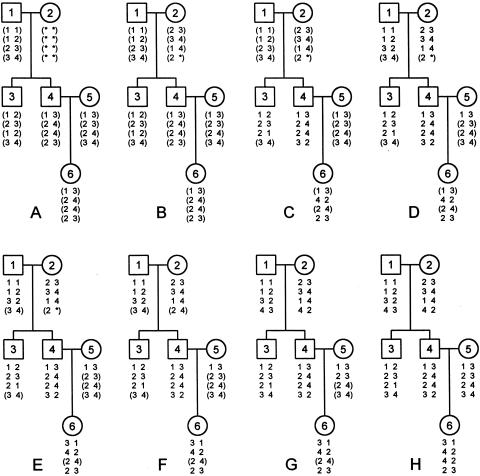
To illustrate rules 1–5, we consider a three-generation pedigree with genotypes at four markers in five genotyped individuals (1 and 3–6) and one completely ungenotyped founder individual (2) (fig. 1A). All six individuals should be included in haplotyping analysis, because individuals 1 and 3–6 are informative and because individual 2 is at least partially informative. By the application of rule 1 to parent-offspring trios {1,2,3} and {1,2,4}, seven of eight missing alleles in individual 2 are unambiguously imputable (fig. 1B). When rule 2 is applied to trios {1,2,3}, {1,2,4}, and {4,5,6}, haplotype assignments can be made unambiguously at three loci in offspring 3, all four loci in offspring 4, and two loci in offspring 6 (fig. 1C). GS can also be identified at the two haplotyped loci in offspring 6 by the strategies given in table 3 (results not shown). When rule 3 is applied to nuclear families {1,2,3,4} and {4,5,6}, haplotype assignments can be made unambiguously at three loci in founders 1 and 2 and one locus in founder 5 (fig. 1D), and GS can be determined at 14 of the 18 PS-known alleles in offspring 3, 4, and 6 (results not shown). When rule 4 is applied to the three parent-offspring trios, haplotype assignment and GS can be made at locus 1 in offspring 6 (fig. 1E). When rule 5 is applied to nuclear family {1,2,3,4} with missing genotype (2 *) in parent 2, the two candidate-allele values are 3 and 4 for the unknown allele *. Since the number of recombinants is 1 under candidate genotype (2 3) and 0 under candidate genotype (2 4), the missing allele 4 is accepted (fig. 1F). When rules 2 and 3 are reapplied, only two loci in individual 5 and one locus in individual 6 are unable to be haplotyped unambiguously (fig. 1G). The third locus, with genotype (2 4), is considered as a flexible locus in individuals 5 and 6.
Figure 1.
Step-by-step haplotyping results in a three-generation pedigree with five genotyped individuals and one completely ungenotyped individual. A, Genotype data. B, Results after application of rule 1. C, Results after application of rule 2. D, Results after application of rule 3. E, Results after application of rule 4. F, Results after application of rule 5. G, Results after second application of rules 2 and 3. H, One MRHC with zero recombinants found after application of rule 6 and reapplication of rule 3. This is the only MRHC in the space Hmin=H0. Haplotypes are displayed as paternal on the left and maternal on the right.
Rule 6. Locate a locus with at least one individual in a nuclear family that is flexible at this locus, enumerate the haplotype configuration into multiple configurations with one of two alternative haplotype assignments in each of the flexible loci in these individuals, and retain all configurations with the minimum recombinants.—After the repeated application of rules 1–5 in a pedigree until no further changes can be made to either the genotype or the haplotype in any individual, the haplotypes in each individual are either completely haplotyped at all loci or haplotyped at one or more locus until the first occurrence of a flexible locus. The choices between two alternative haplotype assignments at a flexible locus cannot be made directly by the number of recombinants in offspring at the immediate left and right marker intervals, because one assignment may give fewer recombinants at closer marker intervals and may also give more recombinants at distant marker intervals. Exhaustive enumeration of a haplotype configuration at all flexible loci in all individuals simultaneously is infeasible when the family size and/or the number of markers are large. We propose rule 6 to enumerate haplotype configurations sequentially at each locus within each nuclear family. Applying rule 6 and then rule 3 to the three-generation haplotype configuration in figure 1G, we obtained one MRHC with zero recombinants (fig. 1H).
The proposed rule-based MRH algorithm for haplotyping in pedigrees is an iterative scheme, which can be summarized in several steps. In the first step, rules 1–5 are applied sequentially and repeatedly until no changes can be made to the haplotype configuration under consideration. In the second step, rule 6 is used to enumerate each haplotype configuration at the flexible loci corresponding to a single locus in individuals within a nuclear family, rules 1–5 are then applied until no changes can be made to each enumerated configuration, and configurations showing minimum recombinants are retained for further analysis. In the third step, we examine whether all individuals are haplotyped at all loci or no further changes can be made to each haplotype configuration. If so, we consider that we have obtained all the MRHCs and stop the haplotyping analysis; otherwise, we repeat steps 2 and 3. In current implementation, the haplotyping analysis is performed in a predefined order, in which rules 1–5 are applied in numerical sequence in each haplotyping iteration and the nuclear families in an extended pedigree are analyzed from the eldest generation to the youngest generation. We note that the haplotyping analysis should be performed in both directions—that is, from locus 1 to locus L and from locus L to locus 1—because the results obtained from rules 2–6 may depend on the direction of the analysis.
Results
A Pedigree with Episodic Ataxia (EA)
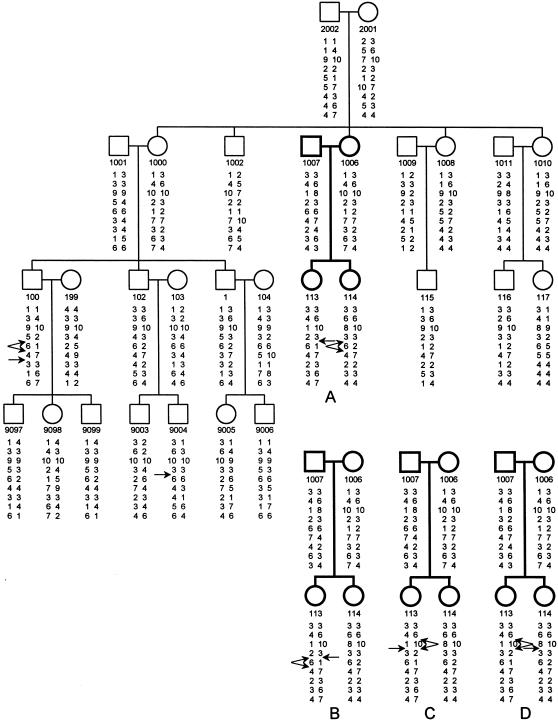
To test our haplotyping algorithm, we analyzed data for a published pedigree from a study of EA by Litt et al. (1994) and compared our results with those reported in other articles. This pedigree, as shown in figure 2, contains 27 individuals genotyped at 9 polymorphic markers on chromosome 12 and 2 individuals 2001 and 1011 completely ungenotyped. The marker names with respect to their linear order are D12S91, D12S100, CACNL1A1, D12S372, pY2/1, pY21/1, KCNA5, D12S99, and S12S93. It is obvious that the 27 genotyped individuals are informative individuals and that the 2 ungenotyped individuals are at least partially informative individuals, and all 29 individuals should be included in haplotyping analysis. The missing genotypes in the 2 ungenotyped individuals and the haplotypes in 22 individuals can be unambiguously identified by the repeated application of rules 1–5 under the criterion of minimum recombinants (results not shown). A total of 11 flexible loci are found in seven individuals: flexible loci 4 and 8 in individuals 1007 and 113, locus 4 in individuals 1009 and 115, loci 4 and 9 in individuals 103 and 9003, and locus 9 in individual 9004. By the application of rule 6 to these flexible loci and the repeat application, after each enumeration, of rules 2–4, four distinct MRHCs, A–D, are found in the space Hmin=H5 (fig. 2).
Figure 2.
Four MRHCs, A–D, in the space Hmin=H5 reconstructed from the pedigree with EA with 27 genotyped individuals and 2 ungenotyped individuals (i.e., individuals 2001 and 1011) (Litt et al. 1994). One nuclear family (i.e., individuals 1007, 1006, 113, and 114, shown by bold symbols) has four distinct haplotype configurations, A–D, and all the other family members belong to a single haplotype configuration. Paternal haplotypes are given on the left, and maternal haplotypes are given on the right. A single arrow indicates a recombination event between two loci. A double arrow originating from a locus indicates a recombinant at either of the two marker intervals but not both.
Since the locations of the nine markers were estimated by the recombination fractions as 0, 0.01, 0.02, 0.05, 0.06, 0.08, 0.09, 0.10, and 0.11 (Dausset et al. 1990; Litt et al. 1994), the relative probabilities of the four MRHCs—A, B, C, and D—can be estimated as .10, .10, .40, and .40, respectively, in the haplotype space H5. In contrast, Litt et al. (1994) found an optimal configuration with 10 recombinants by use of data on 25 individuals. Sobel et al. (1996) analyzed the pedigree data in figure 2 by using a random-walk algorithm via simulated annealing and found that configuration B was the one with maximum likelihood in the whole haplotype space H. Lin and Speed (1997) analyzed the same pedigree data by using a Gibbs-Jump algorithm and concluded that configurations C and B, with probabilities .41 and .09, respectively, were the two most probable ones in the space H and that any other configuration had a probability of <.03. The haplotype configurations reported in these articles were either not optimal or incomplete as compared to the four MRHCs that we found in the haplotype space Hmin=H5.
A Simulation Study
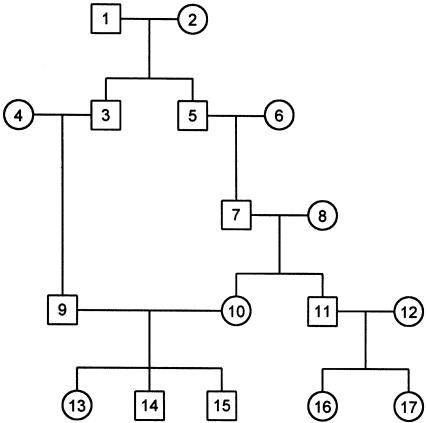
A total of 11 data sets were generated for the evaluation of haplotyping performance, and 100 pedigrees in each data set were simulated under a fixed pedigree structure of J family members and a set of L linked marker loci. Each pedigree in data sets 1–3, 7, and 9 contains 15 individuals, shown in figure 2 (i.e., the three-generation pedigree consisting of individuals 1001 and 1000 and all their descendants on the left side of the pedigree). Each pedigree in data sets 4–6, 8, and 10 contains 29 individuals in a same structure as in figure 2. Each pedigree in data set 11 contains 17 individuals in a looped marriage structure, shown in figure 3. The simulated chromosome segments in data sets 1 and 4 contain 10 microsatellite markers; those in data sets 2 and 5 contain 25 microsatellite markers; those in data sets 3 and 6 contain 50 microsatellite markers; and those in data sets 7–11 contain 10 diallelic markers. Microsatellite markers were generated by a 10-allele random-density function and diallelic markers were generated by a diallelic random-density function. A constant number of R=4 recombinants were randomly generated in nonfounder family members in each pedigree in data sets 1–8, and R=0 recombinants was generated in each pedigree in data sets 9–11.
Figure 3.
A looped marriage structure in a pedigree with ataxia telangiectasia that is composed of 17 individuals (Lange and Matthysse 1989).
Both the rule-based MRH method presented in the present article and the evolution-based MRH method proposed by Tapadar et al. (2000) were able to recover most of the true haplotype configurations in the 1,100 simulated pedigrees analyzed (table 4). For the rule-based method, the reconstructed MRHCs had fewer than R simulated recombinants in 73 (7%) pedigrees and the same R recombinants with true configuration recovered in the remaining 1,027 (93%) pedigrees. For the evolution-based method, the reconstructed MRHCs had fewer than R simulated recombinants in 73 (7%) pedigrees, R recombinants and true configuration recovered in 994 (90%) pedigrees, R recombinants and true configuration not recovered in 22 (2%) pedigrees, and more than R recombinants in 11 (1%) pedigrees. The MRHCs reconstructed by the two methods were identical in most pedigrees, and similar mean ± SD values were observed for the number of distinct MRHCs and the number of recombinants in reconstructed MRHCs (table 5). The rule-based method found more distinct MRHCs in 63 (6%) pedigrees and fewer MRHCs in 0 pedigrees, as compared to the configurations that were obtained from the evolution-based method. The mean ± SD computational time was approximately on the order of O(J2L3) in the rule-based method and was shorter than the evolution-based method in haplotyping each of the 11 simulated data sets. The mean ± SD haplotyping time for diallelic-marker data was ∼3–10 times longer than what was needed for microsatellite-marker data in the rule-based method due to a larger number of enumerations performed in less-polymorphic data. However, the extra computational time for diallelic-marker data was not observed in the evolution-based method. The simulation results in data set 11 indicated that the ability to reconstruct true simulated haplotypes was similar in pedigrees with and without marriage loops by the both methods, although extra computational time was observed in the haplotyping of pedigrees with marriage loops. We note that the haplotyping performance of the evolution-based method was based on our implementation of the algorithm proposed by Tapadar et al. (2000), which may differ slightly from their original implementation.
Table 4.
A Comparison of True Haplotype Configurations Recovered in Reconstructed MRHCs by the Rule-Based and Evolution-Based MRH Methods in Simulated Data Sets
| Data Set (J, L, R, T)a | Recoveredby Bothb | Rule-BasedAlonec | FewerRecombinantsd |
| 1 (15, 10, 4, micro) | 90 | 2 | 8 |
| 2 (15, 25, 4, micro) | 94 | 0 | 6 |
| 3 (15, 50, 4, micro) | 91 | 7 | 2 |
| 4 (29, 10, 4, micro) | 86 | 1 | 13 |
| 5 (29, 25, 4, micro) | 91 | 1 | 8 |
| 6 (29, 50, 4, micro) | 89 | 0 | 11 |
| 7 (15, 10, 4, SNP) | 82 | 9 | 9 |
| 8 (29, 10, 4, SNP) | 76 | 8 | 16 |
| 9 (15, 10, 0, SNP) | 100 | 0 | 0 |
| 10 (29, 10, 0, SNP) | 97 | 3 | 0 |
| 11 (17, 10, 0, loop) | 98 |
2 |
0 |
| Total | 994 | 33 | 73 |
Each data set contains 100 simulated pedigrees of a fixed structure with parameters (J, L, R, T), where J is the family size, L is the number of marker loci, R is the true simulated number of recombinants within each pedigree, and T is an abbreviation of marker type and pedigree structure (i.e., “micro” and “SNP” for microsatellites and SNPs without a looped structure, respectively, and “loop” for SNPs with looped structure).
Number of pedigrees when the true configuration was recovered in reconstructed ones by both methods.
Number of pedigrees when the true configuration was recovered by the rule-based method and not recovered by the evolution-based method.
Number of pedigrees when MRHC had fewer than the true simulated number of recombinants by both methods.
Table 5.
Haplotyping Performance in 11 Simulated Data Sets[Note]
|
Mean ± SD (Range) |
|||
| Method and Data (J, L, R, T) | No. of Distinct MRHCs | No. of Recombinants | Computational Time |
| Rule-Based MRH: | |||
| 1 (15, 10, 4, micro) | 2.03 ± 1.22 (1–8) | 3.91 ± .32 (2–4) | .4 ± .7 (0–4) |
| 2 (15, 25, 4, micro) | 2.08 ± 1.19 (1–8) | 3.93 ± .29 (2–4) | 4.8 ± 6.1 (0–43) |
| 3 (15, 50, 4, micro) | 1.78 ± .89 (1–4) | 3.98 ± .14 (3–4) | 44.0 ± 46.2 (3–263) |
| 4 (29, 10, 4, micro) | 2.44 ± 3.38 (1–32) | 3.86 ± .38 (2–4) | 1.5 ± 2.2 (0–14) |
| 5 (29, 25, 4, micro) | 2.07 ± 1.20 (1–8) | 3.92 ± .27 (3–4) | 25.6 ± 39.4 (3–219) |
| 6 (29, 50, 4, micro) | 1.93 ± 1.30 (1–8) | 3.88 ± .36 (2–4) | 216.9 ± 226.8 (13–985) |
| 7 (15, 10, 4, SNP) | 3.01 ± 2.35 (1–16) | 3.91 ± .29 (3–4) | 1.4 ± 1.1 (0–7) |
| 8 (29, 10, 4, SNP) | 2.76 ± 2.59 (1–20) | 3.82 ± .44 (2–4) | 13.0 ± 41.9 (1–423) |
| 9 (15, 10, 0, SNP) | 1.01 ± .10 (1–2) | .00 ± .00 (0–0) | .8 ± 1.5 (0–12) |
| 10 (29, 10, 0, SNP) | 1.05 ± .22 (1–2) | .00 ± .00 (0–0) | 8.4 ± 20.7 (0–183) |
| 11 (17, 10, 0, loop) | 1.01 ± .10 (1–2) | .00 ± .00 (0–0) | 2.8 ± 7.6 (0–69) |
| Evolution-based MRH: | |||
| 1 (15, 10, 4, micro) | 1.94 ± 1.06 (1–6) | 3.91 ± .32 (2–4) | 4.4 ± .9 (2–7) |
| 2 (15, 25, 4, micro) | 1.98 ± .99 (1–4) | 3.93 ± .29 (2–4) | 19.1 ± 2.3 (13–26) |
| 3 (15, 50, 4, micro) | 1.77 ± .93 (1–6) | 4.54 ± 2.76 (3–18) | 56.6 ± 4.4 (48–68) |
| 4 (29, 10, 4, micro) | 2.23 ± 1.99 (1–16) | 3.86 ± .38 (2–4) | 45.6 ± 5.8 (34–65) |
| 5 (29, 25, 4, micro) | 2.07 ± 1.20 (1–7) | 3.92 ± .27 (3–4) | 222.4 ± 27.0 (170–305) |
| 6 (29, 50, 4, micro) | 1.91 ± 1.27 (1–8) | 3.88 ± .36 (2–4) | 666.1 ± 68.5 (545–811) |
| 7 (15, 10, 4, SNP) | 2.56 ± 1.68 (1–10) | 3.96 ± .42 (3–6) | 3.8 ± 1.6 (1–12) |
| 8 (29, 10, 4, SNP) | 2.53 ± 1.65 (1–9) | 3.83 ± .46 (2–5) | 49.5 ± 89.4 (24–893) |
| 9 (15, 10, 0, SNP) | 1.01 ± .10 (1–2) | .00 ± .00 (0–0) | 1.8 ± .6 (1–4) |
| 10 (29, 10, 0, SNP) | 1.03 ± .17 (1–2) | .02 ± .20 (0–2) | 22.3 ± 8.3 (11–92) |
| 11 (17, 10, 0, loop) | 1.00 ± .00 (1–1) | .04 ± .28 (0–2) | 3.6 ± .8 (2–6) |
Note.— Each data set contains 100 pedigrees. See footnote a of table 4 for a description of parameters (J, L, R, T). Computational time (in s) is calculated on a Unix computer running Sun operating system, version 5.8, with 12.3 Gb memory.
Haplotyping analyses in the 500 pedigrees of family size 15 (i.e., the pedigrees in simulated data sets 1–3, 7, and 9) were also analyzed by GENEHUNTER 2.0 software (Kruglyak et al. 1996; Kruglyak and Lander 1998). The maximum-likelihood haplotype configuration obtained from GENEHUNTER was identical to one of the MRHCs found by our rule-based MRH method in >99% pedigrees analyzed. A comparison of computational time between the method implemented in GENEHUNTER and our rule-based MRH method is not meaningful due to the different assumptions and input data required by the two methods.
Genotype Errors and Incorrect Marker Order
The genotype data of the pedigree with EA shown in figure 2 were used to generate artificial data sets to evaluate the impact of genotype errors and incorrect marker order on haplotyping. To evaluate the impact of genotype errors, we generated genotype data on 1,000 pedigrees with pedigree structure and genotype data identical to that of the real pedigree with EA, except that each pedigree contained one incorrect allele in a random individual at a random marker that was still consistent with Mendelian inheritance. The mean number of recombinants in reconstructed MRHCs was increased from 5 to 6.2±1.2, and 44% of these additional recombinants were double recombinants. For illustrative purposes, the four five-recombinant MRHCs, for the correct genotypes and correct marker order in figure 2, are hereafter referred to as the correct MRHCs. All four correct MRHCs were recovered in the reconstructed MRHCs in 844 (84%) pedigrees, and at least one correct MRHC was recovered in 871 (87%) pedigrees (table 6).
Table 6.
Impact of Genotype Errors and Incorrect Marker Orders in Haplotyping Analysis
|
Mean ± SD (Range) |
|||
| Data Seta | No. of Pedigrees/Total(Frequency) with One or MoreCorrect MRHC Recovereda | No. of Recombinantsb | No. of CorrectMRHCs Recoveredc |
| Genotype error | 871/1,000 (87%) | 6.2 ± 1.2 (5–11) | 3.4 ± 1.4 (0–4) |
| Loci in wrong order: | |||
| 2 | 9/15 (60%) | 6.9 ± 1.9 (5–10) | 1.6 ± 1.5 (0–4) |
| 3 | 15/40 (38%) | 7.8 ± 1.5 (5–10) | .9 ± 1.2 (0–4) |
| 4 | 30/135 (22%) | 8.1 ± 1.4 (5–11) | .4 ± .8 (0–2) |
| 5 | 31/264 (12%) | 8.3 ± 1.3 (5–11) | .2 ± .7 (0–4) |
| 6 | 20/265 (8%) |
8.3 ± 1.3 (5–11) | .2 ± .6 (0–4) |
| Total | 105/719 (15%) | 8.2 ± 1.4 (5–11) | .3 ± .8 (0–4) |
See text for description of the method used to generate the genotype data in 1,000 pedigrees with genotype errors and in 719 pedigrees with markers incorrectly ordered. At least one of the four correct MRHCs was recovered in the reconstructed MRHCs. (For illustrative purposes, the four MRHCs in figure 2 are referred to as the “correct MRHCs” here and in footnote c.)
In reconstructed MRHCs.
In reconstructed MRHCs. For pedigree with genotype error, a correct MRHC was recovered if the haplotypes in all 29 individuals occurred in a reconstructed MRHC, except at the marker with genotype error in the specific individual.
To test the consequence of incorrect marker order, genotype data on 6!-1=719 pedigrees were generated using the same genotypes as the pedigree with EA and all permutational marker orders at loci 2–7. The number of recombinants in the reconstructed MRHCs increased as the number of marker loci incorrectly ordered increased. Among the 719 different orders analyzed, none of the orderings produced MRHCs with fewer than five recombinants, and only 35 (5%) orderings had the same number of recombinants as the correct ordering. The chances of recovering at least one and all four correct MRHCs, respectively, were 60% and 20% when two marker loci were incorrectly ordered and decreased to 8% and 0% when six marker loci were incorrectly ordered (table 6).
Discussion
The computational requirement of our rule-based MRH method does not increase exponentially with the family size J or the number of marker loci L. The computations in our method come from three sources: (1) the enumeration at flexible loci, (2) the haplotype assignment at unambiguous loci after each enumeration, and (3) the backup of haplotype configurations during the analysis. The number of enumeration to each individual by the repeated application of rule 6 is proportional to the number of marker loci L with an upper bound of 2n at each locus, where n is the size of the corresponding nuclear family and does not depend on the size of the extended pedigree under analysis. With this observation, the computational requirement due to enumeration in an extended pedigree with J family members and L marker loci is on the order of O(JL). After each enumeration, haplotype assignments to unambiguous loci are scanned at all L marker loci by the repeated application of rules 1–5 within a corresponding nuclear family, resulting in a haplotyping computation on the order of O(L). For each enumeration and/or haplotype assignment, a backup of current haplotype configuration in all family members is generated to avoid the loss of the current configuration when the new ones are not acceptable, and it has resulted in a backup computation on the order of O(JL). Therefore, the total computational requirement in current implementation is approximately on the order of O(J2L3). We note that the total computational requirement may be reduced to the order of O(JL2) by more-efficient programming. Specifically, the computational requirement for haplotyping after each enumeration may be reduced to O(1) by the restriction of the haplotype assignment between the two closest flexible loci, and the computation for backup may be reduced to O(L) by the restriction of the backup to family members corresponding to a nuclear family under analysis. We believe that a trade-off between programming clarity and computational performance is of little importance to our algorithm, because the current implementation is running fast enough in pedigrees of reasonable family size with a reasonable number of marker loci.
Both genotype errors and incorrect marker order can produce additional recombinants in reconstructed haplotype configurations and can reduce the ability to recover the true haplotype configuration. The chance of the recovery of the true haplotype configuration was >80% when there was only one genotype error per extended pedigree, and the additional recombinants caused by genotype errors were often (44% in our analysis) double recombinants. Such events can often be identified by the inspection of the pedigrees; Douglas et al. (2000) have provided a discussion on methods for the detection of genotype errors and mutations and have described a hidden Markov approach for use with sibling-pair data. The ability to recover true haplotype configurations was much lower even when two markers were incorrectly ordered. These sensitivity analyses suggest that incorrect marker orderings may have a larger adverse impact than do a small fraction of genotype errors in the haplotype reconstruction in extended pedigrees. Since the number of recombinants under the correct marker order often equals the minimum number of recombinants under all possible permutations of the markers and since the minimum number of recombinants occurs only in a very small fraction of orders, the reconstructed MRHCs may provide useful information for the determination of the correct marker order.
The reconstructed MRHCs can also be used to estimate the IBD status between family members. An interesting phenomenon is that the IBD status estimated from each reconstructed MRHC at each marker locus for each relative pair is almost always identical to the IBD status estimated from the true simulated haplotypes in the simulated data sets we analyzed in the present article. This is true even when the reconstructed haplotypes in some individuals may look quite different in multiple MRHCs. For example, the IBD statuses estimated from MRHCs and true haplotypes were identical in 99.95% relative pairs in pedigrees with 15 individuals and 10 markers and were identical in >99.99% relative pairs in pedigrees with 15 individuals and 50 markers. These results indicate that the IBD statuses estimated by MRHCs may be comparable to or more accurate than those estimated by other methods and therefore could be valuable to linkage analysis.
The rule-based MRH method minimizes the number of recombinants within each nuclear family and retains the haplotype configurations with minimum recombinants for the entire pedigree. Likelihood-based methods may be able to assign haplotypes in individuals that are uninformative by our rule-based method due to missing genotypes and/or insufficient first-degree relatives, and these additional haplotypes may still informative in gene-mapping analyses. In practice, we can first use the rule-based method to reconstruct MRHCs in all analyzable individuals and then use a likelihood-based method to assign haplotypes in individuals who are uninformative by the rule-based method. We noticed that most haplotype-based analyses were based on a single set of reconstructed haplotype configurations per pedigree (Beckmann et al. 2001; Qian and Thomas 2001). The availability of multiple MRHCs may provide more information in the obtainment of more-robust estimates in gene-mapping analyses. It is theoretically possible that a reconstructed haplotype configuration with minimum recombinants within each nuclear family, conditional on previous assignments in other nuclear families, may have more than the minimum number of recombinants in an extended pedigree. However, our simulation results indicated that the number of recombinants in MRHCs was always equal to or less than the simulated value for the 1,100 pedigrees we analyzed (table 5). Finding fewer recombinants than the unobserved true number of recombinants is a limitation of MRH methods, whereas our simulation results indicated that the chance of finding fewer recombinants is low (<10%), even in pedigrees with four recombinants. The haplotyping method is applicable to both microsatellite data and diallelic SNP data. The computational requirements for SNP data are usually ∼3–10 times larger than for microsatellite data, because of a higher fraction of flexible loci. The fraction of ambiguous loci during the haplotyping process and its influencing factors require further investigation. Imputation of missing genotypes is performed via genotypes and haplotypes within each nuclear family, conditional on the Mendelian law of inheritance and the criterion of minimum recombinants, but special pedigrees with uninformative individuals as we defined them cannot be handled in the current implementation. For example, a genotyped individual with neither genotyped parents nor genotyped offspring cannot be analyzed by the current algorithm, even if multiple siblings and other relatives are genotyped. Further investigation of additional rules is needed to handle the haplotyping issues in pedigrees not analyzable by the six-rule algorithm in the current implementation. An implementation (MRH, version 0.1) of the haplotyping algorithm described in the present article is available from the Home Page for Dajun Qian.
Acknowledgments
We thank Dr. Duncan Thomas for advice and comments on the manuscript. This work was supported by National Institutes of Health grants CA52862 and GM58897 (to D.Q.), the Helmholtz-Gemeinschaft Strategiefonds from the Federal Ministry of Education and Research of Germany (01SF9903/3), and the German Academic Exchange Service Deutscher Akademischer Austauschdienst (to L.B.).
Electronic-Database Information
The URL for data in this article is as follows:
- Home Page for Dajun Qian, http://www-rcf.usc.edu/~gqian/ (for MRH, version 0.1)
References
- Beckmann L, Fischer C, Deck KG, Nolte IM, te Meerman G, Chang-Claude J (2001) Exploring haplotype sharing methods in general and isolated populations to detect gene(s) of a complex genetic trait. Genet Epidemiol 21 Suppl 1:S554–S559 [DOI] [PubMed] [Google Scholar]
- Dausset J, Cann H, Cohen D, Lathrop M, Lalouel JM, White R (1990) Centre d'Étude du Polymorphisme Humaine (CEPH): collaborative genetic mapping of the human genome. Genomics 6:575–577 [DOI] [PubMed] [Google Scholar]
- Douglas JA, Boehnke M, Gillanders E, Trent JM, Gruber SB (2001) Experimentally-derived haplotypes substantially increase the efficiency of linkage disequilibrium studies. Nat Genet 28:361–364 [DOI] [PubMed] [Google Scholar]
- Douglas JA, Boehnke M, Lange K (2000) A multipoint method for detecting genotyping errors and mutations in sibling-pair linkage data. Am J Hum Genet 66:1287–1297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES (1998) Faster multipoint linkage analysis using Fourier transforms. J Comput Biol 5:1–7 [DOI] [PubMed] [Google Scholar]
- Lange K, Matthysse S (1989) Simulation of pedigree genotypes by random walks. Am J Hum Genet 45:959–970 [PMC free article] [PubMed] [Google Scholar]
- Lin S, Speed TP (1997) An algorithm for haplotype analysis. J Comput Biol 4:535–546 [DOI] [PubMed] [Google Scholar]
- Litt M, Kramer P, Browne D, Gancher S, Brunt ERP, Root D, Phromchotikul T, Dubay CJ, Nutt J (1994) A gene for episodic ataxia/myokymia maps to chromosome 12p13. Am J Hum Genet 55:702–709 [PMC free article] [PubMed] [Google Scholar]
- O'Connell JR (2000) Zero-recombinant haplotyping: applications to fine mapping using SNPs. Genet Epidemiol 19 Suppl 1:S64–S70 [DOI] [PubMed] [Google Scholar]
- Qian D, Thomas DC (2001) Genome scan of complex traits by haplotype sharing correlation. Genet Epidemiol 21 Suppl 1:S582–S587 [DOI] [PubMed] [Google Scholar]
- Sobel E, Lange K, O’Connell JR, Weeks DE (1996) Haplotyping algorithms. In: Speed T, Waterman MS (eds) IMA volumes in mathematics and its applications. Vol 81: Genetic mapping and DNA sequencing. Springer-Verlag, New York, pp 89–110 [Google Scholar]
- Tapadar P, Ghosh S, Majumder PP (2000) Haplotyping in pedigrees via a genetic algorithm. Hum Hered 50:43–56 [DOI] [PubMed] [Google Scholar]
- Thomas A, Gutin A, Abkevich V, Bansal A (2000) Multilocus linkage analysis by blocked Gibbs sampling. Stat Comput 10:259–269 [Google Scholar]
- Wijsman E (1987) A deductive method of haplotype analysis in pedigrees. Am J Hum Genet 41:356–373 [PMC free article] [PubMed] [Google Scholar]