Paternally Transmitted FMR1 Alleles Are Less Stable than Maternally Transmitted Alleles in the Common and Intermediate Size Range

Abstract

Fragile X syndrome, a form of X-linked mental retardation, results from the hyperexpansion of a CGG trinucleotide repeat located in the 5′ untranslated region of the fragile X mental retardation (FMR1) gene. Relatively little is known about the initial mutation that causes a stable allele to become unstable and, eventually, to expand to the full mutation. In the present study, we have examined 1,452 parent-child transmissions of alleles of common (⩽39 repeats) or intermediate (40–59 repeats) sizes to study the initial mutation events. Of these, 201 have been sequenced and haplotyped. Using logistic regression analysis, we found that parental origin of transmission, repeat size (for unsequenced alleles), and number of the 3′ CGGs (for sequenced alleles) were significant risk factors for repeat instability. Interestingly, transmission of the repeat through males was less stable than that through females, at the common- and intermediate-size level. This pattern differs from that seen for premutation-size alleles: paternally transmitted alleles are far more stable than maternally transmitted alleles. This difference that depends on repeat size suggests either a different mutational mechanism of instability or an increase in selection against sperm as their repeat size increases.

Introduction

Little is known about the mutational pathway that leads to dynamic repeat mutation in the trinucleotide-repeat disorders, such as fragile X syndrome (MIM 309550), Huntington disease, the spinocerebellar ataxias, myotonic dystrophy, spinal and bulbar atrophy, dentatorubral-pallidoluysian atrophy, and Friedreich ataxia (for review, see Wells et al. ¹⁹⁹⁸). Fragile X syndrome, a form of X-linked mental retardation, results from the hyperexpansion of a CGG trinucleotide repeat located in the 5′ UTR of the fragile X mental retardation (FMR1) gene (Fu et al. 1991; Oberle et al. ¹⁹⁹¹; Verkerk et al. ¹⁹⁹¹). The repeat is highly polymorphic with respect to size and can be grouped into four broad repeat-size categories. The first group consists of repeat sizes <40, and these alleles are usually inherited in a stable manner from parent to offspring. Intermediate alleles are defined as those with repeats 40–59, and they may or may not be inherited in a stable manner. The larger premutation alleles, with repeats ⩾60, are inherited in an unstable manner and are often a prelude to the hyperexpansion event that leads to the full mutation and the consequent fragile X syndrome. The size range of full mutation alleles is >200 CGG repeats. Beyond this threshold, hypermethylation of a nearby CpG island is triggered, causing subsequent transcriptional silencing of the gene (Oberle et al. 1991; Sutcliffe et al. ¹⁹⁹²). The absence of the FMR1 gene product FMRP, an RNA-binding protein, gives rise to the fragile X syndrome phenotype (Pieretti et al. 1991).

A multistep mutational pathway has been proposed to explain the progression of a stable allele to its expanded full mutation state. Morton and Macpherson (1992) have suggested a broad framework model with four allelic states: N→S→Z→L. First, the initial mutation occurs on a common-sized (i.e., normal) repeat allele (N) leading to susceptibility to instability. Next, the susceptible repeat allele (S) expands or contracts one or two repeats, and this unstable state may persist for as many as 90 generations (Chakravarti 1992). If the allele repeatedly expands, it can reach the premutation size (Z) and now is prone to hyperexpand to full mutation range (L). In the present study, we have focused on the first two states in this mutational pathway (N→S→). The purpose was to identify FMR1 CGG repeat alleles that are predisposed to the initial mutation and to identify their associated risk factors.

Through haplotype association studies, sperm studies, and fragile X syndrome family studies, several risk factors for instability have been implicated (the most important factor being the structure of the repeat). Sequencing of the CGG repeat in the general population has shown that the repeat is polymorphic, not only with respect to size but also with respect to sequence interspersions. It is usually interspersed by 1–3 AGGs every 9–10 CGGs (Eichler et al. 1994; Hirst et al. ¹⁹⁹⁴; Kunst and Warren ¹⁹⁹⁴; Snow et al. ¹⁹⁹⁴; Zhong et al. ¹⁹⁹⁵). These AGG interspersions are thought to stabilize the repeat during replication. The loss of the most distal 3′ end AGG interspersion is one possible mechanism leading to instability of the repeat (Eichler et al. 1994; Kunst and Warren ¹⁹⁹⁴; Snow et al. ¹⁹⁹⁴). Parent-child transmission studies have shown that alleles with >34–37 consecutive CGG repeats at the 3′ end are transmitted in an unstable manner (Eichler et al. 1994). The question remains of whether the number of AGG interspersions also plays a role. For example, it is unclear whether a 9+35 repeat structure is less stable than a 9+9+35 repeat structure (with the number indicating the number of consecutive CGGs and the plus sign representing the AGG interspersion). The position of the first AGG interspersion may be another important component of repeat structure. Through association studies in white populations, the 9+n structure has been postulated to be more prone to expansion than the 10+n structure (Gunter et al. 1998). However, no evidence of this positional effect was found in a large population of African Americans (Crawford et al. ^2000b).

In addition to CGG-repeat structure, as-yet unidentified cis-acting factors related to haplotype background have been evoked as factors involved in CGG-repeat instability (Eichler et al. 1996). Trans-acting factors have also been suggested, on the basis of observations that the rate of expansion from pre- to full-mutation sizes is more similar within sibships than among sibships (Nolin et al. 1996) and that full mutations are more similar between siblings than between unrelated patients (Burman et al. 2000).

Another possible factor of instability is the parental origin of transmission. This factor plays a major role in the instability of premutation alleles: the repeat hyperexpands when passed from mother to child but usually only expands or contracts by a few repeats when transmitted from father to daughter (Rousseau et al. 1991; Nolin et al. ¹⁹⁹⁶; Ashley-Koch et al. ¹⁹⁹⁸).

In the present study, we have examined 1,452 parent-child transmissions of common- and intermediate-sized alleles, to examine the initial mutation events. Of these, 201 have been sequenced and haplotyped. When tested through logistic regression analysis, parental origin of transmission, repeat size (for unsequenced alleles), and the number of 3′ CGGs (for sequenced alleles) were significant with respect to repeat instability. These findings have implications for the mutational process.

Subjects and Methods

Study Population

Individuals were ascertained through a population-based school survey conducted during 1994–1998, in which DNA samples were collected for fragile X testing from children in special-education classes (Crawford et al. 1999; Meadows et al. ¹⁹⁹⁶). Although these data were drawn from special-education classes, they did not differ from data drawn from ethnically matched control subjects with respect to repeat size (Crawford et al. 1999). Thus, the subset of transmissions studied here was drawn from a population that represents a random sample. For the present study, probands were defined as those children who carried either a common allele (⩽39 repeats) or an intermediate allele (40–59 repeats). To obtain transmission information, samples were collected on all available parents of probands. For those children with an intermediate allele, samples were also collected from extended-family members.

The data were compiled into two major data sets. The first data set consisted of all 1,452 parent-child transmissions and included repeat size, parental origin, and ethnic background information. The second data set was a subset of the first, and, in these transmissions, we were able to obtain the sequence of the repeat structure and genotype-flanking markers (DXS548, FRAXAC1, and FRAXAC2). These 201 transmissions included all intermediate alleles (both stable and unstable), all unstable common alleles, and a random sample of stable common alleles.

Because of the particular complexity of sequencing the CGG repeat in female heterozygotes, only samples from male subjects were sequenced. Therefore, the repeat structure for female samples was inferred on the basis of the assumption that mutations only included an expansion or contraction of the 3′ pure CGG repeats. The AGG interspersion pattern was assumed to be stable. Thus, all female subjects with the same size repeat as their sequenced male relative were assumed to have the same repeat structure.

Statistical Methods

Logistic regression analysis was performed on both data sets to examine factors associated with repeat instability. Each transmission was treated independently; that is, we did not group the transmissions according to family. For the total data set, the dependent variable was transmission stability, and the independent variables were repeat size, parental origin, and ethnic background. Repeat size was treated as a continuous variable. Parental origin was treated as a binary variable in which a paternal transmission was coded as “0” and a maternal transmission was coded as “1.” For ethnic background, there were five race categories—white, African American, Hispanic, Asian, and other—as well as a category of unknown race. Each race category was treated as a dummy variable.

For the sequenced data set, the dependent variable was transmission stability, and the independent variables were parental origin, position of the first AGG interspersion, number of AGG interspersions, length of the 3′ end of the CGG repeat, midsection length of the repeat, and ethnic background. In addition, the FRAXAC1 genotype was used to represent the flanking marker haplotype, as it is in the strongest linkage disequilibrium with the full mutation and with specific repeat structures. Its five alleles were represented as dummy variables. For the position of the first AGG interspersion, the absence of AGGs was treated as a 0th position. The 0th, 10th, 11th, and “other” positions were treated as dummy variables. The number of AGG interspersions, as well as the length of the 3′ end, was treated as a continuous variable. For the midsection length, the length was defined as the second section of consecutive CGGs after the first AGG interspersion. The midsection length was coded as “1” if the second section was greater than the first section and as “0” if the second section was equal to or shorter than the first section. Since there were only two transmissions of an ethnic group other than white or African American, ethnic background was treated as a binary variable in which white was coded as “0” and African American and others were coded as “1.” Results of logistic regression are reported as odds ratio (OR) with 95% CI and correspond to the probability of an allele being unstably transmitted from parent to child.

Linear regression analysis was also performed on both data sets to identify factors associated with the magnitude and direction of repeat change. Here, the dependent variable was the difference between the parental and offspring repeat sizes; negative numbers represented contractions, and positive numbers represented expansions. Those with no change were not included in the analyses. The independent variables were the same as those used in both logistic regression analyses. All statistical analyses were performed by use of Statistical Analysis System (SAS) software for Windows (release 8.0).

Laboratory Methods

FMR1 CGG-repeat sizes were determined by a fluorescent-sequencer method, as described elsewhere (Meadows et al. 1996). Samples from parent-offspring pairs and from other relatives, if available, were run side-by-side on the same gel to investigate repeat-size changes. If a change was observed, the samples were reamplified and were run a second time to confirm the observation. This protocol distinguished between PCR artifact and true changes. All genotypes were scored independently by at least two investigators.

The STR markers DXS548, FRAXAC1, and FRAXAC2 were multiplexed, and allele sizes were determined by use of a fluorescent sequencer method, as described elsewhere (Murray et al. 1996). Allele assignments were based on the numbering of Eichler et al. (1996).

The AGG interspersion pattern was determined by sequencing the CGG-repeat array. The sequencing protocol used is detailed in Crawford et al. (2000b). The primers used in the sequencing reactions were 5′-GACGGAGGCGCCGCTGCCAGG-3′, 5′-GTGGGCTGCGGGCGCTCGAGG-3′, and 5′-CCTGCTAGCGCCGGGAGC-3′ (Hirst et al. 1994; Brown et al. ¹⁹⁹³).

Results

Observed Mutation Rates Based on CGG-Repeat Size

A total of 1,452 parent-child transmissions was examined and was drawn from 1,345 families of various ethnic backgrounds. There were 1,072 white families, 198 African American families, 24 Hispanic families, 11 Asian families, 37 families of other ethnicities, and 3 families of unknown ethnicity. Each transmission was categorized by parental origin of transmission, ethnic background, and overall repeat size (table 1). They were grouped within six specified repeat-size ranges, and the number of unstable transmissions for each group was calculated. The first three repeat-size categories include all common allele transmissions, defined in the present study as being <40 repeats. The second three categories include all intermediate allele transmissions defined in the present study as being 40–59 repeats. The percentage of unstable transmissions in each group represents the minimal mutation rate. It is minimal because it is based only on a repeat-size change in the gamete. It does not include unstable transmissions that have a change in repeat structure but not in repeat size.

Table 1.

Mutation Rate of each CGG Repeat Size categorized by Parental Origin

Parental Origin,Repeat Size, andNo. and Race of Transmissionsa	No. of UnstableTransmissions (%)b	Overall μ(%)c
Maternal:
< 20:	…	…
10 W	…	…
20–29:	…	.27
291 W	1 (.34)	…
64 AA	…	…
20 Other	…	…
30–39:	…	.81
480 W	4 (.84)	…
103 AA	1 (.97)	…
37 Other	…	…
40–49:	…	2.34
106 W	3 (2.83)	…
18 AA	…	…
4 Other	…	…
50–54:	…	9.52
21 W	2 (9.52)	…
55–59:	…	14.29
7 W	1 (14.29)	…
Paternal:
< 20:	…	…
1 W	…	…
20–29:	…	3
84 W	3 (3.57)	…
7 AA	…	…
9 Other	…	…
30–39:	…	3.03
113 W	4 (3.54)	…
11 AA	…	…
8 Other	…	…
40–49:	…	7.69
31 W	3 (9.68)	…
3 AA	…	…
5 Other	…	…
50–54:	…	11.11
9 W	1 (11.11)	…
55–59:	…	54.55
11 W	6 (54.55)	…

^aAA = African American; W = white.

^bData are the total number of unstable transmissions within one ethnic group. Ellipses indicate absence of unstable transmissions.

^cPercentage of unstable transmissions of all ethnic groups combined.

Transmissions of white origin have higher point-estimate mutation rates than those of other ethnic groups. However, because of small numbers of transmissions in the other ethnic groups, there is no statistically significant difference.

For all allele sizes and ethnic groups, the mutation rates were estimated to be 5.82% and 1.03% for paternal and maternal transmissions, respectively. When analyzed according to repeat-size category, the estimates for paternal and maternal transmissions were 3% and 0.6% for common alleles and 16.95% and 3.87% for intermediate alleles.

Identification of Risk Factors for Instability Using All Transmission Data

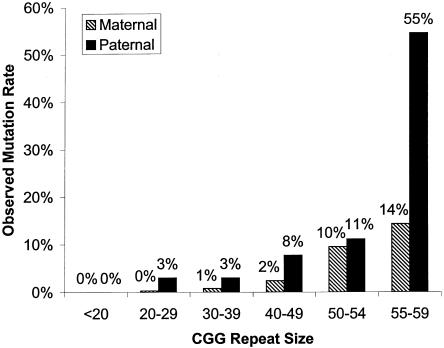
We used logistic regression to determine the importance of repeat size, parental origin, and ethnic background on repeat instability. Only repeat size and parental origin were statistically significant in this data set (table 2). Again, the number of transmissions—specifically, unstable transmissions among the other ethnic groups—was small, and results for ethnic background are therefore inconclusive. Figure 1 shows the observed mutation rate for paternal and maternal transmissions based on repeat size.

Table 2.

Factors that Impact the Rate of CGG Repeat Instability^[Note]

IndependentVariables	ParameterEstimates	P	OR (95% CI)
Total data set:
Y-intercept	−7.07
CGG-repeat size	.12	<.0001	1.12 (1.08–1.17)
Parental origin	−1.50	.0002	.22 (.10–.49)
Sequenced data set:
Y-intercept	−4.02
Length of 3′ end	.09	.0002	1.10 (1.05–1.15)
Parental origin	−1.46	.0129	.23 (.07–.73)

Note.— The dependent variable is transmission stability. The posterior probability (or predicted risk) for instability can be calculated as follows: for total data set, P(x)=1/[1+e^{-[(-7.07)+(0.12)(CGG-repeatsize)+(-1.50)(parentalorigin)]}]; for sequenced data set, P(x)=1/[1+e^{-[(-4.02)+(0.09)(lengthof3′end)+(-1.46)(parentalorigin)]}].

Figure 1.

Percentages of unstable maternal and paternal transmissions and the corresponding predicted risk for instability, according to repeat size.

Identification of Risk Factors for Instability Using Sequenced Transmission Data

For a subset of transmissions, we were able to haplotype and sequence all alleles for which DNA was available, including all stable and unstable intermediate alleles, all unstable common alleles, and a random sample of stable common alleles. Only the male involved in the transmission (or, if an involved male was unavailable, a male relative) was sequenced, because of the complexity of sequencing female heterozygotes. This sequenced data set consists of 201 transmissions consisting of 69 white families (141 transmissions), 54 African American families (59 transmissions), and 1 Hispanic family (1 transmission) (Appendix A). Only one unstable transmission was identified on a nonwhite chromosome; thus, we restricted the logistic regression analyses to white subjects only.

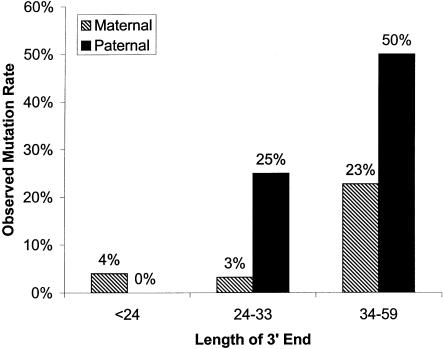
Using logistic regression analysis, we first examined each independent variable separately. We found that the following variables were significant: (1) the length of the 3′ end of the repeat (OR [95% CI] = 1.095 [1.048–1.145]); (2) the number of AGG interspersions (OR [95% CI] = 0.253 [0.12–0.531]); and (3) the parental origin of transmission (OR [95% CI] = 0.236 [0.085–0.654]). When all variables were entered together, the most parsimonious model included parental origin of transmission and the length of the 3′ end (table 2). Thus, the part of the risk explained by the number of AGG interspersions could be better explained by the length of the 3′ end. Figure 2 shows the observed mutation rate for paternal and maternal transmissions based on length of the 3′ end.

Figure 2.

Percentages of unstable maternal and paternal transmissions and the corresponding predicted risk for instability based on the length of the 3′ end.

These findings suggest that the small number of unstable transmissions among the African American sample was a consequence of the small number of “at-risk” alleles. With respect to the length of the 3′ end, there were 3.23% (2/62), 9.3% (4/43), and 33.33% (12/36) of transmissions of white origin that were unstable and had 3′ repeat lengths of <24, 24–33, and 34–59, respectively. For transmissions of African American origin, there were 0% (0/45), 0% (0/8), and 16.67% (1/6) of those with unstable 3′ repeat lengths of <24, 24–33, and 34–59, respectively. Similarly, only 3.39% (2/59) of the sample consisted of paternal transmissions in the African American population, versus 21.28% (30/141) paternal transmissions in the white population. Thus, the small number of unstable transmissions seen in the African American population is due to the vast majority of transmissions having short 3′ repeat lengths (being in the common range) and being of maternal origin, a different distribution from that of the white population.

Identification of Risk Factors for the Magnitude and Direction of Repeat Change

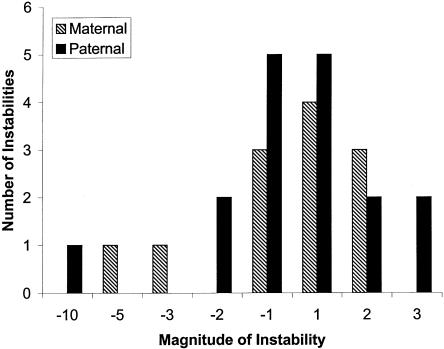
Linear regression analyses and χ² tests were performed on both data sets, to see whether parental origin and repeat size or repeat structure had an impact on the magnitude and direction of change of the repeat. Only the unstable transmissions were included in the analyses (29 transmissions for the total data set and 18 transmissions for the sequenced data set). In both analyses, no variables were significant. The proportion of expansions and contractions did not differ between maternal and paternal transmissions (58% and 53% for the total data set [fig. 3] and 88% and 70% for the sequenced data set, respectively).

Figure 3.

Magnitude of the change in repeat size of maternal and paternal unstable transmissions.

Discussion

Three approaches have been taken to study the mutational pathway of repeat instability: (1) association studies using haplotype data from normal and fragile X chromosomes (e.g., Macpherson et al. ¹⁹⁹⁴; Eichler et al. ¹⁹⁹⁶; Falik-Zaccai et al. ¹⁹⁹⁷; Gunter et al. ¹⁹⁹⁸; Crawford et al. ^2000c, Dombrowski et al. ²⁰⁰²); (2) sperm studies (Mornet et al. 1996; Kunst et al. ¹⁹⁹⁷; Nolin et al. ¹⁹⁹⁹; Crawford et al. ^2000a); and (3) family studies looking at parent-child transmissions (e.g., Nolin et al. ¹⁹⁹⁶; Murray et al. ¹⁹⁹⁷; Ashley-Koch et al. ¹⁹⁹⁸). Each approach has its advantages and disadvantages. For example, haplotype-association studies can only infer mutational pathways but have the advantage of using observations from a large time scale. Sperm studies directly examine the stability of one allele through, potentially, thousands of one-generation transmissions. However, sex and family factors are more difficult to study. Family studies fall in between the above two approaches, in terms of the time scale being studied, and can be used to examine sex and family factors. However, the limitation is the small number of unstable events available for study. We had the advantage of a large population from which to identify unstable transmissions and therefore took this last approach.

Risk Factors for Instability

CGG-repeat structure

In terms of repeat structure, the length of the 3′ end of the repeat has been consistently identified as a risk factor for repeat instability. For example, Eichler et al. (1994) showed that alleles with 34–37 repeats at their 3′ end were unstably transmitted from parent to child, and Kunst and Warren (1994) reported that alleles with >24 repeats at their 3′ end shared a common haplotype background with full mutation alleles. Results from two sperm studies suggest that the number of AGG interspersions may be a risk factor. In the study by Crawford et al. (2000a), an individual with a 28-repeat allele with no AGG interspersions had a higher rate of sperm variants than did an individual who had a 9+23 repeat structure. Similarly, in the study by Nolin et al. (1999), an individual with a 68-repeat allele with no AGG interspersions exhibited a higher rate of sperm variants than did individuals with 9+65, 9+68, or 9+9+80 repeat structures.

In the present study, the length of the 3′ end of the repeat was the only significant factor related to repeat structure. Thus, this feature appears to play a larger role in repeat instability than do the number of AGG interspersions, at least in this data set. One limitation of this conclusion is that we sequenced only male samples. Female repeat structures were inferred.

Not only repeat structure but also cis-acting factors related to haplotype background have been suggested to play a role in repeat instability. Eichler et al. (1996) proposed two main mutational mechanisms by which an allele becomes unstable. They suggested that the CGG-repeat structure was resistant to the loss of AGG interspersions on the 2-1-3 haplotype background, and thus an increase in 3′ CGG repeats occurred through multiple small expansions. In contrast, on the 6-4-4 or 6-4-5 haplotype background, the CGG-repeat structure was suggested to be prone to lose the 3′-most AGG interspersion and to expand rapidly to the premutation state. Crawford et al. (2000b), however, did not find such evidence and suggested that the haplotype associated with repeat structure was primarily due to aspects of population history. Our results are similar to those of Crawford et al. (2000b), in that the haplotype background, as represented by FRAXAC1, was not a significant risk factor for repeat instability. Simple examination of the list of haplotypes in Appendix A among white subjects shows an excess of 2-1-3 haplotypes among the larger repeat sizes, as expected from haplotype studies. However, this haplotype does not appear to be more frequent on unstable transmissions than on stable transmissions.

Recently, Dombrowski et al. (2002) sequenced and haplotyped intermediate-size alleles drawn from a population-based sample of 10,572 male subjects. They found that 48 of the 49 intermediate alleles had one or two AGG interspersions and were enriched for a specific fragile X syndrome–related haplotype. They concluded that loss of AGG interspersions is not necessary for expansion of normal alleles to intermediate alleles. Instead, they inferred that the loss of AGG interspersions is a late event that leads to greatly increased instability and may be related to haplotype background. Our data on parent-offspring transmissions did not implicate haplotype background as a risk factor for instability. Our conclusions must be taken with some caution, because of the relatively small number of unstable events and because of the small number of ethnic groups.

Parental Origin of Transmission

This is the first study to investigate the effect of parental origin of transmission of intermediate and common alleles on repeat instability. We found that, on average, paternal transmissions were less stable than maternal transmissions. This finding contrasts with the parental effect on transmission of premutation alleles, and this difference may indicate different mutational mechanisms and/or different selection processes in males than in females. For premutation alleles, an increase in the size of maternal repeat increases the risk of having large expansions (i.e., full-mutation offspring) on average, whereas paternal premutations never expand to full mutations when transmitted. Furthermore, the frequency of contractions increases with increasing paternal repeat size (Nolin et al. 1996). Ashley-Koch et al. (1998) investigated whether this observation resulted from a mechanistic difference or from selection against the full mutation in sperm but not in eggs. They compared male premutation transmissions with the subset of female premutation transmissions that had not expanded to the full mutation, and they found no significant difference in the risk of expansion compared with contraction, on the basis of parental origin. This evidence supported the hypothesis that there is a different selection process in sperm versus eggs.

In other repeat-mutation disorders in which the repeat is in the coding region, the repeat-size range that leads to instability or produces the disorder (∼35–60 repeats) is primarily equivalent to the intermediate size range for the fragile X mutation. The parental effect in these disorders is similar to the findings of the present study, in that paternal transmissions are less stable than maternal transmissions (Ashley and Warren 1995; Sutherland and Richards ¹⁹⁹⁵; Gusella and MacDonald ¹⁹⁹⁶; Wells et al. ¹⁹⁹⁸). For example, in Huntington disease, the CAG repeat is highly unstable when transmitted from father to child but usually remains relatively stable when passed from mother to child (e.g., De Rooij et al. ¹⁹⁹³; Trottier et al. ¹⁹⁹⁴; Kremer et al. ¹⁹⁹⁵; Norremolle et al. ¹⁹⁹⁵). Leeflang et al. (1999) conducted a study of 26 males with Huntington disease who had large repeat alleles (50–62 CAG repeats). They found an extremely high germline mutation rate (mean 98%) and proposed a germline mitotic model in which trinucleotide-repeat instability occurs over many premeiotic mitotic divisions, rather than in one meiotic division.

The same type of model could be true for the FMR1 CGG repeat. In females, there is only one period of premeiotic mitotic division, which occurs prenatally, whereas males experience premeiotic mitotic divisions throughout their lives. If repeat expansion occurs in this phase, there are many more chances for replication slippage to occur in males than in females. Thus, the mutational distribution of sperm would have a higher mean (assuming expansion bias) and, possibly, a larger variance than that of eggs. The proposed selection against sperm that carry high-repeat alleles (⩾90 repeats) and not against eggs, would truncate the high-end tail of the mutational distribution of sperm among males with ⩾70 repeats. Such males would appear to have more contractions than expansions and to have a smaller variance than do females who carry the same repeat size. If this selection process does exist, the observed instability pattern for a disorder would depend on the repeat-size range of the disease alleles. For those trinucleotide disorders that have unstable repeat sequences within the coding sequence, a paternal bias for greater instability would be expected, because disease alleles are in the range of 35–60 repeats. This is observed for most of the disorders with this characteristic, for example, Huntington disease and the spinocerebellar ataxias. For those trinucleotide disorders with unstable repeat sequences outside the coding region, a maternal bias for greater instability would be expected, because disease alleles are >200 repeats. This pattern is observed for the fragile X syndrome, as well as myotonic dystrophy and Friedreich ataxia.

FMR1 CGG Repeat Mutation Rate

For common and intermediate-sized FMR1 repeat alleles, we found a surprisingly high mutation rate for this STRP. The mutation rate was defined as a change in repeat size during transmission from parent to offspring. We classified every mutation, whether it was an expansion or contraction, as an instability. The mutation rate was found to increase with increasing FMR1 CGG-repeat size and to be high both for common alleles (1%) and for intermediate alleles (8%). Even compared with the average mutation rate of other di-, tri-, and tetranucleotide loci (0.12%) (Weber and Wong 1993), the mutation rate is 10–80-fold higher, showing the unstable nature of this unique STRP. As discussed previously, the mutation rate was found to depend on the parental origin of transmission. The mutation rate of paternal transmissions was higher than the mutation rate of the maternal transmissions among both the common (3.00% and 0.60%, respectively) and intermediate alleles (16.95% and 3.87%, respectively). The maternal mutation rates for common (0.03% [1/2,869]) and intermediate (2.64% [4/151]) alleles in a large white population have been reported elsewhere (Youings et al. 2000) and are similar to those in the present study.

Another way to compute mutation rate would be to classify a mutation as being either “forward” or “backward.” From this analysis and previous studies, the length of the repeat is known to be an important risk factor for repeat instability. Thus, an expansion could be described as a forward mutation, because it leads to a greater chance of instability. A backward mutation or a contraction could be considered advantageous, because it leads to stability. When all transmissions—both maternal and paternal—were considered, the forward mutation rate was estimated to be 0.4% among common alleles. The ratio of forward to backward mutation rates was 1.2. For the intermediate alleles, the forward mutation rate was estimated to be 5.15%, which is 13 times higher than that for the common alleles. The ratio of forward to backward mutation rates increased to 2.2.

We also investigated the magnitude of the change in repeat size that occurs in these mutational events. The changes observed ranged from a contraction of 10 repeats to an expansion of 3 repeats (Appendix A; fig. 3). As with other STRs, the majority of changes were within two repeats. None of the studied factors explained the size of the change or the direction of the change. However, our study was limited because of the small number of unstable transmissions.

Applications of Repeat-Instability Model

The logistic regression model developed from our sequenced data can be used to identify alleles predisposed to instability, as well as the proportion of those alleles in a population. We defined “predisposed” as any allele predicted to be unstable in ⩾10% transmissions. When the sequenced data from ∼200 randomly selected white alleles published by Gunter et al. (1998) were analyzed, 0.05% of alleles were found to be predisposed to instability if maternally transmitted, and 1.1% were found to be predisposed to instability if paternally transmitted. When the sequenced data from ∼200 African American alleles published by Crawford et al. (2000b) were used, 0.05% of alleles were found to be predisposed to instability if maternally transmitted and 0.9% if paternally transmitted. Clearly, application of this model can be useful in the prediction of mutation rates in a population of alleles that have repeat-structure data and no parental-origin information, as is the case in most association studies.

One of the goals of the present project was to predict the risk of instability for an intermediate-sized allele. This information is critically needed both in the clinical setting and in a population-screening setting. In typical situations, repeat structure is unknown, and the risk is dependent on repeat size and parental origin only. Use of the model presented here could provide an estimate of that risk. For example, a male individual with 50 repeats who was identified from the general population would have a 22% chance of transmitting his allele unstably to his offspring, and a female individual would have a 6% chance. Although there is no risk of an intermediate-sized allele expanding to a full mutation, such a finding may indicate a need for further workup in extended relatives to rule out the possibility of expanded, premutation alleles. More transmission studies are necessary before this information can be used in such critical settings; however, the data presented here provide important parameters for further study.

In summary, using 1,482 parent-child transmissions of common and intermediate size FMR1 repeat alleles, we confirmed that the length of the 3′ end is a risk factor for repeat instability. More importantly, we found that paternal transmissions are less stable than maternal transmissions in this size range. This information, combined with that from other trinucleotide repeat disorders, suggests that selection against sperm with large alleles may explain differences in the observed pattern of instability by parental origin of the mutation.

Appendix A

Table A1.

Results from Parent-Child Transmissions for the Sequenced Data Set

Race andTransmissiona	CGG-RepeatStructureb	Haplotype (DXS548,FRAXAC1,and FRAXAC2)	ParentalOrigin
White:
1	25→26	2 3 4	P
2	52→54	7 3 4	M
3	57→58	4 1 3	P
4	57→60	4 1 3	P
5	58 →57	4 1 3	M
6	58→61	4 1 3	P
7	58→60	4 1 3	P
8	9+9+30→9+9+32	2 1 3	P
9	9+9+35→9+9+36	6 3 4	P
10	9+9+38→9+9+37	7 1 2	P
11	9+34→9+32	2 1 3	P
12	9+39→9+40	6 4 6+	M
13	9+41*→9+9+33	2 1 3	M
14	9+51**→9+57	5 1 3	M
15	10+9+8→10+9+10	7 3 4	M
16	10+9+9→10+9+10	7 3 4+	M
17	10+9+27→10+9+26	7 3 4+	P
18	10+31→10+32	7 3 4+	M
19	13→13	7 3 ?	M
20	52→52	7 3 4	M
21	52→52	7 3 4	M
22	58→58	4 1 3	M
23	9+9+13+7→9+9+13+7	6 3 4	M
24	9+9+13+7→9+9+13+7	6 3 4	M
25	9+9+9→9+9+9	7 4 6+	M
26	9+9+9→9+9+9	6.5(+) 4 5	M
27	9+9+9→9+9+9	6 4 6+	M
28	9+12+9→9+12+9	6 4 4+	M
29	9+12+9→9+12+9	6 4 4	M
30	9+12+9→9+12+9	6 4 5	P
31	9+12+9→9+12+9	6 4 3	P
32–35	9+9+20→9+9+20	2 1 3	M
36–37	9+9+20→9+9+20	2 1 3	M
38	9+9+20→9+9+20	2 1 3	P
39–41	9+9+21→9+9+21	2 1 3	M
42	9+9+21→9+9+21	2 1 3	M
43	9+9+21→9+9+21	6 3 4	M
44	9+9+21→9+9+21	7 3 4+	M
45–47	9+9+21→9+9+21	2 1 3	P
48–49	9+9+22→9+9+22	2 1 3	M
50	9+9+22→9+9+22	2 1 3	M
51–52	9+9+23→9+9+23	2 1 3	M
53–55	9+9+23→9+9+23	2 1 3	M
56	9+9+23→9+9+23	2 1 3	P
57–58	9+9+26→9+9+26	2 1 3	M
59	9+9+26→9+9+26	2 1 3	M
60	9+9+27→9+9+27	? 3 ?	M
61	9+9+27→9+9+27	? 3 ?	M
62–63	9+9+30→9+9+30	2 1 3	M
64	9+9+30→9+9+30	2 1 3	P
65–66	9+9+32→9+9+32	2 1 3	M
67	9+9+34→9+9+34	2 1 3	M
68–71	9+9+35→9+9+35	6 3 4	P
72	9+9+38→9+9+38	7 1 2	M
73	9+9+38→9+9+38	7 1 2	M
74	9+9+38→9+9+38	7 1 2	P
75	9+22→9+22	6 4 5	M
76	9+22→9+22	6 4 4	P
77	9+25→9+25	7 4 6+	P
78	9+26→9+26	7 4 6+	P
79–80	9+30→9+30	7 4 5	M
81–82	9+30→9+30	7 4 5	M
83–85	9+30→9+30	7 4 5	P
86	9+31→9+31	7 3 4+	M
87	9+31→9+31	7 3 4+	M
88	9+32→9+32	6 4 4	M
89–90	9+33→9+33	6 4 4	M
91	9+33→9+33	6 4 4	M
92–93	9+33→9+33	6(+) 4 ?	M
94–95	9+33→ 9+33	6(+) 4 ?	M
96–97	9+34→9+34	2 1 3	P
98	9+35→9+35	2 1 3	M
99	9+39→9+39	6 4 5	M
100	9+39→9+39	6 4 6+	M
101	9+41→9+41	2 1 3	M
102–103	9+41→9+41	2 1 3	M
104	9+48→9+48	5 1 3	M
105	9+48→9+48	5 1 3	M
106	10+9+9+10→10+9+9+10	7 4 −2	M
107	10+9+10+9→10+9+10+9	7 3 4+	M
108–109	10+9+8+10→10+9+8+10	7 3 4+	M
110	10+9+8+10→10+9+8+10	7 3 4+	P
111	10+9+8+10→10+9+8+10	7 3 4+	M
112	10+9+15+10→10+9+15+10	7 3 ?	M
113	10+9+15+10→10+9+15+10	7 3 ?	M
114	10+17+9+4→10+17+9+4	7 3 4+	M
115	10+9+20→10+9+20	7 3 4+	M
116	10+9+20→10+9+20	7 3 4+	M
117	10+9+27→10+9+27	7 3 4+	P
118	10+6→10+6	7 3 4+	M
119	10+30→10+30	7 3 4+	M
120	10+30→10+30	7 3 4+	P
121	10+31→10+31	7 3 4+	M
122–123	10+31→10+31	7 3 4+	M
124	10+31→10+31	7 3 4+	P
125	10+36→10+36	7 3 4+	M
126	10+36→10+36	7 3 4+	M
127	10+46→10+46	7 3 4+	M
128	8+10+8+14→8+10+8+14	2 1 4+	M
129	8+18+13→8+18+13	8 3 4+	M
130–131	8+18+13→8+18+13	8 3 4+	M
132–133	8+19+12→8+19+12	6 4 5	M
134–135	8+19+15→8+19+15	2 1 3	P
136	8+19+15→8+19+15	2 1 3	M
137	8+19+15→8+19+15	2 1 3	M
138	8+19+25→8+19+25	6 3 4	P
139–140	8+19+25→8+19+25	6 3 4	M
141	12+9→12+9	7 3 4	P
African American:
142	36→33	4(+) 45	M
143	23→23	7 3 6	M
144	30→30	7 4 3	M
145	36→36	4(+) 4 5	M
146	40→40	7 3 5+	M
147–149	9+9+9+9→9+9+9+9	7 6 5+	M
150	9+9+9+9→9+9+9+9	2(−) 1 3	M
151	9+9+9→9+9+9	5 3 6+	M
152	9+9+9→9+9+9	4 2 5+	M
153	9+9+9→9+9+9	5.5(−) 3 5+	M
154	9+9+9→9+9+9	4 3 5	M
155	9+9+9→9+9+9	4(−) 3 3	M
156	9+9+9→9+9+9	7(+) 3 4	M
157	9+9+9→9+9+9	4(−) 3 5	M
158	9+9+13→9+9+13	2 1 3	M
159	9+9+19→9+9+19	7 3 4	M
160	9+19→9+19	3(−) 4 5	M
161	9+19→9+19	4 4 5	M
162	10+9+9+10→10+9+9+10	7 4 −3	M
163	10+9+9+10→10+9+9+10	7 4 −3	M
164	10+9+9+10→10+9+9+10	7 4 6+	M
165–167	10+9+9→10+9+9	7 3 4+	M
168	10+9+9→10+9+9	7 3 3	M
169	10+9+9→10+9+9	11 4 4	M
170	10+9+9→10+9+9	6 3 3	M
171–172	10+9+9→10+9+9	6 3 4+	M
173	10+9+10→10+9+10	7.5(−) 4 3+	M
174–175	10+10+9→10+10+9	6 3 6	M
176	10+10+9→10+10+9	5 3 6	M
177	10+10+9→10+10+9	6(+) 3 6	M
178	10+9+15→10+9+15	6 3 5+	M
179	10+14→10+14	7 3 4+	M
180	10+20→10+20	7 3 4+	M
181	10+27→10+27	7 3 5	M
182	10+29→10+29	3(−) 3 6	P
183	10+30→10+30	7 3 6	M
184	10+30→10+30	7 3 6	M
185–186	10+30→10+30	7 3 4+	M
187	10+30→10+30	7 3 4+	M
188	10+34→10+34	7 6 5+	M
189	10+34→10+34	7 6 5+	M
190	10+34→10+34	5 3 4+	M
191–192	8+19+11→8+19+11	7 3 6	P
193	12+9→12+9	2 3 6	M
194	14+9→14+9	6 4 3+	M
195	17+9+10→17+9+10	6 4 ?	M
196	19+9→19+9	4(+) 4 5	M
197–198	19+9→19+9	6 4 5	M
199–200	20+9→20+9	4(+) 4 5	M
Hispanic:
201–202	9+9+12+10→9+9+12+10	6 4 4	P

^aTransmissions 1–18 and 142 are unstable.

^bThe underlined repeat structures are those that have been sequenced, and the others are inferred; * = maternal sequence was inferred from her son’s sequence of the same repeat size (shown in transmission 101); ** = 61-repeat allele that was identified through a proband with 58 repeats (shown in transmission 105) and was included in the analysis based on the ascertainment rule (i.e., proband transmissions and their extended relatives).

Table A1.

Results from Parent-Child Transmissions for the Sequenced Data Set

Race andTransmissiona	CGG-RepeatStructureb	Haplotype (DXS548,FRAXAC1,and FRAXAC2)	ParentalOrigin
White:	10+9+9+10→10+9+9+10
1	25→26	2 3 4	P
2	52→54	7 3 4	M
3	57→58	4 1 3	P
4	57→60	4 1 3	P
5	58 →57	4 1 3	M
6	58→61	4 1 3	P
7	58→60	4 1 3	P
8	9+9+30→9+9+32	2 1 3	P
9	9+9+35→9+9+36	6 3 4	P
10	9+9+38→9+9+37	7 1 2	P
11	9+34→9+32	2 1 3	P
12	9+39→9+40	6 4 6+	M
13	9+41*→9+9+33	2 1 3	M
14	9+51**→9+57	5 1 3	M
15	10+9+8→10+9+10	7 3 4	M
16	10+9+9→10+9+10	7 3 4+	M
17	10+9+27→10+9+26	7 3 4+	P
18	10+31→10+32	7 3 4+	M
19	13→13	7 3 ?	M
20	52→52	7 3 4	M
(continued)

Table A1 (continued).

Race andTransmissiona	CGG-RepeatStructureb	Haplotype (DXS548,FRAXAC1,and FRAXAC2)	ParentalOrigin
White:	10+9+9+10→10+9+9+10
21	52→52	7 3 4	M
22	58→58	4 1 3	M
23	9+9+13+7→9+9+13+7	6 3 4	M
24	9+9+13+7→9+9+13+7	6 3 4	M
25	9+9+9→9+9+9	7 4 6+	M
26	9+9+9→9+9+9	6.5(+) 4 5	M
27	9+9+9→9+9+9	6 4 6+	M
28	9+12+9→9+12+9	6 4 4+	M
29	9+12+9→9+12+9	6 4 4	M
30	9+12+9→9+12+9	6 4 5	P
31	9+12+9→9+12+9	6 4 3	P
32–35	9+9+20→9+9+20	2 1 3	M
36–37	9+9+20→9+9+20	2 1 3	M
38	9+9+20→9+9+20	2 1 3	P
39–41	9+9+21→9+9+21	2 1 3	M
42	9+9+21→9+9+21	2 1 3	M
43	9+9+21→9+9+21	6 3 4	M
44	9+9+21→9+9+21	7 3 4+	M
45–47	9+9+21→9+9+21	2 1 3	P
48–49	9+9+22→9+9+22	2 1 3	M
50	9+9+22→9+9+22	2 1 3	M
51–52	9+9+23→9+9+23	2 1 3	M
53–55	9+9+23→9+9+23	2 1 3	M
56	9+9+23→9+9+23	2 1 3	P
57–58	9+9+26→9+9+26	2 1 3	M
59	9+9+26→9+9+26	2 1 3	M
60	9+9+27→9+9+27	? 3 ?	M
61	9+9+27→9+9+27	? 3 ?	M
62–63	9+9+30→9+9+30	2 1 3	M
64	9+9+30→9+9+30	2 1 3	P
65–66	9+9+32→9+9+32	2 1 3	M
67	9+9+34→9+9+34	2 1 3	M
68–71	9+9+35→9+9+35	6 3 4	P
72	9+9+38→9+9+38	7 1 2	M
73	9+9+38→9+9+38	7 1 2	M
74	9+9+38→9+9+38	7 1 2	P
75	9+22→9+22	6 4 5	M
76	9+22→9+22	6 4 4	P
77	9+25→9+25	7 4 6+	P
78	9+26→9+26	7 4 6+	P
79–80	9+30→9+30	7 4 5	M
81–82	9+30→9+30	7 4 5	M
83–85	9+30→9+30	7 4 5	P
86	9+31→9+31	7 3 4+	M
87	9+31→9+31	7 3 4+	M
88	9+32→9+32	6 4 4	M
89–90	9+33→9+33	6 4 4	M
91	9+33→9+33	6 4 4	M
92–93	9+33→9+33	6(+) 4 ?	M
94–95	9+33→ 9+33	6(+) 4 ?	M
96–97	9+34→9+34	2 1 3	P
98	9+35→9+35	2 1 3	M
99	9+39→9+39	6 4 5	M
100	9+39→9+39	6 4 6+	M
101	9+41→9+41	2 1 3	M
102–103	9+41→9+41	2 1 3	M
104	9+48→9+48	5 1 3	M
(continued)

Table A1 (continued).

Race andTransmissiona	CGG-RepeatStructureb	Haplotype (DXS548,FRAXAC1,and FRAXAC2)	ParentalOrigin
White:	10+9+9+10→10+9+9+10
105	9+48→9+48	5 1 3	M
106	10+9+9+10→10+9+9+10	7 4 −2	M
107	10+9+10+9→10+9+10+9	7 3 4+	M
108–109	10+9+8+10→10+9+8+10	7 3 4+	M
110	10+9+8+10→10+9+8+10	7 3 4+	P
111	10+9+8+10→10+9+8+10	7 3 4+	M
112	10+9+15+10→10+9+15+10	7 3 ?	M
113	10+9+15+10→10+9+15+10	7 3 ?	M
114	10+17+9+4→10+17+9+4	7 3 4+	M
115	10+9+20→10+9+20	7 3 4+	M
116	10+9+20→10+9+20	7 3 4+	M
117	10+9+27→10+9+27	7 3 4+	P
118	10+6→10+6	7 3 4+	M
119	10+30→10+30	7 3 4+	M
120	10+30→10+30	7 3 4+	P
121	10+31→10+31	7 3 4+	M
122–123	10+31→10+31	7 3 4+	M
124	10+31→10+31	7 3 4+	P
125	10+36→10+36	7 3 4+	M
126	10+36→10+36	7 3 4+	M
127	10+46→10+46	7 3 4+	M
128	8+10+8+14→8+10+8+14	2 1 4+	M
129	8+18+13→8+18+13	8 3 4+	M
130–131	8+18+13→8+18+13	8 3 4+	M
132–133	8+19+12→8+19+12	6 4 5	M
134–135	8+19+15→8+19+15	2 1 3	P
136	8+19+15→8+19+15	2 1 3	M
137	8+19+15→8+19+15	2 1 3	M
138	8+19+25→8+19+25	6 3 4	P
139–140	8+19+25→8+19+25	6 3 4	M
141	12+9→12+9	7 3 4	P
African American:
142	36→33	4(+) 45	M
143	23→23	7 3 6	M
144	30→30	7 4 3	M
145	36→36	4(+) 4 5	M
146	40→40	7 3 5+	M
147–149	9+9+9+9→9+9+9+9	7 6 5+	M
150	9+9+9+9→9+9+9+9	2(−) 1 3	M
151	9+9+9→9+9+9	5 3 6+	M
152	9+9+9→9+9+9	4 2 5+	M
153	9+9+9→9+9+9	5.5(−) 3 5+	M
154	9+9+9→9+9+9	4 3 5	M
155	9+9+9→9+9+9	4(−) 3 3	M
156	9+9+9→9+9+9	7(+) 3 4	M
157	9+9+9→9+9+9	4(−) 3 5	M
158	9+9+13→9+9+13	2 1 3	M
159	9+9+19→9+9+19	7 3 4	M
160	9+19→9+19	3(−) 4 5	M
161	9+19→9+19	4 4 5	M
162	10+9+9+10→10+9+9+10	7 4 −3	M
163	10+9+9+10→10+9+9+10	7 4 −3	M
164	10+9+9+10→10+9+9+10	7 4 6+	M
165–167	10+9+9→10+9+9	7 3 4+	M
168	10+9+9→10+9+9	7 3 3	M
(continued)

Table A1 (continued).

Race andTransmissiona	CGG-RepeatStructureb	Haplotype (DXS548,FRAXAC1,and FRAXAC2)	ParentalOrigin
African American:	10+9+9+10→10+9+9+10
169	10+9+9→10+9+9	11 4 4	M
170	10+9+9→10+9+9	6 3 3	M
171–172	10+9+9→10+9+9	6 3 4+	M
173	10+9+10→10+9+10	7.5(−) 4 3+	M
174–175	10+10+9→10+10+9	6 3 6	M
176	10+10+9→10+10+9	5 3 6	M
177	10+10+9→10+10+9	6(+) 3 6	M
178	10+9+15→10+9+15	6 3 5+	M
179	10+14→10+14	7 3 4+	M
180	10+20→10+20	7 3 4+	M
181	10+27→10+27	7 3 5	M
182	10+29→10+29	3(−) 3 6	P
183	10+30→10+30	7 3 6	M
184	10+30→10+30	7 3 6	M
185–186	10+30→10+30	7 3 4+	M
187	10+30→10+30	7 3 4+	M
188	10+34→10+34	7 6 5+	M
189	10+34→10+34	7 6 5+	M
190	10+34→10+34	5 3 4+	M
191–192	8+19+11→8+19+11	7 3 6	P
193	12+9→12+9	2 3 6	M
194	14+9→14+9	6 4 3+	M
195	17+9+10→17+9+10	6 4 ?	M
196	19+9→19+9	4(+) 4 5	M
197–198	19+9→19+9	6 4 5	M
199–200	20+9→20+9	4(+) 4 5	M
Hispanic:
201–202	9+9+12+10→9+9+12+10	6 4 4	P

^aTransmissions 1–18 and 142 are unstable.

^bThe underlined repeat structures are those that have been sequenced, and the others are inferred; * = maternal sequence was inferred from her son’s sequence of the same repeat size (shown in transmission 101); ** = 61-repeat allele that was identified through a proband with 58 repeats (shown in transmission 105) and was included in the analysis based on the ascertainment rule (i.e., proband transmissions and their extended relatives).