Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Oct 7;3:2879. doi: 10.1038/srep02879

Polarized linewidth-controllable double-trapping electromagnetically induced transparency spectra in a resonant plasmon nanocavity

Luojia Wang 1, Ying Gu 1,a, Hongyi Chen 1, Jia-Yu Zhang 2, Yiping Cui 2, Brian D Gerardot 3, Qihuang Gong 1,b
PMCID: PMC3791453  PMID: 24096943

Abstract

Surface plasmons with ultrasmall optical mode volume and strong near field enhancement can be used to realize nanoscale light-matter interaction. Combining surface plasmons with the quantum system provides the possibility of nanoscale realization of important quantum optical phenomena, including the electromagnetically induced transparency (EIT), which has many applications in nonlinear quantum optics and quantum information processing. Here, using a custom-designed resonant plasmon nanocavity, we demonstrate polarized position-dependent linewidth-controllable EIT spectra at the nanoscale. We analytically obtain the double coherent population trapping conditions in a double-Λ quantum system with crossing damping, which give two transparent points in the EIT spectra. The linewidths of the three peaks are extremely sensitive to the level spacing of the excited states, the Rabi frequencies and detunings of pump fields, and the Purcell factors. In particular the linewidth of the central peak is exceptionally narrow. The hybrid system may have potential applications in ultra-compact plasmon-quantum devices.

Surface plasmons in metallic nanostructures, which originate from the collective oscillations of free electrons in metal1, have attracted great interest in light-atom interaction2. Compared with other photonic structures, plasmon nanostructures provide large and anisotropic Purcell factors caused by an ultrasmall volume of optical modes3,4,5,6,7. Together with the strong near field enhancement near the resonant plasmonic structure, the superiority of its Purcell factor has been applied in the nanoscale realization of quantum phenomena, such as enhancement and quenching of fluorescence of molecules and quantum dots8,9,10,11,12,13, single surface plasmon sources14,15,16, resonance fluorescence of single emitters17,18, modification of spontaneous emission19, etc.

Coherent population trapping (CPT) in the stable state of light-atom interaction is the origin of many quantum coherence effects. Two kinds of mechanisms for CPT are widely investigated. One is the ordinary two-photon resonance leading to the conventional electromagnetically induced transparency (EIT)20,21, where the populations are coherently trapped in the two lower levels of the three-level Λ or four-level double-Λ system22,23. Due to elimination of absorption and deceleration of the group velocity at the transparent point, EIT has many substantial applications in nonlinear quantum optics, such as large Kerr nonlinearity24,25,26, four- and six-wave mixing27,28,29,30,31,32,33, cross phase modulation24,26,34,35, etc. EIT has also played an important role in quantum information processing, such as quantum memories36,37,38,39,40, quantum state transfer41,42, quantum gates16,24,43, quantum entanglement44,45, etc.

Another mechanism for CPT is related to the crossing damping between two closely lying upper levels, which originates from the interaction with the common vacuum of the electromagnetic field. By involving the crossing damping into the trapping condition, the populations can be coherently trapped in the upper levels of a three-level V-system or four-level system containing V-configuration, which leads to several spontaneously generated coherence (SGC) effects, i.e., spontaneous emission cancelation46, quantum beats of population oscillations47, and narrowing of spectral lines near the trapping condition48,49. Crossing damping terms are closely related to the Purcell factors in the electromagnetic environment50. Plasmonic structures with ultrasmall optical mode volume have the advantage of providing large and anisotropic Purcell factors3,4,5,6,7, thus they can be used to affect the SGC effects of quantum systems. However, the SGC-induced transparency in the four-level double-Λ system is scarcely investigated51,52.

Here, using the custom-designed resonant plasmon nanocavity with both large anisotropic Purcell factors and strong near-field excitation, we demonstrate linewidth-controllable and position-dependent polarized EIT spectra of a quantum system at the nanoscale (Fig. 1). we first analytically derive the double trapping of coherent populations in the double-Λ quantum system with the crossing damping. One is the two-photon resonance with the populations trapped in the two lower levels and the other is assisted by the crossing damping, where the populations can be coherently pulled into the two upper levels, yielding two transparent points in the EIT spectra. Using the evolution of the master equation, three-peaked and linewidth-controllable EIT spectra are obtained, in agreement with the outcomes from a dressed state analysis. The linewidths of three peaks can be effectively modulated by the level spacing of the upper levels, the Rabi frequencies and detunings of pump fields, and the Purcell factors. In particular, the linewidth of the central peak is extremely narrow, much less than the natural linewidth. This ultracompact plasmon-quantum combined system may have potential applications in the nonlinear quantum optics and quantum information processing.

Figure 1. The plasmon-quantum combined system.

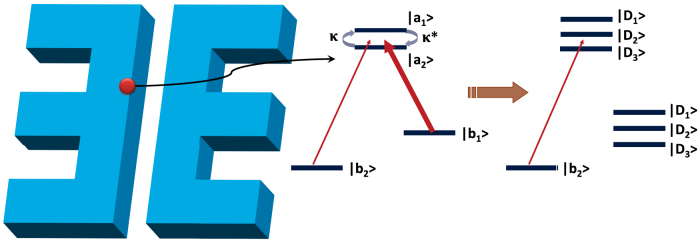
Figure 1

Open in a new tab

The schematics of a resonant silver nanocavity, a double-Λ quantum system with crossing damping between two closely lying upper levels, and its dressed states.

Results

Double trapping of coherent populations

Consider a closed double-Λ system with two closely lying upper levels |a1〉 and |a2〉 and two ground levels |b1〉 and |b2〉 (Fig. 1). Both transitions from upper levels |a1〉 with energy 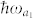Inline graphic and |a2〉 with energy 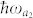Inline graphic to the lower level |b1〉 with energy 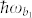Inline graphic are driven by a strong field with the frequency ν1 and detunings defined as 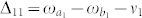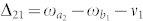Inline graphic, Inline graphic. Simultaneously, a weak probe field with the frequency ν2 acts on both transitions from |a1〉 and |a2〉 to |b2〉 with energy 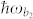Inline graphic and detunings are 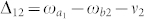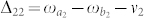Inline graphic, Inline graphic, respectively. These transitions are also coupled by the vacuum modes of electromagnetic fields. In the weak coupling region, with the Weisskopf-Wigner approximation, the spontaneous decay rate from the upper level |ai〉 to the ground level |bj〉 is γij, and the crossing damping between two close upper states is κ = κ1 + κ2. With the dipole and rotation-wave approximations, the interacting system can be described by the Hamiltonian in the interaction picture

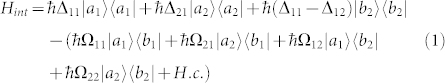graphic file with name srep02879-m1.jpg

where 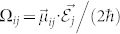Inline graphic, for i, j = 1, 2, is the Rabi frequency of the coherent field with the complex amplitude 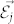Inline graphic coupling the transition from the upper level |ai〉 to the lower level |bj〉 with the corresponding electric dipole moment 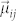Inline graphic. In the following, the coherent field 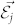Inline graphic can be provided at the nanoscale by a resonant plasmon cavity.

We can gain some physical insights underlying the transparency windows associated with the phenomena of coherent population trapping by finding the eigenstates of the state vectors which are decoupled from the vacuum modes to eliminate the fluorescense and thus the absorption. The trapping eigenstates corresponding to a zero eigenvalue will be the steady solution of equation (7) (see Methods), the existence of which requires

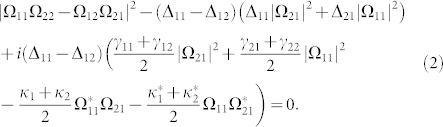graphic file with name srep02879-m2.jpg

This equation gives i) the conventional two-photon resonance condition (Δ11 = Δ12), which makes the population trapping in ground levels |b1〉 and |b2〉; and ii) the SGC-induced trapping condition

graphic file with name srep02879-m22.jpg
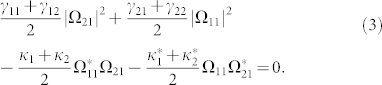graphic file with name srep02879-m3.jpg

The SGC-trapping leads to the population trapping in levels |a1〉, |a2〉, and |b1〉. According to the symmetry of the system, analogous trapping conditions for levels |a1〉, |a2〉, and |b2〉 exist. To obtain complete SGC-induced transparency, dipole moments between the closely lying transitions have to be parallel to generate the maximum destructive interference even with anisotropic Purcell factors. When double trapping occurs at the same point with Δ11 = Δ12 = ω12|Ω11|2/(|Ω11|2 + |Ω21|2), where 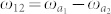Inline graphic is the upper spacing, the zero eigenvalue of equation (7) has twofold degeneracy and all the superpositions of the two corresponding eigenstates are trapping states. As shown in the methods, plasmon nanostructures can be used to control the decay rates γij and κi for i, j = 1 or 2 through nanoscale anisotropic Purcell factors.

Predictions of dressed state analysis

To explain the characteristics of the numerical absorption spectral profile in the following (Figs. 2, 3, and 5), now we give the dressed state analysis53. Writing the interaction Hamiltonian involving the strongly coupled levels |a1〉, |a2〉, and |b1〉 as

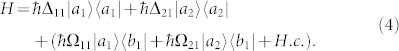graphic file with name srep02879-m4.jpg

We obtain expressions for its eigenvectors corresponding to eigenvalues λ1, λ2, and λ3

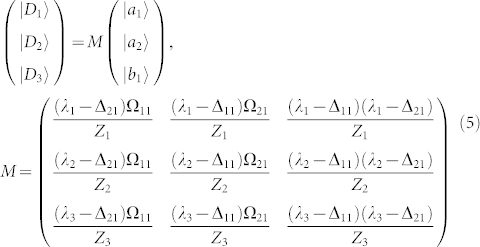graphic file with name srep02879-m5.jpg

where Zi = [(λi − Δ11)2(λi − Δ21)2 + (λi − Δ11)2|Ω21|2 + (λi − Δ21)2|Ω11|2]1/2. After considering the dissipation and the coupling of the weak probe field, we get the equations of motion for the density matrix of dressed states and especially the diagonal elements (for more details see Supplementary Equation 2). The absorption lines of the probe field are related to the fluorescence of spontaneously emitted photons for the same transition. Thus for simplicity we only pay attention to the modified decay rates of the diagonal matrix elements Inline graphic, since they determine separately the linewidths of the peaks in the absorption spectra and the spontaneously emission spectra, given by the expression

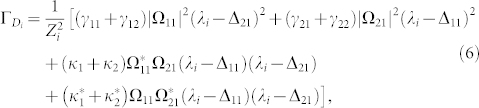graphic file with name srep02879-m6.jpg

where i = 1, 2, 3. According to the dressed state analysis, the positions and linewidths of the absorption lines can be predicted. The linewidths of the three-peaked absorption spectra can be effectively controlled by the level spacing, the Rabi frequencies and detunings of pump fields, and the Purcell factors.

Figure 2. Double trapping three-peaked EIT spectra.

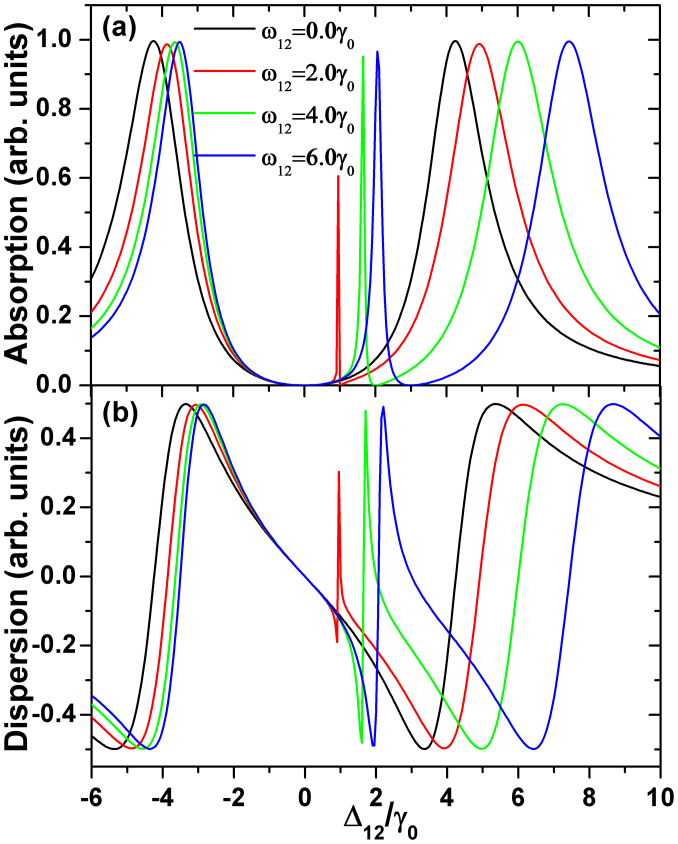
Figure 2

Open in a new tab

(a) Absorption and (b) dispersion as a function of the probe detuning Δ12 in a double-Λ system with parallel dipoles in an isotropic vacuum for upper spacing ω12 = 0.0γ0 (black), ω12 = 2.0γ0 (magenta), ω12 = 4.0γ0 (green), and ω12 = 6.0γ0 (blue). Ω11 = Ω21 = 3.0γ0, Ω12 = Ω22 = 0.03γ0, Γxx = Γzz = 1.0γ0, and the coupling detuning Δ11 = 0.0ω12.

Figure 3. The linewidth control of three peaks.

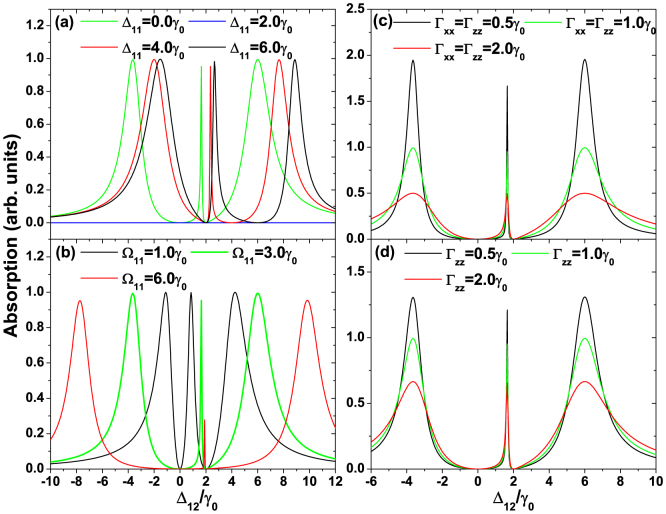
Figure 3

Open in a new tab

Absorption as a function of the probe detuning Δ12 in a double-Λ system with varying (a) coupling detunings Δ11, (b) coupling Rabi frequencies Ω11, (c) isotropic Purcell factors Γxx = Γzz, and (d) anisotropic Purcell factors Γzz. Other parameters remain the same as in Fig. 2 and ω12 = 4.0γ0.

Figure 4. The resonant silver nanocavity with the near field and Purcell factor distributions.

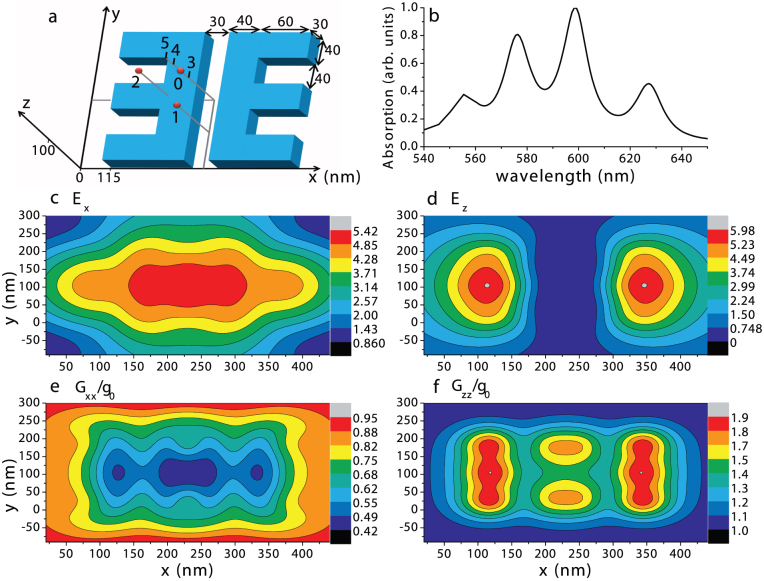
Figure 4

Open in a new tab

(a) Schematic of a resonant silver nanocavity and (b) its absorption. Near field distributions (c) Ex and (d) Ez, and anisotropic Purcell factors (e) Γxx/γ0 and (f) Γzz/γ0 on the xy-plane 70 nm from the metallic surface and at the wavelength of λ = 600 nm.

Figure 5. Polarized EIT spectra in a resonant plasmon nanocavity.

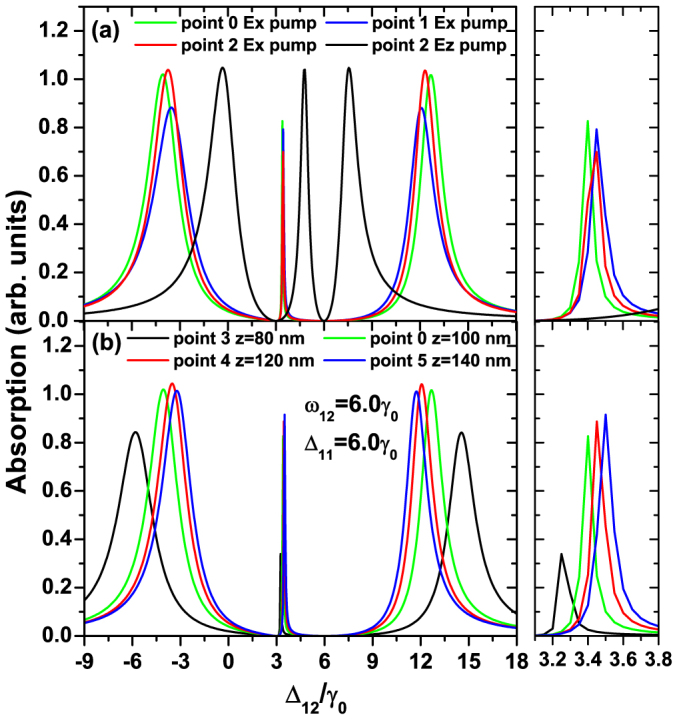
Figure 5

Open in a new tab

EIT spectra of the quantum system as a function of the probe detuning Δ12 for (a) different locations on the xy-plane of z = 100 nm and (b) different distances for z = 80, 100, 120, 140 nm. Right insets are the amplified center peaks.

Linewidth-controllable three-peaked EIT spectra

To fully investigate the double trapping on varies parameters, we numerically calculated the absorption spectra from the ground level |b2〉 to upper levels |a1〉 and |a2〉 through the standard approach based on the master equation for the density matrix elements (for more details see Supplementary Equation 1). The response of the quantum system to the probe field is governed by its polarization 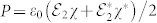Inline graphic and the susceptibility χ(ν2) is proportional to 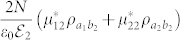Inline graphic. Dipole moments from the upper levels to one ground level in the double-Λ atomic system are assumed to be parallel to demonstrate double-trapping EIT and all dipole moments are set to be equal. Dipoles from the upper levels to different ground levels are orthogonal, one pair of which are along the z axis and the other along the x axis.

Full numerical calculations for the complex susceptibility as a function of the detuning of the probe field are presented in Fig. 2. The Rabi frequencies are Ω11 = Ω21 = 3.0γ0 and Ω12 = Ω22 = 0.03γ0, the detuning of the coupling field is fixed at Δ11 = 0.0ω12, and the Purcell factors are set to be Γxx = Γzz = 1.0γ0. The absorption spectra of the imaginary part of the susceptibility (Fig. 2a) show two transparency channels in an isotropic vacuum with the presence of the maximal SGC. The first type of transparency occurring at Δ12 = 0.0ω12 corresponds to the conventional EIT in a double-Λ system under the two-photon resonance condition, which is retained as the upper spacing ω12 varies. The corresponding dark state is the superposition of |b1〉 and |b2〉, the populations of which are inversely proportional to the square of Rabi frequencies. According to the population distribution for ω12 = 0.0γ0, the only transparency window in the spectrum should be classified as the first type. The second one at Δ12 = 0.5ω12, induced by SGC51, fulfils the condition in equation (3). In contrast to the EIT dark state with empty upper levels, the trapping state induced by the destructive interference has the distribution of 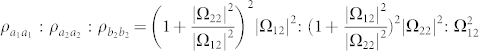Inline graphic. Thus, the population in |b2〉 increases with ω12. The population distributions from the analytical eigenstates for the zero eigenvalue of equation (7) are confirmed by the numerical results.

The real part of the susceptibility is proportional to the probe refraction and its dispersion is related to the group velocity. The double-Λ system provides a positive dispersion as in the usual EIT system and leads to subluminal light propagation with Vg < c. In Fig. 2b, the SGC-induced transparency is accompanied by a remarkably large slope for the real part of the susceptibility and therefore slow light propagation compared to the conventional EIT. The group velocity at the conventional EIT is invariant but the group velocity at the SGC-induced transparency drops as the upper spacing decreases, which confirms the different origin of the two types of transparency. Similar SGC effects for the group velocity in a V-type atomic system have been reported54. Removing SGC doesn't change the group velocity at the conventional EIT.

Since the ground level |b1〉 is coupled to two closely lying upper levels with a strong field, three peaks appear in the absorption spectrum, which characterizes the energy structure of the dressed state regardless of SGC. As shown in Fig. 2, the three peaks shift with the upper spacing ω12 in the absorption spectra and their positions exactly correspond to the eigenvalues of equation (4). Linewidths of the central peaks for ω12 = 2.0γ0, 4.0γ0, 6.0γ0 are increased as 0.010γ0, 0.101γ0, 0.257γ0, respectively, in agreement with the prediction of the dressed state analysis. In this case, the right peak widens but the left peak narrows with increasing upper level spacing. The destructive interference between parallel dipoles makes the sideband linewidths larger and the linewidth of central peak smaller.

The positions and linewidths of the absorption peaks also depend on the coupling detuning Δ11, the coupling Rabi frequency Ω11, and the anisotropic Purcell factors as shown in Fig. 3. As the coupling detuning grows, the conventional EIT window shifts along the same direction due to the two-photon resonance and the peak positions move with it, but the SGC-induced transparency point is fixed at the probe detuning of Δ12 = 2.0γ0. When Δ11 = 2.0γ0, the SGC-induced trapping condition for the coupling transition is satisfied and the transparency window extends within the whole range of the probe detuning as shown in Fig. 3a. Deviating from this value of the coupling detuning in both directions broadens the central peak, in agreement with a previous report52. Furthermore, as the coupling Rabi frequencies are increased, the separation between the peaks increases, but the two transparent points are fixed since both trapping conditions are not destroyed (Fig. 3b). Simultaneously, the central peak approaches the SGC-induced transparent point and becomes narrower and lower.

Figures 3c, d present the dependence of spectral linewidths on the Purcell factors. The Purcell factors don't affect the transparent points and the trapping population distributions. We can alter the decay rates and the cross damping of all the channels through an isotropic vacuum or change either pair of decay rates and cross damping to the same ground state by an anisotropic vacuum. When isotropic Purcell factors increase, the linewidths of three absorption peaks grow proportionally and the heights of peaks drop inversely. When only the Purcell factor along the z axis Γzz increases, similar effects happen with reduced magnitude. All numerical calculations of positions and linewidths of absorption peaks are consistent with the predictions of the dressed state analysis. The above results demonstrate the possibility to control the linewidths of the double-trapping EIT spectra by a custom-designed resonant plasmon nanocavity, which we now present.

Polarized EIT spectra in a resonant plasmon nanocavity

To realize the mechanism for double trapping of populations and allow experimental investigation of the three-peaked linewidth-controllable EIT spectra at the nanoscale, we propose a custom-designed hybrid system of the quantum system and the resonant plasmon nanocavity. The designed silver nanocavity has several features. In order to ensure effective near field excitation of the quantum system, the resonance wavelength of the plasmon nanocavity must match the wavelength of the pumping transition channels, i.e., the transitions from the upper levels |a1〉 and |a2〉 to the lower level |b1〉. The proposed back to back “E”-shaped design in Fig. 4a guarantees uniform distributions of electric fields and Purcell factors within an area of at least 100 × 100 nm2, where the quantum system can be located. Furthermore, in this area the near field is strongly enhanced, and the absolute values of the Purcell factors are reasonable and their anisotropy is very large, i.e., generally the value of Γzz/γ0 is much larger than that of Γxx/γ0. Crucially, using present nanofabrication techniques, this silver nanostructure can be successfully fabricated in the laboratory.

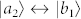To demonstrate the above properties, we use Green's tensor method55,56 (see Methods) with the mesh of 10 nm, to characterize the resonant silver subwavelength cavity of dimensions x × y × z = 230 × 200 × 30 nm3, as shown in Fig. 4a. Figure 4b displays its absorption spectrum showing several peaks, but the largest resonance is at the wavelength of λ = 600 nm which matches the transitions of Inline graphic and Inline graphic of the quantum system. It is noted that, for matching different quantum system, the resonant wavelength of plasmon nanocavity can be designed on demand. Then, we explored the near field distributions and Purcell factor distributions at λ = 600 nm. It is found that from z = 60 nm to z = 140 nm there are strong near field enhancement and large anisotropic Purcell factors. Increasing the distance from the metallic surface to the quantum system decrease the near fields and the Purcell factors approach 1.0. Most importantly, in the xy-plane, there is an area of about 100 × 100 nm2 with almost uniform electric fields and Purcell factors as shown in Figs. 4c–f. Generally, the larger the electric field Ex and the Purcell factor Γxx/γ0, the smaller Ez and Γzz/γ0, and vice versa. The anisotropy of electric fields guarantees both the polarized excitation of the quantum system and linewidth control using the near field (or Rabi frequencies) in EIT spectra, and the anisotropy of Purcell factors provides the effective control of linewidths of three EIT peaks.

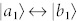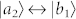In the xy-plane of z = 100 nm, we choose three points 0, 1, and 2, at which the quantum system can be located. They are shown in Fig. 4a, point 0 is at the center and points 1 and 2 are set as front and right 50 nm from the center. We let two sets of dipoles be orthogonal, one is along the x-axis and the other z-axis. 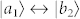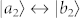First, we let the dipoles of Inline graphic and Inline graphic be excited by the optical near field Ex of the silver nanocavity and the dipoles of Inline graphic and Inline graphic are scanned by the probe field. It is found that the positions and linewidths of the three peaks in EIT spectra are not very sensitive to the location of the quantum system, shown as the green, blue and red curves in Fig. 5a (the right part of which shows the linewidth details of the central peak), which comes from the uniform design of electric field and Purcell factor distributions. Next, we let the channels of excitation and scanning be exchanged. At points 0 and 1, the three-peaked EIT spectra are not presented due to very weak near fields (not shown in the figure). However, for point 2, when the quantum system is excited by the near field of the z direction, there is an obvious change in positions and linewidths of three peaks, shown as black curves in Fig. 5a. Thus for the near field excitation of different directions, polarized EIT spectra are clearly observed.

Finally, we calculate the EIT spectra of the quantum system at the center for the different distance from the metallic surface at z = 80 nm (point 3), 100 nm, 120 nm (point 4), and 140 nm (point 5), respectively. The results, shown in Fig. 5b with the right part of amplified central peaks, indicate that the peaks and widths of three peaks are very sensitive to the distance of the quantum system from the metallic surface due to the strong modification of near fields and Purcell factors. To sum up, position-dependent linewidth-controllable polarized EIT spectra of the designed quantum system is realized at the nanoscale in a plasmon nanocavity.

Discussion

It is noted that, in the above SGC-induced trapping condition [equation (3)] of a quantum system with crossing damping, it is required that the two sets of dipoles are strictly parallel. This is difficult to fulfil in a general atomic system, thus experimental realizations of this kind of system are seldom investigated52,57. One possible scheme to observe the phenomena experimentally is using the Rubidium 85 hyperfine structure52. The two ground states |b1〉 and |b2〉 are 5S1/2, F = 3 and 5S1/2, F = 2. The upper state 5P1/2, F = 3 is coupled to 5D3/2, F = 4 by a strong field. Thus the upper state splits into two dressed states corresponding to |a1〉 and |a2〉, according to the dressed state analysis. 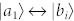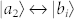Then the atomic system can fulfill the trapping condition that dipoles between Inline graphic and Inline graphic (for i = 1, 2) are parallel. Another potential quantum system to form the above four-level system is dual CdSe/ZnS/CdSe nanocrystals58,59. Their photoluminescence peak positions lie in the optical window, such as λ = 600 nm, and their lifetime is on the order of nanoseconds. The position of each state in both the nanostructures isolated by the wide band gap barrier can be independently tuned, which leads to a design of the desired four-level system by changing materials and sizes. Furthermore, altering the thickness of the barrier layer can control the coupling between the two upper states.

In summary, we have theoretically investigated the EIT of the four-level double-Λ quantum system and its nanoscale realization in the resonant plasmon nanocavity. We have first analytically derived the double trapping conditions of populations, leading to two transparent points in the EIT spectra. By evaluating the master equations, we have numerically obtained the three-peaked linewidth-controllable EIT spectra, and found the positions and linewidths of peaks in agreement with the predictions of the dressed state analysis. Further numerical investigations indicate that the linewidths of these peaks can be well modulated by the level spacing of two upper levels, pump Rabi frequencies and detunings, and isotropic and anisotropic Purcell factors. Finally, the combined system, composed of the custom-designed resonant plasmon nanocavity and the quantum system, has been proposed to realize the three-peaked linewidth-controllable polarized EIT spectra at the nanoscale. This study bridges the fields of traditional quantum optics and plasmonics associated with the strong near field enhancement and ultrasmall optical mode area and will benefit low photon number quantum nonlinear optics and quantum information processing.

Methods

The equations of motion for the state vectors

With the Weisskopf-Wigner approximation, the dissipation is incorporated via the equations of motion for the state vectors, A1(t), A2(t), B1(t), and B2(t):

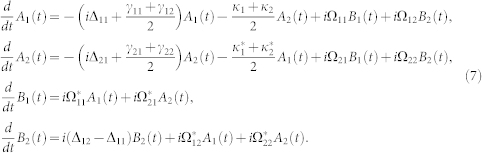graphic file with name srep02879-m7.jpg

The upper spacing ω12 is much less than the dipole transition frequencies, guaranteeing that the dipole moments between the upper levels and one of the ground levels interact with the common electromagnetic vacuum. This leads to crossing damping terms κ = κ1 + κ2 and 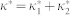Inline graphic, which represent the quantum interference between the spontaneous emission pathways and strongly depend on the properties of the vacuum. In a general vacuum with anisotropic Purcell factors, the intersection angle between the dipole moment 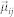Inline graphic and the x axis is θij, for i, j = 1, 2. 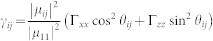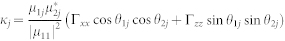If we let the y axis be the quantum axis, the damping terms are given by Inline graphic and Inline graphic, for i, j = 1, 2, where Γzz/γ0 and Γxx/γ0 are the Purcell factors in the x and z directions, and 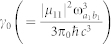Inline graphic is the decay rate in a vacuum for the transition between |a1〉 and |b1〉. According to these expressions, large values of crossing damping, which lead to destructive interference, appear in a vacuum only with nearly parallel dipoles48 or in an anisotropic vacuum even with orthogonal dipoles19,49.

Green's tensor method

In the design of resonant plasmon nanostructure, Green's tensor method for solving the near field and anisotropic Purcell factors is used55,56. When an arbitrary shaped subwavelength structure with the electric permittivity Inline graphic embedded in the homogeneous bulk material with Inline graphic, the field E(r) at any point r satisfies the Lippmann-Schwinger equation

graphic file with name srep02879-m8.jpg

where V denotes the clusters subspace, 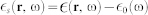Inline graphic, and Green's tensor in a three dimensional system is

graphic file with name srep02879-m9.jpg

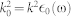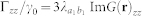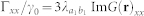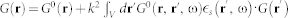where R = |R| = |r − r′| and Inline graphic. The needed anisotropic Purcell factors17,18,60 can be expressed as the Green's tensor coefficients Inline graphic and Inline graphic in the x and z directions, where Inline graphic.

Author Contributions

Y.G. and L.J.W. conceived the study. L.J.W. derived the formulas and wrote the computational program. Y.G. and H.Y.C. designed the plasmon structure. J.Y.Z., Y.P.C., and B.D.G. designed the energy structure of quantum systems. L.J.W., Y.G., and Q.H.G. analysized the results and wrote the paper. B.D.G. polished the paper. Q.H.G. supervised the study and commented on the paper.

Supplementary Material

Supplementary Information

Polarized linewidth-controllable double-trapping electromagnetically induced transparency spectra in a resonant plasmon nanocavity

srep02879-s1.pdf (29.7KB, pdf)

Acknowledgments

This work was supported by the National Key Basic Research Program under Grant No. 2013CB328700 and National Natural Science Foundation of China under Grants No. 11374025,91121018,91221304, and 11121091. BDG acknowledges financial support from the Royal Society, EPSRC UK, and the ERC.

References

  1. Raether H. Surface Plasmons (Springer-Verlag, Berlin, 1988). [Google Scholar]
  2. Brongersma M. L. & Shalaev V. M. The case for plasmonics. Science 328, 440–441 (2010). [DOI] [PubMed] [Google Scholar]
  3. Chance R. R., Prock A. & Silbey R. J. Comments on the classical theory of energy transfer. J. Chem. Phys. 62, 2245–2253 (1975). [Google Scholar]
  4. Ruppin R. Decay of an excited molecule near a small metal sphere. J. Chem. Phys. 76, 1681–1684 (1982). [Google Scholar]
  5. Jun Y. C., Kekatpure R. D., White J. S. & Brongersma M. L. Nonresonant enhancement of spontaneous emission in metal-dielectric-metal plasmon waveguide structures. Phys. Rev. B 78, 153111 (2008). [Google Scholar]
  6. Chen Y., Nielsen T. R., Gregersen N., Lodahl P. & Mørk J. Finite-element modeling of spontaneous emission of a quantum emitter at nanoscale proximity to plasmonic waveguides. Phys. Rev. B 81, 125431 (2010). [Google Scholar]
  7. Andersen M. L., Stobbe S., Sørensen A. S. & Lodahl P. Strongly modified plasmon-matter interaction with mesoscopic quantum emitters. Nat. Phys. 7, 215–218 (2011). [Google Scholar]
  8. Lakowicz J. R. Plasmonics in biology and plasmon-controlled fluorescence. Plasmonics 1, 5–33 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Anger P., Bharadwaj P. & Novotny L. Enhancement and quenching of single-molecule fluorescence. Phys. Rev. Lett. 96, 113002 (2006). [DOI] [PubMed] [Google Scholar]
  10. Kühn S., Håkanson U., Rogobete L. & Sandoghdar V. Enhancement of single-molecule fluorescence using a gold nanoparticle as an optical nanoantenna. Phys. Rev. Lett. 97, 017402 (2006). [DOI] [PubMed] [Google Scholar]
  11. Bharadwaj P. & Novotny L. Spectral dependence of single molecule fluorescence enhancement. Opt. Express 15, 14266–14274 (2007). [DOI] [PubMed] [Google Scholar]
  12. Kulakovich O. et al. Enhanced luminescence of CdSe quantum dots on gold colloids. Nano Lett. 2, 1449–1452 (2002). [Google Scholar]
  13. Tam F., Goodrich G. P., Johnson B. R. & Halas N. J. Plasmonic enhancement of molecular fluorescence. Nano Lett. 7, 496–501 (2007). [DOI] [PubMed] [Google Scholar]
  14. Akimov A. V. et al. Generation of single optical plasmons in metallic nanowires coupled to quantum dots. Nature 450, 402–406 (2007). [DOI] [PubMed] [Google Scholar]
  15. Chang D. E., Sørensen A. S., Hemmer P. R. & Lukin M. D. Quantum optics with surface plasmons. Phys. Rev. Lett. 97, 053002 (2006). [DOI] [PubMed] [Google Scholar]
  16. Chang D. E., Sørensen A. S., Demler E. A. & Lukin M. D. A single-photon transistor using nanoscale surface plasmons. Nat. Phys. 3, 807–812 (2007). [Google Scholar]
  17. Gu Y., Huang L., Martin O. J. F. & Gong Q. Resonance fluorescence of single molecules assisted by a plasmonic structure. Phys. Rev. B 81, 193103 (2010). [Google Scholar]
  18. Marty R., Arbouet A., Paillard V., Girard C. & Colas des Francs C. Photon antibunching in the optical near field. Phys. Rev. B 82, 081403(R) (2010). [Google Scholar]
  19. Gu Y. et al. Surface-plasmon-induced modification on the spontaneous emission spectrum via subwavelength-confined anisotropic Purcell factor. Nano Lett. 12, 2488–2493 (2012). [DOI] [PubMed] [Google Scholar]
  20. Harris S. E. Electromagnetically induced transparency. Phys. Today 50, 36–42 (1997). [Google Scholar]
  21. Fleischhauer M., Imamoglu A. & Marangos J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005). [Google Scholar]
  22. Alzetta G., Gozzini A., Moi L. & Orriols G. Experimental-method for observation of RF transitions and laser beat resonances in oriented Na vapor. Nuovo Cimento B 36, 5–20 (1976). [Google Scholar]
  23. Arimondo E. Coherent population trapping in laser spectroscopy. Progress in Optics 35, 257–354 (1996). [Google Scholar]
  24. Schmidt H. & Imamoğlu A. Giant Kerr nonlinearities obtained by electromagnetically induced transparency. Opt. Lett. 21, 1936–1938 (1996). [DOI] [PubMed] [Google Scholar]
  25. Wang H., Goorskey D. & Xiao M. Enhanced kerr nonlinearity via atomic coherence in a three-level atomic system. Phys. Rev. Lett. 87, 073601 (2001). [DOI] [PubMed] [Google Scholar]
  26. Kang H.-S. & Zhu Y.-F. Observation of large kerr nonlinearity at low light intensities. Phys. Rev. Lett. 91, 093601 (2003). [DOI] [PubMed] [Google Scholar]
  27. Wu Y., Saldana J. & Zhu Y.-F. Large enhancement of four-wave mixing by suppression of photon absorption from electromagetically induced transparency. Phys. Rev. A 67, 013811 (2003). [Google Scholar]
  28. Li Y.-Q. & Xiao M. Enhancement of nondegenerate four-wave mixing based on electromagnetically induced transparency in rubidium atoms. Opt. Lett. 21, 1064–1066 (1996). [DOI] [PubMed] [Google Scholar]
  29. Zhang Y., Brown A. W. & Xiao M. Opening four-wave mixing and six-wave mixing channels via dual electromagnetically induced transparency windows. Phys. Rev. Lett. 99, 123603 (2007). [DOI] [PubMed] [Google Scholar]
  30. Kang H.-S., Hernandez G. & Zhu Y.-F. Slow-light six-wave mixing at low light intensities. Phys. Rev. Lett. 93, 073601 (2004). [DOI] [PubMed] [Google Scholar]
  31. Lu B.-L., Burkett W. H. & Xiao M. Nondegenerate four-wave mixing in a double-Lambda system under the influence of coherent population trapping. Opt. Lett. 23, 804–806 (1998). [DOI] [PubMed] [Google Scholar]
  32. Braje D. A., Balić V., Goda S., Yin G. Y. & Harris S. E. Frequency mixing using electromagnetically induced transparency in cold atoms. Phys. Rev. Lett. 93, 183601 (2004). [DOI] [PubMed] [Google Scholar]
  33. Petch J. C., Keitel C. H., Knight P. L. & Marangos J. P. Role of electromagnetically induced transparency in resonant four-wave-mixing schemes. Phys. Rev. A 53, 543–561 (1996). [DOI] [PubMed] [Google Scholar]
  34. Li S. et al. Enhanced cross-phase modulation based on a double electromagnetically induced transparency in a four-level tripod atomic system. Phys. Rev. Lett. 101, 073602 (2008). [DOI] [PubMed] [Google Scholar]
  35. Shiau B.-W., Wu M.-C., Lin C.-C. & Chen Y.-C. Low-light-level cross-phase modulation with double slow light pulses. Phys. Rev. Lett. 106, 193006 (2011). [DOI] [PubMed] [Google Scholar]
  36. Fleischhauer M. & Lukin M. D. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094–5097 (2000). [DOI] [PubMed] [Google Scholar]
  37. Lobino M., Kupchak C., Figueroa E. & Lvovsky A. I. Memory for light as a quantum process. Phys. Rev. Lett. 102, 203601 (2009). [DOI] [PubMed] [Google Scholar]
  38. Eisaman M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837–841 (2005). [DOI] [PubMed] [Google Scholar]
  39. Mucke M. et al. Electromagnetically induced transparency with single atoms in a cavity. Nature 465, 755–758 (2010). [DOI] [PubMed] [Google Scholar]
  40. van der Wal C. H. et al. Atomic memory for correlated photon states. Science 301, 196–200 (2003). [DOI] [PubMed] [Google Scholar]
  41. Liu C., Dutton Z., Behroozi C. H. & Hau L. V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490–493 (2001). [DOI] [PubMed] [Google Scholar]
  42. Bergmann K., Theuer H. & Shore B. W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 70, 1003–1025 (1998). [Google Scholar]
  43. Kok P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007). [Google Scholar]
  44. Choi K. S., Deng H., Laurat J. & Kimble H. J. Mapping photonic entanglement into and out of a quantum memory. Nature 452, 67–u4 (2008). [DOI] [PubMed] [Google Scholar]
  45. Lukin M. D. & Imamoğlu A. Nonlinear optics and quantum entanglement of ultraslow single photons. Phys. Rev. Lett. 84, 1419–1422 (2000). [DOI] [PubMed] [Google Scholar]
  46. Zhu S.-Y. & Scully M. O. Spectral line elimination and spontaneous emission cancellation via quantum interference. Phys. Rev. Lett. 76, 388–391 (1996). [DOI] [PubMed] [Google Scholar]
  47. Gu Y. et al. Intrinsic quantum beats of atomic populations and their nanoscale realization through resonant plasmonic antenna. Plasmonics 7, 33–38 (2012). [Google Scholar]
  48. Zhou P. & Swain S. Ultranarrow spectral lines via quantum interference. Phys. Rev. Lett. 77, 3995–3998 (1996). [DOI] [PubMed] [Google Scholar]
  49. Paspalakis E. & Knight P. L. Phase control of spontaneous emission. Phys. Rev. Lett. 81, 293–296 (1998). [Google Scholar]
  50. Purcell E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946). [Google Scholar]
  51. Wang D. & Zheng Y. Quantum interference in a four-level system of a 87Rb atom: Effects of spontaneously generated coherence. Phys. Rev. A 83, 013810 (2011). [Google Scholar]
  52. Wang C.-L. et al. Investigation of spontaneously generated coherence in dressed states of 85Rb atoms. Opt. Lett. 33, 687–689 (2008). [DOI] [PubMed] [Google Scholar]
  53. Cohen-Tannoudji C. & Reynaud S. Dressed-atom description of resonance fluorescence and absorption spectra of a multi-level atom in an intense laser beam. J. Phys. B 10, 345–363 (1977). [Google Scholar]
  54. Antón M. A. & Carreño F. Optical light storage in an ensemble of V-type atoms mediated by vacuum induced coherence. Opt. Commun. 282, 3964–3976 (2009). [Google Scholar]
  55. Gu Y., Chen L., Zhang H. & Gong Q. Resonance capacity of surface plasmon on subwavelength metallic structures. Europhys. Lett. 83, 27004 (2008). [Google Scholar]
  56. Martin O. J. F., Girard C. & Dereux A. Generalized field propagator for electromagnetic scattering and light confinement. Phys. Rev. Lett. 74, 526–529 (1995). [DOI] [PubMed] [Google Scholar]
  57. Xia H.-R., Ye C.-Y. & Zhu S.-Y. Experimental Observation of spontaneous emission cancellation. Phys. Rev. Lett. 77, 1032–1034 (1996). [DOI] [PubMed] [Google Scholar]
  58. Battaglia D., Blackman B. & Peng X. Coupled and decoupled dual quantum systems in one semiconductor nanocrystal. J. Am. Chem. Soc. 127, 10889–10897 (2005). [DOI] [PubMed] [Google Scholar]
  59. Tyagi P. & Kambhampati P. Independent control of electron and hole localization in core/barrier/shell nanostructures. J. Phys. Chem. C 116, 8154–8160 (2012). [Google Scholar]
  60. Barnett S. M., Huttner B., Loudon R. & Matloob R. Decay of excited atoms in absorbing dielectrics. J. Phys. B 29, 3763–3781 (1996). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Polarized linewidth-controllable double-trapping electromagnetically induced transparency spectra in a resonant plasmon nanocavity

srep02879-s1.pdf (29.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES