Chiral heliconical ground state of nanoscale pitch in a nematic liquid crystal of achiral molecular dimers

Significance

The appearance of new nematic liquid crystal (LC) equilibrium symmetry (ground state) is a rare and typically important event. The first and second nematics were the helical phase and blue phase of chiral molecules, both found in 1886 in cholesteryl benzoate by Reinitzer, discoveries that marked the birth of LC science. The third nematic, the achiral uniaxial phase, also found in the 19th century, ultimately formed the basis of LC display technology and the portable computing revolution of the 20th century. Despite this achievement, the 20th can claim only the fourth nematic, the lyotropic biaxial phases found by Saupe. Now, early in the 21st, the heliconical structure of the fifth nematic is observed, an exotic chiral helix from achiral molecules.

Abstract

Freeze-fracture transmission electron microscopy study of the nanoscale structure of the so-called “twist–bend” nematic phase of the cyanobiphenyl (CB) dimer molecule CB(CH₂)₇CB reveals stripe-textured fracture planes that indicate fluid layers periodically arrayed in the bulk with a spacing of d ∼ 8.3 nm. Fluidity and a rigorously maintained spacing result in long-range-ordered 3D focal conic domains. Absence of a lamellar X-ray reflection at wavevector q ∼ 2π/d or its harmonics in synchrotron-based scattering experiments indicates that this periodic structure is achieved with no detectable associated modulation of the electron density, and thus has nematic rather than smectic molecular ordering. A search for periodic ordering with d ∼ in CB(CH₂)₇CB using atomistic molecular dynamic computer simulation yields an equilibrium heliconical ground state, exhibiting nematic twist and bend, of the sort first proposed by Meyer, and envisioned in systems of bent molecules by Dozov and Memmer. We measure the director cone angle to be θ_TB ∼ 25° and the full pitch of the director helix to be p_TB ∼ 8.3 nm, a very small value indicating the strong coupling of molecular bend to director bend.

Recently there has been growing interest in the liquid crystal (LC) phase behavior of achiral dimer molecules, such as cyanobiphenyl-(CH₂)_n-cyanobiphenyl (CBnCB), shown for n = 7 in Fig. 1A (1, 2). This arises from the observation of a transition in these mesogens from a typical nematic (N) to a lower-temperature (NX) phase, also apparently nematic, which exhibits a variety of unusual characteristics (3–10). These include: (i) textural features in depolarized transmission light microscopy (DTLM) similar to those found in fluid, lamellar smectic phases but with no X-ray scattering to indicate lamellar ordering of molecules (8); (ii) a variety of other completely unfamiliar DTLM textures (6), including the spontaneous appearance of director field deformation and evidence for small Frank elastic constants (3); (iii) evidence for the chiral molecular organization on the NMR timescale (4), and in macroscopic conglomerate domains in electrooptic experiments on monodomain textures (9); (iv) distinctive odd/even effects in the linker length n, including, in particular, that i–iii are found only in the n-odd homologs (6).

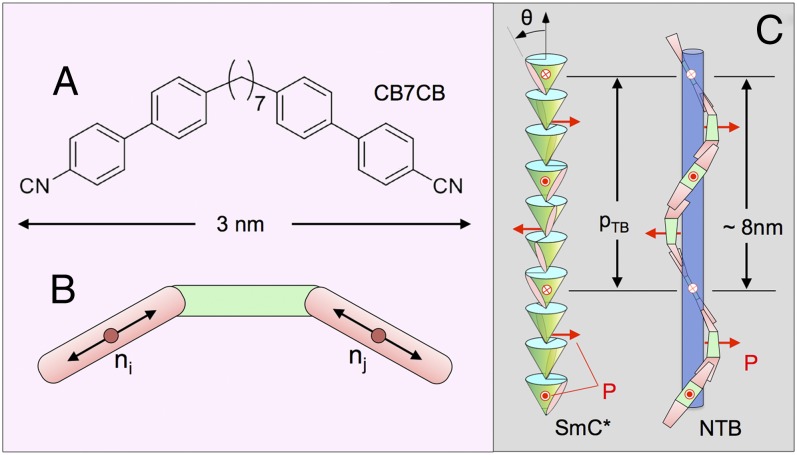
Fig. 1.

(A) Structure of CB7CB [4′,4′-(heptane-1,7-diyl)bis(([1′,1″-biphenyl]-4″-carbo-nitrile))]. The end-to-end length of its van der Waals surface is ∼3.0 nm in the all-trans molecular configuration. (B) CB7CB molecule can be viewed as having three parts, each ∼1 nm in length: two rigid end groups connected by a flexible spacer. The nematic director field n(r) is the local average orientation of the n_i, the long axes of the rigid end groups, each contributing to n(r) at its red circles. (C) Schematic illustration of the heliconical TB structures in the layered chiral SmC* phase and in the layerless NTB phase. The NTB drawing is a qualitatively correct representation of the TB structure found in CB7CB, in which any interval along the helix of single pitch length p_TB ∼ 8 nm includes, on average, four overlaps of 1-nm-long rigid ends and four intervals of 1-nm-long flexible spacers.

These observations, combined with the fact that the all-trans conformations of the n-odd homologous dimers are distinctly bent (Fig. 1B), have led to the notion that the NX is a “twist–bend” (TB) phase, sketched in Fig. 1C, a nematic having a conically helixed ground state of the sort originally proposed by Meyer as the result of the spontaneous appearance of bend flexoelectric polarization (11). More recently Dozov proposed such a ground state as a spontaneously chiral conglomerate domain stabilized by molecular bend (12), and Memmer obtained such structures in computer simulations of systems of bent Gay–Berne dimers (13). This ground-state helix can be written for CB7CB in terms of a half-molecular director n(z), in this case the local average orientation of the long axis of a biphenyl half-molecular core, taken to be located at the center of the bond between its rings (Fig. 1B). Given by n(z) = zcosθ_TB + sinθ_TB(xsinφ + ycosφ) (11), the half-molecular director of the TB ground state reorients on a cone of angle θ_TB coaxial with the helix axis z through azimuthal angle φ = 2πz/p_TB, where θ is the average over the distribution of core tilts from z and p_TB is the pitch, in a fashion similar to that of the molecular director helix in a chiral smectic C, shown in Fig. 1D, but in this case without smectic layering. Because such a helical nematic has no molecular positional layering and, in addition, has the same signs and magnitudes of director deformation (bend and twist) everywhere, the director distortion magnitude has complete translational symmetry. As a result, scattering probes of either mass or electron density, such as nonresonant X-ray or neutron scattering, should not exhibit Bragg diffraction from the helix (14). To date there have been no structural observations to confirm a nematic TB ground state, nor measurement of pitch, p_TB, its basic parameter, predicted by modeling (12) and suggested in simulations of bent-core mesogens (13) to be on the order of a few molecular lengths. Here we report the results of a combined freeze-fracture transmission electron microscopy (FFTEM), synchrotron X-ray diffraction (XRD), and atomistic molecular dynamic (MD) computer simulation study of the nanoscale structure of the NX phase of the CB7CB dimer. The FFTEM experiments show 2D fracture faces modulated by textures of quasiperiodic nanoscale stripes, indicative of a 3D bulk layer-like ordering that the XRD shows to be of spatially uniform density, and thus nematic rather than smectic (molecularly positioned) in nature. Equilibration of structures of the measured p_TB ∼ 8 nm spacing using MD simulation robustly relaxes to the heliconical nematic TB ground state of Meyer (11), Dozov (12), and Memmer (13), showing that the “layers” in 3D found in the FFTEM are not images of molecular scale interfaces, but rather are 2D surfaces of constant azimuthal phase of the heliconical precession. We will therefore follow ref. 4 and refer to the NX phase of CB7CB as the NTB phase.

CB7CB (1) was synthesized from 1,7-bis(4′-bromophenyl)heptane-1,7-dione (SI Appendix, Materials and Methods), and the resulting sample characterized with respect to its LC phase behavior using differential scanning calorimetry and depolarized transmitted light microscopy (DTLM) with a temperature-controlled hot stage. The observed transitions, isotropic (I) → 112 °C → N → 99 °C → NTB (cooling), and I ← 113 °C ← N ← 100 °C ← NTB (heating), are in substantial agreement with literature values (1, 2, 8, 15).

Results

Typical fracture topography of CB7CB in the NTB phase (T = 90 °C) is shown in Fig. 2, where the red arrow indicates the azimuthal direction of incidence of the Pt evaporation and the image is such that the shadowed areas having least Pt are darkest. A pattern of quasiperiodic, curved stripes of spacing d_p(x, y) covers most of the image area of the x, y fracture plane of Fig. 2A. To begin the discussion of these images, we point out explicitly that the term “layers” refers to elements of a periodic stacking of fluid sheet-like structures in 3D space, whereas “stripes” refers to the 2D periodic patterns of intersection of this 3D structure with the 2D fracture surface. We show explicitly in the discussion of the atomistic computer simulations below that the 3D periodic stacking is a heliconical spiral of the director of pitch p_TB so that the layers are 2D surfaces of constant azimuthal phase in this heliconical precession, spaced by p_TB. The spatial variation of d_p(x, y) indicates that ψ(x, y), the angle between the fracture plane normal and the helix axis z, depends on position in the image (SI Appendix, Fig. S1). For a 3D bulk layered system of period d, the apparent 2D stripe spacing d_p in the fracture plane when the 3D helix axis z is at an angle ψ with respect to the fracture surface normal is d_p = d/sinψ, so that the smallest stripe period corresponds to the bulk spacing at ψ = 90°. The persistent texture of intersecting sets of nested rings of stripes in the 2D fracture planes reveals a 3D structural theme of fluid, quasiperiodically spaced layers in the form of focal conic domains (SI Appendix, Fig. S1). Quite remarkable are the lines corresponding to the conic sections defining the domains (circles), identified by rows of cusps in the 2D stripes (Fig. 2B) (16). In such cases, the conic sections in the fracture plane yield sets of rings that run down to very small radii (Fig. 2C), and, because the d_p is smallest in these areas, these layers must be perpendicular to the fracture plane (ψ ∼ 90°) (16). Therefore, the in-plane stripe spacing d_p(x, y) in these domains, which we find by direct measurement on the images and Fourier analysis to be d = 8.3 ± 0.2 nm, can be taken to be the bulk layer spacing d, in this case at T = 90 °C in the thermotropic NTB phase.

Fig. 2.

FFTEM image of CB7CB quenched from the NTB phase at T = 95 °C, with the Pt shadowing direction indicated by the magenta arrow. (A) The fracture face exhibits a 2D texture of curved, periodically arrayed stripes indicative of a bulk, fluid, layered structure of 3D focal conics domains with conic section lines, respectively, parallel to and normal to the fracture surface in B and C. The bulk layer spacing is that observed in C, where the layers are normal to the fracture plane (SI Appendix, Fig. S1). The evident tendency for the fracture plane to run normal to the layers distinguishes TB layering from smectics, where fractures are mostly between the layers (SI Appendix, Figs. S2 and S3). (Scale bar, 100 nm.)

The FFTEM image of a 2D slice of 3D focal conics exemplified by Fig. 2A exhibits FFTEM imaging characteristics that are distinctly different from those of fluid layered liquid crystal systems such as chiral nematics, smectics, and columnar phases, as follows. In FFTEM images of the 1D and 2D ordering of smectic and columnar LCs, respectively, fracture planes have a strong tendency to follow the interfaces between layers, so that the images are dominated by smooth layer interface surfaces with only occasional layer edges (SI Appendix, Figs. S2 and S3, ref. 17). In columnar phases, the translational ordering within the layers is then evident in the smooth layer surfaces (SI Appendix, Fig. S3). The FFTEM images of CB7CB show none of these features, but rather exhibit a strong tendency to fracture in planes nearly normal to the layers. We take this observation to be evidence for the translational invariance of the helical structure, i.e., the absence of distinct layer interfaces on the molecular scale enabling a less well-confined fracture plane. Even in Fig. 2B, where the layers reorient to be nearly parallel to the fracture plane, the layer steps remain rather indistinct compared with those of typical smectics (SI Appendix, Figs. S1 and S2). The proposed TB nematic is basically a continuous network of overlapping dimers with no weak interfaces parallel to the layers susceptible to fracture. In contrast, fracture parallel to the helix axis requires only the breaking of side-to-side molecular contacts. Additionally, the fractures exhibit no periodicity other than the d ∼ 8 nm layer modulation, i.e., the fracture faces are quite irregular, even where the layers are oriented normal to the fracture plane, showing no evidence for 2D ordering. The distinction between the fracture of end-to-end contacts and side-to-side contacts enables freeze fracture to visualize director distortion in nematics (18, 19), including the helical ordering of chiral nematic (18, 20) and blue phases (18, 20, 21) on the >100-nm length scale. The present results extend the application of the FFTEM technique down to the 8-nm scale in nematics, where it also appears to be quite effective.

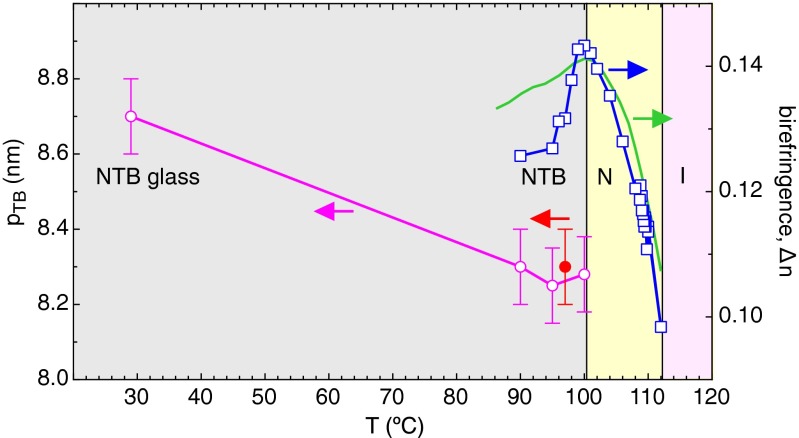
A selection of images from replicas of the NTB phase, quenched from T = 90, 95, 100, and 105 °C (SI Appendix, Figs. S1, S4–S10, S14, and S15), shows that at T = 90 and 95 °C, virtually all areas of the replicas that are recovered and imaged exhibit ∼8-nm stripes. At T = 100 °C, patches without stripes begin to appear, coexisting with striped domains and exhibiting only larger-scale roughness (SI Appendix, Figs. S9 and S10). Fig. 3 compares this stripeless state to examples of the stripe texture at higher magnification. At T = 105 °C no stripes are seen anywhere on the replicas: only the larger-scale roughness is observed, confirming that the stripe pattern is a property of the NTB phase. Remarkably, the NTB layering can also be observed near room temperature (T = 29 °C) in the deeply supercooled NTB glassy state, i.e., when the sample is cooled over a 1-min period from T = 95 °C to T = 29 °C and then quenched (SI Appendix, Figs. S11–S13). The stripe contrast, bulk layer spacing, and patterns exhibit only subtle changes over this entire range of thermotropic and supercooled NTB phase (Fig. 4). A mixture with 25% by weight of the monomer cyanobiphenyl 5CB yielded d = 8 nm layer spacing.

Fig. 3.

(A and B) Comparison of CB7CB FFTEM images of the N phase quenched at T = 105 °C and of the NTB phase quenched at T = 95 °C, showing the absence of fracture surface periodicity in the N phase. (Scale bar, 100 mn.)

Fig. 4.

Temperature dependence of the helix pitch of the NTB phase p_TB(T) and of the birefringence Δn(T) (□) of CB7CB in the N and NTB phases. The pitch obtained from the FFTEM images (○) exhibits little variation with T (less than 5% over the whole NTB range). The solid circle (●) gives p_TB from the MD computer simulation of Fig. 6. Birefringence grows on cooling in the N phase, as is typical. The deuterium magnetic resonance (DMR) splitting-determined orientational order parameter of deuterated 8CB solute in CB7CB, proportional to the solid green line (8), is a measure of Δn(T) in the N phase and is consistent with the optical Δn(T) in the N phase. In the NTB phase Δn(T) decreases with the onset of biaxial ordering, in a fashion different from the DMR splitting.

Pursuit of the idea that the stripe patterns in the FFTEM images represent the TB helix in the NTB phase requires determining the relationship between the bulk stripe period d, as determined from the FFTEM, and the pitch of the TB helix p_TB, defined in Fig. 1. Considering the predominant case in the FFTEM where the helix axis is nearly parallel to the fracture plane, Fig. 1B shows that, whereas at each z within the 2π azimuthal reorientation period defining p_TB the helix has a distinct azimuthal orientational state, the cases of n(z) being either parallel or normal to the fracture plane actually occur twice within each pitch. If, for example, each dark stripe corresponded to a position where the molecules were simply parallel to the surface, then the TB helix pitch would be p_TB = 2d, twice the FFTEM stripe period. However, in such a case alternate stripes would correspond to alternate tilt of n relative to z in the fracture plane. Given the broad range of fracture circumstances evident in the FFTEM images shown in this article, such an alternation in tilt would inevitably, under some conditions, lead to an alternation in the appearance of the even and odd stripes. The stripe pattern would then exhibit a cell doubling, indicating a unit cell of two stripes and a pitch of 2d. However, we have never found any evidence for such a cell doubling in any of the hundreds of FFTEM images of the CB7CB NTB phase that we have studied, including the ones presented here. In the Fourier transforms of the stripe pattern intensity, such a cell doubling would show up as a subharmonic Bragg reflection at q ∼ 0.5*(2π/(8.3 nm)), at half the wavevector of the fundamental stripe period. We have searched our images for both stripe alternation and half-order reflection and have found neither, as exemplified in the images and Fourier transforms presented here. From this we conclude that at every fracture surface there is a unique relation between the azimuthal orientation in the TB helix and topographic height on the fracture face, so that the FFTEM stripe spacing is identical to the TB helix pitch, i.e., d = p_TB ∼ 8.3 nm and q_TB ≡ 2π/p_TB ∼ 0.76 nm⁻¹.

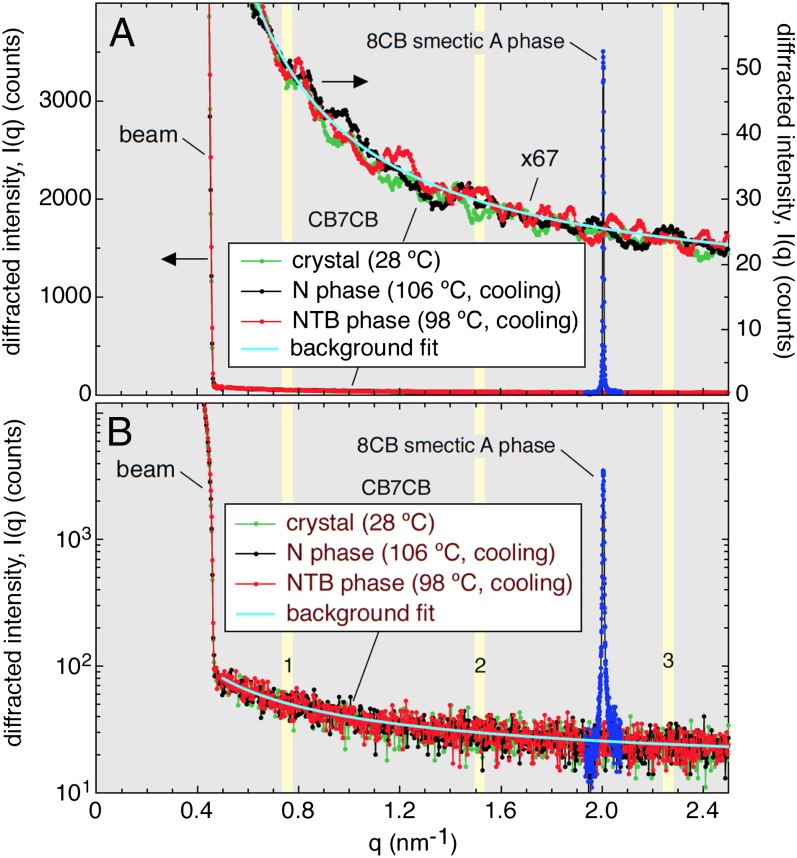
The FFTEM observation of the bulk periodicity in the thermotropic NTB phase motivated and guided a synchrotron X-ray scattering search for a corresponding X-ray Bragg reflection. In these experiments the samples were unoriented “powders” of CB7CB or the reference material 8CB in 1-mm–diameter capillaries. The scattered intensity vs. wavevector I(q) was measured with a scanning diffractometer (SI Appendix, Materials and Methods), with results shown in Fig. 5 and SI Appendix, Fig. S16. I(q) for several sample conditions, including the starting room-temperature crystal phase, and the N and NTB LC phases obtained upon cooling, are compared in Fig. 5 with a scan of the fundamental smectic A lamellar reflection of 8CB at T = 24 °C with the same experimental conditions and counting time.

Fig. 5.

XRD from CB7CB and 8CB. An electron density modulation (EDM) associated with the periodic structure observed in FFTEM images of CB7CB would generate sharp XRD peaks at wavevector q ∼ 2π/8 nm⁻¹ and its harmonics (yellow bands). Here, in a search for this scattering, synchrotron-based powder XRD from CB7CB is compared with that from the smectic A layering in 8CB, which computer simulation shows to have a fractional EDM of 0.25. Subtraction of the background (cyan line) leaves only the shot noise from the background to limit detectability of a peak. No peaks above this limit are observed, indicating that the fractional EDM in any TB scattering structure in CB7CB must be less than 0.005. (A) Linear intensity scale. (B) Log intensity scale.

This search began by considering what scattering characteristics might be expected from the d ∼ 8.3 nm modulation found in FFTEM: (i) Wavevector: The FFTEM data, which indicate that scattering at wavevector q_TB = 2π/(8.3 nm) ∼ 0.76 nm⁻¹ and its harmonics, indicated by the vertical yellow bars in Fig. 5, would be of most interest. (ii) Bragg peak intensity: LCs exhibit nonresonant XRD because of variation in electron density. The SmA Bragg peak of 8CB, included in Fig. 5, can serve as an intensity standard because computer simulation of SmA 8CB (22) shows that at T = 24 °C the peak-to-peak modulation of mass density in the smectic A phase is from ρ = 0.87 g/cm³ to ρ = 1.13 g/cm³, so that the 8CB smectic reflection is from a 1D wave of electron density with a fractional modulation amplitude of δρ/ρ ∼ 0.25. With this information, comparison of the intensity of any Bragg scattering from the NTB phase with that of SmA 8CB can be used to determine a maximum possible fractional electron density in the NTB. (iii) Bragg peak lineshape: The Bragg peak shown in Fig. 5 for SmA 8CB has nearly the shape of the diffractometer resolution function, with a full width at half height (FWHH) δq = 0.005 nm⁻¹, enhanced slightly in the tails by the thermal undulations of the smectic layers via the Landau–Peierls (LP) effect, which limits smectic order in 3D to be quasi–long-ranged order (QLRO) (23). The NTB modulation should also exhibit only QLRO, but the well-defined nature of the focal conics found in DTLM and in the FFTEM images of the NTB phase, and the weak layer positional decorrelation in some FFTEM images, for example SI Appendix, Fig. S13, suggest that, as in smectics, the LP disordering is probably weak. Evidence for this is available from data on the similarly structured SmC_α phase (ignoring the smectic layering for purposes of this argument), which exhibits a precession of period ∼10 nm of the azimuthal orientation of molecules on the SmC tilt cone, forming a TB helix of the type considered here for the NTB phase (14, 24, 25). Resonant X-ray Bragg scattering from the SmC_α TB director helix shows FWHH values of δq ∼ 0.02 nm⁻¹ (25), a value we might also expect for the NTB phase because the TB helices in the two cases are of comparable elasticity, and our diffractometer has sufficient resolution. We therefore would expect a sharp peak from the NTB modulation if it scatters at all. (iv) Background: Background comes from stray scattering from along the beam path. The high angular resolution of the diffractometer rejects nearly all of the intensity of diffuse scattering features from the sample, but passes essentially all of peaks that are near the resolution limit in width. These are ideal conditions to search for weak scattering from a well-ordered modulation such as that found in the FFTEM.

In fact, the X-ray scans show no evidence for Bragg reflection near q_TB or any of its harmonics in the NTB phase. An upper limit on possible NTB Bragg intensity can be established as follows. The background at the nominal first harmonic is I_b(q_TB) = 48.0 ± 0.2 counts, determined precisely by fitting a low-order polynomial to the background over the range 0.5 nm⁻¹ < q < 2.4 nm⁻¹, as shown in Fig. 5. Subtracting the fitted function from the data leaves only its shot noise, ∼±7 counts at q ∼0.76 nm⁻¹, as the uncertainty on each point (Fig. 5B). Fig. 5A shows these data smoothed over 10 adjacent points, such that any peak would have the width of that observed for the SmC_α helix, as discussed above (δq = 0.03 nm⁻¹). This smoothing leaves fluctuations of ∼±2 counts for each point (Fig. 5A), and ∼ ±2 × 10 = ±20 counts of local fluctuation in the area. The area of the 8CB SmA peak is 60,000 counts above background, so that these shot noise fluctuations are equivalent to a ratio of area of a putative TB reflection peak to that of SmA 8CB of 20/60,000 which, because δρ/ρ ∝ √I(q), corresponds in turn to fractional TB phase electron density modulation fluctuations of (δρ/ρ)_fluc ∼ 0.25/√3000 = ∼±0.005. The absence of any features in the scattering above this noise level therefore confirms that the amplitude of any density modulation wave of period p_TB is at most δρ/ρ ∼ <0.005 in the NTB phase.

Motivated by these observations and by recent examples of the very successful description of the physical properties of the nematic and smectic A phases of CBs by atomistic computer simulation (22, 26, 27), we have carried out MD simulations of the ground-state structure of the nematic phases of CB7CB, and, for comparison, of the nematic phase of CB6CB (Fig. 6 A and B). These simulations, which combine a widely tested, fully atomistic force field (28) with advanced MD techniques (refs. 29, 30; SI Appendix, Materials and Methods), were set up in an orthorhombic (L_x = 5.6 nm) × (L_y = 5.6 nm) × (L_z = 8 nm) cell. Initially, simulations were conducted with a biasing potential that aligned the mesogens along z, achieved by applying weak forces to the cyano groups at the end of each molecule, pulling them in the opposite (+z and −z) directions. As a result, the initially equilibrated configurations were in a well-defined nematic (N) phase with the average orientation n of the nematic half-molecular directors n_i, as defined in Fig. 1, initially aligned, apart from fluctuations, in a periodic box along the L_z = 8 nm cell dimension, as suggested by the FFTEM data. The biasing potential was then turned off and each system was simulated in the constant-N, constant-P_z, constant T ensemble in the 370–410K temperature range with the three box dimensions fluctuating, allowing the system to relax to atmospheric pressure on all faces.

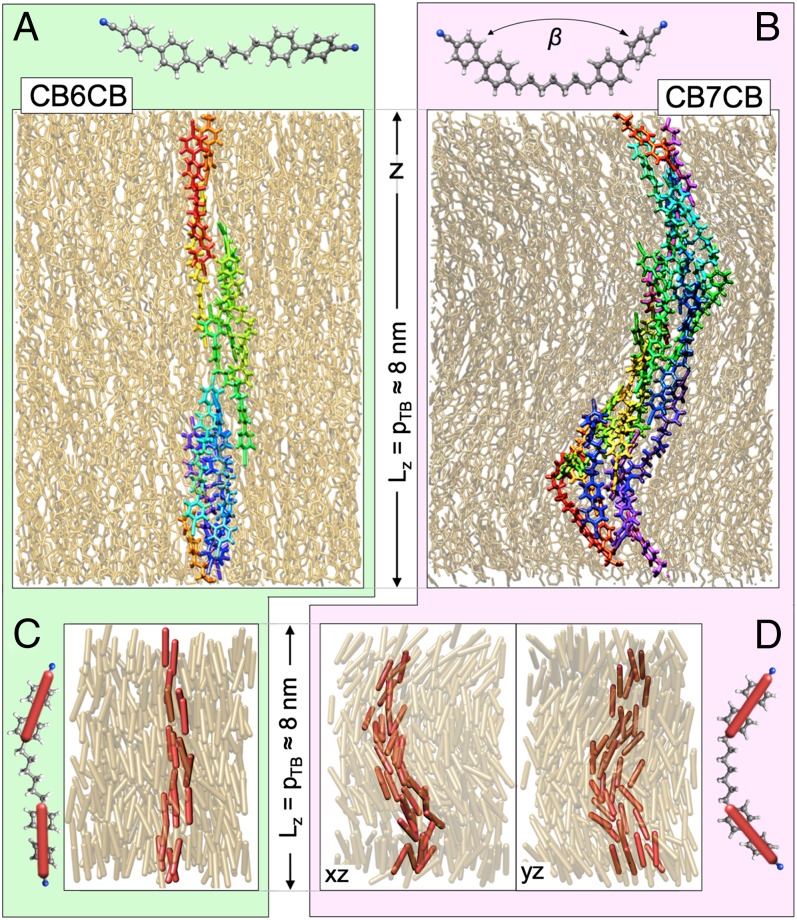
Fig. 6.

Fully atomistic MD simulations of equilibrium nematic phases at T = 370 K in CB6CB, a linear molecule (A), and CB7CB, a bent molecule (B), showing a periodic box of a nominally 5.6 × 5.6 × 8.0 nm dimension. Initial equilibration is carried out with opposed forces in the z direction on the molecular ends, giving a form of field-induced nematic monodomain. As these forces are relaxed, CB6CB remains a nematic, with n along z (A), whereas CB7CB relaxes into a heliconical TB structure, of pitch p_TB = 8.1 nm and cone angle θ_TB = 25° (B). The periodic box adjusts in length along z to equilibrate the pressure. (C and D) Example configurations showing explicitly the orientations n_i of the biphenyl groups that determine the half-molecular director field n. CB6CB shows conventional nematic ordering whereas there is clearly heliconical ordering in CB7CB (SI Appendix, Figs. S17 and S18).

The comparison of nematic ordering obtained in the two mesogens at 370 K clearly highlights the difference between an odd and even number of carbons in the alkyl spacer. For the CB6CB, simulations over 15 ns equilibrated a conventional N structure as illustrated in Fig. 6A and C. However, the CB7CB system, which started with a similar nematic structure due to the biasing during initial equilibration, within a few nanoseconds after the biasing was removed showed a spontaneous deformation into a helical structure having its axis oriented along the original nematic director, n = z, as illustrated in Fig. 6 B and D. The mean square deviation of orientation of the n_i from a local director n(r) is now minimized for the heliconical director state precessing on a cone with a complete period of azimuthal orientation on a p_TB ∼8 nm length scale (SI Appendix, Fig. S17). Equilibration will adjust the box length L_z to match the repeat distance of a periodic structure along z if the latter is initially sufficiently close to L_z. Extended equilibration with L_z initially in the range 7.5 nm < L_z < 8.5 nm relaxed to L_z = 8.3 ± 0.2 nm, determining p_TB = 8.3 nm as the TB period for this simulated molecular system.

Our analysis of the simulation configurations shows that few of the molecules in the simulated N and NTB phases have the lowest energy, all-trans conformations shown in Fig. 6A and B. Nevertheless, calculation of β, the relative orientation of two CB units on the same molecule (Fig. 6), shows that in the NTB phase the CB7CB molecules maintain a significant average bend with 〈β〉 = 133°, whereas the CB6CB molecules in the N phase are almost linear, with 〈β〉 = 166°. In CB6CB the nematic eigenstate is along z, with a half molecular core nematic order parameter of 0.82. In CB7CB the nematic eigenstate is the perfect heliconical director precession, and the order parameter for fluctuations of the half molecular cores away from this eigenstate is is 0.73. The eigenstate cone angle is θ_TB = 25° and the pitch p_TB = 8.3nm. (SI Appendix, Fig. S18).

Discussion

The striking lack of temperature dependence of the TB helix pitch p_TB found in the NTB phase, shown in Fig. 4, and the first-order nature of the N–NTB transition found in a variety of experiments, suggests that the TB helix is a principally enthalpically stabilized structure and calls into question the picture of the N–NTB transition as being driven by a negative bend Frank constant. Rather, these features suggest specific molecular pairing motifs, perhaps into living polymerized-like helical chains that can lock in a particular pitch, as suggested by figure 2b of Dozov’s paper (12) and Fig. 1D above. As a result, variation of chemical structure, for example by further MD study of the dependence of θ_TB and p_TB on n in the n-odd CBnCB homologous series, should be particularly interesting. A Landau model providing a first-order transition to a state of preferred bend, driven by a Frank energy having a term linear in the bend deformation, of the type suggested by Meyer (11), may be a better picture of the transition to the TB state in CB7CB.

The external force-induced stabilization of the N phase in CB7CB observed in our simulations is a quadrupolar analog of the “heliconical to field-polarized” transition in the helimagnet MnSi (31). These simulations make it clear that inducing the N phase by any of a variety of possible model couplings tending to align the CB end groups along z should be a powerful way of exploring the nature of the N–NTB phase transition. This relationship with helimagnets further suggests the possibility of a TB nematic analog of the MnSi “A” phase wherein, at higher temperature, the conical helix reorganizes into a 2D hexagonal blue phase lattice of double twist cylinders (31).

Another aspect of the NTB structure that can be discussed in the light of these observations and the implied local chirality of the TB helix is macroscopic chirality. Currently there is no direct information on the dimensions of homochiral domains in the CB7CB NTB phase in the absence of external perturbation, although they must be large enough for the local handedness to persist on the NMR timescale (∼1 ms) (4), and electric field treatment generates macroscopic conglomerate domains (9). The lower-magnification FFTEM images presented here cover areas of ∼2 µm × 2 µm square, and in such images we have not identified any places where the handedness is clearly changing sign. Qualitatively, we would expect such a conglomerate domain boundary to be marked locally by a disappearance of the layers if the boundary were running normal to the layers, or by an irregularity in the layer spacing if running parallel to the layers. The absence of such features indicates that the as-grown conglomerate domains are of multimicrometer dimension, in agreement with recent observations (32), approaching being macroscopic with respect to optical probes and suggesting that they may exhibit optical rotation (OR) or circular dichroism. Having such large domains in the field-free state may account for the reported observation of electric field induction of truly macroscopic, conglomerate domains of dimensions >100 µm (9).

Nevertheless, the conglomerate domains of the helix in the as-grown NTB phase exhibit little detectable optical rotation (OR) in the absence of applied electric field, and barely detectable OR in the large conglomerate domains obtained by field treatment, although the latter show a chiral, electroclinic-like field-induced reorientation of the uniaxial optic axis (33). The magnitude of chiral optical effects such as OR to be expected in macroscopic NTB domains can be estimated by comparison with those of the nanoscale-pitch conical helices found in the B2 phases of bent-core molecules (34–37). The NTB helix of 8-nm pitch is nearly identical in structure to the effective director helix in the SmC_AP_A phase (pitch = 7 nm) (35, 36), and should exhibit comparable optical properties. Optical characterization of focal conic domains of a typical SmC_AP_A yields an OR = 0.05°/µm (37), in agreement with optical modeling of TB structures in bent-core mesogens (36), and shows that this OR is extremely difficult to detect in the presence of the birefringence of the TB helix. Such modeling also shows that the OR of NTB domains having the helix axis normal to the cell surfaces should be even smaller, by several orders of magnitude (34, 35).

A heliconical NTB helix of the sort sketched in Fig. 1C is accompanied by a commensurate helical precession of a polarization density field, locally always normal to both n and z, also shown in Fig. 1C. The field-induced chiral electroclinic optic axis reorientation can be understood as a coupling of applied field to this helielectric polarization field P(r), a resulting distortion of the helix by local rotation of P(r) toward the field direction, and a consequent tilt of the average director orientation, ω ∝ z × E (38, 39). This effect is weak in the NTB phase because p_TB is so small (39), but, for the same reason, the converse effect, the induction of macroscopic polarization by flow (40), ought to be large.

Materials and Methods

FFTEM experiments were carried out by filling a few micrometers thick gap between 4 mm × 6 mm glass plates with CB7CB, heating the cell to the isotropic phase, and cooling under DTLM observation into the N and NTB phases. The N phase showed typical Schlieren DTLM textures and the NTB phase appeared via a first-order phase transition as domains of a broken fan texture with slightly lower birefringence. Once T was reduced and stabilized at a chosen temperature, the sample was rapidly quenched to T < 90 K by ejection from the hot stage into liquid propane, and then maintained at T = 77 K in liquid nitrogen. As shown in X-ray scattering experiments (SI Appendix, Fig. S16), the NTB phase readily supercools to room temperature even under conditions of slow cooling, in agreement with prior observations (15), so that there is no chance for any ordering but that of the N or NTB to appear in samples so rapidly quenched. Samples were then transferred cold into a Balzers BAF-060 freeze-fracture apparatus and the LC fractured by pulling apart the glass plates cold under vacuum. Shadowing of the topographic structure of the fracture face was carried out by oblique evaporation of a 1.5-nm-thick platinum film, which was then embedded in a thicker evaporated carbon film to form an electron absorption replica with which the interface topography could be viewed in a TEM.