Distortional binding of transition state analogs to human purine nucleoside phosphorylase probed by magic angle spinning solid-state NMR

Significance

Enzymes are efficient at bringing reactants to the transition state. Transition state analogs mimic the transition state but are chemically stable. What forces do enzymes apply to transition state analogs? Solid-state NMR is used to answer this question for human purine nucleoside phosphorylase. When imperfect and near-perfect transition state analogs are analysed on and off the enzyme, greater distortions are observed for the imperfect transition state analog. The distortion is energetically large and is toward the transition state geometry. In contrast, the near-perfect analog experiences almost no distortion, stabilizing the enzyme in a favored conformation near the transition state. Both inhibitors bind with picomolar dissociation constants, but the enzyme expends more energy distorting the imperfect inhibitor toward the transition state.

Abstract

Transition state analogs mimic the geometry and electronics of the transition state of enzymatic reactions. These molecules bind to the active site of the enzyme much tighter than substrate and are powerful noncovalent inhibitors. Immucillin-H (ImmH) and 4′-deaza-1′-aza-2′-deoxy-9-methylene Immucillin-H (DADMe-ImmH) are picomolar inhibitors of human purine nucleoside phosphorylase (hPNP). Although both molecules are electronically similar to the oxocarbenium-like dissociative hPNP transition state, DADMe-ImmH is more potent than ImmH. DADMe-ImmH captures more of the transition state binding energy by virtue of being a closer geometric match to the hPNP transition state than ImmH. A consequence of these similarities is that the active site of hPNP exerts greater distortional forces on ImmH than on DADMe-ImmH to “achieve” the hPNP transition state geometry. By using magic angle spinning solid-state NMR to investigate stable isotope-labeled ImmH and DADMe-ImmH, we have explored the difference in distortional binding of these two inhibitors to hPNP. High-precision determinations of internuclear distances from NMR recoupling techniques, rotational echo double resonance, and rotational resonance, have provided unprecedented atomistic insight into the geometric changes that occur upon binding of transition state analogs. We conclude that hPNP stabilizes conformations of these chemically distinct analogs having distances between the cation and leaving groups resembling those of the known transition state.

When substrate molecules associate with the active sites of enzymes to form the Michaelis complex, they may adopt a conformation that is different from their lowest energy conformation in solution. This distortion, usually called “ground state destabilization,” often lowers the barrier to catalysis by preparing the molecule to achieve the transition state geometry. Enzymes bind several orders of magnitude tighter to analogs of the transition state by converting catalytic energy into binding energy. Ground state destabilization and transition state stabilization therefore work in concert to facilitate catalysis (1–3). Experimental and theoretical kinetic isotope effects (KIEs) have been used extensively for the quantitative determination of the transition state geometry (4). Binding isotope effects (BIEs), X-ray crystallography, vibrational spectroscopy, NMR spectroscopy, and computational studies have been used to probe ground state destabilization effects (i.e., the phenomenon of distortional binding) (5–7). However, due to the small magnitude of molecular distortional effects, high-precision experimental methods are needed to quantify distortional binding.

Transition state analogs are chemically stable molecules designed to capture the transition state stabilization energy by mimicking the geometric and electrostatic features of the transition state. As a result, these molecules bind tighter than the substrate, although remaining chemically inert, resulting in inhibition of the catalytic reaction (8, 9). When transition state analogs bind to the enzymatic active site, they are initially subject to the same distortional forces that are responsible for ground state destabilization of substrate molecules. However, because the electrostatics of these inhibitors resemble those of the transition state rather than the substrate, the enzymatic changes will tend to distort the complex toward the transition state geometry. A transition-state analog closely resembling the transition state will exhibit minimal distortional binding. Distortional binding of a molecule that can adopt the transition state conformation will reflect the difference between its lowest energy conformation and that of the transition state conformation induced by enzyme binding. The energy difference between free and bound conformations subtracts from its observed binding energy. A comparison of free and bound conformations of transition state analogs informs on similarity to the transition state and provides a means for quantitation of distortional binding.

Human purine nucleoside phosphorylase (hPNP) catalyzes the reversible phosphorolysis of inosine to hypoxanthine and α-d-ribose 1-phosphate. The reaction proceeds via a first-order dissociative (S_N1) transition state (Fig. 1), with a completely severed C-N bond (∼3.0 Å) and a fully developed ribocation, as determined by multiple KIE measurements (10). The active site of hPNP is designed to facilitate C-N bond cleavage by promoting hydrogen-bonding interactions to activate the nucleobase (leaving group stabilization) and to form the ribocation (11). The bound phosphate nucleophile, although not chemically bonded at the transition state, is known to form a contact ion pair with the ribocation.

Fig. 1.

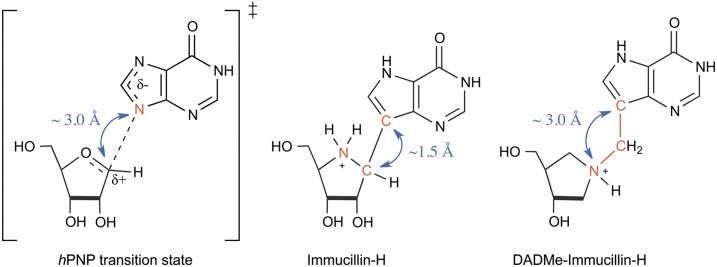
(Left to Right) Transition state for the reaction catalyzed by hPNP. First-generation inhibitor of hPNP: ImmH. Second-generation inhibitor of hPNP: DADMe-ImmH. The double-headed arrows indicate the crucial internuclear distances.

The first two generations of transition state analogs, Immucillin-H (ImmH) (12) and 4′-deaza-1′-aza-2′-deoxy-9-methylene Immucillin-H (DADMe-ImmH) (13), are picomolar inhibitors of hPNP (Fig. 1). Both molecules are good electrostatic and geometric matches to the transition state features of hPNP. The iminoribitol ring (when protonated) mimics the ribocation, and the 9-deazahypoxanthine prevents phosphorolysis due to the chemical stability of the C-C bond. The N7-H proton of 9-deazahypoxanthine mimics the protonation occurring at hypoxanthine N7 in the hPNP transition state. Geometrically, however, ImmH and DADMe-ImmH transition state analogs differ significantly from each other. Whereas the protonated iminoribitol in ImmH mimics the oxocarbenium ion character of the ribose ring, the directly bonded deazahypoxanthine (C-C bond length of ∼1.5 Å) falls considerably short of mimicking the fully dissociated C1′-N9 bond distance (∼3.0 Å) at the hPNP transition state. In DADMe-ImmH, a methylene group bridges the iminoribitol and the deazahypoxanthine moieties, and they are separated by ∼2.5 Å, a distance more closely resembling the hPNP transition state (the three relevant internuclear distances are indicated by blue double-headed arrows in Fig. 1). These differences allow DADMe-ImmH to bind eightfold more tightly to hPNP than ImmH, despite the increased flexibility and lack of a 2′-hydroxyl group in DADMe-ImmH. Our working hypothesis is that hPNP invests energy to distort ImmH by elongation of the C-C bond to achieve geometry near the transition state, whereas DADMe-ImmH requires only minimal distortion to achieve a geometry that captures the transition state binding energy.

Frieden and colleagues (14) have studied the nature of the structural change in adenosine deaminase that accompanies formation of the catalytic transition state using Stern–Volmer titrations of ground state and transition state analogs. To our knowledge, there are no reports addressing high-resolution structural changes occurring in the transition state analogs as they achieve the enzymatically optimized transition state geometry. If the key internuclear distances in ImmH and DADMe-ImmH (double-headed arrows in Fig. 1) are measured in their free and bound states with meaningful precision, it will provide an unprecedented quantitative insight into the force that enzymes exert on molecules to achieve the transition state geometry.

We report the results from a solid-state NMR (ssNMR) study using isotope-edited ImmH and DADMe-ImmH as NMR probes of the distortional binding of these picomolar inhibitors to hPNP. By selectively installing ¹³C and ¹⁵N labels at relevant positions, high-precision internuclear distance measurements were obtained using magic angle spinning (MAS) recoupling techniques, namely, rotational echo double resonance (REDOR) for heteronuclear spin pairs and rotational resonance (R²) experiments for homonuclear spin pairs. The results unambiguously demonstrate distinct enzyme-induced ligand changes and provide atomistic insights into the distortional binding of these transition state analogs to the active site of hPNP.

Results and Discussion

Synthesis of Labeled Transition State Analogs.

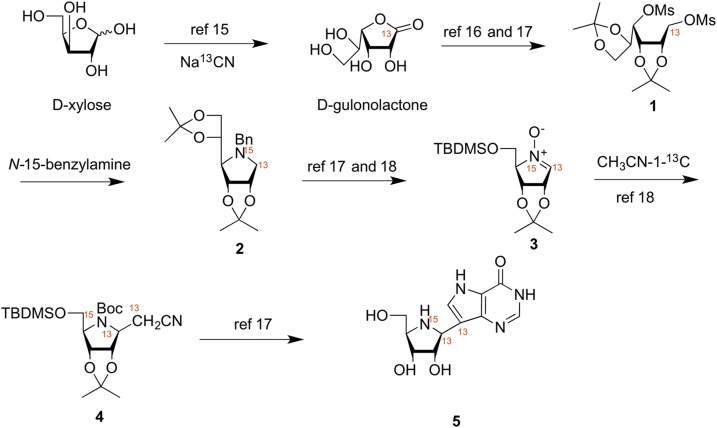
Key to the success of our study was the synthesis of isotope-edited ImmH and DADMe-ImmH (Figs. 2 and 3). Triply labeled ImmH (5) was prepared via a linear 19-step synthesis as previously described for unlabeled 5 (15–21). Specifically, the ¹³C label in the 1′-position of 5 was incorporated via the reaction of d-xylose with [¹³C]-sodium cyanide to afford labeled 1-[¹³C]-d-gulonolactone (15). The 1-[¹³C]-d-gulonolactone was converted to the dimesylate 1 in 3 steps and was then treated with [¹⁵N]-benzylamine, in a neat suspension at 80 °C, to afford the 1-[¹³C]-[¹⁵N]-pyrrolidine 2 in an analogous manner to our previous work. Conversion of compound 2 to nitrone 3 was achieved in 6 synthetic steps via the chemistry outlined by Furneaux et al. (17) and Evans et al. (18). Nitrone 3 was reacted with lithiated 2-[¹³C]-acetonitrile to afford a single product 4, and this was converted to the hydrochloride salt of the title compound 5 in an additional 8 steps.

Fig. 2.

Synthetic scheme for synthesis of triply labeled ImmH. TBDMSO, tert-butyldimethylsilyl linked via the 5'-oxygen.

Fig. 3.

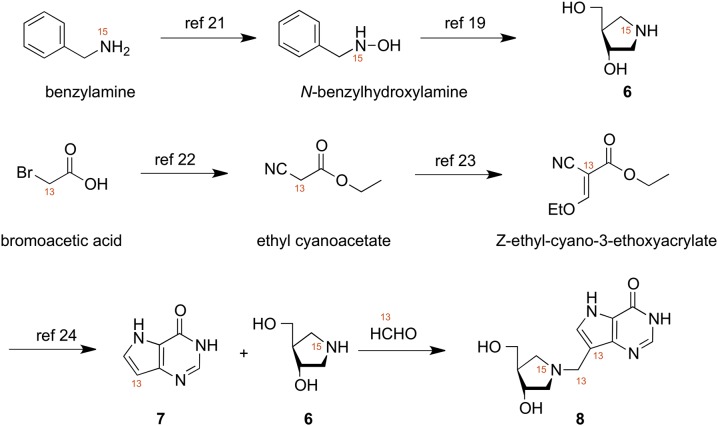
Synthetic scheme for synthesis of triply labeled DADMe-ImmH.

The triply labeled title compound 8 was prepared via a nine-step convergent synthesis as described earlier for unlabeled 8 (19, 20). The key and final step involved the Mannich reaction between [¹⁵N]-(3S,4S)-4-(hydroxymethyl)pyrrolidin-3-ol (6), 9-[¹³C]-9-deazahypoxanthine (7), and [¹³C]-formaldehyde (20). The [¹⁵N]-(3S,4S)-4-(hydroxymethyl)pyrrolidin-3-ol (6) was obtained from [¹⁵N]-benzylamine via [¹⁵N]-N-benzylhydroxylamine, prepared as described by the method of Shiino et al. (21) in eight synthetic steps overall. The 9-[¹³C]-9-deazahypoxanthine (7) was synthesized, as previously described, via [¹³C]-bromoacetic acid, which was converted to [¹³C]-ethyl cyanoacetate (22) and then transformed into [¹³C]-Z-ethyl-2-cyano-3-ethoxyacrylate (23), which was further reacted as described by Kamath et al. (24) to afford 7. The [¹⁵N]-(3S,4S)-4-(hydroxymethyl)pyrrolidin-3-ol (6) and [¹³C]-9-deazahypoxanthine (7) were combined with aqueous [¹³C]-formaldehyde as previously described (20) to afford 8.

ssNMR Chemical Shift Analysis.

Solid samples of cationic ImmH and hPNP–[1′-¹³C, 4′-¹⁵N, 9-¹³C]ImmH–PO₄ complex were prepared as described earlier (11). The preparation of the corresponding samples for DADMe-ImmH is described in Materials and Methods. The ssNMR experiments were conducted on Bruker BioSpin four-channel Avance 750-MHz and 900-MHz spectrometers with low-E and regular HCN probes (Bruker BioSpin). The data were collected at rf fields of 30 kHz for ¹⁵N, 50 kHz for ¹³C, and 80 kHz for ¹H. Typical acquisition time was 15 ms with two-pulse phase modulated (TPPM) decoupling (25). The spinning frequency varied between 9 kHz and 15 kHz depending on the experiment, and the experiments were rotor-synchronized. All the experiments were performed with ¹H-¹³C cross-polarization with a typical cross-polarization time of 3 ms and 20–50% ramp. The number of scans varied between 64 and 256, and the recycle delay was 3 s. The number of points in the free induction decay (FID) was 2,048. The spectra were zero-filled to 4,096 points and apodized with 50- to 100-Hz line broadening.

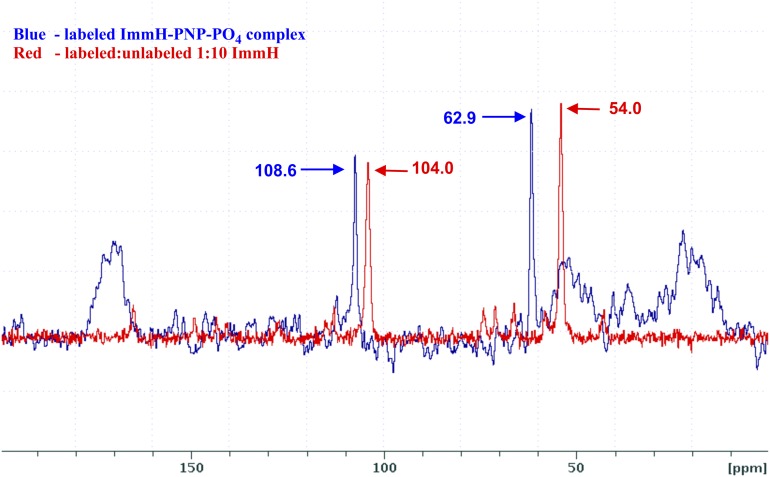
A 8.9-ppm high-frequency change in chemical shift (∆ppm = 8.9) in the 1′-¹³C signal was observed for the hPNP–[1′-¹³C, 4′-¹⁵N, 9-¹³C]ImmH–PO₄ complex relative to the sample of cationic ImmH (Fig. 4). The high-frequency shift is qualitatively consistent with the increased “oxocarbenium-like” character (sp²) of the 1′-C of the bound ImmH. Additionally, a high-frequency ∆ppm = 4.6 for the 9-¹³C signal suggests that the increased sp² character is due to the stretching of the C1′-C9 bond. The magnitude of the change in chemical shift of the two carbon atoms in this nonpolar σ-bond upon binding of the inhibitor molecule to hPNP suggests that the extent of distortion ought to be large enough for accurate quantification.

Fig. 4.

Overlay of ssNMR spectra of [1′-¹³C, 4′-¹⁵N, 9-¹³C]ImmH and hPNP–[1′-¹³C, 4′-¹⁵N, 9-¹³C]ImmH–PO₄ complex. Chemical shifts are referenced to the chemical shift of adamantine set to 40.5 ppm. The peaks at 108.6 and 104 ppm correspond to the 9-¹³C label in bound and free ImmH, respectively. The peaks at 62.9 and 54.0 correspond to the 1′-¹³C label in bound and free ImmH, respectively.

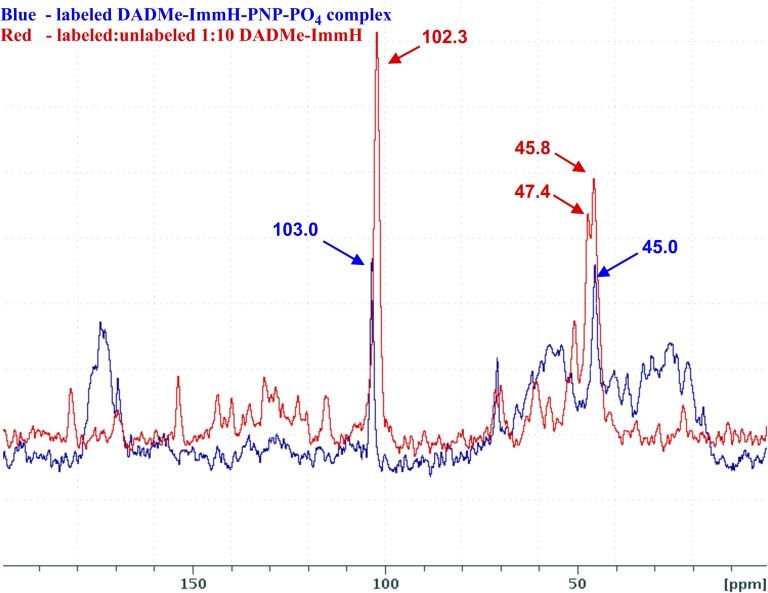
The ssNMR spectrum of DADMe-ImmH is complicated by the chiral nature of the 1′-¹⁵N center: Protonation of either face of the tertiary amine results in diastereomeric molecules. These diastereomers have different ¹³C chemical shifts for the methylene group but, fortunately, the 9-C chemical shift is identical for the two diastereomers. As a result, the ¹³C spectrum of the labeled protonated DADMe-ImmH has three peaks instead of the expected two peaks for a single diastereomer. This problem is not present in the sample of the bound inhibitor because the enzyme binds only one diastereomer. An additional complication was that samples of cationic DADMe-ImmH prepared by lyophilization of pH-adjusted solutions (same procedures used for the preparation of cationic samples of ImmH) resulted in broad line widths (>1 kHz) for each of the three peaks presumably due to amorphous line broadening. We were able to narrow the line widths (∼200–300 Hz) by growing 1:1 cocrystals of cationic DADMe-ImmH/m-bromobenzoic acid. In the NMR spectrum of these cocrystals, two signals for the methylene carbon were at δ 45.8 ppm and δ 47.4 ppm, whereas that of 9-¹³C was at δ 102.3 ppm. In the hPNP–DADMe-ImmH–PO₄ sample, the methylene peak was at δ 45.0 ppm and the 9-¹³C peak was at δ 103.0 ppm (Fig. 5). In comparison to the change in chemical shift observed in free vs. bound ImmH (Fig. 4), the differences in the corresponding spectra of DADMe-ImmH are minimal (a low-frequency ∆ppm = 0.8 or 2.4 for the methylene peak, depending on which of the methylene peaks in the free DADMe-ImmH sample is chosen for comparison with the corresponding peak in the enzyme-bound sample and a high-frequency ∆ppm = 0.7 for the 9-C signal.)

Fig. 5.

Overlay of ssNMR spectra of triply labeled DADMe-ImmH and hPNP–[1′-¹⁵N, ¹³CH₂, 9-¹³C]DADMe-ImmH–PO₄ complex. Chemical shifts are referenced to the chemical shift of adamantine set to 40.5 ppm. The peaks at 103.0 ppm and 102.3 ppm correspond to the 9-¹³C label in bound and free DADMe-ImmH, respectively. The peaks at 47.4 and 45.8 ppm correspond to the ¹³CH₂ label in the two diastereomers of free protonated DADMe-ImmH, and the peak at 45.0 ppm corresponds to the ¹³CH₂ label in the sole diastereomer present in the hPNP—bound protonated DADMe-ImmH.

Further evidence for bond distortions upon binding is found in the comparison of the ¹⁵N chemical shifts of the free and bound inhibitors. A low-frequency shift of 6.6 ppm (δ 67.7 ppm to δ 61.1 ppm) was observed from comparing the ¹⁵N chemical shifts of free and bound ImmH, whereas a similar comparison for DADMe-ImmH revealed only a 0.5 ppm (δ 64.55 ppm to δ 64.05 ppm) low-frequency shift. These results provide qualitative support for the hypothesis that the enzyme distorts ImmH more than DADMe-ImmH.

High-Precision Distance Measurements for Free and Bound Transition State Analogs.

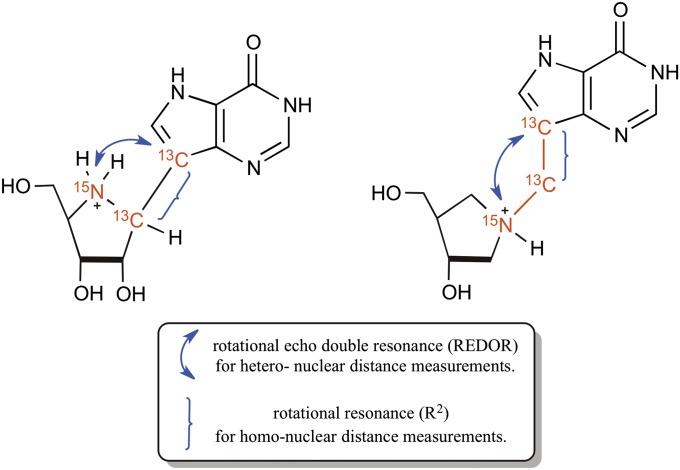
The chemical shift changes that occur upon binding of ImmH and DADMe-ImmH to hPNP are a qualitative measure of the bond distortions that occur upon binding of these inhibitors. Our next goal was to obtain high-precision data for the specific internuclear distance measurements between the ¹³C and ¹⁵N labels present in each of the triply labeled inhibitor molecules. An overview of the chemically incorporated NMR-sensitive labels and the MAS recoupling technique used to obtain each distance measurement is shown in Fig. 6.

Fig. 6.

Labeling scheme and proposed MAS distance measurement experiments.

One of the key distances relevant to this study is the nonbonded ¹³C-¹⁵N distance between the iminoribitol ring and the deazahypoxanthine moiety. This distance was determined using the REDOR technique as described by Gullion and Schaefer (26). In the REDOR method, a special pulse sequence is used to manipulate the effect of the dipolar interaction between the two spins to yield the dipolar coupling constant. The value of this dipolar coupling constant is inversely proportional to the cube of the internuclear distance between the two spins.

The second key distance we interrogated was the ¹³C-¹³C covalent bond distance in both inhibitors. This distance is a function of the force that the enzyme exerts on the two ends of the inhibitor molecule (deazahypoxanthine and iminoribitol) for the complex to mimic the transition state geometry. A carbon-carbon bond length for a C(sp³)-C(sp²) single bond, such as the ones between the ¹³C labels in the two inhibitors, rarely exceeds 1.50 Å. Based on the chemical shift analysis of these two carbon atoms, we were intrigued to find if the large change in chemical shift in ImmH and the minimal change in DADMe-ImmH correlated with the extent of the distortion of this bond upon binding to hPNP. We conducted this measurement for both free and bound inhibitors using the R² technique used for determination of internuclear distance of homonuclear spin systems (27). This method relies on the restoration of the dipolar interaction between a homonuclear spin pair, thereby permitting the determination of the dipolar coupling constant, and hence the internuclear distance. The two nuclei are said to be in rotational resonance when the spinning rate is adjusted to a frequency that is a multiple of the difference of isotropic resonant frequency of the two spins. Under these conditions, these internuclear distances can be determined with very high precision. The signal intensities from the REDOR and R² experiments were fitted using SPINEVOLUTION (28) to yield high-precision internuclear distances.

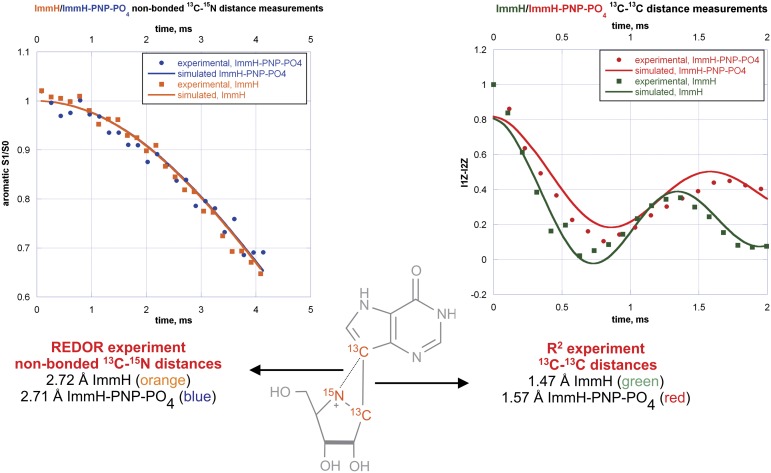
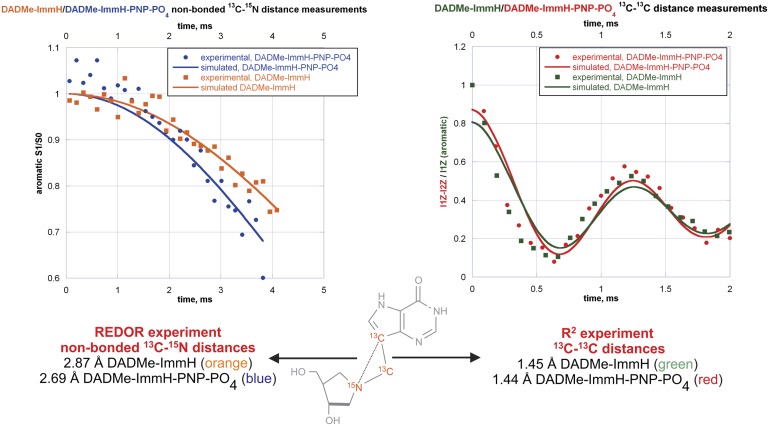
The results from the high-precision distance determinations from NMR experiments along with the simulated results for ImmH and DADMe-ImmH show ImmH to exhibit a 0.10-Å increase in the ¹³C-¹³C bond length, from 1.47 Å to 1.57 Å, upon binding to the active site of hPNP (Fig. 7, Right). In contrast, there is no increase in the corresponding ¹³C-¹³C bond length distance in DADMe-ImmH (Fig. 8, Right). In the case of DADMe-ImmH, the most notable change that occurs upon binding is a decrease of 0.18 Å in the nonbonded ¹³C-¹⁵N distance, from 2.87 Å to 2.69 Å (Fig. 8, Left). In comparison, there is virtually no change in the corresponding ¹³C-¹⁵N distance in ImmH from the free (2.72 Å) to the bound (2.71 Å) state (Fig. 7, Left). It is significant to note, however, that this ¹³C-¹⁵N distance (between the deazahypoxanthine moiety and the protonated nitrogen) is nearly identical in the bound state of both transition state analogs. Confidence limits for all the internuclear distance measurements, obtained from an error analysis, are provided in SI Appendix. (The average error for the four internuclear distances measured for ImmH is 0.05 Å. Due to complications arising from the presence of diastereomers in the DADMe-ImmH sample, the average error for the four distances measured for DADMe-ImmH is slightly higher at 0.1 Å.)

Fig. 7.

Key internuclear distances for free and bound ImmH. S1/S0 is the REDOR dephasing curve. I1Z and I2Z are the signal intensities of the aromatic and aliphatic carbon atoms, respectively, in the R² experiment.

Fig. 8.

Key internuclear distances for free and bound DADMe-ImmH. S1/S0 is the REDOR dephasing curve. I1Z and I2Z are the signal intensities of the aromatic and aliphatic carbon atoms, respectively, in the R² experiment.

Taken together, the above results reveal that hPNP orchestrates the binding of the two transition state analogs to the active site via two distinct distortional events. Although ImmH experiences a significant stretching force upon binding to the active site of hPNP, the enzyme simply “repositions” the two portions of DADMe-ImmH, consistent with rotation about the ¹⁵N-¹³C single bond.

An estimation of the force hPNP exerts on ImmH can be obtained using the Pauling relationship [n_x = n_o exp([r_o − r_x]/0.6)] for calculating bond order of transition structures. Distortion to 1.57 Å (r_x) from 1.47 Å (r_o) indicates a loss of 0.154 of the Pauling bond order [assuming the 1.47-Å C-C bond to have a bond order of 1.00 (n_o)]. This corresponds to a significant fraction of the total bond energy (∼13.1 kcal/mol). Another approach is to calculate the Wiberg bond index for the two geometries with the C-C bond fixed at 1.47 Å and 1.57 Å. This calculation, performed at the B3LYP/6-31+G** level of theory, resulted in a loss of 0.064 of the “atom-atom overlap-weighted Natural Atomic Orbital (NAO) bond order,” which corresponds to an energy of 5.5 kcal/mol (full computational details are provided in SI Appendix). Both methods used to estimate this energy have inherent errors associated with them, but the safe conclusion that can be drawn is that the energy of ImmH distortion by hPNP is significant. In contrast, the simple rotation about the C-N single bond in DADMe-ImmH as it binds to hPNP is unlikely to be energetically significant.

The distance between the cationic nitrogens in both inhibitors and the deazahypoxanthine moiety differs in solution (ImmH = 2.72 Å, DADMe-ImmH = 2.87 Å) but becomes approximately the same in the enzyme-bound complexes (ImmH = 2.71 Å, DADMe-ImmH = 2.69 Å). This result suggests an enzymatically favored geometry to best resemble the electrostatic nature of the transition state. In the enzyme-stabilized transition state, KIEs (10) indicated a geometry of ∼3.0 Å for this distance (Fig. 1). In subsequent computational analysis of the PNP transition state by transition path sampling, a C1′-N9 distance of 2.58 Å was indicated for the transition state (29), similar to within 0.13 Å of the on-enzyme cation-C9 distances for ImmH and DADMe-ImmH (Figs. 7 and 8).

Why does the carbon-carbon bond of ImmH elongate to 1.57 Å upon binding? The answer lies in the electrostatics of the 1′-C position. Whereas the position analogous to the ribocation is occupied by a carbon atom in ImmH, a protonated nitrogen atom occupies this position in DADMe-ImmH. The proton on the 1′-nitrogen atom in DADMe-ImmH better mimics the electrostatics of the 1′-H atom that is attached to the positively charged 1′-C atom of the ribocation at the hPNP transition state. In the ground state of protonated ImmH, there is virtually no polarization of the 1′-H atom. The elongation of the carbon-carbon bond in ImmH to 1.57 Å polarizes the 1′-CH bond toward the electrostatics of the transition state. The energetic penalty of bond stretching is clearly compensated by tighter binding of ImmH to the active site of hPNP. Thus, the ΔH = −21.2 kcal/mol for this interaction, even with the entropic penalty of 7.1 kcal/mol (30), far exceeds the investment in analog distortion (5.5–13.1 kcal/mol) to optimize interactions that mimic the transition state.

Conclusions

Interactions between enzymes and ligands at catalytic sites are essential in understanding binding forces leading to catalysis and to interactions with transition state analogs. Crystallography gives superb information with error limits to a few tenths of an angstrom. However, bond energy and distortion related to catalysis are more informative when bond information is known to a higher resolution. For example, distortion of 0.05 Å in a carbon-carbon single bond length represents a loss of ∼10% of the Pauling bond order. In cases where detailed transition state information is known, distortion of bound ligands reveals forces leading to the transition state. The transition state analog of hPNP, ImmH, is short in its central C-C bond axis relative to the known transition state. Consequently, the enzyme stretches the molecule 0.10 Å in this dimension to best fit the evolved optimal geometry of the enzyme to form the transition state. The more geometrically suitable transition state analog, DADMe-ImmH, fits near optimally after low-energy bond rotation, and thus binds more tightly without energy-requiring enzyme-induced strain. Methods to measure enzyme-induced ligand strain by spectral and BIE approaches are documented well (31–34), but these rarely give high-resolution specific bond information available from the NMR methods reported here.

Materials and Methods

Protein Expression and Purification.

Native hPNP was expressed and purified as the N-terminal histidine-tagged fusion protein as previously described (10).

ssNMR Sample Preparation.

Samples of ImmH and ImmH–hPNP–PO₄ complex were prepared as previously described (11).

Preparation of DADMe-ImmH Sample.

DADMe-ImmH was cocrystallized with 3-bromobenzoic acid using the following procedure. A 15:1 mixture (62 mg/4 mg) of labeled to unlabeled DADMe-ImmH was dissolved in 700 μL of water to which was added 50.2 mg of 3-bromobenzoic acid. A clear solution was obtained by the addition of 400 μL of isopropyl alcohol. The solution was then frozen and subsequently lyophilized to obtain the 3-bromobenzoate salt of DADMe-ImmH as confirmed by NMR analysis in D₂O. The solid was then dissolved in a minimum volume of a 10:2:2.5 mixture of acetonitrile/water/isopropanol and left in a closed vial on the benchtop for 6 h. The recrystallized salt was then washed twice with 1 mL of water, and residual water was removed under reduced pressure.

Preparation of DADMe-ImmH–hPNP–PO₄.

A 1.7-mL sample of a 43-mg/mL stock of purified hPNP (∼0.73 μmol of the hPNP trimer) was dialyzed in a pH 7.5 Tris⋅HCl buffer to obtain a 1,560-μL solution of 2.2 μmol hPNP. To this was added 220 μL of an 8.2-mg/mL solution of phosphate (2.65 μmol) and 220 μL of a 3.2-mg/mL solution of labeled DADMe-ImmH (2.65 μmol) so that a final volume of 2,000 μL was obtained, which was allowed to stand for 2 h. The resulting solution of DADMe-ImmH–hPNP–PO₄ complex was split into two portions, and to each portion was added 300–400 μL of 50:50 PEG 400/water solution, and the resulting mixture was left overnight at 4 °C to induce growth of microcrystals. The two vials were centrifuged, the liquid was drained, and the sample was stored at −78 °C until NMR analysis.